On the fate of hydrogen during zirconium oxidation by water: effect of oxygen dissolution in α-Zr

Abstract

Zirconium oxidation by water is accompanied by hydrogen conversion, either H₂ is released or hydrogen is picked up by the alloy. Strategies are sought to mitigate the detrimental hydrogen uptake into the metal. The corrosion phenomenon is subdivided into anode and cathode processes caused by electron release upon O²⁻ oxidation at the metal/oxide interface in the case of the former and electron–proton recombination resulting in hydrogen pick-up or H₂ evolution in the case of the latter. In a previous study, the additive dependence of the cathodic hydrogen evolution reaction was analysed. The present study examines the oxygen concentration dependence of the anode potential, presents the impact of oxygen concentration on the co-absorption of hydrogen and merges the anode and cathode processes. The computational model is validated by semi-quantitatively reproducing the experimental solubility limit for oxygen in α-Zr. The impact of the emerging conceptual understanding for material development is discussed.

---

I. Introduction

Over more than half a century, zirconium alloys have been the dominating cladding material to enclose the nuclear fuel in light water reactors,^1,2 and it is expected that zirconium alloys will retain their important role in nuclear reactor technology for decades to come. Over the years, extensive knowledge about zirconium alloys in reactor conditions has been acquired, but there are still important unanswered questions to address as well as complex phenomena that need to be understood. Today, the trend in reactor technology is to increase the fuel burnup, which is to let the fuel stay in the reactor for a longer time. A consequence of this is that the corrosion properties of the zirconium cladding become increasingly important. Ideally, with water being the oxygen carrier the oxidation process should be accompanied by molecular hydrogen release into the surrounding. Yet, it was found very early^3,4 that a significant amount of hydrogen is absorbed into the alloy causing embrittlement as well as deformations of the fuel rods, both being decisive to the longevity of the fuel.

In order to make new progress, computational approaches are presently being explored. The objective of several of these undertakings, as well as the present, is to utilize Density Functional Theory,^5,6 DFT, to gain complementary insights into the mechanism for water induced corrosion of zirconium. The general approach to achieve this involves describing various ways that structural dislocations and alloying elements, e.g. Nb, Sn, Fe, Ni and O, interact in order to arrive at rates for oxygen and hydrogen diffusion, as well as to describe structural sinks for hydrogen in the alloy, see e.g. ref. 7–11. In contrast, our effort emphasizes the hydrogen evolution reaction that is the competing pathway to hydrogen pick-up during oxidation of zirconium by water. This implies reformulating the corrosion of the cladding in terms of electrochemistry, i.e. electron release (oxidation) at the anode and electron capture (reduction) at the cathode. The cathode processes comprise hydrogen evolution at oxide grain boundaries or at the oxide/water interface, i.e.

2e⁻ + 2H⁺ → H₂. (R1)

In two recent studies,^12,13 the electro-catalytic aspect of the cathode process occurring predominantly at inter-grain interfaces between ZrO₂ particles was analysed. An alternative cathode process is that hydrogen become dissolved in the oxygen saturated alloy, so-called hydrogen pick-up, according to

2e⁻ + 2H⁺ → 2H (R2a)

Zr_mO_n + 2H → H₂Zr_mO_n. (R2b)

Yet, irrespective of hydrogen evolution or hydrogen absorption, an electron source is required for both (R1) and (R2a). This anode process occurs at the metal/oxide interface and may be effectively written as

mZr + O²⁻ → Zr_mO + 2e⁻. (R3)

It reflects how the dissolution of oxygen ions in the zirconium alloy implies discharge of electrons to be consumed in (R1) or (R2a).

Given the high solubility of oxygen in Zr, i.e. ∼28 at% oxygen,¹⁴ the main objectives of the present study are to determine (1) how the anode potential depends on the oxygen concentration, (2) how the hydrogen solubility in zirconium is affected by the dissolution of oxygen in the metal, and (3) merge the anode and cathode processes to arrive at a comprehensive understanding. The computational approach is validated semi-quantitatively by estimating the experimental solubility limit for oxygen in α-Zr. From the fact that zirconia is a large band gap insulator it is inferred that a large overall cell potential will allow the cathode process to take place far from the metal/oxide interface thus increasing the probability for H₂ evolution, while the opposite is true for small cell potentials.

II. Modelling considerations

The present study constitutes a central part in a comprehensive effort aiming at a detailed mechanistic understanding for the oxidation of zirconium alloys by water. It relies exclusively on atomistic modelling where density functional theory is employed exclusively. The heart of this study is, for different oxygen concentrations, to compute the stabilities of various oxygen distributions in the hexagonal α-Zr matrix.

II.A Computational details

The CASTEP program package¹⁵ within the Material Studios framework¹⁶ was utilized and the PBE GGA functional¹⁷ was employed for all calculations. Core electrons were described by ultrasoft pseudopotentials¹⁸ in conjunction with 300 eV cut-off energy. Zr₈ and Zr₁₆ super-cells of the hexagonal closed packed Zr metal were employed to investigate the oxygen concentration dependence of the anode potential resulting from oxidation by water. (2a, 2b, c) and (4a, 2b, c) super-cells of the Zr₂ unit cell were considered to obtain the Zr₈ and Zr₁₆ host matrices, respectively. The k-point sampling of the Brillouin zone was sampled by means of the Monkhorst–Pack scheme.¹⁹ The Zr₈ and Zr₁₆ based super-cells utilized a 4 × 4 × 4 and 2 × 4 × 4 k-points mesh, respectively. Internal consistency of the emerging energetics was checked by reproducing the values obtained for Zr₈O, Zr₈O₂, Zr₈O₃, and Zr₈O₄ by the formally equivalent Zr₁₆O₂, Zr₁₆O₄ a Zr₁₆O₆, and Zr₁₆O₈, respectively. Moreover, the oxygen affinity at the low concentration limit was estimated by comparing Zr₁₆O to Zr₆₄O. The latter supercell was obtained by means of a (4a, 4b, 2c) super-cell in conjunction with a 2 × 2 × 2 k-points mesh. All results presented include optimization of bond lengths, bond angles, as well as unit cell dimensions and angles.

The present study builds on semi-quantitative arguments to arrive at an internally consistent conceptual understanding. While it does neither include vibrational zero-point corrections nor entropy changes, still it is gratifying to find that the reactivity of Zr to form ZrO₂ by means of H₂O was found to be only 0.37 eV/H₂O too small, i.e. ΔE (0 K) = 2.72 eV compared to ΔG (298 K) = 3.09 eV, given the shortcomings of present day density functionals. Finally, it is acknowledged that any successes of studies such as the present rely extensively on the cancellation of errors achieved by making appropriate comparisons.

In order to further assess the findings produced by the PBE GGA functional, comparisons are provided for some structures by means of the PBE0 hybrid functional.²⁰ For the PBE0 functional, the norm conserving pseudopotentials²¹ was used in conjunction with a 750 eV cut-off energy for the Zr₈ super-cell with 4 × 4 × 4 k-points sampling.

The Linear/Quadratic Synchronous Transit method²² was employed to estimate transition states for redistributions of oxygen atoms in the zirconium matrix.

II.B Strategy for sampling structures among Zr_mO_n structures

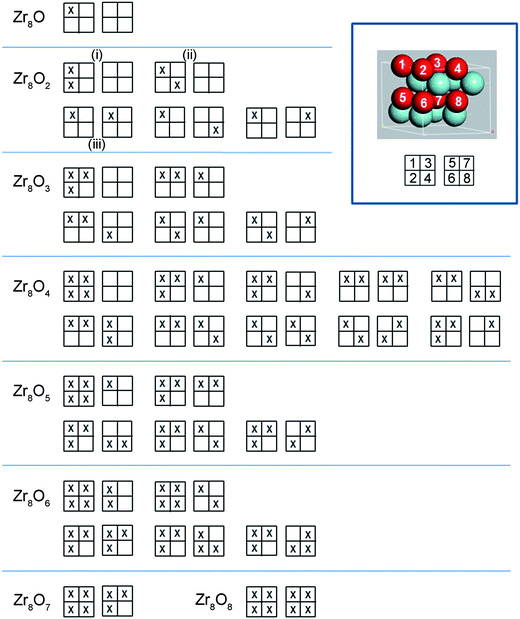
There are two types of interstitial sites in the Zr matrix, octahedral and tetrahedral. Both site types were tested and it was found that octahedral sites are energetically favourable at low concentrations, but a mixed occupancy of both octahedral and tetrahedral sites are preferred at oxygen concentrations in the vicinity of 50 at% O and above. In order to obtain candidate octahedral structures, an alternative procedure to that in ref. 23 was employed here. In this study, full configuration sampling in a structural sub-space of the hexagonal α-Zr host matrix was performed in conjunction with a few complementary candidate structures for interpolation and extrapolation purposes. Thus, all possible permutations of putting one up to eight oxygen atoms in the eight octahedral interstitial sites in the Zr₈ structure were evaluated; rotational and reflection symmetry was assumed as well as that the two planes of interstitial sites were identical. Optimized structures for five oxygen concentrations are displayed in Fig. 1, and the sampling procedure for the Zr₈O₁–Zr₈O₈ structures can be seen in Fig. 2. The Zr₈O_n structural ensemble was extended to include complementary Zr₁₆O_n structures. These where related to the Zr₈O_n structures by doubling the unit cell in the a-direction and by adding or removing oxygen atoms to obtain oxygen concentrations not accessible with the Zr₈O_n supercell. One Zr₆₄O structure was included to address the low oxygen concentration limit. Finally, a suite of structures with different oxygen concentrations from described set was used to study the energy dependence of hydrogen dissolution in these structures.

Fig. 1 Optimized zirconium structures with dissolved oxygen for oxygen concentrations (a) 1.5 at% O, (b) 11 at% O, (c) 20 at% O, (d) 28 at% O, and (e) 33 at% O. (a) and (b) display Zr₆O octahedral sites, (c) display chains of edge-sharing octahedra, (d) and (e) constitute sheets of face-sharing octahedra including octahedral.

Fig. 2 Sampling procedure for Zr₈O₁–Zr₈O₈. All possible permutations to put one up to eight oxygen atoms in the eight octahedral interstitial sites in the Zr₈ structure were tested. The most stable structures for each concentration is the top left structure and the stability of the structure is decreasing when going to right. Rotational and reflection symmetry was assumed as well as that the two planes of interstitial sites were identical.

II.C Rebuilding of electronic structure owing to oxygen dissolution in zirconium

In order to connect the understanding of oxygen dissolution in zirconium to the familiar nature of the large band gap insulators such as ZrO₂, the gradual rebuilding of the density of states as a result of oxygen concentration increase is displayed in Fig. 3. The oxidation can be understood as a titration of electrons at the Fermi energy such that the top of the resulting oxygen associated bands end up ∼3–6 eV below the Fermi level (E_F).

Fig. 3 The rebuilding of the electronic structure owing to increased oxygen concentration in α-Zr eventually resulting in a 4 eV band gap of ZrO₂; red is PDOS for O 2p, green is PDOS for Zr 4d. Dashed line represents the energy of the highest occupied state in all cases. Vertical axis units are in number of states per eV. Horizontal axis units are in eV.

III. Results and discussion

The interest in the Zr–O phase diagram¹⁴ extends beyond its relevance to nuclear technology, as its use includes solid oxide fuel cell applications as well as thermal barrier coatings. The objective of the present study is to determine how the remarkable solubility of oxygen in hexagonal close-packed zirconium affects the corrosion properties of zirconium alloys. Thus it offers the missing pieces of information to a previous mechanistic investigation on the electro-catalytic additive dependence of the competitiveness of the hydrogen evolution reaction versus hydrogen pick-up in the metal.^12,13 Indeed, crucial to application is the ability to control the hydrogen evolution reaction, rendering it competitive with the hydrogen pick-up reaction channel. In what follows, the drive for ZrO₂ dissolution is quantified from a set of different oxygen distributions, and concentrations and the rates for transitions between metastable structures are estimated to assess their relative importance. Often, the activation energies for structural changes among oxygen distributions are large rendering long lifetimes of meta-stable structures. The examined structures are used to assess how the magnitudes and variations of anode potential change upon increased dissolution of oxygen in zirconium, i.e. if there is an oxygen concentration dependence of the ability of the anode potential to drive the cathode process. In addition, the impact of oxygen concentration on the hydrogen pick-up energetics is addressed.

III.A On the dissolution of m-ZrO₂ in α-Zr

Zirconium is known for its remarkable capacity to dissolve oxygen to the extent that oxygen is considered an alloying element in α-Zr. It is interesting to note that while the Zr PDOS at the Fermi level is gradually being depleted, nothing remarkable occurs in the vicinity of ∼28 at% O,¹⁴ see Fig. 3, which is the experimentally reported solubility limit. This suggests that it is the crowdedness of oxygen atoms rather than change in work function, which is decisive for the resulting maximum oxygen solubility in zirconium.

In what follows, the ensemble of structures described in Section II.C, are first ranked with respect to their reaction energies for the reaction

The numbers obtained by the GGA PBE density functional are displayed in Fig. 4 where the oxygen concentration in at% is defined as .

Fig. 4 The energetics of formation of dissolved oxygen structures from ZrO₂ and Zr according to (R4). The spread in energy for a given oxygen concentration comes from different configurations of the oxygen in the Zr matrix.

It comes out clearly that ZrO₂ dissolves in Zr(s). Moreover, it is noted that for every oxygen concentration, the spread in energy is less that 0.5 eV. In order to make any prediction regarding the solubility limit, only the most stable structures, one for each oxygen concentration, are analysed further. These are plotted in the blue curve in Fig. 5. Employing the Boltzmann distribution to the various structures in Fig. 4 does not change the concentration dependence in Fig. 5. Moreover, an overestimate of the configuration entropy as function of oxygen concentration would be to assume degeneracy among configurations, respectively. The stabilities come out comparatively insensitive to the configurational entropy change. In case of 33 at% O the shift is −0.064 eV at 700 K.

In spite of irregularities, the curve clearly displays a minimum. This energy minimum was validated by employ the PBE0 hybrid density functional, which includes 25% exact exchange, see red curve in Fig. 5. It is tempting to take the crossing of the E = 0 eV line in Fig. 5 to reflect the solubility limit, but this is not done here. Rather, the solubility limit is obtained from the chemical potentials for further ZrO₂ dissolution in already formed Zr_mO_n. This is computed according to

in order to employ the residual drive for dissolution of additional oxygen as a measure of remaining ability to dissolve ZrO₂ for each oxygen concentration. The results for m = 8 and 0 ≤ n ≤ 8 are displayed in Fig. 6a for both PBE and PBE0 functionals, while the findings for the extended set including results for m = 16 are displayed in Fig. 6b.

Fig. 5 The energetics of formation of the most stable structures from Fig. 4. Structures calculated with the PBE functional are represented as blue circles and the energetics for some of these structures calculated with the PBE0 functional are represented as red triangles.

Fig. 6 The chemical potential for ZrO₂ dissolution in Zr_mO_n forming Zr_mO_n+1 according to (R5) for m = 8 and m = 16 in (a) and (b), respectively. Blue circles represent calculations with the PBE functional and red triangles represent calculations with the PBE0 functional.

Support for the existence of the largest drive for ZrO₂ dissolution into Zr_mO_n at ∼20 at% O is again obtained by comparing PBE and PBE0 results. Besides this global minimum in the oxygen concentration dependent drive for ZrO₂ dissolution, spikes emerge in Fig. 6 at concentrations where plateaus are found in Fig. 5. These are taken to reflect transitions between various oxygen orderings in the α-Zr matrix.^14,23 It is emphasized that the mere process whereby water oxidizes zirconium alloys tells of a system, which is not in equilibrium. During oxidation, the drive to reach the most stable structure for each local oxygen concentration competes with the continuous inwards dissolution of oxygen into the alloy. For each oxygen concentration, this lends increased importance to the metastable oxygen distributions as compared to the single most stable one. Additional support for this understanding was obtained by calculating activation energies for transitions between typical structures, as summarized in Fig. 1. The obtained numbers, ranging between 0.8 and 2.6 eV, represent displacement along the a- or b-directions of the former, while activation energies close to the latter are associated with transport along the c-direction. The activation barrier of 0.8 eV was calculated between the two Zr₈O₂ structures (ii) and (iii) in Fig. 2 and the 2.6 eV barrier was calculated between the (iii) and (i) structures. Repeatedly, when computational data are compared to experiment in the present study, it should be born in mind that periodic boundary conditions have been employed throughout. Yet, both realistic non-equilibrium and equilibrium scenarios exist, which violate the imposed translational symmetry. Hence, segregation of coexisting domains with higher and lower oxygen concentrations is not unexpected to find in systems studied under limited experimental durations when taking into account the large diffusion barriers normal to the basal plane. Neither would spontaneous such symmetry breaking into coexisting sub-micron domains with different oxygen concentrations be unexpected to find at equilibrium. Hence, employing the experimental solubility limit to validate the computational approach is at best suggestive. Having said this, the PBE functional predicts the solubility limit to be at ∼29 at% O while the value comes out close to 34 at% O in case of PBE0. While it is gratifying to note how these computed numbers come out in agreement with experimental observations, the lower number is commonly reported in the literature,¹⁴ but the upper one is also found in atom probe studies.^13,24

III.B Impact of oxygen dissolution in zirconium on the anode potential

In order to examine the anode potential, H₂(g), was employed as reference electrode. The oxygen concentration dependent anode potential is estimated according to

Zr_mO_n + H₂O(g) → Zr_mO_n+1 + H₂(g) (R6)

and is depicted in Fig. 7 (blue curve) for the most stable structures for each oxygen concentration.

Fig. 7 The oxygen concentration dependent anode potential is represented by the blue circles. The residual drive for the dissolved oxygen structures to form ZrO₂ is represented by the red squares. H₂(g) is the reference electrode for both reactions, see (R6) and (R7).

The residual drive for ZrO₂ formation as function of oxygen concentration for these structures is also included in Fig. 7 (red curve). The residual drive is computed from the reaction

The crossing region in Fig. 7 provides a complementary representation of the solubility limit discussed in Section III.A, where the process beyond the solubility limit corresponds to the disproportionation reaction

as long as any Zr_mO_ns remains. This reaction is the reverse of (R5) but has Zr_mO_ns as the composition at the solubility limit.

Only the energetics of (R6) and (R7) for the most stable structures are displayed in Fig. 7. However, the activation energies for oxygen diffusion have already added importance to the meta-stable oxygen distributions when addressing the actual corrosion process. Indeed, the energetics for (R6) and (R7) are greatly affected when also including the meta-stable structures, see Fig. 8, which includes all structures in Fig. 2. The relevance of this finding to the previously discussed cathode process comes out clearly when taking into account that an anode potential of 2.1 eV was required to drive all cathode processes in those studies.^12,13 For the most stable structures, in the range 20–33 at% O, the anode potential is sufficient to drive all cathode processes, see Fig. 7. This is questionable when taking into account the meta-stable structures. In case of the latter, the instantaneous anode potential is no longer expected to comprise a unique number but it comes with a range of locally varying values.

Fig. 8 The energetics of (R6) in blue and (R7) in red for all structures in Fig. 2. The energetics of (R6) is greatly affected by the choice of structures. For some combinations the solubility limit decreases to less than 20 at% O.

III.C Electronic structure perspectives on the ability of Zr_mO_n to act hydrogen sink

Oxidation of zirconium by water occurs by inwards oxide growth. The necessary proton reduction may occur either by H₂ release or by hydrogen being picked up by the alloy. Mechanisms which lead to H₂ release were discussed in previous studies.^12,13 The reaction, employed to gauge this property here, is

Zr_mO_n + H₂(g) → H₂Zr_mO_n. (R9)

The reaction energy for (R9) is plotted as function of oxygen concentration in Fig. 9, where it comes out clearly that the zirconium–oxygen solid solutions act as hydrogen sink versus H₂(g) well beyond the solubility limit of oxygen.

Fig. 9 Energetics for H₂(g) to be dissolved in various structures with already dissolved oxygen, see (R9). In (a), the oxygen concentrations on the x-axis for the structures are before H₂ is dissolved in the structures. The hydrogen concentration in (b) is for the structures where 2H is dissolved. The blue cross indicates oxygen concentrations ≤ 50 at% O and the red circles indicates concentrations > 50 at% O.

The drive for hydrogen pick-up is further underscored by the fact that it occurs at the metal/oxide interface where it competes with the H₂ formation inside the confining oxide grain boundaries, which introduce an additional ∼1.1 eV penalty for the hydrogen evolution due to the confinement.²⁵

The impact of co-absorption of oxygen and hydrogen on the electronic structures is displayed in Fig. 10, where the partial densities of states (PDOS) owing to co-absorption of oxygen and hydrogen are shown. The dispersion of the hydrogen associated contributions to the density of states (DOS) is seen to correlate with the edges of the oxygen 2p band, which also envelops the 4d contribution to the emerging valence band of monocline ZrO₂. It is not unexpected to find the spread in hydrogen affinities in Fig. 9 to be analogous to the spread in anode potentials in Fig. 8, owing to the relationship between the oxygen and hydrogen bands, compare the p-contribution (red: oxygen) in the left panel of Fig. 10, with the s-band (blue) in the PDOS for 2H in the right panel of Fig. 10.

Fig. 10 Influence of hydrogen pick-up on the electronic structure of the zirconium structures with already dissolved oxygen as function of oxygen concentration. The left panel is total DOS and the right panel is the PDOS for the H contribution. Green, red and blue represents d-orbital, p-orbitals and s-orbitals, respectively. Vertical axis units are in number of states per eV. Horizontal axis units are in eV.

III.D Impacts of magnitudes and spreads in anode potentials on the cathode process

In this section, the spreads in anode potentials for three different oxygen concentrations, cf. Fig. 8, are merged with the elemental dependence of the energetic for the hydride–proton recombination reactions reported for binary Zr alloys,^12,13 see Fig. 11. Also included in Fig. 11 are the spreads in energies (green band) for the dissolution of H₂ corresponding to the different oxygen concentrations, cf. Fig. 9.

Fig. 11 The blue curve is the elemental dependence on the energetics for the cathode process.^12,13 The shades area in orange is the spread in anode dependence due to the meta-stable structures in Fig. 3 for 20 at% O, 27 at% O and 33 at% O. The anode potential is not able to drive all cathode reactions in case of 27 at% O and 33 at% O. The shades are in green is the spread in dissolution of 2H in the some structure with initial oxygen concentrations of 20 at% O, 27 at% O and 33 at% O. The dashed line at 0 eV corresponds to H₂(g) and the dashed line at 1.1 eV corresponds to H₂ in a oxide grain boundary.²⁵

As the oxygen concentration increases, the spread in anode potentials increases. In as much as these values represent the energy required to form intermediate transition metal hydrides,^12,13 overlaps between anode potentials and the additive associated curve implies inability to access the hydrogen evolution channel for those elements and potentials.

The energy for H₂ dissolution was indeed found to depend on oxygen concentration, yet, the drive for H₂ dissolution remains large, i.e. in the range 3–4 eV, see Fig. 11. It is concluded that the H₂ dissolution reaction is significantly less sensitive to the variation among oxygen distributions than the hydrogen evolution reaction in the grain boundary. The latter can by appreciated by considering the distance between the orange ribbons and the dashed line at 1.1 eV, the former representing the ranges of anode potentials for different oxygen concentrations while the latter is the energy for H₂ release into the grain boundary as compared to free H₂.²⁵ Hence, the hydrogen pick-up fraction is expected to increase late in the oxidation process, when approaching the so-called pre-transition regime, because the hydrogen evolution process becomes increasingly suppressed. This conclusion is in agreement with what has been observed by Harada et al.²⁶ and by Couet et al.^27,28

IV. Concluding remarks

Because the cell potential for hydrogen evolution during water induced corrosion of α-Zr is less than that for hydrogen pick-up, avoidance of hydrogen pick-up can only rely on kinetics, i.e. hydride–proton recombination^12,13 occurring more frequently than hydrogen absorption. Indeed, for all relevant oxygen concentrations, co-absorption of hydrogen is preferred relative to free H₂. The findings of the electro-catalytic scenario developed here and in previous studies,^12,13 provide clear implications regarding how to mitigate hydrogen uptake: the anode and cathode processes must be separated in space. Whereas the anode process occurs at the metal/oxide interface, it is preferred that the cathode process takes place in the barrier oxide. Improved electron conductivity in the oxide is required in order for the required proton reduction, followed by hydride–proton recombination reaction, to occur further away from the metal/oxide interface. One way to achieve this would be to exploit second-phase particles as electron conductors, since these extend into the oxide and stay metallic as long as contact with the alloy is maintained. A second way is to n-dope ZrO₂ by substituting small amounts of Zr^IV by Nb^IV. Third, would be to improve the electron conductivity in the grain boundaries by additives, which segregate there.²⁹ It is cautioned thought, that even if electrons are able to access this cathode site, the residual drive might not suffice to produce H₂ in the grain boundary because metastable distributions of oxygen in α-Zr may give rise to insufficient local cell potentials. Moreover, it should be born in mind that improved electron conductivity per se, while it reduces the hydrogen pick-up, may cause accelerated zirconium oxidation.

Acknowledgements

The Swedish Research Council, Westinghouse Electric Sweden, Sandvik Materials Technology, Vattenfall and the EPRI are gratefully acknowledged for financial support.

References

1. H. G. Rickover, L. D. Geiger and B. Lustman, in US Report, Division of Naval Reactors, Washington, DC, 1975.
2. D. E. Thomas, in Metallurgy of Zirconium, ed. B. Lustman and F. Kerze, McGraw-Hill, New York, 1955.
3. S. Kass, J. Electrochem. Soc., 1960, 107, 594.
4. H. H. Klepfer, J. Nucl. Mater., 1963, 9, 77–84.
5. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
6. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
7. M. V. Glazoff, A. Tokuhiro, S. N. Rashkeev and P. Sabharwall, J. Nucl. Mater., 2014, 444, 65–75.
8. M. Christensen, W. Wolf, C. M. Freeman, E. Wimmer, R. B. Adamson, L. Hallstadius, P. E. Cantonwine and E. V. Mader, J. Nucl. Mater., 2014, 445, 241–250.
9. P. A. Burr, S. T. Murphy, S. C. Lumley, M. R. Wenman and R. W. Grimes, J. Nucl. Mater., 2013, 443, 502–506.
10. P. A. Burr, S. T. Murphy, S. C. Lumley, M. R. Wenman and R. W. Grimes, Corros. Sci., 2013, 69, 1–4.
11. S. C. Lumley, S. T. Murphy, P. A. Burr, R. W. Grimes, P. R. Chard-Tuckey and M. R. Wenman, J. Nucl. Mater., 2013, 437, 122–129.
12. M. Lindgren and I. Panas, RSC Adv., 2013, 3, 21613–21619.
13. M. Lindgren, G. Sundell, I. Panas, L. Hallstadius, M. Thuvander and H. O. Andrén, in Zirconium in the Nuclear Industry: Seventeenth International Symposium, ed. R. J. Comstock, ASTM, W. Conshohocken, tentatively accepted.
14. J. P. Abriata, J. Garcés and R. Versaci, Bull. Alloy Phase Diagrams, 1986, 7, 116–124.
15. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
16. Materials Studio 6.0, Accelrys Inc. p. Simulation software.
17. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
18. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
19. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
20. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
21. D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494–1497.
22. N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, Comput. Mater. Sci., 2003, 28, 250–258.
23. B. Puchala and A. Van der Ven, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094108.
24. Y. Dong, A. T. Motta and E. A. Marquis, J. Nucl. Mater., 2013, 442, 270–281.
25. M. Lindgren and I. Panas, Confinement Dependence of Electro-Catalysts for Hydrogen Evolution from Water Splitting, Beilstein J. Nanotechnol. , accepted.
26. M. Harada and R. Wakamatsu, in Zirconium in the Nuclear Industry: 15th International Symposium, ed. B. Kammenzind and M. Limback, ASTM, W Conshohocken, 2009, pp. 384–402.
27. A. Couet, A. T. Motta, R. J. Comstock and R. L. Paul, J. Nucl. Mater., 2012, 425, 211–217.
28. A. Couet, A. T. Motta and R. J. Comstock, Hydrogen Pickup Measurements in Zirconium Alloys: Relation to Oxidation Kinetics, J. Nucl. Mater. , accepted.
29. G. Sundell, M. Thuvander and H. O. Andrén, Corros. Sci., 2012, 65, 10–12.

---