Lithium iron(II) pyrophosphate as a cathode material: structure and transport studies

Abstract

A single phase cathode material Li₂FeP₂O₇ was synthesized by a solid state reaction using inexpensive precursors and optimization of the calcination conditions. Reitveld refinement of the XRD data reveals the value of R_wp and reduced-χ² as 0.97% and 1.006, respectively. Impedance spectroscopy indicates an electronically dominated conduction mechanism with a conductivity of 3.4 × 10⁻⁹ S cm⁻¹ at 303 K.

---

Lithium ion secondary batteries are one of the most promising alternate energy sources that provide a high energy density and operating voltage which are useful for a range of applications from household devices to hybrid electric vehicles (HEV).^1–3 The cathode materials in lithium ion secondary batteries not only dictate its capacity and cycle life, but also determine the cost and safety. Lithium cobalt oxide (LiCoO₂) showing an average potential of 3.9 V with a practical capacity of 150 mA h g⁻¹ is a successfully commercialized cathode material.⁴ However, the high cost and adverse effects of cobalt on the environment have directed researchers to search for cathode materials based on other transition metals. Olivine structured materials, such as lithium iron phosphate (LiFePO₄), are anticipated to be promising cathode materials as they portray appreciable electrochemical properties (average potential 3.4 V, practical capacity 160 mA h g⁻¹).⁴ However, the poor electronic conductivity of LiFePO₄ hinders its commercial usage. In order to improve the conduction characteristics several methods, such as decreasing the particle size, doping ions such as Zr⁴⁺, Ti⁴⁺, V⁵⁺ at Fe sites, coating LiFePO₄ particles with carbonaceous compounds, fluorination of LiFePO₄, have been attempted.^5,6

On the other hand, the search has already begun for novel cathode materials. Recently, a few pyrophosphate based Li₂MP₂O₇ (M = Mn, Fe, Co) materials have been synthesized and tested for application as cathode materials.^7–13 Out of these only Li₂FeP₂O₇ showed appreciable electrochemical activity with an average voltage of 3.5 V and practical capacity of 85 mA h g⁻¹. Li₂MnP₂O₇ was found to be electrochemically inactive while Li₂CoP₂O₇ depicted a voltage of 4.9 V which is higher than the breakdown voltage of most electrolytes. Attempts have also been made to refine the structure of Li₂FeP₂O₇.^8–10 These reports mention the presence of impurity phases in Li₂FeP₂O₇.

We present here the exact preparation conditions to obtain pure phase Li₂FeP₂O₇ and the precise crystallographic data. Electrochemical data concerning Li₂FeP₂O₇ has been reported in the literature but no report seems to be available on the conduction characteristics. We have investigated the basic electrical properties of Li₂FeP₂O₇ using impedance spectroscopy as an experimental tool.

Fig. 1 shows a schematic for the preparation of Li₂FeP₂O₇. In order to find the exact phase formation temperature and the reason behind the presence of the impurity phases, such as Fe₂P₂O₇, LiFePO₄ and LiFeP₂O₇ in Li₂FeP₂O₇,^8,10 the XRD patterns were recorded after each sintering temperature up to 873 K and it is observed that the impurity phase LiFePO₄ creeps-in upon calcining at temperatures above 853 K. In previous reports the samples were calcined at higher temperatures leading to the formation of impurity phases. Also, we prepared the cathode material from inexpensive and easily available starting materials.

Fig. 1 Schematic for the preparation of single phase lithium iron(II) pyrophosphate.

A probable reason for the impurity phase (LiFePO₄) may be the decomposition of P₂O₇⁴⁻ units (pyrophosphate) to PO₄³⁻ (orthophosphate) and PO₃⁻ units (metaphosphate) due to prolonged heat treatment at higher temperatures.¹⁴ The impurity LiFeP₂O₇ is avoided by calcining the sample in a reductive atmosphere of 85% Ar + 15% H₂. The impurity phase Fe₂P₂O₇ may be present due to some initial non-stiochiometry, however, no such phase is observed in our sample (Fig. 2). Room temperature Rietveld refinement of the X-ray diffraction data for the Li₂FeP₂O₇ sample is shown in Fig. 2. The data was refined using the General Structure Analysis System (GSAS) software.¹⁵ Shifted Chebyschev function was used to refine the background while the pseudo-Voigt function was used to refine the profile shape. The Bragg peaks are indexed using the monoclinic space group P2₁/c (no. 14). The refined lattice parameters are a = 11.02260(9) Å, b = 9.75443(10) Å, c = 9.80898(7) Å, β = 101.5321(8)° and V = 1033.363(16) ų. The fitting parameters (R_wp = 0.97%, R_p = 0.75%, goodness of fit (GOF), reduced-χ² = 1.006) obtained are better than those mentioned in previous reports which establish the phase purity of the above prepared Li₂FeP₂O₇. The fractional atomic coordinates, occupancies and the thermal displacement parameters are listed in the ESI.†

Fig. 2 Rietveld refinement of the X-ray diffraction data for lithium iron(II) pyrophosphate.

Fig. 3 shows the refined crystal structure of Li₂FeP₂O₇ drawn using Vesta software.¹⁶ The structure of Li₂FeP₂O₇ reveals that the Fe1 sites are octahedrally coordinated as FeO₆ while the Fe2 and Fe3 sites are coordinated as distorted FeO₅ trigonal bipyramids. The P atoms are coordinated as corner sharing PO₄ tetrahedra forming the P₂O₇⁴⁻ units. The Fe polyhedron are edge sharing and the three edge sharing Fe polyhedron share a corner with one of the PO₄ tetrahedron of the P₂O₇⁴⁻ unit. The Fe2 and Fe3 atoms share their sites with lithium atoms Li5 and Li4, respectively. The Li1 and Li3 atoms exist as edge sharing distorted LiO₅ trigonal bipyramids, while Li2 exists as a LiO₄ tetrahedron. The Li1, Li2 and Li3 atoms are stacked along the b–c plane, which may provide the possible pathways for lithium ion diffusion (Fig. 3).

Fig. 3 Crystal structure of lithium iron(II) pyrophosphate obtained using refined parameters.

A standard redox titration of Mohr's salt and potassium dichromate was used to estimate the total iron content (Fe²⁺ and Fe³⁺) and Fe²⁺ in Li₂FeP₂O₇.¹⁷ A 0.05 N solution of Mohr's salt containing 50 mg of Li₂FeP₂O₇ is titrated against 0.05 N solution of K₂Cr₂O₇ revealing that the total iron content and Fe²⁺ content in the sample are 11.43 and 11.40 mg, respectively. The above quantitative analysis establishes that iron is present only as Fe²⁺ in the above prepared Li₂FeP₂O₇.

The stoichiometry of the sample was also checked by Energy-Dispersive X-ray Spectroscopy (EDS) studies (Fig. 4). The average crystallite size as calculated using the Scherrer formula, D = 0.9λ/(β cos θ) (D = crystallite size, λ = wavelength of X-ray, β = Full Width at Half Maxima (FWHM)) turns out to be 0.3 μm. The FWHM used for the calculation was obtained from the Rietveld refinement and was hence free from instrumental and temperature factors. The SEM image gives the average particle size as ∼1 μm (inset of Fig. 4) indicating each particle consists of several crystallites.

Fig. 4 Energy-dispersive X-ray spectroscopy (EDS) for lithium iron(II) pyrophosphate. Inset shows an SEM image of the sample indicating the particle size.

Fig. 5 shows the TGA and DSC scans for Li₂FeP₂O₇. The DSC scan does not show any transition up to the melting peak, which is observed at 988 K. Also, no appreciable weight loss is observed in the sample up to the melting temperature. The above observations indicate that the cathode material is thermally stable up to its melting point. The thermal stability may be attributed to the presence of corner sharing PO₄ tetrahedrons forming the P₂O₇⁴⁻ units in the structure (Fig. 3).

Fig. 5 Thermogravimetric Analysis (TGA) and Differential Scanning Calorimetry (DSC) of lithium iron(II) pyrophosphate at a heating rate of 10 K min⁻¹.

To carry out the conductivity measurements, the sample was pelletized and sintered progressively up to a temperature of 853 K. The density of the pellet was calculated using the Archimedes principle to be 3.02 g cm⁻³ (96.4% of the theoretical value). Silver electrodes were applied on the opposite faces of the pellet and it was loaded in a spring tight arrangement. Potentiostatic DC polarization measurements were performed to quantify the electronic transport. A constant voltage was applied to the ion blocking cell assembly and the resulting current was recorded as a function of time.

Fig. 6 shows the variation of polarization current as a function of time at a typical temperature of 503 K. A high temperature was chosen for the measurement to observe the signature of any ionic transport. The current increased in a step towards a stationary value as soon as the voltage was applied and decreased in a corresponding manner on turning off the DC voltage, indicating the conductivity is dominated by the electrons in Li₂FeP₂O₇.

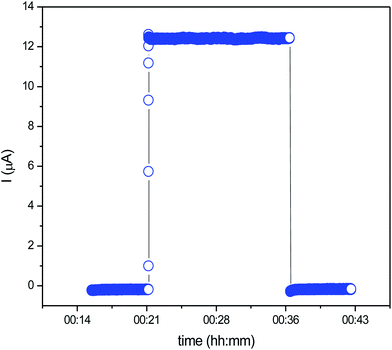Fig. 6 Variation of polarization current as a function of time at 503 K, the DC voltage applied was 0.2 V.

Furthermore, Fig. 7 shows the complex impedance plot at four typical temperatures. Depressed semicircles are observed in the temperature range 293–473 K indicating a distribution of relaxation times. However, the presence of a single depressed semicircle circle is consistent with the absence of any other impurity phase and grain boundaries in the sample.

Fig. 7 Complex impedance plot for the cathode material lithium iron(II) pyrophosphate at four typical temperatures.

The impedance data can also be analyzed in conductivity formalism (σ′ = (Z′/|Z|²)(L/A), where L is the thickness and A is the area of cross-section of the pellet) and several important parameters, such as hopping frequency and activation for the conduction process, can be calculated. Fig. 8 shows the variation of the real part of conductivity (σ′(ω)) with frequency (ω) at four typical temperatures. The data can be analyzed using the Almond–West relation¹⁸

σ′(ω) = σ_dc[1 + (ω/ω_c)^s] (1)

where, σ_dc is the dc conductivity, s is a parameter, 0 ≤ s < 1, and ω_c is the characteristic relaxation frequency. The fitting parameters are mentioned in Table 1. We did not observe any temperature dependence for the parameter s. However, ω_c gives a good estimate of the hopping frequency¹⁹ and shows Arrhenian temperature dependence giving the activation energy for the conduction process as 0.52 ± 0.01 eV. The same value of activation energy was obtained from the Arrhenian temperature dependence of DC conductivity (inset Fig. 8).

Fig. 8 AC conductivity as a function of frequency. Solid lines represent the fitting using the Almond–West relation. The inset shows the variation of dc conductivity (σ_dc) with temperature.

Table 1 DC conductivity (σ_dc), s parameter and hopping frequency (ω_c) at four typical temperatures

Temperature (K)	σdc (S cm^−1)	s	ωc (rad s^−1)
293	1.8 ± 0.1 × 10^−9	0.65	1.9 × 10^3
303	3.4 ± 0.1 × 10^−9	0.65	3.6 × 10^3
313	6.2 ± 0.1 × 10^−9	0.66	6.9 × 10^3
323	1.1 ± 0.1 × 10^−8	0.66	1.2 × 10^4

---

Conclusions

In summary, we have synthesized pure phase Li₂FeP₂O₇ by a solid state reaction method using cheap starting materials. Impurity phases, such as LiFePO₄ and LiFeP₂O₇, are avoided by calcining the sample only up to 853 K in a reductive environment. Rietveld refinement of the sample reveals that Li₂FeP₂O₇ crystallizes in the monoclinic space group P2₁/c with lattice parameters a = 11.02260(9) Å, b = 9.75443(10) Å, c = 9.80898(7) Å and β = 101.5321(8)°. The fitting parameters (R_wp = 0.97%, GOF = 1.006) are better than those obtained in previous reports. The structural studies reveal that the lithium ions are stacked around the b–c plane which may provide possible diffusion pathways for lithium ions. The structure consists of corner sharing PO₄ tetrahedrons which provide thermal stability to the structure, as evident from the TGA and DSC studies. DC polarization and impedance spectroscopy measurements indicate an electronically dominated conduction mechanism with a conductivity of 3.4 × 10⁻⁹ S cm⁻¹ at 303 K. The conduction process was found to be thermally activated with an activation energy of 0.52 eV.

Notes and references

1. M. Armand and J. M. Tarascon, Nature, 2008, 451, 652.
2. J. W. Fergues, J. Power Sources, 2010, 195, 939.
3. L. X. Yuan, Z. H. Wang, W. X. Zhang, X. L. Hu, J. T. Chen, Y. H. Huang and G. B. Goodenough, Energy Environ. Sci., 2012, 5, 5163.
4. J. K. Park, Principles and Applications of Lithium Secondary Batteries, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2012, pp. 21–87.
5. W. J. Zhang, J. Power Sources, 2011, 196, 2962.
6. M. Ueda, M. Ohe, J. H. Kim, S. Yonezawa and M. Takashima, J. Fluorine Chem., 2013, 149, 88.
7. L. Adam, A. Guesdon and B. Raveau, J. Solid State Chem., 2008, 181, 3110.
8. S. Nishimura, M. Nakamura, R. Natsui and A. Yamada, J. Am. Chem. Soc., 2010, 132, 13596.
9. H. Zhou, S. Upetri, N. A. Chernova, G. Hautier, G. Ceder and M. S. Whittingham, Chem. Mater., 2011, 23, 293.
10. H. Kim, S. Lee, Y. U. Park, H. Kim, J. Kim, S. Jeon and K. Kang, Chem. Mater., 2011, 23, 3930.
11. M. Tamaru, S. C. Chung, D. Shimizu, S. Nishimura and A. Yamada, Chem. Mater., 2013, 25, 2538.
12. J. Du, L. Jiao, Q. Wu, Y. Liu, Y. Zhao, L. Guo, Y. Wang and H. Yuan, Electrochim. Acta, 2013, 103, 219.
13. P. Barpanda, G. Rousse, T. Ye, C. D. Ling, Z. Mohamed, Y. Klein and A. Yamada, Inorg. Chem., 2013, 52, 3334.
14. M. Tatsumisago, Y. Kowada and T. Minami, J. Non-Cryst. Solids, 1992, 150, 207.
15. A. C. Larson and R. B. Von Dreele, General Structure Analysis Software (GSAS), Los Alasmos National Laboratory Report LAUR, 2004, pp. 86–748.
16. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272.
17. J. Mendham, R. C. Denney, J. D. Barnes and M. J. K. Thomas, Vogel's Text Book of Quantitative Chemical Analysis, 6th edn, Pearson Education Asia, Singapore, 2002.
18. D. P. Almond and A. R. West, Nature, 1983, 306, 456.
19. M. M. Ahmad, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174303.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra00014e

---