Electronic band structure and specific features of AA- and AB-stacking of carbon nitride (C₃N₄): DFT calculation

Abstract

The state-of-the-art all-electron full potential linear augmented plane wave based on density functional theory was applied for calculating the structural, electronic band structure, effective mass, density of state, and valence electron charge density of AA- and AB-stacking of carbon nitride (C₃N₄). Calculations were performed using four schemes, namely local density approximation (LDA-CA) by Ceperley–Alder, generalized gradient approximation developed by Perdew Burke and Ernzerhof (GGA-PBE), Engel–Vosko generalized gradient approximation (EV-GGA) and the recently developed modified Becke–Johnson (mBJ) potentials. The calculated band structure and total density of states verify the semiconducting nature of the two configurations with band gap of about 2.589 eV and 2.990 eV for AA- and AB-stacking of C₃N₄. The effective mass ratio of electron, heavy hole and light hole were calculated for both AA- and AB-stacking. The upper valence band in AB-stacking is much flatter as compared to AA-stacking, and elucidates a dramatic increase in the effective mass ratio of heavy holes which cause a reduction in group velocity of the wave packet and consequently decrease the mobility of the charge carrier. The partial density of state shows the variation in the orbital state and its strength as one moves from AA- to AB-stacking. The strong hybridization among the orbitals of both stacking (AA- and AB-) shows covalent nature of the bonds. The calculated valence electron charge density contour shows the prevailing covalent nature of C and N bonds with negligible percentage (8.08%) of ionicity.

---

1. Introduction

In recent years carbon nitride (C₃N₄) has attracteded considerable interest as a potential candidate for various biological and technological applications in biomedical, electronic, optical, mechanical and tribological applications.^1–7 The C₃N₄ polymorph, with its high stability and reasonable band gap has been a fascinating research topic for theorists as well as experimentalists. Teter and Hemley⁴ have used the first principle pseudopotential calculation within the local density approximation (LDA) for calculating the structure and physical properties of carbon nitride polymorphs predict a cubic form of C₃N₄ with zero pressure bulk modulus exceeding that of diamond. Liu and Cohen⁵ have used an empirical model and an ab initio calculation to calculate the bulk moduli of β-C₃N₄, they found that β-C₃N₄ have compressibility as compared to diamond structure and the hardness of the compound was exposed to be more than diamond. Numerous theoretical and experimental studies were done on C₃N₄ polymorphs and its forms which focused on its preparation, electronic structure, elastic hardness, linear and nonlinear optical properties.^8–35 Holst and Gillan³⁵ synthesized the nitrogen rich carbon nitride network materials. Their investigations give clear idea about its use as photoactive materials. C₃N₄ is attractive organic semiconductor, gain considerable attention after Wang et al.³⁶ described g-C₃N₄ as a metal free photocatalyst that can absorb more visible light, because of its band gap value (2.70 eV), produce hydrogen from water in comparison to the other oxides. It acquires admirable chemical stability, extraordinary optical characteristics and good thermal solidity that make it potential contestant as a photocatalyst for degradation under visible light. Recently Tahir et al.³⁷ explored the electrochemical properties of tubular g-C₃N₄ which show high suitability as photocatalyst and supercapacitor used to clean environment and energy storage purpose. They highlighted further that improvement in the performance of g-C₃N₄ is due to its high surface area which include more active sites for reaction. The phenomenon of absorbing electromagnetic radiations is very important for photocatalyst, depends on the band gap of the material. Therefore it is necessary to know the accurate band gap's value of the material. Corkill and Cohen³⁸ calculated the electronic band structure of β-C₃N₄ by GW approximation, they obtained a band gap of about 3.11 eV, in close agreement with the previous calculated band gap (3.20 eV) by Liu and Cohen.⁵ The electronic structure and optical properties of β-C₃N₄ were calculated by Yao and Ching.³⁹ They observed that band gap of β-C₃N₄ linearly increases with increasing pressure. Ortega and Sankey⁴⁰ calculated the electronic structure of the planer form of C₃N₄ (p-C₃N₄ and β-C₃N₄). They observed that relative stability of p-C₃N₄ and β-C₃N₄ and found that planer structure of p-C₃N₄ has lower total energy than β-C₃N₄ by at least 0.1 eV per atom. The calculated bulk modulus (189 GPa) of α-C₃N₄ exposed hardness of the reported compound to be approximately half of diamond while the predicted negative Poisson ratio of α-C₃N₄ also leads to fascinating application.⁴¹ We should emphasize that the pseudopotential hybrid functional (B3LYP) presented by Janesko⁴² and Wong and Cordaro⁴³ is the correct way of solving the under-estimated band gaps that they observe in the nitride structures.

From above we noticed that most the reported work were done using non-full potential methods within LDA and GGA approaches. To the best of our knowledge no comprehensive first principles calculations based on full potential method were done for these materials. Therefore, we think it would be worthwhile to perform first-principles calculations, using the state-of-the-art all electron full-potential augmented plane wave plus local orbital approach (FP-APW+lo) based on the density functional theory (DFT) within four approximations namely; local density approximation (LDA-CA) by Ceperley–Alder, generalized gradient approximation developed by Perdew Burke and Ernzerhof (GGA-PBE), Engel–Vosko generalized gradient approximation (EV-GGA) and the recently developed modified Becke–Johnson (mBJ) potentials. Using four schemes for solving the exchange–correlation potentials give accurate result as compared to the previously used methods. This motivate us to carry out more advance computation of electronic band structure, density of states, effective mass and electronic charge density of the AA-stacking and AB-stacking of C₃N₄ using FPLAPW method which has proven to be one of the most precise technique within DFT to calculate the electronic structure of solids.^44,45

2. Crystal structure and computational details

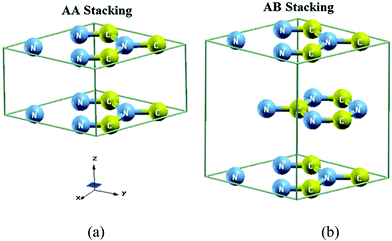
The crystal structure of AA- and AB-stacking of C₃N₄ as shown in Fig. 1a and b are stable in hexagonal symmetry with space group P6̄m2 (no. 187). The crystallographic data of C₃N₄ is taken from ref. 4. The state-of-the-art full-potential augmented plane wave plus local orbitals approach (FP-APW+lo) based on the density functional theory (DFT) within the framework of WIEN2K package⁴⁶ was used. The self-consistent calculations were achieved using four schemes namely; LDA-CA,⁴⁷ GGA-PBE,⁴⁸ EV-GGA⁴⁹ and recently developed mBJ scheme.⁵⁰ LDA works sensibly well but has some shortcomings generally due to the tendency of over binding, which cause too small lattice constants. Perdew et al.⁴⁸ added the gradient terms of the electron density to modify LDA to form a new approximation called generalized gradient approximation developed by Perdew Burke and Ernzerhof (GGA-PBE) which show accurate result in some cases. However both LDA and GGA-PBE have simplest forms that are not sufficiently flexible to accurately reproduce both the exchange–correlation energy and its charge derivative which generally underestimate the energy band gap.⁵¹ Engel and Vosko⁴⁹ considered this deficiency and constructed a new functional form GGA called EV-GGA. Usually EV-GGA acquired by optimizing the exchange–correlation potential V_xc instead of the corresponding energy E_xc. This approach yields better band splitting and structural properties that mainly depend on the accuracy of the exchange–correlation potential^52,53 but still its results for narrow band gap materials and strongly correlated transition-metal compounds are not accurate. Furthermore the mBJ scheme was used.⁵⁰ The mBJ, a modified Becke–Johnson potential, allows the calculation of band gaps with accuracy similar to the very expensive GW calculations.⁵⁰ It is a local approximation to an atomic “exact-exchange” potential and a screening term. This format show best results not only for classical sp-type semiconductors, but also for strongly correlated transition-metal compounds.⁵⁰ For the convergence of energy eigenvalues the wave function in the interstitial regions were expended in plane waves with cutoff R_MTK_max = 7.0. Where R_MT and K_max stand for the muffin-tin (MT) sphere radius and magnitude of largest K vector in plane wave expansion, respectively. The chosen R_MT is 1.24 atomic units (a.u.) for C and N atoms for both of AA- and AB-stacking. The wave function inside the sphere was expended up to l_max = 10 where as the Fourier expansion of the charge density was up to G_max = 12(a.u.)⁻¹. The self-consistent calculations are converged with the difference in total energy of the crystal did not exceed 10⁻⁵ Ryd for successive steps. The self consistent calculations were obtained for both cases by 308k points in irreducible Brillouin zone (IBZ).

Fig. 1 Crystal structure of C₃N₄ unit call (a) AA-stacking (b) AB-stacking.

3. Results and discussion

3.1. Structural optimization

We have performed structural optimization by minimizing the energy with respect to unit cell volume of AA- and AB-stacking of C₃N₄. The exchange–correlation energy was treated by LDA-CA, GGA-PBE and EVGGA schemes to investigate the ground state properties. Fig. 2a–f represent energy verses volume plot for AA- and AB-stacking of C₃N₄ compound. The calculated total energies of C₃N₄ compound are fitted to the Murnaghan's equation of state⁵⁴ to calculate the ground state properties:where E₀, E₀, B₀ and B^′₀ represent ground state energy, volume, bulk modulus and pressure derivative of bulk modulus, respectively. The optimized ground state energy, volume, bulk modulus and pressure derivative of bulk modulus are shown in Table 1. The most stable structure is the one with the lowest total energy.⁵⁵ Both Table 1 and Fig. 1a–f elucidates that EV-GGA show stable volume because of minimum value of the total energy among the other approximations (LDA and GGA). The optimized atomic positions of the investigated compound (AA- and AB-stacking of C₃N₄) are shown in Table 2.

Fig. 2 Optimised energy vs. volume curve of C₃N₄ semiconductor.

Table 1 Present optimized parameters of C₃N₄ semiconductor

	AA-stacking				AB-stacking
	E0 (Ryd)	V0 (a.u^3)	B0 (GPa)	B^′0	E0 (Ryd)	V0 (a.u^3)	B0 (GPa)	B^′0
LDA	−661.853	437.3078	261.6851	3.8487	−1323.726	871.9735	262.7475	3.8393
GGA	−666.533	453.0975	239.7576	3.7503	−1333.044	903.5445	240.7553	3.7432
EVGGA	−672.213	495.9114	181.4819	4.0939	−3344.437	987.9344	193.7032	3.4704

---

Table 2 Present optimized atomic positions of C₃N₄ semiconductor^a

	Atomic coordinates
	Atom	X (Opt.)*	Y (Opt.)*	Z (Opt.)*
a [Present work with GGA-PBE]*.
AA-stacking	C1	0.686	0.843	0.000
	N1	0.333	0.666	0.000
	N2	0.835	0.164	0.000
AB-stacking	C1	0.018	0.509	0.500
	C2	0.686	0.843	0.000
	N1	0.666	0.333	0.500
	N2	0.333	0.666	0.000
	N3	0.168	0.831	0.500
	N4	0.835	0.164	0.000

---

3.2. Band structure

The importance of calculated band structure cannot be ignored for complete understanding the electronic structure and optical properties of the materials because most of the physical properties are directly or indirectly related to it and its basis are linked to the density of states. The energy band gap (E_g) of C₃N₄ is calculated by LDA-CA, GGA-PBE, EV-GGA and mBJ as shown in Table 3. The calculated electronic band structure of AA- and AB-stacking of C₃N₄ is shown in Fig. 3a and b. Following these figures and Table 3, we should emphasize that mBJ shows a better band gap, thus we have selected mBJ to demonstrate the electronic band structure as shown in Fig. 3c and d. The valence band maximum (VBM) and the conduction band minimum (CBM) of AA-stacking are located at A point of the BZ, resulting in a direct band gap. Whereas the VBM and the CBM of AB-stacking are shifted to be situated at the center of the BZ maintaining the direct band gap. The total density of states for AA- and AB-stacking of C₃N₄ are shown in Fig. 4a and b, these figures confirm our observation that mBJ exhibits better band splitting and hence better values of the energy gap.

Table 3 Calculated band gap and effective mass ratio of C₃N₄ semiconductor

	Energy gap
	LDA	GGA	EVGGA	mBJ
AA-stacking
Eg (eV)	0.690	0.870	1.237	2.589
m^*e/me	0.022	0.019	0.022	0.021
m^*hh/me	0.108	0.111	0.143	0.154
m^*lh/me	0.075	0.102	0.110	0.136
AB-stacking
Eg (eV)	1.204	1.357	1.680	2.990
m^*e/me	0.057	0.048	0.059	0.015
m^*hh/me	1.840	1.406	1.324	6.773
m^*lh/me	0.109	1.406	0.771	0.125

---

Fig. 3 Calculated band structure of C₃N₄ semiconductor.

Fig. 4 Calculated total and partial densities of states (States per eV unit cell).

3.3. Effective mass

The electron accelerated in periodic potential of the crystal in the presence of applied electric or magnetic field appear as effective mass (m*). The variation in effective mass of charge carrier depends on its location and energy in the band.⁵⁶ The curvature of the energy band is inversely proportional to effective mass of the charge carrier. An electron moving near the top of allowed energy band acts like a negative mass. The effective mass of charge carrier is approximately equal to rest mass of electron close to the bottom of a nearly-free electron band, but there is considerable increases near the inflection point which turn out to be negative near the zone edge. Therefore the concept of “holes” is introduced in order to avoid the negative m*.⁵⁶

The effective mass of the charge carrier, electron (m^*_e), heavy hole (m^*_hh) and light hole (m^*_lh) were calculated by fitting the dispersion curves around the A and Γ point of BZ following the expression;

or simply it can be written aswhere m_e symbolize the rest mass of electron. We calculated the effective mass ratio of electron (m^*_e/m_e) heavy hole (m^*_hh/m_e) and light hole (m^*_lh/m_e) using the conduction band minimum, upper valence band maximum and the lower valence band maximum. These values are shown in Table 2. There is significant increase in calculated m^*_hh/m_e as one move from AA- to AB-stacking The upper valence band in AB-stacking is much flatter as compared to AA-stacking elucidates dramatic increase in the effective mass ratio of heavy holes which cause to reduce to group velocity of the wave packet and consequently decrease the mobility of the charge carrier.

3.4. Density of states

We have calculated the total and partial density of states (TDOS and PDOS) for AA- and AB-stacking of C₃N₄ using LDA, GGA, EVGGA and mBJ. The TDOS are presented in Fig. 4a and b. Following these figures and also from our prior experience which confirm that the mBJ scheme showed close agreement to the experimental results,^57–63 therefore we have selected mBJ for advance explanation of partial density of state (PDOS). We hope that future experimental works will testify our calculated results. The partial density of states for AA- and AB-stacking of C₃N₄ is shown in Fig. 4c–f. In AA-stacking C-2s state show maximum peak (0.154 states per eV) around −13.5 eV, the same state in AB-stacking also show maximum peak with comparatively small density (0.146 states per eV). The next dominant peak of C-2s in both stacking located around −11.0 eV with same density (0.075 states per eV). As one move towards higher energy, the contribution of C-2s decreases which become very small in the valence band. Its contribution in lower conduction bands is almost zero which again becomes foremost from 6.8 eV to 15.0 eV for both stacking. The first peak of C-2s in the conduction band around 8.0 eV in AA-stacking is about 0.08 states per eV which increases to be 0.10 states per eV for AB-stacking. N-2s state show completely different behaviors for AA- and AB-stacking. There are three dominant peaks in AA-stacking around −13.5, −4.6 and −0.1 eV which shows maximum value of 0.07, 0.05 and 0.08 (states per eV) whereas AB-stacking shows maximum peak of about (0.11 states per eV) around −11.0 eV while N-2s play negligible role in energy range between −11.0 eV and Fermi level. In the conduction band N-2s state show maximum peak (0.05 states per eV) for AA-stacking around 8.0 eV. In case of AB-stacking N-2s state shift towards 7.5 eV with increasing the peak heights to be 0.21 states per eV.

Similarly C-2s/2p and N-2s/2p states show dominant contribution in bands formation. In AA-stacking C-2p state around −7.5 eV is dominant with peak heights of about (0.3 states per eV) which gradually decreases and become zero at Fermi level. The remaining range shows two prevailing peaks around 2.5 eV and 8.0 eV with maximum value of 0.18 states per eV and 0.25 states per eV. In AB-stacking C-2p show dominancy around −7.5 eV and 3.5 eV with the value of 0.28 states per eV and0.45 states per eV. N-2p state play the leading role in bands formation especially in valence band of both stacking. For AA-stacking the first dominant peak is located around −7.5 eV with the value of 0.24 states per eV which increase to be 0.56 states per eV. In AB-stacking the density of the first peak increased to 0.73 states per eV and the second dominant peak is shifted from Fermi energy to −2.0 eV with0.5 states per eV. The contribution of N-2p in conduction band is same as that of C-2p state. From −7.0 eV to Fermi level the N-2p state is dominant and play major role in formation of valence band for AA-stacking. The conduction band is mainly formed by hybridized C-2p and N-2p. In AB-stacking the valence band is fashioned by hybridized C-2p and N-2p with small part of C-2s and N-2s and the conduction band is mainly formed by C-2p.

One can also see strong hybridization between C-2s and N-2s, C-2p and N-2p states. We should emphasize that the strong hybridization among C-s/p state and N-s/p result covalent nature of the bond which can be observed in electronic charge density contour.

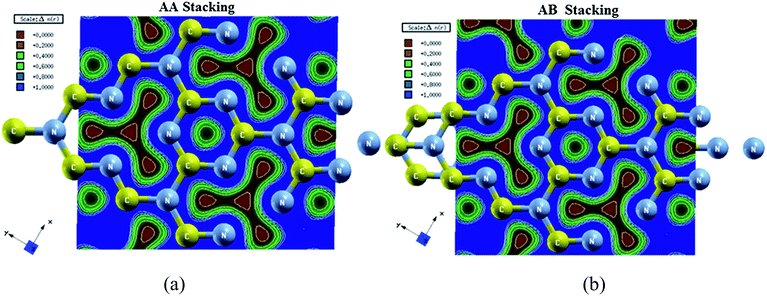
3.5. Electronic charge density

The bonding nature can be accurately explained on the base of electronic charge density plot which is derived from the reliable converge wave function.^64,65 We have calculated the valence charge density in (001) plane for AA- and AB-stacking C₃N₄ by four schemes LDA-CA, GGA-PBE, EVGGA and mBJ-GGA but the results of these formats of exchange correlation potential were almost same, therefore we showed the results of mBJ format which perfectly describe the bonding nature and charge transfer as shown in Fig. 5a and b. We have calculated the electronic charge density of top layer along 2 × 2 × 1 directions in order to completely visualize the bonding nature of the hexagon. The blue color shows the maximum charge intensity as shown in scale while the red color represents zero charge density regions. The blue region in the hexagon representing strong sharing of charge between C and N atom which results the dominant covalent bond among the constituents in the given layer. One can also observe the bonding nature and percentage ionicity by using Pauling scale and Pauling empirical formula used in ref. 66. The electro-negativity difference between C (2.55) and N (3.04) elucidates non polar covalent bond with 8.68% of ionicity.

Fig. 5 Electronic charge density contour of C₃N₄ in (001) plane (a) AA-stacking (b) AB-stacking.

4. Conclusions

We have calculated the electronic band structure, density of state and electronic charge density of AA- and AB-stacking carbon nitride (C₃N₄) using all electron full potential linear augmented plane wave (FPLAPW) method based on DFT within the frame work of Wien2k code. The mBJ potential was preferred due to better band gap for both AA- and AB-stacking in comparison to LDA-CA, GGA-PBE and EV-GGA schemes. The calculated band structures and partial density of states (PDOS) for AA- and AB-stacking were calculated and discussed in details. The calculated effective mass ratio of electron, heavy hole and light hole show variation with bands curvature of AA- and AB-stacking, respectively. The calculated PDOS shows the variation in the states when one move from AA- to AB- stacking. The strong hybridization between C-2s/2p state and N-2s/2p state in AA- and AB-stacking results covalent nature of the bond. The valence electron charge density calculated for both stacking (AA and AB) in (001) plane along 2 × 2 × 1 directions elucidates covalent nature of C and N bond with 8.08% of ionicity.

Acknowledgements

The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme. SA would like to thank CSIR-NPL for financial support.

References

1. E. Kroke and M. Schwarz, Coord. Chem. Rev., 2004, 248, 493.
2. M. H. V. Huynh, M. A. Hiskey, J. G. Archuleta and E. L. Roemer, Angew. Chem., Int. Ed., 2004, 43, 5658 (Angew. Chem., Int. Ed., 2005, 44, 737).
3. L. C. Ming, P. Zinin, Y. Meng, X. R. Liu, S. M. Hong and Y. Xie, J. Appl. Phys., 2006, 99, 033520.
4. D. M. Teter and R. J. Hemley, Science, 1996, 271, 53.
5. (a) A. Y. Liu and M. L. Cohen, Science, 1989, 245, 841; (b) A. Y. Liu and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 10727.
6. Q. Lv, C. B. Cao, C. Li, J. T. Zhang, H. S. Zhu, X. Kong and X. F. Duan, J. Mater. Chem., 2003, 13, 1241.
7. D. R. Miller, D. C. Swenson and E. G. Gillan, J. Am. Chem. Soc., 2004, 126, 5372.
8. T. Sekine, H. Kanda, Y. Bando, M. Yokohama and K. Hojou, J. Mater. Sci. Lett., 1990, 9, 1376.
9. L. Maya, D. R. Cole and E. W. Hagaman, J. Am. Ceram. Soc., 1991, 74, 1686.
10. M. Wixom, J. Am. Ceram. Soc., 1990, 73, 1973.
11. J. J. Cuomo, P. A. Leary, D. Yu, W. Reuter and M. Frisch, J. Vac. Sci. Technol., 1976, 16, 299.
12. H. X. Han and B. J. Feldman, Solid State Commun., 1988, 65, 921.
13. C. Niu, Y. Z. Liu and C. M. Lieber, Science, 1993, 261, 334.
14. D. Marton, K. J. Boyd, A. H. Al-Bayati, S. S. Todorov and J. W. RABlais, Phys. Rev. Lett., 1994, 73, 118.
15. K. M. Yu, M. L. Cohen, E. E. Haller, W. L. Hansen, A. Y. Lu and L. C. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5034.
16. J. P. Riviere, D. Texier, J. Delafond, M. Jaouen, E. L. Mathe and J. Chaumont, Mater. Lett., 1995, 22, 115.
17. Z. M. Ren, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 5274.
18. Y. Yang, K. A. Nelson and F. Adibi, J. Mater. Res., 1995, 10, 41.
19. H. R. Phillip and E. A. Taft, Phys. Rev., 1964, 136, A1445.
20. P. Kroll and R. Hoffmann, J. Am. Chem. Soc., 1999, 121, 4696.
21. H. Yao and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11231.
22. J. Ortegaand and O. F. Sankey, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 2624.
23. M. R. Wixom, J. Am. Ceram. Soc., 1996, 73, 1973.
24. J. E. Lowther, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 5724.
25. S.-D. Mo, L. Ouyang and W. Y. Ching, Phys. Rev. Lett., 1999, 83, 5046.
26. G.-M. Rignanese, J.-C. Charlier and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205416.
27. M. Marqués, J. Osorio, R. Ahuja, M. Flórez and J. M. Recio, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 104114.
28. Y. Zhang, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064109.
29. J. He, L. Guo, X. Guo, R. Liu, Y. Tian, H. Wang and C. Gao, Appl. Phys. Lett., 2006, 88, 101906.
30. J. Hu, W. Cheng, S. Huang, D. Wu and Z. Xie, Appl. Phys. Lett., 2006, 89, 261117.
31. I. Alves, G. Demazeau, B. Tanguy and F. Weill, Solid State Commun., 1999, 109, 697.
32. M. Mattesini, S. F. Matar and J. Etourneau, J. Mater. Chem., 2000, 10, 709.
33. E. Kroke, M. Schwarz, E. Horath-Bordon, P. Kroll, B. Noll and A. D. Norman, New J. Chem., 2002, 26, 508.
34. J. Gracia and P. Kroll, J. Mater. Chem., 2009, 19, 3013.
35. J. R. Holst and E. G. Gillan, J. Am. Chem. Soc., 2008, 130, 7373.
36. X. C. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76.
37. M. Tahir, C. Cao, F. K. Butt, F. Idrees, N. Mahmood, I. Aslam, Z. Ali, M. Tanvir, M. Rizwan and T. Mahmood, J. Mater. Chem. A, 2013, 1, 13949.
38. J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17622.
39. H. Yao and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 11231.
40. J. Ortega and O. F. Sankey, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 2624.
41. Y. Guo and W. A. Goddard, Chem. Phys. Lett., 1995, 237, 72.
42. B. G. Janesko, J. Chem. Phys., 2011, 134, 184105.
43. B. M. Wong and J. G. Cordaro, J. Phys. Chem. C, 2011, 115, 18333.
44. S. Gao, Comput. Phys. Commun., 2003, 153, 190.
45. K. Schwarz, J. Solid State Chem., 2003, 176, 319.
46. P. Balaha, K. Shewartz, G. K. H. Madsen, D. Kvsnicka and J. Luitz, WIEN2K, an Augmented plane wave + local orbitals program for calculating crystals properties,Karlheinz Schewartz, Techn. Universitat, Wien Austria, 2001, ISBN 3-9501031-1-2.
47. D. M. Ceperley and B. I. Alder, Phys. Rev. Lett., 1980, 45, 566.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
49. E. Engel and S. H. Vosko, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164.
50. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
51. P. Dufek, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7279.
52. Z. Charifi, H. Baaziz and A. H. Reshak, Phys. Status Solidi B, 2007, 244(9), 3154.
53. A. H. Reshak, Z. Charifi and H. Baaziz, Eur. Phys. J. B, 2007, 60, 463.
54. F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244.
55. M. Zhou, Y.-H. Lu, Y.-Q. Cai, C. Zhang and Y.-P. Feng, Nanotechnology, 2011, 22, 385502.
56. A. P. Hibbins, PHY3102/3305 Solid State Physics I – 2009/10.
57. A. H. Reshak, X. Chen, S. Auluck and H. Kamarudin, Mater. Chem. Phys., 2012, 137, 346.
58. A. H. Reshak, X. Chen, S. Auluck and H. Kamarudin, J. Appl. Phys., 2012, 112, 053526.
59. A. H. Reshak, I. V. Kityk, O. V. Parasyuk, A. O. Fedorchuk, Z. A. Alahmed, N. AlZayed, H. Kamarudin and S. Auluck, J. Mater. Sci., 2013, 48, 1342.
60. A. H. Reshak and S. A. Khan, Mater. Res. Bull., 2013, 48, 4555.
61. M. Benkraouda and N. Amrane, J. Alloys Compd., 2013, 546, 151.
62. S.-D. Guo and B.-G. Liu, J. Magn. Magn. Mater., 2012, 324, 2410.
63. H. Hakan Gürel, Ö. Akinci and H. Ünlü, Superlattices Microstruct., 2012, 51, 725.
64. R. Hoffman, Rev. Mod. Phys., 1988, 60, 601.
65. C. D. Gellatt, A. R. Willaims Jr and V. L. Moruzzi, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2005.
66. Schlusseltechnologien Key Technologies, 41st IFF Springschool, 2010, p. A1.18.

---