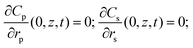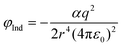Influence of charge compensating cations on propane adsorption in X zeolites: experimental measurement and mathematical modeling
Yunxia Yang*a,
Nick Burkea,
Junfang Zhangb,
Stanley Huangc,
Seng Limd and
Yonggang Zhue
aCSIRO Earth Science and Resource Engineering, 71 Normanby Rd, Clayton North, Victoria 3168, Australia. E-mail: yunxia.yang@csiro.au
bCSIRO, Earth Science and Resource Engineering, 26 Dick Perry Ave, Kensington, WA 6151, Australia
cChevron Energy Technology Company, Houston, TX 77002, USA
dCSIRO Process Science and Engineering, Bayview Ave, Clayton, Victoria 3168, Australia
eCSIRO Materials Science and Engineering, Bayview Ave, Clayton, Victoria 3168, Australia
First published on 6th January 2014
Abstract
Separation of minor components is necessary prior to natural gas liquefaction. There are many methods to achieve this but one that has not been studied in great detail is adsorption of hydrocarbon gases on zeolite materials. A more comprehensive understanding of the fundamentals of hydrocarbon adsorption on zeolites is required in order to determine the efficacy of these materials in natural gas processing. This study investigates the influence of the charge compensating (non-framework) cation on the adsorption of propane on X zeolite by both dynamic experiments and mathematical modeling. This work presents a systematic experimental study examining the effects of the 5 typical types of charge compensating cations (Li+, Na+, K+, Ca2+, La3+) in X zeolites for saturated hydrocarbon adsorption. The dynamic experimental results reveal that for the X zeolites examined, all exhibited an affinity for propane, with LiX being the best, having a propane adsorption capacity of 15.5 wt%. Interestingly, unlike many non-zeolite solid sorbent materials, such as carbons, surface area and pore size alone do not necessarily determine propane adsorption capacity in these X zeolites. It has been shown that the charge compensating cation of the X zeolites of interest, in particular its valence, number of ions and size are the major factors affecting the propane adsorption capacity. Mathematical modeling equations are established by using mass balance in the adsorbent column, macroporous pellets and microporous crystals. The model-predicted results show a good match with our experimental results. The prediction results show that in our current experimental conditions, LiX has a slower adsorption rate than the other zeolites. The obtained adsorption equilibrium constants for all the X zeolites follow the same trend as their propane adsorption capacity, with LiX having the largest constant, suggesting a stronger binding energy between LiX and propane compared to the other zeolites.
1. Introduction
Raw natural gas produced from the wellhead is a mixture consisting of, amongst others, methane and heavier aliphatic hydrocarbons such as ethane and propane, which must be treated to meet production requirements and consumer specifications before pipeline distribution or liquefaction. Among all the emerging technologies available for natural gas processing, separation by adsorption is a very promising chemical engineering method, widely considered because of its reliability, flexibility and low energy consumption but hasn't been widely implemented industrially partly because of the lack of fundamental information on adsorption behaviors of different adsorbent materials.1–4 Ideally, adsorbents should be tailored with attributes that meet the needs of each specific application.5 The past two decades, there has seen a rapid development of new nanoporous materials. Tremendous advances have been made in the ability to control the porosity and surface chemistry of oxide molecular sieves such as zeolites,6–9 metal organic frameworks (MOFs),10–14 structured silica materials15–17 and new forms of carbon such as extremely high surface area activated carbons and templated carbons.18,19 However, adsorption characteristics of many of these materials for hydrocarbon gases, especially in natural gas applications, remain largely unexplored. This is particularly the case with adsorption of non-polar, non-quadrupole moment gases such as alkanes on zeolites.Zeolites are well-known microporous crystalline solids with neutral SiO2 groups and negatively charged (AlO2)− ions compensated by a non-framework cation such as Na+, Li+, K+, Ca2+ or NH4+. It is known that the adsorption interaction within zeolites is significantly influenced by the nature of the cations, this number of cations (Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio) and their positions in the framework. These cations generally assume a certain window position in the framework, constructing specific sized pores accessible to some gases while not accessible to others, which is known as molecular sieving, or trapping. The differences between trapping and sieving are well described in a recent paper by Shang et al.20 When zeolites are used as adsorbents, under the influence of the charge field created, the framework compensating cations interact with the gas molecules through intermolecular dispersion and electrostatic interaction. Polar molecules (for example water) or molecules of high quadruple moment (for example carbon dioxide) will be preferentially adsorbed by virtue of their strong electrostatic interactions with the cations. The practical reality of this phenomenon is that polar and high quadrupole moment gases would need to be removed prior to using a zeolite to separate alkanes in a natural gas mixture. The adsorption behavior of two different zeolites for the same adsorbate with the same compensating cation, say Na+, might be different. This is due to differing extents of cation screening or solvation by lattice oxygen in different zeolite frameworks.21 In order to predict and understand the gas adsorption properties in zeolites, it is very important to know the nature of the charge compensating cations and how they are positioned in the framework. Some early work in the 1970s investigated the locations of the monovalent cations in several types of zeolite and their interaction with adsorbed molecules by isothermal measurement.21–26 Postulations about the cation positions were made but were not confirmed. Up to now, the positions of charge compensating cations have been identified only for A zeolites,27,28 although a recent study has postulated cation position in a chabazite framework by combining empirical measurements and density functional theory (DFT) calculations.20 Extrapolation of these studies to other zeolite frameworks, such as X, is not straightforward; therefore each zeolite framework must be studied independently.
Al ratio) and their positions in the framework. These cations generally assume a certain window position in the framework, constructing specific sized pores accessible to some gases while not accessible to others, which is known as molecular sieving, or trapping. The differences between trapping and sieving are well described in a recent paper by Shang et al.20 When zeolites are used as adsorbents, under the influence of the charge field created, the framework compensating cations interact with the gas molecules through intermolecular dispersion and electrostatic interaction. Polar molecules (for example water) or molecules of high quadruple moment (for example carbon dioxide) will be preferentially adsorbed by virtue of their strong electrostatic interactions with the cations. The practical reality of this phenomenon is that polar and high quadrupole moment gases would need to be removed prior to using a zeolite to separate alkanes in a natural gas mixture. The adsorption behavior of two different zeolites for the same adsorbate with the same compensating cation, say Na+, might be different. This is due to differing extents of cation screening or solvation by lattice oxygen in different zeolite frameworks.21 In order to predict and understand the gas adsorption properties in zeolites, it is very important to know the nature of the charge compensating cations and how they are positioned in the framework. Some early work in the 1970s investigated the locations of the monovalent cations in several types of zeolite and their interaction with adsorbed molecules by isothermal measurement.21–26 Postulations about the cation positions were made but were not confirmed. Up to now, the positions of charge compensating cations have been identified only for A zeolites,27,28 although a recent study has postulated cation position in a chabazite framework by combining empirical measurements and density functional theory (DFT) calculations.20 Extrapolation of these studies to other zeolite frameworks, such as X, is not straightforward; therefore each zeolite framework must be studied independently.
Olefin and paraffin gas adsorption and separation on zeolites have been studied on zeolites such as FAU zeolites, MFI, A zeolites, and ETS (Titanosilicate).1–4,13,26,29–45 However, due to the large number of zeolite frameworks, compensating cations and adsorbate gases, it has been difficult to generalize hydrocarbon gas adsorption and separation properties with respect to the charge compensating cations used, although suggestions were made as to which zeolites are good candidates for separating higher hydrocarbons from natural gas. In order to optimize separation, it is important to fully understand how zeolites and their charge compensating cations interact with hydrocarbons.
As previously stated, propane is very often present in significant quantities in natural gas. Target concentration ranges of propane in natural gas for pipeline and LNG use must be adhered to, and the gas must be treated to meet these requirements. Propane is neither a polar molecule nor a molecule of high quadruple moment. When a zeolite is chosen as the adsorbent, the adsorption potential between the adsorbent and adsorbate reduces to dispersion potential and induction interaction. See chapter 2 in ref. 5, 26 and 30 for details of the relevant equations. In this case, Si/Al ratio (which is inversely related to the total number of the cations) of the zeolite, the positions of the cations in the framework, their charge, accessibility and their polarisability will all play a role in affecting the interaction potential between the gas molecules and the zeolite framework. However, there has been little work done in the past to explore the dynamic adsorption properties of the cations and how they affect adsorption and separation.
In this context, the aim of the current work is to study the effects of the different cations on propane adsorption in X zeolites. A separation rig was designed and used for the dynamic breakthrough experiments for this purpose. The breakthrough results for these ion-exchanged X zeolites were obtained and compared. Mathematical models are established by using mass balance along the adsorbent bed, pellet and crystals. This paper compares theoretical predictions with experimental results in conjunction with the physical and chemical properties of the adsorbents. Factors affecting the propane adsorption properties on these X zeolites are discussed and explained.
2. Experimental
2.1 Materials and synthesis
Faujasite NaX zeolite, was purchased from Sigma Aldrich. LiX, KX, CaX and LaX were synthesized in the current work according to methods described in the literature.46–48 In general, the procedure used was to weigh a certain amount of the zeolite (20 g) in a glass conical flask with a magnetic stirring bar, add in the desired amount of salt solution (0.5 M LiCl, 1 M KCl, 1 M CaCl2, 0.1 M LaCl3, respectively), adjust pH to ∼9 by adding KOH if necessary, place the conical flask in an oil bath, and stir and heat at 65–80 °C overnight. The suspension was then filtered and washed with distilled hot water to remove the excess salt. This procedure was repeated twice. Finally, the sample was filtered and washed with distilled hot water and dried in the oven overnight at 100 °C.2.2 Characterization
Brunauer–Emmett–Teller (BET) surface areas and pore volumes of the synthesized adsorbents were analyzed by a Micromeritics Tristar 3000. Samples were degassed at 350 °C overnight before analysis. BET surface areas were extracted from the adsorption isotherms at a relative pressure p/p0 less than 0.12. Micropore volume was obtained by t-Plot analysis. Elemental analysis was conducted on a Philips PW2404 XRF system. 0.5 g of each of the submitted powders was weighed into 95% Pt/Au crucibles with approximately 5 g of 12–22 lithium metaborate/tetraborate flux. The mixture was fused into a homogeneous glass over an oxy-propane flame at a temperature of approximately 1050 °C and the molten material was poured into a 32 mm diameter 95% Pt/Au mould heated to a similar temperature. Air jets then cooled the melt for approximately 300 seconds. The resulting glass discs were analysed on a Philips PW2404 XRF system using a control program developed by Philips and a self-developed algorithm.2.3 Dynamic experiments
A schematic diagram of the apparatus developed to measure the gas breakthrough curves is shown in Fig. 1. It consists of three main sections: preparation section; adsorption section; and the analytical section. In the gas preparation section, the purge gas was high purity Ar gas (99.999%) which was used to purge the system through the inert gas line and the reactor before the hydrocarbon gas was introduced. The adsorption section used a 2.5 mol% propane gas in helium which passed through the fuel gas line and the reactor. Both lines run into a four-port crossover valve. The whole set up was run isothermally (∼26 °C). Valve positions, gas flowrates, pressure and temperature were completely automated and controlled by an in-house designed Labview program. The exhaust gas from the reactor outlet was analyzed and quantified by a Pfeiffer Mass Spectrometer (MS). The adsorption reactor consisted of a 6 mm i.d. stainless steel column 100 mm in length. All adsorbents were pelletized to an average size of 300–500 μm (without using binder) to avoid pressure drop across the bed. During the breakthrough experiments, the reactor column was filled with adsorbents (0.4 g) which was pre-degassed on a vacuum prep at 350 °C overnight and packed uniformly to about 35 mm in height. After packing, Ar gas from the inert line purged the system and reactor until the MS baselines were stable. The 2.5 mol% propane in helium gas from the fuel gas line was then introduced to the reactor at a flow rate of ∼100 ml min−1 and adsorption was started.The propane adsorption capacity on the adsorbent was obtained by integrating the reactor outlet propane gas concentration profiles over the entire breakthrough period,
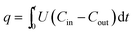 | (1) |
3. Mathematical modeling
In our current work, we have attempted to use a mathematical model to simulate the breakthrough experimental results, aiming to obtain some fundamental information about the adsorption of propane on the FAU zeolites having different types of cations.Consider an element of an isothermal column packed with pellets of zeolite, through which a fluid stream containing concentration of a sorbate, C(z,t) is flowing and assuming the flow pattern is axially dispersed plug flow in which a trace of absorbable species is adsorbed from an inert carrier. At time zero, the 2.5 mol% propane in helium is introduced at the top of the column. The following additional assumptions were made: (1) the ideal gas law applies. (2) The pressure drop through the bed is negligible. (3) The flow pattern is described by the axial dispersed plug flow model. (4) The main resistances to mass transfer for adsorbable species are external fluid film resistance and macropore diffusion, as pointed out by Barcia et al.43
With the above assumptions, the differential fluid phase mass balance over a reactor column element can be expressed as eqn (2):32
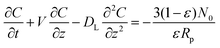 | (2) |
Mass balance over a pellet particle is written as eqn (3):32
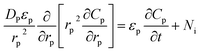 | (3) |
Mass balance over a crystal particle is written as eqn (4) and (5),32
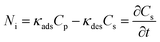 | (4) |
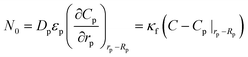 | (5) |
Initial conditions,C(0, t) = C0; C(z, 0) = Cp(rp, z, 0) = Cs(rs, z, 0) = 0;
In order to obtain the transient solution, the Laplace transforms are performed and the solution in Laplace space is inverted numerically by using the so-called Stehfest's method.50,51
4. Results and discussion
4.1 Elemental analysis and cation positions in X zeolite
The elemental analysis of all the X zeolites used in our work, as determined by XRF, is listed in Table 1.| Adsorbent | SiO2/Al2O3 | Lia | Naa | Ka | Caa | Laa | Degree of Na+ ion exchangedd % |
|---|---|---|---|---|---|---|---|
| a mol per 100 gram zeolite.b Under detection limit.c Commercial NaX sample.d Degree of ion exchange = (target ion concentration × target ion valence)/original Na ion concentration. | |||||||
| LiX (LiNaX) | 2.46 | 0.25 | 0.26 | —b | —b | —b | 49 |
| NaXc | 2.45 | —b | 0.59 | —b | —b | —b | —c |
| KX (KNaX) | 2.46 | —b | 0.1 | 0.35 | 0 | —b | 78 |
| CaX (CaNaX) | 2.46 | —b | 0.03 | —b | 0.25 | —b | 94 |
| LaX (LaNaX) | 2.4 | —b | 0.22 | —b | —b | 0.08 | 52 |
It is clear from the elemental analysis results that the ion-exchange of the zeolites is not 100% complete. Because of this, in the ion-exchanged zeolite framework, ions are a mixture of target ions and original Na ions. However, for clarity, we use ion-exchanged ions and their corresponding zeolite framework to represent the ion-exchanged zeolite. For example, LiX represents Li ion exchanged NaX zeolite, even though there are still Na ions present.
The schematic structure of Faujasite (FAU) zeolite and the potential positions of its charge compensating cations are shown in Fig. 2. The zeolite's three-dimensional framework has two main cages: the large supercage assembled with the basic units and the sodalite cages. The spherical supercages are approximately 1.3 nm in diameter. Access to the supercages is by four 12-membered ring windows about 0.74 nm in diameter, which are tetrahedrally distributed around the centre of the supercages. Cations can occupy three positions in the zeolite. Sites I and I′, are located on the hexagonal prism faces between the sodalite units. Sites II and II′, are located on the open hexagonal faces. Site III, is located on the walls of the supercage.53 Cations located in sites I, I′ and II′ are generally screened to some extent and consequently they interact more weakly with adsorbed gas molecules21 while cations in sites II and III are more exposed and accessible. According to the literature, different charge compensating cations occupy different site positions in the framework.21–23,25,28,54,55 The corresponding available void space after gas adsorption and the electric field strength also change. For NaX, it is known that sodium cations assume all of the adsorption sites.42,56 For LiX, the lithium cation's positions will vary with the degree of ion-exchange.26 At a higher degree of exchange (>50%), Li+ may occupy sites II and III.42 But at the ion-exchange degree of 49% (Table 1), Li+ is preferentially positioned at site III positions due to steric considerations.42 According to Dempsey and Harlfinger, cations in the site III position, because of the flat potential troughs, have a higher degree of mobility than cations in the site II position. Also, lithium ions in these positions are well shielded by the six-membered and four-membered oxygen rings of the zeolite framework.57 Exchanging double valent cations such as Ca2+ and larger cations such as potassium and lanthanum will result in the site II positions being occupied first.28,42,57 However, for cations whose size is even bigger, site III positions might be preferred.42
 | ||
| Fig. 2 Faujasite (FAU) zeolite structure and positions of their potential charge compensating cations.52 | ||
4.2 Surface area of the zeolites measured by nitrogen adsorption
After ion-exchange, the Langmuir surface area of the X zeolites followed the trend: LiX > LaX > CaX > NaX > KX (Table 2). There are two main factors affecting the surface area: the size and the number of compensating cations. Li+, Na+ and K+ have the same charge, but their sizes follow the trend: K+ > Na+ > Li+ (Table 2). It can be seen from Fig. 3a that for the monovalent compensating cations, the surface area is inversely proportional to the cation size. Influence on surface area for multi valent cations is more complex because both their size and total number in the framework must be considered. For example, Ca2+ is similar in size to Na+, so we would expect the occupied volume not to change. But since Ca2+ is a divalent ion, the total number of Ca2+ cations in the framework is less than that of NaX (Table 2). Consequently a slightly increased surface area is seen for the CaX zeolite (Table 2 and Fig. 4a). The La3+ ion is larger than Na+, but occupies one exchange site for every three Na+ ions. Also, the degree of exchange of La is not 100%. So any decrease in surface area due to the size of the La3+ ion is offset by its valence and the degree of exchange. This is reflected in the surface area measurements (Table 2, Fig 3a).| Adsorbent | Cation size (Å) | Charge density (+/Å−3) | Total number of cations per g of adsorbent (1021)a | Exchanged cations per g adsorbent (1021)a | Polarizability of cation (10−24 cm3) | Langmuir surface area, (m2 g−1) | C3 adsorption capacity, (wt%) |
|---|---|---|---|---|---|---|---|
| a Na cations are not exchanged but are reported here as total number as the basis for calculation of degree of ion exchange. | |||||||
| LiX | 0.68 | 48.6 | 3.07 | 1.51 | 0.029 | 949 | 15.5 |
| NaX | 0.97 | 16.7 | 3.55 | 3.55 | 0.18 | 789 | 14.4 |
| KX | 1.33 | 6.5 | 2.71 | 2.11 | 0.84 | 771 | 13.3 |
| CaX | 0.99 | 31.5 | 1.69 | 1.51 | 0.471 | 831 | 8.31 |
| LaX | 1.03 | 42 | 1.81 | 0.482 | 0.02 | 841 | 5.47 |
 | ||
| Fig. 4 Model predicted breakthrough curves. (a) LiX (b) NaX (c) KX (d) CaX and (e) LaX (f) Kads influence on the curve shape, CaX. | ||
4.3 Propane adsorption
Propane adsorption was investigated by dynamic breakthrough experiments in an adsorbent bed. The propane breakthrough curve is a plot of the reactor outlet propane concentration against time. When the outlet gas concentration reached the inlet gas concentration breakthrough was taken to be complete. The breakthrough curve gives information about the interactions between the adsorbate and the adsorbent. Propane breakthrough curves are shown for all the X zeolites in Fig. 4b. The slopes of the breakthrough curves give information about the rate of adsorption. The steepest slopes indicate the fastest adsorption. In practice the slope of the curve is very important in determining the length of the adsorption bed. Typically, adsorbent beds must be switched out once breakthrough of the adsorbed material is detected. So, adsorbents with steeper slopes allow for a greater fraction of the adsorption bed to be used. In our case, CaX and NaX have the steepest slopes, indicating a more complete utilization of the adsorbent bed is possible. LaX, LiX and KX have less steep slopes, suggesting a larger fraction of adsorbent is not used.Propane adsorption capacity on different X zeolites is listed in Table 2. Interestingly, the gas adsorption capacity is not proportional to the surface area. One reason for this observation might be explained by the differences between adsorption of propane on the surface of the zeolite and adsorption of nitrogen, which is used in this case as the analyte molecule for surface area measurement. Nitrogen is non-polar and a high quadruple gas molecule whereas propane is a non-polar and non-quadruple gas molecule. Therefore, the surface area extracted from nitrogen adsorption may not reflect the surface area available for propane adsorption.
The interaction between adsorbate and adsorbent is mainly based on:5
(i) dispersion interaction potential and;
(ii) the induced dipole moment.
In the case of charged adsorbents, the induced dipole moment term is the dominant factor in adsorbate/adsorbent interactions, being a few orders of magnitude larger than the dispersion interaction potential. The size of the induced dipole moment is a function of the charge; the polarisability; and the size of the cation, which is related to the induction energy, represented as follows:5
The polarisability of the three single-valent cations (Table 2) follows the trend K+ > Na+ > Li+. However, charge density of the three cations follows the opposite trend (Li+ > Na+> K+). Considering the total number of the exchanged cations in LiX is less than that in NaX and KX, the fact that propane has higher adsorption capacity on LiX would suggest the cation charge density has a greater influence on propane adsorption than polarisability.
Zeolites with multi-valent charge compensating cations show a reduced capacity for the uptake of propane. This is most likely due to the fact that there are fewer compensating cations in the multi-valent exchanged zeolites compared to the single-valent ion-exchanged zeolites (Table 2). The smaller number of compensating ions means that both dispersion interaction potential and induced dipole moment are significantly decreased compared to single valent cation exchanged zeolites. Though LaX has a higher total number of cations than CaX, propane adsorption on LaX is lower than that on CaX, suggesting total number is not the only factor affecting propane adsorption. For CaX, though Ca2+'s charge density is 25% less than that of La3+, the total number of Ca2+ is 3 times more than that of La3+. Also, LaX has a lower polarisability than CaX, which leads to a lower dispersion interaction. Therefore, the over interaction potential in LaX is lower than CaX, resulting in a weaker propane adsorption binding energy. This is in agreement with our experimental observation that LaX has lower propane adsorption capacity than CaX.
4.4 Numerical modeling of breakthrough experiments
The model predicted propane breakthrough curves for the ion-exchanged X zeolite samples at room temperature (299 K) are shown in Fig. 4. Some of the known physical data and model fitted parameters are presented in Table 3.| Parameters | Value |
|---|---|
| Average velocity in the interparticle space, V (m s−1) | 0.07 |
| Longitudinal dispersion coefficient, DL (m2 s−1) | 2.45 × 10−6 |
| Diffusivity in macroparticles, DP (m2 s−1) | 5.0 × 10−6 |
| Mass transfer coefficient, κf (m s−1) | 5.25 |
| Column height, L (m) | 3.5 × 10−2 |
| Particle radius, Rp (m) | 2.0 × 10−4 |
| Macropore porosity, εp | 0.315 |
| Column porosity, ε | 0.310 |
| Adsorption rate constant, Kads (s−1) | LiX, NaX, KX, CaX, LaX 50, 200, 50, 200, 200 |
| Adsorption equilibrium constant KA, m3 m−3 | LiX, NaX, KX, CaX, LaX 640, 620, 620, 560, 400 |
LiX has the highest adsorption equilibrium constant and so has the highest propane adsorption capacity in agreement with experimental observations. LaX has the smallest adsorption equilibrium constant and has the lowest propane adsorption capacity, also in agreement with experimental observations. The predicted adsorption equilibrium constant, KA, for all the adsorbents follows the same trend as their propane adsorption capacity calculated in the experimental section, suggesting the dominant step for gas adsorption in our current dynamic environment is the microscopic adsorption inside the crystal particle of the adsorbent. A high KA generally suggests a strong binding and interaction between adsorbate gas molecule and adsorbent. However, due to intrinsic limitations of this mathematical model, we are not able to identify the specific factors that induced this strong interaction. This conclusion links well with the conclusions from the experimental work related to the importance of the induced dipole moment in gas/solid interactions in these systems.
The predicted results reveal that the best fit longitudinal dispersion coefficient, DL is 2.45 × 10−6 m2 s−1. When DL is less than 2.45 × 10−6 m2 s−1, the curve shape is no longer sensitive to DL, suggesting our previous assumption that little or no dispersion for model establishment is valid. To investigate how the adsorption rate constant, Kads affects the breakthrough curve, model fitting for CaX is explored (Fig. 4f). Changing Kads from 50 to 200, increases the slope of the breakthrough curve, suggesting gas adsorption in a single crystal particle is the dominant step. When the value of Kads is >200, the slope of the breakthrough curve is no longer influenced by the value of the Kads. This is true for all of the adsorbents tested and suggests in this case, that propane adsorption equilibrium step in a single crystal is not the dominant step. CaX has the steepest breakthrough front, suggesting fast propane adsorption equilibrium.
5. Conclusion
Dynamic breakthrough experimental results have demonstrated that X zeolites in general show very good propane adsorption capacity. Among all the X zeolites tested, LiX exhibited the highest adsorption capacity of 15.5 wt%.The breakthrough results also suggest that the surface area of the adsorbent is not the critical determining factor for propane adsorption in X zeolites. Instead, the charge compensating cation, its size, polarisability, and the number of cations have a greater effect on propane adsorption capacity. A careful examination of the results reveals that the charge and size of the charge compensating cations in the adsorbents formed the basis for this phenomenon.
Our mathematical modeling results have demonstrated a good match between the experimental results and the predicted results. Despite the intrinsic limitation of this mathematical model, the modeling results show that the adsorption equilibrium constants obtained by model fitting follow the same trend as their adsorption capacities, suggesting the dominant factor for influencing the adsorption capacity lies in the adsorbate and adsorbent interaction inside a single crystal.
These results provide data that will be critical for the design of natural gas processing equipment using adsorption technology. Most importantly, the model developed in our work and the parameters derived from it may provide meaningful information to researchers in the same field. Future work will study hydrocarbon adsorption in other sorbent materials and will also investigate sorption of mixtures of gases.
Symbol list
| z | is the distance in the flow direction, m |
| t | is time progressing with adsorption, s |
| ε | is the void fraction of the column |
| εp | is macropore porosity in a pellet |
| u | is the gas flow rate, m s−1 |
| V | is the average interstitial velocity in the inter-pellet particle space in the column, u/ε, m s−1 |
| DL | is the longitudinal dispersion coefficient, m2 s−1 |
| DP | is gas diffusivity in pellets, m2 s−1 |
| rp | is the radial distance from the center of a pellet, m |
| rs | is the radial distance from the center of a crystal particle, m |
| Rp | is pellet particle radius, m |
| N0 | is molar flux from fluid to pellet particle in the column, mol m−2s−1 |
| Ni | is the molar gas flux from macroparticle (pellet) to microparticle (crystal), mol m−2s−1 |
| Cp | is the gas concentration in pellets, mol% |
| Cs | is the gas concentration in a crystal, mol% |
| κads | is the adsorption rate constant, s−1 |
| KA | is the adsorption equilibrium constant, KA = κads/κdes, m3 m−3 |
| κf | is the mass transfer coefficient, m s−1. |
Acknowledgements
The authors would like to acknowledge Chevron who, through the Western Australian Energy Research Alliance (WAERA), has supported this work. The authors are also grateful to CSIRO for providing additional financial support and would also like to thank the CSIRO Information Management and Technology for providing Mathematica software and technical support during the course of this work.References
- Z. B. Bao, S. Alnemrat, L. Yu, I. Vasiliev, Q. L. Ren, X. Y. Lu and S. G. Deng, Langmuir, 2011, 27, 13554–13562 CrossRef CAS PubMed.
- A. M. Avila, F. Yang, M. Shi and S. M. Kuznicki, Chem. Eng. Sci., 2011, 66, 2991–2996 CrossRef CAS PubMed.
- M. J. Ahmed, A. Mohammed and A. A. H. Kadhum, Korean J. Chem. Eng., 2011, 27, 1801–1804 CrossRef PubMed.
- M. J. Ahmed, A. Mohammed and A. A. H. Kadhum, Transp. Porous Media, 2011, 86, 245–258 CrossRef.
- R. T. Yang, Adsorbents: Fundamentals and Applications, A John Wiley & Sons, Inc., New Jersey, 2003 Search PubMed.
- E. Brunazzi, A. Paglianti and A. Talamelli, AIChE J., 2003, 49, 41–51 CrossRef CAS.
- E. Van Kemenade, E. Mondt, T. Hendriks and P. Verbeek, Chem. Eng. Technol., 2003, 26, 1176–1183 CrossRef CAS.
- J. C. S. Wu, Z. A. Lin, F. M. Tsai and J. W. Pan, Catal. Today, 2000, 63, 419–426 CrossRef CAS.
- H. MüLler-Steinhagen and Q. Zhao, Chem. Eng. Sci., 1997, 52, 3321–3332 CrossRef.
- T. J. Barton, L. M. Bull, W. G. Klemperer, D. A. Loy, B. Mcenaney, M. Misono, P. A. Monson, G. Pez, G. W. Scherer, J. C. Vartuli and O. M. Yaghi, Chem. Mater., 1999, 11, 2633–2656 CrossRef CAS.
- N. L. Rosi, M. Eddaoudi, J. Kim, M. O'keeffe and O. M. Yaghi, Angew. Chem., Int. Ed., 2002, 41, 284 CrossRef CAS.
- J. L. C. Rowsell and O. M. Yaghi, Microporous Mesoporous Mater., 2004, 73, 3–14 CrossRef CAS PubMed.
- F. N. Ridha, Y. X. Yang and P. A. Webley, Microporous Mesoporous Mater., 2009, 117, 497–507 CrossRef CAS PubMed.
- T. Düren, L. Sarkisov, O. M. Yaghi and R. Q. Snurr, Langmuir, 2004, 20, 2683–2689 CrossRef.
- E. M. Flanigen, J. M. Bennett, R. W. Grose, J. P. Cohen, R. L. Patton, R. M. Kirchner and J. V. Smith, Nature, 1978, 271, 512–516 CrossRef CAS.
- M. A. Uguina, J. L. Sotelo, J. A. Delgado, J. M. Gomez and L. I. Celemin, Sep. Purif. Technol., 2005, 42, 91–99 CrossRef CAS PubMed.
- D. M. Bibby, N. B. Milestone and L. P. aldridge, Nature, 1979, 280, 664–665 CrossRef CAS.
- Y. X. Yang, C. M. Brown, C. X. Zhao, A. L. Chaffee, B. Nick, D. Y. Zhao, P. A. Webley, J. Schalch, J. M. Simmons, Y. Liu, J. H. Her, C. E. Buckley and D. A. Sheppard, Carbon, 2011, 49, 1305–1317 CrossRef CAS PubMed.
- K. Matsuoka, Y. Yamagishi, T. Yamazaki, N. Setoyama, A. Tomita and T. Kyotani, Carbon, 2005, 43, 876–879 CrossRef CAS PubMed.
- J. Shang, G. Li, R. Singh, Q. Gu, K. M. Nairn, T. J. Bastow, N. Medhekar, C. M. Doherty, A. J. Hill, J. Z. Liu and P. A. Webley, J. Am. Chem. Soc., 2012, 134, 19246–19253 CrossRef CAS PubMed.
- V. G. Tsitsishvili and G. T. Andronikashvili, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 217–228 Search PubMed.
- N. N. Avgul, G. A. Bezus and M. O. Dzhigit, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 184–192 Search PubMed.
- M. R. Barrer and J. P. Cram, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 105–131 Search PubMed.
- P. BrÃUer, A. A. Lopatkin and P. H. G. Stepanez, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 97–104 Search PubMed.
- F. Kondis Edward and S. Dranoff Joshua, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 171–183 Search PubMed.
- O. M. Dzhigit, A. V. Kiselev, T. A. Rachmanova and S. P. Zhdanov, J. Chem. Soc., Faraday Trans. 2, 1979, 75, 2662–2677 RSC.
- V. G. Tsitsishvili and G. Andronikashvili, Adv. Chem. Ser., 1971, 217 Search PubMed.
- F. Wolf, F. Danes and K. Pilchowski, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 229–237 Search PubMed.
- M. G. Plaza, A. F. P. Ferreira, J. C. Santos, A. M. Ribeiro, U. Mueller, N. Trukhan, J. M. Loureiro and A. E. Rodrigues, Microporous Mesoporous Mater., 2012, 157, 101–111 CrossRef CAS PubMed.
- P. M. Zimmerman, M. Head-Gordon and A. T. Bell, J. Chem. Theory Comput., 2011, 7, 1695–1703 CrossRef CAS.
- M. Shi, A. M. Avila, F. Yang, T. M. Kuznicki and S. M. Kuznicki, Chem. Eng. Sci., 2011, 66, 2817–2822 CrossRef CAS PubMed.
- H. Leclerc, A. Vimont, J.-C. Lavalley, M. Daturi, A. D. Wiersum, P. L. Llwellyn, P. Horcajada, G. Ferey and C. Serre, PCCP Phys. Chem. Chem. Phys., 2011, 13, 11748–11756 RSC.
- S. Hosseinpour, S. Fatemi, Y. Mortazavi, M. Gholamhoseini and M. T. Ravanchi, Sep. Sci. Technol., 2011, 46, 349–355 CrossRef CAS.
- A. F. P. Ferreira, J. C. Santos, M. G. Plaza, N. Lamia, J. M. Loureiro and A. E. Rodrigues, Chem. Eng. J., 2011, 167, 1–12 CrossRef CAS PubMed.
- C. A. Grande, J. Gascon, F. Kapteijn and A. E. Rodrigues, Chem. Eng. J., 2010, 160, 207–214 CrossRef CAS PubMed.
- C. Peng, Z. Li and X.-m. Sun, J. Zhejiang Univ., Sci., A, 2009, 10, 1636–1641 CrossRef CAS.
- S. E. Siporin, B. C. McClaine and R. J. Davis, Langmuir, 2003, 19, 4707–4713 CrossRef CAS.
- T. H. Yeon, H. S. Han, E. D. Park and J. E. Yie, Microporous Mesoporous Mater., 2009, 119, 349–355 CrossRef CAS PubMed.
- M. Palomino, A. Corma, F. Rey and S. Valencia, Langmuir, 2009, 26, 1910–1917 CrossRef PubMed.
- H. Liu, Z. Zhang, B. H. Chen and Y. Zhao, J. Porous Mater., 2008, 15, 119–125 CrossRef CAS.
- O. Talu, S. Y. Zhang and D. T. Hayhurst, J. Phys. Chem., 1993, 97, 12894–12898 CrossRef CAS.
- R. Harlfinger, D. Hoppach, U. Quaschik and K. Quitzsch, Zeolites, 1983, 3, 123–128 CrossRef CAS.
- P. S. Barcia, J. A. C. Silva and A. E. Rodrigues, Ind. Eng. Chem. Res., 2006, 45, 4316–4328 CrossRef CAS.
- A. Moller, A. P. Guimaraes, R. Glaser and R. Staudt, Microporous Mesoporous Mater., 2009, 125, 23–29 CrossRef PubMed.
- N. Lamia, M. A. Granato, P. S. A. Gomes, C. A. Grande, L. Wolff, P. Leflaive, D. Leinekugel-le-Cocq and A. E. Rodrigues, Sep. Sci. Technol., 2009, 44, 1485–1509 CrossRef CAS.
- W. T. Lim, S. Y. Choi, J. H. Choi, Y. H. Kim, N. H. Heo and K. Seff, Microporous Mesoporous Mater., 2006, 92, 234–242 CrossRef CAS PubMed.
- T. Y. Lee, T. S. Lu, S. H. Chen and K. J. Chao, Ind. Eng. Chem. Res., 1990, 29, 2024–2027 CrossRef CAS.
- S. H. Chen, K. J. Chao and T. Y. Lee, Ind. Eng. Chem. Res., 1990, 29, 2020–2023 CrossRef CAS.
- A. Rasmuson, Chem. Eng. Sci., 1985, 40, 1115–1122 CrossRef CAS.
- H. Stehfest, Commun. ACM, 1970, 13, 47–49 CrossRef.
- H. Villinger, Geophysics, 1985, 50, 1581–1587 CrossRef PubMed.
- J. M. Lee, S. M. Seo, J. M. Suh and W. T. Lim, J. Porous Mater., 2011, 18, 523–534 CrossRef CAS.
- J. Xu, B. L. Mojet and L. Lefferts, Microporous Mesoporous Mater., 2006, 91, 187–195 CrossRef CAS PubMed.
- M. M. Dubinin and A. V. Astakhov, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 69–85 Search PubMed.
- V. A. Kiselev, in Molecular Sieve Zeolites-II, American Chemical Society, 1971, vol. 102, pp. 37–68 Search PubMed.
- D. H. Olson, J. Phys. Chem., 1970, 74, 2758–2764 CrossRef CAS.
- E. Dempsey, Molecular sieves, Society of the Chemical Industry, London, 1968 Search PubMed.
| This journal is © The Royal Society of Chemistry 2014 |