The electronic structure of a graphene quantum dot: electric field-induced evolution in two subspaces
Qing-Rui Dong*
College of Physics and Electronics, Shandong Normal University, Jinan, Shandong 250014, People's Republic of China. E-mail: qrdong@semi.ac.cn
First published on 14th January 2014
Abstract
The tight-binding method is employed to investigate the effects of three typical in-plane electric fields on the electronic structure of a triangular zigzag graphene quantum dot. The calculation shows that the single-electron eigenstates evolute independently in two subspaces no matter how the electric fields change. The electric field with fixed-geometry gates chooses several scattered parts of the zero-energy eigenspace as the new zero-energy eigenstates, regardless of the field strength. Moreover, the new zero-energy eigenstates remain unchanged and the associated levels are linear with the field strength. In contrast, the new nonzero-energy eigenstates mix mutually and the associated levels are nonlinear with the field strength. By comparing the effects of three electric fields, we demonstrate that the degeneracy of the zero-energy eigenstates accounts for the linearity of the associated levels.
1 Introduction
Graphene has attracted enormous interest both in theory and in experiments, due to its exceptional electronic properties1 and great application potential in next-generation electronics.2 However, a gap has to be induced in gapless graphene for real applications in electronic devices.3,4 For this purpose, graphene quantum dots have been proposed as one of the most promising kinds of graphene nanostructures.5 With recent developments in fabrication techniques, it is possible to accurately cut the bulk graphene into different sizes and shapes, such as hexagonal zigzag quantum dots, hexagonal armchair quantum dots, triangular zigzag quantum dots and triangular armchair quantum dots.6The electronic and magnetic properties of graphene quantum dots depend strongly on their shapes and edges.7–9 Moreover, for zigzag graphene quantum dots, especially triangular dots, there appears a shell of degenerate states at the Dirac points and the degeneracy is proportional to the edge size. This unique property of triangular zigzag quantum dots makes them potential components of superstructures acting as single-molecule spintronic devices.10 The electronic structure and total spin of triangular zigzag quantum dots can be tuned by changing a uniform electric field.11,12 Non-uniform electric fields can provide an equal electrostatic potential for the edges of triangular zigzag quantum dots, which allows electrical linear control of the low-energy states.13 The magnetization of triangular graphene quantum dots with zigzag edges also can be manipulated optically.14 In particular, the electrical manipulation of the degenerate zero-energy states of such graphene quantum dots is quite important for the operation of related spintronic devices, since it is easier to generate a potential field through local gate electrodes than an optical or magnetic field.6 So, it is interesting to understand comprehensively the electric field-induced evolution of the electronic structure in graphene quantum dots.
In this paper, we investigated the effects of three typical in-plane electric fields on the low-energy electronic structures of a triangular zigzag graphene quantum dot. The calculations are mainly based on the tight-binding Hamiltonian with the nearest-neighbor approximation, which proves to give the same accuracy in the low-energy range as first-principle calculations.15 Our result shows that the single-electron eigenstates evolute independently in two subspaces, no matter how the electric fields change, which may be useful for the application of graphene quantum dots in electronic and photovoltaic devices.
2 The tight-binding model
The low-energy electrical structure of a graphene quantum dot subjected to an in-plane electric field can be calculated by means of the tight-binding method. The Hamiltonian equation of the system is H|Φ(r)〉 = E|Φ(r)〉 and the tight-binding Hamiltonian with the nearest-neighbor approximation is11,16
 | (1) |
The tight-binding Bloch function can be expressed as a linear superposition
 | (2) |
Usually an electric field is generated by the gates with a fixed geometry and hence Un is proportional to the gate voltage (or the voltage difference) U:
| Un = kUXn, | (3) |
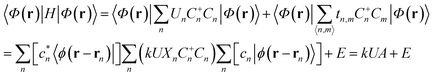 | (4) |
 is a constant and E is the associated level at U = 0. Eqn (4) means that the associated level is linear with U when the eigenstate remains unchanged. If the level is not degenerate, the converse is also true: the eigenstate remains unchanged when the associated level is linear with U. If the level is degenerate, the linearity of the level means that the associated eigenspace is unchanged. So, if the level is not linear with U, the associated eigenstate or eigenspace would change.
is a constant and E is the associated level at U = 0. Eqn (4) means that the associated level is linear with U when the eigenstate remains unchanged. If the level is not degenerate, the converse is also true: the eigenstate remains unchanged when the associated level is linear with U. If the level is degenerate, the linearity of the level means that the associated eigenspace is unchanged. So, if the level is not linear with U, the associated eigenstate or eigenspace would change.
3 The electric fields and the low-energy electronic structures
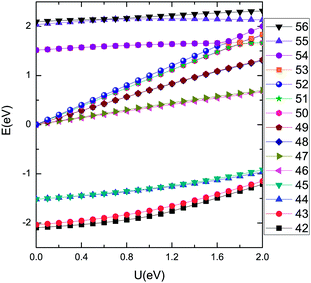
The geometrical structure of a triangular zigzag graphene quantum dot is shown in Fig. 1(a). The number of carbon atoms on each side of the quantum dot is Ns = 8. The low-energy spectrum of the graphene quantum dot in the absence of an electric field is shown in Fig. 1(b), where the lowest fifteen eigenstates are presented and numbered from (42) to (56). The seven orthonormal zero-energy eigenstates (46–52) are degenerate and span a 7-dimensional eigenspace denoted by V1. Other nonzero-energy eigenstates span the orthogonal complement space denoted by V2. The nonzero-energy orthonormal eigenstates (44, 45) as well as the eigenstates (53, 54) are degenerate and span respectively a two-dimensional eigenspace in V2.3.1 In a non-uniform electric field
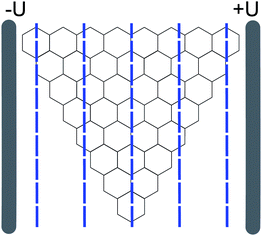
The electric field shown in Fig. 2 possesses the same C3 rotation symmetry as the graphene quantum dot. Moreover, the electric field can provide an equal electrostatic potential for all edge atoms, which is considered to account for the electrical linear control of the zero-energy states.13 The designed gates work in a similar way, as a lateral gated quantum dot is created at a semiconductor heterojunction containing a two-dimensional electron gas.Fig. 3 shows the low-energy spectrum of the graphene quantum dot (Ns = 8) subjected to the electric field. Since the electrostatic potential does not possess a translational symmetry, the zero-energy eigenspace changes from the 7-dimensional subspace V1 into several scattered parts, including one nondegenerate eigenstate (52), two two-dimensional eigenspaces (50, 51) and (48, 49), and one quasi-degenerate eigenspace (46, 47). With increasing U, the seven levels vary linearly, which implies that the associated eigenstates or eigenspaces do not change significantly according to eqn (4). For a nondegenerate eigenstate, its stability can be shown by the corresponding probability density. Fig. 4(a) shows the probability density of eigenstate (52), which indicates that it remains unchanged. Obviously, the electric field, or rather the gate geometry, chooses several scattered parts of the subspace V1 as the new zero-energy eigenstates and then these scattered parts remain unchanged, regardless of the field strength. Hence, the zero-energy eigenstates can be considered to always evolute in V1 with increasing U. The level of the quasi-degenerate eigenspace (46, 47) remains linear on the whole, which implies that the quasi-degenerate eigenspace does not change significantly. If the energy difference between the eigenstates (46) and (47) cannot be neglected, the degenerate eigenspace (46, 47) disappears and the linearity is not perfect. The imperfect linearity implies that the eigenstates (46) and (47) change slightly. The probability density of eigenstate (46) changes slightly (see Fig. 4(b)) and this characteristic can also be seen in the probability density of eigenstate (47). Due to the orthogonality, the eigenstates (46) and (47) can be considered to interact slightly with increasing U, since the other zero-energy eigenstates remain unchanged.
 | ||
| Fig. 3 The low-energy spectra of graphene quantum dot (Ns = 8) subjected to the non-uniform electric field shown in Fig. 2. The eigenstate indexes correspond to those in Fig. 1(b). | ||
 | ||
| Fig. 4 The density of three nondegenerate eigenstates. (a)–(c) correspond to eigenstates (52), (46) and (43) shown in Fig. 3, respectively. | ||
In contrast, the nonzero-energy levels are generally nonlinear with increasing U, which implies that the associated eigenstates or eigenspaces change. As a typical example, the probability density of eigenstate (43) shows that it changes significantly with increasing U (see Fig. 4(c)). Because of the orthogonality, the eigenstates in V1 are perpendicular to the subspace V2 and remain unchanged, which implies that the nonzero-energy eigenstates can be considered to always evolute in V2 with increasing U. In view of the completeness, the eigenstates in V2 can be considered to mix mutually as U increases. At U of about 1.6 eV, some anti-crossings appear and the dependence of related levels in V1 is not linear, which does not agree with eqn (4). This disagreement can be explained by the applicability of the tight-binding method. The tight-binding model as an approximation method requires that the electrostatic potential is a perturbation. When U is larger than about 1.6 eV, the basis vectors |ϕ(r − rn)〉 cannot keep the calculation convergent.
As U increases from 0 to about 1.6 eV, the eigenstates in V1 remain unchanged while the eigenstates in V2 mix mutually. The degeneracy of the zero-energy eigenstates allows enough eigenstates in V1 to meet the requirement of the gate geometry while the electric field lowers the symmetry level of the system. When U is lower than about 1.6 eV, the electrostatic potential can be considered as a perturbation and does not change the eigenstates in V1 significantly, though the corresponding levels vary directly with U. Therefore, it may be a reasonable assumption that the degeneracy of the zero-energy eigenstates accounts for the linearity of the levels in V1. Moreover, it will be shown in the following section that all two-dimensional eigenspaces disappear when the electric field loses C3 symmetry.
3.2 In a uniform electric field
If it is true that the degeneracy of the zero-energy eigenstates accounts for the linearity of the levels, a uniform electric field, always considered not to lead to linearity,12 also can do this. In order to prove this viewpoint, a uniform electric field is presented in Fig. 5, which does not possess C3 symmetry and cannot provide an equal potential for all edge atoms. Moreover, the low-energy spectrum of the graphene quantum dot subjected to this electric field is shown in Fig. 6. | ||
| Fig. 6 The low-energy spectra of the graphene quantum dot (Ns = 8) subjected to the uniform electric field shown in Fig. 5. The eigenstate indexes correspond to those in Fig. 1(b). | ||
Since the electric field leads to a lower level of symmetry than the electric field shown in Fig. 2, the zero-energy eigenspace changes from the 7-dimensional subspace V1 into seven nondegenerate eigenstates. As U increases, the seven associated levels vary linearly, which implies that each zero-energy eigenstate does not change significantly. When U is lower than about 1.6 eV, the calculation is convergent. As a typical example, the probability density of eigenstate (49) is shown in Fig. 7(a), which indicates that it remains unchanged. The other six eigenstates also remain unchanged, which can be seen in the corresponding probability density. Obviously, the seven nondegenerate eigenstates are chosen from the 7-dimensional subspace V1 by the gate geometry and then remain unchanged, regardless of the field strength. This also proves that the degeneracy of the zero-energy eigenstates should account for the linearity of the levels. Without two-dimensional eigenspaces due to the symmetry of the electric field, the interaction between quasi-degenerate eigenstates also does not occur and hence the linearity is more perfect.
 | ||
| Fig. 7 The density of two nondegenerate eigenstates. (a) and (b) correspond to eigenstates (49) and (53) in Fig. 6, respectively. | ||
All nonzero-energy levels are nonlinear, which implies that the associated eigenstates change. As a typical example, the probability density of eigenstate (53) indicates that it changes significantly with increasing U (see Fig. 7(b)). According to the previous analysis, the nonzero-energy eigenstates mix mutually in V2 as U increases.
3.3 In an electric field with a random potential distribution
Since the degeneracy of the zero-energy eigenstates accounts for the linearity of the levels, one can make some predictions on the electric field with arbitrary fixed-geometry gates. The electric field should choose seven nondegenerate eigenstates as the new zero-energy eigenstates, according to the gate geometry, if the arbitrary electric field possesses a lower level of symmetry. Moreover, the electric field, as well as the two electric fields mentioned previously, should keep the new zero-energy eigenstates unchanged in V1 while the new nonzero-energy eigenstates mix mutually in V2.In order to verify these predictions, an imaginary electric field is presented in Fig. 8, which randomly receives an imaginary potential distribution. The low-energy spectrum of a triangular zigzag graphene quantum dot (Ns = 8) subjected to this electric field is shown in Fig. 9. As U increases, the levels of the seven zero-energy eigenstates vary linearly and all levels of the nonzero-energy eigenstates vary nonlinearly, which implies that the effect of the electric field agrees with the above predictions. When U is lower than about 1.4 eV, the calculation is convergent. As a typical example, the probability densities of eigenstates (49) and (53) are shown in Fig. 10. Moreover, the zero-energy levels and the spaces between the levels are dependent on the random potential, which implies that it is more effective to modulate the zero-energy eigenstates by changing the gate geometry.
 | ||
| Fig. 9 The low-energy spectra of the graphene quantum dot (Ns = 8) subjected to the imaginary electric field shown in Fig. 8. The eigenstate indexes correspond to those in Fig. 1(b). | ||
 | ||
| Fig. 10 The density of two nondegenerate eigenstates. (a) and (b) correspond to eigenstates (49) and (53) in Fig. 9, respectively. | ||
3.4 In an arbitrarily changing electric field
If the gate geometry changes, for example, from the electric field in Fig. 2 to the electric field in Fig. 5 and then to the electric field in Fig. 8, the zero-energy eigenstates will also change. However, the evolution of the zero-energy eigenstates is confined to V1 since the zero-energy eigenstates for any gate geometry are chosen from V1. Moreover, the evolution of the nonzero-energy eigenstates is confined to V2 by reason of the orthogonality. That is to say, no matter how the gate geometry and voltage change, the eigenstates evolute independently in the two subspaces V1 and V2.4 Summary
In summary, we investigated the effects of three typical in-plane electric fields on the electronic structure of a triangular zigzag graphene quantum dot. When the electric field is not too strong, the calculation based on the tight-binding model is convergent. The results show that no matter how the electric fields change, the single-electron eigenstates evolute independently in two subspaces V1 and V2. The electric field with fixed-geometry gates chooses several scattered parts of the subspace V1 as the new zero-energy eigenstates. Moreover, the eigenstates in V1 remain unchanged and the associated levels are linear with U due to the degeneracy of the zero-energy eigenstates. In contrast, the eigenstates in V2 mix mutually and the associated levels are nonlinear with U. Two-dimensional eigenspaces can be removed by lowering the symmetry level of the electric field, which helps to keep the zero-energy eigenstates unchanged and to keep the associated levels linear with the field strength. The calculation implies that it is more effective to modulate the zero-energy eigenstates by changing the gate geometry. Our results provide insight into the electric field-induced evolution of electronic states in a graphene quantum dot and may be useful for the application of graphene quantum dots in electronic and photovoltaic devices.Acknowledgements
This work was supported by the Shandong Provincial Natural Science Foundation, China (ZR2013AM010) and the National Natural Science Foundation of China under grant no. 11274205.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- Y. Q. Wu, Y. M. Lin, A. A. Bol, K. A. Jenkins, F. Xia, D. B. Farmer, Y. Zhu and P. Avouris, Nature, 2011, 74, 472 Search PubMed.
- T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Science, 2006, 313, 951 CrossRef CAS PubMed.
- S. Y. Zhou, G.-H. Gweon, A. V. Fedorov, P. N. First, W. A. de Heer, D. Lee, F. Guinea, A. H. C. Neto and A. Lanzara, Nat. Mater., 2007, 6, 770 CrossRef CAS PubMed.
- K. A. Ritter and J. W. Lyding, Nat. Mater., 2009, 8, 235 CrossRef CAS PubMed.
- M. Zarenia, A. Chaves, G. A. Farias and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245403 CrossRef.
- M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245415 CrossRef.
- A. D. Güclü, P. Potasz, O. Voznyy, M. Korkusinski and P. Hawrylak, Phys. Rev. Lett., 2009, 103, 246805 CrossRef.
- P. Potasz, A. D. Güclü, A. Wójs and P. Hawrylak, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075431 CrossRef.
- W. L. Wang, O. V. Yazyev, S. Meng and E. Kaxiras, Phys. Rev. Lett., 2009, 102, 157201 CrossRef.
- R. B. Chen, C. P. Chang and M. F. Lin, Phys. E., 2010, 42, 2812 CrossRef CAS PubMed.
- W. L. Ma and S. S. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045449 CrossRef.
- Q. R. Dong, J. Appl. Phys., 2013, 113, 234304 CrossRef PubMed.
- A. D. Güclü and P. Hawrylak, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035425 CrossRef.
- D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Adv. Phys., 2010, 59, 261 CrossRef CAS.
- W. L. Ma and S. S. Li, Appl. Phys. Lett., 2012, 100, 163109 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2014 |