Optically controlled circling of particles with a particle-decorated fiber probe†
Xiaoshuai Liu,
Jianbin Huang,
Hongbao Xin,
Yao Zhang and
Baojun Li*
State Key Laboratory of Optoelectronic Materials and Technologies, School of Physics and Engineering, Sun Yat-Sen University, Guangzhou, 510275, People's Republic of China. E-mail: stslbj@outlook.com; Fax: +86-20-8411 2260; Tel: +86-20-8411 0200
First published on 10th January 2014
Abstract
With the assistance of a particle-decorated fiber probe, optically controlled circling of particles was demonstrated using 3.14 μm diameter silica particles. The method is based on the temperature gradient and thermal convection when a laser beam of 980 nm (power: 108 mW) is injected into the fibre. Specific currents were created by decorating the tip of the drawn fibre probe with specific geometries of silica particles (diameter: 3.14 μm). Thus, the water was being circulated (convective flow driven by heating), and the particles were drowned into the flow. They were circled anticlockwise along a relatively steady trajectory with a period varying from 3 to 7 s. Once the laser switched off, the particles were immediately stopped. Further experiments show that the circular trajectory can be shifted by moving the fiber probe.
Introduction
The ability to circle particles offers a new degree of control for microobjects, which enables many innovative studies in the fields of rotating motor1–3 and microfluidic pump.4–7 Various schemes have, therefore, been investigated recently to induce circulation of trapped particles. Proposed techniques were based on a magnetic field,8,9 electric field,10 optical forces11,12 and the transfer of orbital angular momentum.13–16 However, these schemes usually employed elaborate magnetrons/electrodes, complex holographic systems, planar waveguide structures or diffraction grating components. Moreover, these methods have requirements for the particles in terms of magnetic susceptibility, electrical conductivity, optical transparency and refractive index, which limit the circling operation to specific particles. As a candidate for manipulating particles, fiber probes have advantages of very small size and ease in fabrication. Therefore, it is expected that particle circling can be realized by using a fiber probe. In this work, we demonstrate an optically controlled particle circling using a particle-decorated fiber probe. The technique is based on temperature gradient and thermal convection induced by the laser beam outputted from the fiber probe, so that it reduces the dependence on the particle physical properties. The organization of the paper is as follows: first, a theoretical analysis is performed to show the influence of decorating particles on the circular motion. Second, experiments were carried out with silica particles (3.14 μm in diameter) by injecting a 980 nm laser into the particle-decorated fiber probe. Finally, the circling stiffness and circling of multiple particles were investigated.Theoretical analysis
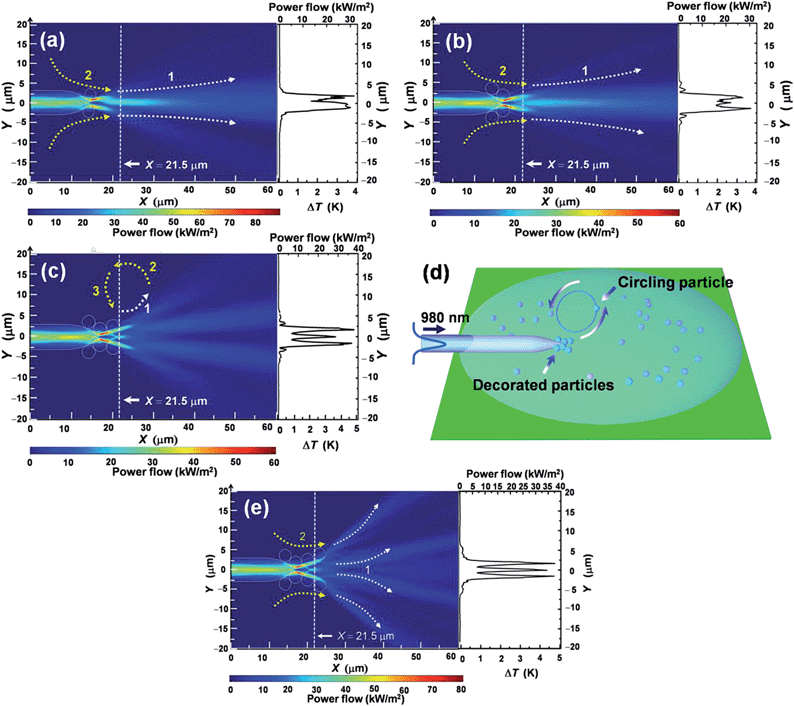
To analyze the mechanism of circling particles using a fiber probe, the power flow distribution of outputted laser from the fiber probe was obtained by a two-dimensional finite element simulation (COMSOL Multiphysics 4.3), as shown in Fig. 1a. The diameter of fiber probe is set to be 6 μm with a parabolic profile. To generate an adequate temperature gradient in water and to avoid thermal damage to biomedical environment, the 980 nm wavelength was used and the laser power should be ranging from 90 to 120 mW. In the simulations, the power of the 980 nm laser was set to be 108 mW which is consistent with the power applied in later experiments. The refractive indices of the silica fiber and water were set to be 1.44 and 1.33, respectively. From Fig. 1a, it can be seen that the laser beam was focused at the end of the bare probe. The upper right inset of Fig. 1a shows the power flow distribution along x direction at y = 0 μm. The focal plane (with the highest light intensity) is at x = 21.5 μm (i.e. 6 μm to the probe end). The right panel shows the power flow at the focal plane (at x = 21.5 μm) in y direction. It can be seen that over 90% power flow distributes within the region from y = −1 to 1 μm. Temperature gradient generated by the light absorption of water can be approximated to be:17| ΔT = ηSτ/(cρd) | (1) |
| F = (n/c)∫∫ΔSdA | (2) |
Since the particle motion depends on the temperature gradient and thermal convection, particle circling can be realized by changing the power flow distribution in water. The most effective and convenient method is to decorate some particles on the probe to change the optical filed distribution at the probe end. By doing so, the temperature gradient in water will be changed and a convection flow will be caused, which drives the other suspended particles near the probe to move along the trajectory of flow. We chose silica particles to decorate the probe because they have same refractive index with the fiber probe so that the reflection loss between the probe and the particles can be weakened. As shown in Fig. 2, the white and yellow dashed arrows indicate the water flow induced by temperature gradient and thermal convection, respectively. The right panel of each graph shows the power flow distribution along y direction at x = 21.5 μm. It should be noted that to provide a stable motion for particles, the optical power flow distribution in water should be symmetric to avoid extra water flow caused by the asymmetric temperature distributions around the probe. Since the fiber probe and the injected laser beam are all axially symmetric, the optical power flow distribution symmetry can be realized by decorating the particles in the same amount on each side of the probe. Therefore, the number of silica particles decorated on the probe should be even. If two particles are decorated at the probe end (Fig. 2a), the power flow is mainly along x direction. The water will flow along the same direction because of the very slight change of the temperature gradient. When four particles are decorated (Fig. 2b), the power flow begin to spread but the change of the temperature gradient is still not enough to cause a circular flow. Thus, when only two or four particles decorated to the fiber probe, the power flow distribution do not change efficiently and the particle will be pushed away along the fiber probe. While if eight particles attached (Fig. 2e), the power flow would be further diverged. Then the flow trajectory will become more complex and uncontrollable, which was consistent with the experiment result. Moreover, the increasing particles will absorb the outputted laser and weaken the optical field distribution in water, which prevented the generation of convection flow. When six particles are decorated as shown in the right panel of Fig. 2c, three peaks appear near the probe end and over 90% power flow is focused within the region from y = −6 to 6 μm. According to the eqn (1), the temperature gradient is along the direction of power flow with a maximum value of 4.7 K μm−1. The water will flow along the changed direction (as shown by the white dashed arrow 1 in Fig. 2c). Meanwhile, due to the liquid continuity, the water will flow toward the heated location (as shown by the yellow dashed arrows 2 and 3 in Fig. 2c). As a result, the particles will be moved along the flow direction and be circled above the fiber probe as schematically described in the Fig. 2d.
Experiment
To verify above theoretical analysis, experiments were carried out using the 980 nm laser with a power of 108 mW. Fig. 3a depicts the experimental setup built around an optical microscope with a charged coupled device (CCD) camera for real-time monitoring. To achieve fine positioning and mechanical stability, a glass slide was mounted on a manual translation stage. A fiber probe with a parabolic profile was drawn from a commercial single-mode fiber by the flame-heating technique. The probe diameter is 6 μm and the length of tapered region is 9.6 μm (Fig. 3b). The radius of curvature of the probe is 0.8 μm. After sheathed with a glass capillary and fixed on a microstage, the probe was immersed in a droplet of silica particle solution on the glass slide. The solution was prepared by diluting 3.14 μm silica particles into deionized water with an ultrasonic treatment for 8 minutes.As mentioned with the theoretical analysis, the decorated particle affected the light field distribution and hence the location of circling. Thus, it was very important to realize the particles being decorated correctly. However, it was indeed a big challenge to efficiently control the number and location of decorated particles. After analyzing and trying some methods, we realized it with the following process: firstly the particle density in solution needs to be controlled accurately. The fiber probe was decorated by attaching the particle one by one. So if the particle density is too high, it will be hard to realize single particle decorated. Then we tried different kinds of particle density and chose the 5 × 107 # per mL as the optimal choice. After the particle solution was prepared, the fiber probe was positioned on the six-axis microstage (resolution: 50 nm) and being adjusted to approach one particle. Then the laser was turned on (power: 70 mW), and the particle was moving toward the fiber probe because of the optical force.21 When the particle touched the fiber probe, the laser was turned off and the particle was attached to the fiber probe under the action of Van der Waals' force. Thus, the first particle was decorated to the fiber probe successfully. Then the fiber probe was adjusted by the microstage to approach the other particle. The decorated location can be changed by adjusting the fiber probe with the microstage. Similarly, the other five particles were successfully decorated to the fiber probe as schematically shown in Fig. 3c.
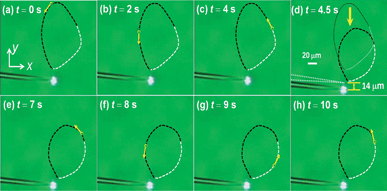
After decorating particles to the fiber probe, particle circling was performed by tuning the 980 nm laser power to 108 mW. Fig. 4 shows the circling of a particle above the six-particle-decorated fiber probe with a circling period of 7 s. The yellow arrows show the moving direction. The white and black dashed curves indicate the circular motion induced by temperature gradient and thermal convection, respectively. It can be seen that the particle was circled above the probe anticlockwise. Detailed process is shown in Movie S1 of the ESI.† Fig. 5 shows the velocity of circling particle. It can be seen that the velocity increases firstly and then decreases. According to the analysis presented in the previous section, the particle circling is mainly driven by the temperature gradient force. Thus, the velocity increases rapidly at the nearest location of circling trajectory to the probe because of the largest temperature gradient. When the particle moves away from the probe, the velocity decreases gradually due to the liquid resistance as well as the decrease of temperature gradient. It should be clarified that the particle circling period varies from 3 to 7 s, which is due to the change of circling trajectory and temperature gradient in water. During the experiment, the water evaporation decreased the effective thickness of solution (d). With the experiment time of 0, 20 and 40 minutes, the values of d are 0.4, 0.35 and 0.3 mm, respectively. According to the eqn (1), the temperature gradient in water became larger so that the particle circling velocity also increased with maximum values of 171, 213 and 239 μm s−1 (the black, red and blue curves in Fig. 5). As a result, the circling periods also changed to 7, 6 and 5 s, respectively.
 | ||
| Fig. 4 Optical microscopic images for the particle circling at different moments in a circling period of 7 s. | ||
 | ||
| Fig. 5 Velocity of particle with the solution effective thickness (d) of 0.4, 0.35 and 0.3 mm. The circling periods were 7, 6 and 5 s, respectively. | ||
To verify that the circling is induced by the outputted beam from the fiber probe, the laser was switched off for 5 s and then turned on again. The particle trajectory and velocity of this process are shown in Fig. 6 and 7, respectively. Firstly, the particle was circled anticlockwise above the fiber probe with a period of 5 s (Fig. 6a–c). At t = 5 s, the laser was switched off. The particle stopped circling immediately and oscillated slightly around the stopped location (Fig. 6d and e) due to the surrounding fluctuations. Turning on the laser at t = 10 s, the particle began to circle again (Fig. 6f–h). Detailed process is shown in Movie S2 of the ESI.† This result indicates that the particle can be positioned at different locations by turning off the laser. Moreover, the particle circling trajectory and velocity nearly keep constant before switching off the laser and after turning on the laser again (Fig. 7).
 | ||
| Fig. 7 Velocity of the particle before switching off the laser (the blue curve) and after turning on the laser again (the red curve). | ||
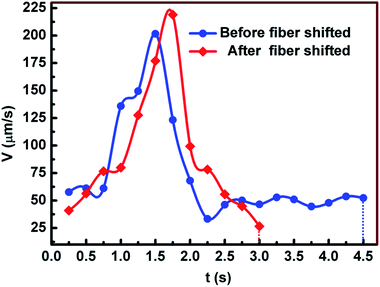
To investigate the stiffness of circling, the fiber probe was shifted by tuning the microstage. The particle motion trajectory and circling velocity are shown in Fig. 8 and 9, respectively. It can be seen from Fig. 8 that the particle was circled above the fiber probe anticlockwise with a period of about 4.5 s. At t = 4.5 s, the fiber probe was shifted along the −y direction with a distance of 14 μm. The particle was also moved with the shift of the fiber while keeping circling above the probe (Fig. 8d). Fig. 9 shows the velocities of the circling particle before and after fiber shifted. In addition, it was also found that multiple particles can be circled above the fiber probe simultaneously. Fig. 10 shows that seven particles were circled above the probe within a period of about 5 s. The maximum and minimum velocities of the seven particles are measured and shown in Fig. 11. Detailed process is shown in Movie S3 of the ESI.† It can be seen that although the trajectories of seven particles are slightly different from each other, the maximum and minimum velocities exhibit a uniformity.
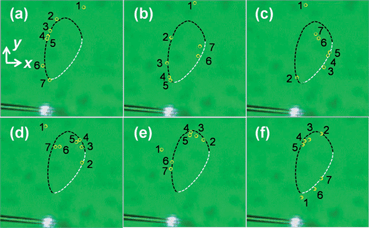 | ||
| Fig. 10 Optical microscopic images for seven particles circling. The yellow circles indicate the particle location. (a) t = 0 s. (b) t = 1 s. (c) t = 2 s. (d) t = 3 s. (e) t = 4 s. (f) t = 5 s. | ||
Conclusion
An optical method was demonstrated for realizing particle circling in water with a particle-decorated fiber probe. By launching a 980 nm laser of 108 mW into the fiber probe, temperature gradient and thermal convection were generated to drive the particle circling above the fiber probe. Once the laser was switched, the circling particle will be stopped immediately. With the shift of fiber probe, the particle kept circling above the fiber probe while the circling trajectory was also shifted along the same direction. Moreover, multiple particles can be circled around the fiber probe simultaneously. Since the circling is due to the temperature gradient and thermal convection, then this technique can be used in the micro-rotors or micro-pumps to realize the actuation of the micro flow and the circulation of the micro-objects.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant no. 61007038, 11274395, and 61205165) and Guangdong Natural Science Foundation (Grant no. S2012010010061).Notes and references
- J. E. Curtis and D. G. Grier, Phys. Rev. Lett., 2003, 90, 133901 CrossRef.
- P. Lenz, J.-F. Joanny, F. Jülicher and J. Prost, Phys. Rev. Lett., 2003, 91, 108104 CrossRef.
- J. Xavier, R. Dasgupta, S. Ahlawat, J. Joseph and P. K. Gupta, Appl. Phys. Lett., 2012, 100, 121101 Search PubMed.
- J. Leach, H. Mushfique, R. D. Leonardo, M. Padgett and J. Cooper, Lab Chip, 2006, 6, 735 RSC.
- K. Ladavac and D. Grier, Opt. Express, 2004, 12, 1144 CrossRef.
- M. Padgett and R. Bowman, Nat. Photonics, 2011, 5, 343 CrossRef CAS.
- A. Terray, J. Oakey and D. W. M. Marr, Science, 2002, 296, 1841 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862 CrossRef CAS PubMed.
- A. Ghosh and P. Fischer, Nano Lett., 2009, 9, 2243 CrossRef CAS PubMed.
- J. S. Kwon, S. P. Ravindranath, A. Kumar, J. Irudayaraj and S. T. Wereley, Lab Chip, 2012, 12, 4955 RSC.
- M. Reichert and H. Stark, J. Phys.: Condens. Matter, 2004, 16, 4085 CrossRef.
- S. Y. Lin, E. Schonbrun and K. Crozier, Nano Lett., 2010, 10, 2408 CrossRef CAS PubMed.
- H. He, M. E. J. Friese, N. R. Heckenberg and H. Rubinstein-Dunlop, Phys. Rev. Lett., 1995, 75, 826 CrossRef CAS.
- A. J. Wright, J. M. Girkin, G. M. Gibson, J. Leach and M. J. Padgett, Opt. Express, 2008, 16, 9495 CrossRef.
- V. Garcés-Chávez, D. McGloin, M. J. Padgett, W. Dultz, H. Schmitzer and K. Dholakia, Phys. Rev. Lett., 2003, 91, 093602 CrossRef.
- A. T. O'Neil, I. MacVicar, L. Allen and M. J. Padgett, Phys. Rev. Lett., 2002, 88, 053601 CrossRef CAS.
- H. B. Xin, H. X. Lei, Y. Zhang, X. M. Li and B. J. Li, Opt. Express, 2011, 19, 2711 CrossRef CAS PubMed.
- K. F. Palmer and D. Williams, J. Opt. Soc. Am., 1974, 64, 1107 CrossRef CAS.
- D. W. James, J. Mater. Sci., 1968, 3, 540 CrossRef.
- D. W. Zhang, X. C. Yuan, S. C. Tjin and S. Krishnan, Opt. Express, 2004, 12, 2220 CrossRef.
- H. B. Xin, R. Xu and B. J. Li, Sci. Rep., 2012, 2, 818 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Video clips (Movies S1, S2, and S3) for detailed processes of particle circling. See DOI: 10.1039/c3ra46822d |
| This journal is © The Royal Society of Chemistry 2014 |