Effect of polyhedral oligomeric silsesquioxane (POSS) on crystallization behaviors of POSS/polydimethylsiloxane rubber nanocomposites

Abstract

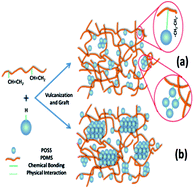
A series of heptaphenylhydrogensilsesquioxane/polydimethylsiloxane (POSS/PDMS) nanocomposites are prepared through grafting and blending. Subsequently, the melting and isothermal crystallization behaviors of the POSS/PDMS nanocomposites are investigated by differential scanning calorimetery (DSC). There is an evident fluctuation in melting temperature though the melting curves of the nanocomposites show similar crystallinities to PDMS. The results indicate that the crystallization rate of the nanocomposites increases with the addition of POSS before POSS loading reaches 3 wt%, but it decreases with further addition of POSS. The maximum crystallization rate of the nanocomposites even achieves more than 2.5 times that of neat PDMS. According to X-ray diffraction (XRD) and scanning electron microscopy (SEM) results, uniformly dispersed POSS is more efficient in behaving as a nucleating agent, while the large agglomerates of POSS tend to crystallize by themselves, whose crystal regions restrict the PDMS chain segments from forming ordered structures. When POSS crystallites are larger than 31.5 nm, the orientation of PDMS chain segments can be significantly depressed.

---

1. Introduction

Polyhedral oligomeric silsesquioxane (POSS), whose molecule has an inorganic and silica-like core surrounded by organic groups, can be considered as the smallest silica particle. Since POSS molecules contain organic substituents on their outer surfaces, they have good compatibility with most polymers.^1–6 To name a few, POSS has been incorporated into polyethylene,⁷ polybutadiene,⁸ norbornyl,^7,9,10 polypropylene,^11,12 polyvinylchloride,^13,14 polystyrene,¹⁵ poly(acrylate),^16,17 polyester,¹⁸ polyamide,¹⁹ polyimide,²⁰ epoxy,²¹etc.

According to types and numbers of functional groups in a POSS molecule, POSS can be incorporated into polymers in four ways:^22,23 (1) POSS containing no reactive group can only be physically blended with the polymer; (2) POSS with one reactive group can be bonded to the backbone of the polymer acting as side chains or endcaps; (3) POSS possessing two reactive groups are able to be bonded into the main chain of the polymer and form a bead-like structure; (4) POSS owning more than two reactive groups can provide cross-linking point for the polymerization.

When POSS is incorporated into polymers, various properties of the resulting composites are expected to be modified, such as thermostability, mechanical property, flame resistance, electric insulativity,²⁴ thermal–mechanical property, shape memory property²⁵ and so on. On the one hand, the modification effect intimately depends upon the incorporation method. In general, physical blending samples from method (1) have more prominent phase separation, but as described in methods (2), (3) and (4), better compatibility can be achieved through grafting, blocking and cross-linking. On the other hand, the modification effect relies on the compatibility of POSS and polymer. For example, Patel et al.²⁶ observed a significant increase in the glass transition temperature (T_g) of the phenyl-substituted POSS/PS copolymer compared with that of alkyl-substituted copolymer, which was partly because of the better miscibility between phenyl rings in POSS and PS.

The aggregation state of POSS and its influence on polymer are very complex, especially in the case of crystalline polymer matrix. Hsiao et al.¹² reported that iPP–POSS samples with different POSS loadings exhibited faster crystallization rates than that of the neat iPP. They deemed that POSS crystals were effective nucleating agents for iPP, whereas dispersed POSS molecules retarded the mobility of iPP molecular chains and thereby decreased crystal growth ability. Nevertheless, an opposite conclusion on high-density PE/octamethyl-POSS nanocomposites was proposed by Joshi et al.²⁷ They found that only the POSS dispersing at the molecular level could act as nucleating agents, while the POSS nanocrystals did not affect the crystallization process. Consequently, how POSS influences the crystallization of polymer is still rich in controversy.

Polydimethysiloxane (PDMS) is considered as the foremost candidate for new materials. Although PDMS is endowed with some exceptional properties such as high and low temperature resistance, ultraviolet resistance, weatherability, electric insulativity and so on, it needs to be further modified. Referring to POSS/PDMS nanocomposites, Ghosh et al.²⁸ indicated that octamethyl-POSS acted as a lubricant in the nanocomposite owing to the small size and good compatibility with PDMS. On the contrary, octaphenyl-POSS formed large chunks of POSS aggregation and set as separate phase in PDMS matrix because of strong π–π interaction between phenyl rings of different octaphenyl-POSS molecules. Liu et al.²⁹ found that in octaisobutyl-POSS/silicone rubber blends prepared at low mixing temperatures, POSS crystals were dispersed as large crystal aggregates in the rubber matrix; while in blends prepared at high temperatures, some of the POSS crystals dissolved into silicone rubber. Nevertheless, what they have studied only related to aggregation and crystalline behaviors of POSS molecules themselves but had little correlation with the crystallization performance of silicone rubber matrix.

In the present work, we aimed at exploring the influence of POSS on the crystallization and melting performances of PDMS. Using differential scanning calorimeter (DSC), X-ray diffraction (XRD) and scanning electron microscopy (SEM), some thought-provoking results were reported firstly.

2. Experimental

2.1 Materials

In this study, both heptaphenylhydrogensilsesquioxane [H(C₆H₅)₇(SiO_1.5)₈, H-POSS, abbreviated as POSS]³⁰ and polydimethylsiloxane (PDMS) rubber having 0.20% vinyl substituents with a molecular weight of 528 000 g mol⁻¹ were synthesized in our laboratory (see ESI†). ²⁹Si NMR spectrum was introduced to characterize the structure of H-POSS. As shown in Fig. 1, the amounts of Si atoms in positions 1, 2 and 3 are 1, 3 and 4, respectively, which corresponds to the three signals at −82.9, −78.5 and −78.2 ppm whose proportion of intensity is 1 : 3 : 4. Platinum(0)-1,3-divinyl-1,1,3,3-tetramethyldisiloxane (Pt(dvs)) was obtained from Tansoole, Shanghai, China. 2,5-dimethyl-2,5-di(tert-butylperoxy)hexane (DBPH) was provided by Dongyang chemical, Haian, China. Toluene was of analytical purity and was purchased from BoDi chemical, Tianjin, China.

Fig. 1 ²⁹Si NMR spectrum of H-POSS.

2.2 Preparation of POSS/PDMS nanocomposites

Neat PDMS and four different POSS loadings of nanocomposites were prepared in the same way. The samples were named H-0, H-1, H-3, H-5 and H-10 where the number meant the weight percentage of POSS in each nanocomposite. POSS and PDMS were dissolved in toluene respectively and stirred adequately, and then the two kinds of solution were mixed directly. After ultrasonic processing and mechanical stirring, the mixture was placed to vacuum oven at 100 °C for 48 hours in order to remove solvent. In two days, the mixture, predetermined amount of Pt(dvs) and DBPH were mixed with an open two-roll mill. Then the product obtained above was placed to plate vulcanizing press at 165 °C with a pressure of 10 MPa for 12 min, followed by post-curing at 180 °C for 4 hours.

2.3 Measurements

FTIR spectra were collected with a spectral resolution of 2 cm⁻¹ on a Nicolet Magna 560 infrared analyzer using KBr disks or pellets at room temperature. Before FTIR characterization, the nanocomposites were firstly extracted by toluene for 3 days in order to remove ungrafted POSS, then wiped with tissue paper and dried in a vacuum oven at 100 °C for 2 days to remove toluene.³¹ X-ray diffraction (XRD) analyses were carried out on a Philips X'Pert Graphics and Identify with Ni-filtered Cu Kα radiation where the 2θ angle ranged from 5 to 45° and the scanning rate was 2.4 deg min⁻¹. Isothermal crystallization was carried out using a TA Q200 differential scanning calorimeter (DSC) calibrated the temperature with indium. All DSC measurements were performed under nitrogen atmosphere. The isothermal crystallization and melting processes were performed as follows: samples were first isothermal at 30 °C for 5 min to remove thermal history, then cooled to −61 °C, −59 °C, −57 °C, −55 °C and −53 °C severally with a cooling rate of −50 °C min⁻¹ for isothermal crystallization until they crystallized completely, finally they were heated to 30 °C at a rate of 10 °C min⁻¹. Scanning electron microscopy (SEM) was performed on a JSM-5900LV scanning electron microscope at a voltage of 20 kV. Samples were first fractured in liquid nitrogen and then coated with a gold coating film of about 100 Å thick and photographed in the microscope.

3. Results and discussion

3.1 Characterization of the grafting reaction

As a good solvent for POSS and uncross-linked PDMS chains, toluene is applied to dissolve them before FTIR characterization. FTIR spectra of POSS, H-0 after extraction (H-0-extraction) and H-3 after extraction (H-3-extraction) as a representation are shown in Fig. 2. Compared with FTIR curve of H-0-extraction, that of H-3-extraction displays broader peaks at 2750–3200 cm⁻¹ and 900–1200 cm⁻¹, where the former is ascribed to C–H in phenyl and the latter is attributed to Si-Phenyl and Si–O–Si structures. Moreover, C–H in Si-phenyl is responsible for peaks at 3053 cm⁻¹, 1581 cm⁻¹ and 1447 cm⁻¹. The above peaks confirm the integrity of POSS cage. In addition, the peak of Si–H can be obviously detected at 2252 cm⁻¹ in the spectrum of POSS, but it disappears in the spectrum of H-3-extraction, indicating the successful grafting of POSS onto PDMS chains.

Fig. 2 FTIR spectra of H-POSS, H-0-extraction and H-3-extraction.

3.2 Study on melting behaviors of POSS/PDMS nanocomposites

For all the five samples of neat PDMS and POSS/PDMS nanocomposites, the shapes of melting curves are similar with each other except for diversity in positions and intensities of the melting peaks. As examples, DSC melting curves of the sample H-3 crystallized at different temperatures and that of samples with different POSS loadings crystallized at the same temperature of −57 °C are presented in Fig. 3(a) and (b) separately. Evidently, only one peak emerges in the DSC endotherms without the appearance of cold crystallization peak. As cold crystallization is the character of less ordered crystals,¹² we can deduce that only one crystal form is shaped and the crystals are quite perfect.

Fig. 3 DSC melting endotherms of H-3 after isothermal crystallization at different temperatures (a) and of the five samples after crystallization at −57 °C (b).

In this study, we choose the peak temperature of DSC curve as melting temperature (T_m). It is obvious in Fig. 3(a) that T_m grows higher with the increase of crystallization temperature (T_c). This is because in higher temperatures, molecular chain segments are more mobile to form ordered structures, thus the crystalline phase tends to be more perfect. Based on a theory by Hoffman and Weeks,³² the equilibrium melting temperature (T⁰_m) where crystalline phase and amorphous phase reach a thermodynamic equilibrium can be deduced by plotting the linear relationship of T_m's versus the isothermal T_c's. As shown in Fig. 4, there is a good linear relationship between T_m's and T_c's for each sample and the intersection of the above straight line with the line T_m = T_c is regarded as T⁰_m. Evidently, T⁰_m values of POSS/PDMS nanocomposites are all substantially higher than that of neat PDMS (240.87 K) where T⁰_m of H-1 is as high as 246.27 K, indicating the formation of more thermal-stable crystals.

Fig. 4 Hoffman–Weeks plots for isothermally crystallized neat PDMS and POSS/PDMS nanocomposites.

According to Hoffman–Weeks equation

λ, a factor depending on the final lamellar thickness of crystals can be considered as the reciprocal of the slope in Fig. 4. λ is assumed to be L_c/L^*_c where L_c and L^*_c are the thickness of a mature crystallite and the critical crystallite nucleus, respectively. From the calculation results of eqn (1), λ values of the nanocomposites stay stable, but are smaller than that of neat PDMS. The result leads us to consider that POSS in the nanocomposites may act as heterogeneous nucleating agent in crystallization of PDMS, so compared with neat PDMS, a larger amount of nucleuses generate and because of impingement and confinement with each other, every nucleus tends to be thinner.

As shown in Fig. 3(b), with the addition of POSS, T_m first increases but then decreases abruptly and finally stays almost stable, which indicates that PDMS crystals could become more intact under a critical POSS loading, but beyond the loading, the integrity of PDMS crystals would no longer change.

The crystallinity (X_c) could be determined from the equation X_c = ΔH_f/ΔH⁰_f × 100% where ΔH_f is the heat of fusion of each sample and ΔH⁰_f is the heat of fusion of a perfectly (100%) crystalline polymer which is 37.4 J g⁻¹ for PDMS rubber.³³ The calculation results show quite comparable values of about 64% for each sample at different temperatures, meaning that the crystallinity is hardly affected by the addition of POSS and crystallization temperature. This seems contradict with the fluctuation of T_m in Fig. 3(b). Whether POSS affects the kinetics of the crystallization of PDMS or not and how does it work? We attempt to trace the origin by isothermal crystallization in the following section.

3.3 Isothermal crystallization kinetic analysis

The isothermal crystallization results show that the influence of T_c on crystallization of the nanocomposites is similar to neat PDMS. Generally, the isothermal crystallization processes can be quantitatively demonstrated through the variation of X(t), the relative crystallinity, which is the weight fraction of crystallized material at time t and is defined aswhere dH/dt, ΔH_t, andΔH_∞, are the rate of heat-flow, heat generated at time t, and total heat generated at the entire crystallization process, respectively. As examples, Fig. 5(a) and (b) displays the development of relative crystallinity during isothermal crystallization. As can be seen, the crystallization kinetics curves of these samples display typical sigmoidal evolution. With the raise of T_c, time to complete isothermal crystallization is prolonged, suggesting a slower crystallization rate. By comparison, the crystallization rate of the nanocomposites is substantially faster than that of neat PDMS. In Fig. 5, time for H-3 to finish crystallization at −53 °C is about 28.5 min, while that for H-0 is more than 2.5 times for H-3, which further confirms that POSS must be a nucleating agent to accelerate the crystallization rate significantly in the isothermal crystallization process of the nanocomposites.

Fig. 5 Plots of relative degree of crystallization X(t) versus time in isothermal crystallization of H-0 (a) and H-3 (b), values in the frames representing isothermal crystallization temperature.

The classic Avrami equation,^34,35 the most frequently used method in isothermal crystallization, is applied to compare the isothermal crystallization behaviors of the five samples. The equation is expressed as follows:

X(t) = 1 − exp(−Ktⁿ) (3)

lg[−ln(1 − X(t))] = n lg t + lg K (4)

where n is the Avrami exponent related to the type of nucleation and the geometry of the growing crystals, and K is the crystallization rate constant. By using eqn (4), plots of lg[−ln(1 − X(t))] versus lg t are shown in Fig. 6(a and b). Similar to most polymers, the curves exhibit two linear stages, expressed as stage I and stage II in sequence. Nevertheless, different from polyethylene terephthalate (PET) and polyamide (PA) whose stage II emerges extremely early and evidently,^36,37 stage II of our samples appears very late and is even hardly detected in the case of neat PDMS.

Fig. 6 Plots of lg[−ln(1 − X(t))] versus lg t in isothermal crystallization of H-0 (a) and H-3 (b), values in the frames representing isothermal crystallization temperature.

In stage II, the curves shift to right, resulting in lower slope values, which is ascribed to the secondary crystallization. As can be deduced from eqn (4), lower slope values suggest lower n values, also indicating lower growth dimensions of the crystals. Because the nanocomposites have more crystal growth points than neat PDMS, their crystals are much easier to be restricted from each other and thus to be smaller in size. The above analysis coincides with the observation result of Fig. 4 that curves of H-3 deviates more obviously.

Stage I represents primary crystallization where Avrami exponent n and the rate constant K can be determined from the slope and intercept through linear regression of these straight lines. The calculated values of n and K are summarized in Table 1. The variation of n value from 2.20 to 3.22 indicates a three-dimensional growth during the isothermal crystallization process of all the samples. Compared with neat PDMS, the nanocomposites have more or less larger values of n, which seems contradict with the Avrami theory that homogeneous nucleation has a larger value of n than heterogeneous nucleation. Bian et al.³⁸ pointed out that n related with the number of growth points in crystal nuclei, namely, the bigger the number, the larger the n value. In POSS/PDMS nanocomposites, as PDMS spherulite is formed by the growth of branches of lamellae induced by POSS, the greater the branching points, the more the growth points and the bigger the n value. Also in the process, the growth and end of PDMS spherulite take place at any time, so n value has a statistical meaning, resulting in that it appears as either integer or decimal.³⁹

Table 1 Kinetic parameters for isothermal crystallization of neat PDMS and POSS/PDMS nanocomposites

Sample	T c (°C)	lg K	n	t 1/2 ^a (min)	t 1/2 ^b (min)
a Obtained from isothermal crystallization exotherms. b Calculated from eqn (5).
H-0	−61	0.019	2.83	0.86	0.86
	−59	−0.922	2.97	1.80	1.81
	−57	−2.038	2.77	4.70	4.77
	−55	−2.735	2.51	10.32	10.62
	−53	−3.719	2.27	35.33	37.02
H-1	−61	0.130	2.51	0.77	0.77
	−59	−0.701	3.22	1.48	1.47
	−57	−1.328	2.89	2.45	2.54
	−55	−2.309	2.78	5.72	5.93
	−53	−2.793	2.20	15.78	15.74
H-3	−61	0.061	2.85	0.83	0.84
	−59	−0.473	2.91	1.29	1.28
	−57	−1.379	2.82	2.52	2.71
	−55	−2.353	2.82	5.82	6.00
	−53	−3.024	2.48	14.18	14.29
H-5	−61	−0.043	2.75	0.89	0.90
	−59	−0.879	2.68	1.85	1.86
	−57	−1.702	2.97	3.22	3.31
	−55	−2.636	2.83	7.38	7.50
	−53	−3.330	2.28	25.13	24.59
H-10	−61	0.067	2.91	0.83	0.84
	−59	−0.789	3.00	1.64	1.62
	−57	−1.823	2.84	3.70	3.85
	−55	−2.717	2.63	9.20	9.39
	−53	−3.350	2.24	26.68	26.58

---

The parameter t_1/2 is the half-time of crystallization which is defined as the time needed to reach half of the final crystallinity. It can be determined either from the plots of X(t) versus time (Fig. 5) or from the following equation:

The calculation results from both eqn (5) and the plots are listed in Table 1. It is obvious that the values of t_1/2 from the two approaches are consistent well with each other, which in turn proves the validity of the values of n and K.

The dependence of t_1/2 on the isothermal crystallization temperature is illustrated in Fig. 7. With the increase of T_c, t_1/2 also increases, indicating a lower crystallization rate. Comparing t_1/2 values of samples with different POSS loadings, deviations become more remarkable for samples to crystallize at higher temperatures. In general, the crystallization rates of the samples follow the order: H-3 > H-1 > H-5 > H-10 > H-0. Among them, though H-3 shows similar crystallization rate to H-1 at lower T_c's and the difference is obvious only when T_c is high enough, both of them can crystallize at an extremely faster rate than H-5 and H-10. This can be interpreted as the variation of nucleation ability of POSS. When POSS loading is below 3%, it can act as nucleating agent in the crystallization process of PDMS efficiently; while when POSS is at a higher loading, the amount of POSS actually acts as nucleating agent may not increase anymore and contrarily, the crystallization of PDMS is restricted at some extent.

Fig. 7 Plots of the values of t_1/2versus crystallization temperature (T_c) in isothermal crystallization of neat PDMS and POSS/PDMS nanocomposites.

3.4 Crystallization activation energy of POSS/PDMS nanocomposites

The crystallization rate constant K can be described by the Arrhenius equation:⁴⁰

K^1/n = k₀ exp(−ΔE/RT_c) (6)

(1/n)ln K = ln k₀ − ΔE/RT_c (7)

where k₀ is a temperature independent preexponential factor, R is the gas constant, and ΔE is the crystallization activation energy containing both transport activation energy and nucleation activation energy. Fig. 8 presents the case of H-3 as an example. Based on eqn (7), the value of ΔE can be determined as R multiplies by the slope of the Arrhenius plot of 1/n ln K versus 1/T_c. Evidently, there is a perfect linear relationship between the two parameters.

Fig. 8 1/n ln K versus 1/T_c of H-3 in isothermal crystallization.

In order to compare the influence of POSS loadings on ΔE of the samples intuitively, another graph is drawn in Fig. 9. Since crystallization is a process of energy-releasing, ΔE is of negative value where the negative sign only has a thermodynamics meaning and represents direction of heat-flow rate. Assuming that the negative sign is taken off, obviously in the figure, the value of ΔE drops dramatically with the initial addition of POSS, but it rises notably once beyond 3 wt% loading. As is well-known, ΔE represents the minimum energy for PDMS chain segments to crystallize and the energy can be accumulated with time. Therefore, the chain segments can achieve the necessary energy more readily if ΔE is lower, resulting in a reduced crystallization time. The above results demonstrate the change of nucleation ability of POSS, which is completely coincident with the calculation results of t_1/2.

Fig. 9 Changes of activation energy with POSS content.

3.5 Dispersion of POSS in POSS/PDMS nanocomposites and the influencing mechanism

Previous analyses in the paper have proposed that POSS can act as nucleating agent efficiently below a critical loading, say 3 wt%, but the nucleation ability would be weakened at higher loadings. Why POSS loading affects the crystallization of PDMS is a problem we are looking forward to resolve.

SEM photographs of distributions of various POSS loadings in PDMS matrix are displayed in Fig. 10. As can be seen, POSS is dispersed quite uniformly in PDMS matrix where the nanocomposites with lower loadings of POSS (H-1 and H-3) show better dispersion than their higher loading counterparts (H-5 and H-10). In H-1 and H-3, POSS is dispersed with molecular level or as tiny agglomerates formed through self-assembling in PDMS matrix. While in H-5 and H-10, a larger amount of POSS agglomerates appear in PDMS matrix and moreover, the agglomerates are of larger size.

Fig. 10 SEM images of neat PDMS and the nanocomposites: H-0 (a), H-1 (b), H-3 (c), H-5 (d) and H-10 (e).

The distribution state was further characterized by XRD. XRD patterns of POSS, neat PDMS and the POSS/PDMS nanocomposites are shown in Fig. 9. Parallel curves can be found for H-1 and H-3 where only a broad diffuse scattering peak corresponding to the amorphous structure of PDMS is detected at almost the same angle. However, when the loading of POSS exceeds 3 wt%, a small diffraction peak assigned to the crystallization structure of POSS can be found on the left side of the amorphous peak, according to the XRD spectrum of POSS, and furthermore, the small peak is becoming stronger with the rise of POSS loading. In addition, the fact that the small diffraction peak of H-10 appears at a slightly smaller angle than that of H-5 indicates the integrity of POSS crystal may be impaired by the increase of POSS loading (Fig. 11).

Fig. 11 XRD patterns of POSS, neat PDMS and the nanocomposites.

The crystallite size of POSS can be calculated using Scherrer's equation:⁴¹

where L_hkl means the crystallite size at reflection of (hkl), K is the Scherrer factor with a value of 0.9, λ is the wave length of the X-rays with a value of 1.54 Å, and β refers to the half width of the diffraction peak in radian, respectively. The calculation results of H-5 and H-10 listed in Table 2 indicate a slight increase in the crystallite size of POSS. Accordingly, we postulate that the transformation of self-assemble structure of POSS happens when POSS loading reaches 5 wt%, around the crystallite size of 31.5 nm as shown in Table 2. Consequently, when POSS loading is below 3 wt%, POSS molecules can be dispersed uniformly in PDMS matrix, with its agglomerates, or crystallites are small in size and hardly detected in XRD. Nevertheless, POSS molecules appear to aggregate at a higher loadings because of intense π–π conjugation effect among phenyl rings. When the crystallite size of POSS is larger than 31.5 nm, its crystallization peaks become obvious in XRD patterns.

Table 2 Crystallite Size of POSS

Sample	Crystallite size (nm)
H-5	31.5
H-10	34.1

---

The diversity in crystallization performances of samples with different POSS loadings can be interpreted as follows: for neat PDMS, crystallization originates from inter- and intrachain interactions, while for the nanocomposites, strong covalent bonding and non-covalent bonding between POSS and PDMS matrix which derived from phenyl–phenyl interactions among the POSS molecules which have been grafted onto PDMS chains accelerate the formulation of ordered structures. Consequently, the difference in crystallization behaviors of the nanocomposites can be attributed to the change of nucleation ability of POSS, which has a close relationship with the distribution of POSS in PDMS matrix.

Two schematics of POSS distribution in PDMS matrix are illustrated in Scheme 1. In samples H-1 and H-3 (lower POSS loadings), most POSS molecules are able to be grafted onto PDMS chains and only a small amount are dissociative from PDMS chains, leading to that most POSS can be dispersed quite uniformly in the rubber matrix and only small size agglomerates appear. Wherein, owing to their rigidity, POSS molecules act as physical cross-linkers that retard the local relaxation of the adjacent PDMS chains, and simultaneously, the surfaces of POSS agglomerates may act as templates for PDMS chain segments to become ordered and crystallize. However, in the case of samples H-5 and H-10 (higher POSS loadings), a larger percentage of POSS would remain independent of PDMS and form their own crystal region after curing because with the increase of POSS loading, steric hindrance from POSS connecting with PDMS chains is becoming so prominent that a growing number of POSS will be hardly grafted onto PDMS chains. Thus, although POSS may still play as nucleating agent in the crystallization of PDMS, its crystal region restricts PDMS matrix from forming ordered structures at some extent, which leads to lower crystallization rate than the fewer loading nanocomposites but higher than neat PDMS. Furthermore, there is a solid evidence that the relationship of T_m in Fig. 3(b) fits well with that of crystallization rate, which can be ascribed to that crystallite in larger size corresponds with more defects and under the condition of constant spherulitic growth rate,⁴² lesser crystallization time lead to the formation of crystallite in smaller size, thus the crystal tends to be more intact. Therefore, although the crystallinities of the samples are almost the same with each other, their T_m values are quite different.

Scheme 1 Schematic drawings of POSS distribution state in PDMS matrix, lower and higher loadings of POSS are illustrated in (a) and (b), respectively.

4. Conclusion

In this work, H-POSS was incorporated into PDMS, then the melting and crystallization behaviors of the POSS/PDMS nanocomposites were studied. The research showed that the addition of POSS facilitated the formation of more thermal-stable crystals. Change in the value of half-time of crystallization t_1/2 suggested that the crystallization rate increased with the addition of POSS before POSS loading reached 3 wt%, beyond that the rate decreased. The result was supported by the findings on activation energy. According to SEM and XRD, distinctions in both melting and crystallization behaviors of the nanocomposites with different POSS loadings originate from the variety of nucleation ability of POSS in crystallization of PDMS. When POSS loading is less than 3 wt%, it can act as nucleating agent efficiently; however, due to the formation of POSS crystallites of larger than 31.5 nm, the nucleation ability of POSS would be weakened when POSS loadings are higher than 3 wt%.

Acknowledgements

The authors thank the National Natural Science Foundation of China (Grant no. 51073097) for financial support.

Notes and references

1. T. S. Haddad and J. D. Lichtenhan, Macromolecules, 1996, 29, 7302–7304.
2. B. X. Fu, B. S. Hsiao, H. White, M. Rafailovich, P. T. Mather, H. G. Jeon, S. Phillips, J. Lichtenhan and J. Schwab, Polym. Int., 2000, 49, 437–440.
3. A. Striolo, C. McCabe and P. T. Cummings, J. Phys. Chem. B, 2005, 109, 14300–14307.
4. R. Hany, R. Hartmann, C. Bohlen, S. Brandenberger, J. Kawada, C. Lowe, M. Zinn, B. Witholt and R. H. Marchessault, Polymer, 2005, 46, 5025–5031.
5. Y. S. Ye, W. Y. Chen and Y. Z. Wang, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 5391–5402.
6. S. W. Kuo and F. C. Chang, Prog. Polym. Sci., 2011, 36, 1649–1696.
7. L. Zheng, R. J. Farris and E. B. Coughlin, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 2920–2928.
8. L. Zheng, S. Hong, G. Cardoen, E. Burgaz, S. P. Gido and E. B. Coughlin, Macromolecules, 2004, 37, 8606–8611.
9. L. Zheng, R. J. Farris and E. B. Coughlin, Macromolecules, 2001, 34, 8034–8039.
10. P. T. Mather, H. G. Jeon and A. R. Uribe, Macromolecules, 1999, 32, 1194–1203.
11. H. X. Zhang, Y. J. Shin, K. B. Yoon and D. H. Lee, Eur. Polym. J., 2009, 45, 40–46.
12. B. X. Fu, C. Yang, R. H. Somani, S. X. Zong, B. S. Hsiao, S. Phillips, R. Blanski and D. Ruth, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 2727–2739.
13. S. Y. Soong, R. E. Cohen, M. C. Boyce and A. D. Mulliken, Macromolecules, 2006, 39, 2900–2908.
14. S. Y. Soong, R. E. Cohen and M. C. Boyce, Polymer, 2007, 48, 1410–1418.
15. Z. Wang, Y. Li and X. H. Dong, et al. , Chem. Sci., 2013, 4(3), 1345–1352.
16. S. W. Kuo, H. C. Kao and F. C. Chang, Polymer, 2003, 44, 6873–6882.
17. N. C. Escude and E. Y. X. Chen, Chem. Mater., 2009, 21, 5743–5753.
18. S. C. Chan, S. W. Kuo and F. C. Chang, Macromolecules, 2005, 38, 3099–3107.
19. L. Ricco, S. Russo, O. Monticelli, A. Bordo and F. Bellucci, Polymer, 2005, 46, 6810–6819.
20. F. Baldi, F. Bignotti, L. Ricco, O. Monticelli and T. Ricco, J. Appl. Polym. Sci., 2006, 100, 3409–3414.
21. A. Strachota, I. Kroutilová, J. Kovárová and L. Matejka, Macromolecules, 2004, 37(25), 9457–9464.
22. G. Kickelbick, Prog. Polym. Sci., 2003, 28, 83–114.
23. M. Joshi and B. S. Butola, J. Macromol. Sci., Polym. Rev., 2004, 44(4), 389–410.
24. G. Z. Li, L. Wang, H. Toghiani, T. L. Daulton and C. U. Pittman, Polymer, 2002, 43, 4167–4176.
25. J. Xu and J. Song, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(17), 7652–7657.
26. R. R. Patel, R. Mohanraj and C. U. Pittman, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 234–248.
27. M. Joshi, B. S. Butola, G. Simon and N. Kukaleva, Macromolecules, 2006, 39, 1839–1849.
28. V. Joshi, M. Srividhya, M. Dubey, A. K. Ghosh and A. Saxena, J. Appl. Polym. Sci., 2013, 130(1), 92–99.
29. L. Liu, M. Tian, W. Zhang, L. Zhang and J. E. Mark, Polymer, 2007, 48, 3201–3212.
30. D. B. Cordes, P. D. Lickiss and F. Rataboul, Chem. Rev., 2010, 110(4), 2081–2173.
31. Y. Meng, Z. Wei and L. Liu, et al. , Polymer, 2013, 54(12), 3055–3064.
32. J. D. Hoffman and J. J. Weeks, J. Chem. Phys., 1962, 37, 1723–1741.
33. M. I. Aranguren, Polymer, 1998, 39, 4897–4903.
34. M. J. Avrami, J. Chem. Phys., 1939, 7, 1103–1112.
35. M. J. Avrami, J. Chem. Phys., 1940, 8, 212–224.
36. X. H. Gu, J. L. Zhou and J. H. Liu, Adv. Mater. Res., 2011, 284, 353–359.
37. S. S. Kadam, H. J. M. Kramer and J. H. ter Horst, Cryst. Growth Des., 2011, 11(4), 1271–1277.
38. J. Bian, S. R. Ye and L. X. Feng, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2135–2144.
39. B. Wunderlich, in Handbook of Macromolecular Physics, Academic Press, New York, 1976, vol. 2, p. 363.
40. P. Cebe and S. D. Hong, Polymer, 1986, 27, 1183–1192.
41. Z. S. Mo, Structure of CrystallinePolymer and X-ray Diffraction [M], Science Press, PRC, 2003, p. 232.
42. F. J. Torre, M. M. Cortazar, M. A. Gomez, G. Ellis and C. Marco, Polymer, 2003, 44, 5209–5217.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis and characterization of H-POSS and PDMS. See DOI: 10.1039/c3ra46711b

---