Unraveling the interplay of different contributions to the stability of the quinhydrone dimer

Abstract

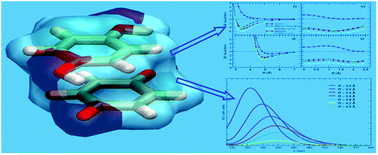
Aim of this paper is to present a computational revisitation of the main structural and spectroscopic features of quinhydrone, a prototype of complexes built on noncovalent interactions, with a view to proposing an accurate yet computationally convenient approach to the characterization of such kind of complexes. Several methods are compared in terms of energy profiles along selected coordinates, which involve the relative distance and/or orientation of the two aromatic rings. MP2 and DFT calculations agree in indicating that H-bonding and dispersion forces play a more important role than charge transfer in stabilizing quinhydrone. Distance- and orientation-dependent overlap of π clouds was found by TD-DFT calculations to be a major determinant of quinhydrone visible absorption and color.

---

1. Introduction

Noncovalent interactions^1–4 certainly play a relevant role in supramolecular^5–8 and biological^9–13 systems, being largely responsible for the specificity and diversity that characterize bio-chemical processes. In many cases, this fine-tuning arises from specific binding motifs, that in turn originate from a delicate interplay among different kinds of noncovalent forces,^12,14 such as H-bonding, dispersion, π–π stacking, or charge-transfer (CT) interactions. Unraveling such complexity by a computational approach could be very useful, given that the method employed is able to take accurately into account all of the above-mentioned contributions. For this reason, persistent efforts were and are still devoted to develop reliable computational methodologies for an accurate representation of noncovalent complexes.^15–40

A good example of noncovalent hetero-dimers is represented by the quinhydrone complex (Fig. 1) whose ubiquitous presence in many aspects of organic matter has motivated an extensive number of experimental and theoretical studies.^41–56 Quinhydrone is made by two units, namely p-benzoquinone and hydroquinone and it is known from a century and an half, being first discovered in 1844 by Wöhler.⁴¹ It can be prepared by a 1 : 1 mixture of the two components or just by partial reduction of p-benzoquinone in ethyl alcohol.⁴² In solution the separate components are colorless (hydroquinone) or pale yellow (p-benzoquinone), while the complex color is intense and goes from deep purple to brown. This effect is solvent-dependent and pH-dependent.⁵⁰ In the solid state, intermolecular hydrogen bond (H-bond) occurs⁴⁵ and attempts have also been made to model the structure,⁴⁸ where H-bonds may be complemented by both π–π stacking and CT interactions between the two moieties. The competition between these forces determines the peculiar structural and spectroscopic features of the complex, which are remarkably different from those exhibited by the two separate units. Furthermore, besides its fundamental interest, quinhydrone can also be seen as a prototype system for the study of oligomeric species involved in the structure of biopolymers of the melanine family, such as that of di-hydroxy indole (DHI) and of its carboxylic counterparts (DHCI). Both these species play an important role in biology and may find interesting practical applications in electronic and photoelectronic devices.^57,58 Finally, the relevance of the quinhydrone species in humic acids has also been recently outlined.^51,55

Fig. 1 Quinhydrone geometries considered for MP2/mod basis set optimization and validation. Face-to-face (FF, top left), side-to-face (SF, bottom left) and parallel displaced (SX SZ top and bottom right, respectively). Reference axes (red, green and blue for x, y and z axis, respectively) and translation vector R (blue arrow) are reported in each panel.

Despite its importance, relatively few computational studies have been reported in literature on the structural and spectral characterization of quinhydrone. The first reliable calculations were performed, to the best of our knowledge, in 1994 by Kurita,⁴⁶ where single point calculations at MP2/6-31G* level, using Counterpoise (CP) correction,⁵⁹ were performed on a geometry reconstructed from experimental (X-ray) data.^43,44 The authors concluded that electron correlation effects are essential to stabilize quinhydrone and that the relative orientation of the stacked complex is determined by the interplay of many interaction terms as steric repulsion, CT interaction energy, dispersion and first order electrostatics. More recently,⁵⁴ the stability and electron density topology of quinhydrone was studied using computational methods of various level of accuracy. The authors aimed to refine Kurita's et al. calculations,⁴⁶ taking into account the role of H-bond, which was found to be relevant by some experiments.⁴⁹ Furthermore, the authors find, through a QTAIM analysis, a small electron transfer of 0.046 a.u., from hydroquinone to p-benzoquinone. As in the previous approach, they also consider a single geometry, taken from experimental X-ray measures. The authors also compare the binding energies computed in vacuo to the experimental value (−2.9 kcal mol⁻¹).⁶⁰ However, the experiments were made in aqueous solution where intramolecular and intermolecular (with neighboring water molecules) hydrogen bonds may compete, while in less interacting solvent the value may be raised up to six times.⁶⁰ The most recent calculations were performed by Tossell in 2009,⁵⁵ who computed quinhydrone structures, stacking energies, as well as UV/vis, IR and NMR spectra. Geometry optimization was performed at the MP2/6-311G* level, in the gas phase and in solution (THF and water) within the PCM approximation. The inter-ring separation in solution was found to increase with solvent polarity, which also affects the position of the OH groups, resulting out of plane in gas phase and coplanar to the benzene ring in water. In gas phase, and correcting for basis set superposition error, the binding energy of quinhydrone, both at MPW1B95 and MP2 level, results ∼6 to 7 kcal mol⁻¹, while it is positive for B3LYP.

Aim of this paper is to investigate the role played by the different sources of interaction, hydrogen bond, CT, π–π stacking, steric repulsion, etc., and their effects on the visible absorption spectrum which characterizes the complex formation. With respect to literature findings, two further issues still call for a deeper investigation and will be addressed in the present paper: (i) only few quinhydrone geometries were considered in previous works, making difficult to evaluate the dependence of the force balance on the reciprocal orientation of the complex forming units; (ii) despite several methods have been employed in previous works, a systematic validation against higher level reference estimates is still missing.

In the past decade, several groups have reported highly accurate calculations for modeling non covalently interacting systems. Among others, the groups of Tsuzuki,^16,17 Hobza,^{11,12,19,40,61} and Sherrill^{18,20–22,24,62,63} have reported interaction energies at the CCSD(T) level, extrapolated at the complete basis set (CBS) limit, which is now often referred to as the “gold standard”⁴⁰ of quantum chemistry. The major drawback of this approach is the extremely high computational cost of the CCSD(T) method, which makes these calculations rapidly infeasible with the increase of molecular dimensions. Computational convenience would suggest resorting to cheaper methods, either density or wavefunction (WF) based.

Methods based on density functional theory (DFT) are generally less expensive, but care must be taken in choosing the appropriate functional,³⁹ i.e. capable to account, in a balanced manner, for all noncovalent interactions involved. The M06-2X functional, was purposely re-parameterized by Truhlar and Zhao^30–32 in order to take dispersion into account, achieving a good agreement^32,34 with reference CCSD(T)/CBS data for benchmark systems.

As far as the WF based methods are concerned, a computationally convenient post-HF method is the Möller–Plesset second order perturbation (MP2) theory. On the other hand, a major drawback of the MP2 method is the remarkable overbinding found for aromatic stacked interactions, when large basis sets are employed.^{16,17,22,27,64,65} Several attempts have been recently made to overcome this problem,^26,27,35 nonetheless, in all these cases, the best agreement with CCSD(T)/CBS reference data was obtained only making use of rather large basis sets.

An alternative choice is the adoption of the standard MP2 method, coupled with a small basis set (6-31G*), where the polarization exponent for the carbon atoms is modified to a smaller value (0.25 instead of the standard 0.80) and therefore named 6-31G*(0.25).¹⁵ The original MP2/6-31G*(0.25) has been also extended to other heteroaromatics compounds, by suitably modifying the polarization exponents of atoms other than carbon in the 6-31G* or similar basis sets.^66–68 The comparison with more expensive computational methods, recently reported for molecular complexes with stacking interactions,^{12,25,33,68,69} is positive, since the interaction energy overestimation found for MP2 calculations performed with larger basis sets is avoided. It should be pointed out that, as the optimized exponent is tailored on the system under study, the resulting specific basis set does not pretend to be transferable to other systems, or, at least, this can be done after verifying its performances.

This procedure (indicated in the following as MP2/mod) and DFT/M06-2X will be applied to the study of quinhydrone and validated by the comparison with the results of accurate CCSD(T) calculations for selected geometries. The two approaches will allow us to quantitatively elucidate the contribution of the various sources of non-covalent interactions to the formation of the complex as well as in determining the observed absorption in the visible.

2. Methods and computational details

Reference data for dimer geometries, interaction and binding energies are obtained by using the gold standard⁴⁰ of quantum chemistry, i.e. the CCSD(T) level of theory, estimated at the CBS limit (CCSD(T)/CBS). This value is obtained from the MP2/CBS value (ΔE^MP2_CBS) corrected with the Δ^CCSD(T)-MP2 term

ΔE^CCSD(T)_CBS = ΔE^MP2_CBS + Δ^CCSD(T)-MP2 (1)

where Δ^CCSD(T)-MP2 is the difference

Δ^CCSD(T)-MP2 = [ΔE^CCSD(T) − ΔE^MP2]_{medium-size basis set} (2)

Despite this procedure has been extensively used by several groups,^{11,12,17,24,63} up to our knowledge, the best route to a correct estimate of both ΔE^MP2_CBS and Δ^CCSD(T)-MP2 values has not yet been assessed. In this work, the MP2 value in the CBS limit is estimated through the procedure proposed by Halkier et al.,⁷⁰ using the augmented Dunning's correlation consistent basis sets, aug-cc-pVDZ and aug-cc-pVTZ basis sets. The Δ^CCSD(T)-MP2 correction term is computed estimating the CCSD(T)-MP2 difference at the aug-cc-pVDZ level.

As the DFT calculations are concerned, the M06-2X functional was chosen in virtue of its good performances for both dispersion based complexes³² and CT interactions.⁷¹ Following Truhlar's suggestions for noncovalent complexes, reported in ref. 32, all calculations were performed with the triple-zeta 6-311+G(2df,2p) basis set, without applying any correction for the basis set superposition error (BSSE). Furthermore, considering the high computational cost due to the presence of the f functions in the adopted basis set, M06-2X calculations were also performed with the smaller 6-311+G(2d,2p) basis set. In this case, due to the reduced dimensions of the basis set, the BSSE is expected to be more relevant, and has been corrected by the CP method.⁵⁹ CP energy correction was also applied to all calculations performed with the wave-function based MP2 method. Moreover, a specifically tailored basis set was coupled to the MP2 method, which will be labeled in the following as 6-31G*(α_C,α_O), where α_C and α_O are the modified polarization exponents for carbon and oxygen atoms, respectively. Whereas the former was set to 0.25, as first suggested by Hobza and coworkers,¹⁵ the α_O was optimized by a fully automated procedure, coded in an “in house” software named Exopt.^66,68 To this end, binding energies were obtained at the CCSD(T)/CBS level for few selected quinhydrone arrangements and thereafter used to obtain the best α_O polarization exponent, through the minimization procedure coded in EXOPT.

All investigated dimer conformations, except those resulting from a complete geometry optimization, were constructed by placing in the chosen arrangements the two molecules, without altering their internal geometry, previously obtained by energy minimizations separately performed for each monomer. In this case interaction ΔE^inter and binding ΔE^bind energies coincide, i.e.

ΔE^inter = E_AB − (E⁰_A + E⁰_B) = ΔE^bind (3)

where E_AB, E⁰_A and E⁰_B are the energy of the dimer AB in the considered conformation and the energy of the two monomers A and B at infinite distance.

Technically, when interaction and binding energies are estimated in the dimer geometry resulting from an optimization performed over the whole dimer, these quantities differ, being

ΔE^inter = E_AB − (E_A + E_B) (4)

and

ΔE^bind = E_AB − (E⁰_A + E⁰_B) = ΔE^inter + (ΔE_A + ΔE_B) (5)

where

ΔE_K = E_K − E⁰_K; K = A,B (6)

is the relaxation/distortion energy of monomer K.

All reference, DFT and MP2 calculations were performed with the GAUSSIAN09 package.⁷²

3. Results

3.1. MP2/mod basis set optimization

As a first step, the basis set to be used with MP2 calculation was tuned following the protocol below:

(i) p-Benzoquinone and hydroquinone monomers have been separately optimized at the B3LYP/aug-cc-pvDz level.

(ii) Four different quinhydrone classes were created, by assembling the previously optimized units varying the intermolecular distance and the relative orientation. Examples of each class are reported in Fig. 1.

(iii) For each class, different geometries were obtained by shifting p-benzoquinone along one direction (see the translation vector R in Fig. 1). The interaction energy for all the resulting conformations was initially computed at MP2/6-31G*(0.25) (ref. 15) level. It may be worth mentioning that no geometry optimization of the whole complex was yet performed at this point.

(iv) CCSD(T)/CBS calculations were performed for 12 quinhydrone conformations, three for each class. Conformations were chosen in the low repulsive region, in the minimum and at medium range attractive distance, with respect to the MP2/6-31G*(0.25) curves.

(v) The polarization exponent for the oxygen atom was then tuned through the EXOPT program, to minimize the energy difference between CCSD(T)/CBS values and those obtained at MP2 level with the tuned basis set. In this procedure, only the FF, SX and SF values were employed, whereas SZ interaction energies were excluded from the training set, with the aim of using them as a first validation of the MP2/mod performances.

The best exponent for oxygen atoms α_O results 0.44, almost half of its value (0.80) in the standard 6-31G* basis set. Reference and MP2/mod binding energies are reported in Table 1 for all geometries employed in the tuning, and for the SZ ones. A good overall agreement was found, being the standard deviation 0.6 kcal mol⁻¹, that improves the performances obtained with the original MP2/6-31G*(0.25,0.8) method (st. dev. ∼1 kcal mol⁻¹). In particular, the fact that MP2/6-31G*(0.25,0.44) energies computed for the SZ class (which was not included in the training set) are also very close to the CCSD(T)/CBS reference values, can be considered a first validation of the reliability of the MP2/mod method.

Table 1 Quinhydrone binding energies (kcal mol⁻¹) computed at CCSD(T)/CBS and MP2/mod level after the exponent optimization. In the last column the difference Δ is also reported. FF, SF SX, SZ labels refer to the geometrical arrangements reported in Fig. 1. The SZ geometries were not included in the training set

Conformation	R (Å)	ΔE^CCSD(T)CBS	ΔE^MP26-31G*(0.25,0.44)	Δ
FF	3.0	+0.49	+0.31	0.18
	3.4	−4.37	−4.73	0.36
	5.0	−1.26	−1.26	0.00
SF	4.4	+1.19	+2.41	−1.22
	4.8	−3.43	−2.94	−0.49
	6.0	−1.73	−1.61	−0.12
SX	1.2	−5.71	−6.01	0.30
	2.4	−4.08	−3.95	−0.13
SZ	1.2	−4.22	−4.53	0.31
	2.4	−5.24	−4.89	−0.35

---

3.2. Quinhydrone interaction curves

The binding energy curves for several quinhydrone arrangements have been computed at different level of theory and reported in Fig. 2, along with the reference CCSD(T)/CBS values. Preliminary tests were performed with the widely used B3LYP functional, with the aug-cc-pvDz basis set, previously employed in the geometry optimization of the separate units. As well known for the benzene molecule and other aromatic compounds,³⁹ standard DFT functionals do not provide stable stacked dimers, due to the lack in accounting for the correlation energy. As appears by looking at Fig. 2, the results for all of the considered quinhydrone geometries, where the two rings are in a stacked conformation (FF, SX and SZ), show the lack of attraction with respect to reference data, clearly indicating the importance of dispersion forces in stabilizing these arrangements. Conversely, similarly to benzene T-shaped conformations, the SF conformations show a definite well, due to favorable electrostatic interactions, but still the binding energy is underestimated with respect of the CCSD(T) values. Furthermore, the relevant role of correlation in the quinhydrone dimer can be also deduced by comparing the MP2 curves, obtained with a standard (aug-cc-pvDz) basis set, to the reference values. Indeed, as already reported in literature for many other aromatic dimers,^{16,17,22,27,64,65} MP2 tends to dramatically overestimate the binding energy in stacked arrangements, whereas works rather well for SF geometries, where correlation is expected to play a less determinant role. Turning to the two methods chosen to investigate quinhydrone interactions in this work, i.e. MP2/mod and M06-2X, they are both in very good agreement with the reference values. More in detail, MP2/mod gives slightly more attractive values, whereas the M06-2X functional tends to neglect some portion of the binding energies, in particular in the region on the right of the minima (in FF and SX classes). It may be worth noticing that the reduction of the basis set dimensions, obtained neglecting the f functions is well compensated by the CP correction, since the M06-2X/6-311+G(2df,2p) and M06-2X/6-311+G(2d,2p) curves are almost superimposed for all considered conformations.

Fig. 2 Quinhydrone interaction energy curves in four different arrangements computed at different levels of theory. Labels and translation vector R refer to Fig. 1. The M06-2X/6-311+G(2df,2p) and M06-2X/6-311+G(2d,2p) results are reported in black and brown curves, respectively.

As computational times are concerned, it appears from Table 2 that, thanks to the small basis set employed, the MP2/6-31Gmod calculations are far less expensive than M06-2X/6-311+G(2df,2p) ones. However, the well known DFT computational efficiency is confirmed by the CPU times obtained with the M06-2X/6-311+G(2d,2p), which are similar to the MP2 ones, notwithstanding the larger basis set employed. More important, both methods can be used for geometry optimizations of this complex and/or extensive sampling of the intermolecular potential energy surface (PES), while, despite the increased efficiency of modern computational resources, CCSD(T) methods still remain out of reach.

Table 2 Average CPU times obtained for quinhydrone by using different methods. All times refer to a single 2 GHz Intel® Xeon® processor

Method	Basis set	CPU time (hours)
a CCSD(T)/CBS are obtained by summing the computational times of all calculations involved in the CBS procedure.
CCSD(T)	CBS^a	1900
CCSD(T)	aug-cc-pvDz	1700
MP2	aug-cc-pvTz	180
MP2	aug-cc-pvDz	8
MP2	6-31G*(0.25,0.44)	1
M06-2X	6-311+G(2df,2p)	7
M06-2X	6-311+G(2d,2p)	1.5

---

However, to confidently employ MP2/mod and M06-2X in geometry optimizations of quinhydrone, some further validation tests should be carried out.

3.3. Validation

To confirm the reliability of the two methods, several calculations were performed for two other conformations, not considered in the training set. A first test was performed on the crystallographic geometry,⁴³ reported in the left panel of Fig. 3, which allows also for a comparison with previous literature findings.^46,54 All results are reported in Table 3, where it is apparent that both MP2/mod and M06-2X (with both basis sets) well agree with the computed CCSD(T)/CBS binding energy: the error of the WF based method is only of ∼0.2 kcal mol⁻¹, whereas the DFT approach overestimates the reference data by less than 0.8 kcal mol⁻¹. Conversely, the literature data tend to severely underestimate the stability of the dimer by about 3 kcal mol⁻¹, making the use of both standard basis set with MP2 and the MPW1B95 functional rather questionable. In particular, it may be worth noticing that if on the one hand it is confirmed that the use of rather large basis sets with MP2 (as 6-311++G(2d,2p),⁵⁴) leads to large overestimation of the binding energy, on the other the polarization exponents of the small 6-31G* set need to be suitably tuned to reproduce the reference CCSD(T) values.

Fig. 3 Quinhydrone geometries considered for validation of the MP2/mod and M06-2X methods. (a) Experimental crystalline geometry.⁴³ (b) Geometry obtained after a complete optimization in vacuo at the MP2/6-31G*(0.25,0.44) level. Some geometrical features as ring–ring distances or torsional dihedrals are reported in blue.

Table 3 Binding energies of the experimental crystalline dimer⁴³ (see Fig. 3, panel a) computed using different methods

Source	Method	Basis set	ΔE (kcal mol^−1)
This work	CCSD(T)	CBS	−5.67
Ref. 46	MP2	6-31G*	−2.70
Ref. 54	MP2	6-311++G(2d,2p)	−6.89
This work	MP2	6-31G*(0.25,0.44)	−5.86
Ref. 54	MPW1B95	aug-cc-pvTz	−2.25
This work	M06-2X	6-311+G(2df,2p)	−6.40
This work	M06-2X	6-311+G(2d,2p)	−6.20

---

A last, more stringent, validation may come from the comparison of the interaction and binding energies, computed at different levels of accuracy, on the optimized structure of the dimer. The optimization has been done by the MP2/mod method, starting from two different arrangements, taken from the local minima of the FF and SX curves of Fig. 2. Both calculations converged to a unique minimum (ΔE^inter = −12.7 kcal mol⁻¹), reported in the right panel of Fig. 3. The interaction and binding energies of such conformation were subsequently computed with both M06-2X and CCSD(T)/CBS methods. It is worth mentioning that the derivation of the relaxation/distortion ΔE_k energy at CCSD(T)/CBS level (see equation (6) and (1)–(2)), is not strictly defined, hence the ΔE^bind cannot be precisely computed from eqn (5). However, ΔE_k was computed for both monomers at CCSD(T)/aug-cc-pvDz level, resulting in a ΔE^bind_CCSD(T) value of −6.1 kcal mol⁻¹. From the results reported in Table 4, it appears once again that MP2/6-31G*(0.25,0.44) energies are in excellent agreement with CCSD(T)/CBS reference values. It should be noticed that the above mentioned optimization was carried out with and without considering CP correction. The results of the two calculations differ by less than 0.1 kcal mol⁻¹. From a different point of view, it can be inferred that geometry optimization performed with the MP2/mod method leads to very reliable geometries.

Table 4 Interaction (ΔE^inter) and binding energies (ΔE^bind) computed with different methods on the quinhydrone dimer geometry previously optimized at the MP2/6-31G*(0.25,0.44) level. The ΔE^bind value at CCSD(T)/CBS level is not reported as the calculation of the relaxation/distortion energy at CBS is not strictly defined

Method	Basis Set	ΔE^inter (kcal mol^−1)	ΔE^bind (kcal mol^−1)
CCSD(T)	CBS	−12.7	—
M06-2X	6-311+G(2df,2p)	−15.6	−7.3
M06-2X	6-311+G(2d,2p)	−13.9	−5.8
MP2	6-31G*(0.25,0.44)	−12.7	−6.2

---

Despite M06-2X/6-311+G(2df,2p) method is found to slightly overestimate the interaction energy, a complete quinhydrone optimization was performed also with this functional, and the resulting geometry showed no significant difference with respect to that obtained with the MP2 approach. In conclusion, both methods can be considered reliable in handling quinhydrone interactions and confidently used to investigate structural and/or spectroscopic features of this complex. It may be worth pointing out that if on the one hand MP2/mod method yields the best energy values, on the other hand the specific derivation of the employed basis set does not grant any transferability, and care should be taken in extending it to other molecules.

3.4. Energy contributions

A deeper insight into the nature of the different energy contributions responsible for quinhydrone stability could be obtained by adopting symmetry adapted perturbation theory (SAPT⁷³) or other energy decomposition analysis (EDA⁷⁴) techniques. However, the computational cost of such approaches is rather high, and their application goes beyond the scopes of the present work. Nonetheless, an analysis of the results obtained with the MP2/mod optimization can still be carried out. Two main differences arise between the optimized structure and both the crystal geometry and the investigated arrangements (FF, SX, etc.) reported in Fig. 3 and 1, respectively: the formation of rather strong H-bonds and the (consequential) rotation of the –OH bond out of the hydroquinones ring plane. More in detail, both dihedrals driving the OH rotation are found at 50°, and the OH⋯O distance is within the H-bond range (1.88 Å) for both protons. The formation of two Hydrogen bonds increases remarkably the interaction energy, reaching values larger than 10 kcal mol⁻¹. However, from a closer look to the different energy contributions (see Table 5), it seems that the role of the H-bonds is to pull both rings closer to each other, hence enhancing the correlation energy (E_corr), which increases, in absolute value, to more than 20 kcal mol⁻¹. Conversely, the electrostatic E_HF term increases, mainly because of the repulsive short range term. A further proof of this picture, may come by computing the energy on a dimer arrangement obtained from the optimized structure reported in Fig. 3, by rotating the –OH bonds to 0°, i.e. by making them coplanar with the aromatic ring. All energy contributions of such geometry are reported in the last row of Table 5. It appears that whereas the correlation energy remains almost constant, since the inter-ring distance was not varied, the E_HF contribution, which contains the H-bond energy, increases by 11.6 kcal mol⁻¹, because the planar constraint prevents the formation of intermolecular H-bonds, since the H⋯O distance increases to 2.5 Å. This also gives a rough estimate of the H-bond energy in the optimized complex of ∼6 kcal mol⁻¹ for each H-bond.

Table 5 Interaction energy contributions computed on different geometries at the MP2/6-31G*(0.25,0.44) level. The correlation energy is obtained as E_corr = ΔE_MP2 − ΔE_HF. All contribution are in kcal mol⁻¹

Geometry	ΔEMP2	Ecorr	ΔEHF
Crystal^43	−5.9	−12.0	6.1
FF (R = 3.4 Å)	−3.5	−9.2	5.7
Optimized	−12.7	−23.3	10.6
Optimized and planarized	−1.1	−24.7	23.6

---

A further contribution which was not accounted for in the previous analysis is the CT energy. Recently, Steinmann and coworkers⁷¹ have questioned the role of CT in stacked compounds. On the contrary, CT contribution has been invoked in previous works⁵⁴ to explain quinhydrone stability. To clarify this issue, as the optimized structure is concerned, Mulliken, ESP and NBO population analysis have been performed with both MP2 and M06-2X methods, and the results reported in Table 6. All methods employed to compute charge population density agree, both at MP2 and DFT level, in estimating the charge transfer, from hydroquinone to p-benzoquinone around 0.15 a.u. To get a deeper insight, charge populations have been computed also along the FF interaction curve, previously reported. Since the interaction energy in these configurations is smaller than the one considered in the optimized geometry, it is expected that also the CT effects will be reduced in intensity. Nevertheless, the comparison between the complexed structure and the separated units can help to investigate in more detail the mechanism of the transfer. From the computed values it results again that all three methods agree in indicating hydroquinone as the electron donor and p-benzoquinone as the electron acceptor, whereas the charge transfer seems to be not negligible only at the shorter distances (R < 3.5 Å). It is worth reminding that the minimum in the FF arrangement is around 3.4 Å: in the minimum region, the charge transfer is around 0.1 a.u., it increases to 0.15 by lowering the inter-ring distance down to 2.8 Å (repulsive intermolecular energy) and it drops to zero when the two units are drawn more than 3.5 Å apart. From this analysis it can be inferred that CT is not the main source of attraction between the quinhydrone forming units, while H-bond and dispersion forces play a much more determinant role.

Table 6 Sum of the point charges localized over the two monomers in the optimized quinhydrone dimer. Population analysis was performed with three different methods for both MP2 and M06-2X calculations. All charges are in a.u.

Monomer	MP2/6-31G*(0.25,0.44)			M06-2X/6-311++G(2d,2p)
	Mulliken	ESP	NBO	Mulliken	ESP	NBO
p-Benzoquinone	−0.14	−0.15	−0.14	−0.09	−0.15	−0.17
Hydroquinone	0.14	0.15	0.14	0.09	0.15	0.17

---

3.5. Spectroscopic properties

To further clarify the role of noncovalent forces on the properties of quinhydrone, exploiting the rather good agreement found between MP2/mod and DFT calculations, the latter method has been used to investigate its spectroscopic behavior. To this end, electronic absorption spectra have been computed through the time extension of the DFT theory, TD-DFT. In fact, this approach is extensively used^75–79 to investigate electronic spectra of organic compounds, and, among a plethora of functionals, M06-2X is often found to yield the best performances.⁷⁷ Thanks to the availability of extended computational and experimental data (see ref. 80 and references therein) on the absorption transition of p-benzoquinone, the TD-M06-2X reliability in the calculation of optical properties can be tested on one of the forming units of quinhydrone. This has been done by computing the first excited states and comparing them to available literature data, as reported in Table 7.

Table 7 Transition energies of p-benzoquinone for its first seven excited states, computed at different levels of accuracy. CIS, CISD and TD-B3LYP calculations were performed⁵⁵ with the 6-311+G(2d,p) basis set, whereas a specific basis set was employed in CASPT2 calculations.⁸⁰ Finally, all TD-M06-2X calculation performed in this work were carried out with the 6-311+G(2df,2p) basis set. All energies are in eV

Transition	CIS^55	CISD^55	TD-B3LYP^55	CASPT2 (ref. 80)	Exp.^80	This work
1	4.06	3.02	2.53	2.50	2.48	2.78
2	4.25	3.18	2.75	2.50	2.48	3.08
3	5.10	4.85	3.85	4.19	4.07	4.51
4	6.36	5.57	4.94	5.15	5.12	5.50
5	7.94	6.75	5.42	5.15	—	6.21
6	8.19	7.27	5.69	4.80	—	6.36
7	8.22	8.21	6.01	5.76	—	6.70

---

It is important to note that not all transitions are allowed, because the computed oscillator strength for most states are negligible, except for that relative to transition to the fourth excited state (0.3 and 0.4 for TD-B3LYP and TD-M06-2X calculations, respectively). It results that TD-M06-2X transition energies are in fair agreement with experimental data and higher level calculations (CASPT2 (ref. 80)), being systematically blue-shifted by 0.3–0.4 eV for all considered states. On the contrary, it may be worth noticing that in TD-B3LYP results⁵⁵ no systematic shift appears with respect to the reference values. Considering the rather good agreement obtained for the optical properties of p-benzoquinone, TD-M06-2X approach was used also to study the absorption spectrum of quinhydrone, as it should be capable to capture the main physics involved in the transitions.

To this end, TD-M06-2X vertical transition energies have been computed for the two units and for quinhydrone, in its vacuo optimized, crystalline and completely stacked conformations. The spectra are obtained by a convolution with Gaussian functions of 0.333 eV half width at half height and reported in Fig. 4 and 5. From the comparison, reported in Fig. 4, between the spectra of the isolated units and the one of the optimized quinhydrone it is apparent that upon complex formation, the absorption is shifted toward the visible region, and a broad band results in the 370–580 nm range. This is in partial agreement with experimental observations, where a change of color was registered upon complexation of benzo- and hydro-quinone species in 100% ethanol solution.⁵¹ Whereas benzoquinone species were found yellow in color and hydroquinone colorless, quinhydrone yields a brilliant purple color. If, on the one hand, the absorption in the visible region due to complexation is accounted for by M06-2X calculations, on the other hand the computed spectrum of benzoquinone does not show any absorption peak in the visible region. As a matter of facts, the first two computed transitions, reported in Table 7, lie in the visible region, but their contribution to the p-benzoquinone spectrum is null, since both their oscillator strengths are zero. As already noticed in ref. 55, taking into account vibronic contributions could overcome this lack, however this is beyond the scopes of the present work.

Fig. 4 TD-DFT electronic absorption spectra computed at the M06-2X/6-311++G(2d,2p) level, for p-benzoquinone (red line), hydroquinone (green line) and quinhydrone (blue line) in vacuo. The complex geometry is the one optimized with MP2/mod and shown in the right panel of Fig. 3.

Fig. 5 TD-DFT electronic absorption spectra computed at the M06-2X/6-311++G(2d,2p) level, for different arrangements of quinhydrone: in vacuo (blue line), FF (magenta) and in the crystalline geometry (dark green). It may be worth noticing that the inter-ring separation for the FF arrangement is 3.4 Å.

Turning to quinhydrone absorption, TD spectra have been computed also for three different arrangements, namely in vacuo optimized, the crystalline geometry reconstructed from X-ray data⁴³ (see Fig. 3) and a completely stacked one, i.e. in the minimum of the FF interaction curve. Results are shown in Fig. 5. It is apparent that the position and the intensity of the absorption peak in the visible region strongly depend on the relative orientation and on the inter-ring distance between the two monomers upon complexation. More in detail, it seems that a displacement that alters the perfect symmetry of the FF arrangement, without varying consistently the inter-ring separation (i.e. like the one that takes place in going from FF to the crystalline geometry) has the main effect of changing the intensity with minor effects on the band position. Conversely, decreasing the inter-ring separation (on going from crystal structure to the optimized geometry) leads to a not negligible red shift of the band. This remarkable dependence of the spectral properties on the complex conformation could be ascribed to a difference in the overlap of the π clouds of the two rings, hence to a variation on the balance of noncovalent interactions that have been found to characterize the complex stability.

To investigate the sensitivity of the absorption spectra to the extent of the π–π overlap, TD-DFT calculations have been performed on the geometries previously considered in the FF and the SX curves, thus exploring the response to the transverse (FF) and longitudinal (SX) perturbations to the overlap. Results are shown in Fig. 6. It appears that both the position of the vertical absorption peak and its intensity are indeed more sensitive to displacements along the normal of the ring planes (FF) than to shifts parallel to the rings (SX). Furthermore, these results agree with the ones reported by Tossell,⁵⁵ where an increase in absorption energy was accompanied by an increase in absorption intensity. Despite from an energetic point of view displacements of the SX type are more probable, as they involve much smoother gradients, large amplitude oscillations of the ring–ring separations should also be induced by temperature as shown by the computed FF interaction energy curves reported in Fig. 2. From the previous spectra, this motion is expected to broaden the absorption band up to wavelengths in the visible region, resulting in dark colors in agreement with the experiment.

Fig. 6 TD-DFT electronic absorption spectra computed at the M06-2X/6-311++G(2d,2p) level, for different arrangements of the quinhydrone dimer, obtained by varying the inter ring distance R in the FF conformation (lower panel) or the displacement in the SX geometry (upper panel). Both FF and SX classes refer to the conformations shown in Fig. 1.

4. Conclusions

The role of different kinds of noncovalent interactions, as hydrogen bond, dispersion and charge transfer on the formation and stability of quinhydrone in vacuo has been investigated by different computational methods. In particular, the M06-2X DFT functional and the MP2/mod method have been tested and validated against reference data, purposely obtained with CCSD(T) calculations extrapolated at the complete basis set limit. Both approaches result in good agreement with the reference calculations, as far as both structural and energetic features are concerned. More in detail, MP2/mod shows a better agreement with CCSD(T) values and it is computationally more efficient, although it requires some expensive calculation for the basis set tuning. However, care should be taken in extending the use of the MP2/mod purposely tuned basis set to other classes of molecular compounds, whereas M06-2X approach, although less accurate for quinhydrone, is indeed of more general applicability.

In agreement with experimental findings,⁴⁹ the H bond is found by both methods to play a relevant role in the complex stability, at least in absence of solvent. However, the competition of the hydrogen bonds that can take place between quinhydrone's forming moieties and those that can occur when protic solvents are employed certainly deserves further investigations, and some work in this direction is already in progress in our group. The importance of CT appears to be more controversial: in contrast with previous findings,⁵⁴ the amount of charge transferred from one monomer to another is 0.15 a.u. at most, and it seems a secondary effect with respect to both H-bond and dispersion forces. This well agrees with recent computational results,⁷¹ where the most important source of attraction was identified in dispersion interactions, which can be estimated only employing methods that correctly account for electron correlation. Indeed, the π–π interactions that can take place between the aromatic rings of the two units in the quinhydrone complex, are found to be dependent not only from the ring–ring separation but also from their relative orientation. In conclusion, the MP2/mod method resulted an useful tool to investigate a noncovalent complex as quinhydrone, as it correctly accounts, in a balanced manner, for most of the interactions that may compete in the stability of such aggregates. More important, its low computational cost, allows for employing it in geometry optimizations, extensive sampling of intermolecular PES's or calculations involving quinhydrone-like units, embedded in very large aromatic stacked complexes.

Finally, exploiting the possibility of employing the M06-2X functional in TD-DFT calculations, the role of noncovalent interactions in the peculiar quinhydrone spectroscopic behavior has been also investigated. It turns out that the overlap in the π clouds, which is both distance and orientation dependent, strongly affects the absorption transition energies, and may be responsible of the change of color experimentally found upon complex formation.

Acknowledgements

The Italian Ministry of Instruction, University and Research (MIUR) is acknowledged for financial funding through the PRIN 2010-11 project (PROxi).

References

1. A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, 1996.
2. I. G. Kaplan, The Interatomic Potential Concept and Classification of Interactions, in Handbook of Molecular Physics and Quantum Chemistry, ed. S. Wilson, P. F. Bernath and R. McWeeny, Wiley, Chichester, West Sussex, England, 2003.
3. V. A. Parsegian, Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists, Cambridge University Press, Cambridge, 2005.
4. J. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 2010.
5. Y. Ma, S. V. Kolotuchin and S. C. Zimmerman, J. Am. Chem. Soc., 2002, 124, 13757.
6. T. C. Dinadayalane, L. Gorb, T. Simeon and H. Dodziuk, Int. J. Quantum Chem., 2007, 107, 2204.
7. K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600.
8. P. J. Cragg, Supramolecular Chemistry – From Biological Inspiration to Biomedical Applications, Springer, Netherlands, 2010.
9. G. A. Jeffrey and W. Saenger, Hydrogen bonding in biological structures, Springer-Verlag, Berlin, 1994.
10. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210.
11. P. Hobza, R. Zahradník and K. Müller-Dethlefs, Collect. Czech. Chem. Commun., 2006, 71, 443.
12. K. Riley, M. Pitoňák, J. Černý and P. Hobza, J. Chem. Theory Comput., 2010, 6, 66.
13. G. Villani, ChemPhysChem, 2013, 14, 1256.
14. L. R. Rutledge, H. F. Durst and S. D. Wetmore, J. Chem. Theory Comput., 2009, 5, 1400.
15. J. Špóner, J. Leszczynski and P. Hobza, J. Phys. Chem., 1996, 100, 5590.
16. S. Tsuzuki, T. Uchimaru, K. Matsamura, M. Mikami and K. Tanabe, Chem. Phys. Lett., 2000, 319, 547.
17. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104.
18. M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, J. Am. Chem. Soc., 2002, 124, 10887.
19. J. Sponer, K. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2595.
20. M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200.
21. M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656.
22. C. D. Sherrill, T. Takatani and E. Hohenstein, J. Phys. Chem. A, 2009, 113, 10146.
23. A. Hasselmann and G. Jansen, J. Chem. Phys., 2005, 122, 014103.
24. A. Vasquez-Mayagoitia, C. D. Sherrill, T. Aprà and B. G. Sumpter, J. Chem. Theory Comput., 2010, 6, 727.
25. K. Riley and P. Hobza, J. Phys. Chem. A, 2007, 111, 8257.
26. S. Grimme, J. Chem. Phys., 2003, 118, 9095.
27. M. Pitoňák, P. Neogrády, J. Černý, S. Grimme and P. Hobza, ChemPhysChem, 2009, 10, 282.
28. S. Grimme, J. Comput. Chem., 2004, 25, 1463.
29. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
30. Y. Zhao and D. Truhlar, J. Chem. Theory Comput., 2007, 3, 289.
31. Y. Zhao and D. Truhlar, J. Chem. Phys., 2006, 125, 194101.
32. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
33. L. Rutledge, H. Durst and S. Wetmore, J. Chem. Theory Comput., 2009, 5, 1400.
34. E. Honenstein, S. Chill and C. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996.
35. M. Pitoňák and A. Heßelmann, J. Chem. Theory Comput., 2010, 6, 168.
36. A. Vazquez-Mayagoitia, C. D. Sherrill, E. Apra and B. G. Sumpter, J. Chem. Theory Comput., 2010, 6, 727.
37. B. K. Mishra, J. S. Arey and N. Sathyamurthy, J. Phys. Chem. A, 2010, 114, 9606.
38. L. A. Burns, A. Vázquez-Mayagoitia, B. G. Sumpter and C. D. Sherrill, J. Chem. Phys., 2011, 134, 084107.
39. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211.
40. J. Rezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9(5), 2151–2155.
41. F. Wöhler, Justus Liebigs Ann. Chem., 1844, 51, 145.
42. G. Ciamician and P. Silber, Ber., 1901, 34, 1350.
43. T. Sakurai, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 403.
44. J. De Boer and A. Vos, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 720.
45. K. Kalnish, R. Gadonas, V. Krasauskas, A. Pelakauskas and A. Pugzhlys, J. Photochem. Photobiol., A, 1994, 77, 9.
46. Y. Kurita, C. Takayama and S. Tanaka, J. Comput. Chem., 1994, 15, 1013.
47. D. T. Scott, D. M. McKnight, E. L. Blunt-Harris, S. E. Kolesar and D. R. Lovley, Environ. Sci. Technol., 1998, 32, 2984.
48. Y. Shigeta, Y. Kitagawa, H. Nagao, Y. Yoshioka, J. Toyoda, K. Nakasuji and K. Yamaguchi, J. Mol. Liq., 2001, 90, 69.
49. F. D'Souza and G. R. Deviprasad, J. Org. Chem., 2001, 66, 4601.
50. J. Regeimbal, S. Gleiter, B. L. Trumpower, C.-A. Yu, M. Diwakar, D. P. Ballou and J. C. Bardwell, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13779.
51. F. Ariese, S. van Assema, C. Gooijer, A. G. Bruccoleri and C. H. Langford, Aquat. Sci., 2004, 66, 86.
52. R. M. Cory and D. M. McKnight, Environ. Sci. Technol., 2005, 39, 8142.
53. J.-M. Lü, S. V. Rosokha, I. S. Neretin and J. K. Kochi, J. Am. Chem. Soc., 2006, 128, 16708.
54. M. J. G. Moa, M. Mandado and R. A. Mosquera, J. Phys. Chem. A, 2007, 111, 1998.
55. J. Tossell, Geochim. Cosmochim. Acta, 2009, 73, 2023.
56. C. Gambarotti, L. Melone, C. Punta and S. Shisodia, Curr. Org. Chem., 2013, 17, 1108.
57. M. D'Ischia, A. Napolitano, A. Pezzella, P. Meredith and T. Sarna, Angew. Chem., Int. Ed., 2009, 48, 3914.
58. Y. Tsuji, A. Staykov and K. Yoshizawa, J. Phys. Chem. C, 2012, 116, 2575.
59. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
60. A. Kuboyama and S. Nagakura, J. Am. Chem. Soc., 1950, 77, 8.
61. H. Valdes, K. Pluháčková, M. Pitoňák, J. Řezáč and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2747.
62. S. Arnstein and C. D. Sherrill, Phys. Chem. Chem. Phys., 2008, 10, 2646.
63. C. D. Sherrill, B. Sumpter, M. O. Sinnokrot, M. Marshall, E. Hohenstein, R. Walker and I. Gould, J. Comput. Chem., 2009, 30, 2187.
64. R. L. Jaffe and G. D. Smith, J. Chem. Phys., 1996, 105, 2780.
65. P. Hobza, H. L. Selzle and E. W. Schlag, J. Phys. Chem., 1996, 100, 18790.
66. I. Cacelli, C. Lami and G. Prampolini, J. Comput. Chem., 2009, 30, 366.
67. I. Cacelli, A. Cimoli and G. Prampolini, J. Chem. Theory Comput., 2010, 6, 2536.
68. I. Cacelli, A. Cimoli, P. R. Livotto and G. Prampolini, J. Comput. Chem., 2012, 33, 1055.
69. I. Cacelli, G. Cinacchi, G. Prampolini and A. Tani, J. Am. Chem. Soc., 2004, 126, 14278.
70. A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, H. Koch, J. Olsen and A. Wilson, Chem. Phys. Lett., 1998, 286, 243.
71. S. N. Steinmann, C. Piemontesi, A. Delachat and C. Corminboeuf, J. Chem. Theory Comput., 2012, 8, 1629.
72. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, P. V. Parandekar, N. J. Mayhall, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fo, Gaussian09, revision c.01, Gaussian, Inc., Wallingford CT, 2009.
73. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
74. R. J. Azar and M. Head-Gordon, J. Chem. Phys., 2012, 136, 024103.
75. Fundamentals of Time-Dependent Density Functional Theory, ed. M. A. L. Marques, F. M. S. Nogueira, E. K. U. Gross and A. Rubio, Springer-Verlag, Heidelberg, 2012.
76. V. Barone, R. Improta and N. Rega, Acc. Chem. Res., 2008, 41, 605.
77. S. S. Leang, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2012, 136, 104101.
78. R. Baer, L. Kronik and S. Kmmel, Chem. Phys., 2011, 391, 1.
79. C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845.
80. R. Pou-Amerigo, M. Merchan and E. Orti, J. Chem. Phys., 1999, 110, 9536.

---