The effect of drop size on contact angle measurements of superhydrophobic surfaces

Abstract

In this study, the effect of drop volume on contact angle (CA) values and also on the applicability of the Cassie–Baxter equation is experimentally investigated. To do this, dimethyldichlorosilane (DMDCS) coated different sized square pillar surfaces with varying f^CB_s(geo) values were used. Varying water drop volumes between 0.5 μl and 19 μl were used to measure CA's on square pillar surfaces with different pattern sizes changing from 8 μm to 40 μm. It was found that experimental CA values remained constant for each drop volume, indicating that increase or decrease in drop volume had no significant effect on experimentally measured CA values of square pillar surfaces with varying pattern sizes and f^CB_s(geo) values. When the relationship between the applicability of the Cassie–Baxter equation and the drop volume was investigated, it was also found that variation in volume of the drop did not cause a significant change in deviations between the theory and the experiments. Δθ^CB values remained almost constant for all samples at varying drop volumes.

---

1. Introduction

Contact angle (CA) measurements can be used quantitatively to determine the wettability of a solid surface by a liquid drop.^1–4 Surface chemical heterogeneity and roughness are the key parameters that affect the wettability of a solid surface. Surfaces that have water CA larger than 150° are called “superhydrophobic” and the tilt angle of the inclined plane used during CA measurements should be very low for superhydrophobic surfaces.^2–7 Superhydrophobic surfaces should also have small contact angle hysteresis (CAH) values, which is the difference between advancing (θ_a) and receding (θ_r) contact angles.^3–8

Firstly, Wenzel⁹ and Cassie–Baxter¹⁰ theories were developed to explain the effect of surface roughness and chemical heterogeneity on CA measurements. Both theories explained the equilibrium CA results of superhydrophobic surfaces depending on the liquid–solid interfacial contact area. However in 2007, Gao and McCarthy made a statement that Wenzel and Cassie–Baxter equations were wrong to be use to explain the CA behavior of water droplets on surfaces.¹¹ They experimentally showed that CA of water droplets on a surface is only dependent on the solid–liquid interaction at the three phase contact line alone and do not depend the liquid–solid interfacial area under the droplet. Similarly, Extrand displayed that experimental results of sessile drops suggest that the wetting is controlled by interactions on three phase contact line.¹² He also made simple experiments by using capillary tubes to demonstrate that the liquid–solid interfacial areas are not important in wetting phenomenon and showed that capillary forces acting in the vicinity of contact line controls the wetting.¹³ Erbil and Cansoy developed a simple method to test the applicability of Wenzel and Cassie–Baxter equations for superhydrophobic surfaces.¹⁴ According to their method, the Wenzel equation cannot be used for superhydrophobic surfaces especially for cylindrical pillar micro-structured surfaces other than a few exceptions. They also reported that according to their calculation results large deviations from Cassie–Baxter equation for the patterned surfaces were found and concluded that the Cassie–Baxter equation can be applied to superhydrophobic surfaces with caution.^8,14

In some theoretical publications, it is specified that volume of the liquid drop used in CA measurements is an important parameter to understand the applicability of Wenzel and Cassie–Baxter equations to chemically heterogeneous and rough surfaces.^15–18 In Wolansky and Marmur paper,¹⁵ they pointed out that CA value is in concordance with Wenzel equation in the case of an infinitely large drop compared with the scale of roughness.

In another Marmur paper, it is reported that with increasing the volume of the drop, the CA value is found to approach to the value predicted according to Cassie–Baxter equation.¹⁶ He also mentioned that, to assure the validity of Cassie–Baxter and Wenzel equations, using large drops is essential and also this minimizes the dependence of advancing and receding angles on drop volume.¹⁷ In 2009, Marmur and Bittoun¹⁸ commented on the findings of Gao and McCarthy.¹¹ They stated that, since the volume of the drops used in the experiments of Gao and McCarthy¹¹ were very small, their results contradicted with Cassie–Baxter and Wenzel equations and concluded that only relatively large drops are useful for the measurement of CA on rough or chemically heterogeneous surfaces. They^15–18 defined the relative size of the drop as the ratio of the diameter of the cylindrical drop before touching the solid, to the wavelength of surface heterogeneity. They explained the large drops as two or three orders of magnitude of the roughness scale. Oppositely to these comments, Shahraz et al.¹⁹ used drop volumes varying between 0.4 nl and 4.5 μl in their work and reported that increase in drop size also causes an increase in the experimentally measured CA values and in the case of using larger drops (the largest drop used in their work was 4.5 μl) CA values became larger when compared with Cassie–Baxter theory. However, when small drops (the smallest drop volume used in their work was 0.4 nl) were used, their experimental CA values were in agreement with Cassie–Baxter and Wenzel theories. Similarly, Bormashenko²⁰ theoretically explained in his publication that Young, Wenzel and Cassie–Baxter CA's are insensitive to external fields when interfacial tensions are independent of these fields under very general assumptions. He also demonstrated that these CA's are insensitive to drop sizes and shapes²¹ and even also to the rotation of the substrates.²²

The aim of this experimental work is to show the independency of CA results of superhydrophobic surfaces on the variation of drop volumes. To do this, dimethyldichlorosilane (DMDCS) coated square pillar structured surfaces with varying pattern sizes and also solid area fractions, were used to display the independency of drop volumes on experimentally measured CA results. DMDCS coated square pillar samples were prepared by deep reactive ion etching (DRIE) technique, as described before.⁸ Water drops with varying volumes between 0.5 μl and 19 μl (drop radiuses changing from 270 μm to 1175 μm) were used to measure CA values on square pillar surfaces. The measured CA values on the same patterned surface were approximately equal to each other for each drop volumes. These results showed that there is no effect of drop volume on the experimentally measured CA values on micro patterned superhydrophobic surfaces. In addition, the dependency of the deviations between Cassie–Baxter theory and the experimental data on drop volumes, (Δθ^CB), were also investigated for the patterned surfaces by using the derived equations in ref. 14. According to the calculation results, it was found that Δθ^CB values remained nearly constant for varying drop volumes for each square pillar surface.

2. Results and discussion

Square pillar samples were coded according to their dimensions as d_sidelengthS_sep.distanceh_height. Side length (d), separation distance (S), height (h), solid area fraction (f^CB_s(geo)) and the theoretical Cassie–Baxter CA's (θ^CB) of DMDCS coated square pillar surfaces were reported in Table 1. The difference between theoretical Cassie–Baxter CA and the experimentally measured CA value (Δθ^CB) can be calculated by using the equation,

Δθ^CB = θ^CB − θ^exp_e (1)

Table 1 Side length (d), separation distance (S), height (h), solid area fraction (f^CB_s(geo)) and theoretical Cassie–Baxter contact angle (θ^CB) of DMDCS coated square pillars

Sample code	d (μm)	S (μm)	h (μm)	f ^CBs(geo)	θ ^CB (°)
d 8.09 S 8.09 h 31	8.09	8.09	31	0.250	145
d 20.59 S 20.59 h 31	20.59	20.59	31	0.250	145
d 39.71 S 41.18 h 33	39.71	41.18	33	0.241	146
d 20.59 S 25.00 h 31	20.59	25.00	31	0.204	148
d 20.59 S 30.88 h 32	20.59	30.88	32	0.160	152
d 20.59 S 34.56 h 32	20.59	34.56	32	0.139	154
d 9.56 S 25.00 h 30	9.56	25.00	30	0.077	161

---

d _8.09 S _8.09 h ₃₁, d_20.59S_20.59h₃₁, d_39.71S_41.18h₃₃, d_20.59S_25.00h₃₁, d_20.59S_30.88h₃₂, d_20.59S_34.56h₃₂ and d_9.56S_25.00h₃₀ coded square pillar samples were used to investigate the effect of drop volume on CA results of superhydrophobic surfaces. Square pillar samples with solid area fractions varying from 0.007 to 0.250 and also pattern sizes changing between 8 μm and 40 μm were used to examine the drop volume effect on a wide range of superhydrophobic pillar structures.

To investigate the drop volume effect on each square pillar sample, equilibrium CA's (θ_e) with varying drop volumes were measured on each patterned surfaces. Water drops with volumes changing between 0.5 μl and 19 μl were formed on square pillar surfaces by using a HAMILTON syringe. The drop volume interval was determined depending on the limitations of the equipment used in CA measurements. Distortions in the spherical shape of the drop were also observed after the volume of 16 μl. In practice it is not convenient to use such large drop volumes in CA measurements. Contact radiuses of the sessile drops were varying between 270 μm and 1175 μm.

For the square pillar sample with the largest solid area fraction (f^CB_s(geo)) of 0.250 and the smallest pattern size of 8.09 μm (d_8.09S_8.09h₃₁), experimental θ_e values were measured 159° ± 2° for each drop volumes. As it is shown in the given plot in Fig. 2a, increase in drop volume did not change the experimentally measured θ_e values of d_8.09S_8.09h₃₁ sample and θ_e remained nearly constant as 159° ± 2°. Similar measurements were done for the square pillar sample with the same f^CB_s(geo) but larger pattern size of 20.59 μm (d_20.59S_20.59h₃₁). CA measurements were done with varying drop volumes of 0.5 μl to 19 μl and increase in water drop volume did not cause a change in θ_e value of the sample, as shown in Fig. 2b. θ_e values were measured 157° ± 2° and constant for d_20.59S_20.59h₃₁ sample for each drop volume. For the sample with the largest pattern size of 40 μm but approximately same f^CB_s(geo), (d_39.71S_41.18h₃₃), conformable results were obtained. Experimental θ_e values were measured 156° ± 2° for each drop volume for the d_39.71S_41.18h₃₃ sample and when drop volume increased from 0.5 μl to 19 μl, experimental CA remained constant as it is shown in Fig. 2c.

Fig. 1 SEM images of d_8.09S_8.09h₃₁, d_20.59S_20.59h₃₁, d_39.71S_41.18h₃₃, d_20.59S_25.00h₃₁, d_20.59S_30.88h₃₂, d_20.59S_34.56h₃₂ and d_9.56S_25.00h₃₀ samples with 1500× magnification.

Fig. 2 Variation of θ_e values with the change of water drop volumes for (a) d_8.09S_8.09h₃₁ (b) d_20.59S_20.59h₃₁ (c) d_39.71S_41.18h₃₃ samples.

The effect of drop volume on CA values of square pillar surfaces with smaller f^CB_s(geo) values such as 0.204 (d_20.59S_25.00h₃₁ sample), 0.160 (d_20.59S_30.88h₃₂ sample), 0.139 (d_20.59S_34.56h₃₂ sample) and 0.077 (d_9.56S_25.00h₃₀ sample) were also investigated. The variation of CA values with the increase of drop volume for d_20.59S_25.00h₃₁ sample with f^CB_s(geo) value of 0.204 was plotted in Fig. 3a. As it can be seen from the figure, θ_e values were measured as 157° ± 2° and constant for each drop volume from 0.5μ to 19 μl. Similar results were obtained for the other square pillar samples with smaller f^CB_s(geo) ratios and all plots were given in Fig. 3b–d. For d_20.59S_30.88h₃₂ sample with f^CB_s(geo) value of 0.160, θ_e values were measured as 157° ± 1° and constant for each drop volume (Fig. 3b), for d_20.59S_34.56h₃₂ sample which has a f^CB_s(geo) value of 0.139, measured CA values were also constant and was 158° ± 2° (Fig. 3c) for the drop volumes varying between 0.5 μl and 19 μl. Lastly, for d_9.56S_25.00h₃₀ sample which had the smallest f^CB_s(geo) value of 0.077, θ_e values were measured as 162° ± 2° and constant for varying drop volumes, as given in the plot in Fig. 3d.

Fig. 3 Variation of θ_e values with the change of water drop volumes for (a) d_20.59S_25.00h₃₁ (b) d_20.59S_30.88h₃₂ (c) d_20.59S_34.56h₃₂ and (d) d_9.56S_25.00h₃₀.

Consequently, varying water drop volumes between 0.5 μl and 19 μl were used to measure CA's on square patterned surfaces with different pattern sizes changing from 8 μm to 40 μm and also solid area fractions, f^CB_s(geo), varying between 0.077 and 0.250. As it was reported above, it was found that experimental CA values remained constant for each drop volume and these finding indicate that there is no effect of drop size on experimentally measured CA results of square patterned surfaces.

Furthermore, to analyze the effect of drop volume on the applicability of Cassie–Baxter equation, deviations between the theory and the experiment, (Δθ^CB), was also calculated for each drop volume, by using eqn (1). Theoretically calculated Cassie–Baxter CA (θ^CB) values of each patterned sample were reported in Table 1. Larger experimental θ_e values were measured on each square pillar sample when compared with theoretically calculated Cassie–Baxter CA's. However, for the d_9.56S_25.00h₃₀ sample with the smallest f^CB_s(geo) value of 0.077, theoretical and experimental CA values were almost similar. Decrease in f^CB_s(geo) values caused an increase in θ^CB values as it can be seen from Table 1, and this resulted in smaller deviations (Δθ^CB) between the experimental and theoretical results. In the case of larger experimental θ_e values, Δθ^CB values were negatively calculated. These results showed that there is a partial liquid–solid contact at the top layer of the pillars and water drop sits on air more than the calculated area fraction of the air from Cassie–Baxter equation.¹⁴ Oppositely, in the case of larger theoretical CA's than the experimental CA's, Δθ^CB values were calculated positive. This means that, liquid–solid contact area is more than the calculated full contact area at the top of the pillars and water drop also contacts with the lateral sides of the pillars to a specific depth.¹⁴ When experimental and theoretical CA's were equal, Δθ^CB was calculated zero.

When the change in drop volume versus Δθ^CB was plotted for the square pillar sample with the largest f^CB_s(geo) of 0.250 and the smallest pattern size of 8.09 μm (d_8.09S_8.09h₃₁) in Fig. 4a, it was found that Δθ^CB values did not change with the varying drop volume and remained nearly constant as Δθ^CB = |15° ± 3°|. Similarly, for both d_20.59S_20.59h₃₁ and d_39.71S_41.18h₃₃ samples with the similar f^CB_s(geo) values, the effect of water drop volume on Δθ^CB was also investigated (Fig. 4b and c). Δθ^CB values were calculated constant and |12° ± 2°| for d_20.59S_20.59h₃₁ and |10° ± 2°| for d_39.71S_41.18h₃₃ samples. As it is seen from Fig. 4b and c, the findings were similar with the results of d_8.09S_8.09h₃₁ sample and increase in drop volume did not vary Δθ^CB for both d_20.59S_20.59h₃₁ and d_39.71S_41.18h₃₃ samples.

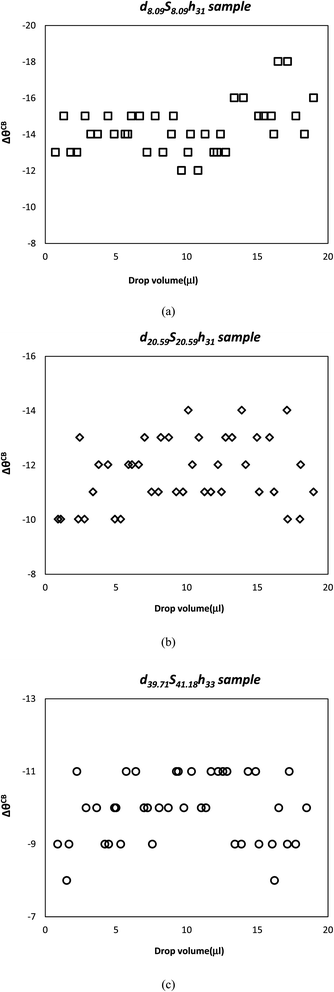Fig. 4 Variation of Δθ^CB values with the change of water drop volumes for (a) d_8.09S_8.09h₃₁ (b) d_20.59S_20.59h₃₁ and (c) d_39.71S_41.18h₃₃ samples.

In the case of smaller f^CB_s(geo) values such as 0.204, 0.160, 0.139 and 0.077, the effect of drop volume on Δθ^CB was also investigated and the results were in concordance with the samples that have larger f^CB_s(geo) values. Δθ^CB values remained almost constant (|9° ± 2°|) with the change of drop volume between 0.5 μl and 19 μl for d_20.59S_25.00h₃₁ sample (Fig. 5a). Similarly, Δθ^CB = |5° ± 1°| was calculated for d_20.59S_30.88h₃₂ sample (Fig. 5b), Δθ^CB = |4° ± 2°| for d_20.59S_34.56h₃₂ sample (Fig. 5c) and Δθ^CB = |0° ± 2°| for d_9.56S_25.00h₃₀ sample (Fig. 5d). This result indicated that experimentally measured and theoretically calculated CA's for d_9.56S_25.00h₃₀ sample were approximately equal to each other. Decrease in f^CB_s(geo) values also caused a decrease in Δθ^CB results showing that smaller deviations from Cassie–Baxter equation can be obtained only when f^CB_s(geo) was lower.⁸

Fig. 5 Variation of Δθ^CB values with the change of water drop volumes for (a) d_20.59S_25.00h₃₁ (b) d_20.59S_30.88h₃₂ (c) d_20.59S_34.56h₃₂ and (d) d_9.56S_25.00h₃₀ samples.

In summary, it is found that increase or decrease in drop volume has no significant effect on experimentally measured CA values of square pillar surfaces with varying pattern sizes and also f^CB_s(geo) values. Conversely to the discussions in the literature,^15–19 drop size did not affect the experimental CA's of chemically heterogeneous and rough surfaces. When larger drops with a volume of 19 μl were used to measure the experimental CA's on superhydrophobic surfaces, approximately equal CA values were measured similar to the measurements done with smaller drop volumes. When the concordance of experimental and theoretical Cassie–Baxter results were examined, it was found that increase in volume of the drop did not caused a significant change in deviations from the theory and Δθ^CB values remained constant for each sample. Δθ^CB values were negatively calculated for most of the patterned samples showing that larger experimental CA's were measured when compared with the theoretically calculated CA's. This result was similar to some part of ref. 19 conclusions where they reported that increase in drop size also caused an increase in the experimentally measured CA values and in the case of using larger drops (the largest drop used in their work was 4.5 μl) CA values became larger when compared with Cassie–Baxter theory. However, they found that their experimental results were in concordance with Cassie–Baxter and Wenzel theories when small drops such as 0.4 nl or 12 nl, were used. These drop volumes are very small and in practice cannot be used in CA measurements.

When f^CB_s(geo) values were low, a decrease was found in deviations between the experiment and the theory. According to these experimental findings, we cannot generalize that meaningful measurements of CA's on rough or chemically heterogeneous surfaces requires sufficiently large drops.¹⁸

3. Materials and methods

3.1. Preparation and hydrophobization of the square pillar samples

Regular square pillar surfaces with varying diameters and separation distances and constant heights of approximately 32 μm ± 2 were prepared by DRIE techniques as described in previous work.⁸ Square patterned surfaces used in this work have varying f^CB_s(geo) values between 0.077 and 0.250. These surfaces were hydrophobized by using dimethyldichlorosilane (FLUKA) coating as described before.⁸

3.2. Contact angle measurements

Apparent CA's (θ_e) of water drops were measured under air by using KSV Attension Theta Lite Optical Tensiometer with manually controlled HAMILTON syringe. MERCK spectroscopic grade water was used to measure all apparent CA values. Water drops with varying volumes between 0.5 μl and 19 μl were formed on each square pillar surface. Volume of the drops was controlled by checking the height of the drop during the CA measurements by using the software of the optical tensiometer. All apparent CA values were measured at room temperature (23 ± 2 °C) and 3 different measurements were done for each volume and each sample. Average CA results were reported with standard deviations of ±2° and all measured apparent CA values are in concordance with the CA values reported in previously published work.⁸ The contact angle measured on flat DMDCS coated surface was θ_e = 106° and this value was used in calculations of theoretical Cassie–Baxter contact angles.

3.3. Scanning electron microscopy (SEM)

SEM images of all square pillar surfaces were taken by using JEOL JSM-7500F SEM with ×1500 magnification and 45° tilt angle. SEM images of the square pillar samples are given in Fig. 1.

4. Conclusions

In this work, it was experimentally shown that CA results of micro patterned superhydrophobic surfaces were not dependent on the variation of drop volumes. It was found that experimental CA values remained constant for every drop volume varying between 0.5 μl and 19 μl. However, distortions in the spherical shape of the drop were also observed after the drop volume of 16 μl. In practice it is not convenient to use drop volumes smaller than 3–4 μl or larger than 10 μl in CA measurements, acceptable drop volumes used in CA measurements generally vary between 5 μl and 10 μl. However, experimental results showed that measured CA's did not vary depending on drop volumes used. According to the findings, it was shown that increase or decrease in drop volume has no significant effect on experimentally measured CA values of square pillar surfaces with varying pattern sizes and f^CB_s(geo) values.

The effect of drop volume on applicability of the Cassie–Baxter equation was also investigated within this study. Larger experimental θ_e values compared to the theoretical Cassie–Baxter CA's were measured on each square pillar sample for each drop volume, except for the smaller f^CB_s(geo) values. In order to calculate smaller deviations from Cassie–Baxter equation, patterned surfaces with lower f^CB_s(geo) should be used. Increase in volume of the drop did not change the deviations from the theory significantly, and Δθ^CB values remained constant with the increase of drop size for each square pillar sample with varying f^CB_s(geo) values.

Acknowledgements

The author would like to thank to Mr Bahadir BAYRAK from TERRALAB, for providing KSV Attension Theta Lite Optical Tensiometer used in this work. Also, I would like to thank to METU-MEMS Centre for preparing square pillar samples and SEM images.

References

1. H. Y. Erbil, Surface Chemistry of Solid and Liquid Interfaces, Blackwell Publishing, Oxford, UK, 2006.
2. H. Y. Erbil, A. L. Demirel, Y. Avci and O. Mert, Science, 2003, 299, 1377.
3. D. Oner and T. J. McCarthy, Langmuir, 2000, 16, 7777.
4. G. McHale, N. J. Shirtcliffe and M. I. Newton, Langmuir, 2004, 20, 10146.
5. W. Li and A. Amirfazli, J. Colloid Interface Sci., 2005, 292, 195.
6. M. Callies, Y. Chen, F. Marthy, A. Pepin and D. Quere, Microelectron. Eng., 2005, 78–79, 100.
7. B. Bhushan and Y. C. Jung, Ultramicroscopy, 2007, 107, 1033.
8. C. E. Cansoy, H. Y. Erbil, O. Akar and T. Akin, Colloids Surf., A, 2011, 386, 116.
9. R. N. Wenzel, Ind. Eng. Chem., 1936, 28(8), 988.
10. A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546.
11. L. Gao and T. J. McCarthy, Langmuir, 2007, 23, 3762.
12. C. W. Extrand, Langmuir, 2003, 19(9), 3793.
13. C. W. Extrand and S. I. Moon, Langmuir, 2012, 28, 15629.
14. H. Y. Erbil and C. E. Cansoy, Langmuir, 2009, 25(24), 14135.
15. G. Wolansky and A. Marmur, Colloids Surf., A, 1999, 156, 381.
16. S. Brandon, N. Haimovich, E. Yeger and A. Marmur, J. Colloid Interface Sci., 2003, 263, 237.
17. A. Marmur, Soft Matter, 2006, 2, 12.
18. A. Marmur and E. Bittoun, Langmuir, 2009, 25, 1277.
19. A. Shahraz, A. Borhan and K. A. Fichthorn, Langmuir, 2012, 28, 14227.
20. E. Bormashenko, Colloids Surf., A, 2009, 345, 163.
21. E. Bormashenko, J. Colloid Interface Sci., 2011, 360, 317.
22. E. Bormashenko, Colloids Surf., A, 2013, 432, 38.

---