High-pressure close-packed structure of boron

Abstract

Based on ab initio evolutionary algorithms, a high-pressure close-packed phase of boron with hexagonal P6₃/mcm symmetry is predicted, named as B₁₀, which is stable over α-Ga phase above 375 GPa to at least 500 GPa. High pressure makes the typical B₁₂ icosahedron collapse to form an incompressible linear atomic chain arrangement together with an isosceles triangle arrangement. The electron localization function calculations confirm that the B₁₀ has strong covalency in this special atomic arranged structure. The vibration of the three atom's isosceles triangle in the framework of linear atomic chains induces an unusual superconductivity in B₁₀. Electron–phonon calculations indicate that electron–phonon coupling parameter λ is 0.82 and the superconducting critical temperature is 44 K at 400 GPa.

---

Introduction

Boron is a fascinating and important element because of its chemical complexity in nature. Many pure polymorphs of boron have been reported such as α-boron,¹ rhombohedral β-boron,^2,3 and orthorhombic γ-B₂₈.^4–6 The B₁₂ icosahedron is an extremely important unit in those boron polymorphs with an incompact atomic arrangement, which is necessary for forming denser phases. Under pressure, the B₁₂ icosahedra are compressed into much denser forms. A much denser phase should be more stable at high temperature and high pressure.⁴ The metallic α-Ga (ref. 7) phase is the densest phase composed of the modification of B₁₂ icosahedra. Unique structure makes the boron have many unique properties among elemental materials. The abnormal ionicity has been found in identical atoms chemically bonded boron phase. The maximum ionicity of boron–boron bonds occurs between polar atoms of two neighboring icosahedron in α-boron.⁸ The ionicity of boron–boron bonds in icosahedra is responsible for the decrease in hardness of α-boron. The γ-B₂₈ structure resembles a NaCl-type structure. The ionicity can be reflected by the B₁₂ icosahedra ‘anions’ and B₂ pairs ‘cations’. The ionicity of γ-B₂₈ affects its electronic and optical properties.⁴ The high-pressure phase of boron presents metallic properties. The α-Ga structure was regard as the metallic phase of boron. It is more stable than other usual metallic phases (bct, fcc) in energy.⁷ The electron–phonon calculations show that the α-Ga phase is superconducting with a low electron–phonon coupling parameter (∼0.39).⁹ Recently, high-pressure research reveals that many simple elements have unique properties under high pressure. The molecular form of nitrogen transforms to single-bonded cubic form at temperature above 2000 K and pressures above 110 GPa.¹⁰ The sodium transforms to a transparent dielectric at pressures above 200 GPa because of the emergence of p–d hybridizations of valence electrons and their repulsion by core electrons into the lattice interstices.¹¹ Simple lithium also shows a complex structural behavior. An unusual metal to semiconductor transition has been found in high pressure.^12,13 Boron is located in the juncture of metals and insulators in the periodic table. Upon high pressure, the bonding properties and electronic behavior of simple boron are very interesting. The form of B₁₂ icosahedron under high pressure is still not clearly. The search for possible superconducting phase of boron under high pressure is very important for low-Z elements. So it is desirable to solve the crystal structure of boron under high pressure.

In this paper, by means of the ab initio evolutionary algorithm (USPEX method), we predict a new high pressure close-packed phase of elemental boron with P6₃/mcm symmetry under hydrostatic pressure that has very intriguing physical properties. We call this novel hexagonal high-pressure phase as B₁₀. The B₁₂ icosahedron collapses in this high pressure phase. This structure is more energetically favorable than α-Ga phase above 375 GPa. The calculation of electron localization function and Mulliken overlap population confirms the existence of various strong covalent bonds in B₁₀. There are linear atomic chains along the c-axis, which make B₁₀ have a highly incompressible property. Electronic structures reveal that it is a metal. The electron–phonon calculations indicate that the B₁₀ phase is superconducting with a high critical temperature (T_c = 44 K@400 GPa) among the low-Z elements, induced by structure modulation.

Computational details

Most calculations are performed within the density functional theory,^14,15 carried out within the Vienna ab initio simulation package (VASP),^16,17 with the projector augmented wave method.¹⁸ The 2s²2p¹ electrons are treated as valence electrons. The generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) functional¹⁹ for the exchange correlation is employed. The plane-wave cutoff energy is taken as 1400 eV. A Gamma-point-centered k-mesh of 12 × 12 × 14 k-point sampling is used for the calculations. The geometries are optimized when the remanent Hellmann–Feynman forces on the ions are less than 0.01 eV Å⁻¹. The calculation of electron–phonon coupling (EPC) parameter λ are performed using the pseudopotential plane-wave method within the density functional perturbation theory as implemented in the PWscf code.²⁰ A 7 × 7 × 8 q-point mesh in the first Brillouin zone is used in the EPC calculation. The technique for the calculation of EPC has been described in detail in our previous publication.^21,22 A grid of 20 × 20 × 24 is used to ensure k-point. The Mulliken population calculation is performed by CASTEP code.²³ The details of convergence tests have been described elsewhere.^22,24–26

Results and discussion

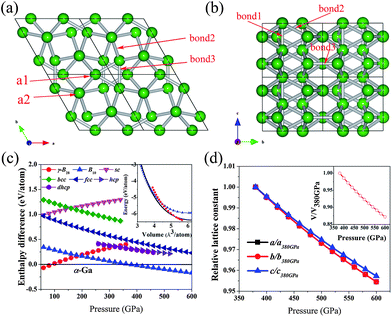
Using ab initio evolutionary algorithm,^27–29 we perform variable-cell structure prediction simulations for boron containing two-twenty atoms in the simulation cell at 100, 200, 300, 400 and 500 GPa, respectively. Our simulations reveal a novel hexagonal structure B₁₀ with P6₃/mcm symmetry as depicted in Fig. 1(a and b). There are 10 atoms in its unit cell. At 400 GPa, the equilibrium lattice parameters are a = 3.73 Å, c = 2.89 Å. Within this structure, two inequivalent atoms occupy the crystallographic 6g and 4d sites in the unit cell, which are (0.751, 0.0, 0.25) (a1) and (0.333, 0.667, 0.0) (a2) positions.

Fig. 1 (a and b) The crystal structure of B₁₀. (c) The enthalpies per atom of γ-B₂₈, B₁₀ and normal high-pressure phases of simple elements as functions of pressure with respect to α-Ga phase. The energy dependence of cell volume is shown in the inset. (d) Pressure dependence of lattice constants a, b, and c for B₁₀. The pressure dependence of cell volume is also shown in the inset.

The B₁₀ is composed of three-atom's isosceles triangles (composed of a1 positions) and linear atomic arranged chains (composed of a2 positions) which are the unit elements of B₁₀ and can be clearly observed in B₁₀. And B₁₀ can be thought as the linear atomic chains are surrounded by isosceles triangles with a little rotation in different layers. The enthalpy difference curves (relative to α-Ga phase) as a function of pressure for various structures are presented in Fig. 1(c). It can be found that the γ-B₂₈ phase transforms to α-Ga phase at 89 GPa, which is consistent with previously report.⁴ And the α-Ga phase transforms to B₁₀ at 375 GPa. The calculated total energy per atom against the volume per atom for γ-B₂₈, α-Ga phase and B₁₀ gives the same conclusion as shown in the insert of Fig. 1(c). The Fig. 1(c) also shows that the closed-packed B₁₀ structure is more stable than other normal high-pressure structures of simple elements. We have calculated the phonon dispersion within a wide pressure range up to 500 GPa. No imaginary frequencies are observed throughout the whole Brillouin zone, confirming dynamically structural stability of B₁₀. The B₁₀ is stable at above 375 GPa and up least to 500 GPa. However, the B₁₀ cannot be quenched down to ambient conditions because of the presence of imaginary frequencies at lower pressures. The standard B₁₂ icosahedrons of γ-B₂₈ transform to a defective forms in α-Ga phase. In the last, the B₁₂ icosahedron collapses in B₁₀. There are three types of bonds in B₁₀ as shown in Fig. 1(b). The lengths of bonds in B₁₀ are 1.436, 1.597, and 1.606 Å. The shortest bonds (bond 1) are located in the linear atomic chains, connecting two adjacent atoms along c axis. The shortest bonds indicate that a very strong interaction in two adjacent atoms of the linear atomic chains. The linear atomic chains are very important for the structural stability of B₁₀ and can give a strong support for B₁₀ along c-axis direction. The predicted pressure dependence of lattice constants confirms this point. As shown in Fig. 1(d), the c axis is the most incompressible crystallographic direction, while a and b axes exhibit similar compressibility. The pressure dependence of cell volume is also shown in the inset. The calculated ratio B/G (bulk modulus/shear modulus) of B₁₀ is 1.76 at 400 GPa. With the pressure increasing, the value of B/G is also increasing. At 500 GPa, the value reaches to 1.86, indicating that the pressure effect makes the ductility of the B₁₀ phase increase, because a high (low) B/G value is associated with ductility (brittleness), and the critical value which separates ductile and brittle materials is about 1.75.³⁰ The compressibility and ductility of B₁₀ are all related to the chemical bonds.

To get quantitative intensity of bonds in B₁₀, the Mulliken overlap population,³¹ bond length, are calculated as shown in Table 1. The length of shortest bonds in B₁₀ is 1.436 Å at 400 GPa, which is much smaller than that of the other phases, indicating that the linear atomic chain arrangement of B atoms is the most compact atomic arrangement in the phases of boron. The Mulliken overlap population for the three types of bonds in B₁₀ are 0.38, 0.42, and 0.47 as shown in Table 1. The Mulliken overlap population is widely used as a measure of the covalency of a material.³¹ The maximum Mulliken overlap population 0.47 of boron–boron bonds (bond 1) occurs in the linear atomic chains, which indicates that those bonds have stronger covalency among the bonds of B₁₀. However, an abnormal phenomenon is found that the length of bond 3 with the medium Mulliken overlap population (0.42) is 1.606 Å, which is larger than that of bond 2 (1.597 Å). This is very different from our normal understanding that the longer bonds have the weaker interaction. It is interesting to note that under compression, the B atom arrangement is more compact and the B₁₂ icosahedron disappears in B₁₀ phase. The interaction of B atoms becomes stronger than that in low-pressure. However, the types of bonds in B₁₀ are still not clearly.

Table 1 Calculated Mulliken population POP, bond length d from first-principles calculations at 400 GPa

Bond	POP	d (Å)
Bond 1	0.47	1.436
Bond 2	0.38	1.597
Bond 3	0.42	1.606

---

In order to analysis the features of bonds in B₁₀ and to get the reason of the abnormal phenomenon, we calculate the electron localization function (ELF)^32–34 of B₁₀. The isosurface of the electron localization function of B₁₀ is shown in Fig. 2. As we know, the ELF has value between 0 and 1, where 1 corresponds to the perfect localization and 0.5 corresponds to electron-gas-like pair probability.³² It is found that the isosurface of ELF with isovalue ELF = 0.5 forms a three-dimensional network as shown in Fig. 2(a and b). The value of the localization function remains nearly constant in this isosurface. This is the characteristic of the metallic materials indicating that the B₁₀ is a metallic phase.

Fig. 2 (a and b) The isosurface of the electron localization function of B₁₀ with isovalue 0.5. (c and d) The isosurface of the electron localization function of B₁₀ with isovalue 0.75.

With the isovalue increasing to ELF = 0.75, the localization domain reduces to several localization domains containing fewer attractors as shown in Fig. 2(c and d), which is very important to classify the chemical bonds as depicted in ref. 33. There is one bond attractor between the core-attractors of the atoms involved in the bond, which is consistent with the covalent bonding. The attractor between two atoms of the isosceles triangle is located in the middle of the bond, forming a symmetrical distribution (be marked as u) as a show in Fig. 2(c). The attractor between two atoms in linear atomic arranged chains is also located in the middle of bond (be marked as v). However, there is an especial attractor between linear atomic arranged chain and the isosceles triangle which is an asymmetrical distribution (be marked as w) as shown in Fig. 2(c and d). The attractor w is smaller than that (u) in the isosceles triangle. An asymmetrical distribution of attractor between linear atomic chain and the isosceles triangle atoms makes the bond 2 form a weaker covalent bond in B₁₀. Whereas the symmetrical distribution of attractor u in the isosceles triangle make the bond 3 form a stronger covalent bond. This can explain that the bond 3 has larger bond length but has a large Mulliken overlap population than the bond 2. The bond 1 has a symmetrical largest attractor v among the bonds of B₁₀, indicating the bond 1 is the strongest covalent bond in B₁₀. As a result, the B₁₀ has a highly incompressible property in c-axis direction and strong ductility.

The calculated electronic band structure and density of state (DOS) for the B₁₀ structure at 400 GPa reveal again that the B₁₀ is metallic because of the finite DOS at the Fermi level (E_f) as shown in Fig. 3(a). The strong hybridization between s and p orbitals especially in conduction bands is found. Note that many bands crossing Fermi level, which lead to a larger electronic DOS at the Fermi level N(E_f). This larger N(E_f) could contribute to a higher T_c. The phonon DOS and phonon dispersion curves of B₁₀ are depicted in Fig. 3(b). The acoustic modes are pictured in red line. The acoustic and optical modes are separated by dot line at 17 THz in the phonon DOS. The absence of imaginary frequencies in the phonon DOS and phonon dispersion curves suggests that the B₁₀ structure is dynamically stable.

Fig. 3 (a) Calculated electronic band structure and partial density of state of B₁₀ at 400 GPa. (b) Phonon dispersion and total phonon DOS of B₁₀ at 400 GPa. (c) The Eliashberg phonon spectral function, the integrated electron–phonon spectral coupling parameter λ at 400 GPa. (d) The projected phonon DOS of B₁₀ at 400 GPa.

We now discuss the superconductivity in B₁₀. The calculated phonon DOS projected on linear atomic chain and isosceles triangle atoms for B₁₀ at 400 GPa is compared to the Eliashberg phonon spectral function α²F(ω)/ω (ref. 35) and the integrated electron–phonon spectral coupling (EPC) parameter λ in Fig. 3(c). The acoustic mode constitutes 56% of the total λ. The remaining parts of the λ are derived from the optical mode. Both the acoustic and optic modes can contribute the superconductivity of B₁₀. The calculated EPC parameter λ is 0.82, indicating that the EPC of B₁₀ is very strong, and the phonon frequency logarithmic average ω_log calculated directly from the phonon spectrum is 892 K. To estimate T_c, the standard effective Coulomb repulsion parameter μ* value is used. Using μ* = 0.1, the critical temperature T_c for B₁₀ structure, estimated from the Allen-Dynes modified McMillan equation,³⁶ is 44 K, compared to the famous superconductor MgB₂.³⁷ And the EPC of B₁₀ phase is much stronger than the α-Ga phase which has smaller λ value of 0.38, 0.39, and 0.39 at 160, 215, 273 GPa by ab initio calculations.⁹ The T_c of B₁₀ phase is also higher than the experimental observed value (11.2 K) at 250 GPa.³⁸ As we know, the superconducting temperature of the elemental oxygen is only 0.6 K under high pressure.³⁹ One of sulphur at 93 GPa is 10 K.⁴⁰ Lithium has the highest observed T_c value (20 K) at 48 GPa in elemental materials.⁴¹ So the T_c of B₁₀ phase is also larger among the elemental materials. The stronger s–p hybridization's bonds are probably responsible for the stronger λ of B₁₀ phase.

In order to study the relations between the crystal structure and its superconductivity, the projected phonon DOS of B₁₀ for isosceles triangle and linear atomic chain atoms are calculated, shown in Fig. 3(d). It is found that the phonon DOS at the range of 0–17 THz is composed of the isosceles triangle atoms and linear atomic chain atoms as shown in Fig. 3(c). However, the contribution of isosceles triangle atoms is a little higher than that of linear atomic chain atoms. So the vibration of isosceles triangle atoms contributes a little bigger part than that of linear atomic chain atoms for the acoustic part of λ. The distribution of total phonon DOS at range of 17–45 THz is major composed of isosceles triangle atoms. So the vibration of isosceles triangle atoms is very important for the optical part of λ. The phonon DOS at the frequency range of 45–60 THz is only contributed by the linear atomic chain atoms, but their contribution for EPC is obviously very small as shown in the Eliashberg phonon spectral function α²F(ω)/ω and the integrated electron–phonon spectral coupling (EPC) parameter λ. However, the vibration of linear atomic chains has a smaller effect for EPC in the whole frequency range. The vibration of linear chains above 50 THz has little contribution to EPC, nearly be negligible because of the restriction of shortest covalent bonds. So it is concluded that the vibration of isosceles triangle units in the framework of linear atomic chains is responsible for the stronger λ of B₁₀ phase. The pressure dependence of T_c and λ for B₁₀ is shown in Fig. 4(a). The T_c of B₁₀ decreases with the pressure increasing. At 500 GPa, the T_c value is 34 K. According to the McMilan equation, the λ and ω_log are two important factors for the T_c. The variation of T_c follows the same trend as that of λ. But the T_c and ω_log show an almost opposite evolution with pressure. The N(E_f) is a less important factor, decreasing upon compression as shown in the insert of Fig. 4(a). So the reduction of T_c is mainly affected by λ. Moreover, evolution of the spectral function is a reflection of phonon behaviors. As pressure increases, the spectral function curves shift to high frequency ranges as shown in Fig. 4(b). A clear phonon frequency harden is observed. The insert of Fig. 4(b) shows that the λ decreases during the phonon frequency harden. So the phonon frequency harden results in a decreased T_c of B₁₀ upon compression.

Fig. 4 (a) Calculated pressure dependence of T_c and λ. The inset shows the evolution of logarithmic average phonon frequency and electronic DOS at the Fermi level N(E_f) with pressure. (b) The Eliashberg phonon spectral function α²F(ω)/ω of B₁₀ at selected pressures. The electron–phonon coupling integral λ(ω) is plotted in the inset.

Conclusions

In conclusion, we have predicted a high pressure close-packed phase of boron with space group P6₃/mcm. We name it as B₁₀, which has an incompressible atomic arrangement because of the linear atomic chains. This high pressure phase is stable over α-Ga phase above 375 GPa. Both electron localization function and Mulliken overlap population confirm strong covalent bond's characteristic in B₁₀. The calculations on the electronic and dynamics properties of B₁₀ show that it is a metal and stable in the range of 375 up to 500 GPa at least. The EPC calculations indicate that B₁₀ is a superconductor with a high transition temperature (T_c = 44 K). The modulation of the framework of linear atomic chains is responsible for the stronger λ of B_10. The phonon frequency harden results in a decreased T_c of B₁₀ upon compression. The current study has deeply implications on high-pressure phase of other simple substances.

Acknowledgements

The authors wish to thank Aitor Bergara for much valuable discussions. This work was supported by the National Basic Research Program of China (no. 2011CB808200), Program for Changjiang Scholars and Innovative Research Team in University (no. IRT1132), the National Natural Science Foundation of China (no. 51032001, 11074090, 10979001, 51025206). Parts of calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.

Notes and references

1. R. Lazzari, N. Vast, J. M. Besson, S. Baroni and A. Dal Corso, Phys. Rev. Lett., 1999, 83, 3230.
2. D. E. Sands and J. L. Hoard, J. Am. Chem. Soc., 1957, 79, 5582.
3. R. E. Hughes, C. H. L. Kennard, D. B. Sullenger, H. A. Weakliem, D. E. Sands and J. L. Hoard, J. Am. Chem. Soc., 1963, 85, 361.
4. A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863 ( Nature , 2009 , 460 , 292 ).
5. E. Yu. Zarechnaya, L. Dubrovinsky, N. Dubrovinskaia, N. Miyajima, Y. Filinchuk, D. Chernyshov and V. Dmitriev, Sci. Technol. Adv. Mater., 2008, 9, 044209.
6. E. Y. Zarechnaya, L. Dubrovinsky, N. Dubrovinskaia, Y. Filinchuk, D. Chernyshov, V. Dmitriev, N. Miyajima, A. El Goresy, H. F. Braun, S. Van Smaalen, I. Kantor, A. Kantor, V. Prakapenka, M. Hanfland, A. S. Mikhaylushkin, I. A. Abrikosov and S. I. Simak, Phys. Rev. Lett., 2009, 102, 185501.
7. U. Haussermann, S. I. Simak, R. Ahuja and B. Johansson, Phys. Rev. Lett., 2003, 90, 065701.
8. J. He, E. Wu, H. Wang, R. Liu and Y. Tian, Phys. Rev. Lett., 2005, 94, 015504.
9. Y. Ma, J. S. Tse, D. D. Klug and R. Ahuja, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 214107.
10. M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Nat. Mater., 2004, 3, 558–563.
11. Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182.
12. T. Matsuoka and K. Shimizu, Nature, 2009, 458, 186–189.
13. J. Lv, Y. Wang, L. Zhu and Y. Ma, Phys. Rev. Lett., 2011, 106, 015503.
14. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
15. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
16. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
17. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
18. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
19. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
20. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. d. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
21. X. Jin, X. Meng, Z. He, Y. Ma, B. Liu, T. Cui, G. Zou and H.-K. Mao, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9969.
22. D. Duan, F. Tian, Z. He, X. Meng, L. Wang, C. Chen, X. Zhao, B. Liu and T. Cui, J. Chem. Phys., 2010, 133, 074509.
23. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
24. X. Wang, K. Bao, F. Tian, X. Meng, C. Chen, B. Dong, D. Li, B. Liu and T. Cui, J. Chem. Phys., 2010, 133, 044512.
25. F. Tian, J. Wang, Z. He, Y. Ma, L. Wang, T. Cui, C. Chen, B. Liu and G. Zou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235431.
26. H. Lu, Y. Mu and S. Li, ACS Nano, 2013, 7, 879.
27. A. R. Oganov, C. W. Glass and S. Ono, Earth Planet. Sci. Lett., 2006, 241, 95.
28. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
29. C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713.
30. S. F. Pugh, Philos. Mag., 1954, 45, 823.
31. M. D. Segall, R. Shah, C. J. Pickard and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16317–16320.
32. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
33. A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed., 1992, 31, 187–188.
34. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
35. P. B. Allen, Phys. Rev. B: Solid State, 1972, 6, 2577.
36. P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905.
37. J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, Nature, 2001, 410, 63–64.
38. M. I. Eremets, V. V. Struzhkin, H. K. Mao and R. J. Hemley, Science, 2001, 293, 272.
39. K. Shimizu, K. Suhara, M. Ikumo, M. I. Eremets and K. Amaya, Nature, 1998, 393, 767–769.
40. V. V. Struzhkin, R. J. Hemley, H. K. Mao and Y. A. Timofeev, Nature, 1997, 390, 382.
41. K. Shimizu, H. Ishikawa, D. Takao, T. Yagi and K. Amaya, Nature, 2002, 419, 597.

---