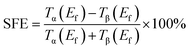Structural, magnetic and transport properties of carbon chains sandwiched between zigzag graphene nanoribbons

Abstract

We investigate the structural, magnetic properties and spin polarized transport of monatomic carbon chains covalently interconnected between zigzag graphene nanoribbon (ZGNR) leads with first-principles and non-equilibrium Green's function methods. It is revealed that an even numbered carbon chain is nonmagnetic when connected at the center of the armchair side of ZGNRs, but it becomes spin polarized and a net magnetic moment (about 0.1 μ_B) is developed when it moves to the edge. In contrast, an odd-numbered carbon chain is magnetic when it lies at the center of the armchair side and the magnetic moment decreases when the carbon chain moves to the edge. The total magnetic moment of the ZGNR/C_n/ZGNR junction depends on the magnetic alignment between two zigzag edges. Compared with that of ZGNR/C₉/ZGNR with C₉ chain anchoring at the center, the magnetic moment of the junction increases by 2.2 μ_B in the antiferromagnetic configuration and decreases by 1.5 μ_B in the ferromagnetic alignment when the carbon chains migrate from the center to one edge. Thus, the ZGNR/C_n/ZGNR junctions show rich magnetic varieties by modulating the carbon chain anchoring sites and the zigzag edge magnetic coupling. Further, spin-dependent transport calculations indicate that the ZGNR/C₉/ZGNR junction behaves as a perfect spin-filter in spintronic circuits.

---

1. Introduction

At the thinnest constrictions, the linear monatomic carbon chains consisting of sp-hybridized atoms directly interconnected between two metallic electrodes have attracted great interest and exhibit various novel quantum transport phenomena, such as spin-valve effect,¹ negative differential resistance,² and parity conductance oscillations with the number of carbon atoms in the chain.³ In such a case, their spin-polarized transport properties are associated with the anchoring atoms (nitrogen,⁴ dinaphthylpolyynes,⁵ transition metal atoms⁶ and C₆₀⁷ ) and the transferred charge from the metallic electrodes.⁸ Recently, an interesting advance associated with carbon chains is that long stable free-standing carbon chains have been fabricated by employing energetic electron irradiation of graphene inside a transmission electron microscope.⁹ As a matter of fact, carbon chains can migrate along the side of graphitic nanofragments which was obviously observed by experiment¹⁰ and prefer to stay at the edges.¹¹ However, so far, there have not been any extensive studies on the effect of migration on the electronic structure of graphene nanofragments.

With the above-mentioned technique,^9,10 it is very easy to create junctions in which monoatomic carbon chains are interconnected between two graphene nanoribbons (GNR) via sp² bonding, herein referred to as GNR/C_n/GNR. Such all-carbon junctions have aroused much research interest.^12–16 Experimentally, the conductance of such junctions could be ballistic, independent of structural imperfections such as distortion and absorbent except for oxygen impurities.¹⁷ Moreover, the equilibrium conductance parity oscillation differs from that of carbon chains directly interconnected to metallic electrodes in that the former is much more pronounced and could appear as the difference between on- and off-states, while the latter is not.¹⁸ In addition, in such a pure carbon-based junction, spin transport is feasible due to its long spin-coherence distance and time in the presence of weak spin–orbit coupling.¹⁹ Fürst et al. found a completely spin-polarized transmission due to the intrinsic spin-polarization of zigzag graphene nanoribbon (ZGNR).²⁰

Yet in addition, it is well known that ZGNRs possess electron states localized near the edges with energies very close to Fermi energy (E_f),²¹ which may greatly affect the magnetic and transport behaviors of the sandwiched carbon chains. However, until now there have been few concerns²² on the effects of ZGNR's edge states on the magnetic and spin polarized transport properties of carbon chains. Therefore, in this work, we pay special attention to the magnetic and spin transport properties of the ZGNR/C_n/ZGNR junctions when the carbon chain migrates from the center to one zigzag edge along the armchair side of the cutting ZGNR. It is found that the magnetic moments of the carbon chain and whole junction and the spin-polarized transport of such junctions are dramatically altered as the carbon chain moves from the center to the edge, due to the change of spatial symmetry.²³ The ZGNR/C_n/ZGNR complex systems can be modulated to show magnetic varieties by tailoring the magnetic coupling of ZGNR edges, the parity of carbon chains, and the anchoring sites to achieve various characteristics, such as semiconducting non-spin-polarized, metallic spin-polarized, and even semiconducting spin-polarized.

The paper is organized as follows. In Section II, we briefly describe the simulation model and computational method. The results and discussions are presented in detail in Section III. The paper ends with Section IV where a short summary is given.

II. Simulation model and calculation method

In this work, the simulated junction is composed of a carbon chain covalently connected to two 12-ZGNRs at an angle of ∼114° and divided into three regions (see Fig. 1): the left and right electrodes (shown in shadow) and the scattering region between them. In ZGNR/C_n/ZGNR junctions, all of the edge carbon atoms are saturated with hydrogen atoms. About the carbon chain, the most interesting thing is the odd–even oscillation in the conductance, so two typical kinds of carbon chains consisting of an even (8) or odd-number (9) of carbon atoms are investigated, respectively. Although we pay special attention to these two cases (C₈ and C₉), the conclusion applies to all other cases. In order to simulate the migration effects of carbon chains,¹⁰ two different anchoring sites for the carbon chain are adopted: the center (yellow) and edge (blue) sites. When the carbon chain contacts in the central region of the armchair side of ZGNR, the total energy is about 0.311 or 0.018 eV higher than that of the junction with the C₉ or C₈ chains anchoring at the edge site, respectively. Namely, the carbon chain prefers to stay at the edges.¹¹ Therefore, four different kinds of junctions are considered in total, such as cZGNR/C₈/cZGNR, eZGNR/C₈/eZGNR, cZGNR/C₉/cZGNR, and eZGNR/C₉/eZGNR, where cZGNR or eZGNR means that the carbon chain lies at the center or edge sites along the armchair side of ZGNR.

Fig. 1 Schematic illustration of the atomic model used to probe spin transport properties in the case of the C₉ chain covalently contacted to 12-ZGNR leads at the center (yellow) or edge (blue) sites.

The vacuum layers between two sheets are 20 Å so that each junction is laterally isolated from its periodic images. Firstly, we need to obtain the suitable electrode/electrode distance along the z direction. As a first step, we assume that the carbon atomic chains are in the ideal cumulene configuration and the initial distance between carbon atoms in the chain is set to 1.283 Å which is the C–C bond length of an infinite carbon chain.²⁴ And then, by specifying several electrode/electrode distances varying, all the junctions are fully optimized by using SIESTA code²⁵ until the absolute value of forces acting on each atom is less than 0.03 eV Å⁻¹. In f

Further, the total energy as a function of z spacing is obtained. At last, a least-squares fit of the energy as the distance yields the optimal lattice constants, which corresponds to the minimum total energy.

And then, the spin-polarized transport calculations are carried out with the SMEAGOL program²⁶ which combines density functional theory with non-equilibrium Green's function method. In ZGNR/C_n/ZGNR junctions, the valence electrons of carbon atoms are 2s²2p² and don't contain localized d or f electrons, so density functional theory is shown to be very suitable in predicting the ground states.^27,28 However, the DFT + U method should be used when the interaction of graphene with 3d transition-metal adatoms is investigated. Because it is found that the electronic configuration and the adsorption geometries are very sensitive to the effects of local on-site Coulomb interactions U in the transition-metal d orbitals. All the calculations were performed within the generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof²⁹ and with standard norm-conserving pseudopotentials.³⁰ The real-space grid cutoff energy is 300 Ry and a Fermi–Dirac distribution function with an electronic temperature of 20 meV is used to populate the energy levels. The k-point sampling mesh for the leads is 1 × 1 × 20. Basis set quality, k-point sampling, kinetic energy cutoff, and electronic temperature have been tested with convergence studies on the structural, magnetic, and spin-polarized transport properties of ZGNR/C_n/ZGNR junctions.

3. Results and discussion

First of all, the geometry optimization was carried out for all ZGNR/C_n/ZGNR junctions. The variation of carbon–carbon bond length with respect to the bond index is presented in Fig. 2. For a carbon chain containing n atoms (C_n), there are n − 1 bonds inside the chain, and two bonds connected to ZGNRs on two ends. Therefore, we have (n − 1) + 2 = n + 1 bond indices (labeled starting from 1 to n + 1 in Fig. 2). The index 1 and n + 1 are for the bond length (d₀) between the carbon chain and ZGNRs and the others are for the bond length (d_i) inside the carbon chain.

Fig. 2 The variation of carbon–carbon bond length with respect to C–C bond index for the carbon chain in all ZGNR/C_n/ZGNR systems.

For cZGNR/C_n/cZGNR junctions, there is a reversal symmetry for the carbon–carbon bonds. For even n, the inversion symmetry point is on a bond and makes no restrictions on the character of the central bond. Due to a Peierls-type distortion, the single and triple bond alternation has a much lower energy. So the bond length for the seven C–C bonds (d_i) inside the chain of the cZGNR/C₈/cZGNR junction oscillates in the range of 1.301 to 1.422 Å. However, if n is odd, the symmetrical point is at the center carbon atom and this carbon atom forms double bonds with its neighbors and all the other bonds thus have to be double bonds. Therefore, the bond length alternation for the cZGNR/C₉/cZGNR junctions is less than that of the cZGNR/C₈/cZGNR junctions and is in the range of 1.317 to 1.391 Å. But the d₀s for the cZGNR/C_n/cGNR junctions are nearly the same and 1.498 and 1.478 Å for the cZGNR/C₈/cZGNR and cZGNR/C₉/cZGNR junctions, respectively. When the carbon chain moves to the edge site, the d_is of eZGNR/C₈/eZGNR junctions are similar to those of cZGNR/C₈/cZGNR junctions. But for the eZGNR/C₉/eZGNR junctions, d_is change a lot in comparison with those of cZGNR/C₉/cZGNR junctions due to the mutual effects and actions between the edge states and the states localized on the carbon chains, which will be discussed in detail in the following section. In general, the length of a single σ bond is 1.47 Å, whereas the double (σ + π) and triple (σ + 2π) bonds shrink to 1.380 and 1.210 Å, respectively. In conclusion, the bond length d₀s are nearly close to the single σ bonds. The bonds in the inner C_n chains with odd n are close to a double (σ + π) bond. Whereas for the even n carbon chains, the bond lengths, d_is, show single–triple bond alternation.

Extensive calculations were carried out for all the junctions using a ferromagnetic (FM, ZGNR/C_n/ZGNR↑↑) and an antiferromagnetic (AFM, ZGNR/C_n/ZGNR↑↓) coupling between the opposite edges of ZGNRs. It is shown that the total energies of the ZGNR/C_n/ZGNR↑↑ junctions are larger than those of the ZGNR/C_n/ZGNR↑↓ junctions, which is similar to the previous results.³¹ However, the total energies of ZGNR/C₉/ZGNR↑↓ and ZGNR/C₉/ZGNR↑↑ systems only differ at most by 7.76 meV when the carbon chain migrates from the center to the edge along the armchair side of ZGNR, suggesting that the alignment of edge magnetization in eZGNR/C₉/eZGNR junctions can be easily influenced by thermal fluctuation.³²

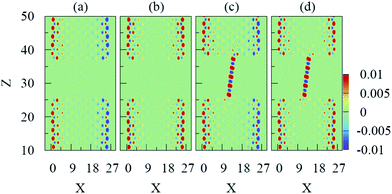
In the following, we investigate how the magnetic properties of all ZGNR/C_n/ZGNR systems change when carbon chains migrate from the center to one edge. It is found that the considered ZGNR/C_n/ZGNR junctions display an interesting magnetic behavior during the migration. The spin density (ρ_↑ − ρ_↓) is computed and presented in Fig. 3 and 4 when carbon chains anchored at the center and edge site, respectively. The magnetization of the ZGNR/C_n/ZGNR junctions is predicted to reside mainly on zigzag edges (shown in Fig. 3 and 4), in agreement with the predicted magnetism of zigzag edges in GNRs.³³ However, the presence of a net spin density localized on the chain atoms depends exclusively on the parity of the chain and not the edge magnetic coupling of ZGNR. The same dependence of magnetization on the chain parity has also been reported by Ravagnan et al.³⁴ for C_n chains with n from 4 to 12 with different kinds of termination.

Fig. 3 Spin densities (ρ_↓ − ρ_↓) on the cZGNR/C_n/cZGNR systems: (a) cZGNR/C₈/cZGNR↑↓; (b) cZGNR/C₈/cZGNR↑↑; (c) cZGNR/C₉/cZGNR↑↓; (d) cZGNR/C₉/cZGNR↑↑. Red and blue correspond to positive and negative isodensities of ρ_↓ − ρ_↓.

Fig. 4 Spin densities (ρ_↓ − ρ_↓) on the eZGNR/C_n/eZGNR systems: (a) eZGNR/C₈/eZGNR↑↓; (b) eZGNR/C₈/eZGNR↑↑; (c) eZGNR/C₉/eZGNR↑↓; (d) eZGNR/C₉/eZGNR↑↑. Red and blue correspond to positive and negative isodensities of ρ_↓ − ρ_↓.

This is because that the spin polarization of linear carbon chains is in fact an intrinsic property of the chains themselves, only depending on the resulting presence of unpaired electrons which is responsible for magnetism in all-carbon nanostructures.^35–38 In a free-standing carbon chain with n atoms, 2s and 2p_z valence electrons are hybridized, and then form two σ bonds with adjacent atoms making the carbon chain linear and stable. Then, the remaining two-fourth valence electrons (2p_x and 2p_y) make π bonds, which are 2-fold degenerate. Thus, there are (n − 1)/2 fully occupied π orbitals for odd n and (n/2 − 1) fully occupied π orbitals plus one half-filled π orbital for even n. Due to Hund's rule, a free odd-numbered carbon chain has 0 μ_B magnetic moment while a free even-numbered carbon chain has a 2 μ_B magnetic moment. When a carbon chain is covalently connected to ZGNR electrodes, it will accept two electrons from the electrodes. So, a new unoccupied π orbital is added for odd n or the partially occupied π orbital is filled for even n. This leads to the completely oppositive magnetic moment of carbon chain. Hence, for ZGNR/C₈/ZGNR junctions, all the bonds inside the carbon chain are occupied with paired electrons and no magnetism is expected (shown in Fig. 3(a) and (b)). While, for ZGNR/C₉/ZGNR junctions, a net spin density is observed (shown in Fig. 3(c) and (d) and Fig. 4(c) and (d)). As is well known that half-filled orbitals contribute to the electrical conduction while fully occupied orbitals do not. Obviously, the above-mentioned magnetic features will also be reflected in the transport properties of ZGNR/C_n/ZGNR junctions which will be discussed later.

In addition, comparing the spin density of eZGNR/C₈/eZGNR junctions (Fig. 3(a) and (b)) with that of cZGNR/C₈/cZGNR junctions (Fig. 4(a) and (b)), a small spin density is excited by edge states of ZGNRs when C₈ chain moves from the center to one edge. The concrete magnetic moment per carbon atom inside the chain is analyzed by Mulliken population and shown in Fig. 5 and Table. 1. The magnetic moment of the C₈ chain changes very little and increases from 0 to ∼0.1 μ_B. For ZGNR/C₉/ZGNR junctions, an oscillating spin density is obviously observed on C₉ chain as illustrated in Fig. 3(c) and (d) and 4(c) and (d), which is consistent with the analysis of Mulliken population (Fig. 5(c) and (d)). When the C₉ chain anchors at the center site of the armchair side of ZGNRs, the magnetic moment on the chain is about 1.6 μ_B, as reported in Table 1. When the C₉ chain migrates from the center site to the edge site, the magnetic moment on the C₉ chain decreases from 1.653 to 1.207 μ_B for the AFM coupling and from 1.620 to 1.221 μ_B for the FM coupling, respectively. In conclusion, the magnetic moment of C₈ chain increases from 0.0 to 0.1 μ_B, while that of the C₉ chain decreases by 0.4 μ_B when the chain migrates from the center to the edge site along the armchair side of ZGNRs. It seems that the changes in the magnetic moment of carbon chains also depend on the parity during the migration.

Fig. 5 Magnetic moment (μ_B) per atom as a function of carbon atom index (shown in Fig. 1) when the C₈ (up panel) or C₉ (down panel) chains are contacted by ZGNR↑↓ (left panel) or ZGNR↑↑ (right panel) from the center to the edge.

Table 1 Magnetic moment (μ_B) on the C_n chains and on the whole ZGNR/C_n/ZGNR junctions

	Mchain (μB)	Mtotal (μB)
cZGNR/C8/cZGNR↑↓	0.000	0.001
eZGNR/C8/eZGNR↑↓	0.093	0.001
cZGNR/C8/cZGNR↑↑	0.008	11.707
eZGNR/C8/eZGNR↑↑	0.087	11.640
cZGNR/C9/cZGNR↑↓	1.653	1.933
eZGNR/C9/eZGNR↑↓	1.207	4.163
cZGNR/C9/cZGNR↑↑	1.620	13.448
eZGNR/C9/eZGNR↑↑	1.221	11.927

---

The total magnetic moment on the whole ZGNR/C₈/ZGNR junction is nearly zero for AFM coupling and 11.7 μ_B for FM coupling, respectively. In addition, the magnetic moment of ZGNR/C₈/ZGNR junctions is hardly affected by the magnetic coupling of ZGNR. For ZGNR/C₉/ZGNR junctions, the magnetic moments are more complex and all of them are spin-polarized regardless of the carbon chain anchoring sites and the magnetic coupling between the opposite edges of ZGNR. The total magnetic moment on the whole ZGNR/C₉/ZGNR junctions has completely reversed charge and increases from 1.933 to 4.163 μ_B for the AFM coupling and decreases from 13.448 to 11.927 μ_B for the FM coupling, respectively.

For the FM alignment, one zigzag edge magnetic moment is suppressed and the other zigzag edge magnetic moment is hardly affected (shown in Fig. 4(d)), which makes the total magnetic moment decrease for the ZGNR/C₉/ZGNR↑↑ junctions. This is consistent with the detailed magnetic moment per carbon atom as a function of the carbon index (shown in the Fig. 1) along the armchair side of ZGNRs in the Fig. 6. Nevertheless, the understanding of the magnetic moment changes for ZGNR/C₉/ZGNR↑↓ junctions may be somewhat complicated. As is well known, graphene is composed of two different kinds of sublattice and the 1 and −1 (as denoted in Fig. 1) sites are the same. For odd-numbered carbon chains in contact with ZGNR leads, if they connect to the same sublattice, the sublattice symmetry is conserved and the electrodes have slight effects on the magnetic moments of the carbon chains. Otherwise, the symmetry is broken and the magnetic moment of carbon chains will decrease when the odd carbon chains are in contact with two different sublattices. So, the carbon chain in the ZGNR/C₉/ZGNR junction has less than 2 μ_B magnetic moments. When the odd carbon chains migrate from the center to the edge, the magnetic moment will further decrease because edge states of ZGNR exponentially decay from the edge to the center. In contrast, for even carbon chains, no matter whether it is connected to the same sublattice or different sublattices, it always obtains a small finite magnetic moment which will increase with the carbon chain migrating from the center to the edge.

Fig. 6 Magnetic moment (μ_B) per atom as a function of carbon atom index (shown in Fig. 1) when the C₉ chain is contacted by ZGNR↑↓ ((a) and (b)) or ZGNR↑↑ ((c) and (d)) from the center ((a) and (c)) to the edge ((b) and (d)).

Further, with n increasing, the odd–even conductivity oscillation magnitude becomes smaller and smaller and finally saturates to a constant, namely, 1 G₀. This trend is easy to understand since the effect of the electrodes on the electronic structure of a long carbon chain is smaller than that on a short carbon chain.¹⁷ However, the above-mentioned conclusions are still applicable. The magnetic moment of ZGNR will also increase for AFM and decrease for FM whilst carbon chains move to the edge, because the symmetry is broken.

The transmission spectra of ZGNR/C_n/ZGNR junctions for the C₈ and C₉ chains are shown in Fig. 7 and 8, respectively. As mentioned above, the ZGNR/C₈/ZGNR junctions are indeed semiconducting, regardless of the anchoring site and the magnetic ordering. From Fig. 7(a), we see that the transmission spectra of cZGNR/C₈/cZGNR↑↓ junctions do not show spin-polarization. In contrast, when the carbon chain deviates from the center, the removal of degeneracy for β- and α-spin makes the junction a semiconducting spin-polarized structure (as shown in Fig. 7(b)). All ZGNR/C₈/ZGNR↑↑ junctions also exhibit semiconducting spin-polarized features.

Fig. 7 Transmission spectra of the cZGNR/C₈/cZGNR systems: (a) cZGNR/C₈/cZGNR↑↓; (b) eZGNR/C₈/cZGNR↑↓; (c) cZGNR/C₈/cZGNR↑↑; (d) eZGNR/C₈/cZGNR↑↑.

Fig. 8 Transmission spectra of the cZGNR/C₉/cZGNR systems: (a) cZGNR/C₉/cZGNR↑↓; (b) eZGNR/C₉/cZGNR↑↓; (c) cZGNR/C₉/cZGNR↑↑; (d) eZGNR/C₉/cZGNR↑↑.

However, it is quite different for the ZGNR/C₉/ZGNR junction. It is metallic in the FM state and semiconducting in the AFM state with an energy gap of 350 meV which is ∼295 meV in previous calculations.²⁸ Outside the gap region, the conductance is no larger than 1 G₀ (G₀ denotes the quantum conductance and equals e²/h for each spin) in the presence of the scattering since the carbon atomic chain could provide at most one channel. The transmission spectra of ZGNR/C₉/ZGNR↑↓ junctions show that it is always semiconducting and spin-polarized, no matter where the C₉ chain anchors at the armchair profile of ZGNR↑↓ (as shown in panels (a) and (b) of Fig. 8). As far as we know, the FM alignment of ZGNR makes it conducting and the transmission is nonzero around E_f. However, the conductance also never exceeds 1 G₀, as mentioned above. All the transmission spectra of ZGNR/C₉/ZGNR↑↑ junctions are spin-polarized. The conductance around E_f becomes larger and larger when the carbon chain deviates from the edge, which shows that the contact between the carbon chain and ZGNRs is increasingly strong. As seen in panel (c) of Fig. 8, the obtained spin-resolved conductance at E_f is 0.019 G₀ or 0.608 G₀ for α- or β-spin channels, when the C₉ chain locates at the center. When the C₉ chain moves to the edge, the obtained spin-resolved conductance at E_f is 0.051 G₀ and 0.003 G₀ for α- and β-spin channels, respectively. To quantify the transmission spin polarization, the spin filter efficiency (SFE)³⁹ in the linear response regime is then calculated from the transmission by its definition

where the transmission coefficients are taken at E_f for the α- and β-spin channel, respectively. The SFE values for the center and edge locations vary as 94% and −90%, respectively, which shows ZGNR/C₉/ZGNR↑↑ junctions are perfect spin-filters.

4. Conclusions

We investigate how ZGNR's edge states affect the structural, magnetic properties and spin transport of a monatomic carbon chain when it is covalently interconnected between ZGNR leads within first-principles methods. It was found that there was a small impact on the magnetic moment of ZGNR/C₈/ZGNR junctions while it played an important role on the structural and magnetic moment of ZGNR/C₉/ZGNR junctions. When the C₉ chain moves to the edge site, the magnetic moments on the C₉ chain and the whole ZGNR/C₉/ZGNR↑↑ junction decrease and the total magnetic moment of ZGNR/C₉/ZGNR↑↓ increases. Thus, the ZGNR/C_n/ZGNR junctions can show magnetic varieties by modulating the C_n chain anchoring site and the edge magnetic coupling of ZGNR. Further, the C₉-ZGNR junction could be used as a perfect spin-filter.

Acknowledgements

This work was partially supported by China Postdoctoral Science Foundation under Grant no. 2013M530756 (RNW), the National Science Foundation of China under Grant no. 11174289 (XQS) and 11104272 (XHZ), the special Funds for Major State Basic Research Project of China (973) under Grant no. 2012CB933702(ZZ), Knowledge Innovation Program of Chinese Academy of Sciences under Grant no. KJCX2-YW-N35 (ZZ), Hefei Center for Physical Science and Technology under Grant no. 2012FXZY004 (ZZ), and Director Grants of CASHIPS, The calculations were performed in Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center and Computer Network Information Center of Chinese Academy of Science.

Notes and references

1. Y. Wei, Y. Xu, J. Wang and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 193406.
2. K. H. Khoo, J. B. Neaton, Y. W. Son, M. L. Cohen and S. G. Louie, Nano Lett., 2008, 8, 2900.
3. N. D. Lang and P. Avouris, Phys. Rev. Lett., 1998, 81, 3515.
4. Z. Y. Li, W. Sheng, Z. Y. Ning, Z. H. Zhang, Z. Q. Yang and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115429.
5. D. Fazzi, F. Scotognella, A. Milani, D. Brida, C. Manzoni, E. Cinquanta, M. Devetta, L. Ravagnan, P. Milani, F. Cataldo, L. Lüer, R. Wannemacher, J. Cabanillas-Gonzalez, M. Negro, S. Stagira and C. Vozzi, Phys. Chem. Chem. Phys., 2013, 15, 9384.
6. C.-S. Liu, H. An and Z. Zeng, Phys. Chem. Chem. Phys., 2011, 13, 2323.
7. R. N. Wang, X. H. Zheng, L. L. Song and Z. Zeng, J. Chem. Phys., 2011, 135, 044703.
8. N. D. Lang and P. Avouris, Phys. Rev. Lett., 2000, 84, 358.
9. A. Chuvilin, J. C. Meyer, G. Algara-Siller and U. Kaiser, New J. Phys., 2009, 11, 083019.
10. C. Jin, H. Lan, L. Peng, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 205501.
11. E. Hobi, R. B. Pontes, A. Fazzio and A. J. R. da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 201406.
12. B. Standley, W. Bao, H. Zhang, J. Bruck, C. N. Lau and M. Bockrath, Nano Lett., 2008, 8, 3345.
13. R. Rivelino, R. B. dos Santos, F. de Brito Mota and G. K. Gueorguiev, J. Phys. Chem. C, 2010, 114, 16367.
14. I. E. Castelli, N. Ferri, G. Onida and N. Manini, J. Phys.: Condens. Matter, 2012, 24, 104019.
15. J. Zhu and D. Shi, J. Appl. Phys., 2011, 110, 104311.
16. M. G. Zeng, L. Shen, Y. Q. Cai, Z. D. Sha and Y. P. Feng, Appl. Phys. Lett., 2010, 96, 042104.
17. L. Shen, M. Zeng, S.-W. Yang, C. Zhang, X. Wang and Y. Feng, J. Am. Chem. Soc., 2010, 132, 11481.
18. B. Akdim and R. Pachter, ACS Nano, 2011, 5, 1769.
19. A. R. Rocha, V. M. García-suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335.
20. J. A. Fürst, M. Brandbyge and A.-P. Jauho, Europhys. Lett., 2010, 91, 37002.
21. T. Liao, C. Sun, Z. Sun, A. Du, D. Hulicova-Jurcakova and S. C. Smith, J. Mater. Chem., 2012, 22, 13751.
22. Y. Xu, B.-J. Wang, S.-H. Ke, W. Yang and A. Z. Alzahrani, J. Chem. Phys., 2012, 137, 104107.
23. Z. Zanolli, G. Onida and J.-C. Charlier, ACS Nano, 2010, 4, 5174.
24. M. Brandbyge, J.-L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
25. J. M. Soler, E. Artacho, J. Gale, D. A. Garacia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
26. A. R. Rocha, V. M. García-Suárez, S. Bailey, C. Lambert, J. Ferrer and S. Sanvito, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 085414.
27. Y.-W. Son, J. Ihm, M. L. Cohen, S. G. Louie and H. J. Choi, Phys. Rev. Lett., 2005, 95, 216602.
28. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
30. D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494.
31. S. B. Kumar and J. Guo, Nanoscale, 2012, 4, 4222.
32. O. V. Yazyev and M. I. Katsnelson, Phys. Rev. Lett., 2008, 100, 047209.
33. K. Wakabayashi, M. Fujita, H. Ajiki and M. Sigrist, Phys. Rev. B: Condens. Matter, 1999, 59, 8271.
34. L. Ravagnan, N. Manini, E. Cinquanta, G. Onida, D. Sangalli, C. Motta, M. Devetta, A. Bordoni, P. Piseri and P. Milani, Phys. Rev. Lett., 2009, 102, 245502.
35. K. W. Lee and C. E. Lee, Phys. Rev. Lett., 2011, 106, 166402.
36. Z. Zanolli and J.-C. Charlier, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165406.
37. S. Lisenkov, A. N. Andriotis and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165454.
38. O. V. Yazyev, Rep. Prog. Phys., 2010, 73, 056501.
39. M. Smeu and G. A. Dilabio, J. Phys. Chem. C, 2010, 114, 17874.

---

Footnote

† Current address: Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, P. R. China.

---