Simulation and optimization of a horizontal ammonia synthesis reactor using genetic algorithm
Abstract
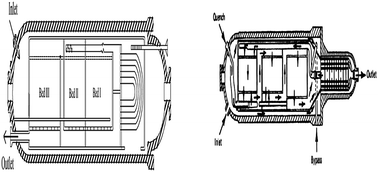
The synthesis of ammonia from nitrogen and hydrogen is one of the most important processes in petrochemical industry. In this study simulation and optimization of a horizontal ammonia synthesis reactor is presented in two cases: first, an intercooled horizontal ammonia synthesis reactor of the Khorasan petrochemical plant, second, a horizontal ammonia synthesis reactor with two quench flows. The one-dimensional heterogeneous mathematical model consists of two point boundary value differential equations for the catalyst pellets which were used in the simulations. Also, the effectiveness factor was calculated by both an empirical relation and considering the diffusion-reaction equations. The differential equations of boundary and initial value problems are solved with a combination of the Runge–Kutta method and an improved shooting method. The simulation was done for two cases. The first case is an intercooled horizontal ammonia converter, and the second one is a horizontal ammonia converter with two quench flows. Good agreement is achieved between simulated results, i.e., the outlet component mole fraction and temperature, and industrial data (Khorasan plant data and SRI report). Then the effect of parameters like inlet temperature, total feed flow rate, and operating pressure on ammonia production is studied. Finally, optimum solutions for the maximum mass flow rate production of ammonia are determined using a genetic algorithm (GA). The adjustable parameters are inlet temperature, total feed flow rate and operating pressure. The results of optimization show that a maximum ammonia mass flux of 52 433 kg h−1 and 73 979 kg h−1 was produced in both cases, respectively, in which the inlet temperature, feed flow rate, and operating pressure were, respectively, 524 °C, 217 005 kg h−1 and 167 atm in the first case and 437 °C, 354 986 kg h−1 and 237 atm in the second one.

 Please wait while we load your content...
Please wait while we load your content...