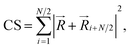Atomistic view of thin Ni/Ni₃Al (0 0 1) under uniaxial tension of twist grain boundaries

Abstract

Atomic motion and the structure response of grain boundaries (GBs) are essential to the plastic deformation of small-volume polycrystal systems, especially for thin materials that exhibit some dramatic characteristics. Here, the microstructure and properties of thin Ni/Ni₃Al (0 0 1) with the uniaxial tension of twist GBs are investigated using molecular dynamics (MD) simulations with an embedded atom (EAM) potential. We find that low angle twist GB dislocations propagate mainly from the corners to the center of the interface, and for high angle twist GBs they originate from the edge of the interface but do not extend to the center. In the process of plastic deformation, both low angle and high angle twist GB fractures occur in the center of the interface, which is completely different from the situation of thick materials reported by other references. More interestingly, the fracture patterns between low angle and high angle twist GBs exhibit extremely different performance due to the different characteristics of the initial dislocation structures in the interfaces.

---

1. Introduction

Grain boundaries (GBs) play a crucial role in the properties of polycrystal materials.¹ Traditional materials processing mainly aimed to control the grain size and number. However, more important are the characteristics of GBs for designing and controlling the functional properties in engineering applications. Therefore, understanding the microstructure and properties of GBs is significantly important. In practice, a large number of two-phase interfaces (GBs) that possess a variety of twin GBs, title GBs and twist GBs in the process of crystallization exist in materials. Recently, there has been a considerable number of reports about the properties of GBs, both from experimental and theoretical studies. The tensile properties of twin GBs' and growth of superlattice nanowires have been studied by Erin L. Wood and Frederic Sansoz.² They showed that coherent twinning superlattices hold great promise for tuning and enhancing the physical and mechanical properties of crystalline nanowires without compromising one property over another. Hossein et al.³ presented an approach of GB engineering involving multiple twinning in nickel layers by electrodeposition. Regarding the study of tilt GBs, Chen et al.⁴ researched the tilt GBs of Ni, Al and Ni₃Al by EAM potentials, and Zhang et al.⁵ discovered the rate of GB migration of Ni (0 0 1) tilt GBs that are significantly influenced by the GB structure and misorientation. The relationship between equilibrium fluctuations and the shear-coupled motion of GBs has been researched by Karma et al.⁶ They elucidated the fundamental link between GB fluctuations and the linear response to shear for pure coupling and pure sliding regimes, and the transition between these regimes warrants further study. For twist GBs, the energy analysis for twist GBs⁷ in noble metals and twist boundary formation and Eshelby twists⁸ in metal nanowires under torsion have been researched. A new physical mechanism for GB rotations in solids has been reported by Bobylev et al.,⁹ and they found that such rotations are energetically favorable processes over a wide rage of GB parameters. Rajabzadeh et al.¹⁰ discovered an important mechanism of shear-coupled GB migration that can be applied to numerous GBs including the low-, high-angle and asymmetrical GBs in various materials.

Thin nickel-based superalloys which have a mass of inherent GBs are widely used as high-temperature structural materials, for example in blades and vanes in advanced gas turbine engines,^11,12 due to their high creep resistance, and good oxidation and corrosion resistance at a relatively high temperature.¹³ Therefore, gaining an in-depth understanding of the GBs' effect on the mechanics is critical for the material’s wide application. The basic Ni-based superalloy consists of the γ′ (Ni₃Al) phase precipitate coherently dispersed on the γ (Ni) phase matrix. The industrial application of Ni-based superalloys are mainly associated with the characteristics of γ/γ′ interfaces (GBs) which prevent dislocation motion at high temperature.^1,14 Since it is experimentally difficult to precisely control the generation of the Ni-based superalloy's twist GBs, the characteristics of GB twist and migration have not been comprehensively studied.

In this work, the uniaxial tension properties of thin Ni/Ni₃Al (0 0 1) twist GBs are investigated by MD studies. We focus on the propagation of dislocations for low angle and high angle twist GBs under uniaxial tension to provide a clearly atomistic comprehension of the evolution of dislocations. The relationship between the twist angle and yielding stress, as well as stress–strain curves, has been calculated and discussed in detail. Then, the progress of the fractures and different fracture patterns for low angle and high angle twist GBs of thin Ni/Ni₃Al (0 0 1) are analyzed by the CS method. Finally, the evolution of different disordered dislocations such as stacking faults, perfect surfaces (considered as a special kind of defect), surface steps and excited point dislocations has been studied.

2. Simulation model and methodology

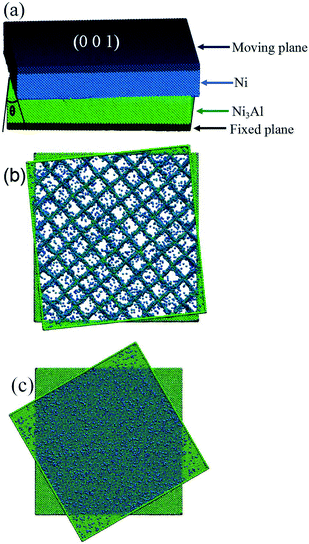
The MD simulations were carried out using the open code LAMMPS program.¹⁵ The interactions between atoms were adopted by the EAM potential¹⁶ which has been proven to be very efficient to describe interface effects on the microstructure and properties.¹⁷ The system is modeled by two grains: 66a_γ′ × 66a_γ′ × 12a_γ′ cubic box with the Ni₃Al lattice constant, and the 67a_γ × 67a_γ × 12a_γ cubic box with the Ni lattice constant a_γ for the case of a twist [0 0 1] GB. The purpose of extending the 66 × 66 unit cells for the Ni₃Al box and 67 × 67 unit cells for the Ni box, respectively, in the directions of the interface is to match the initial model with zero twist degree. The average value of the two lattice constants is chosen as the contact distance between the two blocks. Fig. 1(a) shows the twist model at a certain twist degree. In order to make a comparison analysis in the following discussions, we show Fig. 1(b) and (c) which correspond to the screw dislocations of low angle (6 degree) twist GBs and high angle (30 degree) twist GBs, respectively, at an ambient temperature of 300 K. Here, we investigate the different twist degree GBs from 0 to 42 degrees with 6 incremental values.

Fig. 1 (a) Schematic view of the simulation model with 6 twist angles. (b) Dissociation of low angle (6 degrees) twist GB screw dislocations corresponding to (a). (c) Dissociation of high angle (30 degrees) twist GB screw dislocations.

The energy minimization is performed by the conjugate gradient (CG) algorithm before the adoption of ensembles for different models. Five layer atoms at the bottom and top are fixed as a plane in the model, and a displacement with a movement rate of 0.5 Å ps⁻¹ is applied to the top plane, which is a reasonable value for MD tension simulations. Free boundary conditions are maintained throughout all of the simulations. The MD simulations are carried out as a NPT isothermal isobaric ensemble. The time step is chosen to be 1 fs. The stress is calculated by the virial theorem.

In order to clearly visualize the defects, the centrosymmetry (CS) parameter¹⁸ for each atom in the system, except the fixed plane atoms, is calculated. In solid-state systems, the CS parameter is a useful measure of the local lattice disorder around an atom, and can be used to characterize whether the atom is part of a perfect lattice, a local defect (for instance, point dislocations or stacking faults), or a surface.

3. Results and discussion

In this work, all the GB energies and stresses are considered as per unit GB contact area in order to eliminate the difference caused by different twist degrees. Fig. 2(a) presents the average GB energy of the equilibrium state of the system as a function of the twist angle. It shows that the GB energy rapidly augments with the increase of the twist degree during the low angle (about 0 to 24 degrees) twist GBs. However, in the range of high twist angles (about 24 to 42 degrees), the GB energy increases slowly. Fig. 2(b) shows the GB yielding stress of the material with different twist angles. We can see that with the increase of the twist angle, the yielding stress first rapidly increases to a maximum value in the vicinity of 24 degrees. Then it shows a slight decrease and maintains a constant value after a 30 degree twist angle. These results can be explained as follows: for the left part of the dotted line in Fig. 2 that represents the situation of low angle twist GBs, the GB energy is significantly augmented due to the rapid increase of the dislocation networks' density. Additionally, the yielding stress is about 12.87% higher at a twist of 24 degrees than the stress at 0 degrees due to the reinforcement of GBs which is caused by the enhancement effect of mutual dislocation networks piling up. In the region of screw dislocations, the slip systems mainly consist of the {111} plane,^19,20 and their cross stacking leads to the difficulty of dislocations' extension. Therefore, the more intensive dislocation networks, the greater the strengthening effect of the GB. For the high angle twist GBs that are in the right part of the dotted line, almost no distinctive dislocation planes are formed in the interface, which is totally different from the dislocation networks of the low angle twist GBs. The dislocation defect density of the GB does not change with the increase of the twist degree. Therefore, for high angle twist GBs, there is little change in the GB energy, and the yielding stress almost remains a constant.

Fig. 2 (a) The average GB energy as a function of the twist angle. (b) The different GBs' yielding stress as a function of the twist angle. The dotted line roughly separates the area of the low angle twist GB and the high angle twist GB.

Fig. 3 shows the stress–strain curves for different twist angle GBS of the thin Ni/Ni₃Al (0 0 1) under uniaxial tension. The stress–strain responses for the different GBs of the materials are almost the same before yielding. The linear elastic tangential modulus is approximately equal to 10.6 GPa. As shown in Fig. 3, during the plastic strain, the downward trend of the tensile stress for the low angle twist GBs is slower than that for the high angle twist GBs, indicating that the structures of low angle twist GBs are more stable than those of high angle twist GBs. This illustrates that the screw dislocation networks for low angle twist GBs have a better capability of fracture resistance than those of plane dislocations for high angle twist GBs.

Fig. 3 Stress–strain curves for different twist GBs under uniaxial tension.

To further understand the different yielding responses of the GBs, top views and lateral views of the thin Ni/Ni₃Al (0 0 1) interface dislocation snapshots (as representatives, we choose 6 degrees for the low angle twist GB and 30 degrees for the high angle twist GB) are shown in Fig. 4. Fig. 4(a) and (e) are the GB dislocations of the low angle twist and high angle twist, respectively. In the vicinity of the yielding stress, the GBs begin to lose their stability. We can see that before the yielding stress, the primary {111} slip system has already switched on and the density of the slip system for the low angle twist GB is much higher than that of the high angle twist GB.

Fig. 4 Snapshots of the top views and lateral views for the evolution of the low angle twist GB (6 degrees) and high angle twist GB (30 degrees) under different strains. (a)–(d) are the top views of the dislocations' evolution with strain for the low angle GB case. In (a), the arrows represent the propagative orientation of stacking faults and the yellow area represents the original dislocation network. The yellow area in (c) represents the fracture area in the interface. (a′)–(d′) are the lateral views of the low angle twist GB, which show the surface steps on the surfaces. (e)–(h) are the top views of the dislocations' evolution with strain for the high angle case. The red areas represent the evolution of stacking faults and the yellow areas represent the fracture area in the interface. (e′)–(h′) are the lateral views of the high angle twist GB which show the surface steps on the surfaces.

During the plastic deformation for the low angle twist GB, most of the dislocations, which are nucleated from the dislocation networks, propagate across the wire cross-section and escape from the nanowire.¹⁹ For the phenomenon of the thin Ni/Ni₃Al (0 0 1) system, as shown in Fig. 4(a) and (b), the dislocation networks' slip system originates from the edge (especially from the corners, which is consistent with ref. 21) of the GB and propagates across the interfacial cross-section. The reason is that dislocations in the vicinity of the GB’s edge, and closer to free surfaces, have more priority to transfer them to the surfaces and at the corners the same proportion of the dislocations atoms are close to more free surfaces than those that are at the edges. When the strain continues to increase, the surface steps which are caused by the movement of the slide system are left on the free surfaces, as shown in Fig. 4(a′)–(d′). Meanwhile, the fracture occurs from the GB center and extends to the edge of the GB, as shown in Fig. 4(c) and (d). Fig. 5(a) and (b) show the cross-sectional and top views of Fig. 4(c), respectively. The reason for this phenomenon is that the free surface can not accommodate so many surface steps, which are caused by the propagation of dislocations in the thin system. The fracture, therefore, is formed in the center of the GB and evolves towards the edge of the interface with an uneven ruptured face.

Fig. 5 (a) and (b) show the cross-sectional view and top view respectively of the fracture for Fig. 4(c), which display the uneven ruptured faces for the low angle twist GB. (c) and (d) show the cross-sectional view and top view respectively of the fracture for Fig. 4(g), which display the even ruptured faces for the high angle twist GB.

For high angle twist GBs, no different dislocation planes are formed at the interface, and the detailed interfacial structures are described under different strains, as shown in Fig. 4(e)–(h). The corresponding lateral snapshots are shown in Fig. 4(e′)–(h′). In the course of plastic deformation, the slip system is still the dominating method of dislocation propagation, which mainly originates from the edge of the interface, especially from the sides of the surfaces. With the increase of the strain, the slip system remains at the edge of the interface instead of extending to the center of the GB. At the same time, a fracture directly forms in the interface with the even ruptured face. Fig. 5(c) and (d) show the cross-sectional view and top view respectively of Fig. 4(g).

Obviously, in Fig. 5, we can see two different fracture models corresponding to low and high angle twist grain boundaries under uniaxial tension. For low angle twist GBs, the initial interface structures are covered with dislocation networks (e.g. grid line of Fig. 1(b)) and ideal fcc crystal structures (e.g. blank mesh areas of Fig. 1(b)). Therefore, the evolution modes between dislocation networks and ideal structures, which are entirely different, can lead to uneven ruptured interfaces as in Fig. 5(a) and (b). However, for high angle twist GBs, plane dislocations uniformly distribute on the GB interface. Under uniaxial tension, uniform dislocation planes have almost the same evolution models everywhere in the interface. So the even ruptured interface, as in Fig. 5(c) and (d), is formed.

To observe the relationship between different types of dislocation behavior and localized responses, the fraction of dislocations (containing all dislocations, stacking faults, point dislocations, perfect surfaces and surface steps) has been recorded as a function of strain for the 6 degrees (low) and 30 degrees (high) angle twist GBs, as shown in Fig. 6(a) and (b), respectively. We tested the approximate CS parameters for these dislocations and the defects in these systems. The CS parameter is defined as follows:

where N is the number of neighbors for each atom, and R⃑_i and R⃑_i+N/2 are the vectors or bonds corresponding the N/2 pairs of the opposite nearest neighbors in the system.

Fig. 6 Evolution of different disordered dislocations (including stacking faults, point dislocations, perfect surfaces and surface steps) and the sum of all dislocations as a function of strain. (a) represents the situation of the low angle twist GB. (b) represents the situation of the high angle twist GB.

The value of CS for all of the dislocations of our systems is greater than 1. The CS for stacking faults is greater than 4 and less than 11. The CS for point dislocations, which may be caused by thermal fluctuation and external stress on the nucleation and propagation of defects, is greater than 1 and less than 4. The CS for perfect surfaces is greater than 11 and less than 19, and the CS for surface steps is greater than 19.

The pink lines as shown in Fig. 6(a) and (b) represent the fraction of surface steps. We can see that although the fraction of surface steps for both lines shows a slight increase after yielding, the content of surface steps is still low in all disordered atoms due to the limited thinness of the system. This will lead to the creation of fractures in the GBs. The crack phenomenon can be well reflected by the fraction of perfect surfaces and point dislocations which are represented by cyan lines and blue lines, respectively, as shown in Fig. 6(a) and (b). For low angle twist GBs, although the fraction of perfect surface atoms remains at almost the same level after yielding, this does not mean that no fractures occur at the interface. Fractures form in the center of the interface and extend to the border. The shape of the ruptured faces is extremely uneven, which does not contribute to the content of perfect surfaces but to the fraction of point dislocations. For high angle twist GBs, the fraction of perfect surface has an abrupt jump at the yielding point, and then increases linearly with further strain. This illustrates that the GB fracture occurs suddenly with the even ruptured face, which is completely different to the uneven ruptured face of low angle twist GBs. These results are consistent with the foregoing descriptions of Fig. 4 and 5.

For both low angle and high angle twist GBs, the fraction of all disordered atoms, represented by the black lines shown in Fig. 6(a) and (b), increases abruptly when the GBs become yielding, which represents a large number of nucleated dislocations. However, with further stretching, the fraction of high angle twist GBs shows a more obviously downward trend than that for low angle twist GBs. The reason is that stacking faults, which possess the major proportion of disordered atoms, have different propagation behavior for both low angle and high angle twist GBs. For low angle twist GBs, stacking faults originate primarily from dislocation networks which distribute uniformly on the interface, and decrease slightly with the evolution of the fracture. However, for high angle twist GBs, stacking faults form mainly in the edges of the GBs, and show an obvious decrease with an abrupt fracture under further strain.

4. Conclusions

By using the molecular dynamics simulation method, the GB tension properties and structure response for different twist GBs of thin Ni/Ni₃Al (0 0 1) are performed. The structures of low twist angle GBs are more stable than those of high angle twist GBs. The slip system of dislocation networks for low angle twist GBs propagates from the edge of the interface, especially from the corners, to the center. For high angle twist GBs, they originate mainly from the edge of the GBs but do not propagate to the center. Dramatically, the fracture appears during the plastic deformation in twist GBs of thin Ni/Ni₃Al (0 0 1). The shapes of ruptured faces are extremely uneven for low angle twist GBs, but are even for high angle twist GBs. The interface fractures for screw dislocation networks of low angle twist GBs extend from the center to the border, while the interface fractures for plane dislocations of high angle twist GBs exhibit an abrupt rupture. These different fracture patterns stem from the different propagation of interfacial dislocation structures. We expect that testing these results of thin Ni/Ni₃Al (0 0 1) will provide some useful insight into the atomistic mechanism for the elastic and plastic behavior of GBs.

Acknowledgements

The work was supported partly by the National Basic Research Program of China (no. 2012CB921300) and partly by the NSF of China (Grant no. 11104254 and 11274280).

References

1. J. X. Zhang, Y. Koizumi, T. Kobayashi, T. Murakumo and H. Harada, Metall. Mater. Trans. A, 2004, 35A, 1911.
2. E. L. Wood and F. Sansoz, Nanoscale, 2012, 4, 5268.
3. H. Alimadadi, A. B. Fanta, M. A. J. Somers and K. Panteon, Appl. Phys. Lett., 2013, 103, 031981.
4. S. P. Chen, D. J. Srolovitz and A. F. Voter, J. Mater. Res., 1989, 4, 62.
5. H. Zhang, D. J. Srolovitz, J. F. Douglas and J. A. Warren, Acta Mater., 2007, 55, 4527.
6. A. Karma, Z. T. Trautt and Y. Mishin, Phys. Rev. Lett., 2012, 109, 095501.
7. J. M. Zhang, X. M. Wei and H. Xin, Appl. Surf. Sci., 2005, 243, 1.
8. C. R. Weinberger and W. Cai, Nano Lett., 2010, 10, 139.
9. S. V. Bobylev and I. A. Ovid'ko, Phys. Rev. Lett., 2012, 109, 175501.
10. A. Rajabzadeh, F. Mompiou, M. Legros and N. Combe, Phys. Rev. Lett., 2013, 110, 265507.
11. M. Gell, D. N. Duhl and A. F. Giamei, Superalloys, 1980, 205.
12. S. Walston, A. Cetel, R. Mackay, K. O'Hara, D. Duhl and R. Dreshfield, Superalloys, 2004, 15.
13. T. M. Pollock and A. S. Argon, Acta Metall. Mater., 1992, 40, 1.
14. M. Okazaki and M. Sakaguchi, Int. J. Fatigue, 2008, 30, 318.
15. S. Plimpton, J. Comput. Phys., 1995, 117(1), 1.
16. Y. Mishin, Acta Mater., 2004, 52, 1451.
17. Y. Mishin and M. Asta, Acta Mater., 2010, 58, 1117.
18. C. L. Kelchner, S. J. Plimpton and J. C. Hamilton, Phys. Rev. B: Solid State, 1998, 58, 11085.
19. X. M. Liu, X. C. You, Z. L. Liu, J. F. Nie and Z. Zhuang, J. Phys. D: Appl. Phys., 2009, 42, 035404.
20. F. Leroy, J. Eymery, P. Gentile and F. Fournel, Appl. Phys. Lett., 2002, 80, 3078.
21. T. Zhu, J. Li, A. Samanta, A. Leach and K. Gall, Phys. Rev. Lett., 2008, 100, 025502.

---