Cyclic 3-hydroxymelatonin, a key metabolite enhancing the peroxyl radical scavenging activity of melatonin
Abstract
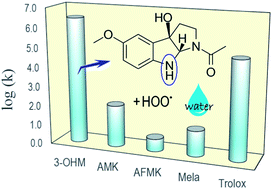
The reactions of cyclic 3-hydroxymelatonin (3-OHM) with hydroxyl (˙OH) and hydroperoxyl (˙OOH) radicals were studied using Density Functional Theory. Two environments, mimicking lipid and aqueous solutions, have been modelled. Three mechanisms of reaction were considered: radical adduct formation (RAF), hydrogen transfer (HT), and single electron transfer (SET). Their relative importance for the free radical scavenging activity of 3-OHM was assessed. It was found that 3-OHM reacts with ˙OH at diffusion-limited rates, regardless of the polarity of the environment, which supports its excellent ˙OH radical scavenging activity. The overall reactivity of 3-OHM towards this radical was found to be similar, but slightly higher than those of melatonin and two other metabolites (N1-acetyl-5-methoxykynuramine, AMK; and N1-acetyl-N2-formyl-5-methoxykynuramine, AFMK). For the reaction with ˙OOH, 3-OHM was found to react several orders of magnitude faster, in aqueous solution, than melatonin, AMK and AFMK. Furthermore, under these conditions 3-OHM was found to react with ˙OOH about 98.4 times faster than Trolox. This seems to be a very important finding since it has been proposed that melatonin, AMK and AFMK are rather ineffective as peroxyl radical scavengers, while 3-OHM is predicted to be very efficient. Therefore, it is proposed that the protective effects of melatonin against peroxyl radicals become important after being metabolized into 3-OHM. Accordingly, the results presented in this work not only support the continuous protection against oxidative stress exerted by melatonin, through its free radical scavenging cascade, but also the important role of 3-OHM on the peroxyl radical scavenging activity of melatonin.
- This article is part of the themed collection: Organic chemistry collection

 Please wait while we load your content...
Please wait while we load your content...