Conformation versus cohesion in the relative stabilities of gabapentin polymorphs†
Abstract
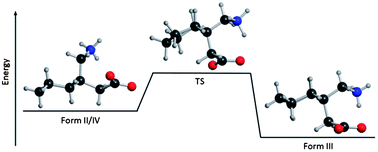
Polymorphism in molecular solids is driven by the competition between internal molecular conformational strain and external binding forces. The pharmaceutical gabapentin exhibits three polymorphic forms each differing in molecular conformation and intermolecular interactions. To improve the understanding of the polymorphic formation, terahertz spectroscopy and solid-state density functional theory have been applied in the analysis of the factors leading to these particular crystalline arrangements. It was found that the most stable solid-state polymorph contained gabapentin molecules under considerable internal strain. The origins of this unexpected stability are described in terms of intramolecular conformational changes and the amount of cohesive binding energy present in each polymorph. Finally, the temperature dependence of the polymorph stabilities is investigated by calculation of the free–energy curves of each form and determining the solid–solid transition points connecting the various phases.

 Please wait while we load your content...
Please wait while we load your content...