Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stability of star-shaped RAFT polystyrenes under mechanical and thermal stress†
Ozcan
Altintas
abc,
Mahdi
Abbasi
b,
Kamran
Riazi
b,
Anja S.
Goldmann
ac,
Nico
Dingenouts
b,
Manfred
Wilhelm
*b and
Christopher
Barner-Kowollik
*ac
aPreparative Macromolecular Chemistry, Institut für Technische Chemie und Polymerchemie, Karlsruhe Institute of Technology (KIT), Engesserstr. 18, 76128 Karlsruhe, Germany. E-mail: christopher.barner-kowollik@kit.edu
bPolymeric Materials, Institut für Technische Chemie und Polymerchemie, Karlsruhe Institute of Technology (KIT), Engesserstr. 18, 76128 Karlsruhe, Germany. E-mail: manfred.wilhelm@kit.edu
cInstitut für Biologische Grenzflächen, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
First published on 8th May 2014
Abstract
Well-defined three-arm and four-arm star polymers designed via a Z-group approach carrying trithiocarbonate functionalities at the core are prepared via reversible addition-fragmentation chain transfer (RAFT) polymerization featuring molecular weights of Mn,SEC = 156 kDa, Đ = 1.16 (3-arm) and Mn,SEC = 162 kDa, Đ = 1.15 (4-arm) based on multi-angle laser light scattering (MALLS) detection, respectively. The star-shaped polystyrenes are subjected (in bulk) to thermal stress in the temperature range between 140 and 200 °C from 10 minutes up to 96 h. The thermally treated 3-arm and 4-arm star polymers are analyzed via size exclusion chromatography (SEC) to quantify the degradation process at variable temperatures as a function of time under an argon atmosphere. Cleavage rate coefficients of the star polymers are deduced as a function of temperature, resulting in activation parameters for the cleavage process, i.e. Ea = 131 kJ mol−1; A = 3.93 × 1011 s−1 (Mn,SEC = 156 kDa, Đ = 1.16, 3-arm star) and Ea, = 134 kJ mol−1; A = 9.13 × 1011 s−1 (Mn,SEC = 162 kDa, Đ = 1.15, 4-arm star), respectively. Processing of the star-shaped polymers is mimicked via a small scale counter rotating twin screw extrusion to achieve nonlinear shear and elongation flow under pressure. Furthermore, a rheological assessment via the linear shear deformation region (small amplitude oscillatory shear, SAOS) allows for a correlation of the processing conditions with the thermal degradation properties of the star polymers in the melt. Zero shear viscosity (η0) as a criterion of the degradation process is measured in the rheometer and correlated to the weight-average molecular weight, Mw.
Introduction
Molecular and mechanistic knowledge of the fundamental processes occurring in polymeric materials carrying functional groups under thermal and mechanical stress is highly relevant for enabling their large scale processing via e.g. extrusion and injection molding as well as techniques involving the shaping and manufacturing of polymer based products. The most common polymer architectures – from an application point of view – are linear, branched and cross-linked network structures. A branched polymer structure is described as a non-linear polymer topology with multiple backbone chains tethered to focal points within the structure, i.e. the backbones or side arms. Branched polymers have gained significant attention in both academia and industry due to their unique physical and chemical properties and potential applications in various fields from film forming and coatings to drug delivery.1,2 Star polymers constitute the simplest form of branched macromolecules in which all the polymer chains (or arm segments) of one macromolecule are linked to a central focal core.3–6 It has been demonstrated that branching results in a more compact structure in comparison to linear counterparts of similar molecular weight, due to the higher segment density of the branched structure, which changes the solution, melt and solid-state properties of the polymer.7–9Ionic, mostly anionic polymerizations have been widely utilized to generate complex macromolecular architectures with controlled molecular weights, well-defined chain ends, low polydispersity and various compositions.10–12 However, there has been rapid growth in the area of controlled/living radical polymerizations (LRP) in the last two decades due to the variety of applicable monomers and the more tolerant experimental conditions than living ionic polymerization routes.13 LRP techniques such as atom transfer radical polymerization (ATRP),14–17 nitroxide mediated radical polymerization (NMP),18,19 and reversible addition fragmentation chain transfer (RAFT)20–23 polymerization are relatively new methods that are used to achieve star-shaped architectures with various compositions.24
Star polymers are usually synthesized via one of three common methodologies, i.e. core-first, arm-first or coupling-onto.24,25 RAFT polymerization is unique among all the star synthesis techniques because the core-first strategy can be further subdivided into two strategies: the R-group approach and the Z-group approach.26 The Z-group design is typically preferred over the R-group approach, as it avoids the formation of higher-order coupling products (see Scheme S1 in the ESI†). In the Z-group approach, the RAFT agent is covalently attached to the structural framework of the core and thus the core never carries radical functions excluding the possibility of core–core couplings.27,28 In contrast – in ATRP and NMP – the core carries the radical species by default and thus core–core coupling reactions occur, which can only be minimized by carefully selecting the reaction conditions e.g. low conversions, low radical fluxes or the use of rapidly propagating monomer. However, a disadvantage of the Z-group approach is the fact that all chains are tethered to the central core via a RAFT agent linkage, which is a potentially weak connection when processing Z-group based RAFT designed polymers.
Recently, we investigated the stability of linear RAFT-based polystyrene and polyacrylate melts that carry a mid-chain trithiocarbonate function emulating a Z-group linkage under thermal and mechanical stress with the aim of developing an encompassing mechanistic, kinetic and rheological image of the degradation process.29 In the previous study, we provided systematic knowledge regarding the stability of the generated linear polymers in the melt under extrusion (i.e. 200 °C) conditions and the associated typical shear rates and pressure30 with regard to the trithiocarbonate functionality at elevated temperatures as a function of processing time. The results showed that Z-group designed materials (featuring a specific trithiocarbonate mid-chain function) can be processed via melt extrusion at elevated temperatures, provided the extrusion times are on average below 3 minutes at 200 °C or 22 minutes at 180 °C leading to an acceptable 10% reduction of molecular weight.
In the present study – a significant extension of our previous work on linear polymer into branched polymer melt29 – highly pure and well-defined star-shaped polymers were prepared via RAFT polymerization via the Z-group approach. The stability of such star-shaped polymer is investigated under thermal and mechanical stress under an inert atmosphere (nitrogen or argon) to understand their cleavage kinetics as well as rheological behavior in order to provide guidelines for their potential thermal processing. Well-defined star-shaped polystyrenes carrying trithiocarbonate functionalities at the core of the polymer with 3-arms (Mn,SEC = 156 kDa, Đ = 1.16 based on multi-angle laser light scattering (MALLS) detection) and 4-arm (Mn,SEC = 162 kDa, Đ = 1.15 also based on MALLS detection) have thus been prepared. The thermal stability of RAFT-functionalized star polystyrenes was studied at elevated temperatures and a detailed kinetic investigation of the degradation of the star-shaped RAFT polymers was carried out at variable temperatures under an inert atmosphere. In addition, the prepared polymers were subjected to extrusion experiments and a detailed rheological assessment to correlate the obtained kinetic data with actual processing conditions. Importantly, rheological assessments are very sensitive to molecular changes within the polymer structure due to the approximately cubic dependence of the zero shear viscosity, η0, on the weight-average molecular weight, η0 ∼ M3.4w as shown by the reptation theory for linear, monodisperse homopolymers,31–34 thus providing a fine sensor for possible polymer cleavage reactions. Highly branched polymer melts have a lower zero shear viscosity, η0, than the linear ones with the same total molecular weight.35–37 However, the zero shear viscosity of symmetric star polymers with entangled branches depends on the length of the arm, Ma, normalized to the entanglement molecular weight, Me, and not the number of arms or total molecular weight of star polymer38 (e.g. η0 = k (Ma/Me)α exp(νMa/Me) with α = 1.5 and ν = 0.47 for polyisoprene, where k is a temperature dependent prefactor). However, a modest deviation for 3-arm and 4-arm stars has been observed.39,40
Experimental section
All manipulations of air-sensitive processes such as the stability studies of RAFT star polystyrenes were performed under the rigorous exclusion of oxygen and moisture in Schlenk-type glassware on a dual manifold Schlenk line interfaced with a high vacuum line (10−3 bar).Materials
Styrene (99% extra pure, Acros) was destabilized by passing through a basic alumina column and stored at −19 °C. Toluene (extra dry over molecular sieve, 99.85%, Acros) was used as received. All other chemicals were purchased from Aldrich and used without further purification. Trimethylolpropane-tris-3-(S-benzyl-trithiocarbonyl)-propanoate (1) and pentaerythritol-tetrakis-(3-(S-benzyl-trithiocarbonyl)-propanoate) (2) were synthesized according to literature procedures (see Scheme 1).41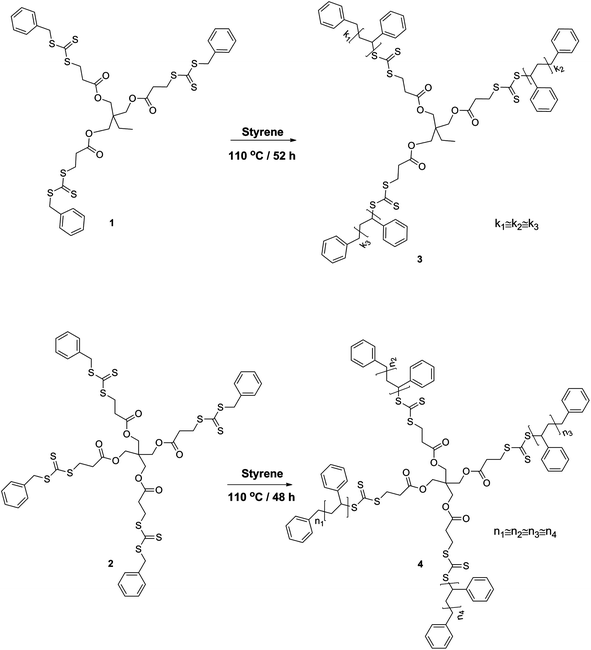 | ||
| Scheme 1 Synthetic strategy for the preparation of 3 and 4-arm star-shaped polystyrenes via a Z-group approach carrying trithiocarbonate moieties in the center of the architecture. | ||
Instrumentation
| Polymer | [CTA]0/mM | Monomer | Time/h | M n /Mnc/kg mol−1 | Đ /Đc | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The structure of the employed chain transfer agents (CTAs) are shown in the Scheme 1. b Determined via SEC using THF as the eluent, calibrated with linear polystyrene standards. c Absolute number-average molecular weights obtained by SEC-MALLS. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3-arm star (3) | 0.84 (1a) | Styrene | 52 | 116/156 | 1.33/1.16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-arm star (4) | 0.55 (2a) | Styrene | 48 | 130/162 | 1.52/1.15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Results and discussion
RAFT polymerization (within the controlled/living radical polymerization family) is a potential candidate for use in variable industrial applications due to its non-demanding reaction conditions, tolerance to a wide variety of monomers as well as similarity to conventional free radical polymerization processes. Star-shaped polymers mimic branched polymers – on a simplified level – and thus constitute an ideal starting point for understanding the stability of branched polymers carrying the most commonly employed RAFT function, namely trithiocarbonates, at the focal point under both thermal and mechanical stress. Thus, Z-type trithiocarbonate functional star-shaped polystyrenes with 3-arm and 4-arm featuring a Z-group design have been prepared via RAFT polymerization with high molecular weight and relatively low polydispersity. The resulting molecular weight distributions obtained by on-line multi-angle laser light scattering (MALLS) are depicted in Fig. S1 in the ESI† section and the relevant reaction conditions are collated in Table 1.Understanding the degradation of polymer systems in an ambient atmosphere is challenging.43–45 Since extrusion is typically conducted at high temperatures (e.g. 200 °C) and pressures (e.g. 300 bar) in closed vessels, the oxygen content is substantially reduced. Thus – to simplify the experimental approach and to mimic the conditions present during extrusion processes – the thermal stability of trithiocarbonate core-functional star-shaped polymers has been studied first at various temperatures in inert atmospheres via time-dependent size exclusion chromatography. Such an approach allows quantifying the core cleavage processes by determining the cleavage kinetics and activation energy of the thermal degradation process. The kinetic analysis allows for a comparison between the thermal stability of Z-group trithiocarbonate RAFT star polystyrenes as a function of time and their extrusion processes under thermal and mechanical stress.29
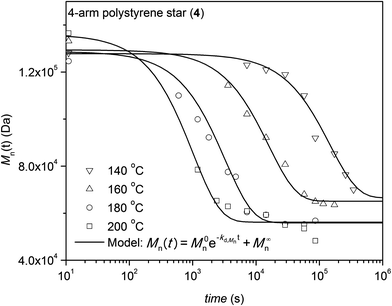
The kinetic degradation studies under inert atmosphere were carried out employing 3-arm and 4-arm star-shaped polystyrene architectures and trithiocarbonate core-functional RAFT polymers (3 and 4 see Table 1) to assess if the number of arms and local packing has a significant influence on the cleavage process of the central core. The kinetics of the cleavage process are investigated under isothermal conditions in the melt at different temperatures with the polymers being kept at various temperatures for pre-set time intervals. SEC was employed to determine the degradation kinetics of the star RAFT polymers by monitoring the number-average molecular weight after each time interval. Exemplary evolutions of the full molecular weight distribution are depicted for the degradation at 180 °C for both polystyrenes 3 and 4 in Fig. 1 and 2, respectively. The number-average molecular weights of the polymers 3 and 4 are plotted vs. the reaction time at different temperatures as depicted in Fig. 3 and 4, respectively. The weight-average molecular weights of polymer 3 and 4 are plotted vs. the reaction time at variable temperatures as depicted in Fig. S2 and S3 in the ESI section.† Degradation rate coefficients, kd,Mn, are obtained by fitting the Mn(t) data depicted in Fig. 5 to eqn (1a) (see below for a detailed description of fitting process). As evident from Fig. 3 and 4 both polymers show increased degradation rates with increasing temperature. To allow for an optimum comparability of the SEC data, all SEC analyses were conducted on the same day on the same instrument for each degradation temperature. An Mn-based kinetic analysis yields the rate coefficient associated with the occurring elemental reaction (see below).
 | ||
| Fig. 1 Evolution of the molecular weight distribution of the trithiocarbonate core functional 3-arm star polystyrene 3 at 180 °C as a function of time in an argon atmosphere. | ||
 | ||
| Fig. 2 Evolution of the molecular weight distribution of the trithiocarbonate core functional 4-arm star polystyrene 4 at 180 °C as a function of time in an argon atmosphere. | ||
 | ||
| Fig. 5 Comparison of Arrhenius plots (based on data employing Mn(t) as a measure for cleavage) for the degradation of RAFT based 3-arm and 4-arm star-shaped polystyrenes as well as linear polystyrenes (2-arm, Mn = 102 kDa) all featuring trithiocarbonate core-functionalities in an inert atmosphere.29 | ||
The rate coefficients, kd,Mn, (refer to Table 2) for the thermal degradation of the corresponding polymers under argon atmosphere in the temperature range between 140 °C and 200 °C were determined using eqn (1a) (see below). Where M0n is the molecular increment added to M∞n at t = 0 corresponding to the initial molecular weight of M0n + M∞n, t is the time the polymer exposed to each temperature and Mn(t) is the observed number-average molar mass after heating for time t. The parameter M∞n is the molar mass of the polymer at infinite time reflecting the maximum possible degradation. Eqn (1a) was fitted – not forcing the fit through any data point (including the starting Mn value) as all data points are assumed to feature an identical SEC error – to the data in Fig. 3 and 4. Note that for the initial star polymer the molecular weight relative to linear polystyrene standards is employed. A deeper inspection of the data contained in Fig. 3 reveals an interesting point: the final molecular weight obtained after degradation at the highest temperature is, in the case of the 3-arm star polymer, approximately 3 times smaller than the MALLS determined molecular weight (3 times 53 kDa equals 159 kDa compared to 156 kDa (MALLS)). In the case of the 4-arm star polymer, the final molecular weight observed at the highest degradation temperature agrees reasonably well with the initial MALLS determined molecular weight divided by a factor of four (162 kDa/4 = 40.5 kDa compared to approx. 48 kDa as determined, see Fig. 4). The kinetic analysis additionally demonstrates that the degradation process can be described by first order kinetics, in analogy to the degradation of mid-chain functional linear RAFT polystyrenes.29 The synthesized star polystyrenes were of relatively low dispersity, however to capture the effect of polydispersity on the rheological behavior, we analyzed the thermal degradation process using both the number-average molecular weight, Mn, and the weight-average molecular weight, Mw. Rheological properties (e.g. longest relaxation times, zero shear viscosity (η0) and zero shear compliance) are highly sensitive to high molecular weight polymer fractions which have more influence on the Mw than Mn, as Mw reflects the volumetric occupancy of the polymer weight distribution.
 | (1a) |
 | (1b) |
| T/°C | k d,Mn/s−1 (3) | M 0n (3) | M ∞n (3) | k d,Mn/s−1 (4) | M 0n (4) | M ∞n (4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Note: the units of M0n and M∞n are in kDa. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 140 | 9.26 × 10−6 | 48.6 | 60.0 | 6.79 × 10−6 | 61.3 | 66.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 160 | 6.57 × 10−5 | 55.5 | 59.0 | 6.31 × 10−5 | 64.3 | 65.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 180 | 3.22 × 10−4 | 57.7 | 56.8 | 3.07 × 10−4 | 72.8 | 55.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 200 | 1.17 × 10−3 | 63.3 | 52.6 | 0.99 × 10−3 | 79.8 | 56.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
M 0w, M∞w and kd,Mw have the similar definitions as presented before for the Mn based analysis. These parameters are determined by fitting the Mw data shown in the Fig. S2 and S3† using eqn (1b) for 3-arm and 4-arm stars, respectively and are reported in Table 3.
| T/°C | k d,Mw/s−1 (3) | M 0w (3) | M ∞w (3) | k d,Mw/s−1 (4) | M 0w (4) | M ∞w (4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Note: the units of M0w and M∞w are in kDa. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 140 | 5.56 × 10−6 | 70 | 77 | 5.03 × 10−6 | 119 | 82 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 160 | 3.36 × 10−5 | 76 | 75 | 4.11 × 10−5 | 118 | 84 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 180 | 2.03 × 10−4 | 71 | 73 | 2.25 × 10−4 | 118 | 79 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 200 | 1.01 × 10−3 | 84 | 71 | 0.83 × 10−3 | 128 | 79 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Subsequently, kd,Mn(T) and kd,Mw(T) were employed to construct Arrhenius plots for both the number-average molecular weight and the weight-average molecular weight. Activation energies, Ea, for the thermal degradation of polymer 2 and 4 were deduced from the slopes of the Arrhenius plots according to eqn (2), where R is the gas constant (8.314 J mol−1 K−1), T is the temperature in Kelvin and A is the frequency factor:
 | (2) |
Plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kdvs. 1/T, the slope and intercept provide −Ea/R and ln(A), respectively. The Arrhenius analysis indicates that the activation energy (Ea) does not show significant differences for different architectures for the trithiocarbonate functional polymers (131 kJ mol−1 for 3 and 134 kJ mol−1 for 4 based on Mn) within experimental error. The degradation process itself proceeds most probably via a Chugaev-type elimination46 as evidenced in our previous study,29 as similar RAFT agents have been utilized in the previous and current study. In addition, it is found that Ea,Mw is slightly higher than Ea,Mn for both star polymers (refer to Fig. S2†).
kdvs. 1/T, the slope and intercept provide −Ea/R and ln(A), respectively. The Arrhenius analysis indicates that the activation energy (Ea) does not show significant differences for different architectures for the trithiocarbonate functional polymers (131 kJ mol−1 for 3 and 134 kJ mol−1 for 4 based on Mn) within experimental error. The degradation process itself proceeds most probably via a Chugaev-type elimination46 as evidenced in our previous study,29 as similar RAFT agents have been utilized in the previous and current study. In addition, it is found that Ea,Mw is slightly higher than Ea,Mn for both star polymers (refer to Fig. S2†).
It is important to compare the values obtained for the star-shaped polymers with their linear mid-chain functional trithiocarbonate analogues (Ea = 116 kJ mol−1, A = 6.24 × 109 s−1; Mn,SEC = 102 kDa, Đ = 1.35).29 The activation energy (based on Mn data) for both star-shaped architectures is close to 132 kJ mol−1, while it reads 116 kJ mol−1 for the earlier investigated linear mid-chain functional trithiocarbonate polymers,29 thus demonstrating that the activation energy is increased (by approximately 16 kJ mol−1) for the star-shaped polymers due to the altered chemical embedding of the RAFT agent: the RAFT agent utilized for the linear polymers has a symmetrical structure in terms of the R-group (styryl groups on both sides), while the RAFT agents employed generating the star-shaped polymers are asymmetrical featuring a primary Z-group, thus likely affecting the activation energies of thermal elimination processes associated with the bond cleavage. Further inspection of Fig. 5 reveals that – while the activation energies are slightly different between linear and star-shaped polymers – a factor exceeding 100 is observed for the pre-exponential factor. As a consequence and as an important finding, the star-shaped polystyrenes 3 and 4 degrade faster than their linear equivalents at similar temperatures. While such an observation may seem surprising at first, it has a possible explanation: within the star-shaped polymers the multiple trithiocarbonate functions are located at the focal point of the architecture in a region of significant compactness, constituting a center where molecular stress and steric strain are exerted by the attached arms. Therefore, the rate at which the trithiocarbonate functions in star-shaped topology undergo cleavage is enhanced.
In a subsequent step, the melt rheological and extrusion behavior of the star-shaped polystyrenes was investigated. The polymers may undergo degradation caused by temperature in the presence of an inert atmosphere as well as additional mechanical stresses during processing. The rheological properties can be monitored continuously in time (e.g. 1 data point per oscillation period) and therefore the degradation process of the samples are assessed via their rheological properties, especially the absolute value of the complex viscosity, |η*|, in the linear regime throughout the degradation process. In the following section, the changes in zero shear viscosity,  , assuming the validity of the Cox–Merz rule will be utilized.47
, assuming the validity of the Cox–Merz rule will be utilized.47
The zero shear viscosity, η0, is directly related to the molecular weight of a polymer.32–34 For polystyrene below the critical molecular weight Mc (≈3Me; Meca. 18 kDa for polystyrene) the zero shear viscosity scales linear with the weight-average molecular weight, Mw. For Mw larger than Mc, reptation theory describes the linear polymer's behavior and leads to a η0 ∼ M3.4w power law dependence of the viscosity on molecular weight. However, as already noted in the introduction, the zero shear viscosity η0, of symmetric star polymers with entangled branches depends on the length of the branch and not the total molecular weight of polymer or number of branches,38i.e. η0 = k (Ma/Me)α exp(νMa/Me) with α = 1.5 and ν = 0.47 for polyisoprene, where k is temperature dependent prefactor.39 The absolute value of the complex viscosities as well as weight-average molecular weights as a function of time at a temperature of 180 °C at a frequency of ω/2π = 0.05 Hz and γ0 = 0.25 strain for the star polystyrenes 3 and 4 are depicted in Fig. 6. Dynamic frequency sweep test depicted in Fig. S7† shows that the zero shear viscosity,  , has been reached for frequency below 5 Hz for degraded polystyrenes. Consequently, it is expected that the initial polystyrenes 3 and 4 before the cleavage process have the longest relaxation time, τ, proportional to the inverse of the cross over frequency, 1/ωc, and M3.4w:
, has been reached for frequency below 5 Hz for degraded polystyrenes. Consequently, it is expected that the initial polystyrenes 3 and 4 before the cleavage process have the longest relaxation time, τ, proportional to the inverse of the cross over frequency, 1/ωc, and M3.4w:
| τ ∼ 1/ωc ∼ M3.4w | (3) |
With respect to eqn (3) and the initial molecular weights M3-arm ≈ 3Ma and M4-arm ≈ 4 Ma, the cross over frequencies ωc of 0.1 and 0.05 Hz for polystyrenes 3 and 4, respectively, are assumed and consequently a test frequency of 0.05 Hz was selected. These expected cross over frequencies show that the applied shear frequency ω/2π = 0.05 Hz is sufficient to use the Cox–Merz rule and the assumption  , during the cleavage process time. Inspection of Fig. 6 indicates that the zero shear viscosities and weight-average molecular weight of polystyrene 3 and 4 remain constant up to 10 minutes and subsequently decrease with increasing time at elevated temperatures. Decrease in the zero shear viscosities and weight-average molecular weight demonstrate almost similar behavior. With respect to the Fig. 6, the plateau viscosity η0 before the dynamic time sweep measurement is close to 5900 Pa s for the polystyrene 3, while it is strongly reduced to 1200 Pa s after about 104 seconds and then decreases with a slower slope. These findings demonstrate that η0 is approximately a factor 5 lower than the initial η0 before the cleavage process for polystyrene 3 and the further decrease of η0 after about 104 seconds (see Fig. 6) is related to the thermal degradation of linear arms. Moreover, the star polystyrene 4 and polystyrene 3 show qualitatively similar η0 time dependencies during cleavage and the later potential arm degradation process. After applying both thermal and mechanical stress (in the linear regime) in the above experiment, SEC analysis revealed that the molecular weight distributions of polystyrene 3 has experienced the expected change, reflecting a reduction in molecular weight from Mn = 156 kDa (based on MALLS detection) to Mn = 52 kDa (linear polystyrene calibration) (see Fig. S3 in the ESI section†). The change in number-average molecular weight, Mn, observed for the 4-armed polystyrene 4 is similar to the change observed for polystyrene 3. However, the 4-armed polystyrene 4 shows an even more pronounced reduction from Mn = 162 kDa (based on MALLS detection) to Mn = 51 kDa (linear polystyrene calibration) (see Fig. S5 in the ESI section†). These results agree well with the SEC data obtained in the time resolved SEC analysis for polymer subjected to only thermal stress. Thus, mechanical stress has (as expected) no distinct effect on the cleavage and degradation process in these polymers and rheological properties in the linear regime (i.e. zero shear viscosity, η0). Therefore, the time dependency of zero shear viscosity and molecular weight should be similar (e.g. exponential time dependence).
, during the cleavage process time. Inspection of Fig. 6 indicates that the zero shear viscosities and weight-average molecular weight of polystyrene 3 and 4 remain constant up to 10 minutes and subsequently decrease with increasing time at elevated temperatures. Decrease in the zero shear viscosities and weight-average molecular weight demonstrate almost similar behavior. With respect to the Fig. 6, the plateau viscosity η0 before the dynamic time sweep measurement is close to 5900 Pa s for the polystyrene 3, while it is strongly reduced to 1200 Pa s after about 104 seconds and then decreases with a slower slope. These findings demonstrate that η0 is approximately a factor 5 lower than the initial η0 before the cleavage process for polystyrene 3 and the further decrease of η0 after about 104 seconds (see Fig. 6) is related to the thermal degradation of linear arms. Moreover, the star polystyrene 4 and polystyrene 3 show qualitatively similar η0 time dependencies during cleavage and the later potential arm degradation process. After applying both thermal and mechanical stress (in the linear regime) in the above experiment, SEC analysis revealed that the molecular weight distributions of polystyrene 3 has experienced the expected change, reflecting a reduction in molecular weight from Mn = 156 kDa (based on MALLS detection) to Mn = 52 kDa (linear polystyrene calibration) (see Fig. S3 in the ESI section†). The change in number-average molecular weight, Mn, observed for the 4-armed polystyrene 4 is similar to the change observed for polystyrene 3. However, the 4-armed polystyrene 4 shows an even more pronounced reduction from Mn = 162 kDa (based on MALLS detection) to Mn = 51 kDa (linear polystyrene calibration) (see Fig. S5 in the ESI section†). These results agree well with the SEC data obtained in the time resolved SEC analysis for polymer subjected to only thermal stress. Thus, mechanical stress has (as expected) no distinct effect on the cleavage and degradation process in these polymers and rheological properties in the linear regime (i.e. zero shear viscosity, η0). Therefore, the time dependency of zero shear viscosity and molecular weight should be similar (e.g. exponential time dependence).
With respect to the above findings and the zero shear viscosity experimental data in Fig. 6, a double mode exponential function was applied to describe the time dependency of η0:
 | (4) |
 | (5) |
| 3-arm | ||||||
|---|---|---|---|---|---|---|
| T/°C | k D0/s−1 (3) | k D0/kd,Mw (3) | η 00/Pa s (3) | k D1/s−1 (3) | η 0 1/Pa s (3) | η ∞0/Pa s (3) |
| 180 | 3.04 × 10−4 | 1.24 | 4740 | 1.35 × 10−5 | 770 | 400 |
| 4-arm | ||||||
|---|---|---|---|---|---|---|
| T/°C | k D0/s−1 (4) | k D0/kd,Mw (4) | η 00/Pa s (4) | k D1/s−1 (4) | η 0 1/Pa s (4) | η ∞0/Pa s (4) |
| 180 | 2.98 × 10−4 | 1.32 | 10360 | 1.20 × 10−5 | 1250 | 564 |
Comparing the weight-average molecular weight cleavage rate coefficient, kd,Mw, (refer to Table 3 at T = 180 °C) and its relevant zero shear viscosity reduction rate coefficient, kD0, (refer to Table 4) of the corresponding polymers shows that the ratio kD0/kd,Mw represents a relationship for the normalized zero shear viscosity and molecular weight in the range of cleavage time:
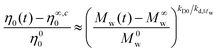 | (6) |
A detailed derivation of eqn (6) is provided in Appendix I (see I8) in the ESI section.†Eqn (6) reveals that the normalized zero shear viscosity has a power law behaviour with an exponent of kD0/kd,Mw. This power law index is 1.24 and 1.32 for the 3-arm and 4-arm star polystyrenes, respectively (see Table 4). However, for more investigations the absolute value of the zero shear viscosity, η0, is plotted as a function of the absolute weight-average molecular weight in Fig. 7a. Zero shear viscosity of linear polystyrene are also shown in Fig. 7a from ref. 48 at the reference temperature Tref = 170 °C, η0,linearPS = 8.8 × 10−14M3.4w, and the WLF shift factor, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aT = −5.47(T − 170)/(119 + (T − 170)), where T is given in Celsius. Using this shift factor, the zero shear viscosity for linear polystyrene was re-calculated for T = 180 °C:
aT = −5.47(T − 170)/(119 + (T − 170)), where T is given in Celsius. Using this shift factor, the zero shear viscosity for linear polystyrene was re-calculated for T = 180 °C:
| η0,linearPS = 3.31 × 10−14M3.4w; T = 180 °C | (7) |
Eqn (7) for linear PS along with eqn (6) for star polystyrenes 3 and 4 are plotted in Fig. 7a. The experimental data in Fig. 7a for η0 and Mw of the star polystyrenes 3 and 4 are reported using the data for Mw(t) from SEC in Fig. S2 and S3† and η0(t) at the same times from rheometry in Fig. 6. Fig. 7a evidences that the experimental data as well as the relevant predictions of eqn (6) for star polystyrenes 3 and 4 are lower than the zero shear viscosity of linear PS with the same total molecular weights. This is in agreement with the experimental data of 3-arm and 4-arm polybutadiene stars when the branch length, Ma, are below the 3 or 4 times Me.49 Molecular weight dependency of zero shear viscosity in the log–log scale, η0 = kMαw, is an important rheological property, where α = 3.4 is for linear polymers. With respect to these criteria, the analytical molecular weight derivative of zero shear viscosity in eqn (6) is derived on a natural log–log scale:
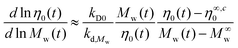 | (8) |
More details on the derivation of eqn (8) are provided in Appendix I in ESI section.†Eqn (8) presents the slope of η0 as a function of Mw on a log–log scale with the data plotted numerically in Fig. 7b for 3-arm and 4-arm star polystyrenes. These curves show that pure star polymers, before degradation, have a slope 2 and 1.8 for 3-arm and 4-arm polystyrene, respectively, which is lower than the slope of linear PS (α = 3.4). This behaviour was related to the contour length fluctuation and constraint release mechanisms, which are dominant relaxation mechanisms compared to the reptation mechanism for star polymers.40 By decreasing the molecular weight via the cleavage process, this slope increases and approaches 3.4, which is an indication that linear counterparts are produced during the decrease of the molecular weight. However, the slope never fully reaches 3.4, because the degradation process of linear polymers (arms) starts for times larger than 1–2 × 104 seconds. This effect was neglected in eqn (8).
Polymer processing provides a simple means to shape and to manufacture plastic objects products from polymer granules. The extrusion process represents a continuous shaping of a polymer in the melt and subsequent solidification into the final product. To mimic the extrusion process of the star-shaped polystyrenes (3 and 4) with trithiocarbonate functionalities, a 5 minute residence time in the extrusion barrel – consistent with the mixing average residence time typically given in extrusion – was selected. However, feeding of the polymers took close to 7 minutes, therefore the total residence time is rather close to 12 minutes at 180 °C. The change in molar mass after extrusion can provide a measure for the combined effects of thermal and mechanical degradation via pressure and shear. The molecular weight reduction observed during extrusion can be compared to the reduction in molecular weight observed viaeqn (1a) for polystyrenes 3 and 4. During the entire extrusion experiment the polymers were exposed to 180 °C for 12 minutes (see above). The expected Mn values for polystyrene 3 and 4 after exposure to thermal stress based on eqn (1a) read 103 kDa and 114 kDa, respectively (using the kinetic rate coefficients provided in Table 2). The number-average molecular weight of polystyrene 3 and 4 after extrusion was determined via size exclusion chromatography to assess the change in molecular weight (refer to Fig. 8). The apparent values for the number-average molecular weight based on SEC before/after extrusion were found to be Mn = 115 kDa (linear PS calibration) vs. Mn = 93 kDa (linear PS calibration) and Mn = 127 (linear PS calibration) vs. Mn = 102 kDa (linear PS calibration) (corresponding to a 20% decrease in both cases) for 3-arm polystyrene 3 (refer to Fig. 8a) and 4-arm polystyrene 4 (refer to Fig. 8b), respectively. Comparing the number-average molecular weight obtained for polystyrene 3 and 4viaeqn (1a) with the value obtained for the same polymer after extrusion, it appears that the extrusion process had an enhanced reduction effect on the Mn values due to mechanical stress in the non-linear deformation regime. In our previous study, no additional effect of the extrusion process on the degradation behavior of the linear mid-chain functional trithiocarbonate polymers (extrusion at 200 °C for 20 min) was observed.29
Conclusions
The stability of trithiocarbonate functional Z-group designed star-shaped RAFT polymers with 3 and 4 arms was investigated under thermal and mechanical stress in an inert atmosphere at elevated temperatures ranging from 140 °C to 200 °C. The thermally treated RAFT star polymeric material was analyzed by size exclusion chromatography as a function of its exposure time to the elevated temperatures. The molar mass of the star-shaped RAFT polystyrenes decreased following first order kinetics during 8 hours most probably via a unimolecular Chugaev-type cleavage process. First order rate coefficients for the 3-arm and 4-arm polystyrene 3 and 4 under inert atmosphere as well as the associated activation parameters (Ea = 131 kJ mol−1; A = 3.93 × 1011 s−1 and Ea = 134 kJ mol−1; A = 9.13 × 1011 s−1) for the thermal degradation were determined from the time dependant evolution of the number-average molecular weight. On-line monitoring of the zero shear viscosity, , (complex viscosity at 0.05 Hz) indicates that the cleavage process commences after 10 minutes. Cleavage reactions of the arms are almost completed after 5/kD0 ≈ 1–2 × 104 seconds and secondary arm degradation process occur subsequently at 0.1/kD1 ≈ 1–2 × 104 seconds. Combining the high time resolution of the kinetic of zero shear viscosity and the quantitative cleavage kinetics as determined via SEC leads to a very detailed molecular weight dependency of zero shear viscosity, which was compared with linear polystyrenes. Furthermore, SEC traces recorded after extrusion for 12 minutes under inert atmosphere at 180 °C demonstrated that the number-average molecular weight of the trithiocarbonate core-functional both star polystyrenes decreases by 20% while the related reduction is only 10% in the presence of thermal stress alone, indicating that mechanical stress in the non-linear deformation regime leads to an additional degradation of the star-shaped polystyrenes. Thus – considering all results obtained in the present and previous studies – it is clear that star Z-group designed polystyrenes featuring a trithiocarbonate moiety are more prone to degradation during thermal and mechanical stress than their linear mid-chain functional analogs.
, (complex viscosity at 0.05 Hz) indicates that the cleavage process commences after 10 minutes. Cleavage reactions of the arms are almost completed after 5/kD0 ≈ 1–2 × 104 seconds and secondary arm degradation process occur subsequently at 0.1/kD1 ≈ 1–2 × 104 seconds. Combining the high time resolution of the kinetic of zero shear viscosity and the quantitative cleavage kinetics as determined via SEC leads to a very detailed molecular weight dependency of zero shear viscosity, which was compared with linear polystyrenes. Furthermore, SEC traces recorded after extrusion for 12 minutes under inert atmosphere at 180 °C demonstrated that the number-average molecular weight of the trithiocarbonate core-functional both star polystyrenes decreases by 20% while the related reduction is only 10% in the presence of thermal stress alone, indicating that mechanical stress in the non-linear deformation regime leads to an additional degradation of the star-shaped polystyrenes. Thus – considering all results obtained in the present and previous studies – it is clear that star Z-group designed polystyrenes featuring a trithiocarbonate moiety are more prone to degradation during thermal and mechanical stress than their linear mid-chain functional analogs.
Acknowledgements
C.B.-K. and M.W. gratefully acknowledge financial support from the German Research Council (DFG). C.B.-K. acknowledges long term funding from the Karlsruhe Institute of Technology (KIT) in the context of the Helmholtz BIF and STN programs. The authors thank Dr Maria Schneider-Baumann (KIT) for the multi-angle laser light scattering (MALLS) measurements.Reference
- C. Gao and D. Yan, Prog. Polym. Sci., 2004, 29, 183–275 CrossRef CAS PubMed.
- C. R. Yates and W. Hayes, Eur. Polym. J., 2004, 40, 1257–1281 CrossRef CAS PubMed.
- T. Neidhoefer, S. Sioula, N. Hadjichristidis and M. Wilhelm, Macromol. Rapid Commun., 2004, 25, 1921–1926 CrossRef CAS.
- N. Hadjichristidis, M. Pitsikalis, S. Pispas and H. Iatrou, Chem. Rev., 2001, 101, 3747–3792 CrossRef CAS PubMed.
- N. Hadjichristidis, H. Iatrou, M. Pitsikalis and J. Mays, Prog. Polym. Sci., 2006, 31, 1068–1132 CrossRef CAS PubMed.
- A. Hirao, M. Hayashi, S. Loykulnant and K. Sugiyama, Prog. Polym. Sci., 2005, 30, 111–182 CrossRef CAS PubMed.
- J. Roovers, in Star and Hyperbranched Polymers, ed. M. K. Mishra and S. Kobayashi, Marcel Dekker, New York, 1998 Search PubMed.
- A. Hult, M. Johansson and E. Malmstrom, Adv. Polym. Sci., 1999, 143, 1–34 CAS.
- W. Burchard, Adv. Polym. Sci., 1999, 143, 113–194 CrossRef CAS.
- N. Hadjichristidis, J. Polym. Sci., Part A: Polym. Chem., 1999, 37, 857–871 CrossRef CAS.
- N. Hadjichristidis, S. Pispas, M. Pitsikalis, C. Vlahos and H. Iatrou, Adv. Polym. Sci., 1999, 142, 71–127 CrossRef CAS.
- A. Hanisch, H. Schmalz and A. H. E. Müller, Macromolecules, 2012, 45, 8300–8309 CrossRef CAS.
- U. Tunca, Z. Ozyurek, T. Erdogan and G. Hizal, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 4228–4236 CrossRef CAS.
- J. S. Wang and K. Matyjaszewski, J. Am. Chem. Soc., 1995, 117, 5614–5615 CrossRef CAS.
- K. Matyjaszewski and J. Xia, Chem. Rev., 2001, 101, 2921–2990 CrossRef CAS PubMed.
- V. Percec and B. Barboiu, Macromolecules, 1995, 28, 7970–7972 CrossRef CAS.
- D. M. Haddleton, M. C. Crossman, B. H. Dana, D. J. Duncalf, A. M. Heming, D. Kukulj and A. J. Shooter, Macromolecules, 1999, 32, 2110–2119 CrossRef CAS.
- C. J. Hawker, Angew. Chem., Int. Ed., 1995, 34, 1456–1459 CrossRef CAS.
- C. J. Hawker, A. W. Bosman and E. Harth, Chem. Rev., 2001, 101, 3661–3688 CrossRef CAS PubMed.
- R. T. A. Mayadunne, E. Rizzardo, J. Chiefari, Y. K. Chong, G. Moad and S. H. Thang, Macromolecules, 1999, 32, 6977–6980 CrossRef CAS.
- C. Barner-Kowollik, T. P. Davis, J. P. A. Heuts, M. H. Stenzel, P. Vana and M. Whittaker, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 365–375 CrossRef CAS.
- C. Barner-Kowollik, M. Buback, B. Charleux, M. L. Coote, M. Drache, T. Fukuda, A. Goto, B. Klumperman, A. B. Lowe, J. B Mcleary, G. Moad, J. M. Monteiro, R. D. Sanderson, M. P. Tonge and P. Vana, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 5809–5831 CrossRef CAS.
- H. Willcock and R. K. O'Reilly, Polym. Chem., 2010, 1, 149–157 RSC.
- O. Altintas, A. P. Vogt, C. Barner-Kowollik and U. Tunca, Polym. Chem., 2012, 3, 34–45 RSC.
- H. F. Gao and K. Matyjaszewski, Prog. Polym. Sci., 2009, 34, 317 CrossRef CAS PubMed.
- A. Gregory and M. H. Stenzel, Prog. Polym. Sci., 2012, 37, 38–105 CrossRef CAS PubMed.
- L. Barner, T. P. Davis, M. H. Stenzel and C. Barner-Kowollik, Macromol. Rapid Commun., 2007, 28, 539–559 CrossRef CAS.
- H. Chaffey-Millar, M. H. Stenzel, T. P. Davis, M. L. Coote and C. Barner-Kowollik, Macromolecules, 2006, 39, 6406–6419 CrossRef CAS.
- O. Altintas, K. Riazi, R. Lee, C. Y. Lin, M. L. Coote, M. Wilhelm and C. Barner-Kowollik, Macromolecules, 2013, 46, 8079–8091 CrossRef CAS.
- M. Kempf, D. Ahirwal, M. Cziep and M. Wilhelm, Macromolecules, 2013, 46, 4978–4994 CrossRef CAS.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, London, UK, 1979 Search PubMed.
- M. T. Shaw, Introduction to Polymer Rheology, John Wiley & Sons, New Jersey, USA, 2012 Search PubMed.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, USA, 1999 Search PubMed.
- C. W. Macosko, Rheology: Principles, Measurements, and Applications, Wiley-VCH, Weinheim, Germany, 1994 Search PubMed.
- M. Abbasi, N. G. Ebrahimi and M. Wilhelm, J. Rheol., 2013, 57, 1693–1714 CrossRef CAS.
- H. M. Hassanabadi, M. Abbasi, M. Wilhelm and D. Rodrigue, J. Rheol., 2013, 57, 881–899 CrossRef CAS.
- M. Abbasi, N. G. Ebrahimi, M. Nadali and M. K. Esfahani, Rheol. Acta, 2012, 51, 163–177 CrossRef CAS.
- J. M. Dealy and R. G. Larson, Structure and Rheology of Molten Polymers, Hanser, Germany, 2006 Search PubMed.
- L. J. Fetters, A. D. Kiss, D. S. Pearson, G. F. Quack and F. J. Vitus, Macromolecules, 1993, 26, 647–654 CrossRef CAS.
- S. T. Milner, T. C. B. McLeish, R. N. Young, A. Hakiki and J. M. Johnson, Macromolecules, 1998, 31, 9345–9353 CrossRef CAS.
- D. Boschmann, R. Edam, P. J. Schoenmakers and P. Vana, Polymer, 2008, 49, 5199–5208 CrossRef CAS PubMed.
- C. Strazielle, H. O. Benoit and O. Vogl, Eur. Polym. J., 1978, 14, 331–334 CrossRef CAS.
- T. Gruendling, S. Weidner, J. Falkenhagen and C. Barner-Kowollik, Polym. Chem., 2010, 1, 599–617 RSC.
- G. Luo, I. Marginean and A. Vertes, Anal. Chem., 2002, 74, 6185–6190 CrossRef CAS.
- X. Jiang, P. J. Schoenmakers, J. L. J. van Dongen, X. Lou, V. Lima and J. Brokken-Zijp, Anal. Chem., 2004, 75, 5517–5524 CrossRef.
- L. Chugaev, Ber. Dtsch. Chem. Ges., 1899, 32, 3332 CrossRef.
- W. P. Cox and E. H. Merz, J. Polym. Sci., 1958, 28, 619–622 CrossRef CAS.
- J. Hepperle, H. Münstedt, P. K. Haug and C. D. Eisenbach, Rheol. Acta, 2005, 45, 151–163 CrossRef CAS PubMed.
- G. Kraus and J. T. Gruver, J. Polym. Sci., Part A: Gen. Pap., 1965, 3, 105–122 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4py00484a |
| This journal is © The Royal Society of Chemistry 2014 |