 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Critically evaluated rate coefficients in radical polymerization – 7. Secondary-radical propagation rate coefficients for methyl acrylate in the bulk†
Christopher
Barner-Kowollik
*ab,
Sabine
Beuermann
c,
Michael
Buback
d,
Patrice
Castignolles
e,
Bernadette
Charleux
f,
Michelle L.
Coote
g,
Robin A.
Hutchinson
h,
Tanja
Junkers
*i,
Igor
Lacík
j,
Gregory T.
Russell
k,
Marek
Stach
j and
Alex M.
van Herk
lm
aPreparative Macromolecular Chemistry, Institut für Technische Chemie und Polymerchemie, Karlsruhe Institute of Technology (KIT), Engesserstraße 18, 76131 Karlsruhe, Germany. E-mail: christopher.barner-kowollik@kit.edu
bInstitut für Biologische Grenzflächen, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
cInstitute of Technical Chemistry, Clausthal University of Technology, Arnold-Sommerfeld-Straße 4, 38678 Clausthal-Zellerfeld, Germany
dTechnical and Macromolecular Chemistry Group, Institut für Physikalische Chemie, University of Göttingen, Tammannstraße 6, D-37077 Göttingen, Germany
eUniversity of Western Sydney, Australian Centre for Research on Separation Science (ACROSS), School of Science and Health, Parramatta Campus, Locked Bag 1797, Penrith 2751, Australia
fUniversité de Lyon, Univ. Lyon 1, CPE Lyon, CNRS UMR 5265, Laboratoire de Chimie Catalyse Polymères et Procédés (C2P2), Equipe LCPP Bat 308F, 43 Bd du 11 Novembre 1918, F-69616 Villeurbanne, France
gARC Centre of Excellence for Free-Radical Chemistry and Biotechnology, Research School of Chemistry, Australian National University, Canberra ACT 0200, Australia
hDepartment of Chemical Engineering, Dupuis Hall, Queen's University, Kingston, Ontario K7L 3N6, Canada
iPolymer Reaction Design Group, Institute for Materials Research, Universiteit Hasselt, Agoralaan D, BE-3590 Diepenbeek, Belgium. E-mail: tanja.junkers@uhasselt.be
jDepartment for Biomaterials Research, Polymer Institute of the Slovak Academy of Sciences, Dubravska cesta 9, 845 41 Bratislava, Slovakia
kDepartment of Chemistry, University of Canterbury, Private Bag 4800, Christchurch 8140, New Zealand
lInstitute of Chemical and Engineering Sciences, 1 Pesek Road, Jurong Island, Singapore 627833
mEindhoven University of Technology, Polymer Reaction Engineering, PO Box 513, 5600 MB Eindhoven, The Netherlands
First published on 10th July 2013
Abstract
Propagation rate coefficient (kp) data for radical polymerization of methyl acrylate (MA) in the bulk are critically evaluated and a benchmark dataset is put forward by a task-group of the IUPAC Subcommittee on Modeling of Polymerization Kinetics and Processes. This dataset comprises previously published results from three laboratories as well as new data from a fourth laboratory. Not only do all these values of kp fulfill the recommended consistency checks for reliability, they are also all in excellent agreement with each other. Data have been obtained employing the technique of pulsed-laser polymerization (PLP) coupled with molar-mass determination by size-exclusion chromatography (SEC), where PLP has been carried out at pulse-repetition rates of up to 500 Hz, enabling reliable kp to be obtained through to 60 °C. The best-fit – and therefore recommended – Arrhenius parameters are activation energy EA = 17.3 kJ mol−1 and pre-exponential (frequency) factor A = 1.41 × 107 L mol−1 s−1. These hold for secondary-radical propagation of MA, and may be used to calculate effective propagation rate coefficients for MA in situations where there is a significant population of mid-chain radicals resulting from backbiting, as will be the case at technically relevant temperatures. The benchmark dataset reveals that kp values for MA obtained using PLP in conjunction with MALDI-ToF mass spectrometry are accurate. They also confirm, through comparison with previously obtained benchmark kp values for n-butyl acrylate, methyl methacrylate and n-butyl methacrylate, that there seems to be identical family-type behavior in n-alkyl acrylates as in n-alkyl methacrylates. Specifically, kp for the n-butyl member of each family is about 20% higher than for the corresponding methyl member, an effect that appears to be entropic in origin. Furthermore, each family is characterized by an approximately constant EA, where the value is 5 kJ mol−1 lower for acrylates.
Introduction
The precise knowledge of rate coefficients for the individual reactions in radical polymerization is crucial for the modeling of polymerization processes and for the understanding and development of new polymerization methodologies. The fundamental reactions governing radical polymerization processes are initiation, propagation and termination, with the propagation reaction taking a prominent role, since it defines the rate of monomer consumption and thus directly affects the overall rate of polymerization. As a consequence, the propagation rate coefficient, kp, is of utmost importance, and most other rate coefficients, such as those for termination or transfer, are measured relative to it. The IUPAC Subcommittee on Modeling of Polymerization Kinetics and Processes recommended the so-called pulsed-laser polymerization-size-exclusion chromatography (PLP-SEC) technique1 as the method of choice to reliably determine kp.2 A series of benchmark papers have reported accurate Arrhenius data for kp of a broad range of monomers.2–7 With PLP-SEC, kp becomes available by the correlation of the time between two consecutive laser pulses with the chain length of the generated polymeric material. This correlation is based on the almost instantaneous initiating and terminating action of each laser pulse, which gives rise to a specific molar-mass distribution (MMD) exhibiting patterns of peaks according to the darktime t0 and multiples thereof, these reflecting the circumstance that some of the growing radicals survive one or more laser pulses and continue their growth over such an extended time period. kp is directly accessed from eqn (1):8| DPi = ikpcMt0 | (1) |
One family of monomers that has proven to be difficult to access viaPLP-SEC is the acrylates. Undefined MMDs may occur with these monomers, as well as a dependence of the obtained (apparent) propagation rate coefficient on the pulse-repetition rate. Thus the clear correlation between t and DPi may be obscured.9,10 The importance of the transfer-to-polymer reaction in acrylate polymerizations was foreseen by Scott and Senogles.11–13 However, only after the important finding of Ahmad et al.14 and Chiefari et al.,15 the absence of a characteristic MMD structure was understood to result primarily from the formation of tertiary mid-chain radicals (MCRs). These MCRs exhibit a considerably higher stability and thus lower propagation activity than secondary chain-end radicals (see Scheme 1), thereby broadening the radical MMD and thus invalidating eqn (1).16 Transfer-to-polymer may occur via inter- or intra-molecular reactions.17 Intermolecular transfer only matters in terms of kinetics of polymerization at higher polymer concentrations, which do not occur in typical PLP-SEC experiments. Intramolecular transfer, on the other hand, which occurs either via a random transfer step or, more frequently, via a six-membered cyclic transition state, is an important process even at low degrees of monomer conversion. The latter reaction is referred to as backbiting.18,19
 | ||
| Scheme 1 Formation of mid-chain radicals by the intramolecular transfer-to-polymer reaction of secondary chain-end radicals in acrylate polymerization, where i + j = n + 1; for the most favored backbiting process via a six-membered ring transition structure, j = 2. | ||
The impact of intramolecular chain transfer on PLP was suggested16 and the consequences were addressed in an IUPAC benchmark paper on kp of n-butyl acrylate (BA).6 Reliable kp values of secondary BA radicals were determined at low temperatures (<20 °C), where laser pulsing could be applied at repetition rates that are sufficiently high to minimize the occurrence of MCR formation. As Arrhenius parameters for kp of BA were reported, propagation rate coefficients could be extrapolated to technically relevant temperatures. It is, however, important to note that such an extrapolation yields kp data of secondary chain-end macroradicals, whereas actual polymerizing systems at these higher temperatures contain a mixture of secondary and (much more slowly propagating) tertiary radicals. The propagation rate of secondary radicals should thus not be confused with the effective rate of propagation that applies in acrylate polymerization above low temperatures and refers to the joint action of propagating secondary and tertiary radicals.9,20
Significant advances have been made in the understanding of acrylate (transfer) kinetics since the benchmark report on BA.6 Online discrimination and quantification of MCRs and secondary propagating radicals (SPRs) became available via electron paramagnetic resonance (EPR) spectroscopy.21–23 Rate coefficients for backbiting have been reported and the rate of monomer addition to BA MCRs has been studied in detail.10,22,23 With the advent of pulse lasers with repetition rates as high as 500 Hz, successful PLP-SEC experiments on BA were carried out up to 60 °C.24 The resulting values are in excellent agreement with the ones extrapolated from the previously reported benchmark data determined at lower polymerization temperatures, underpinning the quality of both datasets. The results, however, also indicated another limitation, namely β-scission of the MCRs.25,26 At temperatures above 60 °C, a deviation from Arrhenius behavior of the evaluated rate coefficients was observed. This could not be explained by transfer-to-polymer steps, but was attributed to β-scission of MCRs.24 This scission reaction, which is associated with a relatively high activation energy,27 yields significant amounts of unsaturated macromonomer species at temperatures above 100 °C, especially during polymerizations at low radical concentrations.15,28 Each β-scission step is preceded by a transfer-to-polymer step. The scission step poses additional problems for PLP-SEC experiments, as radicals are formed that are smaller than the preceding MCR. However, at moderate temperatures the impact of β-scission may be neglected and, as was demonstrated for BA, kp of SPRs may be deduced by extrapolation.
In conclusion, the understanding of acrylate kinetics has advanced significantly during recent years, and although some uncertainties still exist, propagation rate coefficients of secondary chain-end radicals may be accurately measured. The present report focuses on providing benchmark data for bulk polymerization of methyl acrylate (MA), a monomer that is of both application-oriented and academic interest.
Collation of data
Due to the inherent difficulties in the determination of reliable acrylate propagation rate coefficients, only a limited number of kp datasets exist for MA. Earlier data from methods other than PLP-SEC exhibit a large scatter and are not considered for the present evaluation. The following groups have provided the critically evaluated kp data for bulk MA that are collated in Table 1:| θ/°C | f/Hz | E p/mJ | c I/mmol L−1 | k p/L mol−1·s−1 | Ref. |
|---|---|---|---|---|---|
| a Characteristic MMDs were determined via MALDI-ToF rather than by SEC. b PLP experiments performed with interrupted sequences of laser pulses (see text). | |||||
| −28 | 100 | 4 | 5 | 3300 | 32 |
| −26.4 | 250 | 3.0 | 0.5 | 2992 | This work |
| −25.8 | 250 | 3.0 | 5 | 3166 | This work |
| −25.5 | 250 | 3.0 | 5 | 3359 | This work |
| −25 | 60 | 60 | 5 | 3290 | 31 a |
| −25 | 60 | 40 | 5 | 3321 | 31 a |
| −25 | 500 | 3.0 | 5 | 3378 | This work |
| −24.6 | 250 | 3.0 | 20 | 3684 | This work |
| −24.2 | 500 | 3.0 | 20 | 3553 | This work |
| −19.3 | 100 | 25 | 5.3 | 3790 | 29 |
| −19.1 | 100 | 25 | 5.3 | 3740 | 29 |
| −18.5 | 100 | 25 | 5.3 | 3680 | 29 |
| −17.9 | 100 | 25 | 5.3 | 3860 | 29 |
| −17.5 | 100 | 25 | 5.3 | 3920 | 29 |
| −17.1 | 100 | 25 | 5.3 | 3870 | 29 |
| −16.6 | 100 | 25 | 5.3 | 3930 | 29 |
| −16.3 | 100 | 25 | 5.3 | 4060 | 29 |
| −16.2 | 100 | 25 | 5.3 | 4120 | 29 |
| −16.0 | 100 | 25 | 5.3 | 3930 | 29 |
| −15.8 | 500 | 3.0 | 5 | 4135 | This workb |
| −15.7 | 80 | 60 | 5.00 | 4643 | 31 a |
| −15.6 | 80 | 40 | 5.00 | 4567 | 31 a |
| −15 | 100 | 4 | 5.00 | 5300 | 32 |
| −11.3 | 100 | 25 | 1.1 | 5410 | 29 |
| −11.3 | 100 | 25 | 1.1 | 5370 | 29 |
| −11.3 | 100 | 25 | 1.1 | 5290 | 29 |
| −11.3 | 80 | 25 | 1.1 | 5060 | 29 |
| −11.3 | 100 | 25 | 2.4 | 5240 | 29 |
| −11.3 | 100 | 25 | 2.4 | 5200 | 29 |
| −11.3 | 100 | 25 | 2.4 | 5340 | 29 |
| −8 | 100 | 60 | 5.00 | 5788 | 31 a |
| −8 | 100 | 40 | 5.00 | 5797 | 31 a |
| −2.9 | 100 | 25 | 2.4 | 6560 | 29 |
| −2.7 | 100 | 25 | 1.1 | 6600 | 29 |
| −2.7 | 100 | 25 | 2.4 | 6540 | 29 |
| −2.5 | 100 | 25 | 1.1 | 6680 | 29 |
| −1.9 | 100 | 25 | 1.1 | 6790 | 29 |
| −0.5 | 100 | 25 | 2.4 | 6790 | 29 |
| −0.3 | 80 | 25 | 1.1 | 6170 | 29 |
| 0 | 250 | 3.0 | 5 | 7031 | This work |
| 0 | 250 | 3.0 | 5 | 7198 | This work |
| 0 | 500 | 3.0 | 5 | 7655 | This work |
| 0 | 500 | 3.0 | 5 | 7421 | This work |
| 0 | 250 | 3.0 | 20 | 7523 | This work |
| 0 | 250 | 3.0 | 20 | 7322 | This work |
| 0 | 500 | 3.0 | 20 | 7286 | This work |
| 0 | 500 | 3.0 | 20 | 7725 | This work |
| 0.1 | 500 | 3.0 | 5 | 7325 | This workb |
| 0.9 | 100 | 60 | 5.00 | 7593 | 31 a |
| 0.9 | 100 | 40 | 5.00 | 7619 | 31 a |
| 1.9 | 100 | 20 | 1.2 | 6170 | 29 |
| 2.2 | 100 | 20 | 1.2 | 6370 | 29 |
| 3.8 | 100 | 25 | 1.0 | 6130 | 29 |
| 3.8 | 100 | 25 | 1.0 | 6740 | 29 |
| 4.0 | 100 | 25 | 1.0 | 6530 | 29 |
| 4.2 | 100 | 20 | 1.2 | 5990 | 29 |
| 7.8 | 100 | 60 | 5.00 | 9308 | 31 a |
| 7.8 | 100 | 40 | 5.00 | 9299 | 31 a |
| 11.3 | 500 | 1.5 | 5.00 | 9401 | 33 |
| 11.9 | 500 | 1.5 | 5.00 | 10 320 | 33 |
| 12.4 | 100 | 25 | 1.1 | 9740 | 29 |
| 15 | 100 | 30 | 5.00 | 11 397 | 31 a |
| 15 | 100 | 15 | 5.00 | 11 397 | 31 a |
| 19.8 | 500 | 1.5 | 5.00 | 13 011 | 33 |
| 19.8 | 500 | 3.0 | 5 | 11 578 | This workb |
| 20 | 250 | 3.0 | 0.5 | 10 892 | This work |
| 20 | 500 | 3.0 | 0.5 | 11 812 | This work |
| 20 | 250 | 3.0 | 5 | 10 850 | This work |
| 20 | 250 | 3.0 | 5 | 11 054 | This work |
| 20 | 500 | 3.0 | 5 | 11 842 | This work |
| 20 | 500 | 3.0 | 5 | 12 046 | This work |
| 20 | 250 | 3.0 | 20 | 10 924 | This work |
| 20 | 250 | 3.0 | 20 | 11 004 | This work |
| 20 | 500 | 3.0 | 20 | 11 792 | This work |
| 20 | 500 | 3.0 | 20 | 12 101 | This work |
| 20.4 | 500 | 1.5 | 5.00 | 12 826 | 33 |
| 21.8 | 100 | 30 | 5.00 | 13 727 | 31 a |
| 22.3 | 100 | 15 | 5.00 | 13 808 | 31 a |
| 25.0 | 100 | 20 | 0.45 | 14 600 | 29 |
| 25.0 | 100 | 20 | 0.45 | 13 800 | 29 |
| 25.0 | 100 | 20 | 0.45 | 14 000 | 29 |
| 25.0 | 100 | 10 | 0.45 | 14 000 | 29 |
| 25.0 | 100 | 10 | 0.45 | 13 500 | 29 |
| 25.0 | 100 | 10 | 0.45 | 14 000 | 29 |
| 25.0 | 80 | 20 | 0.45 | 13 400 | 29 |
| 25.0 | 80 | 20 | 0.45 | 12 900 | 29 |
| 29.7 | 500 | 1.5 | 5.00 | 15 851 | 33 |
| 29.8 | 100 | 30 | 5.00 | 16 461 | 31 a |
| 29.9 | 100 | 30 | 5.00 | 16 317 | 31 a |
| 30.8 | 500 | 1.5 | 5.00 | 13 944 | 33 |
| 32.0 | 100 | 2 | 1.2 | 15 100 | 29 |
| 32.0 | 100 | 2 | 1.2 | 14 700 | 29 |
| 35.7 | 500 | 3.0 | 5 | 16 796 | This workb |
| 36.5 | 100 | 30 | 5.00 | 19 376 | 31 a |
| 37.2 | 100 | 15 | 5.00 | 19 578 | 31 a |
| 40 | 500 | 3.0 | 0.5 | 17 756 | This work |
| 40 | 500 | 3.0 | 5 | 17 419 | This work |
| 40 | 500 | 3.0 | 5 | 17 379 | This work |
| 40 | 500 | 3.0 | 20 | 17 244 | This work |
| 40 | 500 | 3.0 | 20 | 17 499 | This work |
| 40 | 500 | 3.0 | 5 | 17 900 | This work |
| 40 | 500 | 3.0 | 5 | 18 151 | This work |
| 40.3 | 500 | 1.5 | 5.00 | 21 079 | 33 |
| 40.3 | 500 | 1.5 | 5.00 | 21 480 | 33 |
| 50.2 | 500 | 1.5 | 5.00 | 26 041 | 33 |
| 50.4 | 500 | 1.5 | 5.00 | 26 297 | 33 |
| 60 | 500 | 3.0 | 20 | 24 211 | This work |
| 60 | 500 | 3.0 | 20 | 23 930 | This work |
| 60 | 500 | 3.0 | 5 | 25 019 | This work |
| 60 | 500 | 3.0 | 5 | 25 740 | This work |
| 60.5 | 500 | 1.5 | 5.00 | 31 654 | 33 |
| 60.6 | 500 | 1.5 | 5.00 | 31 965 | 33 |
van Herk and co-workers (Eindhoven laboratories)
The group of van Herk reported two datasets, one of which was measured by Manders via classical PLP-SEC at a pulse repetition rate of 100 Hz and temperatures from −20 to +30 °C.29 Bulk polymerization of MA was investigated with 2,2-dimethoxy-2-phenylacetophenone (DMPA) as the photoinitiator at concentrations from 0.00045 to 0.0024 mol L−1. For analysis of molar mass distributions from SEC, the Mark–Houwink–Kuhn–Sakurada (MHKS) values provided by Hutchinson et al.,30α = 0.66 and K = 19.5 × 10−5 dL g−1, were employed. In the more recent study of this group, molar masses of poly(MA) from PLP were analyzed by the matrix-assisted laser-desorption ionization-time of flight (MALDI-ToF) technique. The latter method, which avoids the band broadening problems of SEC, was used between −30 and +40 °C by Willemse et al.,31 with PLP repetition rates up to 100 Hz. The advantages of MALDI-ToF over SEC for determination of DPi and the resulting accuracy of kp data will be addressed below.Buback and co-workers (Göttingen laboratories)
Buback et al. investigated kp of MA under high-pressure conditions between −15 and −28 °C with DMPA as the photoinitiator.32 Consistent kp data adhering to the criteria for reliable kp determination were obtained. The pressure dependence of kp is associated with an activation volume of (11.7 ± 0.4) cm3 mol−1 at −28 °C and (11.2 ± 0.7) cm3 mol−1 at −15 °C. Extrapolation of the kp data to ambient pressure yields 3360 L mol−1 s−1 for −28 °C and 5270 L mol−1 s−1 for −15 °C. The MHKS parameters provided by Hutchinson et al.30 were used for SEC analysis.Barner-Kowollik, Junkers, Castignolles and co-workers (Karlsruhe laboratories)
Junkers et al.33 provided data from DMPA-initiated PLP-SEC of MA in the range from 11.3 to 81.2 °C. To successfully carry out measurements up to the highest temperatures, fast pulsing with a 500 Hz laser was applied in order to largely eliminate the influence of backbiting on the resulting molar mass distributions. Excellent repeatability of MMDs, including higher-order inflection points, was observed at all temperatures. In order to stay on the safe side, Junkers et al.33 used only the restricted temperature range up to 60 °C for deriving Arrhenius parameters of kp. Above 60 °C, a leveling-off of kp was seen and was attributed to the influence of β-scission on the polymer MMD,15,25 an effect that would lead to underestimation of kp due to an increased polymer background in the sample stemming from the scission fragments.9,10 MHKS parameters for a broad temperature range using PLP-generated poly(MA) samples were determined to be: α = 0.74 and K = 10.2 × 10−5 dL g−1 (THF, 30 °C). Additionally, all samples were assessed with respect to the error margins associated with size-exclusion chromatography and to the local dispersity profile resulting from multiple detection analysis of branched polymer. Relatively homogeneous branching distributions were observed, confirming that SEC can indeed be used with high accuracy for determination of MMDs of poly(MA), as was also found for BA. However, this finding must not necessarily hold true for other acrylates, such as 2-ethylhexyl acrylate34 or tert-butyl acrylate.35Stach and Lacik (Bratislava laboratories)
In the framework of the current kp collation, a new dataset for bulk MA polymerization has been compiled by Stach and Lacík, also using high pulse repetition rates of 250 and 500 Hz. Temperatures from −26 to +80 °C were covered (see the ESI† for experimental details) with 0.0005, 0.005 and 0.020 mol L−1 DMPA as the photoinitiator. The same MHKS parameters as in the study of Junkers et al.33 were used for SEC analysis. Also in this study a leveling-off of kp data was observed at temperatures above 60 °C, although points of inflection for both i = 1 and 2 in eqn (1) could be seen even at 70 °C. In addition to producing polymer by a single sequence of laser pulses applied at high repetition rate, in a second type of experiment polymer samples were made by applying several sequences of laser pulses with a reduced number of pulses per sequence. With this second approach, the reaction mixture can equilibrate back to the thermostat temperature during an experiment, meaning that any enhancement of temperature as a consequence of rapid pulsing (and hence rapid polymerization) should become visible from comparison of kp values obtained by the two pulsing strategies. It is gratifying to note that no significant difference in kp has been found upon applying the two pulsing procedures (see Table 1 for the comparison).Deriving benchmark values
The kp datasets in Table 1 were estimated using slightly different monomer densities (for the calculation of bulk monomer concentration). In addition, different MHKS parameters were applied for SEC analysis depending on the type and temperature of the eluent. The associated error is small compared with the limits of accuracy of size-exclusion chromatographic analysis. Thus, as within the previous benchmark report on BA, no recalculation of kp data has been performed. The kp data in Table 1 refer to different temperatures, laser repetition rates, f, average laser pulse energies, Ep, and initiator concentrations, cI. All data were obtained using the photoinitiator DMPA, which has proven to be an excellent choice for acrylate PLP-SEC experiments. In fulfillment of the IUPAC reliability criteria,2 close matching of data obtained at different laser pulse energies is observed. Consistent kp values are thus derived upon variation of initial radical concentrations. The combined datasets display good agreement and exhibit very satisfactory Arrhenius-type behavior, as depicted in Fig. 1. The scatter of the kp data provided by the different groups is relatively small and well within the general error margin of 20 per cent that is associated with PLP-SEC measurements.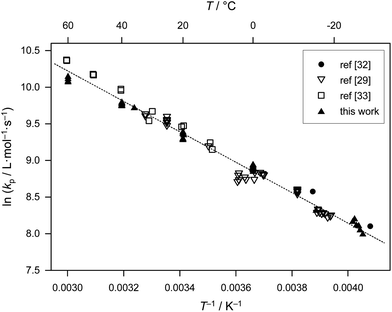 | ||
| Fig. 1 Arrhenius plot of values of propagation rate coefficient, kp, for bulk methyl acrylate from Table 1. Eqn (2), the best-fit line to all the points, is also shown. | ||
The unweighted Arrhenius fit of the kp data in Fig. 1 is given as:
| ln(kp/L mol−1 s−1) = 16.46 (±0.11) − 2080 (±30) K/T | (2) |
Eqn (2) gives activation energy EA = 17.29 kJ mol−1 and frequency (pre-exponential) factor A = 1.41 × 107 L mol−1 s−1. The error margins of both Arrhenius parameters are represented via the 95% confidence interval in Fig. 2. The estimate is made on the assumption of a constant relative error of 20% for each individual kp value. The resulting uncertainties amount to 16.3 kJ mol−1 < EA < 18.2 kJ mol−1 and 0.9 × 107 L mol−1 s−1 < A < 2.0 × 107 L mol−1 s−1. These error margins are very close to the ones of the benchmark kp dataset for BA.6 The error limitations obtained from the joint confidence interval mostly depend on the scatter of the data, whereas trying different relative errors of 10, 15 and 20% in kp yielded very similar contour plots.
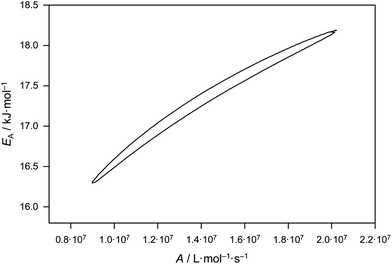 | ||
| Fig. 2 95% joint-confidence interval for the Arrhenius parameters for kp of bulk MA, as estimated from fitting of the data in Fig. 1 (see text). | ||
The kp data of Willemse and van Herk in Table 1 play a special role, as these values were determined via MALDI-ToF analysis of MMDs, and thus should not suffer from the SEC problems of imperfect calibration and band broadening. On the other hand, features in the measured number distributions may not always be unambiguously identified. Additional uncertainties exist with regard to the question of whether the distribution from MALDI-ToF reflects the true distribution, as mass spectrometry is inherently prone to mass discrimination effects, especially for higher molar masses and broad distributions,36 as occur in PLP experiments. It is gratifying to note that, irrespective of these limitations of PLP–MALDI-ToF, very pleasing agreement of the data from the two methods of molar mass analysis is seen: plotting the PLP-SEC data together with the PLP–MALDI-ToF data yields excellent agreement of the kp values deduced from the two PLP-based methods (Fig. 3), with the Arrhenius parameters being more or less identical. One remark can be made at this point; because band broadening in SEC systematically underestimates the kp-values (taking the low-molecular weight inflection point, this point is shifted to lower values due to band broadening) the MALDI-ToF data are systematically slightly higher than the SEC data, as observed in Fig. 3. These statements do not, however, prove the general applicability of the PLP–MALDI-ToF method. Nevertheless, the close agreement hints at the good applicability of the MALDI-ToF approach. This notwithstanding, and in order to follow the IUPAC suggestion of using PLP-SEC for reliable kp determination, the values provided by Willemse et al. were not included in the joint fit shown in Fig. 1.
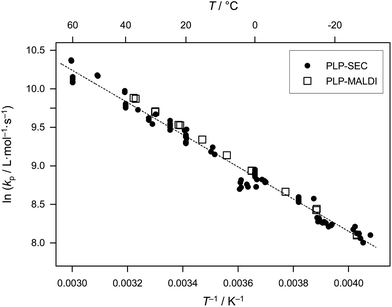 | ||
| Fig. 3 Comparison of literature kp data for bulk MA obtained viaPLP-SEC (data from Fig. 1, full circles) and PLP–MALDI-ToF (data from Willemse et al.,31 open squares); the dashed line represents the Arrhenius fit (equation not given) to the combined dataset, i.e., from both PLP-based methods. | ||
Discussion
Benchmark data are of more than just empirical use. For example, they may serve to definitively elucidate mechanistic trends, and also to establish the utility of predictive calculation methodologies.Comparison with quantum-chemical calculations
With increasing computational power and ongoing refinement of models, it seems worthwhile to compare the experimental benchmark data with results from quantum-chemical (QM) calculations, as were performed for kp of bulk MA by Coote and co-workers.37 Using the G3(MP2)-RAD methodology for calculation of gas-phase rate coefficients and accounting for solvation effects by applying the COSMO-RS model, an activation energy of 21.8 kJ mol−1 and a frequency factor of A = 3.2 × 107 L mol−1 s−1 were obtained for the addition of a dimer radical to the monomer in bulk monomer solution. The absolute kp at 20 °C calculated from these parameters underestimates the value from the benchmark dataset (eqn (2)) by a factor of 2.8. The agreement of the quantum-chemically estimated kp and Arrhenius parameters to better than one order of magnitude of the experimental benchmark values indicates the improvements made with such computational methods in recent times. Nevertheless, the approximations required for the QM calculations do not yet allow for ab initio calculations of benchmark kp values.38Comparison with benchmark kp data for other monomers
Benchmark kp values for a series of methacrylate monomers as well as for BA have previously been published.2–7 Largely based on the more extensive results for methacrylate monomers, a family-type behavior was proposed, this being that within a family of monomers, kp shows a minor but systematic increase with the size of the alkyl ester group due largely, perhaps entirely, to A variation. The observed trends may help to predict kp values of family members which have been less thoroughly studied. The comparison of benchmark values for bulk BA and bulk MA with the corresponding values for n-butyl methacrylate (BMA) and methyl methacrylate (MMA) is illustrated in Fig. 4.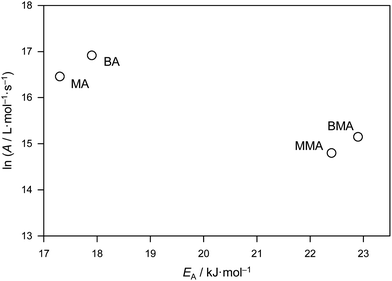 | ||
| Fig. 4 Arrhenius parameters for the benchmark propagation rate coefficients of bulk methyl acrylate (MA), n-butyl acrylate (BA), methyl methacrylate (MMA) and n-butyl methacrylate (BMA).5,6 | ||
Fig. 4 undoubtedly represents a very significant achievement of experimental science in the way it neatly establishes both family behavior and at the same time the differences between families: the methyl and n-butyl members of each family are close to each other while the differences between families are distinct. The activation energies of MMA and BMA differ by only 0.5 kJ mol−1 and the frequency factor only by about 40%, which poses problems toward safely establishing whether one or the other or both Arrhenius parameters are different. On the other hand, it is clearly established that bulk kp of BMA is above the associated value for MMA, e.g., for 20 °C the numbers are 272 L mol−1 s−1 (MMA) and 314 L mol−1 s−1 (BMA). The ratio of these values, kp(MMA)/kp(BMA), is 0.87. The benchmark data for MA enable a similar comparison for MA and BA. Both acrylates exhibit lower activation energies than the corresponding methacrylates, but differ marginally from each other, i.e., by 0.6 kJ mol−1, which is within the limits of experimental accuracy. The frequency factors for bulk BA and MA are also close to each other. Again, the n-butyl member exhibits higher kp than the methyl member of the same family, e.g. at 20 °C it is found that kp(MA)/kp(BA) = 0.81. The systematic effect of ester chain length on kp of bulk (meth)acrylic esters is a genuine kinetic one, as is explained in more detail elsewhere.39 Also pointed out in ref. 39 is the fact that the increase of kp with the size of the ester group, which is seen with bulk radical polymerization of alkyl acrylates and alkyl methacrylates, may not occur in solution polymerization or may even be inverted, e.g., in toluene solution, as might be seen from the data provided by Couvreur et al.,40 although the accuracy of the kp is not established in this latter case due to multiple-detection SEC not having been available to use. Theoretical studies of MA polymerization indicate that intramolecular hydrogen bonding plays a greater role in low polarity environments compared with bulk monomer,37 and this may provide an explanation for the differing behavior.
Future activities of our IUPAC Subcommittee will focus on the quantitative analysis of the effects of substituents and molecular environment on kp.41 These effects are basically related to the extent of internal rotational freedom of the transition state for propagation, as was first pointed out by Heuts et al.42 Significant hindrance to such internal rotational motion is associated with a lower pre-exponential factor and thus with lower kp, which effect also explains the large difference between acrylate and methacrylate kp (although this is also due to the difference in EA). As compared with acrylates, methacrylates suffer from severe hindrance to rotational mobility because of the α-methyl groups present on the polymer backbone.
Given the above-mentioned kinetic argument, which is a purely entropic one, the BA and MA kp data are fitted in Fig. 5 assuming identical EA, viz. 17.6 kJ mol−1, the arithmetic mean of the BA value from ref. 6 (17.9 kJ mol−1) and the present MA value (17.3 kJ mol−1). This yielded frequency factors of A(MA) = 1.6 × 107 L mol−1 s−1 and A(BA) = 2.0 × 107 L mol−1 s−1, i.e., a difference of 20%. Certainly to the naked eye it would seem that this fitting approach is perfectly adequate, and therefore the value EA = 17.6 kJ mol−1 may be cautiously recommended for secondary-radical propagation of all n-alkyl acrylates, with A varying along the indicated lines between family members.
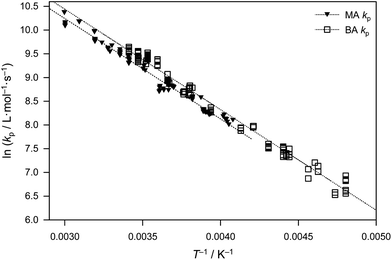 | ||
| Fig. 5 Arrhenius plot comparing benchmark kp data for methyl acrylate (present work) and n-butyl acrylate,6 where each dataset has been fitted using EA = 17.6 kJ mol−1 (see text). | ||
The increase of kp with alkyl ester chain length is illustrated by the numbers in Table 2 for both acrylates and methacrylates. The higher degree of rotational freedom of the transition-state structure for the butyl esters is understood as being a consequence of the more efficient shielding of dipolar interactions by the larger side chain, perhaps associated with some better internal solubilizing effect of butyl as compared to methyl moieties. Variations of kp with solvent environment have been explained via this kind of argument.43,44
| Monomer | A/L mol−1 s−1 | E A /kJ mol−1 | k p(20 °C)/L mol−1 s−1 | Ref. |
|---|---|---|---|---|
| Methyl methacrylate | 2.67 × 106 | 22.4 | 270 | 3 |
| n-Butyl methacrylate | 3.78 × 106 | 22.9 | 310 | 4 |
| Methyl acrylate | 1.41 × 107 | 17.3 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
This work |
| n - Butyl acrylate | 2.24 × 107 | 17.9 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 480 |
6 |
Effective propagation rate coefficient
As mentioned above, under typical conditions of acrylate radical polymerization, both secondary chain-end and tertiary mid-chain radicals occur. It cannot be overemphasized that the benchmark kp values reported in the present study entirely refer only to propagation of the secondary radicals. Monomer addition to mid-chain radicals takes place with a much lower rate coefficient, ktertp. The major effect of mid-chain radicals on the overall propagation rate thus results from the loss of secondary radicals due to their transformation into mid-chain radicals. To account for the presence of two types of radicals, an effective propagation rate coefficient keffp has to be defined, and can be shown to be given by6,9,20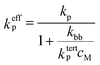 | (3) |
Conclusions
Benchmark data have been collected and analyzed for the chain-growth kinetics of bulk MA secondary propagating radicals at temperatures from −28 to 61 °C. The availability of commercial pulse lasers with pulse repetition rates as high as 500 Hz allows for PLP-SEC studies up to temperatures as high as shown here, for the unfavorable effect of backbiting is largely eliminated by not allowing sufficient time between pulses for it to occur to any significant extent. However, at the highest temperatures the impact of β-scission reactions on the MMD of PLP-structured poly(MA) must be carefully considered. The kp values from PLP-SEC and from PLP–MALDI-ToF are in good agreement, which suggests that the latter technique may also be suitable for reliable kp determination.The Arrhenius pre-exponential factor and activation energy of secondary propagating MA radicals were obtained by fitting of the benchmark dataset to be A = 1.41 × 107 L mol−1 s−1 and EA = 17.3 kJ mol−1 respectively. These numbers are close to the associated ones of n-butyl acrylate (BA). At 20 °C, bulk BA propagates faster than bulk MA by 24%, which difference is close to the one seen between BMA and MMA. Thus, family type behavior of alkyl (meth)acrylate kp is confirmed.
Overall propagation of acrylates may be estimated via effective propagation rate coefficients which, in addition to kp, requires accurate knowledge of ktertp/kbb. So far, the latter two rate coefficients have been determined only for BA. Subsequent activities of our IUPAC Subcommittee may focus on the measurement of these rate coefficients for other acrylates, including MA, on the development of standard protocols for determination of such coefficients, and on solvent effects on (meth)acrylate propagation. With all this information at hand, a complete picture of the propagation kinetics for the acrylate family will be available.
Acknowledgements
Financial support via the IUPAC-funded project 2011-034-2-400 is gratefully acknowledged.References
- O. F. Olaj, I. Bitai and F. Hinkelmann, Makromol. Chem., 1987, 188, 1689–1702 CrossRef CAS.
- M. Buback, R. G. Gilbert, R. A. Hutchinson, B. Klumperman, F.-D. Kuchta, B. G. Manders, K. F. O'Driscoll, G. T. Russell and J. Schweer, Macromol. Chem. Phys., 1995, 196, 3267–3280 CrossRef CAS.
- S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, O. F. Olaj, G. T. Russell, J. Schweer and A. M. van Herk, Macromol. Chem. Phys., 1997, 198, 1545–1560 CrossRef CAS.
- S. Beuermann, M. Buback, T. P. Davis, R. G. Gilbert, R. A. Hutchinson, A. Kajiwara, B. Klumperman and G. T. Russell, Macromol. Chem. Phys., 2000, 201, 1355–1364 CrossRef CAS.
- S. Beuermann, M. Buback, T. P. Davis, N. García, R. G. Gilbert, R. A. Hutchinson, A. Kajiwara, M. Kamachi, I. Lacík and G. T. Russell, Macromol. Chem. Phys., 2003, 204, 1338–1350 CrossRef CAS.
- J. M. Asua, S. Beuermann, M. Buback, P. Castignolles, B. Charleux, R. G. Gilbert, R. A. Hutchinson, J. R. Leiza, A. N. Nikitin, J.-P. Vairon and A. M. van Herk, Macromol. Chem. Phys., 2004, 205, 2151–2160 CrossRef CAS.
- S. Beuermann, M. Buback, P. Hesse, F.-D. Kuchta, I. Lacík and A. M. van Herk, Pure Appl. Chem., 2007, 79, 1463–1469 CrossRef CAS.
- G. V. Schultz and J. Romatovski, Makromol. Chem., 1965, 85, 195–226 CrossRef.
- A. N. Nikitin, P. Castignolles, B. Charleux and J. P. Vairon, Macromol. Rapid Commun., 2003, 24, 778–782 CrossRef CAS.
- A. N. Nikitin, R. A. Hutchinson, M. Buback and P. Hesse, Macromolecules, 2007, 40, 8631–8641 CrossRef CAS.
- G. E. Scott and E. J. Senogles, J. Macromol. Sci., Chem., 1970, A4, 1105–1117 Search PubMed.
- G. E. Scott and E. J. Senogles, J. Macromol. Sci., Rev. Macromol. Chem., 1973, C9, 49–69 CrossRef.
- G. E. Scott and E. J. Senogles, J. Macromol. Sci., Chem., 1974, 8, 753–773 CrossRef CAS.
- N. M. Ahmad, F. Heatley and P. A. Lovell, Macromolecules, 1998, 31, 2822–2827 CrossRef CAS.
- J. Chiefari, J. Jeffery, R. T. A. Mayadunne, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1999, 32, 7700–7704 CrossRef CAS.
- C. Plessis, G. Arzamendi, J. M. Alberdi, A. M. van Herk, J. R. Leiza and J. M. Asua, Macromol. Rapid Commun., 2003, 24, 173–177 CrossRef CAS.
- T. Junkers and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 7585–7605 CrossRef CAS.
- D. Cuccato, E. Mavroudakis, M. Dossi and D. Moscatelli, Macromol. Theory Simul., 2013, 22, 127–135 CrossRef CAS.
- J. Vandenbergh and T. Junkers, Macromolecules, 2012, 45, 6850–6856 CrossRef CAS.
- C. Plessis, G. Arzamendi, J. R. Leiza, H. A. S. Schoonbrood, D. Charmot and J. M. Asua, Macromolecules, 2000, 33, 4–7 CrossRef CAS.
- R. X. E. Willemse, A. M. van Herk, E. Panchenko, T. Junkers and M. Buback, Macromolecules, 2005, 38, 5098–5103 CrossRef CAS.
- M. Buback, P. Hesse, T. Junkers, T. Sergeeva and T. Theis, Macromolecules, 2008, 41, 288–291 CrossRef CAS.
- J. Barth, M. Buback, P. Hesse and T. Sergeeva, Macromolecules, 2010, 43, 4023–4031 CrossRef CAS.
- C. Barner-Kowollik, F. Günzler and T. Junkers, Macromolecules, 2008, 41, 8971–8973 CrossRef CAS.
- T. Junkers, S. P. S. Koo, T. P. Davis, M. H. Stenzel and C. Barner-Kowollik, Macromolecules, 2007, 40, 8906–8912 CrossRef CAS.
- S. P. S. Koo, T. Junkers and C. Barner-Kowollik, Macromolecules, 2009, 42, 62–69 CrossRef CAS.
- T. Hirano and B. Yamada, Polymer, 2003, 44, 347–354 CrossRef CAS.
- T. Junkers, F. Bennet, S. P. S. Koo and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 3433–3437 CrossRef CAS.
- B. Manders, PhD thesis, TU Eindhoven, Eindhoven, The Netherlands, 1997.
- R. A. Hutchinson, D. A. Paquet, Jr, J. H. McMinn, S. Beuermann, R. E. Fuller and C. Jackson, DECHEMA Monogr., 1995, 131, 467–492 CAS.
- R. X. E. Willemse and A. M. van Herk, Macromol. Chem. Phys., 2010, 211, 539–545 CrossRef CAS.
- M. Buback, C. H. Kurz and C. Schmaltz, Macromol. Chem. Phys., 1998, 199, 1721–1727 CrossRef CAS.
- T. Junkers, M. Schneider-Baumann, S. P. S. Koo, P. Castignolles and C. Barner-Kowollik, Macromolecules, 2010, 43, 10427–10434 CrossRef CAS.
- P. Castignolles, Macromol. Rapid Commun., 2009, 30, 1995–2001 CrossRef CAS PubMed.
- P. Castignolles, R. Graf, M. Parkinson, M. Wilhelm and M. Gaborieau, Polymer, 2009, 50, 2373–2383 CrossRef CAS PubMed.
- C. M. Guttman, K. M. Flynn, W. E. Wallace and A. J. Kearsley, Macromolecules, 2009, 42, 1695–1702 CrossRef CAS.
- C. Y. Lin, E. I. Izgorodina and M. L. Coote, Macromolecules, 2010, 43, 553–560 CrossRef CAS.
- B. B. Noble and M. L. Coote, Int. Rev. Phys. Chem., 2013, 32, 467–513 CrossRef CAS.
- M. Buback, Macromol. Symp., 2009, 275–276, 90–101 CrossRef CAS.
- L. Couvreur, G. Piteau, P. Castignolles, M. Tongue, B. Coutin, B. Charleux and J. P. Vairon, Macromol. Symp., 2001, 174, 197–207 CrossRef CAS.
- S. Beuermann and M. Buback, Prog. Polym. Sci., 2002, 27, 191–254 CrossRef CAS.
- J. P. A. Heuts, R. G. Gilbert and L. Radom, Macromolecules, 1995, 28, 8771 CrossRef CAS.
- S. Beuermann, M. Buback, P. Hesse and I. Lacik, Macromolecules, 2006, 39, 184–193 CrossRef CAS.
- S. Beuermann, Macromol. Rapid Commun., 2009, 30, 1066–1088 CrossRef CAS PubMed.
- J. Barth, M. Buback, G. T. Russell and S. Smolne, Macromol. Chem. Phys., 2011, 212, 1366–1378 CrossRef CAS.
- T. Junkers, PhD thesis, Georg-August Universität Göttingen, Göttingen, Germany, 2006.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3py00774j |
| This journal is © The Royal Society of Chemistry 2014 |
