Unraveling polar Diels–Alder reactions with conceptual DFT analysis and the distortion/interaction model

Abstract

The reaction energetics of 280 polar Diels–Alder (DA) reactions between 70 dienophiles and 4 dienes have been studied in detail using the B3LYP/6-31G* level of theory, combining conceptual density functional theory (DFT) analysis and the distortion/interaction model. The barrier heights are governed by a fine balance between the energy required to distort the reactants from their initial to their transition state geometries (ΔE^‡_d) and the binding energy between the deformed reactants in the TS (ΔE^‡_i). The ΔE^‡_i values strongly correlate with the electrophilicity index, ω, which measures the stabilization energy when the system acquires an additional electronic charge from the environment, whereas the ΔE^‡_d was found to depend mainly on the nature of the diene, structural parameters of the dienophile (degree of substitution and ring size) and the asynchronicity of the TS. A detailed analysis to account for the geometrical parameters of the strained diene and dienophile moieties that influence the energy strain of the distorted fragments is also reported.

---

Introduction

The Diels–Alder reaction (DA) represents an important and useful process in modern organic chemistry, and it would be hard to find many chemical transformations that match its power in organic synthesis.¹ The 1950 Nobel Prize in Chemistry went to Prof. Otto Paul Hermann Diels and Kurt Alder for “the discovery and development of the diene synthesis”,² which became a milestone for creating complex molecular architectures, as two simple bonds can be formed in a regio- and stereocontrolled manner, yielding six-membered rings and up to four stereogenic centers in a single step.¹ For that reason, it remains one of the most theoretically studied chemical transformation of all times.³ The DA reaction usually requires electron-withdrawing groups in the dienophile and electron-rich dienes, or vice versa, to afford acceptable reaction rates. The first case, known as normal-electron-demand DA, is the most widely used to enhance the reactivity of the system.¹ This pericyclic transformation is governed by the HOMO_diene–LUMO_dienophile interaction according to frontier molecular orbital (FMO) theory,^3b but can be alternatively seen as a nucleophilic attack of the diene to the dienophile. The amount of charge transferred from the nucleophile (the diene) to the electrophilic counterpart (the dienophile) is related to the electron-deficient and electron-rich character of the dienophile and the diene, respectively. A direct relationship between the charge transfer (CT) during the bond formation process with the decrease of the DA activation barrier was found.^4,5

The development of conceptual DFT analysis arising from modern density functional theory offers a paramount opportunity for the rationalization of several insights regarding different chemical transformations.^3c,6 One of the key advantages is that it allows the prediction and interpretation of experimental and theoretical data with only the information provided by the reagent molecules in their ground state geometries. In this context, the global electrophilicity index ω, which measures the stabilization energy when the system acquires an additional electronic charge ΔN from the environment,⁷ becomes a useful quantity to classify the electrophilicity of a series of dienes and dienophiles within a unique relative scale.⁸ Domingo has pioneered the use of this index to rationalize different aspects of a variety of organic reactions.⁹ In a recent publication, Domingo and Sáez proposed that DA reactions can be classified according to the polarity of the process, that is, the amount of charge transferred at the TS. Therefore, non-polar (N-DA, CT < 0.15e), polar (P-DA, 0.15e < CT < 0.40e) and ionic (I-DA, CT > 0.40e) Diels–Alder reactions were defined.¹⁰ They also found a good linear relationship between the activation energy (ΔE^‡) and CT (R² = 0.89), and between ΔE^‡ and ω (R² = 0.92) for twelve representative dienophiles and cyclopentadiene as the dienic counterpart at the B3LYP/6-31G* level of theory. As a consequence of the good correlation, they proposed that the classification can be related to the electrophilicity of the dienophile as well. Therefore, N-DA, P-DA and I-DA are represented by dienophiles with ω < 1.5 eV, 1.5 eV < ω < 5 eV, and ω > 5.0 eV, respectively.¹⁰ According to this finding, the activation barriers of polar DA reactions, which represent the vast majority of normal-electron-demand DA, can be properly estimated from the electrophilicity of the reagents in their ground state geometries.

However, the present author and co-workers recently found that the ω index did not account properly for the reactivity trends experimentally observed in DA reactions between α-halo enones with a variety of dienes.¹¹ Instead, the distortion/interaction model could be successfully used to explain both the experimental and theoretical observations. In this fragment approach, also known as the activation strain model, the activation energy is decomposed into two main components: the distortion energy (ΔE^‡_d, also known as the strain energy), and the interaction energy ΔE^‡_i, as shown in eqn (1).¹²

ΔE^‡ = ΔE^‡_d + ΔE^‡_i (1)

The ΔE^‡_d is the energy required to distort the reactants from their initial geometries to their transition state geometries, while the ΔE^‡_i is the binding energy between the deformed reactants in the transition state.¹²

Bickelhaupt and co-workers (activation strain model),¹³ and Houk and co-workers (distortion/interaction model),¹⁴ independently developed this useful methodology to understand different issues such as reactivity trends and TS geometries.^12–14

Among the wide variety of reactions that were computationally studied with this method, the Diels–Alder cycloaddition has not been forgotten, though the reports are limited. Only three studies have been fully devoted to this reaction within the strain activation framework. The first one deals with 1,4-dihydrogenations and DA cycloadditions of aromatic molecules and ethylene,^14c the second one was conceived to explain the reactivity trends in DA reactions of cycloalkenones and cyclic dienes^14b and the third one accounts for the selectivity in DA reactions between C₆₀ and cyclopentadiene.^13a

In this work the first study is presented combining conceptual DFT and the distortion/interaction model to fully account for the reactivity trends in polar Diels–Alder reactions.

Computational methods

All calculations were carried out with the B3LYP¹⁵ exchange-correlation functional coupled with the standard 6-31G* basis set¹⁶ using Gaussian 09.¹⁷ The performance of this computationally affordable level of theory has been shown to be suitable for the geometric, electronic and energetic features of DA reactions.^{3b,c,5,9,10,18} All stationary points were characterized by frequency calculations, and all TSs were confirmed to have only one imaginary frequency corresponding to the formation of the expected bonds. The CT were computed with the natural bond order (NBO) method.¹⁹ The global electrophilicity index, ω,⁷ was computed according to the following expression, ω = μ²/2η (eV), where μ is the electronic chemical potential and η the chemical hardness. Both quantities were estimated on the basis of the one-electron energies from the HOMO and LUMO, ε_H and ε_L, as μ ≈ (ε_H + ε_L)/2 and η ≈ (ε_L − ε_H).²⁰ The nucleophilicity index, N, was computed as N = E_HOMO(diene) − E_HOMO(TCE) (eV),²¹ where TCE stands for tetracyanoethylene. The local electrophilic indices, ω_k,²² were computed according to the following expression: ω_k = ωP⁺_k, where P⁺_k is the electrophilic Parr function of atom k,²³ which was computed using the Mulliken atomic spin density (ASD) by single-point UB3LYP/6-31G* calculations of the anion resulting from adding one electron to the optimized neutral B3LYP/6-31G* geometry.²³ The ANOVA analysis was carried out using the Historical Data Response Surface Method (RSM) implemented in the software Design-Expert™.

Results and discussion

In this study 280 polar DA reactions were studied combining a set of 70 dienophiles and 4 representative dienes (cyclopentadiene, CP, 1,3-cyclohexadiene, CH, 1,3-butadiene, BU, and 2,3-dimethyl-1,3-butadiene, DMB), Fig. 1. The selection of dienes was done to account for their cyclic/acyclic nature, and because they exhibit different electron-rich character: while CH is the most nucleophilic diene under study, BU is the most electrophilic one (vide infra). In addition, their symmetry avoided dealing with competing regioisomeric channels of addition, simplifying the overall study. Regarding the dienophiles 1–70 (40 acyclic and 30 cyclic), the selection was done to provide a wide variety of molecular architectures, substitution patterns and functional groups.²⁴ The effect of Lewis acids was introduced by BH₃-complexes, and the effect of substitution by alkyl groups was simplified by the use of methyl groups.

Fig. 1 Dienophiles and dienes used in this study.

In the cases of unsymmetrically substituted dienophiles, two modes of addition are plausible, namely endo and exo. To simplify the analysis and reduce the number of calculations, only the [4 + 2] endo channels were taken into consideration,¹⁰ as they typically represent the most stable TSs in DA reactions.^{1,3,5,10,11,14b} Moreover, for levoglucosenone (64) and its derivatives 65–70, only the TSs resulting from the attack of the diene on the α face of the molecule were taking into account as the β-face is efficiently hindered by the 1,6-anhydro bridge.^11,25

After exhaustive exploration of the potential energy surface (PES) all the 280 TSs corresponding to the [4 + 2] endo channels were located, and were found to range from totally concerted and synchronous to a one-step two-stage mechanism.^10,26 This term was coined to refer to highly asynchronous TSs, from which the lengths of the two σ bonds that are forming in the reaction are sharply different (Δd = d_2–3 − d_1–6 > 0.5 Å), Fig. 1. During the first stage, one of the two C–C bonds is formed via a nucleophilic–electrophilic two-center interaction. Once this bond is formed, the second C–C bond begins to develop, comprising the second stage of the mechanism.^10,26 Other authors might prefer the term “concerted and asynchronous”, but as stated by Brinck the difference between both are flavors of a mechanism that lacks stationary intermediates.²⁷ In the ESI† can be found the most relevant geometric and energetic features of all TSs under study.

Asynchronicity

The average asynchronicity (Δd)²⁸ is 0.39 Å, the TSs resulting from DMB and CH being slightly more asynchronous than those arising from CP and BU (0.42 Å, 0.41 Å, 0.34 Å and 0.38 Å, respectively). Birney and Houk proposed that the Δd can be understood in terms of frontier molecular orbital (FMO) theory.²⁹ Briefly, polar DA reactions are dominated by the HOMO_diene–LUMO_dienophile interaction. The larger the difference in the LUMO coefficients on the dienophile C1 and C2 (ΔLUMO_1,2), the stronger and weaker the interactions between C1–C6 and C2–C3, respectively, and the more asynchronous the corresponding TS. However, in this work this was found to be true only for simple monosubstituted alkenes. The correlation between (ΔLUMO_1,2) and Δd becomes increasingly diffuse with the degree of substitution of the dienophile.³⁰ For instance, the 1,1 substitution pattern leads to more asynchronous TSs than the corresponding 1,2 analogue. Comparing the pairs 9–10, 13–14 and 20–19 (Fig. 1) replacement of a methyl group from the β to the α position involves an increase of ∼0.18 Å in the Δd. Interestingly, FMO theory points in the opposite direction, the difference between Cα and Cβ LUMO coefficients being higher for the 1,2-disubstituted isomers 10, 14 and 19 (ΔLUMO_1,2 = 0.19, 0.24 and 0.13, respectively) than for the corresponding 1,1-disubstituted counterparts 9, 13 and 20 (ΔLUMO_1,2 = 0.16, 0.21 and 0.07, respectively).³⁰ As discussed later, having access to at least a rough estimate of the asynchronicity of the TS using properties computed for the reactants in their ground state geometries was an important need. Therefore, by similar reasoning with the FMO theory arguments indicated above, the local electrophilicity index (ω_k) was evaluated next as asynchronicity descriptor. This index measures the distribution of the global electrophilicity in different sites of a molecule, and is commonly used to explain regioselectivity of polar DA reactions. Briefly, the carbon atom that displays higher ω_k is said to be the most electrophilic, and is expected to interact preferentially with the most nucleophilic center of the asymmetric diene to afford the corresponding regioisomer. The levels of regioselectivity are usually related to the local electrophilic difference (Δω_k) between both C=C atoms of the dienophile.^11,31 In addition, it has been suggested that the Δω_k accounted for the differences in asynchronicity in DA reactions of cyano-substituted dienophiles and cyclopentadiene, though no explicit correlation data was provided.⁵ Continuing this line of thought, in this work an acceptable correlation between Δω_k and Δd was found (R² = 0.77), suggesting that the asynchronicity of the TS can be fairly predicted from conceptual DFT analysis (Δd ≈ 0.39Δω_k + 0.07).³⁰

Activation energies

Probably B3LYP is still the most popular among the vast array of functionals that modern DFT offers. However, that does not prevent it giving unsatisfactory performance in some particular areas, such as underestimating the barrier heights of heavy atom transfer, nucleophilic substitution and unimolecular reactions, inability to accurately describe noncovalent interactions and affording unreliable results for transition metal chemistry.³² To validate the computational results herein obtained, the activation barriers of the reactions between a selected 35 of the 70 dienophiles shown in Fig. 1 and CP were next computed using the high-accuracy composite method CBS-QB3.³³ The complete basis set (CBS) methods were developed by Petersson and co-workers to remove errors from the basis set truncation using asymptotic convergence of pair natural orbital expansions to extrapolate the estimated complete basis set limit.³⁴ CBS-QB3, which starts on B3LYP/6-311G(d,p) geometries, has been found as a benchmark for predicting the activation barriers, reaction energetics and TS geometries of pericyclic reactions.¹⁸ As shown in the ESI,† a good correlation between B3LYP/6-31G* and CBS-QB3 activation barriers was found (R² = 0.95). Similar results were obtained with the increasingly popular meta hybrid exchange-correlation functional M06-2X developed by Truhlar at the 6-31G* basis set (R² = 0.97).^30,32

Next, the effect of strain release in the reactivity trends was first investigated. The lack of significant linear correlation (R² < 0.59) between ΔH^‡ with −ΔH_rxn proved that the Dimroth, Brønsted, Evans–Polanyi, or Marcus relationships,^35–37 which state that ΔΔE^‡ ≈ 1/2ΔΔE_rxn, is only true in a qualitative sense.³⁰

As shown in Fig. 2, the ΔE^‡ did not correlate either with the electrophilicity index ω, consistent with previous observations of Sarotti et al.¹¹ Poor linear correlations (R² < 0.46) are found for the four sets of dienes, concluding that there is not a general relationship between both factors as had been originally proposed.¹⁰ Despite all linear regressions having negative slopes, indicating that the ΔE^‡ tends to decrease with the increase of the electrophilicity of the dienophile, the trend is merely qualitative. For instance, for the DA reactions between dienophiles with similar ω indexes (2.20–2.40 eV) and CP, the ΔE^‡ ranges from 12.6 kcal mol⁻¹ to 29.0 kcal mol⁻¹ (Fig. 2). On the other hand, activation barriers of ∼15 kcal mol⁻¹ are computed to a wide variety of electrophilic alkenes (from 1.50 eV to 6.15 eV).

Fig. 2 Plot of ΔE^‡versus ω.

To understand the causes that affect the activation barriers, a complete activation/distortion analyses for all model reactions was next addressed. In Fig. 3a are shown the averaged values computed for ΔE^‡, ΔE^‡_i and ΔE^‡_d, which was further decomposed as the sum of the diene distortion energy (ΔE^‡_d-diene) and the dienophile distortion energy (ΔE^‡_d–C=C). The ΔE^‡ increases in the order CP < DMB ≈ BU < CH, in agreement with the reactivity trends experimentally observed with these dienes.^11,38 The ΔE^‡_d controls the barrier heights on average, accounting for ∼74% of the activation energy. The ΔE^‡_d-diene is the most relevant factor, comprising ∼60% of the distortion energy. The average energy required to distort all dienes from their equilibrium geometries to the corresponding geometries at the TSs are in the same order of reactivity indicated above. CH, the least reactive diene under study, requires additional 4.7 kcal mol⁻¹ than CP to achieve the TS. This extra distortion is mainly responsible for the higher activation barriers computed for this diene. The averaged ΔE^‡_d–C=C (∼14 kcal mol⁻¹) is slightly higher than the averaged ΔE^‡_i (∼12 kcal mol⁻¹), responsible for ∼26% of the barrier height. However, these energetic terms show an important range between minimum and maximum values (vide infra), therefore any analysis considering the averaged values conceal the most important effects that this work aimed to unravel. For instance, in the reaction between 24 and CP the ΔE^‡_i is by far the most important factor, leading to a ΔE^‡ much lower than the average, while for the reaction between 63 and CP both the diene and the dienophile are highly strained, and coupled with a relatively low interaction energy, lead to an activation energy much higher than the average (Fig. 3b).

Fig. 3 (a) Average values of ΔE^‡ (dashed line), ΔE^‡_d-diene (in green), ΔE^‡_d–C=C (in red) and ΔE^‡_i (in blue) for the four sets of dienes under study. (b) Two representative examples from which a high deviation from the average is found.

The activation strain has been pointed out as the factor controlling the reactivity trends in a wide variety of pericyclic reactions studied under the distortion/interaction approach.^13c–e,14 However, according to the findings described above it is clear that in polar DA reactions this trend is not fully met, in line with recent studies of Fernández et al.^13a,b

Interaction energy analysis

The −ΔE^‡_i displays a large range between minimum (7.3–7.8 kcal mol⁻¹) and maximum values (20.6–27.5 kcal mol⁻¹) as shown in Fig. 4. The effect of this term on the activation energy varies from 18% to 44% in the lower and upper limits, respectively. The averaged highest and lowest values are found for CH and BU, respectively, as the dienic counterparts. Interestingly, both reagents display the maximum and minimum nucleophilicity indexes (N), respectively, among the dienes evaluated in this study (CP = 3.37 eV; CH = 3.53 eV; BU = 2.83 eV and DMB = 2.98 eV).

Fig. 4 Minimum and maximum ΔE^‡_i values for the four sets of dienes under study.

The interaction energy depends mainly on steric and electrostatic repulsions and charge transfer from occupied orbitals of one fragment to the empty orbitals of the other moiety. Within the Kahn–Sham molecular orbital model, the interaction energy between strained reactants can be further decomposed into three terms as shown in eqn (2):^12,39

ΔE_i = ΔV_elstat + ΔE_Pauli + ΔE_oi (2)

where ΔV_elstat accounts for the classical electrostatic interaction between the unperturbed charge distributions of the deformed reagents (usually attractive), ΔE_Pauli is the Pauli repulsion between occupied orbitals (destabilizing interaction, responsible for the steric repulsion) and ΔE_oi reflects the charge transfer resulting of the interaction between occupied orbitals in one moiety with unoccupied orbitals of the other (for example, HOMO–LUMO interactions and polarization).^12,39 As a result, a good correlation between ΔE^‡_i and the charge transfer (CT) at the TS was not unexpected (Fig. 5).

Fig. 5 Plot of −ΔE^‡_iversus CT.

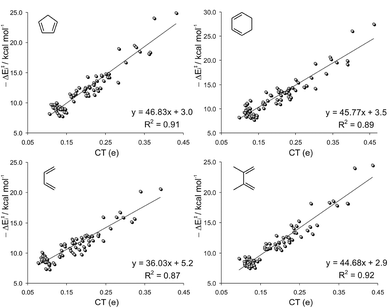
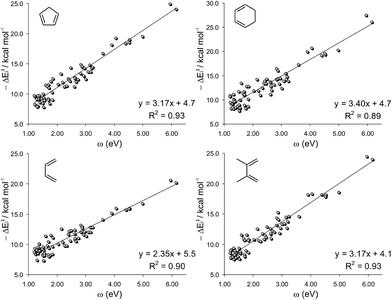
Moreover, since the amount of charge transferred from the diene to the dienophile is higher as the dienophilic counterpart becomes more electrophilic,^8,10 a good correlation between ΔE_i and ω should be expected. Accordingly, both terms matched nicely for each set of dienes under study (0.89 < R² < 0.93), Fig. 6.

Fig. 6 Plot of −ΔE^‡_iversus ω.

The failure of the ω index to correctly reproduce the reactivity trends is due to the fact that the electrophilicity of the dienophile mainly accounts for the ionicity of the process (as measured by the CT along the TS), affecting only the ΔE^‡_i term. This can be proved by the negligible effect that the ω index has on the distortion energy (R² < 0.01).³⁰ When comparing a series of similarly distorted TSs, the reactivity trend depends mainly on the ΔE^‡_i, and therefore, a good correlation between ΔE^‡ and ω is found. This is indeed the reason for the good match between ΔE^‡ and ω previously reported.¹⁰

The slopes of the linear regressions depicted in Fig. 6 increase in the order BU < DMB ≈ CP < CH, which is the exact order of nucleophilicity of those reagents. This can be explained considering that the amount of charge transferred from the diene to the dienophile (and consequently the interaction energy) is higher as the diene becomes more nucleophilic. Although the interaction energy can be fairly expressed from the ω index of the dienophile, a minor dependence on the degree of substitution of the dienophile is also found. The term aω + b (where a and b are the slopes and intercepts of the plots of Fig. 6, respectively) is the interaction energy that would be predicted on the basis of the ω index. The difference between ΔE^‡_i and aω + b is the residual interaction energy, which strongly depends on the number of substituents (NS) of the dienophile (Fig. 7).

Fig. 7 Residual interaction energy versus the number of substituents of the dienophile (NS) for the four sets of dienes under study.

The largest residuals are found for cyclic dienes (mainly CH), for which a range of ±1.5 kcal mol⁻¹ is observed. Nevertheless, the general trend is similar for all dienes: the actual ΔE^‡_i values increase (in absolute value) more than expected from the ω index as the dienophile becomes more substituted. This could be, at least in part, because the ω index only accounts for the stabilizing interaction between occupied/empty orbitals of both distorted fragments. As stated above, the interaction energy also has other terms (such as electrostatic and steric interactions), that are not supposed to be expressed in this simplified aω + b model. Thus, introducing a correction accounting for the NS effect, the ΔE^‡_i can be expressed as follows:

−ΔE^‡_i = aω + bNS + c (3)

where a, b and c are the coefficients that after linear-least squares application minimize the difference between actual and predicted ΔE^‡_i.⁴⁰ The values of these coefficients, along with the correlation R² parameter for each series of dienes, are given in Table 1. The a and b values display the same order that was observed for the nucleophilicity (N) of the dienes and the interaction residuals, respectively. The independent term c might be interpreted as the ΔE^‡_i of a non substituted alkene with ω = 0.0 eV, but is physically meaningless as ω > 0 for all organic molecules.⁸ Nevertheless, the resemblance to the −ΔE^‡_i computed for ethylene (ω = 0.73 eV) and CP, CH, BU and DMB is noteworthy: 4.0, 4.0, 5.1 and 4.5 kcal mol⁻¹, respectively.³⁰

Table 1 Coefficients of eqn (3)

Diene	a	b	c	R ^2
CP	3.13	0.49	3.48	0.95
CH	3.32	0.99	2.25	0.94
BU	2.31	0.45	4.40	0.92
DMB	3.14	0.33	3.32	0.94

---

The correlation between the actual and predicted (from eqn (3)) values of ΔE^‡_i for all 280 reactions under study is very good (see Fig. 17A), concluding that this important term of the activation barrier can be properly estimated considering only the ω index, easily computed from the HOMO and LUMO energies, and the degree of substitution of the dienophile.

Distortion energy analysis

As discussed above, the barrier heights of many pericyclic reactions are controlled by the distortion energy, indicating that ΔE^‡ is linearly dependent on ΔE^‡_d.^13c–e,14 However, only a modest correlation (R² < 0.71) is found for the polar DA reactions under study (Fig. 8), reinforcing the fact that the barrier heights depends on a fine balance between the interaction and distortion energies. Naturally, when comparing the reactivity trends of a series of dienophiles with similar ω indexes, the linearity between ΔE^‡ and ΔE^‡_d is met because the ΔE^‡_i is essentially the same (eqn (3)).³⁰

Fig. 8 Plot of ΔE^‡versus ΔE^‡_d.

In a further attempt to identify the structural and/or electronic factors that influence the distortion energy, a detailed analysis of the strain energy of both diene and dienophile counterparts was next performed.

Dienophile distortion energy (ΔE^‡_d–C=C)

As with the ΔE^‡_i, a wide range between minimum (6.8–7.7 kcal mol⁻¹) and maximum values (18.4–21.7 kcal mol⁻¹) is found for ΔE^‡_d–C=C (Fig. 9a). This term accounts for 20 to 41% of the activation energy in the lower and upper limits, respectively. Interestingly, the dienophile distortion is affected by the nature of the dienic counterpart, being higher for cyclic dienes. Moreover, the ΔE^‡_d–C=C shows a strong dependence on the degree of substitution of the dienophile (NS), increasing an average of ∼2.7 kcal mol⁻¹ per substituent. For cyclic dienophiles, the strain activation energy increases with the ring size (RS), consistent with previous calculations by Houk and co-workers.^14b In a simplistic approach, these observations can be related to the alkene stability. Briefly, as NS and/or RS increase, the alkene becomes more stable and the energy required to distort it from its equilibrium to the TS geometry would be higher.

Fig. 9 (a) Minimum and maximum ΔE^‡_d–C=C values for the four sets of dienes under study. (b) Dependence of ΔE^‡_d–C=C on the number of substituents of the dienophile (NS). (c) Dependence of ΔE^‡_d–C=C on the ring size of the dienophile (RS).

However, detailed analysis of the distorted dienophile-derived fragments suggested that slight variations in geometrical parameters, such as bending and dihedral angles, can generate a great impact on the ΔE^‡_d–C=C. To fully account for the geometrical factors closely linked to the distortion energy, the four torsion angles (θ_1–4), and the three out-of-plane deformations (τ, χ_C1 and χ_C2) were taken into account. The torsion angle (τ, also known as the twisting angle), and the pyramidalization angles (χ, also known as the out-of-plane bending angles) were calculated as described by Winkler and Dunitz to measure the distortion from planarity of amide groups.^30,41 In a non-distorted unstrained alkene, a zero value is expected for τ, χ_C1 and χ_C2, whose geometrical meanings are given in Fig. 10. In addition, two more factors were included: the bond stretching difference, (Δd_C1C2) and the average angle bending difference (Δϕ). The first term accounts for the difference in the C1=C2 bond length between the distorted fragment and the non-distorted alkene (d_{C1C2(distorted)} − d_{C1C2(non-distorted)}), while the second, defined as [∑(ϕ_distorted − ϕ_{non-distorted})]/6), accounts for the average deviation of the six bending angles ϕ_1–6 in the distorted fragments.

Fig. 10 Numbering and geometrical meaning of the dienophile out-of-plane deformations τ, χ_C1 and χ_C2.

After the corresponding 2520 parameters were computed, the next stage was the application of analysis of variance (ANOVA) to determine the statistical significance of the effect of each of the studied factors on the response (in this case, the ΔE^‡_d–C=C). The evidence is based on the probability that differences in the response due to changes introduced by the effects are greater than the differences that could be expected from other sources of factors not considered in the model (random errors).⁴² The design allowed us to obtain the surface response, fitting the data to a mathematical model by the linear-least squares application. The results obtained indicates that Δd_C1C2, Δϕ, τ, χ_C1 and χ_C2 have statistical significance at a 95% confidence level, and the equation that best matches the distortion energy is shown in eqn (4), while the a–k coefficients are given in the ESI:†³⁰

ΔE^‡_d–C=C = aΔd_C1C2 + bΔϕ + cτ + dχ_C1 + eχ_C2 + fΔϕ² + gχ_C2² + hΔϕχ_C1 + iΔϕχ_C2 + jτχ_C2 + k (4)

Interestingly, none of the four dihedral angles taken alone was significant, indicating that the out-of-plane deformations (τ, χ_C1 and χ_C2) are better descriptors for strained alkene intermediates. On average, 75% of ΔE^‡_d–C=C derives from the quadratic term composed of Δϕ, χ_C1, Δϕ² and Δϕχ_C1, proving that the pyramidalization at C1 and the average bending angles difference play a key role in understanding the energy strain of a distorted dienophile. In an asynchronous TS, the bonding between C1–C6 is stronger than C2–C3 (Fig. 1),⁴³ therefore χ_C1 is expected to have a higher impact on the distortion energy than χ_C2. This last term, along with τ, χ_C2², Δϕχ_C1, Δϕχ_C2 and τχ_C2, account for 19% of the ΔE^‡_d–C=C. The remaining 6% is due to the Δd_C1C2 term, whose increment causes a linear increase in the distortion as the a coefficient is positive. The effect of the other parameters is simplified in Fig. 11. The χ_C1 and χ_C2 are not completely independent factors (vide infra), but they are linked to each other. The lowest distortions are located in the southwest zone (lowest Δϕ and χ_C1 + χ_C2), and the highest distortion is found in the north zone (at Δϕ ∼ −3.5°), where χ_C1 + χ_C2 and Δd_C1C2 are maximum. Notably, the highest distortion does not takes place at the highest Δϕ.

Fig. 11 Variation of ΔE^‡_d–C=C with Δϕ. The arrows indicate the direction in which χ_C1 + χ_C2 and Δd_C1C2 increment.

The predicted distortion energy from eqn (4) is highly satisfactory (R² = 0.90), considering that 98% of the cases are between ±1 kcal mol⁻¹ of the actual distortion energy computed at the B3LYP/6-31G* level (see Fig. 17B).

Now that the ΔE^‡_d–C=C can be fairly expressed as function of geometrical parameters of the strained dienophiles, the next question is how those parameters are affected by structural features of the alkene, such as NS and RS. This relationship is disclosed in Fig. 12, indicating that both Δd_C1C2 and Δϕ are affected by the number of substituents (NS) and the ring size (RS) of the dienophile, and tend to increase to the extent that the dienophile becomes more substituted to minimize repulsive interactions.³⁰ Interestingly, a reverse effect is found regarding the ring size of cyclic dienophiles. While Δd_C1C2 increases with the RS, the Δϕ decreases in the same direction. The same trends are found in the non-distorted alkenes and the corresponding DA products, but with different slopes.³⁰

Fig. 12 (a) Dependence of Δd_C1C2 and Δϕ on the number of substituents (NS) and the ring size of the dienophile (RS). (b) Dependence of pyramidalization angles χ_C1 and χ_C2 on the asynchronicity of the TS (Δd) and the number of substituents of the dienophile (NS).

Regarding the out-of-plane bending angles, a strong dependence is found on the synchronicity of the cycloaddition process (Fig. 12b). In a highly asynchronous TS, the bond between C1–C6 is highly advanced, while the bonding at C2–C3 is only emerging.⁴³ As C1 becomes more pyramidalized (higher χ_C1), the pyramidalization at C2 decreases. On the other hand, in a synchronous TS, both carbon atoms are similarly pyramidalized (∼30°). Finally, a minor effect of the degree of substitution is also found, mainly for the χ_C2 parameter. This can be explained, at least in part, considering that the degree of s character of highly strained alkenes (and therefore, the ease of pyramidalization) increases with the Δd_C1C2 (and consequently with NS).³⁰

Diene distortion energy (ΔE^‡_d-diene)

As discussed above, the diene distortion energy is the most relevant term on average, comprising ∼44% of the activation energy. Nevertheless, a wide range between minimum (12.1–15.2 kcal mol⁻¹) and maximum values (22.5–28.4 kcal mol⁻¹) is found for this portion of the total distortion energy (Fig. 13a). Therefore, this term accounts for 31 to 56% of the activation energy in the lower and upper limits, respectively. It would be unnecessary to point out that the diene distortion depends mainly on the nature of the diene, increasing in the order CP < DMB ≈ BU < CH, which is the same order of reactivity computed for those dienes. However, the ΔE^‡_d-diene is also dependent on the structural features of the dienophile, such as the NS and RS (Fig. 13b and c), likewise the ΔE^‡_d–C=C is dependent on the nature of the diene (Fig. 9a). In the strain/activation model, the two infinitely separated reagents begin to interact and deform each other until the TS is reached, where the rates of change of ΔE_d and ΔE_i are opposite (∂ΔE_d = −∂ΔE_i).¹² This result suggest that the distortion of both diene and dienophile fragments is coupled, though a poor correlation is found between ΔE^‡_d-diene and ΔE^‡_d–C=C (R² < 0.58).³⁰ To unravel this issue, the next step was the determination of the geometrical parameters that influence the energy strain of the diene fragments in a similar fashion to the analysis performed for the dienophile distortion.

Fig. 13 (a) Minimum and maximum ΔE^‡_d-diene values for the four sets of dienes under study. (b) Dependence of ΔE^‡_d-diene on the number of substituents of the dienophile (NS). (c) Dependence of ΔE^‡_d-diene on the ring size of the dienophile (RS).

Accordingly, the factors taken into consideration were the eight torsion angles (θ_1–8), and the six out-of-plane deformations (τ₅₆, τ₃₄, χ_C3, χ_C4, χ_C5 and χ_C6) of the two conjugated C=C double bonds, as depicted in Fig. 14. In addition, the approach of the two terminal atoms of the conjugated diene (Δd_C3C6, defined as d_{C3C6(distorted)} − d_{C3C6(non-distorted)}), was also considered a plausible factor. Interestingly, among the 15 parameters considered, only three were found significant after ANOVA analysis was performed: Δd_C3C6 and the two out-of-plane descriptors χ_C3 and χ_C6, which corresponds to the pyramidalization of the terminal atoms of the conjugated diene. The equation that best fits the ΔE^‡_d-diene as a function of Δd_C3C6, χ_C3 and χ_C6 by linear-least squares application is given below, and the a–f coefficients can be found in the ESI.†

ΔE^‡_d-diene = aΔd_C3C6 + bχ_C6 + cχ_C3 + dχ_C6² + eχ_C3² + f (5)

Fig. 14 Numbering and geometrical meaning of the diene out-of-plane deformations τ₁₂, τ₃₄, χ_C3, χ_C4, χ_C5 and χ_C6.

The agreement between actual and predicted values is excellent (R² = 0.97), 98% of the 280 examples being located within ±0.6 kcal mol⁻¹ of the actual distortion energy computed at the B3LYP/6-31G* level (see Fig. 17C).

Analysis of eqn (5) indicates that the most relevant factors are Δd_C3C6, χ_C6 and χ_C6², accounting for 80% of the effect on average. The quadratic dependence on the pyramidalization at C6 has no minimum within the range, therefore the distortion of the diene rises with the extent of pyramidalization at C6. On the other hand, the distortion linearly increases as the terminal atoms of the conjugated diene are increasingly separated. This effect is more pronounced for CH (Fig. 15).

Fig. 15 Variation of ΔE^‡_d-diene with χ_C6 and Δd_C3C6. The plot for DMB is similar to that of BU, and is not shown for simplicity.

The deformation of the diene and dienophile at the TS occur at the geometry that maximizes the orbital interactions between the two moieties at minimal distortion.¹² Thus, a correlation might be expected between Δd_C1C2 and Δd_C3C6, and the factors affecting the former should also alter the second. In fact, as depicted in Fig. 16a, the Δd_C3C6 slightly increases with NS and RS with the same trend observed for Δd_C1C2 (Fig. 12a). Here again, the pyramidalization terms χ_C6 and χ_C3 are strongly correlated with the asynchronicity of the TS (Fig. 16b). In a highly asynchronous TS, χ_C6 will be higher than χ_C3, and the difference between both decreases as the TS becomes more synchronous.⁴² Finally, a minor (almost negligible) effect on the degree of substitution of the dienophile is noted.

Fig. 16 (a) Dependence of Δd_C3C6 on the number of substituents (NS) and the ring size of the dienophile (RS). (b) Dependence of pyramidalization angles χ_C6 and χ_C3 on the synchronicity of the TS (Δd) and the number of substituents of the dienophiles (NS).

Distortion energy model

The distortion energy of both strained diene and dienophile fragments can be accurately predicted considering geometrical parameters of the distorted moieties at the TS (eqn (4) and (5)), which in turn depend on more simple terms, such as NS, RS and Δd. Thus, the final stage of this study was devoted to finding an easy and reliable way to estimate the ΔE^‡_d term. This would provide a better understanding (in a semi-quantitative fashion) of the effects that modify this important term of the activation energy, besides yielding a useful predicting tool. After several trials, the equation that, after linear-least squares application, affords highest accuracy at minimal mathematical complexity is given below:⁴⁴

ΔE^‡_d ≈ aNS + bRS + cω + dΔd + eΔd² + f (6)

ANOVA analysis indicates that all terms are significant at a 95% confidence level. A highly acceptable correlation between actual and predicted distortion energy is found with this simple model (R² = 0.93, Fig. 17D). In Table 2 are shown the coefficients computed for each diene series. Notably, Δd is the only variable of eqn (6) that has to be computed from the TS geometry. Nevertheless, as indicated above, a fair estimation of this term can be achieved using conceptual DFT analysis (Δd ≈ 0.39Δω_k + 0.07). Replacement of Δd in eqn (6) for this finds virtually no changes in the result (R² = 0.97).³⁰ Moreover, the combination of eqn (3) and (6) provides an excellent estimate (considering the simplicity of the calculations) of the B3LYP/6-31G* barrier heights using only conceptual DFT calculations (R² = 0.91).³⁰

Fig. 17 (a) Plot of −ΔE^‡_i (predicted from eqn (3)) versus −ΔE^‡_i. (b) Plot of ΔE^‡_d–C=C (predicted from eqn (4)) versus ΔE^‡_d–C=C. (c) Plot of ΔE^‡_d-diene (predicted from eqn (5)) versus ΔE^‡_d-diene. (d) Plot of ΔE^‡_d (predicted from eqn (6)) versus ΔE^‡_d.

Table 2 Coefficients of eqn (6)

Diene	C=C	a	b	c	d	e	f
CP	Acyclic	3.8	0.0	0.0	9.1	−15.4	20.1
CH	Acyclic	4.8	0.0	0.0	5.7	−8.8	23.5
BU	Acyclic	3.7	0.0	0.0	6.2	−13.2	23.4
DMB	Acyclic	3.6	0.0	0.0	8.3	−15.5	23.8
CP	Cyclic	4.8	2.6	−3.0	−4.0	0	12.6
CH	Cyclic	6.6	2.9	−3.1	−3.0	0	10.3
BU	Cyclic	4.3	2.5	−3.1	−7.5	0	17.6
DMB	Cyclic	4.1	2.2	−3.1	−7.2	0	19.9

---

From the analysis of eqn (6) it is clear that the distortion increases with the degree of substitution of the dienophile, but at different rates. For acyclic dienophiles, each additional substituent accounts for an increase of the strain energy of ∼3.7 kcal mol⁻¹, except when CH is the dienic counterpart (4.8 kcal mol⁻¹). For cyclic dienophiles, the increment of distortion with the NS is higher, requiring ∼0.5 kcal mol⁻¹ (BU and DMB), 1.0 kcal mol⁻¹ (CP) and 1.8 kcal mol⁻¹ (CH) more energy to distort both fragments.

The ring size is also an important term (as found by Houk),^14b increasing ∼2.6 kcal mol⁻¹ when passing from four to five to six-membered rings. On average, the NS and RS terms account for ∼80% of the distortion energy. Interestingly, while the influence of the electrophilic index is negligible for acyclic dienophiles, somehow the distortion tends to decrease as cyclic dienophiles becomes more electrophilic, comprising 5–10% of the ΔE^‡_d. Finally, the asynchronicity at the TS is also significant, accounting for ∼20% and 5–10% of the total distortion in the case of acyclic and cyclic dienophiles, respectively. The quadratic term is only significant for the former (30–50% of the Δd effect in the average). Since the quadratic coefficient e is negative (Table 2), the resulting parabolas are upside-down. The maximum is reached when ∂ΔE^‡_d/∂Δd = 0, and it can be easily proved that this occurs at Δd = −d/2e. In this way, the corresponding stationary points are located at Δd = 0.30 Å, 0.32 Å, 0.23 Å and 0.27 Å for CP, CH, BU and DMB, respectively (Fig. 18). As the TS is more asynchronous, the distortion decreases at a rate indicated by the e coefficient (note that CH is less affected than the other dienes). As a result, a highly asynchronous TS is predicted to be considerably less distorted than more synchronous ones. In the case of cyclic dienophiles, the synchronicity is a minor factor (5–10%), and tends to lower the distortion as the TS is more asynchronous.

Fig. 18 Variation of ΔE^‡_d with Δd. The plot for DMB is similar to that of CP, and is not shown for simplicity.

The effect of the synchronicity on the strain energy can be seen by comparing the large difference in reactivity between the dicyanoethylenes 16 and 18 (Fig. 19). As experimentally determined by Sauer et al., the former is ∼500 times more reactive than the second in DA reactions with CP.⁴⁵

Fig. 19 Diels–Alder reaction between 16 and 18 with CP.

The experimental trend is well reproduced by B3LYP/6-31G* calculations (Fig. 19).⁵ The computed ω indices are similar (2.82 and 3.08 eV), therefore such a difference in reactivity cannot be due to the interaction energy. In fact, the computed −ΔE^‡_i values for TS-16+CP and TS-18+CP are 13.4 and 13.6 kcal mol⁻¹ respectively, and those estimated from eqn (3) are 12.8 and 13.7 kcal mol⁻¹, respectively. Based on the above, the barrier heights must be controlled by the distortion energy. While the B3LYP/6-31G* ΔE^‡_d computed for the system 16+CP is only 22.7 kcal mol⁻¹, for the parent reaction of 18+CP this value rises to 28.3 kcal mol⁻¹. Since both dienophiles are acyclic disubstituted alkenes, from eqn (6) the difference in the distortion energy can only be justified on the asynchronicity of the TSs. The computed ω_k indices for the C1 and C2 carbon atoms of the dienophiles are highly different for 16 (Δω_k = 1.82 eV) and similar for 18 (Δω_k = 0.00 eV), as shown in Fig. 19. Accordingly, TS-16+CP is expected to be much more asynchronous than TS-18+CP. The Δd values computed on the transition structures located at the B3LYP/6-31G* level are 0.81 Å and 0.03 Å, respectively, and the Δd estimated from the Δω_k values are 0.77 Å and 0.07 Å, respectively. Finally, the ΔE^‡_d estimated from eqn (6) are 24.9 kcal mol⁻¹ and 28.0 kcal mol⁻¹ for the systems 16+CP and 18+CP, respectively, in very good agreement with the B3LYP/6-31G* calculated values.

Similar conclusions can be drawn considering the geometrical parameters of the distorted fragments at the TS. The Δd_C1C2, Δϕ and τ values are similar for both strained dienophiles, but they differ significantly in their pyramidalization angles (Fig. 20). While the fragment derived from the asynchronous TS-16+CP is highly pyramidalized on C1 (χ_C1 = 40.9°) and almost unpyramidalized on C2 (χ_C2 = 8.6°), the distorted trans-dicyanoethylene fragment is similarly pyramidalized on both atoms (∼30°). As χ_C1 + χ_C2 is slightly higher for the second (49.5° vs. 60.4°), according to Fig. 11 a narrow difference in the distortion energy of both fragments is expected. In fact, the B3LYP/6-31G* computed ΔE^‡_d–C=C values for TS-16+CP and TS-18+CP are 10.6 kcal mol⁻¹ and 12.0 kcal mol⁻¹, respectively, and the predicted values from eqn (4) are 11.3 kcal mol⁻¹ and 11.8 kcal mol⁻¹, respectively. On the other hand, the distorted cyclopentadiene moieties show significant differences in their geometrical parameters Δd_C3C6, χ_C3 and χ_C6 (Fig. 20), thus are expected to be responsible for the total distortion energy difference. Here again, the B3LYP/6-31G* ΔE^‡_d-diene values for TS-16+CP and TS-18+CP are 12.1 kcal mol⁻¹ and 16.3 kcal mol⁻¹, respectively (ΔΔE^‡_d-diene = 4.2 kcal mol⁻¹), and the estimated values from eqn (5) are 12.5 kcal mol⁻¹ and 16.6 kcal mol⁻¹, respectively (ΔΔE^‡_d-diene = 4.1 kcal mol⁻¹), in perfect agreement with the calculated values.

Fig. 20 Distortion/interaction analysis of the Diels–Alder reactions between 16 and 18 with CP along the reaction coordinate projected onto the average forming C–C distances.

Finally, as pointed out by Bickelhaupt, the activation strain model has to be applied to the entire reaction coordinate.¹² A single-point analysis at the transition states only might yield misleading conclusions. For that reason, a complete activation strain analysis was carried out for 10 representative examples.³⁰Fig. 20 shows the plots of the computed PES along the IRC trajectories for the 16+CP and 18+CP reactions, projected onto the average bond forming distances. Similar plots corresponding to the reactions of 1, 24, 33, 40, 41, 48, 55 and 56 with CP can be found in the ESI.†

In the early stages of the reaction the reactants approach each other and the energy increases. The interaction at this phase is destabilizing, probably due to steric repulsion (Pauli) between reactants,¹² except when the dienophile is highly electrophilic (24 and 33).³⁰ As the reagents come closer, the repulsion is higher but the HOMO_diene–LUMO_dienophile orbitals begins to interact, and the charge transfer starts occurring from the diene to the dienophile. Thus, the overall interaction becomes stabilizing and begins to drop faster as reagents becomes more closer. On the other hand, the distortion energy is always positive and increases constantly as the distance between reagents decreases. Before the TS, the growth trend of the distortion is higher than the downward trend of the interaction (mathematically, ∂ΔE_d > −∂ΔE_i) and the energy of the system increases. At the TS, the ∂ΔE_d = −∂ΔE_i and the stationary point is reached. As the reaction moves forward, now the ∂ΔE_d < −∂ΔE_i and the energy starts to drop. A clear tendency is also observed toward an early transition state as the activation barrier decreases.

Analysis of the CT along the reaction coordinate indicates that the electron density transfer increases in a Gaussian shaped curve, and reaches its maximum at ∼2.1–2.2 Å, which is normally not the geometry of the TS. Interestingly, an inflection point (change in the curvature sign) is also noted at ∼2.5–2.6 Å, corresponding to the average bond forming distance at which the interaction energy begins to fall sharply. Notably, the position of the CT maximum and inflection point seems to be unaffected by the amount of charge transfer and the asynchronicity of the TS, as similar curves are found for the other systems.³⁰

Conclusions

In this work, 280 polar DA reactions were computationally studied at the B3LYP/6-31G* level of theory. From the results obtained, several conclusions can be drawn. The activation barriers show a poor correlation with the reaction enthalpies and with the electrophilicity index ω, in clear opposition to what had been originally proposed. Moreover, in contrast to other pericyclic reactions, the barrier heights do not show a linear relationship with the distortion energy. Instead, the ΔE^‡ values emerge as a delicate balance between the energy required to distort the reactants from their initial geometries to their transition state geometries and the binding energy between the deformed reactants in the TS. The interaction energy shows a strong dependence on the amount of charge transferred from the diene to the dienophile at the TS, and therefore, displays good correlation with the electrophilicity of the dienophile. On the other hand, a detailed analysis of the structural factors that affect the strain energy of both diene and dienophile distorted fragments was also performed. As a result, the distortion energy can be expressed as a function of simple terms, such as the substitution degree, electrophilicity and, when relevant, the ring size of the dienophile, along with the asynchronicity of the TS. This term can be better estimated considering the local electrophilic indices resulting from conceptual DFT analysis than from classical FMO theory. Finally, this study provides a further example on the outstanding ability of the distortion/interaction model for understanding reactivity trends.

Acknowledgements

CONICET, Universidad Nacional de Rosario, and ANPCyT for financial support.

Notes and references

1. (a) F. Fringuelli and A. Taticchi, The Diels-Alder Reaction. Selected Practical Methods, John Wiley & Sons, New York, 2002; (b) I. Fleming, Pericyclic Reactions, Oxford University Press Inc., New York, 1999; (c) K. C. Nicolau, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668.
2. http://www.nobelprize.org .
3. (a) K. J. Cahill and R. P. Johnson, J. Org. Chem., 2013, 78, 1864; (b) K. Black, P. Liu, L. Xu, C. Doubleday and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12860; (c) D. H. Ess, G. O. Jones and K. N. Houk, Adv. Synth. Catal., 2006, 348, 2337; (d) K. N. Houk, J. Gonzalez and Y. Li, Acc. Chem. Res., 1995, 28, 81; (e) K. N. Houk, Y. Li and J. D. Evanseck, Angew. Chem., Int. Ed., 1992, 31, 682; (f) J. Sauer and R. Sustmann, Angew. Chem., Int. Ed. Engl., 1980, 19, 779.
4. L. R. Domingo, M. Arnó and J. Andrés, J. Org. Chem., 1999, 64, 5867.
5. L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, J. Org. Chem., 2003, 68, 3884.
6. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793.
7. R. G. Parr, L. von Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922.
8. L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, Tetrahedron, 2002, 58, 4417.
9. For recent references, see: (a) L. R. Domingo, P. Pérez and D. E. Ortega, J. Org. Chem., 2013, 78, 2462; (b) L. R. Domingo, J. A. Sáez, J. A. Joule, L. Rhyman and P. Ramasami, J. Org. Chem., 2013, 78, 1621; (c) L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615; (d) C. N. Alves, A. S. Carneiro, J. Andrés and L. R. Domingo, Tetrahedron, 2006, 62, 5502; (e) L. R. Domingo and J. Andrés, J. Org. Chem., 2003, 68, 8662.
10. L. R. Domingo and J. A. Sáez, Org. Biomol. Chem., 2009, 7, 3576.
11. A. M. Sarotti, R. A. Spanevello and A. G. Suárez, Tetrahedron Lett., 2011, 52, 4145.
12. W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118.
13. (a) I. Fernández, M. Solà and F. M. Bickelhaupt, Chem.–Eur. J., 2013, 19, 7416; (b) I. Fernández, F. M. Bickelhaupt and F. P. Cossío, Chem.–Eur. J., 2012, 18, 12395; (c) I. Fernández and F. M. Bickelhaupt, J. Comput. Chem., 2012, 33, 509; (d) I. Fernández, F. P. Cossío and F. M. Bickelhaupt, J. Org. Chem., 2011, 76, 2310; (e) I. Fernández, F. M. Bickelhaupt and F. P. Cossío, Chem.–Eur. J., 2009, 15, 13022; (f) A. P. Bento and F. M. Bickelhaupt, J. Org. Chem., 2008, 73, 7290; (g) A. Diefenbach, G. T. de Jong and F. M. Bickelhaupt, J. Chem. Theory Comput., 2005, 1, 286; (h) A. Diefenbach and F. M. Bickelhaupt, J. Phys. Chem. A, 2004, 108, 8460; (i) A. Diefenbach and F. M. Bickelhaupt, J. Chem. Phys., 2001, 115, 4030; (j) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114.
14. (a) S. A. Lopez and K. N. Houk, J. Org. Chem., 2013, 78, 1778; (b) R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366; (c) A. E. Hayden and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 4084; (d) Y.-H. Lam, P. H.-Y. Cheong, J. M. Blasco Mata, S. J. Stanway, V. Gouverneur and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 1947; (e) F. Schoenebeck, D. H. Ess, G. O. Jones and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 8121; (f) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187; (g) D. H. Ess, G. O. Jones and K. N. Houk, Org. Lett., 2008, 10, 1633; (h) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646.
15. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
16. W. J. Hehre, L. Radom, R. v. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
18. V. Guner, K. S. Khuong, A. G. Leach, P. S. Lee, M. D. Bartberger and K. N. Houk, J. Phys. Chem. A, 2003, 107, 11445.
19. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1. For some original literature references, see: (a) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
20. (a) R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512; (b) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
21. L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615.
22. L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, J. Phys. Chem. A, 2002, 106, 6871.
23. L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486.
24. Some of the 280 cycloadditions have been previously theoretically studied by other authors at the B3LYP/6-31G* level of theory (for example, the reactions between CP and 1–4, 16–18, 30 and 33,^5,10 and the reactions between 41, 48 and 57 with CP and CH.)^14b For the cycloadditions between 6–7 with CP see: M. A. Silva, S. C. Pellegrinet and J. M. Goodman, ARKIVOC, 2003,(10), 556.
25. (a) A. M. Sarotti, R. A. Spanevello, A. G. Suárez, G. A. Echeverría and O. E. Piro, Org. Lett., 2012, 14, 2556; (b) A. M. Sarotti, M. M. Zanardi, R. A. Spanevello and A. G. Suárez, Curr. Org. Synth., 2012, 9, 439.
26. L. R. Domingo, J. A. Sáez, R. J. Zaragozá and M. Arnó, J. Org. Chem., 2008, 73, 8791.
27. M. Linder and T. Brinck, J. Org. Chem., 2012, 77, 6563.
28. The asynchronicity of a concerted reaction can be quantified in different manners. A very common and simple definition, used in this work, employs the difference in the lengths of the two bonds forming (Δd). Other methods, such as the difference in Wiberg bond indices of both σ bonds forming (Δ_WBI), and the more complex term introduced by Moyano and co-workers ( A. Moyano, M. A. Pericàs and E. Valenti, J. Org. Chem., 1989, 54, 573 ), have been used by different authors. As shown in the ESI,† good linear correlations were found for all these methods.
29. D. M. Birney and K. N. Houk, J. Am. Chem. Soc., 1990, 112, 4127.
30. See the ESI† for further details on this issue.
31. A. M. Sarotti, A. G. Suárez and R. A. Spanevello, Tetrahedron Lett., 2011, 52, 3116.
32. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
33. Since CBS-QB3 is a highly demanding computational method, the 35 compounds were selected to provide a representative and homogeneous distribution of structural and electronic properties of all dienophiles under study.
34. (a) J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532; (b) J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822; (c) G. A. Petersson, D. K. Malick, W. G. Wilson, J. W. Ochterski, J. A. Montgomery and M. J. Frisch, J. Chem. Phys., 1998, 109, 10570.
35. O. Dimroth, Angew. Chem., 1933, 46, 571.
36. M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1340.
37. R. A. Marcus, J. Chem. Phys., 1956, 24, 966.
38. A. M. Sarotti, P. L. Pisano and S. C. Pellegrinet, Org. Biomol. Chem., 2010, 8, 5069.
39. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558.
40. Note that the a and b coefficients are different from those of the aω + b relationship, and should not be confused.
41. F. K. Winkler and J. D. Dunitz, J. Mol. Biol., 1971, 59, 169.
42. E. Morgan, Chemometrics: Experimental Design, Wiley, New York, USA, 1995.
43. For asynchronous TSs, C1 is arbitrarily defined as the carbon atom of the dienophile with the lowest bond forming distance with the diene moiety. Therefore, C6 is defined as the carbon atom of the diene that bonds to C1.
44. For example, cubic equations afford better correlation between predicted and calculated values, but are more difficult to interpret.
45. J. Sauer, H. Wiest and A. Mielert, Chem. Ber., 1964, 97, 3183.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates and energies for all stationary points, global and local DFT indices for all reagents, geometrical parameters of all distorted fragments, and all further discussion and information related to this work. See DOI: 10.1039/c3ob41628c

---