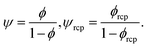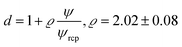Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Length-scale dependent transport properties of colloidal and protein solutions for prediction of crystal nucleation rates†
Tomasz
Kalwarczyk
*a,
Krzysztof
Sozanski
a,
Slawomir
Jakiela
a,
Agnieszka
Wisniewska
a,
Ewelina
Kalwarczyk
a,
Katarzyna
Kryszczuk
a,
Sen
Hou
ab and
Robert
Holyst
*a
aInstitute of Physical Chemistry of the Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: rholyst@ichf.edu.pl; tkalwarczyk@ichf.edu.pl; Tel: +48 22 343-3123
bState Key Laboratory of Medicinal Chemical Biology, Nankai University, China
First published on 25th June 2014
Abstract
We propose a scaling equation describing transport properties (diffusion and viscosity) in the solutions of colloidal particles. We apply the equation to 23 different systems including colloids and proteins differing in size (range of diameters: 4 nm to 1 μm), and volume fractions (10−3–0.56). In solutions under study colloids/proteins interact via steric, hydrodynamic, van der Waals and/or electrostatic interactions. We implement contribution of those interactions into the scaling law. Finally we use our scaling law together with the literature values of the barrier for nucleation to predict crystal nucleation rates of hard-sphere like colloids. The resulting crystal nucleation rates agree with existing experimental data.
1 Introduction
Crystallization is ubiquitous in nature and is a standard way to purify chemical substances or determine the structure of proteins. Surprisingly description of this phenomenon provides an example of one of the largest discrepancies between theory and experiment in science. The dimensionless nucleation rate of colloidal hard-spheres at volume fraction ϕ = 0.52 is I = 10−10 in experiment1,2 and 10−20 in theory3,4 giving 10 orders of magnitude of difference. The nucleation rate I = αP where P = exp(−ΔGcrit/kBT) is the probability of formation of the critical nucleus and ΔGcrit is the height of a barrier for the nucleus formation. α is the kinetic pre-factor defined as2,5,6α = 6/πϕ5/3D/σ5 (cf.ref. 5, page 285), where ϕ is the volume fraction, D is the diffusion coefficient of colloidal particles, and σ is the particle diameter. The probability P is usually calculated from the classical nucleation theory (CNT), and the precision of computation depends only on the proper choice of the equation of state and the crystal–liquid surface tension. ΔGcrit can also be calculated using the umbrella sampling method.3,4,7,8 Determination of the diffusion rate at volume fractions 0.52–0.56 where nucleation takes place is difficult because in this narrow range of volume fractions the viscosity of colloidal solutions increases drastically, reaching a value of 2400 times the viscosity of solvent.9Here we analyse the viscosity of colloidal solutions, and mobility in those solutions in a wide range of concentrations taking into account the length-scale dependent viscosity concept.10,11 We analyse the viscosity for the broad range of volume fractions (10−3–0.56) and on that basis we calculate the mobility of colloidal particles for the most concentrated systems (ϕ > 0.52). Next, using these data in combination with the literature values of the nucleation barrier,4,7 we determine the crystal nucleation rate for hard-sphere colloids which appear in agreement with experimental data.2
Recently we have shown that the transport properties of entangled complex fluids (e.g. polymer and micellar solutions) are, at the nanoscale, strongly influenced by the length-scale dependent viscosity.10,11 The long-time self-diffusion coefficient D = D0/f(rp) is inversely proportional to the effective viscosity experienced by the probe η = η0f(rp), where rp denotes the hydrodynamic radius of the probe. D0 is the diffusion coefficient of the probe in a pure solvent of viscosity η0 (at infinite dilution limit), and f(rp) is an exponential function of the length-scale of flow that corresponds to rp. Note that both expressions D = D0/f(rp) and η = η0f(rp) extend the validity of the Stokes–Sutherland–Einstein12,13 formula D = kT/6πηrp for complex media.10,11 For entangled polymer solutions10,11f(rp) is given by:
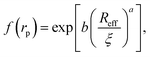 | (1) |
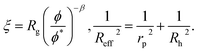 | (2) |
R
g is the radius of gyration of the polymer coil and β is a constant close to unity. 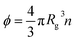 is the volume fraction where n denotes the number of polymer coils per unit volume. ϕ* is the polymer volume fraction for the overlap concentration – the concentration at which the polymer coils start to penetrate each other. ϕ* = 0.52 and corresponds to the maximum packing fraction for a simple cubic lattice. a is a constant of the order of 1. Rh is the hydrodynamic radius of the polymer coils forming the solution. b is inversely proportional to the temperature (b = γ/RT, where R is the gas constant, T is the absolute temperature, and γ is a parameter expressed in kJ mol−1).14Eqn (1), apart from the transport in polymer and micellar solution, surprisingly well describes the transport properties in the cytoplasm of mammalian11,15 or bacterial16,17 cells. Since the cytoplasm of living cells consists of both entangled, elongated structures and non-entangled colloids (proteins), a question arises: Do the transport properties of non-entangled colloidal fluids depend on the length-scale of flow and do they consistently apply across the nano- and macroscopic scale as given by eqn (1)?
is the volume fraction where n denotes the number of polymer coils per unit volume. ϕ* is the polymer volume fraction for the overlap concentration – the concentration at which the polymer coils start to penetrate each other. ϕ* = 0.52 and corresponds to the maximum packing fraction for a simple cubic lattice. a is a constant of the order of 1. Rh is the hydrodynamic radius of the polymer coils forming the solution. b is inversely proportional to the temperature (b = γ/RT, where R is the gas constant, T is the absolute temperature, and γ is a parameter expressed in kJ mol−1).14Eqn (1), apart from the transport in polymer and micellar solution, surprisingly well describes the transport properties in the cytoplasm of mammalian11,15 or bacterial16,17 cells. Since the cytoplasm of living cells consists of both entangled, elongated structures and non-entangled colloids (proteins), a question arises: Do the transport properties of non-entangled colloidal fluids depend on the length-scale of flow and do they consistently apply across the nano- and macroscopic scale as given by eqn (1)?
The transport properties of fluids are influenced by the van der Waals, steric, hydrodynamic, and electrostatic interactions. For example electrostatic repulsion between colloidal particles increases the shear viscosity of their solutions.18,19 Additionally the rates of diffusion-limited reactions in bio-complex systems (i.e. cell cytoplasm) depend on the ionic strength of the cellular interior.15 Here we ask: How do the intermolecular interactions influence f(rp)?
2 Scaling law for transport properties of colloidal solutions
To answer the above stated questions we analysed the viscosity of the following colloidal systems: hard-sphere solutions consisting of monodisperse (standard deviation σ ≈ 0.05) poly(methyl methacrylate) – PMMA particles with hydrodynamic radii Rh ranging from 240 to 500 nm,20,21 SiO2 particles (Rh = 244 nm),9 charged polystyrene latex (PSL) particles (Rh varying from 25 to 35 nm),19 and polydisperse (standard deviation σ ≈ 0.12) SiO2 particles (Rh varying from 28 to 110 nm).22 We also analysed the data on self-diffusion coefficients of probe particles in colloidal and in protein solutions including bovine serum albumin (BSA, rp = 4 nm) and myoglobin (MGB, rp = 2.4 nm).20,23 Additionally, we performed measurements of viscosity of BSA and of lysozyme (LYS, rp = 1.9 nm) solutions as well as self-diffusion of lysozyme. For the experimental details see ESI.†Relative viscosity ηr = η/η0 of an ideal, infinitely-diluted non-interacting hard-sphere solution is given by the Einstein's formula24,25ηr = 1 + kϕ where k = 2.5. The Einstein's formula is derived under assumption that the volume of particles forming the solution is much lower than the volume of the whole system, and the hydrodynamic interactions (HIs) between particles are negligible. In the real hard-sphere systems, however, HIs are not negligible as the screening length of HI is an order of magnitude longer than Rh of spheres forming the solution.26 The formula describing viscosity of the hard-sphere solution and including long-ranged, multi-body HI is derived by Saitô:27ηr = 1 + kψ, where ψ = ϕ(1 − ϕ)−1 and can be expressed as the ratio of the total volume of spheres suspended in the solution, Vk, to the volume of the solvent, Vs (ϕ = Vk/(Vk + Vs); ψ = Vk/Vs).
Following Saitô’s work we adopted eqn (1) in order to describe the viscosity and diffusion in hard-sphere solution and we introduced the dependence on ψ into eqn (1). In the literature one can find many examples of more or less complicated equations describing the viscosity of concentrated suspensions of hard-sphere particles.28–30 In our approach we use the simplest form that includes the long-range, multi-body hydrodynamic interactions that can not be neglected in real systems. From the experience gained in the description of viscosity of rigid and elongated micelles,11 we learned that for rigid systems β = 1 (cf.eqn (1)). For non-entangled hard-sphere systems we defined ξ in the following form:
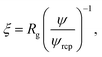 | (3) |
ϕrcp = 0.638 is the volume fraction at random close packing.
We fit 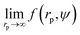 to the data of the macroscopic viscosity (rp → ∞; Reff → Rh) of mono-9,20,21 and polydisperse22 hard-sphere solutions, with a and b as free parameters. We found that for hard-sphere-like particles the average value of the exponent a = 1.29 ± 0.01 and we further used this value for all studied systems.
to the data of the macroscopic viscosity (rp → ∞; Reff → Rh) of mono-9,20,21 and polydisperse22 hard-sphere solutions, with a and b as free parameters. We found that for hard-sphere-like particles the average value of the exponent a = 1.29 ± 0.01 and we further used this value for all studied systems.
For the analysis of the self-diffusion data20 for hard-sphere solutions (rp = Rh) we used a and b obtained from the analysis of macroscopic viscosity. We obtained overestimated values of the D0/D ratio with respect to the relative macroscopic viscosity ηr of hard-sphere solutions (cf. Fig. S1†). We ascribed the discrepancy to the caging effect, similar to the depletion effect in polymer solutions.31–33 In both cases (caging and depletion) the spherical probe diffuses in the region confined by other spheres or polymer chains. This confinement influences the short- and long-time motion of the probe. The cage/depletion effect is correlated with the concentration of the particles/macromolecules constituting the media. In order to obtain the same relation between the relative viscosity and the self-diffusion coefficient, we introduced the concentration dependent term d into Reff (cf.eqn (4)). Fitting of f(rp, ψ) to the data for self-diffusion of the hard-sphere with fixed a and b gave:
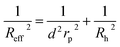 | (4) |
The parameter ϱ was fixed for all studied systems. We assumed that for proteins (similar as for hard-sphere) Rg = Rh(3/5)1/2 and we fit f(rp, ψ) to the macroscopic viscosity and self-diffusion data for protein solutions using as-obtained a and d and with b as a free parameter. We found that b differed between systems and for monodisperse hard-sphere solutions b = 6.2 ± 0.2 while for polydisperse hard-sphere solutions b = 4.771 ± 0.002. b differed also between the types of proteins and was equal to 22.9 ± 0.4, 50 ± 2, and 9.3 ± 0.1 for BSA, LYS, and MGB, respectively. In Fig. 1 we showed scaling plots for all analysed data of viscosity and of diffusion coefficients. Data for the macroscopic viscosity of mono- and polydisperse hard-sphere and protein solutions, as well as for self-diffusion in those systems fell on the master curve defined by eqn (1)–(4) with common parameters a and d and with the system dependent parameter b.
 | ||
| Fig. 1 Scaling plot of the relative viscosity and the reciprocal of the relative diffusion coefficient. (a) shows literature9,20–22 and experimental data for macroscopic viscous flow. The graph shows the data for monodisperse PMMA and SiO2 (Rh = 244 nm) particles,9,20,21 polydisperse SiO2 particles,22 and proteins. Data cover a range of volume fractions from ϕ = 10−3 to ϕ = 0.52. The data follow one master curve given by eqn (1) to (4) with b = 6.2 ± 0.2. (b) shows data for the self-diffusion of PMMA particles (rp = 247 nm),20 and for proteins: bovine serum albumin (BSA, rp = 4 nm),23 myoglobin (MGB, rp = 2.4 nm),23 and lysozyme (LYS, rp = 1.9 nm). | ||
We tested the quality of our scaling formula based on ψ-dependence by comparing it with the analogical model based on ϕ-dependence. The quality of both models can be compared in Fig. S2.†
The scaling law for non-entangled complex fluids (eqn (1)–(4)) exhibited a compressed34 exponential character (exponent a > 1). Analysis of a obtained for hard-sphere systems and for polymer systems11 showed correlation of a with the Rh/Rg ratio. For hard-sphere a = 1.29 ± 0.01, while for polymer systems: a = 0.62 ± 0.02 for polyethylene glycol, and a = 0.71 ± 0.1 for polystyrene.11 To compare, the values of Rh/Rg ratios were equal to: 1.29, 0.61, and 0.75 for: hard-sphere,35 polyethylene glycol,11 and polystyrene,11,36 respectively. The compressed exponential dependence of the macroscopic viscosity of hard-sphere solutions on the concentration was also in agreement with previous Phillies' reports.37
3 Influence of electrostatic repulsion on the transport properties
Results of our previous work14 suggested that b depended on the interactions between particles forming the fluid. We verified this hypothesis and we analysed the data for viscosity of sterically stabilized charged-sphere solutions differing in the ionic strength and in the pH of the solutions.19 We fitted the data with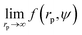 and we found that for charged-sphere solutions b depended on the surface potential ζ of the colloidal particles as:
and we found that for charged-sphere solutions b depended on the surface potential ζ of the colloidal particles as: | (5) |
 | ||
Fig. 2 The plot of the relative viscosity as a function of scaled concentration ψ/ψrcp. In plot (a) we fit  to the macroscopic viscosity data of charged particles19 for different ionic concentrations ci. The inset shows exponential dependence of b on the Debye's screening length κ−1 to Rh ratio. In the inset the solid line corresponds to the function b = (12 ± 1) exp[(1.3 ± 0.2)κ−1/Rh] and the shaded area corresponds to the standard deviation of the fitting parameters. In panel (b) we fit to the macroscopic viscosity data of charged particles19 for different ionic concentrations ci. The inset shows exponential dependence of b on the Debye's screening length κ−1 to Rh ratio. In the inset the solid line corresponds to the function b = (12 ± 1) exp[(1.3 ± 0.2)κ−1/Rh] and the shaded area corresponds to the standard deviation of the fitting parameters. In panel (b) we fit  to the macroscopic viscosity data of charged particles19 for different pH. The inset shows that, at the analysed pH range, b increases with ζ-potential of the particles. to the macroscopic viscosity data of charged particles19 for different pH. The inset shows that, at the analysed pH range, b increases with ζ-potential of the particles. | ||
For monodisperse systems (hard-sphere, charged-sphere, and protein solutions) the lowest value of b = 6.2 ± 0.2 and corresponded to the hard-sphere solutions while the highest, b = 81 ± 2, corresponded to the solution of charged-sphere with low ionic strength where κ−1 ≈ Rh. The only type of intermolecular interactions expected in the hard-sphere system were steric repulsion and hydrodynamic interactions. In the case of charged-sphere systems also attractive (van der Waals) and repulsive electrostatic interactions were present leading to an increase in b values with decreasing ionic strength of the solution.
Interactions between particles forming the solution contribute to the excess activation energy for viscous flow14 defined as:
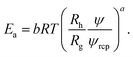 | (6) |
Concentration independent activation energy is then given by Êa = Eaψ−a = ÊHS + ÊvdW + Êε where ÊHS, stands for energy contribution from the steric and hydrodynamic interactions present in the hard-sphere system. ÊvdW and Êε denote contributions to the energy from the van der Waals and electrostatic interactions, respectively. At room temperature ÊHS = 10.3 kJ mol−1. For screened charged-sphere, when κ−1 → 0, Êa ≈ 19.9 kJ mol−1, where approximately 50% of this value originates from the van der Waals interactions, ÊvdW = Êa − ÊHS. For the system of charged-spheres, where κ−1 ≈ Rh, Êa ≈ 73 kJ mol−1 and the contribution of around 53 kJ mol−1 comes from Êε = Êa − (ÊHS + ÊvdW). For the solutions of proteins, an additional contribution to the Êa should be included due to the presence of the so called hydrophobic interactions. It is clearly visible for BSA solutions where b = 22.9 ± 0.4. At pH = 4.7 BSA is slightly charged (the surface potential ζ ≈ 4 mV). In the solution with ionic strength Is = 154 mM the screening length κ−1 = 0.78 nm. Using eqn (5), one can predict that for BSA b ≈ 15 at the above conditions.
From all the systems the lowest value of b was obtained for polydisperse hard-sphere solutions. In that case b was lower by around 23% than for the monodisperse hard-sphere solutions. This was consistent with previous reports where increasing polydispersity of particles decreased the viscosity of the solution.38
4 Transport properties of highly concentrated solutions
Calculation of the hard-sphere crystal nucleation rate requires the probability of nucleation and the kinetic prefactor that depends on the diffusion coefficient of hard-spheres in a given suspension. In the liquid metastable region (ϕ > 0.52), where nucleation takes place, there is a sudden increase in the viscosity, η, of the suspension.9 The analogical sudden change of the diffusion coefficient of particles D occurs at (ϕ > 0.55)39 implying that in the liquid metastable region D can not be calculated directly from D(η−1) dependence provided by the Stokes–Sutherland–Einstein relation.As we showed in preceding sections, eqn (1)–(4) provided a unified description of both viscosity and self-diffusion in the range of volume fractions not exceeding ϕ = 0.52. We also extended the applicability of the Stokes–Sutherland–Einstein relation for highly concentrated solutions as η/η0 = D/D0 = f(rp). We further used this equation to analyse the transport properties of hard-sphere solutions at ϕ > 0.52 obtaining a unified phenomenological description of transport in a liquid and metastable liquid phase (other approaches are shown in the ESI†).
Data for viscosity of hard-sphere solutions at ϕ > 0.52, when plotted against b (Reff/ξ)a, exhibit a sudden increase of the slope (from 1 at ϕ < 0.52 to 3.4 ϕ > 0.52); cf.Fig. 3. Fitting of those data revealed that above ϕ ≈ 0.52 the scaling formula was given by eqn (7)
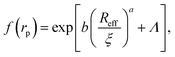 | (7) |
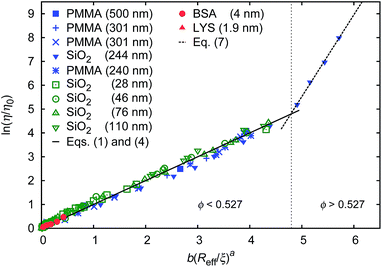 | ||
| Fig. 3 Scaling plot of the relative viscosity and the reciprocal of the relative diffusion coefficient. The figure shows literature9,20–22 and experimental data for macroscopic viscous flow. The graph shows the data for monodisperse PMMA and SiO2 (Rh = 244 nm) particles,9,20,21 polydisperse SiO2 particles,22 and proteins. Data cover a range of volume fractions from ϕ = 10−3 to ϕ = 0.56. The vertical dashed line corresponds to the volume fraction ϕ = 0.527. For SiO2 particles (Rh = 244 nm) at ϕ < 0.52 (the liquid region) the data follow one master curve given by eqn (1) to (4) with b = 6.2 ± 0.2. At ϕ > 0.52 (the metastable region where crystallization occurs) data corresponding to SiO2 particles (Rh = 244 nm)9 follow a master curve given by eqn (7) with b = 21 ± 1 and Λ = −11.7 ± 0.6. | ||
5 Influence of the transport properties on the crystal nucleation rate
f(rp) obtained for hard-sphere solutions in previous sections was used to predict the rates of nucleation I of hard-sphere crystals. In experimental studies the nucleation rate is usually expressed in its reduced, dimensionless form defined as: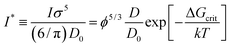 | (8) |
To calculate I* we used values of ΔGcrit/kT calculated in ref. 7 and 4, via the umbrella sampling method, at the volume fractions ϕ = 0.5207, 0.5277, and 0.5342 (ref. 7) and ϕ = 0.526, 0.535, and 0.538 (ref. 4). Those volume fractions were below ϕ = 0.548 (cf. Fig. S3a†), so to calculate the diffusion constants we used eqn (1)–(4) with parameters obtained from fitting of 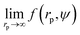 to the data of macroscopic viscosity and diffusion at ϕ < 0.527. Note that for systems where ϕ > 0.548 eqn (7) instead of eqn (1)–(4) should be used to calculate D/D0 and I*. We compared as-predicted I* with corresponding simulation results,4,7 and with experimental data2,40 (Fig. 4). We also compared the data with the nucleation rates obtained from molecular dynamic simulations performed by Filion et al.8 All simulation data presented in Fig. 4 are expressed in the units of the free diffusion as defined by eqn (8). Namely the simulation data of Filion et al.,4 originally expressed in the units of the short-time diffusion coefficient DS (Iσ5/DS), were divided by 6/π, and next multiplied by eqn (S2)† describing the relative short-time diffusion in hard-sphere solution. The same procedure was performed for the data obtained via molecular dynamics by Filion et al.8 who expressed all their results for I in terms of the long-time diffusion coefficient DL (Iσ5/DL). The data taken from Filion's work,8 then, were multiplied by the ratio DL/D0 represented by eqn (S3)† which was originally used by the authors to calculate DL.8 Simulation data4,7,8 and our predicted values of I* followed the experimental data of Harland and van Megen. Although the simulation data got uncertainty of up to 2 orders of magnitude making them in agreement with experiments, the values were systematically higher than the experimental results having uncertainty lower than 0.5 of the order of magnitude. Note that the predicted values of I* obtained with the method used in this work reproduced the experimental data very well as presented in Fig. 4. The presented method required the values of the nucleation barrier for which the accuracy of calculation was of the order of 1 kT (cf. corresponding figures in ref. 4 and 7), leading to a 100% of error for P. This value was higher than the uncertainty for the calculated relative diffusion coefficient (up to 81% for the highest volume fractions). Even so the maximum error for the prediction of log10(I*) was at the level of Δlog10(I*) = 0.56. Additionally the uncertainty of volume fraction4 (Δϕ = 0.005) was included in the calculation of Δlog10 (I*). The change was at the fourth meaning place and therefore was neglected.
to the data of macroscopic viscosity and diffusion at ϕ < 0.527. Note that for systems where ϕ > 0.548 eqn (7) instead of eqn (1)–(4) should be used to calculate D/D0 and I*. We compared as-predicted I* with corresponding simulation results,4,7 and with experimental data2,40 (Fig. 4). We also compared the data with the nucleation rates obtained from molecular dynamic simulations performed by Filion et al.8 All simulation data presented in Fig. 4 are expressed in the units of the free diffusion as defined by eqn (8). Namely the simulation data of Filion et al.,4 originally expressed in the units of the short-time diffusion coefficient DS (Iσ5/DS), were divided by 6/π, and next multiplied by eqn (S2)† describing the relative short-time diffusion in hard-sphere solution. The same procedure was performed for the data obtained via molecular dynamics by Filion et al.8 who expressed all their results for I in terms of the long-time diffusion coefficient DL (Iσ5/DL). The data taken from Filion's work,8 then, were multiplied by the ratio DL/D0 represented by eqn (S3)† which was originally used by the authors to calculate DL.8 Simulation data4,7,8 and our predicted values of I* followed the experimental data of Harland and van Megen. Although the simulation data got uncertainty of up to 2 orders of magnitude making them in agreement with experiments, the values were systematically higher than the experimental results having uncertainty lower than 0.5 of the order of magnitude. Note that the predicted values of I* obtained with the method used in this work reproduced the experimental data very well as presented in Fig. 4. The presented method required the values of the nucleation barrier for which the accuracy of calculation was of the order of 1 kT (cf. corresponding figures in ref. 4 and 7), leading to a 100% of error for P. This value was higher than the uncertainty for the calculated relative diffusion coefficient (up to 81% for the highest volume fractions). Even so the maximum error for the prediction of log10(I*) was at the level of Δlog10(I*) = 0.56. Additionally the uncertainty of volume fraction4 (Δϕ = 0.005) was included in the calculation of Δlog10 (I*). The change was at the fourth meaning place and therefore was neglected.
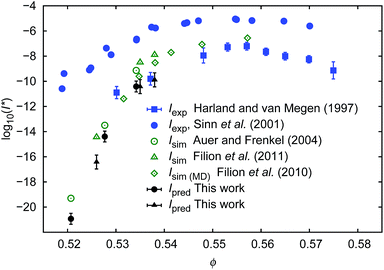 | ||
| Fig. 4 Comparison of the nucleation rates I* = ϕ5/3D/D0P. P = exp[−ΔGcrit/kT] where ΔGcrit is the free energy barrier for the formation of the critical nucleus, taken from literature.4,7Ipred – values predicted in this work; Iexp values obtained experimentally2,40; Isim – values obtained from simulations.4,7,8 To calculate Ipred marked as ● we used ΔGcrit, the same as in simulation results, Isim marked as ○. Analogically to calculate Ipred (▲) we used ΔG from simulation results of Isim marked as Δ. | ||
Our predictions were consistent (to the error bars) with simulation data while both were in disagreement with the experimental data of Sinn et al.40 or of Schatzel et al.1 The reason for this was convincingly described by Russo and co-workers41 and was dedicated to the influence of gravity on the experiments. Shortly, in the gravity unaffected experiments, the time τs, needed for a particle of radius Rh to sediment over the distance σ = 2Rh, was approximately 140 times longer than the time τB, needed for the particle to diffuse over the same distance (for details see also (ref. 41)). In the gravity affected systems (usually where the densities of the hard-sphere particles and of the solvent are not matched) the τs/τB ratios equal to 4.1 (ref. 40) and 2.9.1 Therefore the nucleation rate of the hard-sphere crystal can be significantly increased by the gravitational force acting on the suspended particles leading to the density gradients. This implies a slower transport of particles towards the nuclei in a denser region of the sample. The density gradients at the level of 4% of volume fraction (from 0.52 to 0.56) along the distance of 20 diameters of the particle reduce the diffusion coefficient of the particles by a factor of 36, but also significantly decrease ΔG and change P.
The method of the prediction of the nucleation rates, presented in this work, required the data of the nucleation barrier ΔGcrit obtained via the umbrella sampling method as described in the literature.3,4,7,8 We also calculated the nucleation rates using the classical nucleation theory (CNT; details of calculations and results are shown in the ESI†). It appeared that above ϕ = 0.535 I* calculated from eqn (8) with −ΔGcrit/kT given by eqn (S4)† gave overestimated values. We supposed that for ϕ > 0.535 CNT does not predict ΔG correctly which was also notified by Auer and Frenkel.3
6 Conclusions
The transport properties (long-time self-diffusion and the macroscopic viscosity) of colloids and of protein solutions are described by a phenomenological formula given by eqn (1)–(4). The formula depends on well defined and measurable variables like hydrodynamic radius of the particles or the volume fraction. Validity of the scaling formula in non-entangled complex fluids like colloidal suspensions (primarily used for entangled complex fluids, e.g. polymer solutions) extends its applicability and suggests a universal character.In the scaling formula there is only one free parameter b which is related to the interactions between particles forming the complex fluid. Parameters a and ϱ are the same, for all non-entangled systems, and can be treated as fixed constants. We note, however, that a ∝ Rh/Rg which, in turn, can be easily measured42 or calculated11,16,35 for any (not only hard sphere-like) system. To the best of our knowledge this is the first time that the stretching (or compressing) exponent a, when used with respect to the description of transport properties, can be strictly defined by means of parameters with a well defined physical meaning.
From the macroscopic viscosity of the hard-sphere solution we calculated the diffusion coefficient of spheres (eqn (1–4, 7)) and we used it to predict the nucleation rate of hard-sphere crystal formation. The predictions were made on the basis of both: the calculated diffusion coefficients and the probability of critical nuclei formation taken from simulation studies (ref. 7 and 4). For the volume fractions where experimental data on nucleation rates were available (ϕ > 0.53), our predictions agreed very well with experimental data and with the statistical error with simulation results.4,7,8 Interestingly reasonable results were obtained only when the scaling equation was combined with the simulation results for the nucleation barrier.4,7 When the scaling formula was combined with the calculations of the barrier as described by Sinn et al.,40 the obtained nucleation rates were overestimated for volume fractions exceeding 0.535.
There is a debate in the community about factors influencing the crystal nucleation rate.3,4,41 One of the suggested reasons is gravity that increases the nucleation rates by at least two orders of magnitude.41 The other factor proposed by Radu and Schilling is the viscosity of the solvent.43
In our work we offer a relatively simple tool and a handful of tips on how to predict the crystal nucleation rates for hard-sphere and other colloidal solutions. Predictions of the crystal nucleation rates for charged systems (charged colloids or proteins) would require similar analysis of the transport properties in the liquid–solid coexistence region (eqn (7)) as we performed for the hard-sphere system (cf.Fig. 1(a)). We believe that such studies would be beneficial for better understanding of the protein crystallization phenomenon.
Acknowledgements
T.K. thanks the Polish National Science Centre for funding under the contract DEC1-2011/01/N/ST3/00865. K.S. acknowledges financial support of the Polish Ministry of Science and Higher Education within the Diamond Grant program DI2011 015341. R.H., A.W., and K.K. thank the National Science Center for funding the project from the funds granted on the basis of the decision number: 2011/02/A/ST3/00143 (Maestro grant). S.J. acknowledges financial support from the Polish Ministry of Science and Higher Education under the grant Iuventus Plus – IP2012 015172. E.K. thanks the Polish National Science Centre for funding under the contract DEC-2011/01/N/ST5/02920. S.H. and R.H. acknowledge the collaboration with the State Key Laboratory of Medicinal Chemical Biology, Nankai University, Tianjin, China within the Grant no. 20130301.References
- K. Schätzel and B. J. Ackerson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3766 CrossRef.
- J. L. Harland and W. van Megen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3054 CrossRef CAS.
- S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023 CrossRef CAS PubMed.
- L. Filion, R. Ni, D. Frenkel and M. Dijkstra, J. Chem. Phys., 2011, 134, 134901 CrossRef CAS PubMed.
- J. Duijneveldt and H. Lekkerkerker, in Science and Technology of Crystal Growth, ed. J. Eerden and O. Bruinsma, Springer, Netherlands, 1995, pp. 279–290 Search PubMed.
- T. Palberg, Curr. Opin. Colloid Interface Sci., 1997, 2, 607–614 CrossRef CAS.
- S. Auer and D. Frenkel, J. Chem. Phys., 2004, 120, 3015–3029 CrossRef CAS PubMed.
- L. Filion, M. Hermes, R. Ni and M. Dijkstra, J. Chem. Phys., 2010, 133, 244115 CrossRef CAS PubMed.
- Z. Cheng, J. Zhu, P. M. Chaikin, S.-E. Phan and W. B. Russel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041405 CrossRef.
- R. Holyst, A. Bielejewska, J. Szymański, A. Wilk, A. Patkowski, J. Gapiński, A. Żywociński, T. Kalwarczyk, E. Kalwarczyk and M. Tabaka, et al. , Phys. Chem. Chem. Phys., 2009, 11, 9025–9032 RSC.
- T. Kalwarczyk, N. Ziebacz, A. Bielejewska, E. Zaboklicka, K. Koynov, J. Szymanski, A. Wilk, A. Patkowski, J. Gapinski, H. J. Butt and R. Holyst, Nano Lett., 2011, 11, 2157–2163 CrossRef CAS PubMed.
- W. Sutherland, Philos. Mag. A, 1905, 9, 781–785 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 17, 549 CrossRef CAS.
- K. Sozanski, A. Wisniewska, T. Kalwarczyk and R. Holyst, Phys. Rev. Lett., 2013, 111, 228301 CrossRef.
- M. Tabaka, L. Sun, T. Kalwarczyk and R. Holyst, Soft Matter, 2013, 9, 4386–4389 RSC.
- T. Kalwarczyk, M. Tabaka and R. Hołyst, Bioinformatics, 2012, 28, 2971–2978 CrossRef CAS PubMed.
- M. Tabaka, T. Kalwarczyk and R. Hoyst, Nucleic Acids Res., 2013, 42, 727–738 CrossRef PubMed.
- F. Booth, Proc. R. Soc. London, Ser. A, 1950, 203, 533–551 CrossRef CAS.
- J. Stone-Masui and A. Watillon, J. Colloid Interface Sci., 1968, 28, 187–202 CrossRef CAS.
- P. N. Segre, S. P. Meeker, P. N. Pusey and W. C. K. Poon, Phys. Rev. Lett., 1995, 75, 958 CrossRef CAS.
- S. P. Meeker, W. C. K. Poon and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 5718 CrossRef CAS.
- J. C. Van der Werff and C. De Kruif, J. Rheol., 1989, 33, 421 CrossRef CAS.
- I. V. Nesmelova, V. D. Skirda and V. D. Fedotov, Biopolymers, 2002, 63, 132–140 CrossRef CAS PubMed.
- A. Einstein, Ann. Phys., 1906, 19, 289 CrossRef CAS.
- A. Einstein, Ann. Phys., 1911, 34, 591 CrossRef CAS.
- D. O. Riese, G. H. Wegdam, W. L. Vos, R. Sprik, D. Fenistein, J. H. H. Bongaerts and G. Grübel, Phys. Rev. Lett., 2000, 85, 5460 CrossRef CAS.
- N. Saitô, J. Phys. Soc. Jpn., 1952, 7, 447–450 CrossRef.
- C. Beenakker, Phys. A, 1984, 128, 48–81 CrossRef.
- H. Clercx and P. Schram, Phys. Rev. A: At., Mol., Opt. Phys.Phys. Rev. A, 1992, 45, 860 CrossRef CAS.
- G. L. Hunter and E. R. Weeks, Rep. Prog. Phys., 2012, 75, 066501 CrossRef PubMed.
- N. Ziebacz, S. A. Wieczorek, T. Kalwarczyk, M. Fialkowski and R. Holyst, Soft Matter, 2011, 7, 7181–7186 RSC.
- S. Hou, N. Ziebacz, T. Kalwarczyk, T. S. Kaminski, S. A. Wieczorek and R. Holyst, Soft Matter, 2011, 7, 3092–3099 RSC.
- A. Ochab-Marcinek, S. A. Wieczorek, N. Ziebacz and R. Holyst, Soft Matter, 2012, 8, 11173–11179 RSC.
- E. W. Hansen, X. Gong and Q. Chen, Macromol. Chem. Phys., 2013, 214, 844–852 CrossRef CAS.
- B. Hammouda, J. Appl. Crystallogr., 2010, 43, 716–719 CrossRef CAS.
- T. Cherdhirankorn, A. Best, K. Koynov, K. Peneva, K. Muellen and G. Fytas, J. Phys. Chem. B, 2009, 113, 3355–3359 CrossRef CAS PubMed.
- G. D. Phillies, J. Colloid Interface Sci., 2002, 248, 528–529 CrossRef CAS PubMed.
- S. G. Ward and R. L. Whitmore, Br. J. Appl. Phys., 1950, 1, 286–290 CrossRef.
- L. V. Woodcock, Ann. N. Y. Acad. Sci., 1981, 371, 274–298 CrossRef CAS PubMed.
- C. Sinn, A. Heymann, A. Stipp and T. Palberg, in Trends in Colloid and Interface Science XV, Springer, 2001, pp. 266–275 Search PubMed.
- J. Russo, A. C. Maggs, D. Bonn and H. Tanaka, Soft Matter, 2013, 9, 7369–7383 RSC.
- K. Devanand and J. Selser, Macromolecules, 1991, 24, 5943–5947 CrossRef CAS.
- M. Radu and T. Schilling, arXiv preprint arXiv:1301.5592, 2013.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and some analysis details. See DOI: 10.1039/c4nr00647j |
| This journal is © The Royal Society of Chemistry 2014 |