A distinct atomic structure–catalytic activity relationship in 3–10 nm supported Au particles†
Valeri
Petkov
*a,
Yang
Ren
b,
Shiyao
Shan
c,
Jin
Luo
c and
Chuan-Jian
Zhong
c
aDepartment of Physics, Central Michigan University, Mt. Pleasant, Michigan 48859, USA. E-mail: petko1vg@cmich.edu; Fax: +1 989 774 2697; Tel: +1 989 774 3395
bX-ray Science Division, Advanced Photon Source, Argonne National Laboratory, Argonne, Illinois 60439, USA. E-mail: yren@anl.gov; Fax: +1 630-252-0365; Tel: +1 630-252-8651
cDepartment of Chemistry, State University of New York at Binghamton, New York 13902, USA. E-mail: cjzhong@binghamton.edu; Fax: +1 607-777-4478; Tel: +1 607-777-4605
First published on 25th October 2013
Abstract
Bulk Au is very inert but Au nanoparticles less than 5 nm in size have been found to be catalytically active for several reactions, in particular for low-temperature oxidation of CO. Using high-energy X-ray diffraction coupled with atomic pair distribution function analysis and computer simulations we determine the structure of 3 nm and 10 nm Au particles supported on titania and silica as typical representatives of reducible and irreducible supports, respectively. We find that the synthesis protocol adopted in our work affects strongly and differently the structure of the Au nanoparticles on the different supports. This leads to clearly distinct dependences of the catalytic activity of the nanoparticles on their size. In the case of the silica support the catalytic activity of Au nanoparticles increases and in the case of the titania support it decreases with decreasing nanoparticle size. The experimental results are considered in terms of current theoretical predictions and found to be in good accord with them.
Introduction
The use of nanoparticles (NPs) in catalysis allows for a substantial contact between the nanoparticles' surface area and the surrounding gas or liquid phase thus ensuring an effective use of the catalysts. The increased surface area is, however, not the only reason for good catalytic activity. Particles confined to nanoscale dimensions may further increase the catalytic activity due to interactions with the support,1 induced atomic-level strain2,3 and the presence of particular atomic configurations at the NP surface.4 Preparation conditions may also have a profound effect on the NP catalytic activity.5–12 A typical example is Au. While bulk gold is very inert chemically supported Au NPs catalyze various reactions, in particular low-temperature oxidation of CO.13–15 An example is presented in Fig. 1. As can be seen in the figure, Au particles less than 5 nm in size show a very good catalytic activity. On the other hand, Au particles larger than 5 nm in size show low activity for oxidation of CO. The experimental observations triggered numerous studies aimed at understanding and so getting control over this nanoscale effect. Several explanations have been put forward including quantum size confinement effects,5,15–17 charge transfer to and from the support,18–20 presence of tensile strain2,21 and of low-coordinated atoms at the Au NP surface.5,22–24 In reality it is very likely that some of these factors act simultaneously22 rendering Au NP catalyzed oxidation of CO a very complex process. In our paper we concentrate on studying two of these factors, that is the influence of given preparation conditions and support type on the Au NP atomic-scale structure, in particular that in the vicinity of the NP surface, and, hence, on the dependence of the catalytic activity of Au NPs on their size. For that purpose we study 3 nm and 10 nm Au particles that, according to the data in Fig. 1, should show greatly enhanced and low activity for CO oxidation, respectively. The particles are supported on silica (SiO2) and titania (TiO2) as typical representatives of irreducible and reducible supports, respectively. We determine the atomic-scale structure of the NPs employing high-energy X-ray diffraction (XRD) coupled with atomic pair distribution function (PDF) analysis and computer simulations. We find clear structural differences between the Au/TiO2 and Au/SiO2 NPs of different sizes, in particular in the degree of atomic ordering, atomic-level strain and type of low-coordinated atoms at the NP surface. The structural differences translate into different dependences of the catalytic activity of Au/SiO2 and Au/TiO2 NPs on their size. We offer an explanation for the observed differences by comparing our results with current theoretical predictions. Note, by comparing structural results obtained by NP assembly-averaging experimental techniques, such as XRD, to NP assembly-averaged properties, such as catalytic activity, we put structure–property relationship exploration on the same footing. Furthermore, by generating structure models featuring NPs of real size, i.e. with a size of 3 nm and 10 nm, real shape (that is spherical in our case) and free surface, i.e. surface that has not been constrained to be necessarily made of regular atomic planes, we take into account the fact that real NPs less than 10 nm in size can show various structural characteristics.25 Thus we avoid the limitations of current theory5 and other experimental approaches26 that concentrate either on Au clusters of a few tens of atoms or on fairly small Au NPs that are terminated with a particular set of regular atomic planes. Nevertheless, our experimental results are in good accord with current theoretical predictions5,27 that a reasonable way to understand the catalytic activity of Au NPs is to relate it to the type and number of low-coordinated atoms at the NP surface.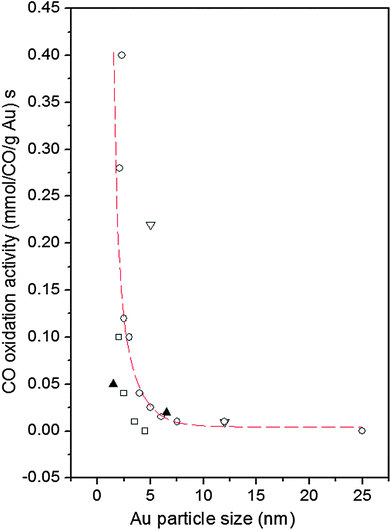 | ||
| Fig. 1 Reported catalytic activities of Au NPs for CO oxidation as a function of Au particle size. Data are taken at 0 °C. The supports are indicated as follows: down triangle – Fe2O3, square – Al2O3, up triangles – SiO2 and circles – TiO2. The broken line fitted to the data scales with the calculated number of atoms located at the corners (coordination number of six) of NPs with the shape of a truncated octahedron (adapted from ref. 5). | ||
Experimental
Sample preparation and characterization
The preparation of Au NPs involved the use of hydrogen tetrachloroaurate(III) hydrate (HAuCl4, 99%), decanethiol (DT, 96%), tetraoctylammonium bromide (TOABr, 99%) and sodium borohydride (99%). All chemicals were obtained from Aldrich. DT-capped gold NPs were synthesized using a standard two-phase protocol.28 Briefly, AuCl4− was first transferred from aqueous solution (10 mM) to toluene by TOABr (36 mM). DT was then added at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio of DT to Au, which was followed by addition of an excess (12 times) of aqueous NaBH4, producing a dark-brown solution of DT-capped Au NPs with a size of ∼2 nm. The solution was subjected to solvent removal in a rotary evaporator, followed by multiple cleaning steps using ethanol and acetone. Gold NPs of a larger size were obtained from the 2 nm sized Au particles by a thermally activated processing route, details of which are described in our previous reports.29–31 Briefly, a concentrated solution of the 2 nm sized Au particles was heated to a temperature of 140 °C, at which the NPs undergo desorption/redeposition, coalescence and aggregative growth in size. The resulting ∼7 nm sized Au particles were subjected to subsequent cleaning in ethanol to ensure a complete removal of the solvent and byproducts. After cleaning, the Au nanoparticles were suspended in hexane.
1 mole ratio of DT to Au, which was followed by addition of an excess (12 times) of aqueous NaBH4, producing a dark-brown solution of DT-capped Au NPs with a size of ∼2 nm. The solution was subjected to solvent removal in a rotary evaporator, followed by multiple cleaning steps using ethanol and acetone. Gold NPs of a larger size were obtained from the 2 nm sized Au particles by a thermally activated processing route, details of which are described in our previous reports.29–31 Briefly, a concentrated solution of the 2 nm sized Au particles was heated to a temperature of 140 °C, at which the NPs undergo desorption/redeposition, coalescence and aggregative growth in size. The resulting ∼7 nm sized Au particles were subjected to subsequent cleaning in ethanol to ensure a complete removal of the solvent and byproducts. After cleaning, the Au nanoparticles were suspended in hexane.
For the preparation of silica and titania supported NP catalysts, we employed a procedure involving suspension of a controlled amount of silica or titania in hexane solution containing a certain concentration of gold NPs overnight. The resulted powder was collected and dried under N2. More details of this preparation protocol are described in our previous report.32
The supported catalysts were further treated in a quartz tube furnace. In particular, the supported NPs were first heated at 260 °C in 15 vol.% O2 (oxidative atmosphere) for 30 min for removing their organic shells, and then treated at 400 °C in 15 vol.% H2 (reducing atmosphere) for 60 min. The weight loadings were about 5% for both silica and titania supported NPs. After the thermal treatment, the NP size increased further due to NP sintering. The actual size of the “smaller” and “larger” NPs was determined by TEM experiments described below. Note our synthesis protocol differs considerably from other reported protocols that are typically based on conventional co-precipitation or impregnation methods. For example, a typical conventional method for preparation of titania supported Au NPs involves an addition of an aqueous mixture of HAuCl4 and a nitrate of titania to an aqueous solution of Na2CO3. The co-precipitate is washed, dried under vacuum overnight and then calcined in air at 400 °C.33 A typical conventional method for preparation of silica supported Au NPs involves deposition–precipitation in a HAuCl4 solution containing gold at a controlled atomic ratio followed by calcination at 300 °C.33
The size and morphology of the Au NPs studied here were determined by transmission electron microscopy (TEM). For the TEM measurements the NP samples were diluted in hexane and drop cast onto carbon-coated copper grids followed by solvent evaporation in air at room temperature. TEM work was done at the Center for Advanced Microscopy, Michigan State University using a JEM-2200FS microscope operated at 200 kV. Fig. S1† shows a representative set of TEM images for the respective Au NPs. Based on the TEM data, the extra thermal treatments in oxidative and reducing atmospheres carried out as a part of our preparation method increased the size of as synthesized “smaller” particles from ∼2 nm to 3.4 ± 1.0 nm and that of the “larger” particles from ∼7 nm to 10 ± 2 nm. These thermally processed catalysts are labeled as “3 nm” and “10 nm” in this report. TEM data also showed that the 3 nm and 10 nm Au particles are largely spherical in shape.
Catalytic property measurements
The catalytic activity for CO oxidation was measured using a custom-built reaction system, which includes a temperature-controlled reactor, gas flow/mixing/injection controllers, an online gas chromatograph (Shimadzu GC 8A) equipped with 5 Å molecular sieve, Porapak Q packed columns and a thermal conductivity detector. The CO was 1 vol.% balanced by N2, O2 was 20 vol.% balanced by N2 and H2 was 15 vol.% balanced by N2. The catalytic data for the Au NPs on different supports are summarized in Table S1† in terms of T1/2 which is the temperature at which 50% CO conversion is achieved. Fig. S2† shows a representative set of CO conversion and oxidation rate data for Au/TiO2 catalysts. Fig. 2 shows turn over frequency (TOF) data for both Au/TiO2 and Au/SiO2 catalysts studied here. TOF data for Au/TiO2 NPs were obtained at 50 °C while that for Au/SiO2 NPs at 160 °C. The reason was that, in line with previous studies (e.g. see Fig. 1), Au/SiO2 NPs showed little to no activity at temperatures close to room temperature (see Table S1†). Also shown in Table S1† are T1/2 data for NPs that have been subjected to different types of post-synthesis thermal treatment, including freshly prepared NPs (i.e. NPs that have been O2–H2 treated followed by air exposure), O2-alone treated NPs and H2-alone treated samples. Significant dependence of the catalytic activity on the particular post-synthesis treatment is observed. The activity increases in the order of freshly prepared NPs < O2-treated NPs < H2-treated NPs. A similar result was reported recently for Au/SiO2 prepared by an impregnation method.34 In a previous report the H2-treated (500 °C) catalyst was found to exhibit a higher activity than the catalyst treated in He2 (500 °C)34 which in turn showed an activity better than that of the catalyst treated in O2 (500 °C). Therefore, we concentrated on the H2-treated Au NPs and compared their structural characteristics to the respective catalytic activity. The structural characteristics were obtained by high-energy XRD experiments coupled with atomic PDFs analysis and computer simulations described below.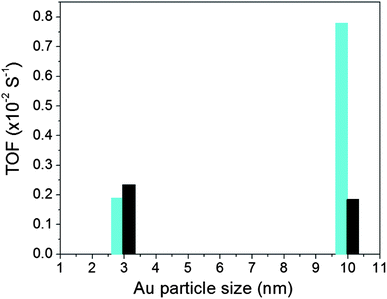 | ||
| Fig. 2 TOF for Au NPs supported on silica (bars in black) and titania (bars in cyan). Data for Au/TiO2 and Au/SiO2 NPs were taken at 50 °C and 160 °C, respectively. | ||
High-energy XRD experiments and atomic PDF derivation
High-energy XRD experiments were carried out at the 11-ID-C beamline of the Advanced Photon Source at the Argonne National Laboratory. All NPs were measured with X-rays of energy 115 keV (λ = 1080 Å). For the measurements the samples were put in glass capillaries. The respective XRD patterns are given in Fig. S3.† XRD data up to wavevectors of 25 Å−1 were collected and corrected for detector dead time, sample absorption and background scattering. The so-corrected XRD data were reduced to structure factors defined as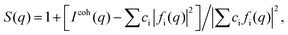 | (1) |
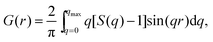 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ), 2θ is the angle between the incoming and outgoing X-rays and λ is the wavelength of the X-rays used. The so-derived atomic PDFs are shown in Fig. 3. High-energy XRD and atomic PDFs have already proven to be very efficient in studying the atomic-scale structure of nanosized materials, including metallic NPs.35,36
θ/λ), 2θ is the angle between the incoming and outgoing X-rays and λ is the wavelength of the X-rays used. The so-derived atomic PDFs are shown in Fig. 3. High-energy XRD and atomic PDFs have already proven to be very efficient in studying the atomic-scale structure of nanosized materials, including metallic NPs.35,36
Results and discussion
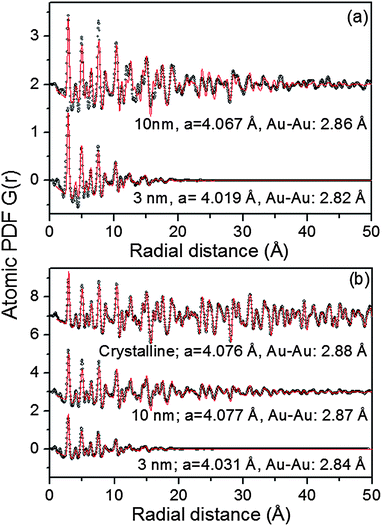
As can be seen in Fig. S3† the Au NPs studied here show rather diffuse XRD patterns, which is a picture typical for nanosized materials. The rather diffuse XRD patterns render traditional crystallography based structure analysis hardly applicable. As we36–40 and others35 have repeatedly shown the task is greatly simplified if not the diffuse XRD patterns but their Fourier transforms, the so-called atomic PDFs, are considered instead. In brief, the frequently used atomic PDF G(r) peaks at distances separating pairs of atoms while the areas under the PDF peaks are proportional to the number of atomic pairs at those distances. In this respect G(r) resembles the so-called Patterson function that is widely applied in traditional X-ray crystallography. However, while the Patterson function peaks at interatomic distances within the unit cell of a crystal, G(r) does not imply any lattice periodicity and so reflects all interatomic distances occurring in the studied material. This allows for a convenient testing and refining of structure models for finite size materials, such as 3 nm and 10 nm particles, whose structure may not necessarily be well described in terms of infinite periodic lattices used for their bulk counterparts.An inspection of the data in Fig. 3 shows that all experimental PDFs have well-defined peaks with distances of a few nm reflecting the presence of well-defined local atomic ordering. The peaks decay to zero faster than those in the PDF for a standard Au sample which extends to high interatomic distances as it should be with a polycrystalline material. The real space distance at which the NP PDFs decay to zero is commensurate to the so-called length of structural coherence. With the 3 nm and 10 nm particles studied here this length appears shorter than the respective NP size indicating the presence of substantial structural distortions. Such distortions are typical for NPs in the 10 nm size domain and are usually due to finite size and surface relaxation effects.
To gain a better insight into the NPs' structure we employed two distinct types of modeling approaches. At first the experimental PDF data were approached with models based on crystalline lattices. In this type of modeling a PDF for an infinite crystalline lattice is first computed. Then each of the coordination spheres of the perfect lattice is broadened by a convolution with a Gaussian function to take into account the presence of thermal (Debye–Waller type) and static local atomic displacements in NPs. At the same time the computed PDF is multiplied by a particle shape (spherical in our case) dependent function which is zero for distances longer than the size of the NPs being modeled. It is a simplistic approximation to the structure of real NPs but is useful since it allows us (i) to verify the type of their atomic ordering and (ii) to obtain a set of structural parameters (e.g., lattice parameters) that may be used to distinguish between different NPs. The calculations were done with the help of the program PDFgui.41 Data from literature sources for the face-centered cubic (fcc)-type lattice occurring with bulk Au were used as starting values in the NP structure modeling.
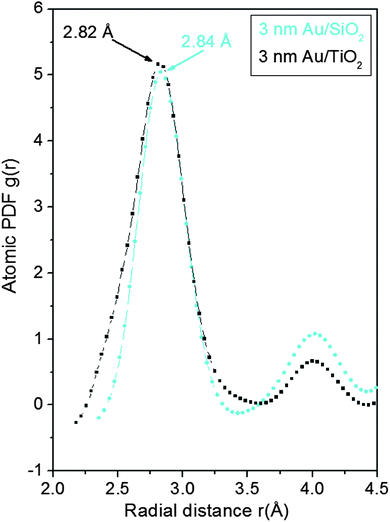
As can be seen in Fig. 3 the experimental atomic PDFs are reasonably well approximated by a model featuring a fcc-type atomic arrangement. The data for the fcc lattice parameters and for the first Au–Au neighbor distances extracted from the position of the first PDF peaks indicate a shrinking of the interatomic distances with diminishing NP size. In particular, the first Au–Au interatomic distance in titania supported Au NPs shrinks from 2.86 Å to 2.82 Å when the size of the particles diminishes from 10 nm to 3 nm. That distance changes from 2.87 Å to 2.84 Å in the case of silica supported NPs. For reference the first Au–Au neighbor distance in bulk Au is at about 2.88 Å. Comparing the shape of the experimental PDFs for Au/SiO2 and Au/TiO2 NPs reveals not only a different degree of shrinking of the interatomic distances but also a different degree of smearing of the respective PDF peaks. As the data in Fig. 4 show, the full width at half maximum (FWHM) of the first PDF peaks is different for the Au samples deposited on different supports. The FWHM is larger with the titania supported NPs indicating stronger NP–support interactions leading to a larger degree of structural distortions. Obviously, given the same preparation conditions, different supports interact differently with the Au NPs deposited on their surface and so the respective NP atomic-scale structures are modified to a different extent. To determine how exactly the underlying fcc-type structure is modified with the different NPs studied here we employed reverse Monte Carlo simulations42 that allow us to reveal structural features extending beyond a single unit cell of the fcc lattice.
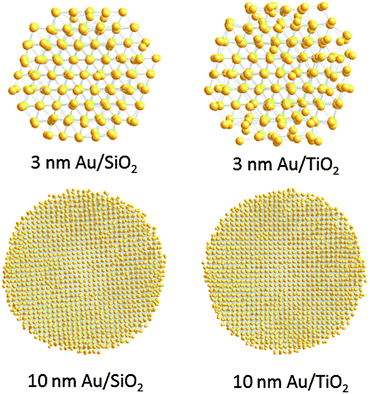
Finite size atomic configurations cut out of a perfect fcc lattice were used to start the reverse Monte Carlo simulations. The configurations were spherical in shape and with diameters of about 3 nm (∼1200 atoms) and 10 nm (∼31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) i.e. with a size and shape similar to those of the NPs studied here. In the simulations the position of each atom from the model atomic configurations was adjusted as to minimize the difference between the RMC model and experimental PDF data. Also, atoms were constrained (i) not to come closer than pre-selected distances of closest approach and (ii) to maintain as maximal (i.e. as close to 12) as possible coordination numbers. The first constraint reflects the fact that metal atoms in Au do not approach each other closer than the sum of the respective atomic radii. The second constraint takes into account the close packing nature of the fcc-type atomic ordering in the Au NPs studied here. At the same time the energy of the RMC configurations was optimized by minimizing pair-wise (Lenard-Jones type) potentials for Au taken from literature sources.43 The simulations were done with the help of a new version of the program RMC++44 expanding on our recent work.45,46 The reverse Monte Carlo simulations refined structure models are shown in Fig. 5. The atomic PDFs computed from them reproduce the experimental PDFs in very good detail as the data in Fig. S4† show. Several structural characteristics such as degree and distribution of the structural disorder across the Au NPs, bond angle distributions, etc. can be assessed from the RMC constructed model atomic configurations. Here we concentrated on assessing the type of atomic configurations, i.e. first coordination numbers (CNs), for the atoms at the NPs' top surface layer since it is this layer that is most important for catalytic reactions. Results are presented in Fig. 6. Surface atoms at the larger size, i.e. 10 nm, particles presumably have 8–9 first neighbors indicative of close packed, planar-type NP surfaces. With diminishing the NP size to 3 nm a substantial number of surface atoms with 7 and 6 first neighbors emerges indicating the appearance of a substantial number of edges/terraces and corners at the NP surface (see Fig. 1 in ref. 4 where the relationship between the geometry of surface atomic configurations and first atomic CNs is very clearly shown). With the 3 nm/TiO2 NPs, however, a substantial number of 3, 4 and 5-fold coordinated atoms also appears indicating surface atomic configurations characteristic for extremely sharp corners. The number of such atomic configurations with the 3 nm Au/SiO2 NPs is almost negligible (see Fig. 6). Theory predicts4,5,47 and experiment48,49 has shown that the catalytic activity of Au NPs for low-temperature oxidation of CO depends strongly on the presence of low-coordinated, in particular 7-fold (sitting on surface edges/terraces) and 6-fold (sitting on regular surface corners i.e. corners that are not extremely sharp) coordinated atoms. The reason is that atoms from closely packed atomic surfaces, i.e. atoms with first CN of 8 and 9, bind oxygen and CO very weakly (see Fig. 5a in ref. 4) resulting in almost negligible rates of the CO oxidation reaction. On the other hand, both the oxygen and CO absorption energies are lowered by almost 0.5 eV, corresponding to stronger binding, for surface atoms with CNs of 7 and 6 resulting in higher rates of the CO oxidation reaction. This may well explain our catalytic data for Au/SiO2 NPs. The number of 6 and 7-fold coordinated surface atoms in 3 nm silica supported particles is much larger than that in 10 nm particles (see Fig. 6) and so the former show an albeit moderately yet clearly higher CO oxidation rate than the latter (see Table S1† and Fig. 3). The situation with 3 nm titania supported Au particles is quite different. They have a substantial number of 3, 4 and 5-fold coordinated surface atoms at which the binding energies of oxygen and CO are lowered by ∼1 eV (see Fig. 5a in ref. 4) resulting in a considerably higher reactivity of those atoms. Too high a reactivity of surface atoms may impede the CO oxidation reaction by blocking the respective atomic sites with strongly absorbed reaction intermediates. Furthermore, 3 nm Au/TiO2 particles are under considerable compressive strain indicated by the shortest Au–Au distance of 2.82 Å among all other NPs studied here. Studies have shown that Au NP catalyzed CO oxidation is promoted by tensile and not compressive strain.2,50 This may give a plausible explanation of our catalytic data for 3 nm Au/TiO2 NPs. The presence of a substantial number of very low-coordinated (3, 4 and 5-fold coordinated), highly reactive surface atoms and the considerable compressive strain may impede the CO oxidation reaction masking the size dependence shown in Fig. 1. Furthermore, studies have shown that the CO oxidation reaction on titania supported Au NPs occurs at dual sites – sites at the NP surface and sites at the Au particle–TiO2 perimeter zone.51 Sites at the perimeter zone for Au NPs on irreducible supports like silica are not active, which may well explain the intrinsically lower catalytic activity of Au/SiO2 NPs compared to that of Au/TiO2 NPs (see Table S1† and Fig. 2). With quite a few atomic sites at the surface of 3 nm Au/TiO2 particles likely blocked what remains as a main driving force of the CO oxidation reaction are the sites at the TiO2–Au perimeter zone. Larger (i.e. 10 nm) Au NPs, though having a considerably smaller number of 6- and 7-fold coordinated surface atoms (see Fig. 6), may have a more significant contribution from the perimeter zone sites and so show higher, than in the case of 3 nm particles, rates of the CO oxidation reaction as our data in Fig. 2, Table S1 and Fig. S2† show.
000 atoms) i.e. with a size and shape similar to those of the NPs studied here. In the simulations the position of each atom from the model atomic configurations was adjusted as to minimize the difference between the RMC model and experimental PDF data. Also, atoms were constrained (i) not to come closer than pre-selected distances of closest approach and (ii) to maintain as maximal (i.e. as close to 12) as possible coordination numbers. The first constraint reflects the fact that metal atoms in Au do not approach each other closer than the sum of the respective atomic radii. The second constraint takes into account the close packing nature of the fcc-type atomic ordering in the Au NPs studied here. At the same time the energy of the RMC configurations was optimized by minimizing pair-wise (Lenard-Jones type) potentials for Au taken from literature sources.43 The simulations were done with the help of a new version of the program RMC++44 expanding on our recent work.45,46 The reverse Monte Carlo simulations refined structure models are shown in Fig. 5. The atomic PDFs computed from them reproduce the experimental PDFs in very good detail as the data in Fig. S4† show. Several structural characteristics such as degree and distribution of the structural disorder across the Au NPs, bond angle distributions, etc. can be assessed from the RMC constructed model atomic configurations. Here we concentrated on assessing the type of atomic configurations, i.e. first coordination numbers (CNs), for the atoms at the NPs' top surface layer since it is this layer that is most important for catalytic reactions. Results are presented in Fig. 6. Surface atoms at the larger size, i.e. 10 nm, particles presumably have 8–9 first neighbors indicative of close packed, planar-type NP surfaces. With diminishing the NP size to 3 nm a substantial number of surface atoms with 7 and 6 first neighbors emerges indicating the appearance of a substantial number of edges/terraces and corners at the NP surface (see Fig. 1 in ref. 4 where the relationship between the geometry of surface atomic configurations and first atomic CNs is very clearly shown). With the 3 nm/TiO2 NPs, however, a substantial number of 3, 4 and 5-fold coordinated atoms also appears indicating surface atomic configurations characteristic for extremely sharp corners. The number of such atomic configurations with the 3 nm Au/SiO2 NPs is almost negligible (see Fig. 6). Theory predicts4,5,47 and experiment48,49 has shown that the catalytic activity of Au NPs for low-temperature oxidation of CO depends strongly on the presence of low-coordinated, in particular 7-fold (sitting on surface edges/terraces) and 6-fold (sitting on regular surface corners i.e. corners that are not extremely sharp) coordinated atoms. The reason is that atoms from closely packed atomic surfaces, i.e. atoms with first CN of 8 and 9, bind oxygen and CO very weakly (see Fig. 5a in ref. 4) resulting in almost negligible rates of the CO oxidation reaction. On the other hand, both the oxygen and CO absorption energies are lowered by almost 0.5 eV, corresponding to stronger binding, for surface atoms with CNs of 7 and 6 resulting in higher rates of the CO oxidation reaction. This may well explain our catalytic data for Au/SiO2 NPs. The number of 6 and 7-fold coordinated surface atoms in 3 nm silica supported particles is much larger than that in 10 nm particles (see Fig. 6) and so the former show an albeit moderately yet clearly higher CO oxidation rate than the latter (see Table S1† and Fig. 3). The situation with 3 nm titania supported Au particles is quite different. They have a substantial number of 3, 4 and 5-fold coordinated surface atoms at which the binding energies of oxygen and CO are lowered by ∼1 eV (see Fig. 5a in ref. 4) resulting in a considerably higher reactivity of those atoms. Too high a reactivity of surface atoms may impede the CO oxidation reaction by blocking the respective atomic sites with strongly absorbed reaction intermediates. Furthermore, 3 nm Au/TiO2 particles are under considerable compressive strain indicated by the shortest Au–Au distance of 2.82 Å among all other NPs studied here. Studies have shown that Au NP catalyzed CO oxidation is promoted by tensile and not compressive strain.2,50 This may give a plausible explanation of our catalytic data for 3 nm Au/TiO2 NPs. The presence of a substantial number of very low-coordinated (3, 4 and 5-fold coordinated), highly reactive surface atoms and the considerable compressive strain may impede the CO oxidation reaction masking the size dependence shown in Fig. 1. Furthermore, studies have shown that the CO oxidation reaction on titania supported Au NPs occurs at dual sites – sites at the NP surface and sites at the Au particle–TiO2 perimeter zone.51 Sites at the perimeter zone for Au NPs on irreducible supports like silica are not active, which may well explain the intrinsically lower catalytic activity of Au/SiO2 NPs compared to that of Au/TiO2 NPs (see Table S1† and Fig. 2). With quite a few atomic sites at the surface of 3 nm Au/TiO2 particles likely blocked what remains as a main driving force of the CO oxidation reaction are the sites at the TiO2–Au perimeter zone. Larger (i.e. 10 nm) Au NPs, though having a considerably smaller number of 6- and 7-fold coordinated surface atoms (see Fig. 6), may have a more significant contribution from the perimeter zone sites and so show higher, than in the case of 3 nm particles, rates of the CO oxidation reaction as our data in Fig. 2, Table S1 and Fig. S2† show.
Conclusion
The obvious difference in molecular capping and in thermal treatment applied in our synthesis method from traditional co-precipitation or impregnation methods results in distinct dependences of the rate of low-temperature CO oxidation reaction on the size of Au/SiO2 and Au/TiO2 NPs. For Au/SiO2 NPs the catalytic activity increases with diminishing particle size in line with the previous findings. For Au/TiO2 NPs the catalytic activity diminishes with diminishing particle sizes (see Fig. 2) which is at odds with the previous findings (see Fig. 1). The reason for the odd behavior of Au/TiO2 NPs is very likely due to the fact that our synthesis method involves removal of the molecules capping the NP surface at rather high temperatures first in oxidizing and then in reducing atmospheres. This increases the Au NP–reducible titania support interactions as the experimental PDFs indicate (see Fig. 4) rendering Au particles less than 5 nm in size rather compressed, structurally disordered and with a significant number of very low-coordinated surface atoms, i.e. with a coarser surface that does not necessarily promote the low-temperature oxidation of CO. Indeed our recent studies showed that metallic particles 5 nm or less in size may undergo a substantial surface reconstruction when thermally treated consecutively in oxidizing and reducing atmospheres.52 This is very likely what we observe with 3 nm Au/TiO2 particles that show a reduced catalytic activity when compared to 10 nm Au/TiO2 particles. A much smaller degree of structural distortions is observed with 3 nm Au particles on SiO2 support and so they show a better catalytic activity for low-temperature CO oxidation than 10 nm Au/SiO2 NPs. The result demonstrates well the importance of synthesis details and support type in determining fine features in the atomic-scale structure of Au particles less than 10 nm in size and, hence, influencing their catalytic behavior. Note, the findings of our work, in particular the catalytic data in Fig. 2, would not have been possible to be given the plausible explanation put forward here without building realistic models for the studied Au NPs based on reverse Monte Carlo simulations guided by experimental atomic PDF data. The approach allows more precise determination of the NP atomic-scale structure, including the type and relative abundance of surface atomic sites in NPs (see Fig. 6), than the widely applied NP structure approximations based on preconceived polyhedra terminated with regular atomic planes. As such it deserves to be applied more often than now in catalysis research, in particular when more precise structural information for real NP catalysts is needed.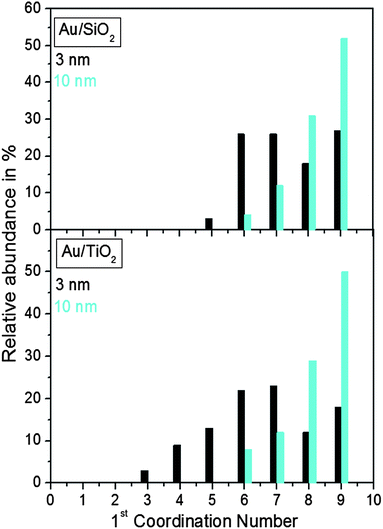 | ||
| Fig. 6 Distribution of the nearest atomic neighbors for the top surface layer of 3 nm and 10 nm Au particles supported on silica and titania. The distributions are extracted from the RMC constructed models shown in Fig. 5. | ||
Acknowledgements
This work was supported by DOE Grant no. DESC0006877. Work at APS is supported by the DOE under Contract no. DE-AC02-06CH11357.References
- M. M. Schubert, S. Hackenberger, A. C. van Veen, M. Muhler, V. Plak and R. J. Behm, J. Catal., 2001, 113, 197 Search PubMed.
- M. Mavrikakis, B. Hammer and J. K. Norskov, Phys. Rev. Lett., 1989, 81, 2819 CrossRef.
- Y. Hu and M. Mavrikakis, J. Phys. Chem. B, 2003, 107, 9298 CrossRef.
- T. Jiang, D. J. Mowbray, S. Dobrin, H. Falsig, B. Hvolbaek, T. Bligaard and J. K. Norskov, J. Phys. Chem. C, 2009, 113, 10548 CAS.
- B. Hvolbaek, T. V. W. Janssens, B. S. Clausen, H. Falsig, C. H. Christensen and J. K. Norskov, Nano Today, 2007, 2, 14 CrossRef.
- M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647 CrossRef CAS.
- G. C. Bond and D. T. Thompson, Catal. Rev.: Sci. Eng., 1999, 41, 319 CAS.
- R. J. H. Grissel and B. E. Nieuwenhuys, J. Catal., 2001, 99, 48 CrossRef.
- M. A. P. Dekkers, M. J. Lippits and B. E. Nieuwenhuys, Catal. Today, 1999, 54, 381 CrossRef CAS.
- S. Carretin, P. McMorn, P. Iohnston, K. Griffin, C. Kiely and G. I. Hutchings, Phys. Chem. Chem. Phys., 2003, 5, 1329 RSC.
- M. D. Hughes, Y.-J. Xu, P. Jenkins, P. McMorn, P. Landon, D. I. Enache, A. F. Carley, E. H. Stitt, P. Johnston, K. Griffin and C. Kiely, Nature, 2005, 437, 132 Search PubMed.
- P. Landon, P. J. Collier, A. J. Papworth, C. J. Kiely and G. Hutchings, Chem. Commun., 2002, 2058 RSC.
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 2, 405 CrossRef.
- M. Haruta, Chem. Rec., 2003, 3, 75 CrossRef CAS PubMed.
- M. Haruta, Catal. Today, 1997, 36, 153 CrossRef CAS.
- M. Valden, S. Pak, X. Lai and D. W. Goodman, Catal. Lett., 1998, 56, 7 CrossRef CAS.
- X. Lai and D. W. Goodman, J. Mol. Catal. A: Chem., 2000, 162, 33 CrossRef CAS.
- Z. Yang, R. Wu and D. W. Goodman, Phys. Rev. B, 2000, 61, 14066 CrossRef CAS.
- A. Sanchez, S. Abbet, U. Heiz, W.-D. Schneider, H. Häkkinen, R. N. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573 CrossRef CAS.
- J. A. van Bokhoven, C. Louis, C. J. T. Miller, M. Tromp, O. V. Safonova and P. Glatzel, Angew. Chem., Int. Ed., 2006, 45, 4651 CrossRef CAS PubMed.
- M. Mavrikakis, P. Stoltze and J. K. Nøskov, Catal. Lett., 2000, 64, 101 CrossRef CAS.
- T. V. W. Janssens, B. S. Clausen, B. Hvolbæk, H. Falsig, C. H. Christensen, T. Bligaard and J. K. Nørskov, Top. Catal., 2007, 44, 15 CrossRef CAS PubMed.
- N. Lopez and J. K. Nørskov, Surf. Sci., 2002, 515, 175 CrossRef CAS.
- R. Burch, Phys. Chem. Chem. Phys., 2006, 8, 5483 RSC.
- L. D. Marks, Rep. Prog. Phys., 1994, 57, 603 CrossRef CAS.
- A. Carlsson, A. Puig-Molina and T. V. W. Janssens, J. Phys. Chem., 2006, 110, 5286 CAS.
- N. Lopez, T. V. W. Janssens, B. S. Clausen, Y. Xu, M. Mavrikakis, T. Bligaard and J. K. Norskov, J. Catal., 2004, 223, 232 CrossRef CAS PubMed.
- M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. J. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801 RSC.
- M. M. Maye, W. X. Zheng, F. L. Leibowitz, N. K. Ly and C. J. Zhong, Langmuir, 2000, 16, 490 CrossRef CAS.
- M. M. Maye and C. J. Zhong, J. Mater. Chem., 2000, 10, 1895 RSC.
- M. J. Schadt, W. Cheung, J. Luo and C. J. Zhong, Chem. Mater., 2006, 18, 5147 CrossRef CAS.
- L. F. Yang, S. Y. Shan, R. Loukrakpam, V. Petkov, Y. Ren, B. N. Wanjala, M. H. Engelhard, J. Luo, J. Yin, Y. S. Chen and C. J. Zhong, J. Am. Chem. Soc., 2012, 134, 15048 CrossRef CAS PubMed.
- M. Haruta, S. Tsubota, T. Kobayashi, H. Kageyama, M. J. Genet and B. Delmon, J. Catal., 1993, 144, 175 CrossRef CAS.
- N. Bogdanchikova, A. Pestryakov, I. Tuzovskaya, T. A. Zepeda, M. H. Farias, H. Tiznado and O. Martynyuk, Fuel, 2013, 110, 40 CrossRef CAS PubMed.
- T. Egami and S. J. L. Billinge, Underneath the Braggs' Peaks, Pergamon/Amsterdam, Netherlands, 2003 Search PubMed.
- V. Petkov, Mater. Today, 2008, 11, 28 CrossRef CAS.
- Th. Proffen, V. Petkov, S. J. L. Billinge and T. Vogt, Z. Kristallogr., 2002, 217, 47 CrossRef CAS.
- V. Petkov, N. Bedford, M. R. Knecht, M. G. Weir, R. M. Crooks, W. Tang, G. Henkelman and A. Frenkel, J. Phys. Chem. C, 2008, 112, 8907 CAS.
- V. Petkov, L. Yang, J. Yin, R. Loukrakpam, S. Shan, B. Wanjala, J. Luo, K. W. Chapman and C. J. Zhong, Phys. Rev. Lett., 2012, 109, 125504 CrossRef CAS.
- X. Tuaev, S. Rudi, V. Petkov, A. Hoell and P. Strasser, ACS Nano, 2013, 7, 5666 CrossRef CAS PubMed.
- C. L. Farrow, P. Juhás, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, Th. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- R. L. McGreevy and L. A. Pusztai, Mol. Simul., 1998, 1, 359 CrossRef.
- H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, J. Phys. Chem. C, 2008, 112, 17281 CAS.
- O. Gereben, P. Jovari, L. Temleitner and L. Pusztai, J. Optoelectron. Adv. Mater., 2007, 9, 3021 CAS.
- M. Welborn, W. Tang, J. Ryu, R. M. Crooks, V. Petkov and G. Henkelman, J. Chem. Phys., 2011, 135, 014503 CrossRef PubMed.
- V. Petkov, I. Moreels, Z. Hens and Y. Ren, Phys. Rev. B, 2010, 81, 241304 CrossRef.
- N. Lopez and J. K. Norskov, J. Am. Chem. Soc., 2002, 124, 11262 CrossRef CAS PubMed.
- S. H. Overbury, V. Schwartz, D. R. Mullins, W. Yan and Sh. Dai, J. Catal., 2006, 241, 56 CrossRef CAS PubMed.
- G. Walter, D. J. Mowbray, T. Jiang, G. Jones, S. Jensen, U. Quaade and S. Horch, J. Catal., 2008, 280, 86 CrossRef PubMed.
- Y. Hu and M. Mavrikakis, J. Phys. Chem. B, 2003, 107, 9298 CrossRef.
- I. X. Green, W. Tang, M. Neurock and J. T. Yates, Jr, Science, 2011, 333, 736 CrossRef CAS PubMed.
- V. Petkov, S. Shan, P. Chupas, J. Yin, L. Yang, J. Luo and C. J. Zhong, Nanoscale, 2013, 5, 7379 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: XRD patterns, and TEM and catalytic activity data. See DOI: 10.1039/c3nr05362h |
| This journal is © The Royal Society of Chemistry 2014 |