Two magnetic phase transitions, driven by symmetry breaking and isostructural phase transitions, in a nickel-bis-dithiolene spin system†
Wei-Hua
Ning
ab,
Xuan-Rong
Chen
ab,
Jian-Lan
Liu
*ab,
Ping-Chun
Guo
ab and
Xiao-Ming
Ren
*abc
aState Key Laboratory of Materials-Oriented Chemical Engineering and College of Science, Nanjing University of Technology, Nanjing 210009, China. E-mail: xmren@njut.edu.cn; Fax: +86 25 58139481; Tel: +86 25 58139476
bCollege of Materials Science and Engineering, Nanjing University of Technology, Nanjing 210009, China
cCoordination Chemistry Institute & State Key Laboratory, Nanjing University, Nanjing 210093, China
First published on 11th October 2013
Abstract
A one-dimensional (1-D) magnetic chain compound, [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2], where (CD3)2C
N-Py][Ni(mnt)2], where (CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py+ = 1-(propan-d6-2-ylideneamino)pyridinium and mnt2− = maleonitriledithiolate, was synthesized and characterized. This compound undergoes two structural phase transitions, at around 267 K and 325 K. The three phases are sequentially labeled as α (below 267 K), β (between 267 and 325 K) and γ (above 325 K). The [Ni(mnt)2]− anions form irregular stacks, with two values of neighboring Ni⋯Ni distances. The cations align in a straight and regular arrangement along the crystallographic a-axis direction in the β phase. The asymmetric unit switches from one anion–cation pair to two anion–cation pairs in the transition from the β to the α phase. This leads to a doubling of the crystallographic axis length, parallel to the anion stack. It also results in the irregular anion stack showing three non-equivalent neighboring Ni⋯Ni distances, as well as making the straight cation arrangement irregular. The β and γ phases are isostructural and exhibit quite similar packing structures. The anion stack shrinks a little with increasing temperature, with all crystallographic axes showing small reduction from the β to γ phase. The two observed magnetic phase transitions are driven by these various structural phase transitions. A thermal hysteresis loop, with a separation of ∼8 K, appears in the transition between the β and α phases. However, this is absent in the transition between the β and γ phases. A dielectric anomaly appears across the phase transition between the β and γ phases but not between the β and α phases.
N-Py+ = 1-(propan-d6-2-ylideneamino)pyridinium and mnt2− = maleonitriledithiolate, was synthesized and characterized. This compound undergoes two structural phase transitions, at around 267 K and 325 K. The three phases are sequentially labeled as α (below 267 K), β (between 267 and 325 K) and γ (above 325 K). The [Ni(mnt)2]− anions form irregular stacks, with two values of neighboring Ni⋯Ni distances. The cations align in a straight and regular arrangement along the crystallographic a-axis direction in the β phase. The asymmetric unit switches from one anion–cation pair to two anion–cation pairs in the transition from the β to the α phase. This leads to a doubling of the crystallographic axis length, parallel to the anion stack. It also results in the irregular anion stack showing three non-equivalent neighboring Ni⋯Ni distances, as well as making the straight cation arrangement irregular. The β and γ phases are isostructural and exhibit quite similar packing structures. The anion stack shrinks a little with increasing temperature, with all crystallographic axes showing small reduction from the β to γ phase. The two observed magnetic phase transitions are driven by these various structural phase transitions. A thermal hysteresis loop, with a separation of ∼8 K, appears in the transition between the β and α phases. However, this is absent in the transition between the β and γ phases. A dielectric anomaly appears across the phase transition between the β and γ phases but not between the β and α phases.
Introduction
Phase transitions in materials occur widely in nature and can often impart functionality to the system, sometimes leading to important technological innovations. The physical properties of a material may change massively across a solid-to-solid phase transition.1–14 For example, vanadium dioxide VO2 undergoes a metal-to-insulator (MI) transition at 341 K and shows dramatic changes in electrical resistivity and infrared transmission across this phase transition.13,15 An organic molecular conductor, based on a spiro-biphenalenyl neutral radical, goes through a structural phase transition near room temperature and simultaneously exhibits bistability in three physical properties, electrical, optical and magnetic.12 As a consequence, materials that undergo fast, reversible, and especially hysteretic phase transitions can be very useful for applications such as switching devices.1–15Generally, a solid-to-solid phase transition is associated with a structural phase transition (SPT) accompanied by a change in its crystallographic structure across critical thermodynamic parameters (most often pressure and temperature). Among the huge number of materials exhibiting SPTs, symmetry breaking is often observed. In these cases, the crystallographic space group changes across the structural phase transition boundary. A typical example is the paraelectric–ferroelectric phase transition, where a crystal is non-polar in the paraelectric phase but polar in the ferroelectric phase.16–20 In fact, there are very few instances in which such a transition is accompanied by a change in neither the crystallographic space group nor the occupied Wyckoff positions. Such transitions have been categorized as “isostructural phase transitions” (IPTs), and have mostly been discovered by mineralogists while investigating minerals. Most IPT materials are characterized by framework structures or a large coordination environment around a cation21 under compression.
One example of these fascinating molecule architectures is the metal-bis-1,2-dithiolene mono-anion (denoted as [M(dithiolato)2]−, normally with M = Ni, Pd or Pt). This features a planar geometry, with a frontier orbital distribution over much, if not all, of the molecule. The negative charge is distributed over the anion skeleton. These features allow [M(dithiolato)2]− ions to form face-to-face one-dimensional (1-D) columnar stacks rather easily.22–24 The magnetic couplings between neighboring [M(dithiolato)2]− ions are extremely sensitive to subtle changes of the crystal packing. This is due to the unpaired electron delocalizing over the whole skeleton of the [M(dithiolato)2]− ion, and the magnetic coupling can be transmitted through non-bonded interatomic contacts, especially through sulfur atoms. As a result, the cell volume contraction or expansion resulting from temperature changes probably triggers a magnetostructural phase transition in such a [M(dithiolato)2]− magnetic system.25 In addition, the 1-D S = 1/2 magnetic system shows intrinsic magnetoelastic instability. This unique structural and magnetic nature leads to 1-D [M(dithiolato)2]− magnetic compounds, which are rich sources of magnetostructural phase transitions driven by a critical thermodynamic parameter (temperature or pressure).10,26
In previous studies, we prepared a series of 1-D compounds, consisting of 1-N-(4′-R-benzyl)pyridinium and bis(maleonitriledithiolato)nickelate monoanion (abbr. as [R-BzPy][Ni(mnt)2] where the substituent R = Cl, Br, I, NO2, CH3 or –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) H2). These compounds experience a symmetry breaking structural phase transition at a critical temperature in the 100–210 K range.6–9 The space group is monoclinic P2(1)/c with both anion and cation stacks arranged regularly in the high-temperature phase. This becomes triclinic P
H2). These compounds experience a symmetry breaking structural phase transition at a critical temperature in the 100–210 K range.6–9 The space group is monoclinic P2(1)/c with both anion and cation stacks arranged regularly in the high-temperature phase. This becomes triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , with both anion and cation stacks dimerized in the low-temperature phase. Meanwhile a spin-Peierls-type transition is accompanied by a symmetry breaking structural phase transition. Most recently, the deuterated analogues, [R-BzPy-d5][Ni(mnt)2] (R = Cl, Br, I, NO2 and CH3), were prepared utilizing pyridine-d5 instead of pyridine in the 1-N-(4-R-benzyl)pyridinium cations. [R-BzPy][Ni(mnt)2] and [R-BzPy-d5][Ni(mnt)2] are isostructural and the deuteration in the diamagnetic counter ion gives rise to diverse isotopic effects on the lattice and magnetic transitions; however, the exact mechanisms are not quite clear.27,28 Thus, more insight into the exact mechanism of the isotopic effect, from more studies and using other examples, is desirable.
, with both anion and cation stacks dimerized in the low-temperature phase. Meanwhile a spin-Peierls-type transition is accompanied by a symmetry breaking structural phase transition. Most recently, the deuterated analogues, [R-BzPy-d5][Ni(mnt)2] (R = Cl, Br, I, NO2 and CH3), were prepared utilizing pyridine-d5 instead of pyridine in the 1-N-(4-R-benzyl)pyridinium cations. [R-BzPy][Ni(mnt)2] and [R-BzPy-d5][Ni(mnt)2] are isostructural and the deuteration in the diamagnetic counter ion gives rise to diverse isotopic effects on the lattice and magnetic transitions; however, the exact mechanisms are not quite clear.27,28 Thus, more insight into the exact mechanism of the isotopic effect, from more studies and using other examples, is desirable.
To extend this area of research, we prepared the deuterated compound [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] where (CD3)2C
N-Py][Ni(mnt)2] where (CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py+ = 1-(propan-d6-2-ylideneamino)pyridinium, which is the analogue of the 1-D magnetic phase transition compound [(CH3)2C
N-Py+ = 1-(propan-d6-2-ylideneamino)pyridinium, which is the analogue of the 1-D magnetic phase transition compound [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2].29 We found that these two compounds show different magnetic and structural phase transitions. The deuterated compound [(CD3)2C
N-Py][Ni(mnt)2].29 We found that these two compounds show different magnetic and structural phase transitions. The deuterated compound [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] is a novel example of a compound showing two structural phase transitions in the temperature range 2–400 K. One of these is an isostructural phase transition and the other is a symmetry breaking structural phase transition. In addition, the two structural phase transitions are associated with a magnetic phase transition.
N-Py][Ni(mnt)2] is a novel example of a compound showing two structural phase transitions in the temperature range 2–400 K. One of these is an isostructural phase transition and the other is a symmetry breaking structural phase transition. In addition, the two structural phase transitions are associated with a magnetic phase transition.
Experimental section
Chemicals and materials
All reagents and chemicals were purchased from commercial sources and used without further purification.The starting materials for the preparation of 1, namely hydroxylamine-O-sulfonic acid,30,31 [N–NH2Py]I (where N–NH2Py+ represents 1-aminopyridinium),32 Na2mnt,33 [N–NH2Py]2[Ni(mnt)2] and [N–NH2Py][Ni(mnt)2]29 were synthesized according to literature procedures.
During evaporation of [N–NH2Py][Ni(mnt)2] solution in (CD3)2CO, [N–NH2Py]+ reacts with acetone-d6 to form [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py]+ (ref. Scheme 1). Single crystals of [(CD3)2C
N-Py]+ (ref. Scheme 1). Single crystals of [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] (1), suitable for X-ray diffraction structure analysis, were obtained at ambient temperature after 7–10 days. The acetone-d6 solution described above, containing 435 mg [N-NH2Py][Ni(mnt)2], gave 452 mg of crystals of 1, representing a yield of more than 94%.
N-Py][Ni(mnt)2] (1), suitable for X-ray diffraction structure analysis, were obtained at ambient temperature after 7–10 days. The acetone-d6 solution described above, containing 435 mg [N-NH2Py][Ni(mnt)2], gave 452 mg of crystals of 1, representing a yield of more than 94%.
 | ||
Scheme 1 Illustration of the formation of the Schiff base cation [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py]+via the reaction of [N–NH2Py]+ with acetone-d6. N-Py]+via the reaction of [N–NH2Py]+ with acetone-d6. | ||
Elemental microanalysis calculated for C16H5D6N6NiS4 (1): C, 40.01; H and D, 3.56; N, 17.50%. Found: C, 40.22; H and D, 3.18; N, 17.79%. IR spectrum (KBr pellet, cm−1) and the assignments for the listed bands: 3112(w), 3087(w) and 3066(w) are attributed to the νC–H of the pyridyl ring, 2208(vs) is assigned to the νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N of the mnt2− ligands, 1619(s) and 1608(w) are attributed to the νC
N of the mnt2− ligands, 1619(s) and 1608(w) are attributed to the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and νC
C and νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N of the pyridyl in the cation, respectively, 1475(s) is assigned to the νC
N of the pyridyl in the cation, respectively, 1475(s) is assigned to the νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of the mnt2− ligands and 1158(vs) and 1043(w) are attributed to νC–S + νC–C of the mnt2− ligands, respectively.
C of the mnt2− ligands and 1158(vs) and 1043(w) are attributed to νC–S + νC–C of the mnt2− ligands, respectively.
Physical measurements
Elemental analyses (C, H and N) were performed using an Elementar Vario EL III analyzer. The IR spectra at room temperature were recorded on a Bruker VERTEX80V Fourier transform infrared spectrometer (KBr disc) under vacuum. Powder X-ray diffraction (PXRD) data were collected on a Bruker D8 Advance powder diffractometer, operating at 40 kV and 40 mA using Cu Kα radiation with λ = 1.5418 Å. Samples were scanned from 2θ = 5–50° with 0.02° per step and 1.2 s per step. Magnetic susceptibility data for polycrystalline samples were measured over a temperature range of 1.8–400 K using a Quantum Design MPMS-5S superconducting quantum interference device (SQUID) magnetometer; no correction was made for the diamagnetic susceptibility of the atomic cores. Differential scanning calorimetry (DSC) was carried out on a Q2000 V24.9 Build 121 instrument over the temperature range of −180 to 20 °C (93–293 K) at a heating rate of 20 °C min−1.The temperature- and frequency-dependent dielectric permittivity (ε′) and dielectric loss tan(δ) were measured using a Concept 80 system (Novocontrol, Germany) between −120 and 110 °C (153–383 K). A plate-shaped single crystal, with dimensions 1.30 mm × 0.50 mm × 0.25 mm, was selected. Conducting silver paste was coated on two opposite surfaces (1.30 mm × 0.50 mm) of the single crystal. Gold wires (80 μm diameter) were used to connect copper electrodes to the single crystal surfaces in order to apply ac frequencies of 1–107 Hz.
X-ray single crystallography
Single-crystal X-ray diffraction data for 1 were collected at 200, 296 and 353 K using graphite monochromated Mo Kα (λ = 0.71073 Å) radiation on a CCD area detector (Bruker-SMART). Data reduction and absorption corrections were performed with the SAINT and SADABS software packages,34 respectively. Structures were solved by a direct method using the SHELXL-97 software package.35 The non-hydrogen atoms were anisotropically refined using a full-matrix least-squares method on F2. All hydrogen/deuterium atoms were placed at the calculated positions and refined as riding on the parent atoms. The details of data collection, structure refinement and crystallography are summarized in Table 1.| a R 1 = Σ||Fo| − |Fc||/|Fo|, wR2 = [Σw(ΣFo2 − Fc2)2/Σw(Fo2)2]1/2. | |||
|---|---|---|---|
| Temp. (K) | 200 K (α phase) | 296 K (β phase) | 353 K (γ phase) |
| Wavelength (Å) | 0.71073 | 0.71073 | 0.71073 |
| Formula | C16H5D6N6NiS4 | C16H5D6N6NiS4 | C16H5D6N6NiS4 |
| Formula weight | 480.29 | 480.29 | 480.29 |
| Space group | P2(1)/n | P2(1)/n | P2(1)/n |
| CCDC no. | 948262 | 948261 | 948263 |
| Crystal system | Monoclinic | Monoclinic | Monoclinic |
| a (Å) | 15.4940(12) | 7.9131(8) | 7.8725(9) |
| b (Å) | 17.3801(12) | 17.7611(19) | 17.8806(17) |
| c (Å) | 16.0217(14) | 14.9879(18) | 15.1206(16) |
| β (°) | 110.099(9) | 99.912(3) | 99.488(11) |
| V(Å3)/Z | 4051.7(5)/8 | 2075.0(4)/4 | 2099.3(4)/4 |
| ρ (g cm−1) | 1.575 | 1.537 | 1.520 |
| F(000) | 1928 | 964 | 964 |
| Abs. coeff. (mm−1) | 1.383 | 1.351 | 1.335 |
| θ Range for data collection (°) | 2.71–26.00 | 1.79–27.49 | 2.66–26.00 |
| Index ranges | −19 ≤ h ≤ 19 | −10 ≤ h ≤ 10 | −9 ≤ h ≤ 8 |
| −21 ≤ k ≤ 21 | −23 ≤ k ≤ 22 | −21 ≤ k ≤ 22 | |
| −19 ≤ l ≤ 19 | −18 ≤ l ≤ 19 | −13 ≤ l ≤ 18 | |
| R int | 0.0591 | 0.0707 | 0.0680 |
| Independent reflect./restraints/parameters | 7950/0/487 | 4739/0/244 | 4123/0/245 |
| Refinement method | The least square refinement on F2 | ||
| Goodness of fit on F2 | 1.024 | 0.999 | 1.024 |
| R 1, wR2a [I > 2σ(I)] | 0.0467, 0.1011 | 0.0619, 0.1549 | 0.0650, 0.1672 |
| R 1, wR2a [all data] | 0.0852, 0.1169 | 0.1512, 0.1955 | 0.1275, 0.2022 |
| Residual (e Å−3) | 0.595/−0.457 | 0.854/−0.439 | 0.547/−0.352 |
Results and discussion
Crystal structures
Compound 1 crystallizes in the monoclinic space group P2(1)/n at room temperature (296 K) and is isostructural with its analogue [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2].29 The two compounds, [(CD3)2C
N-Py][Ni(mnt)2].29 The two compounds, [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] and [(CH3)2C
N-Py][Ni(mnt)2] and [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2], show quite similar lattice parameters at room temperature. As displayed in Fig. 1a, the asymmetric unit of 1 consists of an anion and a cation. The pyridyl ring in the cation moiety is tilted towards the molecular plane of the anion, with a dihedral angle of 51.4°, where the mean-molecular plane of the [Ni(mnt)2]− anion is defined through the four coordinated sulfur atoms. The bond lengths and angles in the planar [Ni(mnt)2]− moiety, listed in Table S1 (ESI†), are normal and comparable to those of its analogue.29 The bond lengths and angles in the cation moiety fall within the expected ranges, and the mean-molecular plane, defined by N6/C14/C15/C16, is approximately perpendicular to the pyridyl ring, with a dihedral angle of 83.3°.
N-Py][Ni(mnt)2], show quite similar lattice parameters at room temperature. As displayed in Fig. 1a, the asymmetric unit of 1 consists of an anion and a cation. The pyridyl ring in the cation moiety is tilted towards the molecular plane of the anion, with a dihedral angle of 51.4°, where the mean-molecular plane of the [Ni(mnt)2]− anion is defined through the four coordinated sulfur atoms. The bond lengths and angles in the planar [Ni(mnt)2]− moiety, listed in Table S1 (ESI†), are normal and comparable to those of its analogue.29 The bond lengths and angles in the cation moiety fall within the expected ranges, and the mean-molecular plane, defined by N6/C14/C15/C16, is approximately perpendicular to the pyridyl ring, with a dihedral angle of 83.3°.
The packing diagram of 1 viewed along the a-axis direction is shown in Fig. 1b. The anions form stacks, with two anions per repeat unit, along the a-axis direction; the neighboring anions are arranged in a slippage fashion along both the long and short molecular axes, with two alternating Ni⋯Ni distances within a stack (Fig. 1b and Table 2). The cations are aligned in a straight and regular arrangement, with one cation per repeat unit, along the a-axis direction. The adjacent cations are arranged anti-parallel and are related to each other through the inversion center. As displayed in Fig. 2a, the anions and cations form a layered arrangement and the molecular layer is parallel to the crystallographic (101) plane. Charge-assisted N⋯H and N⋯C interactions exist between the adjacent hydrogen and carbon atoms of the pyridyl rings and the nitrogen atoms of the nitrile groups, as shown in Fig. 2b, in the intra-layer. Such charge-assisted intermolecular interactions have previously been observed in the ion-pair compounds of [Ni(mnt)2]− with pyridinium derivatives.28 A two-fold interpenetrating two-dimensional (2-D) network is formed through the intermolecular charge-assisted N⋯H and N⋯C interactions (the typical interatomic separations are listed in Table 2), where each grid in an individual 2-D network includes three pairs of anions and cations that can be considered as a 3 + 3 type supramolecular macrocycle. As illustrated in Fig. 2a, if each 3 + 3 type supramolecular macrocycle is defined as a triangle, the supramolecular layer in 1 can be considered as a two-fold interpenetrating six-connected 2-D network.
| Distance/Å | α | β | γ |
|---|---|---|---|
| d1 | 4.4802(8) | 4.2788(9) | 4.2523(10) |
| d2 | 4.1878(8) | 4.1333(9) | 4.1221(10) |
| d3 | 4.2118(8) | ||
| a1 | 3.7034(12) | 3.6262(14) | 3.6128(16) |
| a2 | 3.5093(14) | 3.4980(13) | 3.5003(16) |
| a3 | 3.4704(12) | ||
| b1 | 4.4141(15) | 4.3011(20) | 4.1785(22) |
| b2 | 4.3871(15) | 4.1891(20) | 4.2645(22) |
| b3 | 4.0767(16) | 4.1118(19) | 4.2045(21) |
| b4 | 4.3905(18) | 4.2307(19) | 4.1131(21) |
| b5 | 4.2720(16) | ||
| b6 | 4.2865(16) | ||
| h1 | 3.202(11) | 3.201(12) | |
| h2 | 3.1764(93) | 3.235(12) | |
| h3 | 2.723 | 2.823 | |
| h4 | 2.668 | 2.702 | |
| h5 | 2.648 | 2.619 |
Temperature dependent magnetic susceptibility and DSC measurements reveal that the crystals of 1 experience two phase transitions between 200 and 400 K (see Fig. 8). One phase transition takes place at around 267 K and another phase transition occurs near 325 K during the cooling procedure (see the discussion of magnetic properties below). For convenience, the three phases are sequentially labeled as α (below 267 K), β (between 267 and 325 K) and γ (above 325 K). The crystal structure of 1 was determined at 353 K to show the γ phase and at 200 K to show the α phase. As shown in Table 1, the γ phase is isostructural with the β phase, and the two phases show quite similar lattice parameters. An asymmetric unit of 1 in the γ phase, displayed in Fig. 3, consists of one anion–cation pair. The bond lengths and angles in both the anion and cation moieties, listed in Table S1 (ESI†), are in good agreement with those in the β phase. The values of the equivalent U parameters (Ueq), listed in Table S2 (ESI†), do not change significantly from the β phase to the γ phase with increasing temperature. In addition, the molecular conformation of the cation, which has a dihedral angle of 83.0° between the mean-molecular plane defined by N6/C14/C15/C16 and the pyridyl ring, as well as the relative orientation between the anion and the cation, with a dihedral angle of 50.9° between the mean-molecular plane of the anion and the pyridyl ring, is almost the same as in the β phase. This indicates that there are strong similarities between the molecular structures of both anions and cations for the β and γ phases.
 | ||
| Fig. 3 Molecular structure of 1 in the γ phase with labeling and displacement ellipsoids of non-hydrogen atoms at the 20% probability level. Hydrogen and deuterium atoms are omitted for clarity. | ||
The transition between the β and γ phases is known as an IPT. Interestingly, temperature induced IPTs are among the “rarest of rare” IPT phenomena reported so far.36 IPTs are also known as “Cowley's type zero” transitions37 after Cowley postulated the possibility of such a transition, based on the behavior of acoustic phonons within the framework of displacive structural phase transitions. Consequently, the intermolecular distances within an anion stack, as well as between the anions and cations in a two-fold interpenetrating 2-D supramolecular network, were carefully inspected. Typical distances are illustrated in Fig. 4 and summarized in Table 2. This reveals that the interatomic separations show some shrinkage along the a-axis direction, but slight expansion along the b- and c-axes. For instance, two types of neighboring Ni⋯Ni distances within an anion stack, which are along the a-axis direction, are d1(353 K) = 4.2523(10) and d2(353 K) = 4.1221(10) Å versus d1(296 K) = 4.2788(9) and d2(296 K) = 4.1333(9) Å. This gives Δd1 = d1(353 K) − d1(296 K) = −0.027 Å and Δd2 = d2(353 K) − d2(296 K) = −0.011 Å. The interatomic separations between the N atoms of CN groups and the H atoms of pyridyl rings, which are approximately along the b- and c-axes directions, are h3(353 K) = 2.823 and h4(353 K) = 2.702 Å versus h3(296 K) = 2.723 and h4(296 K) = 2.668 Å. This gives Δh3 = h3(353 K) − h3(296 K) = 0.1 Å and Δh4 = h4(353 K) − h4(296 K) = 0.034 Å. The changes in interatomic distances between the β and γ phases are in agreement with the changes in the lengths of the crystallographic axes. To the best of our knowledge, besides 1, only three other compounds that show an isostructural phase transition associated with a magnetic transition26,29,38 have previously been reported in 1-D [Ni(mnt)2]− magnetic systems.
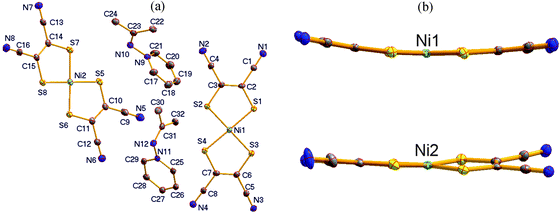
From the β to the α phase, the space group does not change. However, an asymmetric unit switches from an anion–cation pair in the β phase into two pairs of anions and cations in the α phase (as shown in Fig. 5a). This situation is distinct from [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2], where an isostructural phase transition takes place with decreasing temperature from room temperature.29 The bond lengths and bond angles in both anions and cations in the α phase, listed in Table S1 (ESI†), are comparable to those in the β phase. Two crystallographically different [Ni(mnt)2]− anions show distinct molecular shapes (ref. Fig. 5b). The anion containing Ni1 exhibits a banana shape, with its four N atoms moved away from the mean-molecular plane, defined by the four coordinated S atoms at 0.294(4), 0.378(4), 0.546(4) and 0.605(4) Å. In addition, these values are much larger than the values 0.144(8), 0.235(7), 0.251(6) and 0.362(7) Å found in the β phase. The anion containing Ni2 shows non-planar geometry, and the two five-membered chelating rings make a dihedral angle of 8.2°. The molecular conformations of the two non-equivalent cations are also different from each other. The dihedral angle is 58.7° between the mean-molecular plane defined by N10/C22/C23/C24 and the corresponding pyridyl ring in the cation containing N10 but 87.8° between the mean-molecular plane of N12/C30/C31/C32 and the corresponding pyridyl ring in the cation containing N12.
N-Py][Ni(mnt)2], where an isostructural phase transition takes place with decreasing temperature from room temperature.29 The bond lengths and bond angles in both anions and cations in the α phase, listed in Table S1 (ESI†), are comparable to those in the β phase. Two crystallographically different [Ni(mnt)2]− anions show distinct molecular shapes (ref. Fig. 5b). The anion containing Ni1 exhibits a banana shape, with its four N atoms moved away from the mean-molecular plane, defined by the four coordinated S atoms at 0.294(4), 0.378(4), 0.546(4) and 0.605(4) Å. In addition, these values are much larger than the values 0.144(8), 0.235(7), 0.251(6) and 0.362(7) Å found in the β phase. The anion containing Ni2 shows non-planar geometry, and the two five-membered chelating rings make a dihedral angle of 8.2°. The molecular conformations of the two non-equivalent cations are also different from each other. The dihedral angle is 58.7° between the mean-molecular plane defined by N10/C22/C23/C24 and the corresponding pyridyl ring in the cation containing N10 but 87.8° between the mean-molecular plane of N12/C30/C31/C32 and the corresponding pyridyl ring in the cation containing N12.
The packing diagram of 1 in the α phase at 200 K, viewed along the c-axis direction, is displayed in Fig. 6. This is similar to the packing diagram of 1 in the β phase at 296 K, viewed along the a-axis direction. The anions form a columnar stack along the c-axis direction in the α phase, whereas the anion stack runs along the a-axis direction in the β phase at 296 K (Fig. 6). There are three significant changes in the anion and cation arrangements resulting from the transformation from the β to the α phase. (1) The anion stack is irregular, with two different neighboring Ni⋯Ni distances and two anions per repeat unit along the a-axis direction in the β phase. However, the anions form a stack in the form of ⋯Ni1Ni1Ni2Ni2⋯, and there are four anions per repeat unit along the c-axis direction, with three distinct neighboring Ni⋯Ni distances in the α phase (see Fig. 6 and Table 2). (2) The cations forming a linear arrangement show the same orientation in the β phase but two different orientations in the α phase. This is due to the existence of two crystallographically non-equivalent cations in the α phase. The distortion of both anion stack and cation alignments gives rise to the double length of the crystallographic axis, which is parallel to the anion stack or cation alignment. The doubling of axis length indicates that the translation symmetry breaking-of the lattice undergoes from the β to the α phase. (3) The charge-assisted intermolecular interaction patterns are different in the α and β phases, as displayed in Fig. 4b and c and Fig. 7, as well as Tables 2 and 3, respectively. Clearly, there are strongly charge-assisted intermolecular H-bond interactions in the α phase but not in the β and γ phases.
 | ||
| Fig. 7 Illustration showing the charge-assisted H-bond interactions between anions and cations in the α phase. Some H/D atoms are omitted for clarity and the symmetric codes #1–#14 refer to Table 3. | ||
| a Symmetric codes: #1 = −x, 1 − y, 1 − z; #2 = 0.5 − x, −0.5 + y, 1.5 − z; #3 = −0.5 + x, 1.5 − y, −0.5 + z; #4 = −0.5 − x, −0.5 + y, 0.5 − z; #5 = 1 − x, 1 − y, 1 − z; #6 = 0.5 + x, 1.5 − y, 0.5 + z; #7 = −1 + x, y, z; #8 = 1 − x, −0.5 + y, 2.5 − z; #9 = 0.5 + x, 1.5 − y, −0.5 + z; #10 = 0.5 + x, 1.5 − y, 0.5 + z; #11 = 1.5 − x, 0.5 + y, 2.5 − z; #12 = 1 + x, y, z; #13 = −0.5 − x, 0.5 + y, 0.5 − z; #14 = 0.5 − x, 0.5 + y, 1.5 − z. | |||||
|---|---|---|---|---|---|
| N1⋯H26A | 2.733 | C7⋯S5#1 | 3.493(4) | N5#12⋯H18A | 2.768 |
| N1⋯C26 | 3.243(6) | C2⋯C13#1 | 3.372(7) | N5#12⋯C18 | 3.205(7) |
| N2⋯H27A#2 | 2.694 | S1⋯C14#1 | 3.491(4) | N4#5⋯H17A | 2.656 |
| N2⋯H28A#2 | 2.716 | N5⋯D24C#6 | 2.618 | N3#13⋯H29A | 2.640 |
| N2⋯H20A#3 | 2.639 | N5⋯H18A#7 | 2.768 | N3#13⋯C31 | 3.238(6) |
| N3⋯H29A#4 | 2.640 | N5⋯C18#7 | 3.205(7) | N4#1⋯H27A | 2.656 |
| N3⋯C31#4 | 3.238(6) | N6⋯H19A#8 | 2.729 | N2#14⋯H27A | 2.694 |
| N3⋯C11#1 | 3.236(6) | N5#9⋯D24C | 2.618 | N2#14⋯H28A | 2.716 |
| N4⋯H17A#5 | 2.656 | N2#10⋯H20A | 2.639 | ||
| N4⋯H27A#1 | 2.715 | N6#11⋯H19A | 2.729 | ||
Magnetic and phase transition properties
The temperature dependent magnetic susceptibility of 1 is displayed in Fig. 8. The χmversus T plot exhibits the following features. (1) Two magnetic phase transitions appear, at around 267 and 325 K, as the temperature is reduced from 400 K to 2 K, and these phase transitions were further confirmed by DSC measurements. A thermal hysteresis with a ∼8 K loop is observed for the magnetic phase transition around 267 K, but no observable thermal hysteresis effect for the magnetic phase transition around 325 K is observed in the heating–cooling run. A hysteresis effect is generally related to intermolecular cooperative interactions in the crystal.1,10 In this case, the strong hydrogen-bonding interactions in the α phase are probably responsible for highly cooperative interactions during the magnetic phase transition between the α and β phases. As mentioned in the crystal structure description, the changes of interatomic distances are not very significant in the three different phases. However, the magnetic features are obviously different from each other. This observation demonstrates that the magnetic coupling interactions between [Ni(mnt)2]− anions are quite sensitive to the non-bonded interatomic contacts. (2) The χm value drops exponentially below about 100 K upon cooling. This indicates the existence of a singlet ground state with a spin gap.39 (3) The weak Curie–Weiss type of paramagnetism dominates in the low temperature regime, below 50 K. It is worth noting that 1 and its analogue [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] show different magnetic phase transition behaviors. The compound [(CH3)2C
N-Py][Ni(mnt)2] show different magnetic phase transition behaviors. The compound [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] shows a magnetic phase transition at 266 K and its absence around 325 K.
N-Py][Ni(mnt)2] shows a magnetic phase transition at 266 K and its absence around 325 K.
Given that the [Ni(mnt)2]− anion bears an S = 1/2 spin and the unpaired electron is delocalized over the entire anion skeleton, the magnetic exchange interaction between neighboring [Ni(mnt)2]− anions may be transmitted through long non-bonded interatomic contacts involving sulfur atoms. From a structural viewpoint, an anion stack can be considered as an S = 1/2 spin chain, and the magnetic exchange model of a tetrameric S = 1/2 spin chain might be used to fit the variable temperature magnetic susceptibility in the α phase since the anion stack is effectively tetrameric below 267 K. Unfortunately, it is not possible to analyze the magnetic susceptibility data using a tetrameric S = 1/2 spin chain model since there is no useable χm = χm(T) formula. The Curie–Weiss type magnetic susceptibility in the low temperature range was therefore fitted using eqn (1),
 | (1) |
The crystal structure reveals that the anion stack is irregular and shows two different neighboring Ni⋯Ni distances in both the β and γ phases. As a consequence, an alternating S = 1/2 magnetic chain model with two different magnetic coupling constants was used to model the variable temperature magnetic susceptibility in the β and γ phases. The spin Hamiltonian for the Heisenberg alternating linear chain may be written as
 | (2) |
 | (3) |
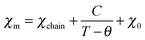 | (4) |
Dielectric properties
The dielectric permittivity of 1 as a function of temperature is plotted in Fig. 9. The dielectric permittivity falls, from 109 to 96, between 153 and 273 K for ac frequencies 1–107 Hz and increases upon heating above 293 K. A rounded peak appears in the plot of dielectric permittivity versus temperature and its maximum, at 328 K, is independent of ac frequency. The peak temperature is close to the critical temperature of the magnetic phase transition between the β and γ phases. This means that the IPT at around 325 K gives rise to both a magnetic phase transition and a dielectric anomaly. It is worth noting that no sizable dielectric anomaly around 267 K was observed in the plot of dielectric permittivity versus temperature (see inset of Fig. 9). Dielectric dispersion is observed for 1 in the high temperature region, especially in the low-frequency regime. This is because the mobility of the molecules begins to increase at higher temperatures. | ||
| Fig. 9 Plots of dielectric permittivity versus temperature over the range 153–383 K for ac frequencies 1–107 Hz (inset shows the enlarged ε′–T plot under f = 1 Hz). | ||
Conclusion
In summary, the 1-D magnetic chain compound [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] experiences two structural phase transitions, at around 267 K and 325 K, while its analogue [(CH3)2C
N-Py][Ni(mnt)2] experiences two structural phase transitions, at around 267 K and 325 K, while its analogue [(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] only undergoes one isostructural phase transition at 266 K. These remarkable differences result from the deuteration of the diamagnetic counterion. The three phases for [(CD3)2C
N-Py][Ni(mnt)2] only undergoes one isostructural phase transition at 266 K. These remarkable differences result from the deuteration of the diamagnetic counterion. The three phases for [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] are sequentially labeled α (below 267 K), β (between 267 and 325 K) and γ (above 325 K). From a structural viewpoint, the transformation is a symmetry breaking structural phase transition between the β and α phases, owing to the translation symmetry breaking of the lattice, while an isostructural phase transition occurs between the β and γ phases. The striking structural feature is that the anion stack shows some shrinking with increasing temperature, which gives rise to a small reduction in the length of the corresponding crystallographic axis, when passing from the β to γ phase.
N-Py][Ni(mnt)2] are sequentially labeled α (below 267 K), β (between 267 and 325 K) and γ (above 325 K). From a structural viewpoint, the transformation is a symmetry breaking structural phase transition between the β and α phases, owing to the translation symmetry breaking of the lattice, while an isostructural phase transition occurs between the β and γ phases. The striking structural feature is that the anion stack shows some shrinking with increasing temperature, which gives rise to a small reduction in the length of the corresponding crystallographic axis, when passing from the β to γ phase.
The two magnetic phase transitions in [(CD3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-Py][Ni(mnt)2] are driven by a different kind of structural phase transition. The significant changes of magnetic susceptibility across the structural phase transitions are attributed to variations of AFM coupling constants within a magnetic chain in the different phases.44,45 A ∼8 K thermal hysteresis loop appears in the magnetic phase transition between the β and α phases. However, no sizable thermal hysteresis effect is observed in the magnetic phase transition between the β and γ phases. This observation is probably related to the presence of strong charge-assisted intermolecular H-bond interactions in the low-temperature α phase but only weak charge-assisted intermolecular H-bond interactions in the high-temperature γ phase. Another striking feature of this 1-D magnetic chain compound is the dielectric anomaly, which only appears across the phase transition between the β and γ phases, not between the β and α phases. To understand this particular issue better, further investigations will be carried out.
N-Py][Ni(mnt)2] are driven by a different kind of structural phase transition. The significant changes of magnetic susceptibility across the structural phase transitions are attributed to variations of AFM coupling constants within a magnetic chain in the different phases.44,45 A ∼8 K thermal hysteresis loop appears in the magnetic phase transition between the β and α phases. However, no sizable thermal hysteresis effect is observed in the magnetic phase transition between the β and γ phases. This observation is probably related to the presence of strong charge-assisted intermolecular H-bond interactions in the low-temperature α phase but only weak charge-assisted intermolecular H-bond interactions in the high-temperature γ phase. Another striking feature of this 1-D magnetic chain compound is the dielectric anomaly, which only appears across the phase transition between the β and γ phases, not between the β and α phases. To understand this particular issue better, further investigations will be carried out.
Acknowledgements
The authors thank the Priority Academic Program Development of Jiangsu Higher Education Institutions, Science and Technology Department of Jiangsu Province and National Nature Science Foundation of China for financial support (grant no. BK2010551, 91122011 and 21271103).Notes and references
- O. Kahn and C. J. Martinez, Science, 1998, 279, 44 CrossRef CAS.
- T. Liu, D. P. Dong, S. Kanegawa, S. Kang, O. Sato, Y. Shiota, K. Yoshizawa, S. Hayami, S. Wu, C. He and C. Y. Duan, Angew. Chem., Int. Ed., 2012, 51, 4367 CrossRef CAS PubMed.
- S. Takaishi, N. Ishihara, K. Kubo, K. Katoh, B. K. Breedlove, H. Miyasaka and M. Yamashita, Inorg. Chem., 2011, 50, 6405 CrossRef CAS PubMed.
- M. Nihei, H. Tahira, N. Takahashi, Y. Otake, Y. Yamamura, K. Saito and H. Oshio, J. Am. Chem. Soc., 2010, 132, 3553 CrossRef CAS PubMed.
- F. Setifi, S. Benmansour, M. Marchivie, G. Dupouy, S. Triki, J. Sala-Pala, J.-Y. Salaün, C. J. Gómez-García, S. Pillet, C. Lecomte and E. Ruiz, Inorg. Chem., 2009, 48, 1269 CrossRef CAS PubMed.
- X. M. Ren, Q. J. Meng, Y. Song, C. S. Lu, C. J. Hu and X. Y. Chen, Inorg. Chem., 2002, 41, 5686 CrossRef CAS PubMed.
- D. B. Dang, C. L. Ni, Y. Bai, Z. F. Tian, Z. P. Ni, L. L. Wen, Q. J. Meng and S. Gao, Chem. Lett., 2005, 680 CrossRef CAS.
- X. M. Ren, T. Akutagawa, S. Nishihara, T. Nakamura, W. Fujita and K. Awaga, J. Phys. Chem. B, 2005, 109, 16610 CrossRef CAS PubMed.
- Z. F. Tian, H. B. Duan, X. M. Ren, C. S. Lu, Y. Z. Li, Y. Song, H. Z. Zhu and Q. J. Meng, J. Phys. Chem. B, 2009, 113, 8278 CrossRef CAS PubMed.
- O. Jeannin, R. Clérac and M. Fourmigué, J. Am. Chem. Soc., 2006, 128, 14649 CrossRef CAS PubMed.
- W. Fujita and K. Awaga, Science, 1999, 286, 261 CrossRef CAS.
- M. E. Itkis, X. Chi, A. W. Cordes and R. C. Haddon, Science, 2002, 296, 1443 CrossRef CAS PubMed.
- C. Z. Wu, J. Dai, X. D. Zhang, J. L. Yang and Y. Xie, J. Am. Chem. Soc., 2009, 131, 7218 CrossRef CAS PubMed.
- J. A. Koza, Z. He, A. S. Miller and J. A. Switzer, Chem. Mater., 2011, 23, 4105 CrossRef CAS.
- Y. Muraoka and Z. Hiroi, Appl. Phys. Lett., 2002, 80, 583 CrossRef CAS.
- K. S. Aleksandrov, I. P. Aleksandrova, V. F. Shabanov, V. I. Yuzvak, Y. Z. Nozik and L. I. Fikin, Phys. Status Solidi A, 1978, 45, 53 CrossRef CAS.
- S. Horiuchi, R. Kumai, Y. Tokunaga and Y. Tokura, J. Am. Chem. Soc., 2010, 130, 13382 CrossRef PubMed.
- G. C. Xu, X. M. Ma, L. Zhang, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588 CrossRef CAS PubMed.
- G. C. Xu, W. Zhang, X. M. Ma, Y. H. Chen, L. Zhang, H. L. Cai, Z. M. Wang, R. G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948 CrossRef CAS PubMed.
- Z. H. Sun, T. L. Chen, J. H. Luo and M. C. Hong, Angew. Chem., Int. Ed., 2012, 51, 3871 CrossRef CAS PubMed.
- A. Christy, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 753 CrossRef.
- W. B. Pei, J. S. Wu, W. H. Ning, Z. F. Tian, J. L. Liu and X. M. Ren, Inorg. Chim. Acta, 2013, 398, 28 CrossRef CAS PubMed.
- E. B. Lopes, H. Alves, I. C. Santos, D. Graf, J. S. Brooks, E. Canadell and M. Almeida, J. Mater. Chem., 2008, 18, 2825 RSC.
- R. Perochon, L. Piekara-Sady, W. Jurga, R. Clérac and M. Fourmigué, Dalton Trans., 2009, 3052 RSC.
- H. B. Duan, X. R. Chen, H. Yang, X. M. Ren, F. Xuan and S. M. Zhou, Inorg. Chem., 2013, 52, 3870 CrossRef CAS PubMed.
- R. D. Willett, C. J. Gómez-Garcí, B. L. Ramakrishna and B. Twamley, Polyhedron, 2005, 24, 2232 CrossRef CAS PubMed.
- G. J. Yuan, S. P. Zhao, C. Wang, X. M. Ren and J. L. Liu, Chem. Commun., 2011, 47, 9489 RSC.
- G. J. Yuan, S. P. Zhao, C. Wang, J. L. Liu and X. M. Ren, Chem.–Asian J., 2013, 8, 611 CrossRef CAS PubMed.
- Z. F. Tian, X. M. Ren, Y. Z. Li, Y. Song and Q. J. Meng, Inorg. Chem., 2007, 46, 8102 CrossRef CAS PubMed.
- F. Sommer, O. F. Schulz and M. Nassau, Z. Anorg. Allg. Chem., 1925, 147, 142 CrossRef CAS.
- J. H. Krueger, P. F. Blanchet, A. P. Lee and B. A. Sudbury, Inorg. Chem., 1973, 12, 2714 CrossRef CAS.
- G. Richard and M. Alwin, Chem. Ber., 1959, 92, 2521 CrossRef.
- A. Davison and H. R. Holm, Inorg. Synth., 1967, 10, 8 CrossRef CAS.
- Software packages SMART and SAINT, Siemens Analytical X-ray Instrument Inc., Madison, WI, 1996 Search PubMed.
- G. M. Sheldrick, SHELX-97, Program for the refinement of crystal structure, University of Göttingen, Germany, 1997 Search PubMed.
- D. Saha, R. Ranjan, D. Swain, C. Narayana and T. N. G. Row, Dalton Trans., 2013, 42, 7672 RSC.
- R. A. Cowley, Phys. Rev. B: Solid State, 1976, 13, 4877 CrossRef CAS.
- J. L. Xie, X. M. Ren, C. He, Y. Song, Q. J. Meng, R. K. Kremer and Y. G. Yao, Chem. Phys. Lett., 2003, 369, 41 CrossRef CAS.
- D. C. Johnston, R. K. Kremer, M. Troyer, X. Wang, A. Klümper, S. L. Bud'ko, A. F. Panchula and P. C. Canfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9558 CrossRef CAS.
- J. H. van Vleck, The Theory of Electric and Magnetic Susceptibilities, Oxford, London, 1932 Search PubMed.
- J. Bonner and M. E. Fisher, Phys. Rev. [Sect.] A, 1964, 235, 640 Search PubMed.
- J. W. Hall, W. E. Marsh, R. R. Weller and W. E. Hatfield, Inorg. Chem., 1981, 20, 1033 CrossRef CAS.
- D. A. Tucker, P. S. White, K. L. Trojan, M. L. Kirk and W. E. Hatfield, Inorg. Chem., 1991, 30, 823 CrossRef CAS.
- G. Leibeling, S. Demeshko, S. Dechert and F. Meyer, Angew. Chem., Int. Ed., 2005, 44, 7111 CrossRef CAS PubMed.
- S. Youngme, G. A. van Albada, H. Kooijman, O. Roubeau, W. Somjitsripunya, A. L. Spek, C. Pakawatchai and J. Reedijk, Eur. J. Inorg. Chem., 2002, 2367 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data are available in CIF format for 1 at 200, 296 and 353 K. Electrospray ionization mass spectra and the packing diagrams at 200 and 353 K, in PDF format. CCDC 948261–948263. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3nj01101a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2014 |