Bio-inspired microvascular exchangers employing circular packing – synthetic rete mirabile

Abstract

Natural systems employ microvascular exchangers with circular packing for both heat and mass transfer that closely conform to the compact, packing of circles of two diameter. Mathematical descriptions of these systems exist, but have rarely been studied in three dimensions for their exchange properties. We focus on four close packed patterns: “Hexagonal” “Dodecagonal”, “Squarer”, and “Double Squarer”. While two of these patterns have natural analogs, the others are abiological. We compare computationally and experimentally the mass and heat transfer characteristics of these various patterns. Intriguingly the “Double Squarer” pattern, had the highest transfer rates within our fabrication constraints.

---

Conceptual insights

This report provides fundamental insight into the design of transport structures modeled on biological systems. Exchange and transport from hierarchical materials is at the heart of many current materials challenges including: batteries, thermal cooling, fuel cells, and solar fuels, but it has been at the heart of biological survival for hundreds of millions of years. In each application, changing the materials shape and hierarchical arrangement to increase transport is necessary to improve the performance. We look to the approaches that biological systems have taken in solving transport problems and elucidate the solutions of natural systems then use the insight to improve transport. The relationship between 3D membrane geometry and transport properties is directly correlated. Some of the structures demonstrated here have never been fabricated or found in nature and are examined for their transport properties for the first time. In total, this report provides insight into new bio-mimetic structures that explore new areas in materials design, 3D membrane topologies, micro-vascular materials, and bio-mimetic mass and heat transport.

Introduction

Micro-structured materials have advanced the fields of heat exchange, chemical analysis, flow chemistry, fuel cells, and carbon capture, and are currently advancing the field of tissue engineering.^1–24 Despite these successes, improved heat and mass micro-exchangers would benefit many applications.^25–28 Alongside human-made exchangers, biological systems developed micro-patterned exchange designs for much of evolutionary history.^29–32 Evolution repeatedly converged on vascular exchange units composed of arrays of circular channels, known as “rete mirabile”. Remarkably, in the 1970s, it was discovered that these bio-exchange designs are the exact solutions to the compact, packing of circles of two diameters.³¹ Despite strong interest in micro-exchangers and their many applications, very little work examines biologically inspired systems composed of close-packed circular microchannels. Here we report the synthesis and study of the transfer characteristics of microvascular exchange units adapted from the solution of close-packed patterns of circles of two diameters. We find that the patterns' exchange coefficients vary and that abiological systems generally employ the more efficient patterns, given our design constraints. However, two patterns have not been found in biological systems and yet we found they are also efficient for both heat and mass transfer.

Our interest in compact packing patterns was first piqued by observations of natural systems as almost all biological systems converge on one of these solutions (Fig. 1a). A complete set of solutions to binary circular packing was recently reported by Kennedy.^33–37 In determining if packing patterns effected transfer, we studied the relative transfer rates among four of the patterns using finite element modeling. As no formal names exist, we refer to the different patterns as “Hexagonal”, “Dodecagonal”, “Squarer”, and “Double Squarer” in this report (Fig. 1c). While the “Hexagonal” and “Squarer” patterns have known natural analogs to the avian lung and piscine gas bladder, respectively, the “Dodecagonal” and “Double Squarer” have no biological analogs that we can identify. Additionally, the “Dodecagonal” and “Double Squarer” patterns were chosen for their similarity to biological patterns (ESI†). Each pattern has an optimal ratio between diameters of the two circle sizes, which allows for the highest occupied density in a regular lattice arrangement. For synthesis and analysis, we modified these ratios to maintain constant minimum inter-channel distances and to account for available fabrication sizes.

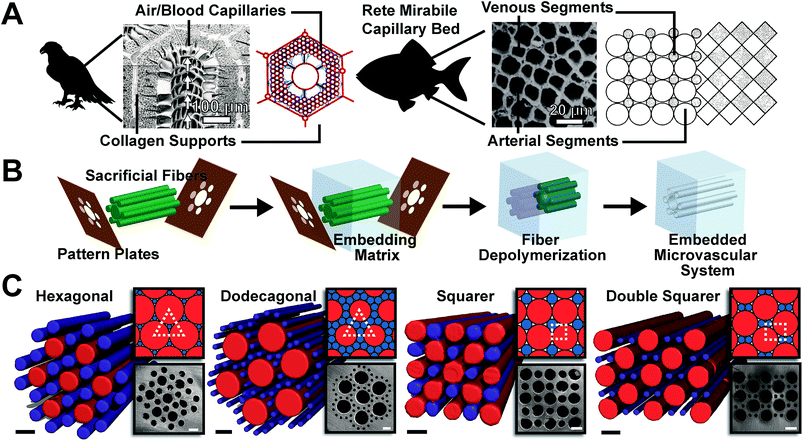Fig. 1 Biological inspiration, design and creation of close packed patterned exchangers. (A) Natural exchange systems. The avian lung contains a modified hexagonal packing structure for the transfer of CO₂ and O₂,^29,32 reproduced with permission from Environmental Health Perspectives and Journal of Anatomy. The piscine gas bladder uses a squarer packing structure for the release of O₂ to control its bouyancy,^30,31 reproduced with permission from Microvascular Research and The Biological Bulletin. (B) VaSC fabrication process of compact, packing elements. Sacrificial fibers are placed in a parallel arrangement using patterning plates. A polymer matrix then fills the space between the fibers. Last, the fibers are depolymerized, resulting in a hollow microvascular system. (C) Microvascular close packed patterns. SEM and μCT images confirm the fabrication of the patterned exchange units. Inset are the ideal geometries for the most densely packed structures. Unit cell shapes are outlined in white. Scale bars are 300 μm.

Intrigued by our observations and preliminary models, we fabricated these four patterns to confirm the model results, including the abiological patterns which were of particular interest. To synthesize such compact patterns, we used the Vaporization of a Sacrificial Component (VaSC) technique. VaSC employs a sacrificial element rather than a lithographic or direct-write approach.^38,39 During the course of experiments, we measured the mass transfer characteristics of each packing structure using a model reaction between carbon dioxide and monoethanolamine (MEA, 30% w/w). The highest mass transfer coefficient, for our samples, occurs in the “Double Squarer”, a previously unknown pattern, and the lowest in the “Hexagonal” close packed patterns. We measured the heat transfer characteristics of each packing structure by using the countercurrent flow of hot and room temperature water. The highest heat transfer coefficient is again found in the “Double Squarer” – an abiological pattern. The general trends found in the mass transfer coefficients were also found in the heat transfer coefficients. It should be noted that the geometries chosen were constrained, by fabrication techniques, to only certain patterns. The primary constraint was to maintain a minimum inter-channel distance of 50 μm. Other parameters such as mean distance, channel ratios, and closeness to ideal sizes were also considered, but not experimentally examined (ESI†).

Experimental

Materials

Monoethanolamine (≥99%, MEA), tin(II) oxalate (98%), and fluorescein were purchased from Sigma-Aldrich. 5-(and-6)-Carboxynaphthofluorescein was purchased from Invitrogen. Tris–HCl was purchased from J. T. Baker. Sylgard® 184 silicone elastomer kit (PDMS) was purchased from Dow Corning. Disperbyk-130 was purchased from BYK Additives & Instruments. Trifluoroethanol (TFE) was purchased from Halogen Inc. Poly(lactic) acid (PLA) fibers were provided by Teijin Monofilament.

VaSC fiber preparation

Tin(II) oxalate was entrapped within PLA fibers to lower its depolymerization temperature from 280 °C to 200 °C. A 800 mL treatment solution was created (400 mL deionized water, 400 mL trifluoroethanol, 50 g tin oxalate, 20 g DISPERBYK-130, 0.5 g malachite green) to infuse the tin oxalate within the fibers and to dye the fibers for visual clarity. Fibers were wound around a custom spindle and placed within the solution. The solution with the fibers was spun at 300 RPM for 48 hours at room temperature. The fibers were then removed from the solution and dried in air at room temperature for 24 hours.

Exchange unit fabrication

PDMS was created using mixtures of the Sylgard 184 silicone elastomer with a 10 : 1 ratio between base and curing agent. VaSC fibers were strung through two laser-cut brass plates containing the desired close-packed patterns. The plates were placed onto a 1 inch long mold box with the fibers tensioned on either side to create a set of parallel fibers in the patterned arrangement within the mold box. The mold box was then filled with PDMS and cured at 85 °C for 1 hour. A second stage of molding with PDMS was performed to separate the channels from the pattern and allow for easier loading of channels. The vascular preforms were heated to 210 °C under vacuum to vaporize and remove the fibers embedded within the PDMS resin resulting in a close packed arrangement of hollow channels.

Mass and heat transfer model

The models were created using the COMSOL Multiphysics Modeling and Simulation software. The models assumed conservation of momentum, mass and energy to describe the movement of fluids and mass. The models use several parameters including diffusion coefficients, reaction rates, fluid properties, heat capacities, thermal conductivities, and densities (ESI†).^40–45

Exchange unit imaging

Scanning Electron Microscope (SEM) images were taken on a FEI Quanta FIB system (Oxford Instruments) and performed at the Laboratory for Electron and X-ray Instrumentation (LEXI) at UC Irvine. The images were taken at a beam current of 8.31 pA and a voltage of 2.00 kV. X-ray computed tomography (μCT) images were taken using a Xradia VersaXRMTM 410 nano-CT system and also performed at LEXI. Images were taken at a 40 kV and 7 W beam settings at 4× magnification. Image reconstruction to form the three-dimensional images was performed using ImageJ image processing software.

Results and discussion

Each microvascular exchange unit was modeled using COMSOL Multiphysics. For mass transfer, the model predicted that the “Double Squarer” pattern had the highest mass transfer coefficient while the “Hexagonal” pattern had the lowest. For heat transfer, similar predictions were made due to the underlying physical laws governing mass and heat transfer. The prediction that the “Double Squarer” pattern has the highest mass and heat transfer rate intrigued us, because it has no known natural analog and a lower degree of rotational symmetry. A full analysis of our model parameters are provided later in the text.

To test our predictions, we fabricated close-packed microvascular exchange units by employing the VaSC fabrication process (Fig. 1b). VaSC uses a positive polymer template to create long, cylindrical microchannels placed in a patterned arrangement. Poly(lactic) acid (PLA) fibers were impregnated with a Tin(II) catalyst to lower its depolymerization temperature using a solution that swells the fibers allowing the catalyst to enter the swollen region. The fibers were then placed in a compact, packed pattern using pairs of laser-cut micromachined plates. The fibers were strung through the plates and then placed under tension to create a parallel arrangement of fibers matching the patterning plates. To create a membrane, the space between fibers was filled with polydimethylsiloxane (PDMS) pre-polymer. PDMS was cured at 85 °C for 30 min to form the embedding matrix of the patterns. Last, the fibers were depolymerized under vacuum at 210 °C for 48 hours. The result was a single exchange unit, consisting of a set of microchannels matching the desired pattern.

Based on the packing patterns for circles of two sizes, a precise ratio between two sizes exists for each pattern to form the densest packing of the circles (ESI†). However, we adjusted the dimensions to accommodate the requirement of 50 μm minimum separations between all fibers and discrete fiber diameters. These two adjustments resulted in average packing densities of ∼57%. For each pattern, multiple unit cells were fabricated. Each exchange unit structure was confirmed using scanning electron microscopy (SEM) and X-ray computed tomography (μCT) imaging techniques. For ease of testing, structures were fabricated with a single unit cell, surrounded by nearest neighbor channels.

First, we examined the mass transfer characteristics of the close-packed systems. The mass transfer model solved the Navier–Stokes equation for fluid flow and Fick's laws of diffusion to predict the mass transport in the close-packed vascular system.^40,41 We then matched model to experiment (Fig. 2a). In our experiment, carbon dioxide flowed through the larger set of channels at the same flow rate as the model (1 mL min⁻¹ per channel). The gas diffuses across the PDMS membrane and reacts with MEA (30 wt% in H₂O) containing a pH sensitive fluorescent dye (5-(and-6)-Carboxynaphthofluorescein, 0.17 mg mL⁻¹) in the smaller channels. To test the micro-vascular exchange, each unit is mounted on a fluorescent microscope. As MEA reacts with carbon dioxide, the carbamic acid formation lowers the pH of the solution. The fluorescence intensity of the probing dye decreases as the pH decreases (from pH ∼12 to ∼8), providing a colorimetric readout of mass transfer. The change in intensity is normalized, reaching 100% change at its lowest intensity value (Fig. 2a). We calculated the mass transfer rate by measuring the time to reach an intensity change of 80% (2.2 M CO₂).

Fig. 2 Close packing mass transfer. (A) Model and experimental comparison. The reaction between CO₂ and monoethanolamine (MEA) was used to obtain the mass transfer characteristics. A CO₂ sensitive fluorescent solution was loaded into the microchannels to visualize the capture of CO₂ by MEA. The normalized change in intensity and predicted model concentration are plotted against time. (B) Mass transfer coefficient. Differences between the patterns were observed, with the “Double Squarer” pattern obtaining the highest mass transfer coefficient. (C) MEA volume normalized mass transfer rate. Differences between the patterns become more pronounced, although the “Double Squarer” pattern still obtained the highest mass transfer rate. (D) MEA volume normalized mass transfer rate using 10% CO₂. Mass transfer rates were similar to the results from the use of 100% CO₂, but decreased by a factor of 10. Reported values are mean ± SD (n = 3).

We initially examined the mass transfer characteristics of the close-packed patterns by comparing the mass transfer coefficients (Fig. 2b). The “Double Squarer” pattern had the highest mass transfer coefficient (36 ± 2.1 μm s⁻¹) of all the synthesized close-packed patterns and was ∼40% greater than that of the lowest rate, found in the “Hexagonal” pattern (26 ± 2.0 μm s⁻¹). Similar trends were found from the computational model, but experimentally obtained mass transfer rates were 3–10% higher than predicted.

The mass transfer rates per total volume of the liquid phase provided further insight into the effects of the packing geometries (Fig. 2c). The patterns containing 100 μm diameter channels consistently obtained the highest mass transfer rates with respect to the volume of MEA used (up to 63 mol m⁻³ s). To simulate an application of a mass transfer device, 10% CO₂ (balance N₂), representing the CO₂ in the flue stream produced by a power plant, was flowed through each pattern (Fig. 2d). Similar trends were found and the measured mass transfer rates were ten times lower than the mass transfer rates obtained using pure CO₂. Again, the model predicted similar, but lower mass transfer rates.

Next, the heat transfer characteristics of the packing patterns were examined. The heat transfer model solved the Navier–Stokes equation again for fluid flow, while the heat equation and Fourier's Law were used for heat transfer.^46,47 We experimentally examined the heat transfer characteristics through the counter-current flow of warm (0.2 mL min⁻¹ per channel, 45 °C) and colder water (0.1 mL min⁻¹ per channel, 25 °C). The three-dimensional geometries of the close-packed patterns created difficulty in using thermocouple elements to measure the temperatures. Instead, a thermally sensitive, fluorescent solution was used.⁴⁸ The solution consists of fluorescein coupled to a Tris-HCl solution (10 μM fluorescein in 10 mM Tris–HCl). The pH of Tris–HCl depends on temperature and the intensity of fluorescein depends on pH (Fig. S3b†). This coupled solution acts as an intensity based temperature probe (Fig. 3a). Using this probe, the temperature gradient within a close-packed structure was measured, allowing for the measurement of heat transfer (Fig. 3b).

Fig. 3 Comparison of heat transfer in close packing patterns. (A) Model and experimental comparison. Warm and cool water flow counter-currently through the exchanger, resulting in a temperature gradient. A temperature-dependent, fluorescent solution was flowed through the microvascular exchange unit to measure the temperature profile of the packing patterns. The solid lines indicate the predicted model temperatures. (B) Sample temperature profile. The changes in temperature across the hot and cool channels are used to calculate the heat transfer characteristics within the exchangers. (C) Heat transfer coefficients. The “Double Squarer” pattern obtained the highest heat transfer coefficient while the other patterns obtained similar coefficients as each other. Reported values are mean ± SD (n = 3).

The heat transfer characteristics were compared using the heat transfer coefficients of each pattern (Fig. 3c). The elastomeric properties of the membrane allow the exchanger to potentially physically deform while fluid flows through the exchanger. This may change the geometry and result in different heat transfer characteristics. We found that the “Double Squarer” pattern again obtained the highest heat transfer coefficient (3000 W m⁻² K). The trends between the patterns were identical to the mass transfer coefficients. These values are lower than conventional micro heat exchangers (∼5000–20000 W m⁻² K).²⁶ However, PDMS is a poor conductor of heat. Heat transfer coefficients would increase with increased thermal conductivities of the material used to cast the micro vascular exchange unit. We expected the agreement found between trends for the mass transfer coefficients and heat transfer coefficients due to the similar governing physical laws behind heat and mass transfer. Nusselt numbers were also calculated for the patterns and the “Hexagonal”, “Squarer”, and “Double Squarer” patterns obtained similar values while the “Dodecagonal” pattern obtained the lowest (ESI†).

Although we had determined that the “Double Squarer” pattern obtained the highest transfer coefficients, we sought to understand the reasoning behind this. To explain why certain patterns obtained higher mass or heat transfer coefficients than others, the distances between two sets of channels were initially examined. The closest distance between one set of channels to the other, over the entire arc length of a channel was calculated. We found that as the root mean square of the nearest channel distances decreased, the transfer coefficients increased (ESI†). However, when we adjusted the models to maintain constant mean distances, the relative transfer coefficients between patterns remained the same. Upon further investigation using the model, we found that channel ratios and use of the ideal channel sizes had a greater impact on the transfer coefficients.

Conclusions

In conclusion, we present a computational and experimental comparison of mass and heat exchange between close packed arrangements of circular microchannels – the first such exploration of bio-inspired exchange structures. The computational models created for the close packed exchangers accurately predicted the experimental mass and heat transfer characteristics of each pattern. This predictive capability will allow for future design optimization of exchangers. The mass transfer rates, normalized to the capture fluid volume showed large differences between the packing patterns. The “Double Squarer” pattern obtained the highest mass transfer rate. Large differences in the heat transfer characteristics were also observed. Again, the “Double Squarer” pattern obtained the highest heat transfer coefficient of all of the patterns for our preliminary experiments. However, only small variations in the Nusselt numbers were found between the patterns, with the “Dodecagonal” pattern obtaining the lowest. Parameters such as minimum inter-channel distances, mean distances, and channel sizes all play an important role in determining transfer characteristics. These parameters are interconnected, restricting the degrees of freedom when designing a system. Access to other packing geometries allows for a new design parameter. Our fabrication constraints resulted in the “Double Squarer” pattern obtaining the highest transfer rates. These differences in mass and heat transfer are likely to become more pronounced as the size scales of the exchangers decrease further.

These close-packed patterns form the basis of most biological exchange systems. We report the first synthesis and analysis of these patterns in model exchange systems. These insights and new techniques, inspired by nature, might facilitate the development of novel cooling devices and gas exchangers with applications in electronics, flow chemistry, fuel cells, and many other areas where exchange is needed. Future work in this area will entail making smaller patterns and adding finer features as well as the adaptation of these patterns to specific applications and devices.

Acknowledgements

This work was supported by the AFOSR Young Investigator Program under FA9550-12-1-0352 and a 3M Non-Tenured Faculty Award. Du T. Nguyen was supported by the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program. Maya Kleiman acknowledges support from a Ben Gurion UCI Postdoctoral Fellowship. The authors would like to acknowledge Steve George, Said Elghobashi, Lalisa Stutts, and Janine Tom for helpful discussion relating to this project. The poly(lactic) acid fibers were generously provided by Teijin Monofilament.

Notes and references

1. M. A. McClain, C. T. Culbertson, S. C. Jacobson, N. L. Allbritton, C. E. Sims and J. M. Ramsey, Anal. Chem., 2003, 75, 5646–5655.
2. V. Hessel, H. Löwe and F. Schönfeld, Chem. Eng. Sci., 2005, 60, 2479–2501.
3. E. Choban, J. Power Sources, 2004, 128, 54–60.
4. A. Brunetti, F. Scura, G. Barbieri and E. Drioli, J. Membr. Sci., 2010, 359, 115–125.
5. G. Mehta, J. Lee, W. Cha, Y.-C. Tung, J. J. Linderman and S. Takayama, Anal. Chem., 2009, 81, 3714–3722.
6. A. Balasubramanian, R. Morhard and C. J. Bettinger, Adv. Funct. Mater., 2013, 23, 4832–4839.
7. C. J. Bettinger, E. J. Weinberg, K. M. Kulig, J. P. Vacanti, Y. Wang, J. T. Borenstein and R. Langer, Adv. Mater., 2006, 18, 165–169.
8. C. J. Hansen, S. R. White, N. R. Sottos and J. A. Lewis, Adv. Funct. Mater., 2011, 21, 4320–4326.
9. D. T. Nguyen, Y. T. Leho and A. P. Esser-Kahn, Lab Chip, 2012, 12, 1246–1250.
10. D. T. Nguyen, Y. T. Leho and A. P. Esser-Kahn, Adv. Funct. Mater., 2013, 23, 100–106.
11. Y. Zheng, P. W. Henderson, N. W. Choi, L. J. Bonassar, J. A. Spector and A. D. Stroock, Biomaterials, 2011, 32, 5391–5401.
12. L. M. Bellan, T. Kniazeva, E. S. Kim, A. A. Epshteyn, D. M. Cropek, R. Langer and J. T. Borenstein, Adv. Healthcare Mater., 2012, 1, 164–167.
13. L. M. Bellan, M. Pearsall, D. M. Cropek and R. Langer, Adv. Mater., 2012, 24, 5187–5191.
14. N. D. Mota, D. A. Finkelstein, J. D. Kirtland, C. A. Rodriguez, A. D. Stroock and H. D. Abruña, J. Am. Chem. Soc., 2012, 134, 6076–6079.
15. J. C. McDonald and G. M. Whitesides, Acc. Chem. Res., 2002, 35, 491–499.
16. P.-X. Jiang, M.-H. Fan, G.-S. Si and Z.-P. Ren, Int. J. Heat Mass Transfer, 2001, 44, 1039–1051.
17. A. Khademhosseini, Proc. Natl. Acad. Sci., 2006, 103, 2480–2487.
18. R. P. Lively, R. R. Chance, B. T. Kelley, H. W. Deckman, J. H. Drese, C. W. Jones and W. J. Koros, Ind. Eng. Chem. Res., 2009, 48, 7314–7324.
19. D. H. Kam and J. Mazumder, J. Laser Appl., 2008, 20, 185.
20. M. D. Determan, D. C. Hoysall and S. Garimella, Ind. Eng. Chem. Res., 2012, 51, 495–502.
21. W. Wu, C. J. Hansen, A. M. Aragón, P. H. Geubelle, S. R. White and J. A. Lewis, Soft Matter, 2010, 6, 739.
22. D. Wang, K. Li and W. Teo, J. Membr. Sci., 1999, 163, 211–220.
23. D. T. Clausi and W. J. Koros, J. Membr. Sci., 2000, 167, 79–89.
24. W. Wu, A. DeConinck and J. A. Lewis, Adv. Mater., 2011, 23, H178–H183.
25. G. L. Morini, Int. J. Therm. Sci., 2004, 43, 631–651.
26. P.-S. Lee, S. V. Garimella and D. Liu, Int. J. Heat Mass Transfer, 2005, 48, 1688–1704.
27. W. Qu and I. Mudawar, Int. J. Heat Mass Transfer, 2002, 45, 3973–3985.
28. S.-M. Kim and I. Mudawar, Int. J. Heat Mass Transfer, 2010, 53, 4002–4016.
29. J. N. Maina, S. A. Jimoh and M. Hosie, J. Anat., 2010, 217, 597–608.
30. R. C. Wagner, R. Froehlich, F. E. Hossler and S. B. Andrews, Microvasc. Res., 1987, 34, 349–362.
31. J. B. Wittenberg and B. A. Wittenberg, Biol. Bull., 1974, 146, 116–136.
32. R. E. Brown, J. D. Brain and N. Wang, Environ. Health Perspect., 1997, 105, 188–200.
33. T. Kennedy, Discrete Comput. Geom., 2005, 35, 255–267.
34. L. F. Tóth, Regular Figures, Pergamon Press, Oxford, 1964.
35. C. N. Likos and C. L. Henley, Philosophical Magazine Part B: Physics of Condensed Matter. Electronics, Optical and Magnetic Properties, 1993, 68, 85–113.
36. J. Molnár, Ann. Univ. Sci. Budapest., 1959, 2, 33–40.
37. A. Heppes and J. Molnár, Mat. Lapok, 1960, 11, 330–355.
38. A. P. Esser-Kahn, P. R. Thakre, H. Dong, J. F. Patrick, V. K. Vlasko-Vlasov, N. R. Sottos, J. S. Moore and S. R. White, Adv. Mater., 2011, 23, 3654–3658.
39. H. Dong, A. P. Esser-Kahn, P. R. Thakre, J. F. Patrick, N. R. Sottos, S. R. White and J. S. Moore, ACS Appl. Mater. Interfaces, 2012, 4, 503–509.
40. P. V. Danckwerts, Chem. Eng. Sci., 1979, 34, 443–446.
41. T. C. Merkel, V. I. Bondar, K. Nagai, B. D. Freeman and I. Pinnau, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 415–434.
42. J. M. Plaza, D. V. Wagener and G. T. Rochelle, Energy Procedia, 2009, 1, 1171–1178.
43. J. E. Mark, Polymer data handbook, Oxford University Press, Oxford, New York, 2009.
44. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC handbook of chemistry and physics: a ready reference book of chemical and physical data, CRC Press, Boca Raton (Fla.), London, New York, 2012.
45. E. D. Snijder, M. J. M. te Riele, G. F. Versteeg and W. P. M. van Swaaij, J. Chem. Eng. Data, 1993, 38, 475–480.
46. T. L. Bergman and F. P. Incropera, Fundamentals of heat and mass transfer, Wiley, Hoboken, NJ, 2011.
47. B. R. Munson, W. W. Huebsch and A. P. Rothmayer, Fundamentals of fluid mechanics, John Wiley & Sons, Inc., Hoboken, NJ, 2013.
48. S. M. Shameli, T. Glawdel, Z. Liu and C. L. Ren, Anal. Chem., 2012, 84, 2968–2973.

---

Footnote

† Electronic supplementary information (ESI) available: Design of packing patterns. Exchange unit fabrication. COMSOL mass and heat transfer modeling. CO₂-MEA reaction mechanism. Mass and heat transfer experimental details. Fluorescent temperature measurement probe information. Heat transfer calculations. Channel distance correlations. See DOI: 10.1039/c4mh00120f

---