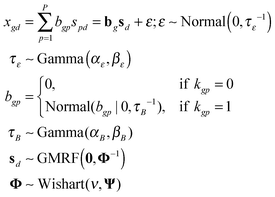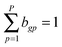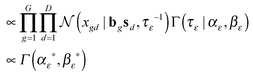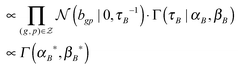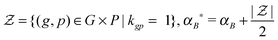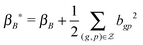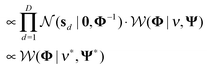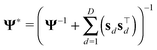Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pathway-based Bayesian inference of drug–disease interactions†
Naruemon
Pratanwanich
and
Pietro
Lió
*
University of Cambridge, JJ Thomson Avenue, CB3 0FD, UK. E-mail: np394@cam.ac.uk; pl219@cam.ac.uk
First published on 3rd April 2014
Abstract
Drug treatments often perturb the activities of certain pathways, sets of functionally related genes. Examining pathways/gene sets that are responsive to drug treatments instead of a simple list of regulated genes can advance our understanding about such cellular processes after perturbations. In general, pathways do not work in isolation and their connections can cause secondary effects. To address this, we present a new method to better identify pathway responsiveness to drug treatments and simultaneously to determine between-pathway interactions. Firstly, we developed a Bayesian matrix factorisation of gene expression data together with known gene–pathway memberships to identify pathways perturbed by drugs. Secondly, in order to determine the interactions between pathways, we implemented a Gaussian Markov Random Field (GMRF) under the matrix factorization framework. Assuming a Gaussian distribution of pathway responsiveness, we calculated the correlations between pathways. We applied the combination of the Bayesian factor model and the GMRF to analyse gene expression data of 1169 drugs with 236 known pathways, 66 of which were disease-related pathways. Our model yielded a significantly higher average precision than the existing methods for identifying pathway responsiveness to drugs that affected multiple pathways. This implies the advantage of the between-pathway interactions and confirms our assumption that pathways are not independent, an aspect that has been commonly overlooked in the existing methods. Additionally, we demonstrate four case studies illustrating that the between-pathway network enhances the performance of pathway identification and provides insights into disease comorbidity, drug repositioning, and tissue-specific comparative analysis of drug treatments.
1 Introduction
Cellular processes before and after drug treatments often result from the concerted interactions of certain sets of genes. Traditionally, microarray-based case–control studies provide the information about such mechanisms through a list of differentially expressed genes. It has currently become of great interest to analyse at the level of pathways/gene sets instead of individual genes. This is because firstly looking at the pathway/group level can reduce the complexity of the analysis due to the dimension reduction. Secondly, some of the important differences may not be detected in the simple gene list because of the dominating noise inherent to the microarray technology.1 Finally, the gene-wise approach limits the scalability of comparative studies, since the gene list profiles may marginally overlap between two independent experiments despite being under the same biological conditions (e.g. drug treatments or disease states).1 In contrast, the pathway-based approach can overcome these limitations since pathways already embody functionally related genes, providing interpretable information with low dimensionality. This also allows a certain variation of genes that are differently expressed under the same biological conditions.Notably, connections between genes may trigger unexpected effects. On one hand, the interactions can cause negative outcomes such as comorbidity, the presence of one or more diseases co-occurring with the primary disease. In particular, Goh et al. have assumed that diseases could comorbid with each other through overlapping disease-causing genes, as represented by the human disease network (HDN).2 On the other hand, the links between genes can also bring medical benefits that enable polypharmacology and drug repositioning. For example, the network of drug targets and disease-related genes can help determine the new potential indications of the existing drugs.3 As connections exist not only within a pathway but also across different pathways, the network of pathway interactions still remains to be established.
To better understand cellular processes in case–control settings, we aim to source microarray data in an efficient manner. Firstly, we have developed a Bayesian matrix factorisation of gene expression data and taken advantage of known gene–pathway memberships to identify pathway responsiveness. Secondly, we have augmented the Bayesian factor model with a GMRF to determine the interactions between pathways. Assuming the GMRF prior of pathway responsiveness, we used the precision (inverse co-variance) matrix of a Gaussian distribution to model the correlations between pathways.4 In this study, we applied the combination of the Bayesian factor models and the GMRF to analyse gene expression data of drug treatments.
GMRF models have been widely developed to learn spatial interactions.5,6 Recently, they have been used for the analysis of genomic data to identify causal or marker genes and simultaneously to reconstruct between-gene interactions.7,8 To the best of our knowledge, this is the first effort to apply the GMRF model to reconstruct the network of between-pathway interactions.
As for responsive pathway identification, many studies extracted responsive pathways by leveraging gene expression data for the network of gene interactions, regardless of the prior knowledge about gene–pathway memberships.9–11 These results would leave a burden of expertise for interpretation. Ma and Zhao developed a Bayesian factor model for identifying pathway responsiveness, called FacPad, which utilises the prior knowledge of gene–pathway memberships.12 Similarly, a well-known method, Gene Set Enrichment Analysis (GSEA), determines whether a pre-defined pathway is enriched in a given gene expression profile using statistical scores.1 However, both have assumed that individual pathways are independent, which limits to reflect the realistic molecular activities. We have overcome this limitation by implementing a GMRF to model the dependencies between pathways. This GMRF extension improves the performance of responsive pathway identification.
Modeling pathway dependencies, which are regarded as latent structures, is challenging because they cannot be observed directly from the data. Although the issue of dependency structure in latent space has been solved,13,14 the literature concerning between-pathway relationships is still limited. Luo et al. connected two pathways through the overlapping perturbed member genes in time series gene expression data,15 but only a few pathways were analysed. Recently, Pang and Zhao developed a large-scale pathway clustering method based on the inferred distances where each pathway was used as a classification tree to predict classes of phenotypes from gene expression data, and two pathways were considered similar if they predicted the same class of phenotypes.16 However, while they predicted the between-pathway relations deterministically after the classification tasks, we probabilistically modeled such interactions concurrently with the pathway responsiveness identification task. Due to the simultaneous tasking in our model, not only can the results from the identification part reflect pathway dependency behaviours, but also the pathway interactions help improve the accuracy to identify pathway responsiveness to drug treatments.
2 Data
Our model requires two types of data inputs – differential gene expression data and known gene–pathway associations informing gene memberships in each pathway. We utilised gene expression data of drug treatments from the human breast epithelial adenocarcinoma cell line (MCF7) provided by CMap (build 02),17,18 and exploited the prior knowledge of gene–pathway memberships from Kyoto Encyclopedia of the Genes and Genomes (KEGG) database.19 After pre-processing (see the ESI† for more details), 3041 genes, 1169 drugs, and 236 known pathways (90% of the total KEGG pathways), 66 of which were disease pathways, remained in our analysis. We applied our model to another gene expression data set of the epithelial cell line of human prostate adenocarcinoma (PC3) from CMap17,18 for tissue comparative analysis as discussed in the final case study.3 Results and discussion
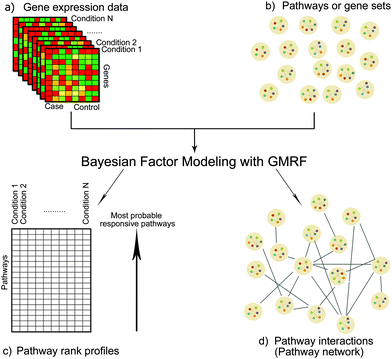
Identifying pathway responsiveness under any biological conditions (e.g. drug treatments and disease conditions) can be accomplished using a Bayesian factor model.12 We modeled pathways as latent variables, of which gene members were pre-defined.12 More importantly, we implemented a GMRF prior in order to capture the network structure of interactions between pathways.Given the differential gene expression data and the prior knowledge of gene–pathway memberships, we inferred the following: (1) pathway responsiveness specific to each biological condition and (2) interactions between pathways (Fig. 1). The novelty of this study lies in the latter, which contributed the network of between-pathway interactions.
In the next section, we show the results of model verification and validation including comparison with the other existing models, followed by four case studies as to how this inferred pathway network helps us to understand the underlying mechanisms among drugs and diseases.
3.1 Model verification with simulation studies
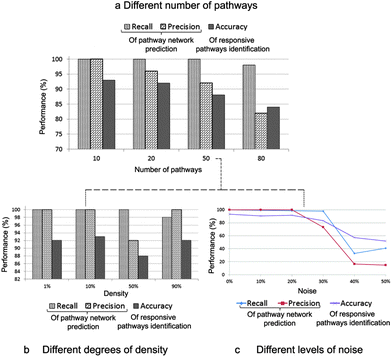
To verify our model, we synthesised different gene expression data sets of 3000 genes and 2000 drugs from a Gaussian distribution with respect to a random but known underlying network of between-pathway interactions that varied over 10, 20, 50, and 80 pathways. Next, we assigned some pathways to each drug as its responsive pathways. Finally, we assessed for our model how many original between-pathway interactions were recovered and how many responsive pathways were identified correctly. We used recall and precision metrics to evaluate the performance of our inference on the pathway network and accuracy metric for the assessment of pathway identification.Fig. 2 shows the overall performance of our model on the different synthetic data sets. Although the performance was dropping when the number of pathways was increasing, it was no less than 80% (Fig. 2a). On the other hand, an increase in density slightly affected the model performance (Fig. 2b). We also conducted the robustness analysis of noise tolerance. Here, noise can be originated from both inputs, the gene expression data and the information of gene–pathway memberships. However, we tested our model only with the noise caused by the latter case because we already incorporated the noise model from the first case. Our model proved its robustness up to 30% of noise (Fig. 2c).
3.2 Model validation and comparative studies
To validate, we applied our model to analyse gene expression data of drug treatments from CMap and exploited the prior information of gene–pathway memberships from KEGG. We then evaluated two outputs: the pathway rank profiles responsive to drug treatments and the network of between-pathway interactions.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 chemical-pathway associations were left for the validation.
502 chemical-pathway associations were left for the validation.
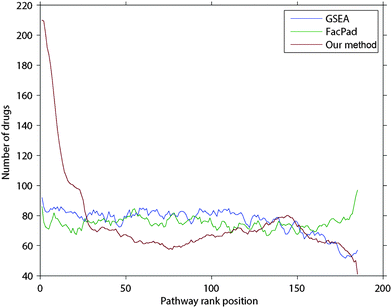
In each drug d, we ranked all pathways according to their inferred responsiveness values. The ranked list of pathways is called a pathway rank profile where pathways at the upper ranks are more likely to be responsive to drug d. Fig. 3 demonstrates the frequency of pathways that were documented in CTD in each rank of the inferred pathway rank profiles. We found that 210 drugs were identified at the first rank, which was 1.5–2.6 times higher than random expectation. Furthermore, our method identified the perturbed pathways at the upper ranks than those inferred by FacPad and GSEA (p < 0.0001).
Using the validation set from CTD, we also calculated the average precision (AP)21 over the recall ranged from 0 to 1, as shown in eqn (1) for each drug d:
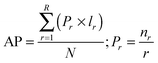 | (1) |
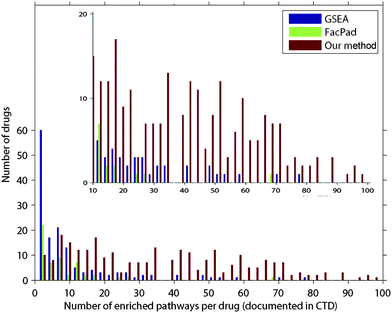 | ||
| Fig. 4 Comparison of the average precision values for evaluating each pathway rank profile from our model, FacPad, and GSEA. We calculated the average precision (eqn (1)) for each profile and compared this metric among the methods. Out of 500 drugs in the validation set, the number of pathway rank profiles with the highest average precision in each model is demonstrated in the y-axis. We classified drugs according to the number of enriched pathways per drug as documented in CTD shown in the x-axis. We found that our model outperformed the others for identifying responsive pathways in the case of drugs that had an effect on more than 10 pathways. These results are illustrated in the refined scale with a y-axis ranging from 0 to 20 in the inset plot. | ||
Theoretically, there are many factors why pathways interact with each other, one of which is the overlapping of their gene members. Thus, we used the number of the overlapping genes between two pathways from the curated KEGG database to quantify the validity of our results. We first ranked the pathway interactions according to their correlations derived from our approach (eqn (5)). We then applied the cumulative gain (CG),22 to determine whether the inferred interactions at the upper ranks were more likely to imply true interactions. Here, the number of overlapping genes indicated the possibility of true interactions between pathways. For each rank r, we calculated the ratio between the CG of our model and that of the random expectation, called fold enrichment of cumulative gain (FE_CGr) as in eqn (2):
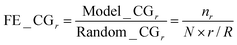 | (2) |
In addition, we calculated the significance of each pathway interaction in terms of perturbed member genes using a hypergeometric distribution15 (see the ESI†). Here, a perturbed gene was a gene with the absolute fold change deviated from the mean of all genes by more than one standard deviation. Let N, n, and x be the number of all perturbed genes under given conditions, in either of a pathway pair, or in both pathways respectively. The significance is the probability of at least X genes that are perturbed in both pathways, which follows the hypergeometric distribution15 as shown in eqn (3):
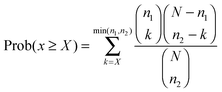 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 interactions stayed unconnected with zero values (see Methodology). Fig. 5b also shows that these interactions significantly contained more overlapping genes than the rest (p < 0.001).
000 interactions stayed unconnected with zero values (see Methodology). Fig. 5b also shows that these interactions significantly contained more overlapping genes than the rest (p < 0.001).
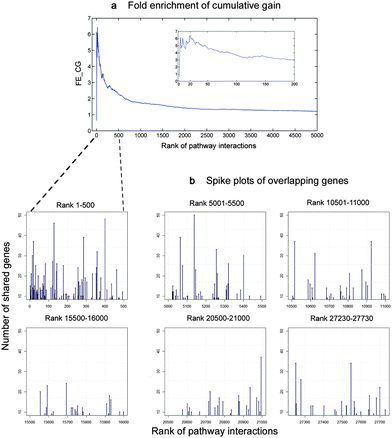 | ||
Fig. 5 Relation of our inferred pathway interactions and the number of overlapping genes. We defined true positives as the interactions of pathways that had genes in common. To validate, we ranked the pathway interactions by their correlations as calculated with our method in a descending order. We then counted the number of genes shared by any two pathways for every interaction. Next, we calculated the cumulative true positives weighted by the number of overlapping genes in each rank, also known as cumulative gain (CG),22 and compared this metric against random expected values. (a) Fold enrichment of cumulative gain (FE_CG) as calculated in eqn (2), which is the ratio between the CG of our model compared to random expectation,12 reached the peak of (6.5 fold) at the upper ranks (20th). Out of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 possible interactions, the top 500 interactions inferred by our model were likely to share genes approximately 2–6.5 fold compared to the random expectation. (b) Number of overlapping genes of each interaction in six intervals, each of which equally spans to 500 rank positions. As shown, the density of spikes at the first 500-rank interval was at the maximum then it continually declined, and reached the minimum at the lower end of the ranks. 730 possible interactions, the top 500 interactions inferred by our model were likely to share genes approximately 2–6.5 fold compared to the random expectation. (b) Number of overlapping genes of each interaction in six intervals, each of which equally spans to 500 rank positions. As shown, the density of spikes at the first 500-rank interval was at the maximum then it continually declined, and reached the minimum at the lower end of the ranks. | ||
However, we also modeled the interactions between pathways that did not share any genes. Fig. 6 compares the networks of the top 500 pathway interactions resulting from two methods. The first network of pathway interactions derived from our Bayesian factor model with GMRF (Fig. 6a). For the second network, two pathways were linked if they shared perturbed member genes15 and their interaction strength was proportional to the number of their overlapping genes (Fig. 6b). We mapped all 236 pathways into 22 classes based on the definition by KEGG with different colours. Fig. 6a contains 67% of inter pathway-class interactions while 42% in Fig. 6b. The high percentage of inter pathway-class interactions resulted from our model may imply the complex relationships beyond gene connections. For example, we uncovered the links between cancer and metabolism (Fig. 6b). According to the recent study,23 metabolism first generates oxygen radicals which contribute to loss of tumor suppressors and finally lead to cancer. These cancer cells will in turn rewire back to metabolic pathways for cell growth and survival. We also rediscovered the interactions between cancer pathways and those of infectious diseases caused by viral,24 bacterial,25,26 and parasitic26 agents (Fig. 6b), while the other model reconstructed only the links with viral agents.
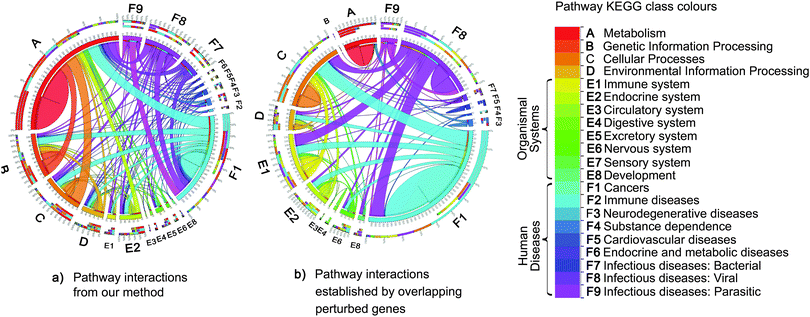 | ||
| Fig. 6 Comparisons of pathway interactions. The colour of each pathway maps to each class of pathway defined by KEGG. The edge size is proportional to the number of interactions from one pathway class to another. Each interaction is established by two methods. (a) Firstly, pathway interactions resulted from our Bayesian factor model with GMRF. (b) Secondly, two pathways were linked if they shared perturbed member genes.15 Of top 500 interactions, our approach yielded more interactions across different classes of pathways, nearly double the number of interactions relative to the second method (b), which discovered more intra pathway-class interactions. For instance, the relationships between cancers and metabolism pathways23 rediscovered by our method were absent from the second method (b). The second method limits to capture the interactions between pathways without overlapping genes. In contrast, our method can model pathway interactions according to both overlapping genes and the co-occurrence of pathways observed in the gene expression data. | ||
3.3 Applications of the pathway network
In this case study, we explored a sub-network of the top 500 interactions, which contained the largest hub namely the hepatitis B pathway. We found that infectious diseases, especially hepatitis B and C, connected with more than half of cancer types in our study (Fig. 7a). This finding agrees with the statistics from a survey of Cancer Research UK in 2008, showing that hepatitis B and C viruses are the third most attributable risk to cancers only after human papillomavirus and helicobacter pylori, which were not included in our study. Additionally, the inferred pathway network suggest that NF-κB, followed by FCεRI and GnRH signaling pathways be the main contributions underlying the comorbidity among infectious diseases and cancers.
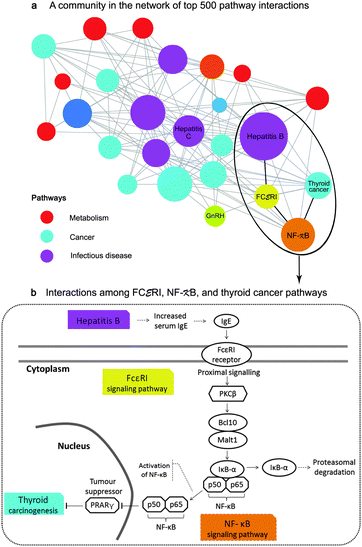 | ||
| Fig. 7 Application of the pathway network for disease mechanisms and comorbidity (case study 1). (a) depicts a sub-network of between-pathway interactions. Each node represents a pathway with the node size proportionate to its degree and each edge represents an inferred interaction. The inferred interactions in this community imply the comorbidity among infectious diseases, especially hepatitis B and C, and more than half of all cancer types in this study through the contribution of the inflammatory signaling pathways namely, NF-κB and FCεRI. (b) illustrates the comorbidity of hepatitis B and thyroid cancer through the interactions of NF-κB and FCεRI. Those mechanisms were previously confirmed by separated studies.30–33 | ||
Particularly, we can make a hypothesis that hepatitis B may comorbid with thyroid cancer through the mechanisms of FCεRI and NF-κB signaling pathways. The processes may begin with the increased level of serum Immunoglobulin E (IgE) in hepatitis B patients30 that theoretically activates FCεRI receptors as described in KEGG (inferred corr = 0.14, rank 33th, overlapping perturbed genes with p < 0.0001 from a hypergeometric test). We then confirmed the inferred interaction between NF-κB and FCεRI (inferred corr = 0.23, rank 10th, overlapping perturbed genes with p < 0.005) by the literature. Klemm and Ruland reported that the inflammatory signals in mast cells could be transmitted between these pathways through the following events: the activation of the receptor-associated tyrosine kinases upon FcεRI ligation, the activation of PKC isoforms and the protein complex of Bcl10/Malt1, the degradation of IκB-α, and finally the activation of NF-κB31 (Fig. 7b). Moreover, we rediscovered the association of the NF-κB signaling pathway and the thyroid cancer pathway (corr = 0.10, rank 64th) even though they had no overlapping genes. Several studies have claimed that the activation of NF-κB blocks the PRARγ tumor suppressor, promoting thyroid carcinogenesis.32,33 As the relevance of NF-κB and FCεRI signaling pathways as well as the high prevalence of thyroid cancer in hepatitis patients34 have recently been reported,35,36 our hypothesis that cancers may comorbid with infectious diseases through these inflammatory signaling pathways should be further studied.
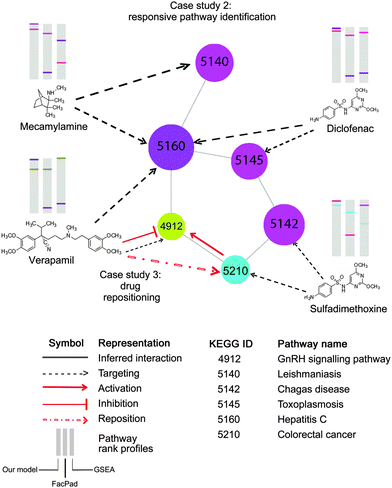 | ||
| Fig. 8 Application of the inferred pathway network to enhance the identification of pathway responsiveness to drug treatments, (case study 2) and drug repositioning (case study 3). Each node represents a pathway with the corresponding KEGG ID. This part of the pathway network derived from Fig. 6b is targeted by four drugs, Mecamylamine, Verapamil, Diclofenac, and Sulfadimethoxine, as documented in CTD. In the diagram, there are three pathway rank profiles inferred by our model, FacPad, and GSEA are shown above each chemical structure. The position of any targeted pathway within each rank profile is represented by a line with the same colour as the corresponding targeted pathway. As seen on the pathway rank profiles inferred by our model, any two pathways that were closely correlated to each other were placed in the upper rank, unlike FacPad and GSEA. This proves that the inferred pathway interactions can help improve the model to identify pathway responsiveness to drug treatments. As seen in case study 3, the pathway network also enables drug repositioning; particularly a repositioning of Verapamil for recovering the colorectal cancer state.41 With the inferred pathway interlinks, we may make an assumption that the GnRH signaling pathway is the underlying mechanism for such repositioning, therefore, providing a bridge for Verapamil to counteract the effects of colorectal cancer. These findings are consistent with the studies claiming that GnRH hormone is activated by colorectal cancer,40 but inhibited by Verapamil.39 | ||
For example, we repositioned Verapamil, which has been currently used for the treatment of angina and hypertension, to the new indication for colorectal cancer. As documented in CTD and inferred by our method, this compound targeted the GnRH signaling pathway, which linked colorectal cancer in the inferred pathway network as shown in Fig. 8 (corr = 0.06, rank 261th, shared perturbed genes with p < 0.001). This suggests the new indication of Verapamil to recover the disease state of colorectal cancer. Our hypothesis is in line with the independent studies claiming that Verapamil could suppress the release of GnRH hormone39 which is over-expressed in colorectal cancer.40 More recently, this drug repositioning has been confirmed by a clinical study concluding that the use of Verapamil with chemotherapy can improve clinical efficacy in metastatic colorectal patients.41
Upon the integration of the pathway network and responsive pathway identification from our method, we can provide informative hypotheses of not only the directions to reposition drugs but also the underlying pathways to explain the new drug–disease mechanisms.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765th in PC3. There exist evidences that both pathways are linked in mast cells;31 however, the study concerning the issue of tissue types is still limited. Generally, FcεRI plays a central role in the initiation and control of atopic allergic inflammation42 and NF-κB involves in many cancers.43 Thus, the existence of the interaction between these two pathways may account for the role of allergic disorders differs between the development of cancer cells in breast and prostate tissues.44 Such a difference in between-pathway interactions in different tissue types can improve our understanding of disease mechanisms, leading to the advance in tissue-specific therapies.45,46
765th in PC3. There exist evidences that both pathways are linked in mast cells;31 however, the study concerning the issue of tissue types is still limited. Generally, FcεRI plays a central role in the initiation and control of atopic allergic inflammation42 and NF-κB involves in many cancers.43 Thus, the existence of the interaction between these two pathways may account for the role of allergic disorders differs between the development of cancer cells in breast and prostate tissues.44 Such a difference in between-pathway interactions in different tissue types can improve our understanding of disease mechanisms, leading to the advance in tissue-specific therapies.45,46
4 Methodology
4.1 Notation
In this paper, we represent a matrix, a vector, and a scalar with a bold capital letter, a bold lowercase letter, and an italic lowercase letter respectively. Moreover, we use double brackets to represent a matrix and its elements such as X = [[xij]], indicating that the matrix X consists of the scalar elements xij where i and j denote a row index and a column index respectively.4.2 Method overview
In this study, we have performed the analysis of the differential gene expression data of G genes under D conditions. Our goal is to identify responsive pathways for each condition and simultaneously to uncover between-pathway relationships. To begin with, we assume that the differential gene expression data arise from the effects of perturbed genes being members of the pathways responsive to each condition e.g. a drug or a disease. This concept can be implemented by a matrix factorisation,12 where the observed differential gene expression data matrix X ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) G×D is decomposed into two matrices: X ∼ BS. The first matrix B ∈
G×D is decomposed into two matrices: X ∼ BS. The first matrix B ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) G×P denotes the strength of gene membership in each pathway, called a gene–pathway matrix. The second matrix S ∈
G×P denotes the strength of gene membership in each pathway, called a gene–pathway matrix. The second matrix S ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) P×D corresponds to the degree of pathway responsiveness to each condition, called a pathway-condition matrix. Note that P is the number of pathways shared by the matrix B and the matrix S, since pathways are regarded as the latent factors underlying both genes and conditions. Similar to FacPad,12 we used the prior knowledge of gene–pathway memberships denoted by a matrix K ∈ {0,1}G×P from KEGG19 to force the sparsity (the pattern of 0's entries) of the matrix B. We developed a GMRF model within the matrix decomposition with the aim of capturing pathway dependencies by imposing a Gaussian distribution on the matrix S with a precision (inverse covariance) matrix Φ ∈
P×D corresponds to the degree of pathway responsiveness to each condition, called a pathway-condition matrix. Note that P is the number of pathways shared by the matrix B and the matrix S, since pathways are regarded as the latent factors underlying both genes and conditions. Similar to FacPad,12 we used the prior knowledge of gene–pathway memberships denoted by a matrix K ∈ {0,1}G×P from KEGG19 to force the sparsity (the pattern of 0's entries) of the matrix B. We developed a GMRF model within the matrix decomposition with the aim of capturing pathway dependencies by imposing a Gaussian distribution on the matrix S with a precision (inverse covariance) matrix Φ ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) P×P. Consequently, we drew the undirected links between any two pathways according to the non-zero off-diagonal elements of the matrix Φ. Meanwhile, we determined pathway responsive to each condition from the matrix S.
P×P. Consequently, we drew the undirected links between any two pathways according to the non-zero off-diagonal elements of the matrix Φ. Meanwhile, we determined pathway responsive to each condition from the matrix S.
Fig. 9 shows our methodology in a schematic view. The following subsections are the brief introduction of GMRF, the mathematical description of our model in detail and our inference method.
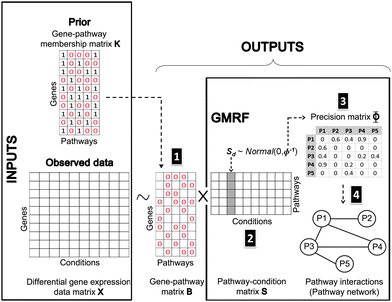 | ||
| Fig. 9 Bayesian matrix factorisation modeling with GMRF. Our model requires two input types: an observed differential gene expression data matrix X under conditions of interest and a pre-defined gene-pathway membership binary matrix K. The main task is to decompose the matrix X into a gene–pathway matrix B and a condition-pathway matrix S: X ∼ BS. The first step (1) is to make inference on the matrix B. The matrix K is used as prior knowledge to guide the sparsity pattern of the matrix B.12 The significant contribution to this work is the modeling of a Gaussian distribution with a zero mean and a precision Φ on the matrix S. Thus, the next two steps (2 and 3) are to infer the matrix S and its precision matrix Φ. The values in each column of the matrix S can reflect the pathway responsiveness to the corresponding drug treatments or disease conditions. According to the concept of GMRF that an undirected graph is encoded by non-zero entries in the off-diagonal precision matrix, the values in the matrix Φ represent the conditional correlation of every pathway pair. In the last step (4), a pathway interaction network can be finally constructed, given the matrix Φ. | ||
4.3 Gaussian Markov Random Field (GMRF)
GMRF, referred to as a Gaussian Graphical model (GGM) interchangeably,47 is a special case of Markov Random Field forming with respect to an undirected graph if it satisfies the Markov properties.48 An N-dimensional random vector x which is defined by GMRF4 is assumed to follow a zero-mean multivariate Gaussian distribution with a precision matrix Φ = [[Φij]]; i,j ∈ {1,…,N} as shown in eqn (4):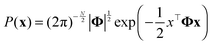 | (4) |
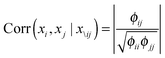 | (5) |
4.4 Model description
The observed differential gene expression data matrix X = [[xgd]] was linearly decomposed into two matrices: a gene–pathway matrix B = [[bgp]] and a pathway-condition matrix S = [[spd]], where g ∈ {1,…,G}, d ∈ {1,…,D}, and p ∈ {1,…,P}. Such decomposition can be represented in an element-wise linear combination with an additive noise model as shown in eqn (6):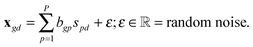 | (6) |
First of all, we modeled the noise ε with a zero-mean Gaussian with the precision τε. We also put a conjugate prior Gamma distribution with the shape parameter αε and the rate parameter βε on τε. This noise model was applied for every entry of the matrix X, known as an isotopic Gaussian noise model.
Likewise, we put a zero-mean Gaussian distribution with the precision τB on every entry of the matrix B. We also exploited the pre-defined gene–pathway memberships matrix K = [[kgp]], where kgp = 1 if gene g belonged to pathway p and kgp = 0 otherwise, to control the sparsity pattern of the matrix B.12 Therefore, the values in the matrix B suggested the strength of the gene membership in each pathway, which was not specified by the binary matrix K.
In order to capture the relations of the latent pathways, we put the zero-mean GMRF with the precision matrix Φ on every condition vector of the matrix S (eqn (4)). With the GMRF, the conditional correlations between any two pathways were described by the parameter Φ = [[Φij]];i,j ∈ {1,…,P} (eqn (5)). We next constructed an undirected graph illustrating such relations. Let G = (V,E) denotes an undirected graph where nodes represent hidden pathways and edges denote any pairwise relations. An edge between node i and j where (i,j) ∈ V × V is drawn if and only if ϕij > 0. The Wishart distribution, a conjugate prior of normal likelihood function, with the degree of freedom ν and the scale matrix Ψ was used as the prior of Φ.
4.5 Inference
According to the models described above, we needed to make inference on τε, τB, B, S, and Φ with a setting of hyper-parameters (αε, βε, αB, βB, ν, and Ψ). However, only the matrix S and the matrix Φ were our main interests for further analysis. Under a Bayesian framework, we developed the correlated pathways Gibbs sampling algorithm to approximate the joint distribution of those five parameters (Algorithm 1).Below is the conditional posterior distribution for each step in the correlated pathways Gibbs sampling. The first two (1–2) demonstrate those of the inverse variances in the noise model ε and the gene–pathway matrix B respectively. The calculation in the third (3) is consistent to that of FacPad.12 The last two (4–5) allow us to learn pathway responsiveness together with between-pathway interactions (see the ESI† for the calculation methods in detail):
(1) τε ∼ P(τε|X, B, S, αε, βε)
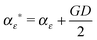 and
and 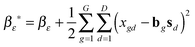 .
.
(2) τB ∼ P(τB|B, αB, βB)
(3) bg ∼ P(bg|X, S, τε, τB)
∝ ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (bg|μB*,(ΦB*)−1) if kgp = 1; p = 1, 2, 3,…,P
(bg|μB*,(ΦB*)−1) if kgp = 1; p = 1, 2, 3,…,P
μ B * = (ΦB*)−1(τεS*xTg), ΦB* = τεS*(S*)T + τBI|S*| and S* = the submatrix of S with the row indices corresponding to the 1-entries of the vector kg.
(4) Φ ∼ P(Φ|S, ν, Ψ)
(5) sd ∼ P(sd|X, B, τε, Φ)
∝![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (xd|Bsd,τε−1IG)·
(xd|Bsd,τε−1IG)·![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (sd|0,Φ−1)
(sd|0,Φ−1)
∝![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (sd|μ*, (Φ*)−1)
(sd|μ*, (Φ*)−1)
μ* = (Φ*)−1(τεBTxd) and Φ* = τεBTB + Φ.
Our MATLAB implementation of the correlated pathway Gibbs sampling is available upon request to the corresponding author. The burn-in period can be selected according to the trace plots. Moreover, to decrease autocorrelation, samples from the Gibbs sampling can be collected subject to the thinning rate, and then be averaged across the collecting iterations to form the final estimations.
5 Conclusions
Given differential gene expression data of drug treatments and the prior knowledge of gene memberships in each pathway of interest, we have presented Bayesian factor modeling with GMRF to identify pathway responsiveness to drug treatments, concurrently with the reconstruction of between-pathway interactions.Specifically, we treated all pathways as latent variables, of which gene members were pre-defined. We then applied a Bayesian matrix factorisation model to determine pathways that were perturbed specific to drug treatments.12 The underlying assumption is that gene expression data arise from the effects of perturbed gene members of the pathways responsive to drug treatments.12 Therefore, a gene expression data matrix was decomposed into a gene–pathway matrix indicating gene membership strength in each pathway and a drug-pathway matrix reflecting pathway responsiveness to each drug.
More importantly, we extended the Bayesian matrix factorisation models with a GMRF prior. This augmentation was inspired by the fact that genes could pass their signals across different groups or pathways.16 We imposed a Gaussian distribution with a zero mean and a precision matrix (an inverse covariance matrix) on the drug-pathway matrix. This precision matrix was mapped to an undirected graph depicting pairwise dependencies between pathways. Here, the interactions between any pair of pathways were drawn if and only if they were direct relationships without the mediation through any other pathway. We quantified the between-pathway interactions by calculating their correlations directly from the precision matrix under the GMRF framework. However, we can explore indirect relationships from the network of all direct interactions.
Our method can infer complex relations between two pathways through other layers of molecules such as proteins or metabolites, which cannot be observed by only overlapping perturbed genes. With our approach, the complexity can be simplified by the replacement of a link between pathways derived from the co-occurrence of pathways from the observed gene expression data.
The combination of the Bayesian factor model and the GMRF prior allows us to identify pathway responsiveness and to extract between-pathway interactions in a unified framework. As a result, our method yielded a higher average precision than the existing methods for identifying pathway responsiveness to drugs that affect multiple pathways. This contribution is advantageous to the analysis of disease gene expression data as the number of associated pathways is increasing in proportion to disease complexity, comorbidity,49 and progression time.50 In addition, the network of between-pathway interactions can also provide the mechanistic insights in terms of pathway-based functionality that accommodate the studies of disease comorbidity, drug repositioning, and tissue-specific comparative analysis.
Acknowledgements
We thank Dr Viet Anh Nguyen for a productive discussion on Bayesian approaches. We thank FP7-ICT Mission T2D for funding. NP acknowledges the Royal Thai Government Scholarship.References
- A. Subramanian, P. Tamayo, V. K. Mootha, S. Mukherjee, B. L. Ebert, M. A. Gillette, A. Paulovich, S. L. Pomeroy, T. R. Golub, E. S. Lander and J. P. Mesirov, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 15545–15550 CAS.
- K.-I. Goh, M. E. Cusick, D. Valle, B. Childs, M. Vidal and A.-L. Barabási, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 8685–8690 CrossRef CAS PubMed.
- Z. Wu, Y. Wang and L. Chen, Mol. BioSyst., 2013, 9, 1268–1281 RSC.
- H. Rue and L. Held, Gaussian Markov Random Fields: Theory and Applications, Chapman & Hall, London, 2005, vol. 104 Search PubMed.
- Y. C. MacNab, Stat. Methods Med. Res., 2011, 20, 49–68 CrossRef PubMed.
- O. Demirkaya, M. H. Asyali and M. M. Shoukri, Bioinformatics, 2005, 21, 2994–3000 CrossRef CAS PubMed.
- B. Peng, D. Zhu, B. P. Ander, X. Zhang, F. Xue, F. R. Sharp and X. Yang, PLoS One, 2013, 8, e67672 CAS.
- Z. Wei and H. Li, Bioinformatics, 2007, 23, 1537–1544 CrossRef CAS PubMed.
- Y. Silberberg, A. Gottlieb, M. Kupiec, E. Ruppin and R. Sharan, J. Comput. Biol., 2012, 163–174 CrossRef CAS PubMed.
- Y.-Q. Qiu, S. Zhang, X.-S. Zhang and L. Chen, Syst. Biol., 2009, 3, 475–486 Search PubMed.
- Y. Wang and Y. Xia, Proc. Optim. Syst. Biol., 2008, 9, 333–340 Search PubMed.
- H. Ma and H. Zhao, Bioinformatics, 2012, 28, 2662–2670 CAS.
- K. Kavukcuoglu, H. Park, Y. He and Y. Qi, NIPS, 2012, pp. 2375–2383 Search PubMed.
- J. D. Lafferty and D. M. Blei, Advances in neural information processing systems, 2005, pp. 147–154 Search PubMed.
- W. Luo, M. S. Friedman, K. D. Hankenson and P. J. Woolf, BMC Syst. Biol., 2011, 5, 82 CrossRef PubMed.
- H. Pang and H. Zhao, BMC Bioinf., 2008, 9, 87 CrossRef PubMed.
- J. Lamb, E. D. Crawford, D. Peck, J. W. Modell, I. C. Blat, M. J. Wrobel, J. Lerner, J.-P. Brunet, A. Subramanian, K. N. Ross, M. Reich, H. Hieronymus, G. Wei, S. A. Armstrong, S. J. Haggarty, P. A. Clemons, R. Wei, S. A. Carr, E. S. Lander and T. R. Golub, Science, 2006, 313, 1929–1935 CrossRef CAS PubMed.
- J. Lamb, Nat. Rev. Cancer, 2007, 7, 54–60 CrossRef CAS PubMed.
- M. Kanehisa, S. Goto, Y. Sato, M. Furumichi and M. Tanabe, Nucleic Acids Res., 2012, D109–D114 CrossRef CAS PubMed.
- A. P. Davis, C. G. Murphy, R. Johnson, J. M. Lay, K. Lennon-Hopkins, C. Saraceni-Richards, D. Sciaky, B. L. King, M. C. Rosenstein, T. C. Wiegers and C. J. Mattingly, Nucleic Acids Res., 2013, 41, D1104–D1114 CrossRef CAS PubMed.
- R. Baeza-Yates and B. Ribeiro-Neto, Modern information retrieval, Addison Wesley, England, 1999 Search PubMed.
- K. Järvelin and J. Kekäläinen, ACM Trans. Inf. Syst., 2002, 20, 422–446 CrossRef.
- C. V. Dang, Genes Dev., 2012, 26, 877–890 CrossRef CAS PubMed.
- C. de Martel, J. Ferlay, S. Franceschi, J. Vignat, F. Bray, D. Forman and M. Plummer, Lancet Oncol., 2012, 13, 607–615 CrossRef.
- J. Parsonnet, Environ. Health Perspect., 1995, 103, 263 Search PubMed.
- V. Samaras, P. I. Rafailidis, E. G. Mourtzoukou, G. Peppas and M. E. Falagas, J. Infect. Dev. Countries, 2010, 4, 267–281 Search PubMed.
- Q. Wang, W. Liu, S. Ning, J. Ye, T. Huang, Y. Li, P. Wang, H. Shi and X. Li, Eur. J. Hum. Genet., 2012, 20, 1162–1167 CAS.
- D.-S. Lee, J. Park, K. A. Kay, N. A. Christakis, Z. N. Oltvai and A.-L. Barabási, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9880–9885 CAS.
- Y. Li and P. Agarwal, PLoS One, 2009, 4, e4346 Search PubMed.
- D. Gutierrez, P. Guardia, J. Delgado, J. Gutiérrez, F. Monteseirin, A. De la Calle, P. Lobatón, A. Senra and J. Conde, J. Invest. Allergol. Clin. Immunol., 1997, 7, 119 CAS.
- S. Klemm and J. Ruland, Immunobiology, 2006, 211, 815–820 CAS.
- I. Palona, H. Namba, N. Mitsutake, D. Starenki, A. Podtcheko, I. Sedliarou, A. Ohtsuru, V. Saenko, Y. Nagayama and K. Umezawa, et al. , Endocrinology, 2006, 147, 5699–5707 CrossRef CAS PubMed.
- Y. Kato, H. Ying, L. Zhao, F. Furuya, O. Araki, M. Willingham and S. Cheng, Oncogene, 2005, 25, 2736–2747 CrossRef PubMed.
- A. Antonelli, C. Ferri, P. Fallahi, A. Pampana, S. M. Ferrari, L. Barani, S. Marchi and E. Ferrannini, Thyroid, 2007, 17, 447–451 CrossRef CAS PubMed.
- F. Al-Mulla, M. S. Bitar, M. Al-Maghrebi, A. I. Behbehani, W. Al-Ali, O. Rath, B. Doyle, K. Y. Tan, A. Pitt and W. Kolch, Cancer Res., 2011, 71, 1334–1343 CrossRef CAS PubMed.
- K. Meyer, M. Ait-Goughoulte, Z.-Y. Keck, S. Foung and R. Ray, J. Virol., 2008, 82, 2140–2149 CrossRef CAS PubMed.
- A. Gottlieb, G. Y. Stein, E. Ruppin and R. Sharan, Mol. Syst. Biol., 2011, 7, 496 CrossRef PubMed.
- F. Napolitano, Y. Zhao, V. M. Moreira, R. Tagliaferri, J. Kere, M. D'Amato and D. Greco, J. Cheminf., 2013, 5, 30 CAS.
- K. Yu, P. Rosenblum and R. Peter, Gen. Comp. Endocrinol., 1991, 81, 256–267 CrossRef CAS.
- J. Engel, G. Emons, J. Pinski and A. V. Schally, Expert Opin. Invest. Drugs, 2012, 21, 891–899 CAS.
- Y. Liu, Z. Lu, P. Fan, Q. Duan, Y. Li, S. Tong, B. Hu, R. Lv, L. Hu and J. Zhuang, Cell Biochem. Biophys., 2011, 61, 393–398 CrossRef CAS PubMed.
- D. Von Bubnoff, N. Novak, S. Kraft and T. Bieber, Clin. Exp. Dermatol., 2003, 28, 184–187 CrossRef CAS.
- B. Rayet and C. Gelinas, Oncogene, 1999, 18, 6938–6947 CAS.
- H. Wang, D. Rothenbacher, M. Löw, C. Stegmaier, H. Brenner and T. L. Diepgen, Int. J. Cancer, 2006, 119, 695–701 CrossRef CAS PubMed.
- P. Oh, Y. Li, J. Yu, E. Durr, K. M. Krasinska, L. A. Carver, J. E. Testa and J. E. Schnitzer, Nature, 2004, 429, 629–635 CrossRef CAS PubMed.
- J. E. Schnitzer, Adv. Drug Delivery Rev., 2001, 49, 265–280 CrossRef CAS.
- S. L. Lauritzen, Graphical models, Oxford University Press, Oxford, 1996, vol. 17 Search PubMed.
- D. Barber, Bayesian Reasoning and Machine Learning, Cambridge University Press, Cambridge, 2012 Search PubMed.
- E. Capobianco and P. Lio, Trends Mol. Med., 2013, 19, 515–521 CrossRef PubMed.
- L. Hood, Rambam Maimonides Med. J., 2013, 4, e0012 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4mb00014e |
| This journal is © The Royal Society of Chemistry 2014 |