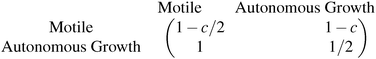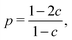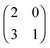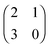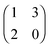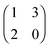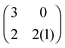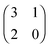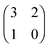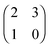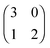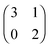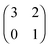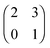Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evolutionary game theory: cells as players
Sabine
Hummert
ab,
Katrin
Bohl
cd,
David
Basanta
e,
Andreas
Deutsch
f,
Sarah
Werner
c,
Günter
Theißen
g,
Anja
Schroeter
c and
Stefan
Schuster
*c
aFachhochschule Schmalkalden, Faculty of Electrical Engineering, Blechhammer, 98574 Schmalkalden, Germany
bFriedrich-Schiller-University Jena, University Medical Centre (Universitätsklinikum) Jena, Institute of Physiology II, 07743 Jena, Germany
cFriedrich-Schiller-University Jena, Faculty of Biology and Pharmacy, Department of Bioinformatics, Ernst-Abbe-Platz 2, 07743 Jena, Germany. E-mail: stefan.schu@uni-jena.de; Fax: +49 (0)3641 946452; Tel: +49 (0)3641 949580
dFriedrich-Schiller-University Jena, Faculty of Biology and Pharmacy, Research Group Theoretical Systems Biology, Leutragraben 1, 07743 Jena, Germany
eIntegrated Mathematical Oncology, H. Lee Moffitt Cancer Center & Research Institute, Tampa, FL, USA
fCentre for Information Services and High Performance Computing (ZIH), Dresden University of Technology, Germany
gFriedrich-Schiller-University Jena, Faculty of Biology and Pharmacy, Department of Genetics, Philosophenweg 12, 07743 Jena, Germany
First published on 7th August 2014
Abstract
In two papers we review game theory applications in biology below the level of cognitive living beings. It can be seen that evolution and natural selection replace the rationality of the actors appropriately. Even in these micro worlds, competing situations and cooperative relationships can be found and modeled by evolutionary game theory. Also those units of the lowest levels of life show different strategies for different environmental situations or different partners. We give a wide overview of evolutionary game theory applications to microscopic units. In this first review situations on the cellular level are tackled. In particular metabolic problems are discussed, such as ATP-producing pathways, secretion of public goods and cross-feeding. Further topics are cyclic competition among more than two partners, intra- and inter-cellular signalling, the struggle between pathogens and the immune system, and the interactions of cancer cells. Moreover, we introduce the theoretical basics to encourage scientists to investigate problems in cell biology and molecular biology by evolutionary game theory.
1. Introduction
Replicating units such as living organisms practically never exist alone. Rather, they interact with each other in various ways, in cooperative or competing relationships. Not least, this applies to cells within multicellular organisms (where usually cooperative types of interaction prevail). Evolutionary theory often tries to understand heritable changes of organisms and cells in terms of better adaptation to a well-defined or even constant environment. This reasoning regarding optimization is, however, often insufficient for understanding biological evolution. It needs to be acknowledged that evolution is almost always co-evolution.1,2 That is, the properties of interacting macromolecules or cells evolve in dependence on each other. This may affect the optimum on all sides and leads to an “open ended” dynamics of evolution rather than to the approximation to a fitness optimum.3An appropriate framework for analysing evolution in dynamic fitness landscapes is evolutionary game theory because it allows one to describe the maximization of fitness of several interacting partners.4–7 Game theory had originally been developed mainly for applications in economics,8 besides inspirations from parlour games such as poker. Later, it was also applied and adapted to applications in biology, resulting in the field of evolutionary game theory.
The metaphor of games is wide-spread in human society. Companies describe themselves as “global players”, the sentence “The game is over” occurs in many thriller movies, and the German word “Beispiel” (example) refers to “Spiel” (game). Especially, the “Games people play”9 have always been of strong interest. Thus, thinking in terms of games helps us to understand complex phenomena in an intuitive way, even if these phenomena are very serious things like conflicts among animals, companies or nations. The book “Game Theory” by Nobel prize winner Roger Myerson10 is thus aptly subtitled “Analysis of Conflict”.
Independently of evolutionary game theory, Eigen and Winkler11 considered many biological processes including prebiotic evolution to have properties of games. In this and an accompanying review,12 however, we use the term “game” in the sense of classical game theory as introduced by Neumann and Morgenstern8 and developed further by Nash13 and Maynard Smith.4 A game describes the interaction of two or more agents (players) in which the outcome of each player depends not only on the own decision, but also on the strategies adopted by the coplayers. Since the pioneering work by Maynard Smith and Price,14 Hamilton15 and others, evolutionary game theory has been applied for decades to the interaction among higher organisms on a macroscopic scale. Examples concern animal behaviour,14,16–20 competition among plants21,22 and interactions between animals and plants.23 Its application to the microscopic scale – the cellular and subcellular levels of life – is much less common, but of increasing interest and importance.
Not only multicellular organisms as a whole, but also cells and some macromolecules within cells can be considered as players in the sense of game theory. Many of their traits can then be regarded as strategies, such as usage of metabolic pathways, expression of virulence factors or generation of different splice variants. The change between strategies can occur by mutations or epigenetic modifications and the succeeding strategy is chosen by natural selection. Therefore, cognitive and rational capabilities are no prerequisites for being considered as a player in the sense of game theory. Merely the property of having a trait (strategy) that is subject to selection and, thus, influences the replicational success (the payoff of the game) makes them potential players.
In this and an accompanying review,12 we provide a broad overview of applications of evolutionary game theory in molecular and cell biology. While the accompanying review12 focuses on the potential of the application of game theory to interactions on the subcellular level, the present one is devoted to interactions between cells. Examples include the formation of biofilms,24 division of labour in consortium pathways,25,26 intercellular signalling,27,28 and tumour biology.29,30 An outline of the mathematical fundamentals of game theory is given in the Appendix.
The sections of this review are ordered according to different biological applications rather than different theoretical game types. Thus, it is structured with respect to biological players. It is worth noting that one and same game type such as the hawk–dove game occurs in different applications.
In our view, the potential of game theory is largely underestimated in molecular and cell biology. One intention of our two reviews is certainly to motivate more researchers to employ the powerful tools of game theory.
2. Respiration versus fermentation
During evolution of metabolic pathways, several alternatives have evolved. Examples are provided by glycolysis and the Entner–Doudoroff pathway, both of which degrade glucose to trioses. While most present-day organisms use glycolysis, the bacterium Zymomonas mobilis (used technologically for producing Tequila) relies on the Entner–Doudoroff pathway, and Escherichia coli and several other bacteria harbour both pathways. Alternatively or in addition, many organisms can use the pathway of respiration (oxidative phosphorylation). Pathway usage can be changed by regulation even during the life-span of one individual.Over the last decade, metabolic games have attracted more and more interest. Different metabolic pathways can be regarded as different strategies in the sense of game theory. Pathways can be restricted to the interior of the cell as well as comprise reactions outside of the cell, as in the case of degradation of substances by means of extracellular enzymes.
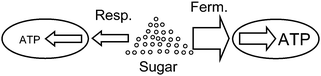
The publication of Pfeiffer and coworkers31 is a pioneering paper on game-theoretical approaches in biochemistry, dealing with cooperation and competition in ATP-producing pathways. They analyse the two ATP-producing pathways of respiration and fermentation. Both pathways start with glycolysis and differ in that respiration involves the tricarboxylic acid cycle and respiratory chain, while fermentation includes one or several steps in which pyruvate is converted to an excreted product such as lactate, acetate or ethanol. The former pathway has an ATP-over-glucose yield of about 20–3032 and a relatively low rate, while fermentation only has a yield of two but its rate of ATP production is usually higher than that of respiration (Fig. 1). For example, in striated muscle cells, where both pathways exist, fermentation is up to 100 times faster (cf. Voet and Voet32). Mixed strategies in the sense of simultaneous usage of two or more pathways occur as well: for example, baker's yeast uses respiro-fermentation, meaning that, when sufficient glucose is available, respiration proceeds at maximum rate and fermentation is used to a large extent in addition. While respiration utilizes the common pool of the resource efficiently, it has the drawback that it leads to a lower growth rate for pure respirators. The proportions in mixed strategies may differ. For example, in baker's yeast, so-called “ants” have lower glycolytic gene dosage and have a small cell size but reach a high carrying capacity, while the “grasshoppers” have higher glycolytic gene dosage, consume glucose more rapidly, and reach a larger cell size and lower carrying capacity.33
In a spatially homogeneous environment, a model of ordinary differential equations leads to a “tragedy of the commons”, where all cells use the shared resource inefficiently by additionally fermenting sugars (defector strategy).31 The “tragedy of the commons” is a situation widely considered in evolutionary game theory to describe evolution towards the inefficient use of a common resource.31,34–36 It also occurs frequently in an economic context, for example, in the overfishing of oceans or over-extraction of groundwater.37 The short-term “advantage” of inefficient resource usage may explain why many micro-organisms such as Saccharomyces cerevisiae (baker's yeast) and Dekkera bruxellensis (used technologically for brewing Belgian beer) mainly rely on fermentation even under aerobic conditions. In contrast, other micro-organisms such as Kluyveromyces marxianus and Pichia fermentans use respiration under aerobic conditions and fermentation under anaerobic conditions. They can be considered as cooperators. A compilation of data on the trade-off between rate and yield in several micro-organisms can be found in MacLean.36 The question arises how they could escape the “tragedy of the commons” during evolution.
A transition to cooperation can be achieved by spatial structure.38 Implementing spatial structure in a model consisting of partial differential equations (PDEs) where cells as well as nutrients are allowed to diffuse can promote respirators. For low resource influx rates as well as low diffusion rates, respirators coexist with respiro-fermenters or even take over the population.31
Frick and Schuster39 study the non-spatial version of the Pfeiffer model31 at the level of competing populations rather than cells. The fermentation–respiration game can then be interpreted as a Prisoner's Dilemma, the two-player analog of the “tragedy of the commons”.40 The cooperative strategy is to use respiration because it uses the common resource more economically. Fermentation is the defector strategy because it provides a short-term advantage but wastes the common resource. In the Prisoner's Dilemma, the only Nash equilibrium is where both players defect, although they would obtain higher payoffs if they cooperated, see Appendix B. This is because the highest payoff is obtained by a defector playing against a cooperator, so that there is an incentive to defect. In fact, this applies to the respiration–fermentation game. As shown by Aledo et al.,34 a similar game can arise when only the glycolytic pathway is considered, but operates in a more efficient and a less efficient mode. Also in this situation, rapid and inefficient use of glucose is favored by natural selection when the environment is spatially homogeneous.
MacLean and Gudelj41 extend the game-theoretical problem of yield versus rate in ATP production by including temporal structure. Their ordinary differential equation model introduces seasonality, resembling a batch culture. Their results are in line with results from ecology saying that oscillations in the environment promote coexistence.
The respiration–fermentation game is also relevant in the competition between cancer cells and healthy cells in humans and higher animals (see Section on Malignant tumour growth). This is one possible explanation for the Warburg effect,42 saying that tumour cells mainly rely on glycolysis. As shown by a simple, analytically tractable model, the choice of optimal pathway depends on protein costs as well.43 If the enzymes of the high-yield pathway are costly in their synthesis, which is the case for the enzymes of the respiratory chain, the low-yield pathway is favoured. If not, then the high-yield, low-rate pathway is favoured.
The secretion of intermediates that are toxic to other cells (ethanol, acetate and lactate in the cases of Saccharomyces cerevisiae, E. coli and tumours, respectively) is a further effect in the competition.41,44 MacLean and Gudelj41 include the ethanol excreted by respiro-fermenters into their model, thus imposing a cost in terms of reduced reproductive yield to those cells. This effect also promotes coexistence of respirators and respiro-fermenters.
Using ordinary differential equation models and calculating evolutionarily stable strategies (ESSs, see Appendix A), Frank45,46 analyses further factors relevant for the trade-off between rate and yield: kin selection, mutation rates and colony demography. Lower genetic relatedness as well as higher mutation rates favour rate over yield. Yield is favoured over rate for long colony survival times.
3. Public goods
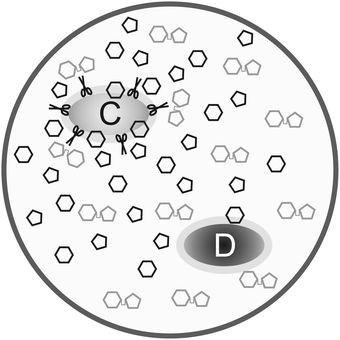
Besides the trade-off between rate and yield, public goods games play a major role in metabolism. The production and secretion of, for example, extracellular enzymes is costly to the cooperating cell and benefits surrounding cells (even if the latter do not contribute to the public good). Productivity is often reduced by “cheater” mutants. This is known since the early 20th century as for the secretion of proteases by Streptococcus lactis in milk and represents a major problem in the dairy industry.47Besides general models on exoenzyme games, models tailored to specific extracellular enzymes have been proposed. Greig and Travisano48 published an experiment on the secretion of invertase in baker's yeast. They find that the individual advantage of cheaters increases with total cell density. Their interpretation that the invertase game would always have the structure of a Prisoner's Dilemma is, however, doubted by several groups, among them Schuster et al.40 Gore et al.49 presented experimental results supported by a phenomenological model. Both their experiments and model show that the secretion of invertase is a harmony game when the cost-to-benefit ratio of secretion is low, hawk–dove game (medium cost-to-benefit ratio) or Prisoner's Dilemma (high cost-to-benefit ratio). The different game types are explained in Appendix B and the transition between them upon parameter change can be seen in Fig. 8. The same conclusion is derived by Schuster et al.,50 based on a model that is closer to biological mechanisms and simulating the effect of total cell density. Coexistence can arise because of spatial gradients of the nutrient – the glucose concentration is lower around defector cells than around cooperators. This is consistent with numerical simulations based on a grid model51 and with experimental studies and a model of protease secretion by Lactococcus lactis.52 These results can be interpreted in that secreting cells do not cooperate due to altruism but because it is favourable to increase glucose concentration locally. Both cell types can coexist when this advantage outweighs the higher costs of production and secretion of the extracellular enzyme (Fig. 2).
In the case of a Prisoner's Dilemma, the defectors may even drive the population to extinction.50,52 An even more detailed model of invertase secretion by yeast (including the metabolism of fructose in addition to that of glucose) is proposed by MacLean et al.53 They derive the interesting conclusion that, under certain conditions, a mixture of cheaters and cooperators can be better for the population than the absence of cheaters. This may be due to a nonlinear upregulation of invertase in cooperating cells when glucose goes down due to cheater cells.
4. Cross-feeding
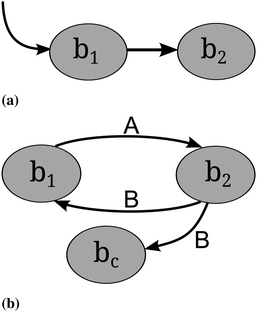
Cross-feeding occurs whenever an organism uses metabolites that are produced by another organism for its own growth and maintenance.54 “Cross-feeding” and “syntrophy” are synonymous terms.55,56 Two different types of cross-feeding can be distinguished. First, sequential cross-feeding in which one species b1 partially degrades the primary resource and excretes an intermediate or waste product, which is then taken up by another species b2 (or another strain of the same species) and used as a secondary resource57 (see Fig. 3). Second, cooperative or reciprocal cross-feeding is the mutually beneficially exchange of nutrients among species.58Examples for cross-feeding in nature involve anaerobic methane oxidation by methanogenic and sulfate-reducing bacteria,59 which leads to microbially mediated pyrite formation, degradation of xenobiotic compounds57,60 and the partial degradation of glucose to acetate.61 It has been known since the end of the 19th century that nitrification is performed in two consecutive steps by two distinct groups of bacteria: ammonia-oxidizing and nitrite-oxidizing bacteria.26
The question arising here is why a homogeneous population that degrades the primary resource completely does not perform better than a population of cross-feeders.57 Some possible explanations are outlined below. Moreover, an intriguing problem is how mutualistic cross-feeding can be robust against cheaters. If species b1 and b2 overproduce and secrete substances A and B respectively, and these substances are taken up by the respective counterpart, a cheater mutant of b1 that does not overproduce nor secrete A would, in a spatially homogeneous habitat, always have an advantage. It saves the cost for overproducing A while still benefitting from taking up B (see Fig. 3).
Several theoretical studies examine the conditions under which cross-feeding can evolve. Doebeli57 uses adaptive dynamics (Appendix A or Hofbauer and Sigmund6) to investigate when an evolutionary branching can occur so that the population splits into two diverging phenotypic clusters representing the two resource specialists coexisting in a (sequential) cross-feeding polymorphism. Doebeli57 compares the situation in a chemostat with that in a serial batch culture. He concluded that cross-feeding is less likely in serial batch cultures, because the secondary nutrient is available at appreciable levels only for a relatively short period of time, thus making conditions harsher for specialists on the secondary resource, which is in agreement with experimental results.61
A different approach to study the evolution of sequential cross-feeding is proposed by Pfeiffer and Bonhoeffer.25 They search for so called evolutionary endpoints, which are analogous to the concept of an evolutionarily stable strategy (ESS, Appendix A), by simulating competing strains that differ in the expression of the enzymes of a certain metabolic degradation pathway. They assume that the rate of ATP production is maximized and that the total concentrations of enzymes and of intermediates of the pathway are minimized. These two assumptions provide a straightforward explanation for the advantage of sequential cross-feeding: both species or strains may thus carry less enzymes and also less intermediates. They predict that partial resource degradation is more advantageous than complete degradation if the resource concentration is high or if the concentration of intermediates is restricted to a low value. They find that for intermediate dilution rates of the chemostat the coexistence of complete and partial degradation and coexistence between two partial degraders is possible. At very high or very low dilution rates a coexistence of these strains is very unlikely, which is in agreement with the results from Doebeli.57 It is concluded that cross-feeding emerges naturally under the above-mentioned extremality principles. On the basis of similar principles, Costa and coworkers26 explained division of metabolic labour by bacteria in nitrification.
A consortium degrading xenobiotics is studied by Katsuyama et al.60 They develop a mathematical model based on Sphingomonas sp. TFEE and Burkholderia sp. MN1 degrading fenitrothion, both lacking the complete pathway. Therefore, both bacteria partially degrade fenitrothion. Burkholderia lives on the intermediate excreted by Sphingomonas. These findings are in accordance with Pfeiffer and Bonhoeffer:25 each bacterium uses a minimum number of enzymes and the total concentration of the intermediates is minimized.
Another, rather different approach is chosen by Gerlee and Lundh.62 They investigate the evolution of cross-feeding in a population of artificial individuals that are capable of successively degrading artificial metabolites from which they extract energy for self-maintenance and reproduction. By computer simulations, Gerlee and Lundh62 find out that cross-feeding is the more favoured the more the flow rate of new metabolites into the system is decreased. This is explained by arguing that with low influx rates of new metabolites each metabolite stays longer in the system, such that its probability to be degraded by several organisms is increased. Thus, interactions between organisms are strengthened. That is in accordance with the result of Pfeiffer and Bonhoeffer25 that a coexistence of bacterial strains is more likely to evolve if the dilution rate of the chemostat is low.
In a theoretical study by Bull and Harcombe,58 a model for the growth of two populations interacting by reciprocal cross-feeding is developed. Therein, ordinary differential equations are used to model a system that resembles Maynard Smith's haystack model.63 Three general factors are found to affect the evolution of cooperative cross-feeding. First, the population needs to be spatially structured in order to ensure that a returned benefit can be directed to individuals or clones, not entire populations. Second, cross-feeding must pre-exist in that, in the beginning, one partner already provides a benefit to the partner by overproduction of, for example, a byproduct. Third, cross-feeding is more easily selected when its cost to the donor is low in comparison to the benefit of the recipient. A further important finding of that paper is that cooperative cross-feeding is favoured during growth at intermediate population densities.
The model by Bull and Harcombe is subsequently revisited by Estrela and Gudelj,64 using non-linear dynamics. The following outcomes contradict those found by Bull and Harcombe: first, instead of cross-feeding being favoured at intermediate densities, cross-feeders may never be able to outgrow non-cross-feeders at intermediate densities. Second, the shape of the trade-off functions between the cost and benefit of cooperation has a profound effect on the success of cross-feeders in comparison to non-cross-feeders. Third, the result that a small population of cheaters cannot invade an already established population of cooperating cross-feeders requires the same carrying capacity for all interacting populations. They come to the conclusion that cooperative cross-feeding is a robust interaction.
Estrela et al.54 study a special interaction: a one-way byproduct cross-feeding in which a cross-feeder species takes up a by-product from a producer species that is toxic to the producer. This cross-feeding interaction is favoured by intermediate toxicity degrees, an increasing by-product production and an increasing consumption of the by-product. Furthermore, the consequences of environmental fluctuations are discussed. The authors speculate that such a one-way by-product interaction could evolve to an obligate interaction.
The evolution of cross-feeding can be explained by the concept of an evolutionarily stable strategy or by adaptive dynamics. Interestingly, in the studies cited above, payoff matrices were not used. Especially for the case of sequential cross-feeding on glucose and acetate we suggest a payoff matrix of the form:
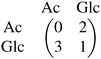 | (4.1) |
However, for reciprocal cross-feeding the concepts of two individuals playing against each other or one individual playing against a population are not sufficient.67 Here, the game is running on the level of two (or more) populations against each other. Usually, cross-feeding is an N-player game.67 Furthermore, we can have four types of players: two partners each of which can cooperate or cheat. Also, the game does not necessarily have to be symmetric. Thus, existing concepts need to be refined or new ones need to be developed. Archetti and Scheuring66 discuss the importance of non-linear public good's games and propose for the problem of cooperative cross-feeding between two species a game of two simultaneous public good's games. Assuming that the fitness function of the public goods are non-linear, they show that, without the ability to discriminate between cheater and cooperator and in the absence of sanctions, a stable coexistence between cooperators and cheaters is possible.
5. Cyclic competition
A central question in evolutionary biology is to identify mechanisms maintaining and even increasing biodiversity. How can different phenotypes (strategies) of the same species coexist?In several ecosystems a non-transitive, cyclic competition of three species has been observed, which resembles the famous rock–paper–scissors (RPS) game, where rock is wrapped by paper, paper is cut by scissors and scissors are crushed by rock. Jackson and Buss68 describe such cyclical dynamics of coral reef invertebrates and Sinervo and Lively69 observe the rock–paper–scissors structure of mating strategies of the side-blotched lizard Uta stansburiana.
An interesting aspect of the RSP game is that it arises from the Prisoner's Dilemma game by adding a strategy called “loner”.70 This additional strategy implies that the players are no longer stuck in the situation “defect, defect” (see Appendix C).
The most famous and frequently investigated example in microbiology is given by colicin producers and non-producers in Escherichia coli populations.71,72 An early work describing the difference between two competing strains and three competing strains is that of Durrett and Levin.73
Strains that produce colicin (P) also have to be resistant against it. Non-producing strains can either be resistant (R) or sensitive (S). Producing toxins against competitors is called allelopathy. Pairwise competitions show that P strains poison S strains, S beats R because of R having the costs of being resistant and R outcompetes P because of P bearing additionally the costs of producing colicin. Neumann and Schuster74,75 investigate a model with intrinsic growth rates and self-limitation terms. Due to the competition for nutrients among the three strains and the poisoning effect caused by the colicin producers, all interaction coefficients are assumed to be negative. This model is structurally stable. Depending on parameter values a stable steady state, stable limit cycle or heteroclinic cycle is obtained. The latter describes an oscillatory dynamics converging to one of the three pure states. Such a dynamics is indeed found in experiments.71 In Neumann and Jetschke76 this model is developed further by the use of adaptive dynamics. This leads to the interesting prediction that the toxicity should decrease during evolution.
In many situations of cyclic dominance in biology, spatial structure is of importance. To include this, partial differential equation (PDE) systems, here reaction-diffusion models, can appropriately be adapted. Nakamaru and Iwasa77 consider the boundaries (traveling waves) between areas dominated by different strains. Adamson and Morozov78 use the spatiotemporal reaction-diffusion scheme based on the three-species Lotka–Volterra competition approach, as considered by May and Leonard.79 Focussing on a variable mobility of the species results in a wide range of spatiotemporal patterns.
Several spatial models using cellular automata that represent structured environments and finite populations have been established, often hand in hand with and in comparison to a differential equation model. In Durrett and Levin73 the spatial model shows coexistence for a long simulation time, in contrast to the mean-field ordinary differential equation model. The ordinary differential equation model of Frean and Abraham81 shows that the populations are not controlled by their own invasion rates, but by the rates of the type they invade. Adapting the spatial model, it still holds that the most aggressive species does not have the largest population (“survival of the weakest”).
An important experimental work is that of Kerr et al.71 They do experiments with three E. coli strains that satisfy a rock–paper–scissors competitive relationship and modify the simulation of Durrett and Levin.73 When dispersal and interaction are local, coexistence occurs over a substantial range of model parameter values. However, regarding a global neighborhood coexistence never occurs and only the resistant strain survives (contrary to ordinary differential equation models). Károlyi et al.82 introduce a mixing step to simulate chaotic flow.
Berr et al.83 investigate asymmetric interaction rates and compare small and large population sizes with the help of ordinary differential equations. Wang et al.84 consider mobile species that can carry a virus. The authors study the epidemic spreading (intra- and interspecific). Ni et al.85 find that the structures of the basins of attraction yielded by a PDE model and by a lattice model are in good agreement.
Müller and Gallas86 try to find an explanation for the different outcomes of the model in Kerr et al.71 (only the resistant strain survives in long-range interactions) and the model in Károlyi et al.82 (the winner is the sensitive strain). They discover that cyclic competition has a characteristic quasiextinction period, during which the sensitive population remains smaller than the other strains, so that the critical factor controlling the final strain surviving is actually the size of the community.
Further cellular automaton models are used to explain the promotion of biodiversity87,88 and to investigate the influence of mutation rates35,89 or of mobility.90,91 Shi et al.80 emphasise the dependence of dynamical properties on initial conditions (see Fig. 4). Venkat and Pleimling92 study mobility and asymmetry effects in one-dimensional rock–paper–scissors games.
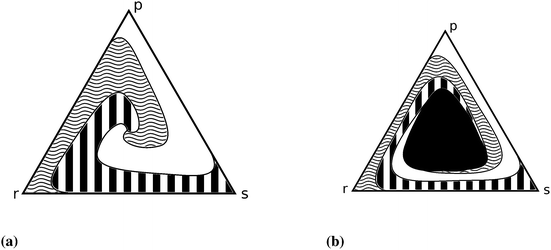 | ||
| Fig. 4 Simplex representation of the different outcomes of the rock–scissors–paper game.80 Each point of the simplex represents an initial three species population and the pattern shows the final state (white, black and white, curled region, respectively). (a) High mobility (parameter) ends up in extinction – only one of the three strains can survive, which one depends on the initial densities, (b) decreasing the mobility parameter leads to an area (black region) in the middle where coexistence is possible. | ||
Szolnoki and Szabó93 and Szabó et al.94 compare the behaviour of the rock–scissors–paper game on different networks (for example square lattice, honeycomb lattice, random networks).
Well-mixed and large but finite populations can be modeled with the help of stochastic processes. This approach also emphasises the underlying stochastic character. It was used, for example, by Tainaka,95 Ifti and Bergersen96 (introducing mutations and migrations), and Traulsen et al.97 (including mutation rates). Claussen and Traulsen98 recall the replicator dynamics for large populations. With the help of microscopic stochastic processes it is shown that also the population size determines whether extinction or coexistence occurs. A critical population size is calculated, above which coexistence is likely.
Last, but not least, there are studies that consider more than three strains.99–102 Different modeling techniques and interaction topologies are investigated.
There is a lot of literature describing the dynamics of the rock–paper–scissors game. Different modeling techniques depending on the investigated population (finite or infinite) and on the space (homogeneous or structured) can be found as well as different parameters of interest. There are studies concerning the invading probability (speed/interaction rate),35,81,83,103 mutation rates,35,89,96–98,104,105 the toxicity of the bacteriocin,73,74,76,88 the death rate,73,88 mobility of the species,78,80,84,85,90–92,96 population size,83,86,98 intraspecific competition85 and even one- or two-dimensional space92,106 and the initial values.
Not all of the literature cited in this section uses game theory in a strict sense. However, as we are interested in the results of the rock–paper–scissors dynamics, we find it worth mentioning all the modeling approaches inspired by this game.
6. Signalling
Signalling is a concept that can be found in many fields like sociology, economics, philosophy and of course in biology.107 The term of signalling is closely related with the concepts of communication and information. Signalling games are two-player games between a sender S and a receiver R.107 Both players have different strategies. The sender has a potentially infinite set of messages and the receiver can choose from a set of actions.107 Furthermore, the sender has a certain type given by nature, which is not known by the receiver. The type could be for example male or female, venomous or non-venomous insects. For example, a non-venomous insect could send the message that it is non-venomous or pretend that it is venomous. In contrast to some classical two-player games, like the Prisoner's Dilemma or the hawk–dove game (see Appendix B), the players in a signalling game always act sequentially rather than simultaneously (Fig. 5). R responds to the message of S. The payoffs for the two players depend on the type of S, the message sent by S and the action of R.108,109 In the signalling games often the term quality is used. It describes a subset of characteristics which are taken into account for the fitness of an individual.Signalling games in biology deal with the following aspects: how costly is the signal for the sender and how to differentiate between honest and dishonest (cheating) signalling. Often not the real payoff values are calculated but only the ESSs are identified on the basis of the payoff relations. Most of these game-theoretical studies are focused on animals like mammals and birds. John Maynard Smith, the developer of the concept of ESS, and David Harper concentrate on animal signals in their homonymous book.110 However, game-theoretical analysis of signalling is not only possible for animals, but also for other multicellular organisms such as plants, and on the cell level.
An important question arising in signalling games is, how evolution produced “honest” or reliable signals between organisms despite the incentive to betray the receiver of the signal. Zahavi111 provides an attempt to explain this with a hypothesis called “Zahavi's handicap principle”. It suggests that reliable signals have also to be costly to the sender, and therefore implying that other individuals without a specific trait could not afford the cost for this honest signal. An ESS model of the handicap principle is derived by Grafen.112 But the handicap principle is not without controversy, e.g. Bergstrom et al.113 find that reliable, honest signals need not be costly.
In a publication by Pagel28 the ESS of signalling between gametes in lower eukaryotic organisms is analysed. The gametes emit pheromones and affect movement or growth of other gametes in the direction of the pheromone. The result is that with increasing quality of the signalling gamete, also the level how strong the signaller displays its fitness and the probability that the receivers prefer that signaller increase.
In bacteria, signalling is often mentioned in the context of quorum sensing. For example in biofilms quorum sensing in combination with cheating plays a very important role.114
Brown and Johnstone27 develop a two-trait ESS function describing the optimal level of cooperation and of signalling depending on the costs to the individual, benefit to the group, colony size and relatedness of the bacteria. For their ESS calculations, they fixed the costs and passive fitness (fitness of a non-cooperating bacterium in a group of non-cooperators). There is only a stable cooperation effort if the relatedness and colony size are higher than certain threshold values. The highest stable signalling effort is at a relatedness near 0.35 and large colony size.
Quorum sensing (QS) with a two-dimensional cellular automaton of toroidal lattice topology is modeled by Czárán and Hoekstra.115 They assume three genetic loci: C for cooperation, S for production of signal molecules and R for signal response. All loci can have an active allele or inactive allele, thus there are eight different genotypes. Different scenarios, with different initial combinations of genotypes and different costs for cooperation are tested. In environments which promote cooperation, the C allele is almost fixed. Simulation of the scenario, in which cooperation is costly, results in a cyclic interaction pattern of the genotypes “Honest” (CSR), “Vain” (CSr) and “Blunt” (Csr) comparable to a rock–scissor–paper game (see Section 5). The “Vain” can invade a population of “Honest”, because it saves the costs for response. The “Blunt” has no costs for the QS, that is why it invades the “Vain”. This unconditional cooperator can be invaded by the “Honest”, because the last one only cooperates if there are QS-signals, so if it is surrounded by “Blunts” it has not to pay the costs for cooperation but benefits from the public good. If cooperation is relatively cheap, the simulation results in a dynamical coexistence of “Honest”, “Vain” and “Blunt” genotypes reminiscent of the rock–scissors–paper game (see Section 5). The authors also investigate other environments with other fixed alleles or no fixed alleles.
The work of Lotem et al.116 deals with unconditional altruism through signalling benefits. Three different strategies are assumed: unconditional altruism, helping all other players; defection by soliciting but never donating help; and conditional altruism or tit-for-tat strategy.117 The latter is a strategy in the iterated Prisioner's Dilemma implying to replicate an opponent's previous action. There are a total of six ESSs. Provided that the signalling benefit of donating help only exceeds the costs for some individuals (high-quality players) and not for others (low-quality players), the ESS is that the high-quality players are unconditional altruists and the low-quality players are defectors or play tit-for-tat.
Traulsen and Nowak118 develop a tag-based model for cooperation. The basic idea is that individuals recognise each other via arbitrary signals, so-called tags. A population of cooperators (or a fraction of this population) is able to change their secret tag when a defector misuses the tag. In the theoretical study of Traulsen and Nowak118 the authors find that there are more cooperators than defectors if b/c > 1 + (2u/v) (with b benefit; c costs; u mutation rate changing only the strategy; v mutation rate changing both strategy and tag). If there are K different tags and the mutation rate between all phenotypes is constant, the constraint is b/c > (K + 1)/(K − 1).
An example for a tag-based system is the csA gene in Dictyostelium discoideum, encoding a homophilic cell adhesion protein.119 In a mixed culture of wild-type and csA-knockout cells, the wild-type cells are more altruistic but they can distinguish between their neighbours and direct the benefit preferentially to other wild-type cells. This effect is called “greenbeard” mechanism,119 meaning that cooperators can recognize each other by a striking trait.
7. Host cells meet parasitic cells
Several papers analyse two-player games between a host and its pathogen.120–122 In Renaud and de Meeüs120 a two-player game between one host and one pathogen is analysed. The two players can choose between an aggressive strategy that seeks to eliminate the adversary (killer strategy) and a less aggressive strategy (diplomat strategy). The killer strategy is always an ESS, whereas the diplomat strategy is a second solution only under certain parameter settings (costs of virulence and resistance).In Frean and Abraham121 an endosymbiont–host association is studied additionally by a two-populations simulation (intra- and inter-specific competition). Huang et al.122 uses focal-point theory to investigate three host-microbe game models (cooperation, dilemma, conflict).
A spatial model on the basis of a cellular automaton is given by Rauch and Bar-Yam.123 The effect of long-range mixing of species is investigated, which occurs for example due to human intervention and to global transport of an infectious disease.
A third general host–pathogen approach (considering infectiousness) is based on epidemiological modeling and adaptive dynamics: ordinary differential equations for susceptible and infected subpopulations are established,124,125 subsequently some fitness functions are found (function A in the Appendix A) with the help of the solution of these ordinary differential equations and final investigations on evolutionary stability.
Studies considering parasites competing within a “constant” host are for example the work of Bremermann and Pickering,126 van Baalen127 and Day et al.128 There, individual parasites are considered as players. In Bremermann and Pickering126 it is assumed that the disease-induced mortality rate of the host grows with the increase of a parasite's reproductive rate. In order to extend the length of reproduction time, competing parasites within a host may prefer to reproduce at rates below their maximum reproductive rates. The work by van Baalen127 shows that different evolutionary outcomes are possible if the parasites coevolve with the host (a common but quite avirulent parasite in a host investing little in defence or a rare but virulent parasite in a heavily defending host). In Day et al.128 parasite's virulence and host clearance rate are considered as strategies. It is found that the total infection-induced mortality can be a by-product of host immune response.
Several studies investigate the evolution of host defence against a fixed parasite strain. While Boots and Haraguchi129 examine resistance strategies of the host, Bonds et al.130 focus on the evolution of host sociality with respect to an infectious disease and Miller et al.131 study the influence of the host life span on different host resistance mechanisms. In Best et al.132 the question why hosts are differently tolerant is analysed.
The coevolution of host and pathogen is modeled for example by Taylor et al.133 The level of virulence that the pathogen exhibits and the level of immune clearance that the host exhibits are used as continuous strategies. Further coevolutionary population models are reviewed in Boots et al.134
The interesting effect of host infection on the evolution of biodiversity of pathogen strains is studied by Morozov and Best.135 It is argued that the role of host–parasite interaction can be important in explaining polymorphism. The model is a combination of an epidemiological model and a predator-prey model and is analysed by adaptive dynamics and evolutionary game theory.
Alonzo and Calsbeek136 build a game with three strategies: a reproductive parasite and two different resource defenders. The model shows continuous sequential invasion and no stable coexistence.
In order to investigate age-dependent behaviour variation137 and heterogeneous host populations,138 epidemic modelling is combined with game theory. Williams138 argues that individuals are differently susceptible and vulnerable to a pathogen and these differences may also influence the pathogen evolution.
In the following, we present some interaction models with specific biological application.
Wolf and coworkers139,140 explore the origin and utility of random phase variation (RPV). This strategy can be described as a random switching of phenotypes in order to adapt to rapidly varying environments without requiring mutation. Bacteria as players have sensors and a number of options to react (e.g. cell states or phenotypes). A strategy is defined as a map from sensor information onto behaviour. Certain sensor defects (unobservable, incorrect, delays, noise) and different environments (time-invariant, time-varying, stochastic) are analysed for combinations that give rise to RPV as an ESS. As RPV can be seen as random alternations between losing strategies, that form a winning strategy when sensing is absent, an example for the Parrondo paradox is found. The Parrondo paradox describes the effect that mixing losing strategies can produce a winning outcome. The problem is solved with a matrix population model, that is based on Markov chains.
Endosymbiosis of proto-mitochondrial prokaryotes into proto-eukaryotic host-cells is investigated in Bivort et al.141 A game-theoretical two-player game analysis suggests that active symbiosis would not have been favourable to both species as an asymmetric Prisoner's Dilemma arises from the payoff matrix, indicating that some assumptions are not adequate. Agent-based model simulations exhibited potential conditions that could lead to a stable symbiosis.
Eswarappa142 studies persistent infections. Bacteria stay in both intracellular (mostly phagocytes) and extracellular compartments of the host. Bacteria are safe inside phagocytes if they can avoid lysis. Here, the bacteria are protected from immune recognition and serum mediated extracellular killing by the host system. Furthermore, bacteria can access the external environment for dissemination. Examples for such bacteria are Helicobacter pylori, Mycobacterium tuberculosis and Salmonella spp. On the other hand, the host can use extracellular or intracellular defense mechanisms. A very basic and heuristic model shows three Nash equilibria: two pure equilibria that are not biologically plausible and a mixed Nash equilibrium that exists independently of the payoff relations and is biologically relevant. Bacteria remain in extra- and intracellular compartments of the host and the host uses extra- and intracellular defense mechanisms.
The polymorphic fungus Candida albicans has two strategies when engulfed by macrophages: avoiding lysis transiently (silencing) or forming hyphae and escaping (piercing) (Fig. 6). Two different games among C. albicans yeast cells inside the macrophage (macrophage is considered as the environment) are developed by Hummert et al.143 In the two-player game it is assumed that each macrophage engulfs exactly two yeast cells. If costs for silencing are not too high, the game is a hawk–dove game with a single mixed ESS.
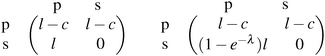 | (7.1) |
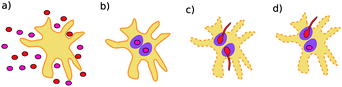 | ||
| Fig. 6 Possible interaction scenarios: (a) C. albicans yeast cell population and a macrophage before ingestion, (b) both ingested cells silence, (c) both ingested cells pierce (d) ingested cells adopt different strategies. Figure taken from Hummert et al.143 | ||
The left matrix of (7.1) shows the payoffs, where p stands for the piercing strategy, s stands for the silencing strategy, l stands for having survived, and c having payed the costs for piercing. In the second game, which is a playing the field game (Appendix A), a Poisson distribution for the number of ingested C. albicans yeast cells is assumed. The fitness matrix is shown in the right part of eqn (7.1). An entry gives the payoff of an individual playing a row strategy against a pure population playing the column strategy. The ESS in a mixed population (under certain parameter conditions) can be calculated, but also a pure piercing population can exist (under contrary parameter conditions). Additionally, survival rates of phagocytosed yeast cells can be calculated. A comparison with experimental studies showed that there exist two different karyotypes, a pure piercing population and a mixed population, the difference is explained in the difference of the costs these two karyotypes have, or in other words, in the ability to secrete proteins that enhance producing hyphae.
Bewick et al.144 investigate two different HIV variants and the corresponding adaptive immune responses. Two different scenarios are analysed and the Nash-equilibria are calculated. In another work Bewick et al.145 model the immune defense against hepatitis B in the liver by comparing the immune defense strategy with military defense strategies.
8. Malignant tumour growth
Cancer is known to be a genetic disease where accumulation of mutations can transform cells from a homeostatic tissue into a complex ecosystem of individualistic cells that compete for limited space and resources.146–148 Cancers are also very heterogeneous, both genotypically and phenotypically. A single tumour may contain several different types of tumour cells,149 with each type potentially having different traits and ways to interact with other cells and the local microenvironment. This heterogeneity is passed on from parent to daughter cells and affects their probability of proliferation and survival. Furthermore, this heterogeneity is key to explain important aspects of cancer such as the emergence of increasingly more aggressive cell types and resistance to treatments.Tumour cells are thus part of an ecosystem where interactions between different cells and the environment determine the somatic evolution.146,147,150 Any given tumour can be made of a number of different highly dynamic microenvironments.149,151 Studying cancer progression requires access to mathematical tools where the competition of different cancer phenotypes and strategies can be taken into consideration.152 The use of evolutionary game theory to model and analyse cancer progression is still a nascent field with only about 15 years of history and just a few papers.153 In that time it has been used to study cancer progression both in vitro (as a loose collection of tumour cell populations growing out of control) and also in vivo in organs such as the brain, bone, prostate or the lung. Indeed, most uses of evolutionary game theory in cancer so far involved studying how certain tumour phenotypes are selected for. This is a particularly important part of cancer progression as new phenotypes emerge in the tumour population and, provided they are fitter than the current mix of phenotypes, grow and become an important (but rarely the only) subpopulation in the tumour. The emphasis on phenotypic transitions as hallmarks of cancer has been previously highlighted154–156 and considered therapeutically.
The evolution of increasingly more aggressive phenotypes is studied in the context of the competition between different cell lines by Anderson and colleagues.157 The study focuses on the emergence of phenotypes with ever decreasing dependence on the local microenvironment, one of the hallmarks of cancer aggressiveness.156 The results of the game between cells that are microenvironmentally independent and those that can rely on the microenvironment, show that the two types are likely to be found coexisting under most circumstances. Other studies on the emergence of aggressiveness focus on glioblastomas, malignant brain cancers characterised especially by high invasiveness and motility of the constituting cancerous glia cells. In particular, the emergence of invasiveness is studied in the context of glioblastomas using a cellular automaton model whose rules are based on game theory but where fitness is not defined explicitly but implicitly via the phenotype.158 A more conventional evolutionary game theory approach30,159 considering invasive and proliferative subpopulations, highlights the importance of the microenvironment in the progression to malignancy. The model results are later corroborated via an agent-based model.30 Both models consider a population of rapidly proliferating cells where a mutation might confer a higher degree of motility to certain cells at the cost that cells that move cannot divide at the same time. In essence, both models present a game that is similar to the standard hawk–dove game4 so that the local population of proliferative cells is better off interacting with the new motile cells than with other proliferative cells but a population composed of proliferative cells is still susceptible to be invaded by invasive ones. This is akin to hawks receiving a higher fitness payoff from their interactions with doves but still being susceptible of being invaded by a small number of doves (under the assumption that injuries can be costly). As in most evolutionary game theory, a payoff matrix completely describes the model:
This simple game leads to an equilibrium described by this equation:
Meanwhile, the invasion/proliferation game mentioned before has been enriched with the addition of cells with a glycolytic phenotype and interpreted in a glioblastoma context.162 The results of this game suggest that invasiveness is more likely to emerge in tumours where there are glycolytic cells present, strengthening the notion that non-competitive interactions between tumour cells play an important role in glioblastoma progression. Further work studying secondary glioblastomas characterised by the IDH1 (isocitrate dehydrogenase) mutation, suggest the following mechanism: rapidly proliferating cells grow beyond oxygen reach leading to glycolytic phenotypes that incentivise the emergence of the invasive phenotypes typical in glioblastomas.161 Building on the research by Basanta162 and Kareva,44 Archetti163 has recently modelled the Warburg effect following the idea of lactic acid viewed as a public good (it helps the tumour in small doses but it harms if there is too much of it). A modelling approach that would allow for a nonlinear dependence of the benefit on lactic acid concentration could yield new insights on its role in cancer progression. Archetti uses a non-linear public goods game based on the properties of Bernstein polynomials and suggests that reducing the acidity of the environment might not significantly change the dynamics of the game and thus should not be a useful therapeutical approach.
Evolutionary game theory is thus a very powerful mathematical modeling tool in which to study how the interactions between different cellular populations could give rise to the different hallmarks of cancer.155 Work by Axelrod and collaborators150 nonetheless suggests that not all tumour cells have to acquire all the traits in the hallmarks for the tumour to develop a cancer. The interactions between tumour cells or even stromal cells are not always exclusively competitive. There is then the potential that tumour cells with different capabilities could cooperate so that while no single cell would have all the hallmarks of cancer, a group of cells would collectively have them. Similar types of interactions between individuals in a population have been studied by Nowak before164 and it is clear now that these interactions play an important role in cancer progression165 (see Fig. 7). They can be mutualistic (if both cells interacting benefit from the interaction), competitive (if both cells can be harmed as a result of the interaction), predatory (if the benefit of one of the cells comes at a huge cost to the other cell), parasitic (if the benefit to one cell comes at a small cost to the other cell) or commensalistic (if the benefit to one cell comes at no cost to the other cell).
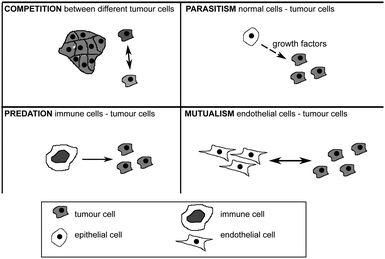 | ||
| Fig. 7 Four types of interaction among tumour cells and among tumour and healthy cells. For further explanation see text. | ||
Interestingly, the first known application of evolutionary game theory in cancer investigates how angiogenesis can emerge if not all tumour cells contribute,166 thus constituting a model of commensalism. In their model, Tomlinson and colleagues consider two subpopulations of tumour cells, one producing VEGF (an angiogenic factor) whereas the other one devotes all its energy to proliferation. The coexistence shown by their game-theoretical model is also later confirmed in a more sophisticated threshold model by Bach and colleagues167 where the benefits of angiogenesis can only be realised when a majority of interacting cells are producing VEGF. The general mechanism describing the dynamics of cancers with cooperating and cheating subpopulations (where cooperation is defined as the production of growth factors such as VEGF) is also studied using a spatial implementation of evolutionary game theory in the paper by Bach et al.168
The interactions between tumour cells and non tumour cells are equally important. It is well known that tumour cells interact with stromal cells such as fibroblasts, endothelial cells and macrophages, in ways that could be considered co-option.169 Dingli et al.170 study interactions between different types of tumour cells and stromal cells in the bone (osteoclasts and osteoblasts) in multiple myeloma. The model shows that targeting the cancer cells directly is unlikely to be an effective long term cure of myeloma but targeting the interactions between the tumour and the stromal cells so that those can effectively outcompete the tumour is a more promising approach. In a similar line, game theory is used to study interactions between a heterogeneous tumour with fibroblasts in prostate cancer.171 In this game tumour cells can co-opt the fibroblasts to obtain certain growth factors or ignore the microenvironment at the cost of having to produce those factors. The study of different treatment options demonstrates the role they have as selection forces. In some occasions, these forces can potentially eliminate the bulk of the tumour but only at the expense of increasing the relative fitness of more aggressive and less treatable phenotypes.
This last study highlights not only the role of evolutionary game theory to understand the role of cell interactions in cancer progression but also how therapies can influence the evolutionary dynamics of a cancer. One example is the use of evolutionarily enlightened therapies such as the evolutionary double bind as advocated by Gatenby and colleagues.172 The evolutionary double bind suggests that combination therapies, where treatments can be considered as tumour cell predators, can be applied so that tumour cells that are resistant to one of the treatments are so at the expense of being even more susceptible to the second treatment. Mathematical models are used to investigate this intriguing hypothesis173 but more recently a game-theoretical approach is used to study a specific case where researchers at the Moffitt Cancer Center find that chemotherapy and a p53 vaccine could work synergistically in lung cancer.174,175 The model assumes that, given the two treatment options, a heterogeneous tumour can be composed of three subpopulations: susceptible to both treatments, resistant to the p53 vaccine and resistant to chemotherapy. The interactions between these populations are important since the clinical work could be explained by the parasitism of the p53 resistant populations (providing protection from the immune system to their neighbours) by the subpopulations that are sensitive. The study also suggests that the key to the synergistic effect is the sequence in which the treatments are applied which results in an increasing reduction of tumour heterogeneity.
In summary, cancer is an evolutionary disease where cells that can adapt to the tumour environment will thrive whereas those that cannot become extinct. The evolutionary dynamics of cancer can be understood with the help of mathematical models based on evolutionary game theory, especially regarding two key and intertwined aspects of evolution: the role of interactions between individuals and the emergence of new traits in a population.
Current evolutionary game theory approaches have a number of limitations: they assume homogeneously mixed populations where all the relevant phenotypic strategies are known from the start. Although not a limitation of evolutionary game theory, current game-theoretical models of cancer usually disregard the role of space and usually consider the proportions of phenotypes in a tumour as opposed to the total numbers. This can obscure the fact that in many situations the proportion of a phenotype could be going down as the number of cells with that phenotype keeps increasing during tumour growth. Despite the limitations, evolutionary game theory is a very useful tool in which to study the emergence of new, increasingly more aggressive phenotypes that characterise tumour evolution and progression. It is also an ideal framework in which to investigate how treatments can affect selection and alter the evolutionary landscape.
9. Application in medicine and biotechnology
As shown in the previous section by the example of cancer treatment, evolutionary game theory is a promising tool also for applications in medicine, producing counter-intuitive results where conventional approaches fail. The same holds for applications in biotechnology. Both directions are discussed in the present section.In medicine, conventional treatments of tumours as well as life-threatening infections by viruses like HIV or bacteria often tend to fight tumour cells or pathogens by (single) drug usage at high dosage. What seems to be a success on short-sight often leads to resistance to the given drug and relapse on the long run.
Optimal drug dosage over time is treated generally by Bewick et al.176 in a model that combines evolutionary game theory with optimal control theory.176 Based on the assumption that viruses have to make a trade-off between replication capacity and drug resistance, their results give advice for an optimal treatment scheme in a rather non-intuitive way: when drug resistance increases faster with mutations, leading to resistance, than the replication rate decreases, the optimal strategy of drug dosage is to give high dosages during the early phase of the treatment regime, and then to lower dosages as the treatment process proceeds. In the other case, if drug resistance increases slower than the replication rate lowers during mutational processes, leading to resistance, the optimal drug strategy is to limit drug application during the first half of the treatment phase, and then to increase the drug load over the second half of the treatment phase.
In a similar manner, Wu and Zhang177 use the combined approach of evolutionary game theory and optimal control theory to propose optimal medication schemes for HIV patients. They come to the conclusion that it is optimal to dose the medication only moderately at later stages of the treatment, so that T cells and HI-viruses attain a stable coexistence rather than maximize the drug load which leads to a rapid resistance mutation of HI-viruses.
Also in cancer treatment, evolutionary enlightened therapies are promising (cf. Section 8). Tumours are now seen as heterogeneous formations consisting of interacting subpopulations, each bearing different properties that can be seen as strategies. Combination therapies successively weaken the cancerous phenotypes, which may be susceptible to all treatments or susceptible to one respective agent of the combination therapy.175 The key to the synergistic effect is the sequence in which the treatments are applied, which results in a stepwise reduction of tumour heterogeneity.
Interactions not only among tumour subpopulations but also with surrounding cells in the microenvironment attracted more and more interest as therapeutical targets in the fight against cancer178 (cf. Section 8). Game-theoretic models illustrated the role of different treatments as selection forces.170,171 Targeting tumour cells directly often merely leads to short-term success, clearing the way for more aggressive and less treatable phenotypes. Instead, targeting interactions between the tumour and surrounding cells, enabling the latter to outcompete the tumour cells, is a promising approach to long-term survival.
Metastasis is one of the clinically most import transitions in tumour progression, leading to more than 90% of cancer deaths.179 Intuitively, “starving out” the primary tumour by limiting its resources to prevent metastasis seems to be a suitable therapeutical approach. However, game-theoretic models show that the contrary is the case. Providing a nutrient rich environment to the tumour increases the fitness of proliferative cells over motile cells, acting as a disincentive for a tumour to become invasive and metastasising.30 Improving tissue oxygenation, which increases the relative fitness costs of tumour cells for switching to anaerobic glycolysis, has a similar effect.162
As mentioned in the title of their paper, “An analogy between the evolution of drug resistance in bacterial communities and malignant tissues” is seen by Lambert et al.180 They suggest a fundamental mechanistic similarity between the rapid evolution of resistance to drugs in communities of cells in malignant tissues and in bacterial communities. As a cause of the evolution, they propose a programmed and collective stress response performed by interacting cells und suggest bacterial communities as a model system for tumour cells. From this perspective, a united view based on game-theoretical models seems to be reasonable.
Bacteriocins are of current interest as probiotic and bioprotective agents181 as well as a potential viable alternative to conventional antibiotics,182–184 showing promising success in experimental studies on the treatment of chronic biofilm-mediated infections.185 Kirkup and Riley72 emphasise the role of bacteriocins in a game of rock–paper–scissors as potential promoters rather than inhibitors of microbial diversity (in the mammalian gut). Indeed, Brown et al.185 identify bacteriocins as potential selective correctors of imbalances in the microbiome that are associated with chronic conditions such as Crohn's disease.
Evolutionary game theory is also a promising tool for biotechnology. Game-theoretical analyses of the production of extracellular enzymes bear a great biotechnological potential, for example, in the context of renewable fuels and biodegradation of xenobiotics. Biotechnological processes are optimized regarding their cost-benefit ratio. High density cell cultivation is thus favourable.186,187 However, if production of extracellular enzymes is involved in the biotechnological process, “cheating” mutants deficient in exoenzyme production can arise, which benefit from the exoenzymes produced by “cooperating” cells. Game-theoretical models predict a high percentage of “cheating” mutants at high cell densities and suggest optimal densities for maximised volumetric productivity to be lower.50
10. Challenges and future prospects
In this and an accompanying review,12 we discuss the use of evolutionary game theory in cell and molecular biology including biochemistry. In spite of its “playful” name, game theory has manifold practical applications, as witnessed by several Nobel prizes in economics. As outlined above (especially in Sections 7–9), evolutionary game theory can be applied beneficially in medicine and biotechnology.While evolutionary game theory has been applied in ecology and behavioral biology since the mid-20th century, applying it to “lower” levels in biology is more recent. As mentioned in the Introduction, an important aspect in this development is that, earlier, it was assumed that the players should have a certain degree of cognitive and rational capabilities, so that only humans and sufficiently complex animals could be considered as players. However, applying the conceptual toolkit of game theory does clearly not require that the players are conscious, rational beings (cf. Maynard Smith and Price14). This becomes even clearer from the numerous examples reviewed above. By selection, certain behaviours or features outcompete others, so that, in retrospect, it may look as if a certain appropriate strategy had been chosen deliberately. Interactions between micro-organisms can obviously be described by game theory very successfully. Importantly, human behaviour is often superimposed by moral and social factors. This enables more complex solutions such as mutualism based on trust leading to non-Nash states, equilibria based on a rationality in favour of the community or apparently irrational responses like defiance or spite. Therefore, it might be argued that the concept of Nash equilibrium is often much better suited to micro-organisms than to human behaviour.
This raises the general question as to what can be gained by applying game theory to non-cognitive systems that is not provided by more conventional approaches such as optimization theory or classical evolutionary theory. The arguably most important aspect is a better understanding of seemingly counter-intuitive findings such as “survival of the weakest”,81 as it can occur in the rock–paper–scissors game. As explained in more detail above, the probably most intriguing example is provided by a bacterial strain that is sensitive to a toxin but can eventually be the only survivor in an oscillatory dynamics because it grows with a higher intrinsic rate than the toxin producer and resistant strains, although it is the least competitive strain. Phenomena like this apparently contradict Darwin's notion of the “survival of the fittest”. Whether they actually do so, however, depends on how fitness is defined. The attribute “weakest” strongly depends on definition. In terms of growth rate, the sensitive strain is actually the fittest. In any case, the rock–paper–scissors game is more complex than traditional Darwinian concepts because the transitivity relation of fitness is violated.102 That is, if A is fitter than B and B is fitter than C, (counter-intuitively) C needs not be fitter than A. This non-transitivity actually implies that there is no weakest, so that “survival of the weakest” is just a provocative notion to make the point.
When analysing multi-cellular organisms, the question arises as to what entities can be considered to be players. One obvious option is to consider entire organisms as players. However, in the case of cancer, the tumours or even the particular tumour cells act (more or less selfishly) as independent agents. This can be considered as an evolutionary regression to unicellular forms of life.188 Interestingly, also adipocytes can act independently to a certain extent. These cells excrete signalling substances, so-called adipokines, regulating glucose metabolism. In obese individuals, that signalling is perturbed so that adipocytes become, in a sense, selfish.189
Game-theoretical approaches can be extended in several directions in the future. They can be extended to involve spatial dimensions, for example, using individual-based models. They can involve a temporal dimension (for example, using differential equations such as in several rock–scissors–paper models, Section 5) and stochastic components. Many dynamical processes can be regarded as iterated games, such as the iterated Prisoner's Dilemma.117 These often show very complicated dynamics or it may even occur that no optimal time pattern exists.117 This is one possible explanation for the open-endedness of evolution.
Here, we have concentrated on spatially homogeneous situations. Of course, many processes of cooperation and competition occur in heterogeneous setups. Accordingly, many game-theoretical analyses have been performed by spatial models, either continuous models31,38 or discrete models on lattices (grids) (e.g. Reichenbach et al.,90 Szolnoki and Perc,190 Allison51). The boundary between game theory and other modelling methods such as lattice models is not clear-cut then. Also in other extensions of game theory, the boundary is not clear-cut, for example, with respect to ordinary differential equation models in population dynamics.74
Appendix A: mathematical background
Typical tools and concepts in evolutionary game theory are payoff matrices, Nash equilibria and evolutionarily stable strategies (ESS). In a Nash equilibrium, no player would gain an advantage (e.g. in terms of growth rate) when changing strategy unilaterally, that is, without coordinated changes by other players. The related concept of ESS describes a strategy that, if adopted by a population, cannot be invaded by any mutant strategy.A.1. Two-player games
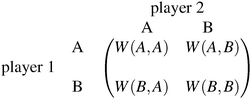
Each player can choose a particular strategy from a predefined strategy set. For each strategy combination there are defined payoffs for each player, written down in the payoff matrix (outcome of the game).Example: A symmetric two-player game with strategy set {A,B}. The payoff for strategy A versus B is given by W(A,B). Because of symmetry it is sufficient to fill the payoff matrix with the outcomes of the row-player (player 1):
 | (A.1) |
A strategy is said to be a dominant strategy if for every choice of strategies of the other players the payoff from choosing this strategy is greater than the payoffs from choosing any other strategy. Strategy A is dominant if W(A,A) ≥ W(B,A) and W(A,B) ≥ W(B,B), for all strategies B ≠ A.
Given a certain amount of pure strategies, a further possibility is to adopt each (pure) strategy with a certain probability. Such a set of probabilities is said to be a mixed strategy. Of course, the probabilities have to sum up to one. In the symmetric two-player game with pure strategies A and B, we write x for the mixed strategy to adopt A with probability x and B with probability (1 − x).
An important notion in game theory is the Nash equilibrium. It is a situation (a certain strategy combination of all players) where no player has an incentive to choose another strategy given that all other players stay at their chosen strategy. In a Nash equilibrium, the strategy of each player is the best response to the strategies chosen by all other players.191
Example: Given the symmetric game formalized in matrix (A.1), possible Nash equilibria in pure strategies are:
• (A,A) is Nash equilibrium, if W(A,A) ≥ W(B,A)
• (B,B) is Nash equilibrium, if W(B,B) ≥ W(A,B)
• (A,B) and (B,A) are Nash equilibria, if W(A,B) ≥ W(B,B) and W(B,A) ≥ W(A,A)
Note that in the cases (A,A) and (B,B) one can also say that the strategies A and B, respectively, are Nash equilibria. In general, in a Nash equilibrium where all players adopt the same strategy, also the strategy itself is called a Nash equilibrium. Further, if the above inequalities hold as strict inequalities, then the Nash equilibria are called strict.
According to the Bishop–Cannings Theorem,192 the idea to find a mixed strategy that is a Nash equilibrium in a symmetric game is the following. Each single pure strategy adopted against this mixed strategy does equally well, i.e. the expected payoff to a player is independent of its adopted strategy: W(A,x) = W(B,x), where W(A,x) = xW(A,A) + (1 − x)W(A,B) and W(B,x) = xW(B,A) + (1 − x)W(B,B). Solving this equation for x gives
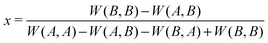 | (A.2) |
Check if the solution is between 0 and 1, because it represents a fraction or probability. If the solution is outside of that range, only the pure Nash equilibria are relevant.
A.2. Evolutionary game theory
If applying the concepts of game theory to animals, plants, micro-organisms, cells or even molecules the prerequisite of rational choices made by the players is not required. Without rational players a Nash equilibrium can be found by an evolutionary process in a population. Individuals using a strategy that is not optimal in the population will reproduce at a lower rate than individuals with an optimal strategy, which will thrive and pass this strategy on to the next generation. New strategies can appear by (epi-)mutation or by immigration into the population.Among an infinite population we consider repeated random encounters of opponents. In terms of a population, a mixed strategy can also define the state of the population, where certain fractions of the population play one of the strategies. Again, the fractions have to sum up to unity.
A strategy is evolutionarily stable if a whole population using that strategy cannot be invaded by a small group with a mutant genotype. Strategy x is evolutionarily stable if and only if for any mutant type p we have: W(x,x) ≥ W(p,x) and if W(x,x) = W(p,x), then W(x,p) > W(p,p). The first condition is the Nash equilibrium condition and the latter one is the evolutionary stability condition, meaning that x can invade any p population.
(2) If all players have a dominant strategy, then the situation where all players adopting it is a Nash equilibrium (NE in dominant strategies).191
(3) Every evolutionarily stable strategy is a Nash equilibrium, but not every Nash equilibrium is evolutionarily stable.193
(4) Every strict Nash equilibrium is evolutionarily stable.191,193
(5) In asymmetric games (asymmetric in payoffs) only strict Nash equilibria are evolutionarily stable.191
Because a Nash equilibrium does not necessarily have to be evolutionarily stable, one has to check for the evolutionary stability of the (mixed) Nash equilibrium.
Evolutionary stability is a particularly useful concept because it says something about the dynamic properties of a system without being committed to any particular dynamic model.
A.3. Dynamic game theory
Dynamic game theory is important if one wants to study the behaviour of a system beyond an “equilibrium based viewpoint”.194 Investigating the long-term change of the strategies' frequencies is only possible when considering dynamics. It can also be used for studying frequency dependent selection.7 Further, the notion of evolutionary stability relies upon implicit dynamical consideration. In certain situations, the underlying dynamics can be modelled by differential equations.6Another point of dynamic game theory is the question whether games do reach a Nash equilibrium, and if so, by what process?191 Further questions include: if there are several Nash equilibria, to which one does the game converge? The answers can be found by studying the behaviour of dynamical systems.
The dynamical behaviour of a game is interesting especially if the long-term outcome is not a Nash equilibrium (this is the case for e.g. variants of the rock–scissors–paper game). In such a case, the behaviour over time is characterized by endless regular or irregular oscillations.7 Hence, the static approach often is not sufficient for a full analysis. Only a dynamical theory can describe e.g. the “Red Queen” aspect of “Alice's Wonderland”. (There, in the kingdom of the Red Queen one has to run to remain on the same spot.) Such phenomena reign in evolution as in the arms races between hosts and parasites or predators and prey.
A.4. Spatial games
Individuals are arranged on a regular lattice (with arbitrary dimension, but usually two- or three-dimensional) playing the game (a two-player game) with its immediate neighbours.7,195 Different neighbourhoods can be defined: the von Neumann or the Moore neighbourhood,193 both using different distances. The update can be either synchronous or asynchronous.7An example for one of the first spatial games is a spatial Prisoner's Dilemma by Nowak and May.196 There, the payoffs from these interactions are added up for each individual. In the following round (i.e. generation) each player adopts the strategy with the highest payoff in its immediate neighbourhood. All cells are updated in synchrony. This and other simple spatial games investigate deterministic evolutionary dynamics without random mutations.
Often, the boundary conditions are defined as periodic boundaries, but also other boundary conditions are possible (e.g. fixed boundaries). Different initial settings (e.g. initial random distribution of strategies) can be chosen. Furthermore, different lattice geometries can be used (e.g. triangular or hexagonal).
To analyze invasion conditions, it is useful to start with one mutant strategy among a homogeneous array. Another aim of exploring spatial games is to find interesting sequences of patterns (e.g. dynamic fractals, evolutionary kaleidoscopes, chaos).196 Empty sites or more than two competing strategies can lead to spiral waves. For example, in the spatial Prisoner's Dilemma, coexistence between cooperators and defectors can be observed.196 Cooperators survive in clusters and under certain conditions, cooperators can invade defectors. Often, spatial structure tends to allow more diversity than well-mixed populations do.7,196
A.5. Evolutionary game dynamics
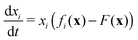 | (A.3) |
• Every Nash equilibrium of a matrix game is a rest point (= fixed point) of the replicator equation, but not every fixed point of the replicator equation is a Nash equilibrium.
• Every evolutionarily stable state of a matrix game is an asymptotically stable fixed point of the replicator equation.
The approach considers a resident population which is invaded by mutants. The most fit mutant (in comparison to the resident population) is chosen by natural selection.197 We assume that the whole population uses strategy x and a mutant uses strategy y = x + h which is close to x. A(y,x) denotes the total payoff obtained by a y strategist against an x-opponent. The relative advantage W(h,x) is calculated by A(y,x) − A(x,x). The adaptive dynamics is then calculated by the differential equation
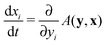 | (A.4) |
Appendix B: types of games
Here we present an overview over all possible symmetric games with two players and two strategies. Similar classifications are proposed by Hauert200 and Stark.201The payoff matrix of any symmetrical two-player game can be written as:
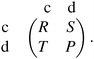 | (B.1) |
The payoffs are termed according to the Prisoner's Dilemma, where they mean R-reward for mutual cooperation (strategy c), T-temptation to defect (strategy d), S-sucker's payoff and P-punishment for mutual defection. If we set R > P, the remaining two values (S and T) span a plane, where 12 different regions can be distinguished. This plane is depicted in Fig. 8. The character of a game does not change if rows and columns are permuted simultaneously. We now characterise the various games with an exemplary payoff.
(1) Prisoner's Dilemma
Cover story: two suspects in a crime are put into separate cells. If they both confess, each will be sentenced to three years in prison. If only one of them confesses, he will be set free and used as a witness against the other, who will receive a sentence of five years. If neither confesses, they will both be convicted of a minor offence and spend one year in prison. The highest payoff represents the best output of this situation (to be set free) and 0 stands for the worst case (five years in prison).
Game properties: the dominant strategy is to defect. It is the only Nash equilibrium and evolutionarily stable strategy (ESS). This solution is Pareto inefficient.
(2) Hawk–dove game (also: game of chicken, snowdrift game) (Leader II)
Cover stories: Hawk–dove game. The opponents are fighting for food, a territory or a potential mate. To be a hawk is an aggressive strategy (defect), while dove is to denote a peaceful (cooperate), surrendering strategy. Two hawks damage each other, two doves share the good (or one dove gets the whole good with probability 0.5). A dove meeting a hawk flees, resulting in no fitness gain nor loss, while the hawk gets the good.
Game of chicken, also Chicken-game. Two cars are speeding towards each other on a collision. The loser must chicken out, or both suffer from a bad accident. If none of them stays on track, they stay unhurt but share the disgrace.
Snowdrift game. Two car drivers are stuck in a snowdrift. If both refuse to shovel, none of them will get home. If one of them shovels, while the other refuses to do so, both will get home. However, the shoveling player cooperates and pays a cost. If both shovel, both will get home, and share the cost of shoveling.
Game properties: the two pure Nash equilibria are on the secondary diagonal (to choose different strategies). The defector has the greater payoff. One mixed Nash equilibrium can be found, which is also an ESS.
(3) Leader (I)
Cover story: a strategic game in economics is played by the leader firm that moves first and by the follower firm that moves sequentially, while competing for quantity. The leader always has an advantage, similar to the hawk–dove game. However, here the cooperator has a lower disadvantage.
Game properties: the two pure Nash equilibria are on the secondary diagonal (to choose different strategies). The defector has the greater payoff. One mixed Nash equilibrium can be found, which is also an ESS (cf. hawk–dove game).
(4) Battle of the sexes (Leader III)
Cover story: a couple wants to meet this evening. The husband prefers to visit the football game, while his wife would like to go to the opera. Both prefer to go out together rather than to different places. They are not able to communicate.
Originally this game is asymmetric (i.e. the payoffs are different, though both choose the same strategy), but it can be transformed into a symmetric one by renaming the strategies in e.g. “my preference” and “his/her preference”.
Game properties: the battle of the sexes has the same properties as the hawk–dove game, but the cooperator (in terms of the Prisoner's Dilemma), the player applying “my preference”, has the greater payoff. The two pure Nash equilibria are on the secondary diagonal. One mixed Nash equilibrium can be found, which is also an ESS (cf. hawk–dove game).
(5) Stag Hunt (Coordination III)
Cover story: two huntsmen have the choice to hunt a stag or a hare. They can only hunt the stag cooperatively and share the stag afterwards. Also, each one can hunt a hare on its own, but half a stag is worth more than a hare. If they are not able to communicate, which is the best strategy?
Game properties: the two pure Nash equilibria are on the main diagonal. One mixed Nash equilibrium can be found, which is not an ESS.
(6) Harmony games
(a) Harmony I
(b) Harmony II
Game properties: cooperation is the dominant strategy that leads to a pure Nash equilibrium where both players receive the highest possible payoff. Thus, they are “in harmony”. The difference between these two versions lies in the “strength” of the dominance of cooperation. In version II cooperation has the stronger dominance.
(7) Route choice (Deadlock II)
Cover story: there are two routes with different capacities: a freeway and a side route. If both players decide to drive the freeway (c strategy), they can drive fast, but have to consider the other car, while a single car on the freeway can speed up. A single car on the side route is still quick, while two cars on the side route hinder each other.
Game properties: driving on the freeway is the dominant strategy. There exists only one Nash equilibrium with the second highest possible payoff. A player has the interest to encourage the opponent to play the dominated strategy.
(8) Coordination games
(a) Coordination game I
(b) Coordination game II
Game properties: the two players have to coordinate their actions (i.e. play the same strategies) to receive a high payoff. The two pure Nash equilibria are on the main diagonal. Thus, the system shows bistability. One mixed Nash equilibrium can be found, which is NOT an ESS.
(9) Own goal (Harmony III)
Game properties: cooperation is the dominant strategy. There exists only one Nash equilibrium with the highest possible payoff. A unilateral deviation of one player from the dominant strategy would be an “own goal” because the loss is very high.
(10) Deadlock (I)
In terms of the cover story of the route-choice game, one may say that when both drivers choose the side road, they are better off (for example, because they can help each other in case of an accident) than a driver that goes alone on the side road.
Game properties: the c strategy is dominant. There exists only one Nash equilibrium with the second highest possible payoff. A player has some interest to encourage the opponent to play the dominated strategy.
The game properties are summarised with the classification tree in Fig. 9.
 | ||
| Fig. 9 Classification tree for two-player games summarising game properties. The dynamics is characterized as in Nowak and Sigmund.7 | ||
Appendix C: rock–scissors–paper game
This popular children's game, where rock is wrapped by paper, paper is cut by scissors and scissors are crushed by rock can also be described by a game-theoretical model. In a biological context the strategies are renamed to producer (P), resistant (R) and sensitive (S), see Section 5. Consider the following payoff matrix: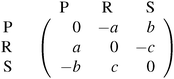 | (C.1) |
There is no Nash equilibrium in pure strategies, because for each entry of the matrix one of the players can increase payoff by changing strategy. For example, if a producer plays against a resistant strain, the producer can improve by switching to any other strategy. A mixed Nash equilibrium can be found by applying the Bishop–Cannings theorem (Appendix A) with the following distribution of strategies p = a/(a + b + c), r = b/(a + b + c), s = c/(a + b + c). In this biological context, the distribution can be interpreted as the corresponding fractions of the population. In the special case of a = b = c, an equal distribution of one third is obtained as is known from the hand game of the same name. However, this mixed Nash equilibrium is not evolutionarily stable. That is why it is interesting to study the dynamics of this game. Different dynamical approaches are reviewed in Appendix A.
To illustrate the dynamics of a three species population, often the simplex, an equilateral triangle, is used. It represents the plane from the three-dimensional Cartesian coordinate system with p + r + s = 1, where each fraction stands for one subpopulation, see Fig. 10.
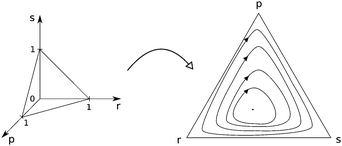 | ||
| Fig. 10 Simplex representation. Left: Simplex in the three-dimensional Cartesian coordinate system, right: simplex without the coordinate system. Here, periodic orbits around a fixed point are shown, similar to ref. 81. Such cyclic orbits correspond to oscillating sub-populations. | ||
Acknowledgements
Financial support by the International Max Planck Research School (Jena), the Leibniz Institute for Natural Product Research and Infection Biology – Hans-Knöll-Institute (Jena), the Jena School of Microbial Communication, and the Virtual Liver Network funded by the BMBF (Germany) is gratefully acknowledged. We thank Ina Weiß for helpful literature search and Sebastian Germerodt for stimulating discussions.References
- Y. K. Lee and S. K. Mazmanian, Science, 2010, 330, 1768–1773 CrossRef CAS PubMed.
- D. J. Schneider and A. Collmer, Annu. Rev. Phytopathol., 2010, 48, 457–479 CrossRef CAS PubMed.
- M. Ebner, R. Watson and J. Alexander, Proceedings of the 2000 Congress on Evolutionary Computation, San Diego, IEEE Press, 2000, pp. 1284–1291.
- J. Maynard Smith, Evolution and the Theory of Games, Cambridge University Press, Cambridge, 1982 Search PubMed.
- R. Axelrod, The Evolution of Cooperation, Basic Books, New York, 1984 Search PubMed.
- J. Hofbauer and K. Sigmund, Evolutionary Games and Population Dynamics, Cambridge University Press, Cambridge, 1998 Search PubMed.
- M. A. Nowak and K. Sigmund, Science, 2004, 303, 793–799 CrossRef CAS PubMed.
- J. V. Neumann and O. Morgenstern, Theory of Games and Economic Behaviour, Princeton University Press, 1944 Search PubMed.
- E. Berne, Games People Play: The Psychology of Human Relationships, Penguin, 1973 Search PubMed.
- R. B. Myerson, Game Theory: Analysis of Conflict, Harvard University Press, 1991 Search PubMed.
- M. Eigen and R. Winkler, Das Spiel. Naturgesetze steuern den Zufall, Pieper, München, 1975 Search PubMed.
- K. Bohl, S. Hummert, S. Werner, D. Basanta, A. Deutsch, S. Schuster, G. Theißen and A. Schroeter, Mol. BioSyst., 2014 10.1039/c3mb70601j.
- J. F. Nash, Proc. Natl. Acad. Sci. U. S. A., 1950, 36, 48–49 CrossRef CAS.
- J. Maynard Smith and G. R. Price, Nature, 1973, 246, 15–18 CrossRef.
- W. D. Hamilton, Science, 1967, 156, 477–488 CAS.
- K. C. Clements and D. W. Stephens, Anim. Behav., 1995, 50, 527–535 CrossRef.
- M. Broom and G. Ruxton, Behav. Ecol., 1998, 9, 397–403 CrossRef.
- J. Brown and T. Vincent, Evolution, 1992, 46, 1269–1283 CrossRef.
- D. W. Dickins and R. A. Clark, J. Theor. Biol., 1987, 125, 301–305 CrossRef.
- R. Poulin and W. L. Vickery, J. Theor. Biol., 1995, 175, 63–70 CrossRef PubMed.
- D. King, Am. Nat., 1990, 135, 809–828 Search PubMed.
- M. Augner, T. Fagerstrom and J. Tuomi, Behav. Ecol. Sociobiol., 1991, 29, 231–234 CrossRef.
- M. Archetti, J. Theor. Biol., 2000, 205, 625–630 CrossRef CAS PubMed.
- J.-U. Kreft, Microbiology, 2004, 150, 2751–2760 CrossRef CAS PubMed.
- T. Pfeiffer and S. Bonhoeffer, Am. Nat., 2004, 163, E126–E135 CrossRef PubMed.
- E. Costa, J. Pérez and J. U. Kreft, Trends Microbiol., 2006, 14, 213–219 CrossRef CAS PubMed.
- S. P. Brown and R. A. Johnstone, Proc. R. Soc. B, 2001, 268, 961–965 CrossRef CAS PubMed.
- M. Pagel, Nature, 1993, 363, 539–541 CrossRef CAS PubMed.
- R. A. Gatenby and T. L. Vincent, Cancer Res., 2003, 63, 6212–6220 CAS.
- D. Basanta, H. Hatzikirou and A. Deutsch, Eur. Phys. J. B, 2008, 63, 393–397 CrossRef CAS.
- T. Pfeiffer, S. Schuster and S. Bonhoeffer, Science, 2001, 292, 504–507 CrossRef CAS PubMed.
- D. Voet and J. Voet, Biochemistry, John Wiley & Sons, 2011 Search PubMed.
- Z. Wang and N. Goldenfeld, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 020902 CrossRef.
- J. C. Aledo and J. A. Perez-Claros, et al. , J. Mol. Evol., 2007, 65, 328–339 CrossRef CAS PubMed.
- J. Juul, K. Sneppen and J. Mathiesen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061924 CrossRef.
- R. C. MacLean, Heredity, 2007, 100, 471–477 CrossRef PubMed.
- I. A. Shiklomanov, Water Int., 2000, 25, 11–32 CrossRef.
- J. Y. Wakano and M. A. Nowak, et al. , Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 7910–7914 CrossRef CAS PubMed.
- T. Frick and S. Schuster, Naturwissenschaften, 2003, 90, 327–331 CrossRef CAS PubMed.
- S. Schuster, J.-U. Kreft, A. Schroeter and T. Pfeiffer, J. Biol. Phys., 2008, 34, 1–17 CrossRef CAS PubMed.
- R. C. MacLean and I. Gudelj, Nature, 2006, 441, 498–501 CrossRef CAS PubMed.
- O. Warburg, Science, 1956, 123, 309–314 CAS.
- S. Schuster, L. F. de Figueiredo, A. Schroeter and C. Kaleta, BioSystems, 2011, 105, 147–153 CrossRef CAS PubMed.
- I. Kareva, PLoS One, 2011, 6, e28576 CAS.
- S. A. Frank, J. Evol. Biol., 2010, 23, 609–613 CrossRef CAS PubMed.
- S. A. Frank, Philos. Trans. R. Soc., B, 2010, 365, 2515–2522 CrossRef PubMed.
- L. A. Harriman and B. W. Hammer, J. Dairy Sci., 1931, 14, 40–49 CrossRef CAS.
- D. Greig and M. Travisano, Proc. R. Soc. B, 2004, 271, S25–S26 CrossRef CAS PubMed.
- J. Gore, H. Youk and A. van Oudenaarden, Nature, 2009, 459, 253–256 CrossRef CAS PubMed.
- S. Schuster, J.-U. Kreft, N. Brenner, F. Wessely, G. Theißen, E. Ruppin and A. Schroeter, Biotechnol. J., 2008, 5, 751–758 CrossRef PubMed.
- S. D. Allison, Ecol. Lett., 2005, 8, 626–635 CrossRef PubMed.
- H. Bachmann, D. Molenaar, M. Kleerebezem and J. E. van Hylckama Vlieg, ISME J., 2011, 5, 929–932 CrossRef CAS PubMed.
- R. C. MacLean, A. Fuentes-Hernandez, D. Greig, L. D. Hurst and I. Gudelj, PLoS Biol., 2010, 8, e1000486 Search PubMed.
- S. Estrela, C. H. Trisos and S. P. Brown, Am. Nat., 2012, 180, 566–576 CrossRef PubMed.
- H. C. Bernstein, S. D. Paulson and R. P. Carlson, J. Biotechnol., 2012, 157, 159–166 CrossRef CAS PubMed.
- B. E. Morris, R. Henneberger, H. Huber and C. Moissl-Eichinger, FEMS Microbiol. Rev., 2013, 37, 384–406 CrossRef CAS PubMed.
- M. Doebeli, Popul. Ecol., 2002, 44, 59–70 CrossRef.
- J. J. Bull and W. R. Harcombe, PLoS One, 2009, 4, e4115 Search PubMed.
- B. Schink, Antonie van Leeuwenhoek, 2002, 81, 257–261 CrossRef CAS.
- C. Katsuyama, S. Nakaoka, Y. Takeuchi, K. Tago, M. Hayatsu and K. Kato, J. Theor. Biol., 2009, 256, 644–654 CrossRef CAS PubMed.
- D. E. Rozen and R. E. Lenski, Am. Nat., 2000, 155, 24–35 CrossRef PubMed.
- P. Gerlee and T. Lundh, Evolution, 2010, 64, 2716–2730 CrossRef PubMed.
- J. Maynard Smith, Nature, 1964, 201, 1145–1147 CrossRef.
- S. Estrela and I. Gudelj, PLoS One, 2010, 5, e14121 CAS.
- M. L. Friesen and E. I. Jones, Methods in Molecular Biology, Springer, New York, 2012, vol. 804, pp. 481–499 Search PubMed.
- M. Archetti and I. Scheuring, J. Theor. Biol., 2012, 318C, 58–67 Search PubMed.
- M. Archetti, I. Scheuring, M. Hoffman, M. E. Frederickson, N. E. Pierce and D. W. Yu, Ecol. Lett., 2011, 14, 1300–1312 CrossRef PubMed.
- J. B. Jackson and L. Buss, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 5160–5163 CrossRef CAS.
- B. Sinervo and C. M. Lively, Nature, 1996, 380, 240–243 CrossRef CAS.
- F. Michor and M. A. Nowak, Nature, 2002, 419, 677–679 CrossRef CAS PubMed.
- B. Kerr, M. A. Riley, M. W. Feldman and B. M. Bohannan, Nature, 2002, 418, 171–174 CrossRef CAS PubMed.
- B. C. Kirkup and M. A. Riley, Nature, 2004, 428, 412–414 CrossRef CAS PubMed.
- R. Durrett and S. Levin, J. Theor. Biol., 1997, 185, 165–171 CrossRef.
- G. Neumann and S. Schuster, J. Math. Biol., 2007, 54, 815–846 CrossRef PubMed.
- G. Neumann and S. Schuster, Discrete Cont. Dyn.-B, 2007, 8, 207–228 CrossRef.
- G. F. Neumann and G. Jetschke, BioSystems, 2010, 99, 155–166 CrossRef CAS PubMed.
- M. Nakamaru and Y. Iwasa, Theor. Popul. Biol., 2000, 57, 131–144 CrossRef CAS PubMed.
- M. W. Adamson and A. Y. Morozov, Bull. Math. Biol., 2012, 74, 2004–2031 CrossRef CAS PubMed.
- R. M. May and W. J. Leonard, SIAM J. Appl. Math., 1975, 29, 243–253 CrossRef.
- H. Shi, W.-X. Wang, R. Yang and Y.-C. Lai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 030901 CrossRef.
- M. Frean and E. R. Abraham, Proc. R. Soc. B, 2001, 268, 1323–1327 CrossRef CAS PubMed.
- G. Károlyi, Z. Neufeld and I. Scheuring, J. Theor. Biol., 2005, 236, 12–20 CrossRef PubMed.
- M. Berr, T. Reichenbach, M. Schottenloher and E. Frey, Phys. Rev. Lett., 2009, 102, 048102 CrossRef.
- W.-X. Wang, Y.-C. Lai and C. Grebogi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 046113 CrossRef.
- X. Ni, R. Yang, W.-X. Wang, Y.-C. Lai and C. Grebogi, Chaos, 2010, 20, 045116 CrossRef PubMed.
- A. P. O. Müller and J. A. C. Gallas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 052901 CrossRef.
- T. L. Czárán, R. F. Hoekstra and L. Pagie, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 786–790 CrossRef PubMed.
- F. Prado and B. Kerr, Evolution, 2008, 62, 538–548 CrossRef PubMed.
- A. A. Winkler, T. Reichenbach and E. Frey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 060901 CrossRef.
- T. Reichenbach, M. Mobilia and E. Frey, Nature, 2007, 448, 1046–1049 CrossRef CAS PubMed.
- T. Reichenbach, M. Mobilia and E. Frey, J. Theor. Biol., 2008, 254, 368–383 CrossRef PubMed.
- S. Venkat and M. Pleimling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021917 CrossRef.
- A. Szolnoki and G. Szabó, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 037102 CrossRef.
- G. Szabó, A. Szolnoki and R. Izsák, J. Phys. A: Math. Gen., 2004, 380, 2599–2609 CrossRef.
- K.-i. Tainaka, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 3401–3409 CrossRef CAS.
- M. Ifti and B. Bergersen, Eur. Phys. J. B, 2004, 37, 101–107 CrossRef CAS.
- A. Traulsen, J. C. Claussen and C. Hauert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041901 CrossRef.
- J. C. Claussen and A. Traulsen, Phys. Rev. Lett., 2008, 100, 058104 CrossRef.
- L. Frachebourg, P. L. Krapivsky and E. Ben-Naim, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6186–6200 CrossRef CAS.
- P. P. Avelino, D. Bazeia, L. Losano and J. Menezes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031119 CrossRef CAS.
- P. P. Avelino, D. Bazeia, L. Losano, J. Menezes and B. F. Oliveira, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 036112 CrossRef CAS.
- A. F. Lütz, S. Risau-Gusman and J. J. Arenzon, J. Theor. Biol., 2013, 317, 286–292 CrossRef PubMed.
- M. Peltomäki and M. Alava, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031906 CrossRef.
- G. Szabó and T. Czárán, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 042902 CrossRef.
- B. Allen and D. I. S. Rosenbloom, Bull. Math. Biol., 2012, 74, 2650–2675 Search PubMed.
- Q. He, M. Mobilia and U. C. Täuber, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051909 CrossRef.
- G. Jäger, J. Theor. Biol., 2008, 253, 131–141 CrossRef PubMed.
- R. Gibbons, A Primer in Game Theory, Financial Times Prentice Hall, 1992 Search PubMed.
- E. Rasmusen, Games and Information: An Introduction to Game Theory, Wiley-Blackwell, 1995 Search PubMed.
- J. Maynard Smith and D. Harper, Animal Signals, Oxford University Press, 2003 Search PubMed.
- A. Zahavi, J. Theor. Biol., 1975, 53, 205–214 CrossRef CAS.
- A. Grafen, J. Theor. Biol., 1990, 144, 517–546 CrossRef CAS.
- C. T. Bergstrom, S. Számadó and M. Lachmann, Philos. Trans. R. Soc., B, 2002, 357, 1595–1606 CrossRef PubMed.
- R. Popat, S. A. Crusz, M. Messina, P. Williams, S. A. West and S. P. Diggle, Proc. R. Soc. B, 2012, 279, 4765–4771 CrossRef CAS PubMed.
- T. Czárán and R. F. Hoekstra, PLoS One, 2009, 4, e6655 Search PubMed.
- A. Lotem, M. A. Fishman and L. Stone, Proc. R. Soc. B, 2003, 270, 199–205 CrossRef PubMed.
- R. Axelrod and W. D. Hamilton, Science, 1981, 211, 1390–1396 CAS.
- A. Traulsen and M. A. Nowak, PLoS One, 2007, 2, e270 Search PubMed.
- D. C. Queller, E. Ponte, S. Bozzaro and J. E. Strassmann, Science, 2003, 299, 105–106 CrossRef CAS PubMed.
- D. Renaud and T. de Meeüs, J. Theor. Biol., 1991, 152, 319–327 CrossRef.
- M. R. Frean and E. R. Abraham, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 051913 CrossRef.
- S.-H. Huang, W. Zhou and A. Jong, J. Biomed. Biotechnol., 2008, 856314 Search PubMed.
- E. M. Rauch and Y. Bar-Yam, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 020903 CrossRef.
- R. M. Anderson and R. M. May, Nature, 1979, 280, 361–367 CrossRef CAS.
- R. M. Anderson and R. M. May, Parasitology, 1982, 85, 411–426 CrossRef.
- H. J. Bremermann and J. Pickering, J. Theor. Biol., 1983, 100, 411–426 CrossRef CAS.
- M. van Baalen, Proc. R. Soc. B, 1998, 265, 317–325 CrossRef CAS PubMed.
- T. Day, A. L. Graham and A. F. Read, Proc. R. Soc. B, 2007, 274, 2685–2692 CrossRef PubMed.
- M. Boots and Y. Haraguchi, Am. Nat., 1999, 153, 359–370 CrossRef PubMed.
- M. H. Bonds, D. C. Keenan, A. J. Leidner and P. Rohani, Evolution, 2005, 59, 1859–1866 CrossRef PubMed.
- M. R. Miller, A. White and M. Boots, Evolution, 2007, 61, 2–14 CrossRef PubMed.
- A. Best, A. White and M. Boots, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20786–20791 CrossRef CAS PubMed.
- P. D. Taylor, T. Day, D. Nagy, G. Wild, J.-B. André and A. Gardner, Theor. Popul. Biol., 2006, 69, 323–331 CrossRef PubMed.
- M. Boots, A. Best, M. R. Miller and A. White, Philos. Trans. R. Soc., B, 2009, 364, 27–36 CrossRef PubMed.
- A. Morozov and A. Best, J. Theor. Biol., 2012, 307, 29–36 CrossRef PubMed.
- S. H. Alonzo and R. Calsbeek, J. Evol. Biol., 2010, 23, 2614–2624 CrossRef CAS PubMed.
- T. Reluga and J. Li, J. Math. Biol., 2012, 66, 1–27 Search PubMed.
- P. D. Williams, Am. Nat., 2012, 179, 228–239 CrossRef PubMed.
- D. M. Wolf, V. V. Vazirani and A. P. Arkin, J. Theor. Biol., 2005, 234, 227–253 CrossRef PubMed.
- D. M. Wolf, V. V. Vazirani and A. P. Arkin, J. Theor. Biol., 2005, 234, 255–262 CrossRef PubMed.
- B. L. d. Bivort, C.-C. Chen, F. Perretti, G. Negro, T. M. Philip and Y. Bar-Yam, J. Theor. Biol., 2007, 248, 26–36 CrossRef PubMed.
- S. M. Eswarappa, PLoS One, 2009, 4, e5383 Search PubMed.
- S. Hummert, C. Hummert, A. Schröter, B. Hube and S. Schuster, J. Theor. Biol., 2010, 264, 312–318 CrossRef CAS PubMed.
- S. Bewick, J. Wu, S. C. Lenaghan, R. Yang, M. Zhang and W. Hamel, Bull. Math. Biol., 2011, 73, 2339–2356 CrossRef PubMed.
- S. Bewick, M. Zhang and W. Hamel, IEEE Trans. Syst. Man Cybern., 2011, 41, 583–588 CrossRef.
- B. Crespi and K. Summers, Trends Ecol. Evol., 2005, 20, 545–552 CrossRef PubMed.
- L. M. F. Merlo, J. W. Pepper, B. J. Reid and C. C. Maley, Nat. Rev. Cancer, 2006, 6, 924–935 CrossRef CAS PubMed.
- P. C. Nowell, Science, 1976, 194, 23–28 CAS.
- M. Gerlinger and A. J. Rowan, et al. , N. Engl. J. Med., 2012, 366, 883–892 CrossRef CAS PubMed.
- R. Axelrod, D. E. Axelrod and K. J. Pienta, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13474–13479 CrossRef CAS PubMed.
- R. J. Gillies, D. Verduzco and R. A. Gatenby, Nat. Rev. Cancer, 2012, 12, 487–493 CrossRef CAS PubMed.
- D. Basanta and A. Deutsch, in Selected Topics in Cancer Modeling: Genesis, Evolution, Immune Competition, and Therapy, ed. N. Bellomo and E. de Angelis, Springer, Birkhäuser Boston, 2008, ch. 5 Search PubMed.
- C. Cleveland, D. Liao and R. Austin, AIP Adv., 2012, 2, 011202 CrossRef PubMed.
- W. C. Hahn and R. A. Weinberg, N. Engl. J. Med., 2002, 347, 1593–1603 CrossRef CAS PubMed.
- D. Hanahan and R. A. Weinberg, Cell, 2000, 100, 57–70 CrossRef CAS.
- D. Hanahan and R. A. Weinberg, Cell, 2011, 144, 646–674 CrossRef CAS PubMed.
- A. R. A. Anderson, M. Hassanein, K. M. Branch, J. Lu, N. A. Lobdell, J. Maier, D. Basanta, B. Weidow, A. Narasanna, C. L. Arteaga, A. B. Reynolds, V. Quaranta, L. Estrada and A. M. Weaver, Cancer Res., 2009, 69, 8797–8806 CrossRef CAS PubMed.
- Y. Mansury, M. Diggory and T. Deisboeck, J. Theor. Biol., 2006, 238, 146–156 CrossRef PubMed.
- M. Martin, J. Natl. Cancer Inst., 2009, 101, 220–222 CrossRef PubMed.
- R. A. Gatenby and R. J. Gillies, Nat. Rev. Cancer, 2004, 4, 891–899 CrossRef CAS PubMed.
- D. Basanta, J. G. Scott, R. Rockne, K. R. Swanson and A. R. A. Anderson, Phys. Biol., 2011, 8, 015016 CrossRef PubMed.
- D. Basanta, M. Simon, H. Hatzikirou and A. Deutsch, Cell Prolif., 2008, 41, 980–987 CrossRef CAS PubMed.
- M. Archetti, J. Theor. Biol., 2014, 341, 1–8 CrossRef PubMed.
- M. A. Nowak, Science, 2006, 314, 1560–1563 CrossRef CAS PubMed.
- D. W. Strand, O. E. Franco, D. Basanta, A. R. A. Anderson and S. W. Hayward, Curr. Mol. Med., 2010, 10, 95–112 CrossRef CAS.
- I. P. Tomlinson and W. F. Bodmer, Br. J. Cancer, 1997, 75, 157–160 CrossRef CAS.
- L. A. Bach, S. M. Bentzen, J. Alsner and F. B. Christiansen, Eur. J. Cancer, 2001, 37, 2116–2120 CrossRef CAS.
- L. A. Bach, D. J. T. Sumpter, J. Alsner and V. Loeschcke, J. Theor. Med., 2003, 5, 47–58 CrossRef.
- M. Billaud and M. Santoro, Cancer Res., 2011, 71, 6572–6575 CrossRef CAS PubMed.
- D. Dingli, F. A. C. C. Chalub, F. C. Santos, S. V. Segbroeck and J. M. Pacheco, Br. J. Cancer, 2009, 101, 1130–1136 CrossRef CAS PubMed.
- D. Basanta, J. G. Scott, M. N. Fishman, G. Ayala, S. W. Hayward and A. R. A. Anderson, Br. J. Cancer, 2012, 106, 174–181 CrossRef CAS PubMed.
- R. A. Gatenby, J. Brown and T. Vincent, Cancer Res., 2009, 69, 7499–7502 CrossRef CAS PubMed.
- A. S. Silva, R. A. Gatenby, R. J. Gillies and J. A. Yunes, J. Theor. Biol., 2010, 262, 601–613 CrossRef PubMed.
- S. J. Antonia, N. Mirza, I. Fricke, A. Chiappori, P. Thompson, N. Williams, G. Bepler, G. Simon, W. Janssen, J.-H. Lee, K. Menander, S. Chada and D. I. Gabrilovich, Clin. Cancer Res., 2006, 12, 878–887 CrossRef CAS PubMed.
- D. Basanta, R. A. Gatenby and A. R. A. Anderson, Mol. Pharmaceutics, 2012, 9, 914–921 CrossRef CAS PubMed.
- S. Bewick, R. Yang and M. Zhang, Engineering in Medicine and Biology Society, 2009. EMBC 2009. Annual International Conference of the IEEE, 2009, pp. 6026–6029.
- J. Wu and M. J. Zhang, IEEE Trans. Syst. Man Cybern., 2010, 40, 694–702 CrossRef PubMed.
- A. Ostman, Nat. Med., 2012, 18, 1332–1334 CrossRef PubMed.
- V. Marx, Nature, 2013, 494, 133–136 CrossRef CAS PubMed.
- G. Lambert, L. Estévez-Salmeron, S. Oh, D. Liao, B. M. Emerson, T. D. Tlsty and R. H. Austin, Nat. Rev. Cancer, 2011, 11, 375–382 CrossRef CAS PubMed.
- O. Gillor, A. Etzion and M. A. Riley, Appl. Microbiol. Biotechnol., 2008, 81, 591–606 CrossRef CAS PubMed.
- P. D. Cotter, R. P. Ross and C. Hill, Nat. Rev. Microbiol., 2013, 11, 95–105 CrossRef CAS PubMed.
- C. T. Lohans and J. C. Vederas, Int. J. Microbiol., 2012, 2012, 386410 Search PubMed.
- M. Montalbán-López, M. Sánchez-Hidalgo, E. Valdivia, M. Martínez-Bueno and M. Maqueda, Curr. Pharm. Biotechnol., 2011, 12, 1205–1220 Search PubMed.
- C. Brown, M. P. Garwood and J. E. Williamson, Biol. Lett., 2012, 8, 729–732 CrossRef PubMed.
- M. R. Silva and M. G. Severo, et al. , Biochem. Eng. J., 2013, 71, 38–46 CrossRef CAS PubMed.
- G. Potvin, A. Ahmad and Z. S. Zhang, Biochem. Eng. J., 2012, 64, 91–105 CrossRef CAS PubMed.
- T. Pfeiffer and S. Bonhoeffer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 1095–1098 CrossRef CAS PubMed.
- H. Cao, M. Sekiya, M. Ertunc, M. Burak, J. Mayers, A. White, K. Inouye, L. Rickey, B. Ercal, M. Furuhashi, G. Tuncman and G. Hotamisligil, Cell Metab., 2013, 17, 768–778 CrossRef CAS PubMed.
- A. Szolnoki and M. Perc, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 026104 CrossRef.
- H. Gintis, Game Theory Evolving, Princeton University Press, Princeton, 2000 Search PubMed.
- D. T. Bishop and C. Cannings, J. Theor. Biol., 1978, 70, 85–124 CrossRef CAS.
- M. A. Nowak, Evolutionary Dynamics – Exploring the Equations of Life, Harvard University Press, 2006 Search PubMed.
- J. Hofbauer and K. Sigmund, Bull. Am. Math. Soc., 2003, 40, 479–519 CrossRef.
- M. A. Nowak, C. E. Tarnita and T. Antal, Philos. Trans. R. Soc., B, 2010, 365, 19–30 CrossRef PubMed.
- M. A. Nowak and R. M. May, Nature, 1992, 359, 826–829 CrossRef.
- K. M. Page and M. A. Nowak, J. Theor. Biol., 2002, 219, 93–98 CrossRef.
- J. Hofbauer, Nonlinear Anal. Theor. Meth. App., 1981, 5, 1003–1007 CrossRef.
- O. Diekmann, Banach Center Publ., 2004, 63, 47–86 Search PubMed.
- C. Hauert, Int. J. Bifurcation Chaos, 2002, 12, 1531–1548 CrossRef.
- H.-U. Stark, Evolution, 2010, 64, 2458–2465 Search PubMed.
| This journal is © The Royal Society of Chemistry 2014 |