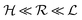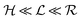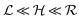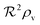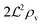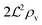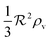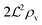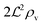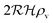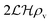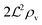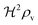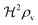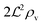DOI:
10.1039/C3MB70230H
(Paper)
Mol. BioSyst., 2014,
10, 103-109
Size of quorum sensing communities†
Received
17th June 2013
, Accepted 2nd October 2013
First published on 3rd October 2013
Abstract
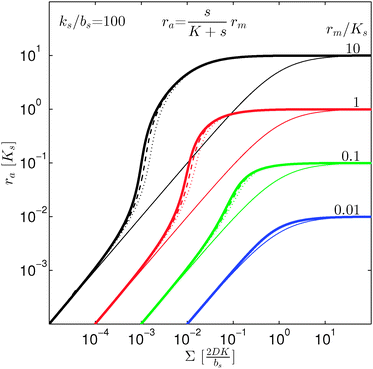
Ensembles of bacteria are able to coordinate their phenotypic behavior in accordance with the size, density, and growth state of the ensemble. This is achieved through production and exchange of diffusible signal molecules in a cell–cell regulatory system termed quorum sensing. In the generic quorum sensor a positive feedback in the production of signal molecules defines the conditions at which the collective behavior switches on. In spite of its conceptual simplicity, a proper measure of biofilm colony “size” appears to be lacking. We establish that the cell density multiplied by a geometric factor which incorporates the boundary conditions constitutes an appropriate size measure. The geometric factor is the square of the radius for a spherical colony or a hemisphere attached to a reflecting surface. If surrounded by a rapidly exchanged medium, the geometric factor is divided by three. For a disk-shaped biofilm the geometric factor is the horizontal dimension multiplied by the height, and the square of the height of the biofilm if there is significant flow above the biofilm. A remarkably simple factorized expression for the size is obtained, which separates the all-or-none ignition caused by the positive feedback from the smoother activation outside the switching region.
1 Introduction
Quorum sensing (QS) is a cell–cell signaling system used by bacteria to keep track of the size, density, and the growth state of the population. The regulation depends on the concentration of diffusible signal molecules which are typically small peptides for Gram positives and acyl homoserine lactones for Gram negatives. The most basic regulatory system consists of a signal molecule synthetase and a transcriptional regulator as illustrated in Fig. 1. At low population “size” the signal molecules are produced at the background level. At higher population “size”, the signal molecules accumulate and activate the transcriptional regulator to induce further transcription of the signal molecule synthetase. This positive feedback loop results in a rapid amplification of the signal.1–4 In these systems the regulator R is produced constitutively and is activated through binding of signal molecules S. The activated regulator concentrationis the intrinsic measure of whether a quorum is formed. This intracellular concentration controls the quorum sensing feedback as well as the transcription of specific quorum regulated target genes. Following this generic design of quorum sensors in Gram negative bacteria we derive a simple expression for the size of a biofilm colony and demonstrate how a single quorum sensor depends on density, geometry, boundary conditions, and maximal regulator concentration. The maximal regulator concentration, in turn, may be sensitive to specific conditions for the growth state required for the quorum conditions to be satisfied.
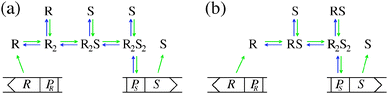 |
| | Fig. 1 Schematic examples of pathways in regulator (R) induction and signal (S) binding that may lead to static activated dimer (R2S2) concentrations of the form (2) or (4). R, PR and S, PS denote the gene and promoter region for the regulator and the signal molecule synthetase respectively. (a) Dimerization drives ligand binding. (b) Ligand binding drives dimerization. | |
The collective behavior displayed in QS was first reported in Vibrio fischeri where it activates the production of light in large cell colonies.1–3 Quorum sensing systems have been reported in many bacterial systems including Aeromonas hydrophila,5–7Agrobacterium tumefaciens,8 and Pseudomonas aeruginosa.9,10
It is our hope that the simple factorized expression for the size of a quorate community presented here will provide a more general guidance on how to speak of the size of a bacterial quorum. In particular we note that boundary conditions and geometrical shape are integral parts of the “size” of the colony.
All variables used in the manuscript are summarized in Table 1 while the size measures for different geometries and boundary conditions are summarized in Table 2.
Table 1 Variables and parameters used in the model
| Variable |
Details |
Explanation |
|
P
R
|
|
Promoter for R synthetase |
| R |
|
Regulator protein |
|
P
S
|
|
Promoter for S synthetase |
| S |
|
Signal molecule/ligand |
|
s
|
[S] |
Signal molecule concentration |
|
b
s
|
|
Background S production |
|
k
s
|
∼100bs |
Maximal induced S production |
|
κ
s
|
b
s < κs < ks |
Induced S production |
|
K
|
10 nM–10 μM |
R2S2 dissociation constant12,14–16 |
|
K
s
|
|
R2S2-PS dissociation constant |
|
r
a
|
[R2S2] |
Activated regulator concentration |
|
r
m
|
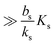
|
Maximal ra |
|
h
|
1–2 |
Regulator oligomerization order |
|
D
|
∼2 mm2 h−1 |
Diffusion constant for S (AHLs) |
|
ρ
v
|
<1 |
Bacterial density (v/v) |
|
r
|
|
Radial coordinate |
|
z
|
|
Height coordinate |
|
Σ
|
|
Colony “size” measure |
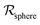
|
10–70 μm |
Radius of colony17,18 |
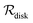
|
10–500 μm |
Radius of colony17 |
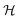
|
10–70 μm |
Height of colony17,19,20 |
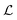
|
2–7 mm |
Degradation length (AHLs pH 8, 7) |
|
λ
s
|
0.03–0.25 h−1 |
S degradation (AHLs, pH 7, 8)21,22 |
|
Table 2 Size measures at the center of the colony for a sphere and for a disk resting on a signal molecule reflecting surface. The radius of the colony is 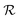 and the height of the disk is
and the height of the disk is 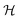 . When the degradation rate λs of signal molecules is significant, i.e. when the length
. When the degradation rate λs of signal molecules is significant, i.e. when the length 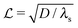 is smaller than one or more of the geometrical dimensions of the colony, this dimension is (approximately) replaced by
is smaller than one or more of the geometrical dimensions of the colony, this dimension is (approximately) replaced by  in the size measure. Eventually all geometrical sizes disappear and the size, Σ, then measures the cell density
in the size measure. Eventually all geometrical sizes disappear and the size, Σ, then measures the cell density
2 Model
2.1 Self consistent description
Typical motifs for activation of regulators involve dimerization as indicated in Fig. 1a where dimerization drives ligand binding and in Fig. 1b where ligand binding drives dimerization. In the quasistatic limit, the concentration of activated regulator may be parametrized as a product of a signal molecule switch of order h and a maximal level rm| | 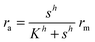 | (2) |
where K is the effective dissociation constant for binding of the signal molecules to the regulator.11 With h = 2 this describes dimerization followed by cooperative binding of signal molecules. Solving for the ligand concentration we get| | 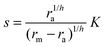 | (3) |
Another form of interest would be| | 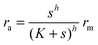 | (4) |
| | 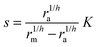 | (5) |
which covers non-cooperative binding of signal molecules as well as typical cases where signal molecule binding drives dimerization.11,12 With h = 1 we have monomer behavior. Though this is not a typical motif in quorum sensors, it is included to illustrate the advantage of designs involving oligomers to achieve the hysteresis leading to robust all-or-none switching seen in many positive feedback systems.13
The binding of the activated regulator to the signal promoter site leads to increased expression of the signal molecule synthetase. In the quasistatic limit the resulting signal molecule production can be expressed
| | 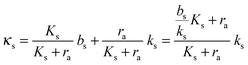 | (6) |
normalized as produced number per time per intracellular volume. This is merely a shift from a low background production
bs when
ra is below
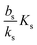
to the higher, active, production
ks when the concentration
ra is above
Ks. Note that the feedback mechanism turns on at the concentration
| | 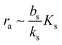 | (7) |
which needs to be a couple of orders of magnitude lower than the dissociation constant
Ks for the feedback system to produce a pronounced switch.
The production of signal molecules and their intercellular diffusion are linked together in the diffusion equation. Given a production rate κs(r) per intracellular volume and a volume fraction ρv(r) occupied by cells, the diffusion equation with the source term reads
| | 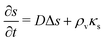 | (8) |
where
D is the diffusion constant for the signal molecules and
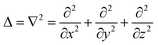
is the Laplace operator. Since single cells are unable to ignite or even maintain an ignited feedback loop the net contribution from binding and dissociation of signal molecules to regulators could be ignored when writing
eqn (8). (Active transport of signal molecules across the cell membrane which, to lowest order, leads to a rescaling between the intracellular and extracellular ligand concentration was not included.) At the steady state
| | 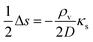 | (9) |
which we shall use to establish qualitative expressions for the conditions required to form a quorum.
2.2 Simple estimates
As a starting point, let us solve eqn (9) for a spherical colony of bacteria with radius 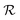 . This also solves the case of a hemispherical biofilm on a reflecting surface. The volume fraction occupied by cells, ρv, is zero outside the biofilm and assumed constant inside the colony.
. This also solves the case of a hemispherical biofilm on a reflecting surface. The volume fraction occupied by cells, ρv, is zero outside the biofilm and assumed constant inside the colony.
If the colony is very small or very large, we can assume that κs is constant and takes the values bs or ks respectively. Further, due to the feedback, the switching on/off is very abrupt which results in the whole colony being in the same state, i.e. κs can be assumed constant throughout the colony. This approximation is confirmed by numerical simulations below.
The solution of the steady state eqn (9) depends on the boundary condition. If the colony is surrounded by tissue or by non-flowing liquid, the boundary condition simply requires s(r) and its derivative to be continuous across the boundary. This leads to
| | 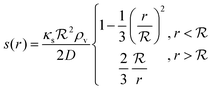 | (10) |
and the density of signal molecules at the center of the colony is
| | 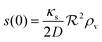 | (11) |
Self consistency dictates that the autoinducer production rate
κs in
(11) be equal to the rate in
(6). When the signal molecule concentration
s is approximately expressed in terms of
ra by
(3), this leads to a fairly simple factorized expression for
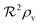
of the colony
| |  | (12) |
as a function of the activated regulator level
ra. With
h = 2
eqn (12) describes quorum switching with cooperative binding of ligands to the regulator. The relevant “size” measure is seen to be
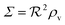
,
i.e. a combination of density and geometrical size of the biofilm. Notably, this size measure is a function of the activated dimer concentration only and can be expressed as a product of a normal forward activation and a feedback switch. Below we shall see that the r.h.s. is unaltered when the geometry and boundary conditions change. This means that all information regarding geometry, density, and boundary conditions is on the l.h.s. of the equation. In this sense
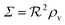
is a proper “size” measure. The forward activation and the feedback switch being dimensionless, the natural unit of size is seen to be 2
DK/
bs.
In Fig. 2 we see that for h = 1 the size dependence does not lead to hysteresis and therefore is not a fully developed all-or-none switch. However, for h = 2 seen in Fig. 3 the forward activation is sufficiently steep to ensure that the feedback switch leads to a robust all-or-none switch implied by the hysteresis.13
 |
| | Fig. 2 Self consistent estimate of the concentration of the activated regulator at the center of a bacterial colony as a function of the colony size. The ligand binding is assumed to be first order. Thin lines indicate the ra level for a first order ligand binding without feedback. The approximate solution is the same for all geometries. The size measure Σ depends on the specific geometry and boundary conditions as indicated in Table 2. At low regulator levels the feedback has no effect. At high regulator levels, the role of the feedback loop is to make the ignition of the QS system happen more abruptly. Dashed lines represent the numerical solution for a spherical colony with open boundary condition 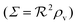 . Dotted curves are the numerical solution for a spherical colony with absorbing boundary . Dotted curves are the numerical solution for a spherical colony with absorbing boundary 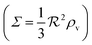 . . | |
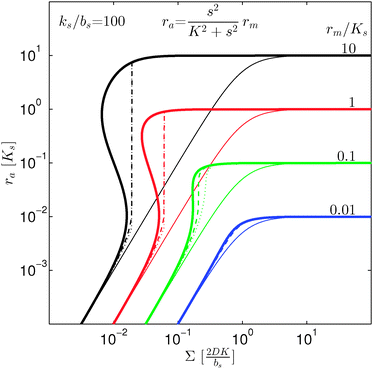 |
| | Fig. 3 Self consistent estimate of the concentration of the activated regulator at the center of a bacterial colony as a function of the colony size. Ligand binding is assumed to be second order and fully cooperative. Thin lines indicate the ra level for a second order cooperative ligand binding without feedback. The size measure Σ depends on the specific geometry and boundary conditions as indicated in Table 2. Dashed lines represent the numerical solution for open boundary condition 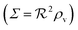 . Dotted curves are the numerical solution with absorbing boundary . Dotted curves are the numerical solution with absorbing boundary 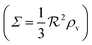 . . | |
If we consider the case (4) where ligand bindings are independent we get instead
| |  | (13) |
with
h = 2. The size measure
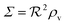
remains unchanged.
As seen in Fig. 4, expressions (12) and (13) have similar behavior at the ignition point, 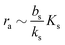 , and have identical asymptotic behavior. It is therefore not critical to the ignition function of the feedback loop that consecutive ligand bindings are cooperative. However, the cooperativity extends the bistable region somewhat and therefore may aid in stabilizing the switch.
, and have identical asymptotic behavior. It is therefore not critical to the ignition function of the feedback loop that consecutive ligand bindings are cooperative. However, the cooperativity extends the bistable region somewhat and therefore may aid in stabilizing the switch.
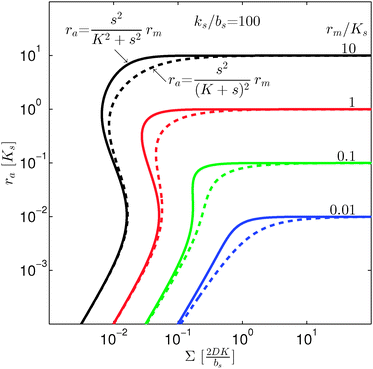 |
| | Fig. 4 Self consistent estimate of the concentration of the activated dimer regulator as a function of the bacterial colony size. The full curves represent the case of fully cooperative ligand binding and the dashed curves represent the independent binding of ligands. When rm ≳ Ks the hysteresis leading to a robust switch is present for cooperative ligand binding as well as for independent binding. The cooperative binding makes the hysteresis accessible at lower rm. | |
When growth conditions result in a maximal regulator concentration rm smaller than 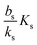 , it is impossible to ignite the feedback loop no matter how high the concentration of signal molecules is. When growth conditions lead to a maximal dimer level significantly higher than
, it is impossible to ignite the feedback loop no matter how high the concentration of signal molecules is. When growth conditions lead to a maximal dimer level significantly higher than 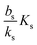 the feedback loop can be ignited. The effect of the feedback is an increased production of signal molecules and an abrupt increase in ra. Even for first order ligand binding (h = 1) the feedback makes the transition to higher ra levels happen quite abruptly as a function of colony “size” as seen in Fig. 2. For the more typical second-order ligand binding (h = 2) shown in Fig. 3 the feedback displays a second order transition, i.e. the transition is practically a Heaviside step function with ra jumping more than a factor ks/bs at the quorum ignition point.
the feedback loop can be ignited. The effect of the feedback is an increased production of signal molecules and an abrupt increase in ra. Even for first order ligand binding (h = 1) the feedback makes the transition to higher ra levels happen quite abruptly as a function of colony “size” as seen in Fig. 2. For the more typical second-order ligand binding (h = 2) shown in Fig. 3 the feedback displays a second order transition, i.e. the transition is practically a Heaviside step function with ra jumping more than a factor ks/bs at the quorum ignition point.
At size, Σ, larger than 2DK/bs the feedback loop has no effect: the activated regulator concentration ra is simply equal to the maximal regulator concentration rm. In such large biofilm communities ra is therefore completely determined by the growth state.
With absorbing boundary condition
| | 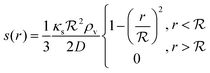 | (14) |
which leads to the approximate size expression
| |  | (15) |
This means that it only takes a three times larger
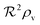
to reach the quorum sensing ignition level with absorbing boundary condition than with free boundary.
For a thin biofilm with height 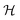 growing on a reflecting surface and covered by rapidly exchanged liquid we get
growing on a reflecting surface and covered by rapidly exchanged liquid we get
| | 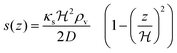 | (16) |
where
z is the height above the surface. Using the value at the bottom we get the size measure
| | 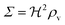 | (17) |
for the ignition.
If the liquid above the biofilm is not moving we get instead
| | 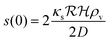 | (18) |
at the bottom of the biofilm and correspondingly the size measure
| | 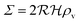 | (19) |
where
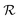
is the radius of the biofilm. (Details of the calculation are given in the ESI
† and
ref. 33.)
In all cases the scaling properties (r.h.s. of (12)) are conserved. Thus, the interpretation of “size” depends critically on the geometry of the assembly of cells. We note that the relevant geometry for different types of growth is dictated by the environmental conditions. The disk geometry is relevant when a biofilm grows as a thin film on a surface17,19,20 whereas the spherical geometry is relevant for a more bulky type of growth.18,19
2.3 Signal molecule degradation
In significantly alkaline environments signal molecules degrade21–23 which suggests the inclusion of a negative term proportional to the signal molecule concentration. Let us consider how this changes our conclusions. The diffusion equation now reads| | 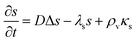 | (20) |
where λs is the degradation rate. Dimensional analysis tells us that loss from degradation competes with loss from diffusion at system dimensions around the characteristic length 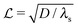 . I.e. when
. I.e. when 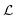 is much smaller than a system dimension, the system dimension should be replaced by the
is much smaller than a system dimension, the system dimension should be replaced by the 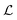 in our size measures Σ.
in our size measures Σ.
In the simple case of an extended biofilm of height 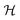 the solution to (20) is
the solution to (20) is
| | 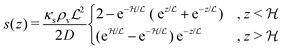 | (21) |
where
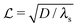
is the characteristic length at which the degradation competes with diffusion. At the bottom of the biofilm,
z = 0, this leads to
| | 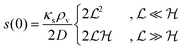 | (22) |
Comparison to
(11) and
(18) tells us that whenever
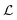
is smaller than a geometrical dimension, the geometrical dimension should be replaced by
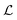
(within a factor of
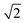
).
Table 2 summarizes the size measures for different geometries and also includes the modifications following from degradation.
2.4 Numerical solution
We saw that even with constant κs throughout the colony the signal molecule concentration s drops to ⅔ of the central value at the edge of the colony. If the colony is surrounded by rapidly flowing liquid, the boundary value drops to zero. Since κs and s are intertwined it is therefore reasonable to check the validity of keeping κs constant (all or none switch). This is now done in a numerical solution. After inserting (2) and (6) in (9) we arrive at the self consistent equation| | 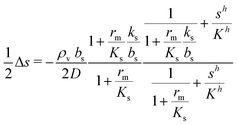 | (23) |
Changing units rm/Ks → rm, ks/bs → ks, s/K → s, and 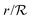 → reqn (23) becomes
→ reqn (23) becomes| | 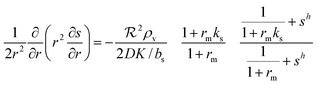 | (24) |
with the boundary condition ∂s(0)/∂r = 0 at the origin. With open boundary the solution is proportional to r−1 outside the colony. Since s as well as the derivative are continuous across the boundary this gives the condition ∂s(1)/∂r = −s(1) at the boundary. For a biofilm surrounded by rapidly exchanged liquid we get instead the boundary condition s(1) = 0.
The numerical solution, s(r), is subsequently used to calculate ravia(2). The values at the center are compared with the approximate expression in Fig. 2 for first order ligand binding. The approximate solution gives an excellent description of the transition from quiet to ignited quorum sensing. In Fig. 3 the numerical solutions at the center are compared to the approximate expression (12) for second order cooperative ligand binding. The second order ligand binding leads to a very abrupt ignition. In the bistable region the numerical solver was initialized with the static solution with no feedback in order to capture the ignition of the quorum sensor. Again, the “size” required to ignite the feedback is captured well by the simple model (12) and favors the approximation of keeping κs constant throughout the colony.
With absorbing boundary condition for the ligand concentration κs(r) approaching the bs eventually. Thus, very near the edge, there is a small region where the approximation of keeping κs constant throughout the colony breaks down. The hysteresis in the second order binding has the effect of narrowing down this region. That is why the fully developed switches for the open boundary and the absorbing boundary for the second order binding in Fig. 3 are practically identical.
3 Discussion
In order to have a significant effect of the positive-feedback loop the induced production of signal molecules must be much larger than the background production, i.e.must be satisfied. Further, in order to be able to fully ignite the feedbackis required. Provided that growth conditions are such that this is the case, the generic switch will turn on when the size Σ becomes sufficiently large to make 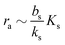 .
.
From systematic studies of activities of constitutive promoters in Escherichia coli24,25 and chemical composition studies of cells26–28 as a function of exponential growth rate we expect that the parameters, e.g. rm, may depend on the growth rate. Further, they may well depend on other physiological parameters like temperature and chemical composition of the environment. Thus, in order to establish when a quorum switch can be ignited and sustained, there is a call for studies of transcription rates, RNA turnover, translation rates, and protein turnover under physiological conditions where the culture approaches the stationary phase and starts forming a biofilm.
Typical biofilm thicknesses range from 13–60 μm mean (34 ± 10) μm in Pseudomonas aeruginosa.19 In flow cells (mixed) cultures of Pseudomonas aeruginosa, Pseudomonas fluorescens, Klebsiella pneumoniae, and Stenotrophomonas maltophilia produced biofilms of thickness (51 ± 19) μm with no flow decreasing to (37 ± 12) μm in flow.17 The horizontal dimension ranged up to 500 μm. This order of magnitude of the dimension of biofilm structures is confirmed across many bacterial strains, Staphylococcus aureus (30–40 μm thick),20Staphylococcus epidermidis (240–590 μm diameter).18 This is to be compared to the degradation range. For acyl homoserine lactones signal molecules at pH = 7, 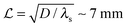 and at pH = 8,
and at pH = 8, 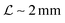 . Thus the reported ranges of the biofilm dimension give confidence that the thickness is typically below the limit for degradation to be important. The radius
. Thus the reported ranges of the biofilm dimension give confidence that the thickness is typically below the limit for degradation to be important. The radius 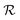 of a biofilm growing on a surface may, however, become similar to the degradation range
of a biofilm growing on a surface may, however, become similar to the degradation range 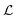 for signal molecules in large colonies.
for signal molecules in large colonies.
Other groups have considered the influence of density and size on ignition of the quorum sensing systems in numerical simulations of specific growth scenarios.29,30 While these simulations specifically address the time dependence of the quorum establishment they do not provide analytical insight into conditions required to ignite and sustain a quorum.
The positive feedback is typical for quorum sensors, even in cases where downregulation is desired. However, it may be worth mentioning that explicit negative feedback in the regulator production has been suggested to play a role in the EsaR transcription factor.31,32 The analysis presented here, i.e. the dependence on density and geometry, remains valid for this type of regulator. However, where the positive feedback leads to an all-or-none switch, the proposed negative feedback would lead to a smooth downregulation of the maximal transcription factor concentration. This results in an expression like (12) without the feedback switch and with the maximal regulator level suppressed at high concentrations of the regulator.
4 Conclusion
We have modeled a generic single-loop quorum sensor with positive feedback. An adequate measure for the size of the quorum sensing ensemble of bacteria has been established and shown to combine the effect of geometric shape, geometric size, cell density, and boundary conditions. Simple expressions for the conditions, (25) and (26), required to sustain an all-or-none quorum switch were established. The results for a thin biofilm suggest that the quorum sensor may act as a flow sensor. When the flow above a biofilm with density ρv, height 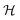 , and radius
, and radius 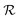 , turns off the “size” measure changes from
, turns off the “size” measure changes from 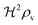 to
to 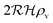 . For a thin biofilm this can cause the ignition of the quorum merely as a consequence of silencing the flow above the biofilm.
. For a thin biofilm this can cause the ignition of the quorum merely as a consequence of silencing the flow above the biofilm.
We emphasize that the qualitative behavior of the generic quorum sensor described here is determined by only three dimensionless parameters, rm/Ks, ks/bs, and h. The influence of the growth state, including growth rate is therefore expected to simply enter through rm/Ks and ks/bs. Furthermore, we have shown that rm/Ks ≳ 1, ks/bs ≳ 100, and h ≳ 1 are sufficient conditions to produce a functioning quorum sensor with an all-or-none switch. The model illuminates the importance of an experimental determination of these parameters under physiological conditions where biofilm colonies are formed.
References
- A. Eberhard, J. Bacteriol., 1972, 109, 1101 CAS.
- K. H. Nealson, T. Platt and J. W. Hastings, J. Bacteriol., 1970, 104, 313–322 CAS.
- S. H. Choi and E. P. Greenberg, J. Bacteriol., 1992, 174, 4064–4069 CAS.
- B. L. Hanzelka and E. P. Greenberg, J. Bacteriol., 1995, 177, 815–817 CAS.
- S. Swift, A. V. Karlyshev, E. L. Durant, M. K. Winson, S. R. Chhabra, P. Williams, S. Macintyre and G. S. A. B. Stewart, J. Bacteriol., 1997, 179, 5271–5282 CAS.
- M. J. Lynch, S. Swift, D. F. Kirke, C. W. Keevil, C. E. R. Dodd and P. Williams, Environ. Microbiol., 2002, 4, 18–28 CrossRef CAS.
- D. F. Kirke, S. Swift, M. J. Lynch and P. Williams, FEMS Microbiol. Lett., 2004, 241, 109–117 CrossRef CAS PubMed.
- M. J. Bottomley, E. Muraglia, R. Bazzo and A. Carfi, J. Biol. Chem., 2007, 282, 13592–13600 CrossRef CAS PubMed.
- C. Fuqua, S. C. Winans and E. P. Greenberg, Annu. Rev. Microbiol., 1996, 50, 727–753 CrossRef CAS PubMed.
- M. I. Moré, L. D. Finger, J. L. Stryker, C. Fuqua, A. Eberhard and S. C. Winans, Science, 1996, 272, 1655–1658 Search PubMed.
- A. V. Hill, Proc. Physiol. Soc., 1910, iv–vii Search PubMed.
- M. Welch, J. Gross, J. T. Hodgkinson, D. R. Spring and T. Sams, Biochem., 2013, 52, 4433–4438 CrossRef CAS PubMed.
- M. Laurent and N. Kellershohn, Trends Biochem. Sci., 1999, 24, 418–422 CrossRef CAS.
- J. B. Andersen, C. Sternberg, L. K. Poulsen, S. P. Bjorn, M. Givskov and S. Molin, Appl. Environ. Microbiol., 1998, 64, 2240–2246 CAS.
- M. Welch, D. E. Todd, N. A. Whitehead, S. J. McGowan, B. W. Bycroft and G. P. Salmond, EMBO J., 2000, 19, 631–641 CrossRef CAS PubMed.
- C. Garde, T. Bjarnsholt, M. Givskov, T. H. Jakobsen, M. Hentzer, A. Claussen, K. Sneppen, J. Ferkinghoff-Borg and T. Sams, J. Mol. Biol., 2010, 396, 849–857 CrossRef CAS PubMed.
- P. Stoodley, Z. Lewandowski, J. D. Boyle and H. M. Lappin-Scott, Biotechnol. Bioeng., 1999, 65, 83–92 CrossRef CAS.
- C. A. Fux, J. W. Costerton, P. S. Stewart and P. Stoodley, Trends Microbiol., 2005, 13, 34–40 CrossRef CAS PubMed.
- P. S. Stewart, B. M. Peyton, W. J. Drury and R. Murga, Appl. Environ. Microbiol., 1993, 59, 327–329 CAS.
- K. K. Jefferson, D. A. Goldmann and G. B. Pier, Antimicrob. Agents Chemother., 2005, 49, 2467–2473 CrossRef CAS PubMed.
- A. L. Schaefer, B. L. Hanzelka, M. R. Parsek and E. P. Greenberg, Methods Enzymol., 2000, 305, 288–301 CAS.
- A. R. Horswill, P. Stoodley, P. S. Stewart and M. R. Parsek, Anal. Bioanal. Chem., 2007, 387, 371–380 CrossRef CAS PubMed.
- E. A. Yates, B. Philipp, C. Buckley, S. Atkinson, S. R. Chhabra, R. E. Sockett, M. Goldner, Y. Dessaux, M. Cámara, H. Smith and P. Williams, Infect. Immun., 2002, 70, 5635–5646 CrossRef CAS.
- S.-T. Liang, M. Bipatnath, Y.-C. Xu, S.-L. Chen, P. Dennis, M. Ehrenberg and H. Bremer, J. Mol. Biol., 1999, 292, 19–37 CrossRef CAS PubMed.
- S.-T. Liang, Y.-C. Xu, P. Dennis and H. Bremer, J. Bacteriol., 2000, 182, 3037–3044 CrossRef CAS.
-
H. Bremer and P. P. Dennis, in Escherichia coli and Salmonella: Cellular and Molecular Biology, ed. F. C. Neidhart, ASM Press, Washington, DC, 1996, ch. 97: Modulation of chemical composition and other parameters of the cell by growth rate Search PubMed.
- S. Klumpp, Z. Zhang and T. Hwa, Cell, 2009, 139, 1366–1375 CrossRef PubMed.
- M. Scott, C. W. Gunderson, E. M. Mateescu, Z. Zhang and T. Hwa, Science, 2010, 330, 1099–1102 CrossRef CAS PubMed.
- P. Nilsson, A. Olofsson, M. Fagerlind, T. Fagerstrom, S. Rice, S. Kjelleberg and P. Steinberg, J. Mol. Biol., 2001, 309, 631–640 CrossRef CAS PubMed.
- M. E. Parent, C. E. Snyder, N. D. Kopp and D. Velegol, Colloids Surf., B: Biointerfaces, 2008, 62, 180–187 CrossRef CAS PubMed.
- C.-S. Tsai and S. C. Winans, Mol. Microbiol., 2010, 77, 1072–1082 CrossRef CAS PubMed.
- S. B. von Bodman, D. R. Majerczak and D. L. Coplin, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 7687–7692 CrossRef CAS.
-
N. H. Asmar, Partial differential equations with Fourier series and boundary value problems, Pearson Prentice Hall, Upper Saddle River, NJ, 2005, pp. 1–690, pp. A1–A112 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3mb70230h |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
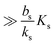
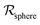
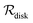
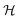
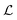
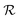 and the height of the disk is
and the height of the disk is 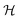 . When the degradation rate λs of signal molecules is significant, i.e. when the length
. When the degradation rate λs of signal molecules is significant, i.e. when the length 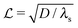 is smaller than one or more of the geometrical dimensions of the colony, this dimension is (approximately) replaced by
is smaller than one or more of the geometrical dimensions of the colony, this dimension is (approximately) replaced by 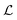 in the size measure. Eventually all geometrical sizes disappear and the size, Σ, then measures the cell density
in the size measure. Eventually all geometrical sizes disappear and the size, Σ, then measures the cell density
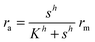
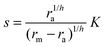
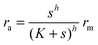

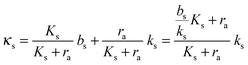
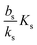 to the higher, active, production ks when the concentration ra is above Ks. Note that the feedback mechanism turns on at the concentration
to the higher, active, production ks when the concentration ra is above Ks. Note that the feedback mechanism turns on at the concentration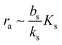
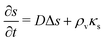
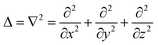 is the Laplace operator. Since single cells are unable to ignite or even maintain an ignited feedback loop the net contribution from binding and dissociation of signal molecules to regulators could be ignored when writing eqn (8). (Active transport of signal molecules across the cell membrane which, to lowest order, leads to a rescaling between the intracellular and extracellular ligand concentration was not included.) At the steady state
is the Laplace operator. Since single cells are unable to ignite or even maintain an ignited feedback loop the net contribution from binding and dissociation of signal molecules to regulators could be ignored when writing eqn (8). (Active transport of signal molecules across the cell membrane which, to lowest order, leads to a rescaling between the intracellular and extracellular ligand concentration was not included.) At the steady state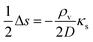
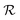 . This also solves the case of a hemispherical biofilm on a reflecting surface. The volume fraction occupied by cells, ρv, is zero outside the biofilm and assumed constant inside the colony.
. This also solves the case of a hemispherical biofilm on a reflecting surface. The volume fraction occupied by cells, ρv, is zero outside the biofilm and assumed constant inside the colony.
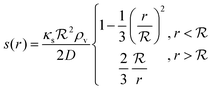
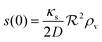
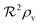 of the colony
of the colony
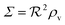 , i.e. a combination of density and geometrical size of the biofilm. Notably, this size measure is a function of the activated dimer concentration only and can be expressed as a product of a normal forward activation and a feedback switch. Below we shall see that the r.h.s. is unaltered when the geometry and boundary conditions change. This means that all information regarding geometry, density, and boundary conditions is on the l.h.s. of the equation. In this sense
, i.e. a combination of density and geometrical size of the biofilm. Notably, this size measure is a function of the activated dimer concentration only and can be expressed as a product of a normal forward activation and a feedback switch. Below we shall see that the r.h.s. is unaltered when the geometry and boundary conditions change. This means that all information regarding geometry, density, and boundary conditions is on the l.h.s. of the equation. In this sense 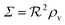 is a proper “size” measure. The forward activation and the feedback switch being dimensionless, the natural unit of size is seen to be 2DK/bs.
is a proper “size” measure. The forward activation and the feedback switch being dimensionless, the natural unit of size is seen to be 2DK/bs.

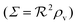 . Dotted curves are the numerical solution for a spherical colony with absorbing boundary
. Dotted curves are the numerical solution for a spherical colony with absorbing boundary 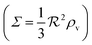 .
.
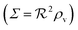 . Dotted curves are the numerical solution with absorbing boundary
. Dotted curves are the numerical solution with absorbing boundary 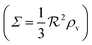 .
.
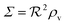 remains unchanged.
remains unchanged.
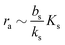 , and have identical asymptotic behavior. It is therefore not critical to the ignition function of the feedback loop that consecutive ligand bindings are cooperative. However, the cooperativity extends the bistable region somewhat and therefore may aid in stabilizing the switch.
, and have identical asymptotic behavior. It is therefore not critical to the ignition function of the feedback loop that consecutive ligand bindings are cooperative. However, the cooperativity extends the bistable region somewhat and therefore may aid in stabilizing the switch.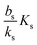 , it is impossible to ignite the feedback loop no matter how high the concentration of signal molecules is. When growth conditions lead to a maximal dimer level significantly higher than
, it is impossible to ignite the feedback loop no matter how high the concentration of signal molecules is. When growth conditions lead to a maximal dimer level significantly higher than 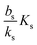 the feedback loop can be ignited. The effect of the feedback is an increased production of signal molecules and an abrupt increase in ra. Even for first order ligand binding (h = 1) the feedback makes the transition to higher ra levels happen quite abruptly as a function of colony “size” as seen in Fig. 2. For the more typical second-order ligand binding (h = 2) shown in Fig. 3 the feedback displays a second order transition, i.e. the transition is practically a Heaviside step function with ra jumping more than a factor ks/bs at the quorum ignition point.
the feedback loop can be ignited. The effect of the feedback is an increased production of signal molecules and an abrupt increase in ra. Even for first order ligand binding (h = 1) the feedback makes the transition to higher ra levels happen quite abruptly as a function of colony “size” as seen in Fig. 2. For the more typical second-order ligand binding (h = 2) shown in Fig. 3 the feedback displays a second order transition, i.e. the transition is practically a Heaviside step function with ra jumping more than a factor ks/bs at the quorum ignition point.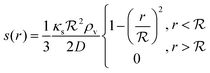

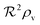 to reach the quorum sensing ignition level with absorbing boundary condition than with free boundary.
to reach the quorum sensing ignition level with absorbing boundary condition than with free boundary.
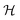 growing on a reflecting surface and covered by rapidly exchanged liquid we get
growing on a reflecting surface and covered by rapidly exchanged liquid we get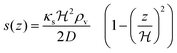
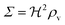
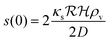
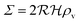
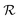 is the radius of the biofilm. (Details of the calculation are given in the ESI† and ref. 33.)
is the radius of the biofilm. (Details of the calculation are given in the ESI† and ref. 33.)
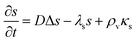
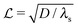 . I.e. when
. I.e. when 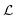 is much smaller than a system dimension, the system dimension should be replaced by the
is much smaller than a system dimension, the system dimension should be replaced by the 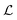 in our size measures Σ.
in our size measures Σ.
 the solution to (20) is
the solution to (20) is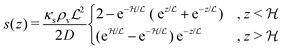
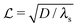 is the characteristic length at which the degradation competes with diffusion. At the bottom of the biofilm, z = 0, this leads to
is the characteristic length at which the degradation competes with diffusion. At the bottom of the biofilm, z = 0, this leads to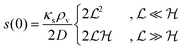
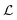 is smaller than a geometrical dimension, the geometrical dimension should be replaced by
is smaller than a geometrical dimension, the geometrical dimension should be replaced by 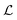 (within a factor of
(within a factor of 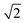 ). Table 2 summarizes the size measures for different geometries and also includes the modifications following from degradation.
). Table 2 summarizes the size measures for different geometries and also includes the modifications following from degradation.

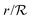 → reqn (23) becomes
→ reqn (23) becomes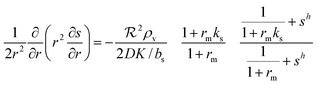
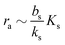 .
.
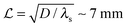 and at pH = 8,
and at pH = 8, 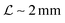 . Thus the reported ranges of the biofilm dimension give confidence that the thickness is typically below the limit for degradation to be important. The radius
. Thus the reported ranges of the biofilm dimension give confidence that the thickness is typically below the limit for degradation to be important. The radius 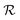 of a biofilm growing on a surface may, however, become similar to the degradation range
of a biofilm growing on a surface may, however, become similar to the degradation range 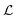 for signal molecules in large colonies.
for signal molecules in large colonies.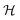 , and radius
, and radius 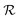 , turns off the “size” measure changes from
, turns off the “size” measure changes from 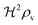 to
to 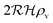 . For a thin biofilm this can cause the ignition of the quorum merely as a consequence of silencing the flow above the biofilm.
. For a thin biofilm this can cause the ignition of the quorum merely as a consequence of silencing the flow above the biofilm.