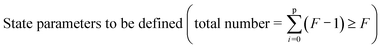Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Control parameters for electrochemically relevant materials: the significance of size and complexity†
J.
Maier
*
Max Planck Institute for Solid State Research, 70569 Stuttgart, Germany. E-mail: s.weiglein@fkf.mpg.de
First published on 18th August 2014
Abstract
This contribution is concerned with the control parameters for arriving at defined, electrochemically relevant materials. The treatment is precise as far as the equilibrium situation of simple crystals is concerned, but becomes more and more qualitative if the distance from equilibrium or the (structural or compositional) complexity increases. It proves useful to distinguish between in situ parameters and ex situ parameters, the number ratio of which decreases with increasing distance from equilibrium. A particularly complex situation is met if not only size, shape and phase distribution are important, but even morphological details are of relevance, as it is the case for modern battery electrodes (“electrochemical integrated circuits”). For such cases archetypical examples along with their advantages or disadvantages for electrochemical storage properties are discussed. In this context, special emphasis is placed upon the dimensionality and distribution topology of building elements.
1. Introduction
As far as applications are concerned, materials under consideration may be as simple as single crystals but also as complex as multiphase composites. Most materials of technological interest contain frozen structure elements. In biology and biotechnology, stationary structures are typically out of equilibrium but not frozen, their stationarity being maintained by export of entropy; at present they do not play an important role in usual electrochemical applications. Here, we rather deal with structures that are stationary and non-dissipative. Table 1 gives an overview on morphologies with increasing deviation from equilibrium. In complete equilibrium not only all fluxes (J), but also all driving forces (F) vanish; while in the case of frozen morphologies some driving forces are non-zero, yet the corresponding fluxes disappear owing to kinetic reasons. Note that in all these cases the entropy production (P, given by the product of forces and fluxes) is zero. This is however not the case for the aforementioned dissipative structures; yet it can be shown that for specified boundary conditions the variation of the entropy production, at least with respect to forces, nullifies.1| Classification | Thermodynamic characteristics | Characteristic properties | Examples |
|---|---|---|---|
| Equilibrium morphology | P = F = J = 0 | Absolutely stable/reproducible/typically boring/low information content | Wulff-shaped single crystals |
| Frozen morphology | P = J = 0 ≠ F | Partially stable/reproducible/most relevant for technology | Technologically relevant materials |
| Dissipative morphology | δ F P = 0 | Living/self-healing/sustained by outer fluxes/dissipative/high information content | Biologically relevant systems |
| F ≠ 0 ≠ J |
This paper considers the control parameter for materials definition for various degrees of complexity. The complexity is determined by the number of (practical) degrees of freedom and hence the information content. Complexity of a given material (Fig. 1) can be increased by varying composition (introduction of zero-dimensional defects), but also by varying morphology (introduction of higher-dimensional defects). As to the latter, nano-structuring has proved to be an efficient means of defining electrochemically relevant materials. Even though not always completely independent, Fig. 2 depicts the two coordinate-axes, size and complexity, along which many modern materials developments have been made possible.
 | ||
| Fig. 1 Increase of materials complexity by introducing zero-dimensional defects (compositional complexity) and higher-dimensional defects (morphological complexity). | ||
Fig. 3 refers to two extreme cases: the uniform single crystal in equilibrium with only point defects present (top) and a multi component composite with many frozen elements (bottom). It illustrates the theme of this paper which investigates: (i) the impact of building elements defining a real electrochemically relevant material on the properties, whereby we mainly concentrate on electrochemical storage, (ii) the parameters that are necessary to define the real material in terms of the constituent building elements.
2. Equilibrium
2.1. Point defect chemistry
The chemistry of real materials includes the chemistry of the perfect state as well as the defect chemistry to be superimposed. The simplest situation as far as charge carrier chemistry is concerned, is met for an infinite crystal in equilibrium. Then only point defects are of significance. They define the equilibrium charge carrier situation we are interested in. Under conditions at which point defect concentrations are small (Boltzmann conditions) and the complexity of charge carrier chemistry is moderate (Brouwer conditions, typically two majority carriers), ideal mass action laws (with mass action constants Kr) can be formulated for inner reactions and outer reactions connecting the inner situation with the component partial pressures (Pp) fixed by neighboring phases (e.g. gas phase).2 For the concentration of any charge carrier (j), then it can be formulated that3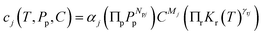 | (1) |
 | (2) |
In words: on positive (negative) doping, i.e. an aliovalent substitution that leads to a fixed effective positive excess charge, the concentrations of all negative (positive) defects are increased and all positive (negative) defects that take part in the defect-chemical equilibrium are decreased (zj: charge number of dopant defect). The non-trivial point here is that it affects all these charge carriers. This is not only a consequence of the electroneutrality condition but also of the mutual mass action laws. To give a well-known example: a partial substitution of Zr4+ by Y3+ does not only result in an increased oxygen vacancy (V••O) concentration, also the hole (h•) concentration is increased while the conduction electron (e′) concentration is decreased.
Eqn (2) ignores elastic effects of dopants. Such effects can even lead to homovalent dopant effects.4
Certainly in most cases the validity range of dilute conditions is exceeded. Then associates and activity coefficients are to be considered, that may introduce further materials constants (dielectric constants, mass action constants) but not further control parameters.
Taking account of an invariant dopant concentration already touches on the next paragraph and the next complication, namely the consideration of a (partially) frozen-in point defect chemistry.5,6 Usually, at least at temperatures significantly below the melting point, not all components are mobile via point defects. Let us consider a binary oxide MO. At very high temperatures M- and O-defects may be mobile and in equilibrium (here creep can occur). On lowering the temperature, the O-lattice may stay mobile, while the M-defects now act as frozen dopants. When at even lower temperatures oxygen defects are also immobile, then we consider the situation typically assumed in semi-conductor physics (immobile ions, mobile electrons). Not only does the situation become more complex, but also the number of practical degrees of freedom increases since new parameters such as freezing-in temperature and partial pressures or even kinetic adjusting screws (cooling kinetics) come into play. Fig. 4 (we now refer to the concentrations not labelled by Q) shows how significantly the freezing procedure changes the defect chemistry.
 | ||
| Fig. 4 Excess electron and electron hole concentrations as a function of oxygen partial pressure under the still reversible quenching conditions (labelled Q, here 800 °C) as well as for quenched state at lower temperatures. Ionic disorder is predominant and is frozen for T < TQ. Reprinted with permission from ref. 6. | ||
Table 2 gives an overview of the electronic concentrations in an oxide in the different temperature regimes characterized by predominant ionic disorder. It assumes infinitely fast quenching which can be approximated by very long annealing at temperatures at which equilibrium takes a rather long time, followed by fast cooling. This temperature is denoted as TQ. The concentrations labelled as Q, refer to the equilibrium values at TQ (as discussed above). The other concentrations refer to situations where the ionic disorder is frozen. These concentrations are discussed as a function of PO2 at TQ. For details the reader is referred to ref. 6. The above introduced distinction between parameters that can be reversibly changed in situ (in situ parameters) and those the definition of which is requiring higher temperatures and then a new preparation (ex situ parameters) is very helpful in this context. Eqn (1) is still valid under these assumptions but freezing is the equivalent of losing in situ parameters (P's) to the benefit of the ex situ parameter C (cf.Table 2).
| Temperature range | Control parameters (total number = F = 3) | ||
|---|---|---|---|
| a The upper index Q labels quenching parameters (Q0 refers to quenching of A-sublattice, Q1 to quenching O-sublattice and Q2 to (unrealistically) quenching the electronic structure). The B-lattice is assumed to be frozen even at the very high temperatures (still far from melting point). Reprinted with permission from ref. 6. | |||
| Very high | Reversible: T, PO2, PAO | In situ: 3 | T, PO2, PAO |
| (3) | |||
| Fixed: ϕ | Ex situ: 0 | ||
| High | Reversible: T, PO2 | In situ: 2 |
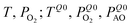
|
| (3 + 2) | |||

|
Ex situ: 1 | ||
| Low | Reversible: T | In situ: 1 |

|
| (3 + 2 + 1) | |||

|
Ex situ: 2 | ||
| (not realistic) | Reversible: ϕ | In situ: 0 |

|
| (3 + 2 + 1 + 0) | |||
Fixed: [h˙], |
Ex situ: 3 | ||
3. Excursion: control parameter and thermodynamic state variables
Here it is important to make some remarks on the terms “control parameters” used in this paper. With this term we designate the parameters available and necessary to define the sample.In the simplest case of the infinite crystal in equilibrium, they are in situ parameters and are identical to the thermodynamic state parameters (e.g. open isobaric system (“intensive system”): T, p, μ's i.e. P's, μ denoting the chemical potential).
This is already different in the case of defining dopant effects or frozen-in defects. Most simply we may take their concentrations as given and consider these concentrations as control parameters which are in fact ex situ parameters. Alternatively as shown in Section 2 one can prepare the situation under regard by freezing an equilibrium situation and instead use the thermodynamic state variables of the freezing conditions. This typically fails if higher-dimensional defects and formally morphological patterns are to be considered. It is for the vast majority of situations not possible to define the transformation from an equilibrium state to such a real situation. Thus, we simply take all the formal frozen structure elements (such as nature, density and orientation of interfaces; phase distribution, phase topology, size etc.) as given and the parameters necessary to describe them as ex situ control parameters.
4. Point defect chemistry in the vicinity of higher-dimensional defects
A further increase of complexity with respect to Section 1 is achieved if higher-dimensional defects are irreversibly introduced. Irrespective of varied mobilities within interfaces or dislocation networks, the defect concentrations near surfaces, interfaces or dislocations may be characteristically varied compared to the infinite bulk. This is particularly the case if we assume abrupt heterogeneities such as a mono-atomic interfacial core layer inserted with negligible structural relaxation. Owing to the novel boundary condition and the concomitant symmetry break, a point defect redistribution will occur such that an excess charge will establish, balanced by space charge zones with greatly varied carrier concentrations.Owing to the enormous impact on e.g. conductivities and the similarity to homogeneous doping (= zero-dimensional doping), the technique of influencing carrier concentrations by implementing higher-dimensional defects has been termed heterogeneous doping (= higher-dimensional doping). Even a similar rule (rule of heterogeneous doping3) can be formulated:
 | (3) |
Here we need to know the compensating interfacial charge density Σ (rather than the effective charge of an atomistic dopant) to predict how the individual concentrations will be varied. Again the rule includes the variation of minority species. The latter is of great significance (but is usually overlooked) for electronic conductors as often ionic point defects are in majority and the electronic effects may be dictated by the behavior of the ions (fellow traveler effect).7
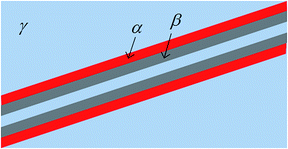
5. Hetero-interfaces and phase combinations
Apart from grain or domain boundaries, interfaces separate different phases. The consequence of such hetero-interfaces on charge carrier redistribution is analogous to what was stated in the previous paragraph, up to one point: here a charge transfer from one phase to the other can occur and a bilateral space charge situation develops without even any excess charge in the interfacial core. (This however can be an additional effect.) Such effects depend critically on the phase combination and it is this circumstance7 that provides a manifold of opportunities to purposefully vary defect chemistry and hence conductivities, reactivities, and related properties. If, e.g., a combination of CaF2 and BaF2 phases result in a net transfer of F− from BaF2 to CaF2 then in the space charge regions BaF2(CaF2) is increased (decreased) while
in the space charge regions BaF2(CaF2) is increased (decreased) while  shows the opposite behavior. The electronic minority species are changed accordingly: [e′] in BaF2(CaF2) is increased (decreased) while [h˙] is oppositely varied.8
shows the opposite behavior. The electronic minority species are changed accordingly: [e′] in BaF2(CaF2) is increased (decreased) while [h˙] is oppositely varied.8
By selecting a suitable second phase contacted with the matrix, ion and electron conductivities in the matrix can be often varied by orders of magnitude, in particular if the density of interfaces is very high as it can be achieved in nano-composites or heterolayers.
This heterogeneous doping effect has been predicted to be of great influence also for fields such as catalysis, superconductivity or thermoelectricity.9
6. Size effects
Size is an expression of the distance of neighboring surfaces. Many properties directly depend on it (nano-ionics).9 As far as transport and storage parameters are concerned, in Fig. 5 L.H.S a distinction was made between explicit and implicit size dependencies.10 The latter which concerns the intensive terms (materials constants), can then be divided into trivial and non-trivial size effects. Explicit size dependence (cf. Ln-term in Fig. 5 L.H.S) refers to the remaining geometry-relevant part of the size dependencies of resistances or capacitances and is often primarily responsible for the enormous influence of size on storage kinetics. R.H.S of Fig. 5 gives a collection of power laws for explicit size dependence for various mechanisms. As we refer to storage kinetics the reader's attention is to be drawn to the second line (τ ∝ L2) highlighting the enormous influence of size on diffusion time. Implicit size dependencies refer, to give an example, to the size dependence of effective conductivities in inhomogeneous systems that may be caused by space charge effects at surfaces or internal boundaries. As long as neighboring space charge zones are well-separated, their contribution to the overall property scales simply with size, in contrast to situations where space charge layers overlap causing non-trivial size effects. Such a distinction is meaningless for homogeneous phenomena such as capillary pressure that can be of enormous consequences on phase stability, partial pressures of components, cell voltage, solubilities, defect concentrations and many others.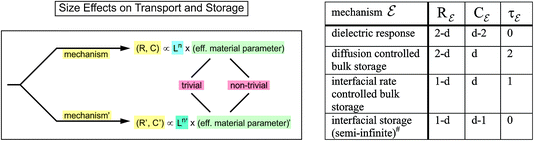 | ||
| Fig. 5 L.H.S.: Implicit and explicit size effects on electrochemical, chemical or electrical resistors and capacitors. The first effects can be divided in trivial and non-trivial effects. Size effects may change R and C such that even another mechanism may become dominant. Reprinted with permission from ref. 10. R.H.S.: Dimensionality dependent exponents (n) of the explicit thickness (L) dependence of resistors, capacitors, relaxation times for various electrochemical mechanisms (ε) in nano-structured materials. The parameter d gives the number of nano-sized dimensions (1 ≤ d ≤ 3) of extension L (taken the same for simplicity). #In the finite size regime the situation also depends on the neighboring phases. Reprinted with permission from ref. 10. | ||
7. Shape and dimensionality in nano-sized systems
While in macroscopic crystals shape and dimensionality are only of influence if anisotropic or extremely surface-sensitive properties are concerned, these parameters are decisive for nano-sized systems.For simplicity we refrain from distinguishing between different surface crystallographies and anisotropies caused by the perfect structure. Then we may be concerned with nano-particles, nano-grains in ceramics, nano-rods or nano-plates, the shapes of which are completely kinetically controlled or controlled by mechanical equilibrium (round nano-particles, nano-ceramics with equilibrium grain-angles11etc.).
It is important to note that having a stationary non-equilibrium structure or composition does not preclude reversible processes. In fact such situations are rather the rule than the exception as far as functional materials are concerned. Thus, oxygen ion conduction or even stoichiometric changes in the oxygen sub-lattice are possible in structures with frozen-in cation sub-lattices; equally, nano-sized or even amorphous electrodes can function as reversible anodes or cathodes in Li-based batteries. Only those processes that immediately affect the frozen-in structure elements cannot be reversible.
Let us concentrate on conductivity and storage properties. As far as the equilibrium storage capacity of a component is concerned it is increasingly varied from nano-2 D (nano-plate) to nano-0 D (nano-dots) via nano-1 D (nano-rods) according to a modified chemical potential of this component. Note that e.g. the excess chemical potential of Li in a crystallite due to capillarity is given by 2(γ/r)υLi (γ: effective surface tension, r: effective radius).12,13 The partial molar volume of Li (υLi) in the compound under regard can be positive or negative depending on whether Li-addition leads to expansion or shrinkage of the crystallite. Even more important are kinetic issues that are dealt with below in the next section by means of a few notable examples.
In terms of transport, percolation efficiency is of great significance. While nano-0 D objects require agglomeration to higher-dimensional ones, nano-1 D objects are ideal as percolating objects provided their intrinsic transport properties are appreciable. If aligned properly, they are favorable solutions as far as covered transport length per mass is concerned. Equally good are nano-plate mixtures that connect two electrodes. Hierarchical geometries as well as fractal geometries can be very favorable, too, in order to achieve a good electrical connectivity.
The complexity is further increased by the presence a multitude of phases. A typical example is a composite electrode consisting of a mixture of an electro-active mass with a current collecting and electrolyte phase. Here the total morphology needs to be considered.
8. Nano-morphology and Li-storage
8.1. The necessity of electrochemical integrated circuits
As a rule an efficient storage electrode consists of a bicontinuous network of electron collector and electrolyte which is heterogeneous on a scale comparable with the size of the electroactive particles, whereby this size is chosen such that diffusion problems become just negligible. If the electroactive mass is identical to the current collector or the electrolyte, the morphology is significantly simplified.The greatest simplification is achieved if the electroactive mass is simultaneously a good electron and Li+ conductor. If then the related chemical diffusion coefficient is very high, the particle size can be very large. A wonderful but exceptional example is Ag2S14 in which Ag can be quickly stored, even if it is present as a macroscopic single crystal. There is no need of nano-structuring or of further network components, and the cell may be as simple as Ag|AgI|Ag2S|C. But let us consider the frequently occurring case that the electroactive mass is electronically and ionically rather insulating.
Nano-0-D electro-active particles are then preferred owing to the fact that diffusion time scales with size squared. Size reduction from a 1 mm particle to an ensemble of 10 nm-size particles reduces the diffusional relaxation time by 1010. On the other hand, the volume scales with size cubed meaning that we decompose the 1 mm-sized particle into 1015 10 nm-sized particles, each of which needs to be sufficiently electronically and ionically connected, obviously requiring highly sophisticated network solutions. The use of liquid electrolyte wetting all the particles is the solution of choice for ion transport while adding carbon particles is the standard method to achieve sufficient electronic contact. On one hand the carbon volume fraction must be high enough to ensure percolation, on the other hand one has to think about connectivity down to nano-size which requires going beyond usual techniques. This is described in detail below.
Nano-1-D electroactive masses are providing special advantages (e.g. percolation efficiency) but may not be the best solution for high energy systems. An elegant example has been given in the literature15 in the form of Si-nanowires growing on copper, where the nanobrush so-formed is embedded in liquid electrolyte. The rate performance is excellent yet the absolute energy stored small (but see 9.2.).
Nanoplates, or better thin films, are preferred in microbatteries as far as the electrolyte is concerned. Arranged parallel to the electrode they may also be useful as a protection layer or separation layer thin enough as not to cause too much resistance. Perpendicular arrangements would be necessary if connectivity is important. One might think of hetero-layered packages as electrolyte or electrode systems to exploit interfacial effects, yet for practical systems they might be too expensive.
Most successful proved composites that use various dimensionalities. Let us describe a few archetypes in the subsequent section and use the following notation: α:β denotes a two-phase system constituted by the phases α and β irrespective of phase distribution; α@β specifies that α and β are distributed more or less equitably (co-arranged rather than sub-ordinated). Characteristic examples are random two-phase systems or bi-continuous two-phase systems. The symbol α ⊂ β denotes a situation where α is completely embedded in a β-surrounding, characteristic examples being non-percolating particles or rods in a solid or liquid matrix or non-percolating particles in a tube. Naturally, this simple nomenclature cannot cover all topological cases. Moreover, the inclusion of the electrolyte phase (i.e. of pores) is also important requiring the description of a three-phase morphology. Whenever avoidable, we will refrain from using a too detailed notation. Note that we use the terms 0 D, 1 D, 2 D to denote extreme aspect ratios on the scale specified by the respective prefix (e.g. nano-1 D means that one dimension is nano-scale (but not atomistic) while the others are macroscopic).
8.2. Electroactive nanoparticles in electronically conducting nanotubes
Lithiation of macroscopic MoS2 leads to conversion to separate Mo and Li2S phases. Reversing the situation is not trivial as it assumes reversible nucleation and fast diffusion.
In the present case we refer to extreme reaction confinement and hence almost to a cluster reaction whereby the cluster is fixed in space. It can be assumed that the transfer of 4e− corresponding to the reaction with 4Li does not lead to a significant spatial separation, rather the reaction will occur at the tiny clusters lowering if not nullifying transport and nucleation problems. Indeed striking reversibility could be achieved for at least thousand cycles. Simultaneously the cell voltage is lowered by the small size, which is favorable for application as an anode.
8.3. Nanocomposites of electroactive mass and electron conductors
If the electroactive mass is not a good electron conductor (such as TiO2 or LiFePO4) a hierarchically porous TiO2 structure is not sufficient to achieve high rate performance; rather it is highly beneficial to incorporate an electronically conducting phase into the nanostructure. This has been achieved in ref. 19 with high capacities even at very high rates.
9. Conclusions
Electrochemically relevant materials can be as simple as macroscopic single crystals but also as complex as multiphase nanostructured composites. In the present paper the focus is on electrochemical impact and on controllability of the building elements involved. While in the extreme case of a single crystal the equilibrium charge carrier situation can be fully defined by a few thermodynamic state parameters (in situ parameter), with increasing complexity and deviation from equilibrium, ex situ parameters become increasingly relevant. According to the increased information content, all morphological details may finally become relevant (electrochemical integrated circuit). Thus only archetypical examples can be discussed rather than a precise thermodynamical description given. Such examples refer to electrochemical storage in specially designed electrode structures.References
- P. Glansdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability and Fluctuations, John Wiley & Sons, Ltd., New York, 1971 Search PubMed.
- G. Brouwer, Philips Res. Rep., 1954, 9, 366 CAS.
- J. Maier, Physical Chemistry of Ionic Materials. Ions and Electrons in Solids, John Wiley & Sons, Ltd, Chichester, West Sussex UK, 2004 Search PubMed.
- D. Zahn, J. Maier and P. Heitjans, Chem.–Eur. J., 2012, 18, 6225 CrossRef CAS PubMed.
- F. A. Kroeger, Chemistry of Imperfect Crystals, North-Holland, 1964 CrossRef CAS; R. Waser, Ber. Bunsen-Ges., 1986, 90, 1223 CrossRef CAS; K. Sasaki and J. Maier, J. Appl. Phys., 1999, 86, 5422 CrossRef PubMed.
- J. Maier, Phys. Chem. Chem. Phys., 2003, 5, 2164 RSC.
- J. Maier, Prog. Solid State Chem., 1995, 23, 171 CrossRef CAS; J. Maier, Ber. Bunsen-Ges., 1989, 93, 1468 CrossRef.
- N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 946 CrossRef CAS PubMed.
- J. Maier, Nat. Mater., 2005, 4, 805 CrossRef CAS; J. Maier, Adv. Mater., 2009, 21, 2571 CrossRef.
- J. Maier, Chem. Mater., 2014, 26, 348 CrossRef CAS.
- W. D. Kingery, H. K. Bowen and D. R. Uhlmann, An Introduction to Ceramics, John Wiley & Sons, Ltd., New York, 1976 Search PubMed.
- R. Defay, I. Prigogine, A. Bellemans and H. Everett, Surface Tension and Adsorption, Longmans, Green & Co, Ltd, London, 1960 Search PubMed.
- J. Maier, Angew. Chem., Int. Ed., 2013, 52, 4998 CrossRef CAS PubMed.
- U. von Oehsen and H. Schmalzried, Ber. Bunsen-Ges., 1981, 85, 7 CrossRef CAS.
- C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31 CrossRef CAS PubMed.
- Y. Yu, L. Gu, C. Zhu, P. A. van Aken and J. Maier, J. Am. Ceram. Soc., 2009, 131, 15984 CrossRef CAS PubMed.
- C. Zhu, X. K. Mu, P. A. van Aken, Y. Yu and J. Maier, Angew. Chem., Int. Ed., 2014, 53, 2152 CrossRef CAS PubMed.
- Y.-S. Hu, P. Adelhelm, B. M. Smarsly, S. Hore, M. Antonietti and J. Maier, Adv. Funct. Mater., 2007, 17, 1873 CrossRef CAS.
- Y.-G. Guo, Y.-S. Hu, W. Sigle and J. Maier, Adv. Mater., 2007, 19, 2087 CrossRef CAS.
- F.-F. Cao, Y.-G. Guo, S.-F. Zheng, X.-L. Wu, L.-Y. Jiang, R.-R. Bi, L.-J. Wan and J. Maier, Chem. Mater., 2010, 22, 1908 CrossRef CAS.
- R. Dominko, M. Gaberscek, J. Drofenik, M. Bele, S. Pejovnik and J. Jamnik, J. Power Sources, 2003, 119–121, 770 CrossRef CAS.
- C. Zhu, K.-P. Song, P. A. van Aken, Y. Yu and J. Maier, Nano Lett., 2014, 14, 2175 CrossRef CAS PubMed.
Footnote |
| † This work is dedicated to Professor Martin Jansen on the occasion of his 70th birthday. |
| This journal is © The Royal Society of Chemistry 2014 |