Influence of different types of natural organic matter on titania nanoparticle stability: effects of counter ion concentration and pH†
Julián A.
Gallego-Urrea
*,
Jenny
Perez Holmberg
and
Martin
Hassellöv
Department of Chemistry and Molecular Biology, University of Gothenburg, Kemivägen 4, 412 96, Gothenburg, Sweden. E-mail: julian.gallego@chem.gu.se
First published on 7th February 2014
Abstract
The effects of biopolymeric (alginate) and refractory macromolecules (humic and fulvic acids) on the aggregation kinetics of anatase titanium dioxide (titania) nanoparticles were evaluated. The particles were synthesized using a wet-chemical method based on the hydrolysis of TiCl4. Stable suspensions of positively-charged titania were obtained at pH 2.5. One batch of this product was shifted above the point of zero charge to pH 12. These dispersions were mixed with three different types of well characterized environmental macromolecules: sodium alginate, fulvic acid and humic acid, and evaluated in terms of the stability. Changes in the particle size were measured using time-resolved dynamic light scattering (TR-DLS) at different concentrations of three electrolytes: NaCl, CaCl2 and Na2SO4, and at different solution pH values. Results were in agreement with DLVO calculations. The use of TR-DLS for determining aggregation rates is critically discussed.
Nano impactThe stability of titania nanoparticles in natural waters is influenced by the concentration of nanoparticles themselves and the physicochemical characteristics of the receiving water. Predominantly, electrolytes and pH determine the extent of repulsion by electrostatic or electrosteric mechanisms, and natural organic matter can provide some additional stabilization or cause aggregation depending on the surface coverage of the particles. This work examines the effects of these parameters on the stability of titania nanoparticles for three types of macromolecules and three electrolytes commonly found in natural waters. Implications of this study are important mainly for near source emissions, spill situations and ecotoxicity tests, where other natural or anthropogenic particles are relatively less significant for determining the ENP fate. |
Introduction
Nanoparticles and nanomaterials are becoming increasingly common in products for multiple applications.1 Therefore, the environmental fate of these novel materials and their transformation products must be predicted in a physically meaningful way.2,3Nanoparticles (NP) in aquatic suspensions are subject to different types of molecular forces that are dependent on the material, the hydraulic conditions and the presence of dissolved substances; these forces can lead to aggregation, stabilization or deposition of the particles in the dispersion. The interactions between the forces encompass the particles, the medium in which they are dispersed and other surfaces. In many cases of environmental interest, the main forces that dominate the stability of the dispersion are long-ranged van der Waals forces, short-ranged electrostatic double-layer forces and steric interactions, and these are modulated by hydrodynamic interactions.4 All of these forces are ubiquitous in environmental waters and ecotoxicological growth medium tests, where macromolecules, ions and surfaces are abundant.
Depending on the entry point into the environment, the concentration of particles may be high or low, from single point or dispersed source. Transformation processes will act concomitant to the particles with a different degree that depends on the physical details of the release. One of these transformation processes involves sorption of ubiquitous natural organic matter (NOM) present in natural waters onto the surface of the engineered NP (ENP); this sorption can lead to aggregation via bridging mechanisms or stabilisation through electrosteric or solely steric effects. The ratio between NOM and ENP, the nature of the specific NOM and the ENP surface and the concentrations of both will be determinants of the extent to which any of these processes will be favoured.
Titania (TiO2) NP are currently used in a great number of consumer products, and the likelihood that individual NP or some of the transformation products reaches the environment is increasing.5,6 The effects of titania on the environment are currently being documented. Since NP in the environment will undergo aggregation due to the forces aforementioned, then the exposure to titania NP is going to be related to the extent of aggregation.
In this study, the stability of synthesized titania NP obtained at pH 2.5 and pH 12 was evaluated. These dispersions were mixed with three different types of organic environmental substances, sodium alginate (ALG), fulvic acid (FA) and humic acid (HA), and evaluated in terms of the stability. The changes in the particle size were monitored using time-resolved dynamic light scattering (TR-DLS) at different concentrations of three electrolytes: NaCl, CaCl2 and Na2SO4, and at different solution pH values.
This new set of data will help to elucidate the behaviour of engineered nanoparticles in aquatic systems where the presence of other particulate matter is not crucial, e.g. ecotoxicological tests or spill situations. Additionally, a new methodology for the use of TR-DLS for determining aggregation rates and measuring simultaneously the size and intensity variations using conventional DLS apparatus is provided.
Previous studies on titania stability and NOM sorption
Several studies have been carried out concerning the aggregation behaviour of titania or other metal oxides. Most of those related to titania NP have been summarized in the review by Liu et al.7 and some of their findings have been compiled and complemented with factors that were considered important according to the focus of the present paper (see Table S1 in the ESI†). Some studies have focused on the effects that NOM has on the final stable suspension while some others have focused on the effects of electrolytes on the stability of NP. Contrastingly, we have investigated the effect of electrolytes with two different valence states on particles stabilized after mixing with NOM at different pH levels.Sedimentation rates and aggregation kinetics are sometimes difficult to compare between experiments even if the same source of material is used. The dispersion of the particles in the medium may have different outcomes in terms of particle size distribution (PSD) and particle number concentration (even if mass concentrations are reported, the number concentration remains unknown); since these two parameters are influential on the collision rates (i.e. more particles will have more encounters and smaller particles will surpass more easily the energy barriers8) then the comparison between experiments is difficult to be made in a straightforward way. Furthermore, the use of hydrolytically synthesized titania NP provides a cleaner surface and a narrower size distribution than dispersed particles from powders; this helps to study the transformation and transport processes (e.g. sorption and aggregation) in a more mechanistic way.
Results and discussion
Measurement of zeta potentials and isoelectric points
Titania NP are positively charged at pH below the isoelectric point (IEP). The IEP was determined using zeta potentials obtained from electrophoretic mobility measurements (EPM), using Henry's equation with corrections suggested by Ohshima to transition to Smoluchowski's equation. The results obtained for the isoelectric points of two batches of titania at pH 3 and one “charged-reversed” batch are presented in Fig. 1.In Fig. 1, it is possible to identify the apparent variation of the IEP with different starting sizes; since the system is unstable close to the IEP, then the measured zeta potentials are an ensemble average of the PSD of the aggregates present. The determination of zeta potentials from EPM was done using the z-average diameters and, therefore, it is not possible to distinguish the relative amount of smaller aggregates and their relative importance on the measured surface potentials due to possible size-dependent surface charge.9
Adsorption of macromolecules on titania NP surfaces
The adsorption of NOM onto the surfaces of the particles was done in small volumes and low concentrations. Table 1 presents the distribution of zeta potentials and z-averaged hydrodynamic diameters at different pH values upon the addition of 3 different types of NOM. Fig. 2 presents the characterization data as a function of HA/titania mass fraction, which shows the destabilization of the particles at low HA.| Concentration of NOM, mg L−1 | Humic acid | Fulvic acid | Alginate | ||||||
|---|---|---|---|---|---|---|---|---|---|
| pH | Zeta potential, mV | Size, nm | pH | Zeta potential, mV | Size, nm | pH | Zeta potential, mV | Size, nm | |
| 0.0 | 3.6 | 43.0 | 21.0 | 3.6 | 43.0 | 21.0 | 3.6 | 43.0 | 21.0 |
| 0.0 | 3.7 | 29.0 | 13.0 | 3.7 | 29.0 | 13.0 | 3.7 | 29.0 | 13.0 |
| 0.0 | 12.2 | −30.0 | 19.0 | 12.2 | −30.0 | 19.0 | 12.2 | −30.0 | 19.0 |
| 10.0 | 3.5 | 16.5 | 261.6 | 3.6 | 31.8 | 789.8 | 4.1 | 35.0 | 133.0 |
| 100.0 | 3.3 | −48.0 | 94.5 | 3.4 | 0.0 | 79.0 | 4.3 | −47.0 | 146.0 |
| 100.0 | 3.6 | −38.0 | 130.7 | 3.8 | −28.0 | 112.7 | 4.3 | −50.0 | 144.0 |
| 100.0 | 3.6 | −30.0 | 117.3 | 3.8 | −35.0 | 100.0 | 5.1 | −70.0 | 138.0 |
| 100.0 | 4.0 | −41.0 | 114.0 | 4.4 | −49.0 | 80.0 | 5.5 | −53.0 | 115.0 |
| 100.0 | 7.4 | −32.0 | 50.3 | 7.1 | −38.0 | 127.7 | 7.0 | −46.0 | 213.0 |
| 100.0 | 12.2 | −34.0 | 30.0 | 12.2 | −40.0 | 28.0 | 12.2 | −1.5 | 25.0 |
| 250.0 | 4.2 | −50.0 | 125.0 | 4.7 | −44.0 | 79.0 | 5.6 | −78.0 | 250.0 |
| 250.0 | 12.2 | −7.0 | 28.7 | 12.1 | −35.0 | 26.0 | 12.3 | −10.0 | 21.0 |
| 500.0 | 2.9 | −42.5 | 96.4 | 3.0 | −34.0 | 93.0 | 5.5 | −76.0 | 198.0 |
| 800.0 | 2.8 | −38.0 | 147.5 | 2.9 | −37.0 | 190.0 | 5.6 | −97.0 | 680.0 |
 | ||
| Fig. 2 Change of size of titania after humic acid addition to a varying mass ratio at pH ~ 3.5. The labels indicate the exact mass ratio. | ||
In Fig. 2, the lowest concentration of humic acid (ratio 0.03) at low pH induced high aggregation (probably due to uncompleted surface coverage) which is also reflected in the data in Table 1 for 10 mg L−1 HA (ratio 0.05). In Table 1, 100 and 250 mg L−1 concentrations of alginate at high pH led to zeta potentials larger than expected whilst the size remained relatively low. This could be due to the absence of attraction between the titania surface and the biopolymers at this pH, and the change in zeta potential could be partly explained by the signals from alginate itself. Generally, the addition of NOM in sufficient amounts to generate stable dispersions resulted in an increase of the z-averaged hydrodynamic diameter as observed in Table 1 and Fig. 2. The charge of the particles for stabilized suspensions with HA, FA and ALG turned negative at almost all pH tested. The adsorption of macromolecules on the available sites of titania NP can occur either by surface complexation with the carboxylic, phenolic, or hydroxyl groups on the NOM or through hydrophobic interactions. Since NOM macromolecules are polyelectrolytes with relatively low pKa (3.76 and 4.35 for FA and HA, respectively10), then the free charged groups (i.e. not complexed to the mineral surface) provide the particles with a net negative charge at the pH values tested.11,12
The evolution of hydrodynamic diameters as a function of added HA in Fig. 2 shows that concentrations below 16.4 mg L−1 HA (mass ratio 0.16) induced fast aggregation and slight destabilization as can be observed by the increase in dH in 30 minutes. By assuming an initial dH of ~20 nm and an average MW for HA of 5.7 kDa (ref. 13) then it is possible to identify approximately the ratio of HA required to stabilize the particles. In this case, 16.4 mg L−1 HA corresponds to 283 mol of HA per mol (part per L, scaled by the Avogadro number) of particles. It is important to note that the mixing conditions and the initial concentration for the sorption of HA are very crucial: in the experiment, high mixing rates were achieved and high concentrations (with respect to expected environmental particle concentrations) of particles were needed to be used, while in the environmental context the expected concentrations can fluctuate from high (i.e. near point sources) to low (in diluted systems with diffuse emission) and shear rates can also vary. Further, the presence of natural particles will influence the behavior of the incoming particles; for instance if these enter uncoated into an aquatic compartment with an elevated concentration of surfaces (particles) exposed to NOM, then they are likely to induce heteroaggregation since there will be no time for the released NP to achieve sorption equilibrium before they get in contact with another coated particle; a similar situation was observed for polymeric coatings which increased the stability between coated surfaces but enhanced deposition in uncoated surfaces.14
Interaction potential calculations
The addition of different electrolytes to the dispersions of bare titania NP causes the compression of the electrical double layer that keeps the particles separated even if aleatory Brownian motion or attractive van der Waals interactions induce collisions between them. This leads to more unstable dispersions in which nanoparticles start to form aggregates at different rates depending on the level of compression of the double layer.Calculations using the DLVO theory were made and stability ratios were determined using the approximation valid if the major contributions to the interaction potential come from the proximity of the maximum potential:15
 | (1) |
 | ||
| Fig. 3 Theoretical stability ratios, W, between 2 spheres, calculated using eqn (5) after determining the height of the energy barrier using the Derjaguin approximation. Non-retarded Hamaker coefficient 3.5 × 10−20 J, temperature 293 K, radii 10 nm. The curves are truncated in log(W) 5 and 0 to allow better visualization. | ||
Aggregation rate measurements by TR-DLS
DLS uses the temporal evolution of the intensity fluctuations to measure the translational diffusion coefficients of the particles in suspension. From the diffusion coefficient the hydrodynamic radius can be determined via the Stokes–Einstein equation. The measured hydrodynamic radius of a coagulating suspension is the average of the hydrodynamic radii of the individual aggregates, weighted by their scattered light intensities. The growth of the aggregates in a coagulation process can thus be observed by performing time-resolved DLS measurements.19The intensity of scattered light is also dependent on the particle concentration and can be calculated as:
 | (2) |
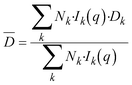 | (3) |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) is the intensity-averaged diffusion coefficient, which is inversely proportional to the hydrodynamic radius according to the Stokes–Einstein equation. The strong particle size influence on the scattering intensity will have a strong effect on the measured size, as a small amount of large particles will have such a large influence that smaller particles can be overlooked.21 The average intensity-weighed hydrodynamic-diameter obtained using this method is called the zeta-average diameter.
is the intensity-averaged diffusion coefficient, which is inversely proportional to the hydrodynamic radius according to the Stokes–Einstein equation. The strong particle size influence on the scattering intensity will have a strong effect on the measured size, as a small amount of large particles will have such a large influence that smaller particles can be overlooked.21 The average intensity-weighed hydrodynamic-diameter obtained using this method is called the zeta-average diameter.
The combination of the above two equations and under the assumption of the limit when time tends to zero so that only duplets are formed generates the following equation that has been widely used to determine aggregation rate constants by combining DLS and static light scattering, SLS:19
 | (4) |
The attachment efficiency (α) used to account for modeling the repulsive forces in solution22 can be calculated based on the aggregation rates obtained from the TR-DLS measurements by dividing the initial slope (fast aggregation) at a particular concentration with the maximum (favorable) slope, and log-plotted against the salt concentration which, with enough data points available, allows determination of the critical coagulation concentration (CCC).8 Another useful quantity to evaluate the stability of the suspension is the stability ratio, W. We can calculate this value with the help of eqn (4) by taking the maximum rate as the theoretical rate, kij, which under stable conditions or slow aggregation rates, is equivalent to k11 but under unstable conditions can take values up to 2 orders of magnitude higher. Here, it was decided to calculate kij using the difference between the first size determined using TR-DLS, Rha, and the initial size, Rh1:
 | (5) |
Since the data here evaluated have been acquired for relatively high number concentrations, the curves obtained for the rates of increase in hydrodynamic radius (zeta-average radius) and intensities (derived count rates) have to be extrapolated to values near time zero. The procedure followed to achieve the final results for stability ratios, W, is presented below.
Since the relative change between Rh2 and Rh1 is one of the parameters obtained when doing simultaneous measurements of DLS and SLS, it has to be adjusted, and this is especially important for the most destabilized suspensions where the variation in intensity starts overwhelming the variation in hydrodynamic ratios. The relative change between Rh2 and Rh1 in eqn (5) was evaluated to be 1.4 (calculations have shown that the hydrodynamic radius of a duplet is approximately 1.38 times the initial diameter19) if the ratio between the initial diameter and the first measurement with the calculated slope was less than 1.4. If this was not the case (as it was found under the most unstable conditions), the expression was calculated assuming Rh2 as the radius 1 second after mixing under the calculated slope. This allows compensating for possible deviations from the assumptions of initial duplet formation. Another compensation done in order to avoid underestimation of the stability ratios due to elevated aggregation rates was to include the total theoretical aggregation rates as explained above.
The values of both size and intensity were plotted and the initial data points (approx. 1–2 minutes after the start of the aggregation process) were selected for a quadratic regression with a forced intercept in the initial value of diameter or intensity (this is the value before starting the aggregation process except for low rates where a slope from a linear fit was more suitable). The first derivative evaluated at time zero for these equations was then selected as the initial rate of increase and used in eqn (5) to determine the stability ratio. This was not done for cases where linearity was evident (i.e. no addition of electrolytes or some cases of low concentrations where the previous method provided misleading information).
Fig. 4 presents an example of the measurement of the rate of increase in size (Fig. 4B) and scattered intensity (Fig. 4A) of a dispersion of 100 mg L−1 titania NP at pH 3 (initial particle size 13 nm) after addition and rapid mixing of different concentrations of NaCl. Fig. 4C corresponds to the PSD (based on intensity and calculated using the CONTIN algorithm) measured by DLS for the same dispersions 1 minute after the addition of different concentrations of NaCl. The size distributions get broader and flatter after the addition of the electrolytes and some bimodal peaks can be distinguished for concentrations higher than 300 mM NaCl.
The stability ratios, W, were calculated as described above for different additions of NOM and rapid mixing of the electrolytes at different concentrations. Fig. 5 presents the results for 100 mg L−1 NOM addition (HA, FA and ALG) at different levels of NaCl, CaCl2 and Na2SO4. The particle number concentrations were calculated with the hydrodynamic diameter assuming spherical particles, the density of titania found in the literature (3900 kg m−3) and the initial mass concentration (100 mg L−1).
 | ||
| Fig. 5 Stability ratios, W, at different values of pH (columns and symbols), organic macromolecules (rows) and salt concentration. A) Sodium chloride. B) Calcium chloride. C) Sodium sulfate. The concentrations of organic molecules and titania NP were kept at 100 mg L−1. Eqn (4) was used to determine W. | ||
In Fig. S1 in the ESI,† the stability ratios for different additions of NOM (10, 100, 250, 500 and 800 mg L−1) at a limited set of pH values can be found.
In general, all additions of electrolytes without NOM followed the DLVO theory. Positively charged NP at low pH were more prone to destabilization by SO4−2 compared to Cl− while the opposite holds for Ca+2 compared to Na+ at high pH. If the pH of the suspension is far from the IEP, the particles have a higher charge (either positive or negative) and this leads to slower aggregation rates at a similar particle concentration than when the pH of the particles is closer to the IEP.
The behaviour of the experimental stability ratios in Fig. 5 is in accordance with DLVO theory, and even the order of magnitude in the absence of NOM (Fig. 5, upper panels) matches those calculated at different surface charges presented in Fig. 3.
The addition of NOM at concentrations which generated stable suspensions increased the stability of the systems with respect to NaCl and Na2SO4 but did not have much influence on the CaCl2 systems. This suggests that there is bridging coagulation between the organic molecules and calcium. Calcium is known to bridge the molecules in the alginate network (β-D-mannuronate and α-L-guluronate) to form gel-like aggregates. Particles with HA have also shown low stability in the presence of calcium.23 Other studies with silica particles (150 nm z-average) have shown that Ca2+ ions destabilize the suspension in the presence of alginate and humic acid but not with fulvic acid.24
The stability of FA coated NP in the presence of CaCl2 was slightly better than for any of the other NOM sources. This is in accordance with other studies and can be due to the lower affinity of FA to form a complex with Ca2+ (ref. 25).
The weight-averaged molecular weight, MW, of SR-HA is about 5700 Da,13 the average molecular weight of FA is 550 Da,26 and that of sodium alginate, between 75 and 200 kDa (provided by the manufacturer). A big part of the MW of NOM is therefore due to HA, and comparing the effects of this with FA on the stability of titania NP, it is possible to see that small amounts of FA are more favourable for stability but as more molecules are added, HA improves the stability probably due to increased steric effects.
The presence of NOM increased the stability in the presence of Na2SO4 in a more efficient way than for the other 2 electrolytes. HA was less effective in stabilizing NP at low pH due to the fact that the carboxylic groups were protonated and, therefore, the overall surface charge was low and there was reduced electrostatic contribution to the repulsion. FA was a better stabilizer even at low pH probably because there were fewer branches available for bridging coagulation with other particles and due to the larger overall charge density per mass of FA compared to HA (Fig. S2 in the ESI†).
Experimental
Synthesis of titania NP
The synthesis of TiO2 was done via low temperature hydrolysis of TiCl4 following previous publications,27 which proceeds according to the reaction:| TiCl4 + 2H2O → TiO2 + 4H+ + 4Cl− | (6) |
Particle growth according to a specific target size was facilitated through temperature control during dialysis and solution storage, with lower temperature for smaller particles. Dialysis was done to reduce the concentration of Cl− ions which screen the TiO2 surface charge and contribute to particle aggregation.27 The suspensions obtained by this method have a concentration of approximately 19 g L−1 of mostly the anatase crystal form and the pH is around 2.5. Even though some Cl− ions and Ti species may remain in solution after dialysis, the expected concentrations estimated are negligible after dilution to the concentrations used in this work.28
In order to perform the experiments at high pH, the surface charge of the NP was modified using a fast addition of NaOH, changing the pH to around 12. One mL of the original suspension of TiO2 was diluted with 5 mL of water and then quickly mixed with 1 mL of 0.1 M NaOH. Because this process of “charge reversal” includes passing through the IEP, some of the particles collide and attach to each other forming larger aggregates resulting in a z-average hydrodynamic diameter of approximately 60 nm as measured by DLS.
Natural organic macromolecules
The representative NOM model compounds chosen were humic and fulvic acids (isolated from Suwanee River) and sodium alginate (isolated from brown algae). HA and FA are typical standard sources of natural organic matter used with the intention to have a material that is well characterized in order to increment the repeatability from laboratory studies; HA and FA were obtained from the International Humic Substances Society (IHSS, University of Minnesota, St. Paul, MN, USA) batches 2S101H and 2S101F, respectively. Sodium alginate (Pronova® UP LVG; chemical name sodium (1→4)-linked β-D-mannuronate and α-L-guluronate) was obtained from NovaMatrix (Sandvika, Norway). Additional information about the physicochemical characteristics of the NOM sources is provided in the ESI.†The particles were mixed with NOM to obtain a final mass concentration of titania of 200 mg L−1 and these batches were stored for a maximum of two weeks at 4 °C in the dark before mixing in the proportion of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 with the corresponding electrolyte prior to TR-DLS measurements.
2 with the corresponding electrolyte prior to TR-DLS measurements.
Dynamic light scattering
A DLS unit (Malvern Zetasizer, Malvern instruments Ltd, Worcestershire, UK) equipped with a 633 nm laser source was used for the measurements of electrophoretic mobility, zeta-averaged hydrodynamic diameters and photon counts per second (count rates) under the initial conditions.The measurements of TR-DLS were done using the Malvern Zetasizer as well. The optimum concentration that was used for the measurements of aggregation rates by DLS was 100 mg L−1 TiO2; this concentration gave good statistical data at low particle diameters with the drawback of having fast aggregation rates. The measurements were done using standard operating procedures with fixed attenuator and measurement positions optimized for each set of samples. All of the liquids were equilibrated at room temperature, and the instrument was adjusted to that temperature as well. The refractive index and viscosity of the solutions of NaCl and CaCl2 were obtained from the Zetasizer software while the values for Na2SO4 were obtained from the literature.29,30 The stabilized particles were thoroughly mixed for approximately 5 seconds and placed inside the instrument before the first measurement was done; the time elapsed between the initial mixing and the first measurement was noted and used as the first time point.
Influential outlier data points in the datasets were removed if the variation in the outcome slope and the intercept were several orders of magnitude higher than the ones obtained when these points were included in the calculations.
The chemicals used in this study were of analytical grade and were acquired from Fischer Scientific.
Conclusions
The aggregation of ENP has a strong influence on the final fate of these in the environment. Here we have shown that a low coverage of NOM on top of bare titania particles can induce aggregation but further coverage can protect them from aggregating even at high ionic strengths; particles stabilized in this way are larger in size and have negative surface charge probably coming from the different functional groups in the macromolecules. The degree of coverage is going to be governed by the concentration ratio between NP and NOM and different approaches in the process of mixing can lead to different states of aggregation:Higher initial number concentrations of particles will, generally, lead to larger sizes of the stabilized particles in the dispersion.
NOM sorption increases the size, probably from small aggregate formation during the mixing process, and lowers the zeta-potential.
Initial mixing strength (gradients) will influence the contact between particles and other additives.
The ionic composition strongly influences the aggregation behaviour, with divalent anions and cations destabilizing more strongly positively and negatively charged titania, respectively. This is in accordance with the Schulze–Hardy rule that states that, depending on the conditions, the CCC of a colloidal dispersion is inversely proportional to the 2nd to 6th power of the counterion valence.31 The pH of the suspension is a major influential factor that will determine the initial charge of the NP and the degree of electrostatic repulsion. pH levels near the IEP of the ENP will lower the absolute value of the surface charge of the particles, with direct consequences on stability.
Besides the ionic strength and pH, the quality and quantity of NOM have a significant influence on the aggregation behaviour of titania. Larger molecules like humic acid and alginic acid will increase steric repulsion in the presence of NaCl and Na2SO4 but will destabilize strongly the particles in the presence of CaCl2 probably due to the bridging of some parts of the macromolecules with the aid of Ca bridges. Therefore, in natural waters with high contents of Ca2+ and NOM, it could be expected that the NP will undergo more aggregation than in other types of water.32
The concentrations of titania tested induced high aggregations rates. At further stages of the aggregation process, the assumptions of sphericity and monodispersity are broken and the values for collision rates (k11) are no longer valid. More sensitive methods for lower concentrations should be developed.
Additionally, the measurements using TR-DLS provide intensity-weighed size averages that can be significantly higher than the number-averaged values and, therefore, attachment efficiencies calculated by this method will probably lead to overestimation of aggregation rates.
Implications of this study are important mainly for near source emissions, spill situations and ecotoxicity tests, where other particles are relatively less important. In ecotoxicity tests, the concentrations used differ in several orders of magnitude and, therefore, the measurement of aggregation rates using TR-DLS is more adequate compared to fate studies where the expected concentrations usually fall below the detection limits of DLS. Due to the dependence of aggregation rates on number concentrations, the actual PSD during an ecotoxicity test is variable with time and the exposure to smaller particles, which is dynamic across different treatments, will differ from the actual mass concentration. Modelling using probabilistic approaches for aggregate size distribution dynamics could be helpful in both ecotoxicity tests and environmental fate studies.
Acknowledgements
Financial support was received from the Swedish environmental research council, the FORMAS and the NanoFATE Project CP-FP 247739 (2010–2014) under the 7th Framework Programme of the European Commission and the Swedish chemical inspectorate. We thank Aldina Bijedic and Mohammad Aurangojeb for the work done in collecting TR-DLS data and Johan Bergenholtz for the initial input on DLVO models. We thank Elisabet Alhberg and Zareen Abbas for previous contributions to the synthesis method, and Caroline Jonsson for valuable comments.Notes and references
- M. Roco, J. Nanopart. Res., 2011, 13, 427–445 CrossRef.
- B. Nowack, J. F. Ranville, S. Diamond, J. A. Gallego-Urrea, C. Metcalfe, J. Rose, N. Horne, A. A. Koelmans and S. J. Klaine, Environ. Toxicol. Chem., 2012, 31, 50–59 CrossRef CAS PubMed.
- G. V. Lowry, K. B. Gregory, S. C. Apte and J. R. Lead, Environ. Sci. Technol., 2012, 46, 6893–6899 CrossRef CAS PubMed.
- D. F. Evans and H. Wennerström, The colloidal domain: where physics, chemistry, biology and technology meet, John Wiley and Sons, 2nd edn, 1999 Search PubMed.
- F. Gottschalk, T. Sun and B. Nowack, Environ. Pollut., 2013, 181, 287–300 CrossRef CAS PubMed.
- U.S. Environmental Protection Agency, Nanomaterial Case Studies: Nanoscale Titanium Dioxide in Water Treatment and in Topical Sunscreen (Final), Washington, DC, 2010 Search PubMed.
- X. Liu, G. Chen, A. A. Keller and C. Su, Environ. Sci.: Processes Impacts, 2013, 15, 169–189 CAS.
- A. R. Petosa, D. P. Jaisi, I. R. Quevedo, M. Elimelech and N. Tufenkji, Environ. Sci. Technol., 2010, 44, 6532–6549 CrossRef CAS PubMed.
- Z. Abbas, C. Labbez, S. Nordholm and E. Ahlberg, J. Phys. Chem. C, 2008, 112, 5715–5723 CAS.
- J. D. Ritchie and E. M. Perdue, Geochim. Cosmochim. Acta, 2003, 67, 85–96 CrossRef CAS.
- L. M. Mosley, K. A. Hunter and W. A. Ducker, Environ. Sci. Technol., 2003, 37, 3303–3308 CrossRef CAS.
- R. Beckett and N. P. Le, Colloids Surf., 1990, 44, 35–49 CrossRef CAS.
- C. Guéguen and C. W. Cuss, J. Chromatogr. A, 2011, 1218, 4188–4198 CrossRef PubMed.
- S. Lin, Y. Cheng, J. Liu and M. R. Wiesner, Langmuir, 2012, 28, 4178–4186 CrossRef CAS PubMed.
- M. Elimelech, J. Gregor, X. Jia and R. I. Williams, Particle deposition and aggregation: measurement, modeling, and simulation, Butterworth-Heinemann, Woburn, 1995 Search PubMed.
- W. B. Russel, D. A. Saville and W. Schowalter, Colloidal dispersions, Cambridge, 1989 Search PubMed.
- H. Ohshima, Biophysical chemistry of biointerfaces, Wiley, Hoboken, NJ, USA, 2010 Search PubMed.
- A. I. Gómez-Merino, F. J. Rubio-Hernández, J. F. Velázquez-Navarro, F. J. Galindo-Rosales and P. Fortes-Quesada, J. Colloid Interface Sci., 2007, 316, 451–456 CrossRef PubMed.
- H. Holthoff, S. U. Egelhaaf, M. Borkovec, P. Schurtenberger and H. Sticher, Langmuir, 1996, 12, 5541–5549 CrossRef CAS.
- M. L. Broide and R. J. Cohen, J. Colloid Interface Sci., 1992, 153, 493–508 CrossRef CAS.
- M. Hassellöv, J. Readman, J. Ranville and K. Tiede, Ecotoxicology, 2008, 17, 344–361 CrossRef PubMed.
- R. Arvidsson, S. Molander, B. A. Sandén and M. Hassellöv, Hum. Ecol. Risk Assess., 2011, 17, 245–262 CrossRef CAS.
- A. Siripinyanond, S. Worapanyanond and J. Shiowatana, Environ. Sci. Technol., 2005, 39, 3295–3301 CrossRef CAS.
- T. Abe, S. Kobayashi and M. Kobayashi, Colloids Surf., A, 2011, 379, 21–26 CrossRef CAS PubMed.
- R. F. Domingos, C. Peyrot and K. J. Wilkinson, Environ. Chem., 2010, 7, 61 CrossRef CAS.
- A. Fattahi and T. Solouki, Anal. Chim. Acta, 2003, 496, 325–337 CrossRef CAS.
- Z. Abbas, J. P. Holmberg, A. K. Hellström, M. Hagström, J. Bergenholtz, M. Hassellöv and E. Ahlberg, Colloids Surf., A, 2011, 384, 254–261 CrossRef CAS PubMed.
- J. P. Holmberg, Dissertation (Ph.D.), Department of Chemistry, University of Gothenburg, Sweden, 2012 Search PubMed.
- S. Urréjola, A. Sánchez and M. N. F. Hervello, J. Chem. Eng. Data, 2010, 55, 2924–2929 CrossRef.
- T. Isono, J. Chem. Eng. Data, 1984, 29, 45–52 CrossRef CAS.
- P. C. Hiemenz and R. Rajagopalan, Principles of colloid and surface chemistry, Marcel Dekker, New York, 3rd edn, 1997 Search PubMed.
- J. Hammes, J. A. Gallego-Urrea and M. Hassellöv, Water Res., 2013, 47, 5350–5361 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A comprehensive table with other studies regarding titania stability in the presence of electrolytes or NOM; a figure presenting stability ratios for other concentrations of macromolecules and equations used for the DLVO simulations; additional information about NOM sources. See DOI: 10.1039/c3en00106g |
| This journal is © The Royal Society of Chemistry 2014 |


