Open Access Article
Open Access ArticleQuantifying the potential of ultra-permeable membranes for water desalination†
David
Cohen-Tanugi
a,
Ronan K.
McGovern
b,
Shreya H.
Dave
b,
John H.
Lienhard
b and
Jeffrey C.
Grossman
*a
aDepartment of Materials Science & Engineering, Massachusetts Institute of Technology, Cambridge MA 02139, USA. E-mail: jcg@mit.edu
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge MA 02139, USA. E-mail: lienhard@mit.edu
First published on 4th February 2014
Abstract
In the face of growing water scarcity, it is critical to understand the potential of saltwater desalination as a long-term water supply option. Recent studies have highlighted the promise of new membrane materials that could desalinate water while exhibiting far greater permeability than conventional reverse osmosis (RO) membranes, but the question remains whether higher permeability can translate into significant reductions in the cost of desalinating water. Here, we address a critical question by evaluating the potential of such ultra-permeable membranes (UPMs) to improve the performance and cost of RO. By modeling the mass transport inside RO pressure vessels, we quantify how much a tripling in the water permeability of a membrane would reduce the energy consumption or the number of required pressure vessels for a given RO plant. We find that a tripling in permeability would allow for 44% fewer pressure vessels or 15% less energy for a seawater RO plant with a given capacity and recovery ratio. Moreover, a tripling in permeability would result in 63% fewer pressure vessels or 46% less energy for brackish water RO. However, we also find that the energy savings of UPMs exhibit a law of diminishing returns due to thermodynamics and concentration polarization at the membrane surface.
Broader contextThe development of affordable, reliable and energy-efficient technologies for converting saltwater into fresh water is one of the most important research goals of this century. Yet the best technology available today, reverse osmosis (RO), remains costly. Recent advances in materials research suggest that new membranes could reject salt while permeating water much faster than nonporous RO membranes. However, considerable confusion exists regarding the likelihood that future RO systems will continue to become smaller, more productive or more energy-efficient. Given the critical importance of water technology research for human development goals, it is essential to carefully evaluate what future RO systems can and cannot achieve on the basis of more permeable membranes. Beginning with fundamental transport equations and extending to applied engineering scenarios, we demonstrate that membranes with 3x higher permeability could reduce the energy consumption of RO by 15-46% for seawater and brackish water respectively, or alternatively reduce the number of pressure vessels by 44-63%. Given many recent advances in the design of RO membranes, this work highlights the likely development of a new generation of desalination plants with higher throughput and a smaller spatial footprint than what is achievable today. |
1 Introduction
Fresh water is becoming an increasingly scarce global resource, and its availability is expected to influence the long-term wealth and wellbeing of nations.1 Desalination provides the attractive possibility of expanding the natural hydrological cycle by supplementing it with water from oceans and brackish reservoirs.RO technology has improved dramatically since the 1950s:2 the most efficient desalination process, reverse osmosis (RO), now requires ∼2.6 kWh per cubic meter of fresh water compared with 8 kWh in 1980.3,4 However, desalination still comes at a high capital and energy cost.5 In particular, RO plants remain expensive to build and often occupy large areas in coastal zones where available land is increasingly limited (see Fig. 1). Fortunately, advances in RO technology have steadily reduced the cost of desalinated water in past decades.6
However, considerable confusion exists regarding the likelihood that future RO systems will continue to become smaller, faster or more energy-efficient. Given the critical importance of water technology research for human development goals, it is crucial to carefully evaluate what future RO systems can and cannot achieve on the basis of more permeable membranes.
2 Motivation and research question
The orders-of-magnitude increase in permeability that UPMs could potentially enable require an in-depth assessment of the physical mechanisms that occur at the membrane's surface. The thin-film composite (TFC) membranes employed in RO today achieve very high salt rejection (>99%), but at the expense of a low water permeability (∼1 L (m2 h bar)−1, compared with 300 L (m2 h bar)−1 for ultrafiltration membranes).7,8 Trends in materials research indicate that future RO membranes will likely exhibit substantially higher intrinsic permeability to water than TFCs. For example, it has been shown that graphene is experimentally capable of separating salts from water,9 and simulations suggest that the permeability of nanoporous graphene could exceed that of TFCs by 2–3 orders of magnitude.10 Other research efforts have highlighted the potential of incorporating zeolites, graphene, carbon nanotubes11,12 or bioinspired aquaporins into membranes.2,13–15 However, it is known that concentration polarization – namely, the accumulation of salt near the membrane surface and the resulting decrease in water flux – will prevent UPMs from performing significantly better than conventional membranes.16–18 Prior work has largely focused on the energy consumption of RO and mostly neglected other ways in which RO systems could produce cheaper water, e.g. reduced system size. Seawater RO plants today can contain >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 membrane elements, with capital costs ranging in the hundreds of millions of US dollars and approximately 20% of the capital cost attributable directly to pressure vessels and the associated membranes and piping.19 Studies have also examined the specific engineering aspects of RO modules – including spacer design and inter-element connectors20 – but the direct effects of increasing membrane permeability have largely been overlooked in the literature.
000 membrane elements, with capital costs ranging in the hundreds of millions of US dollars and approximately 20% of the capital cost attributable directly to pressure vessels and the associated membranes and piping.19 Studies have also examined the specific engineering aspects of RO modules – including spacer design and inter-element connectors20 – but the direct effects of increasing membrane permeability have largely been overlooked in the literature.
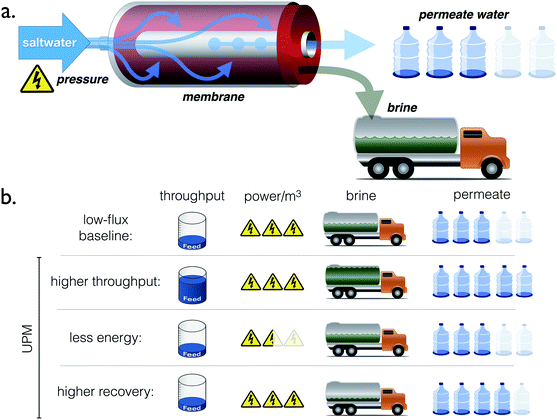
Thus, this paper addresses the following question: would a tripling of water permeability over current membrane technology allow for a significant improvement in the performance of RO? More specifically, for an RO plant of a given capacity and recovery ratio, how much could UPMs reduce the energy consumption or the number of pressure vessels required to produce the plant's total output, as illustrated in Fig. 2? In the remaining Sections, we answer these questions and demonstrate that energy consumption, far from scaling linearly with membrane permeability, is limited by thermodynamics, while the number of pressure vessels could be reduced more significantly than had been appreciated previously.
2.1 Methodological approach
In order to evaluate how membrane permeability affects the energy consumption and number of pressure vessels in an RO plant, we model the mass transport and fluid dynamics of an RO system. Unless mentioned otherwise, we use the term UPMs to refer to membranes whose permeability would be at least three times greater than their TFC counterparts with equivalent salt rejection performance. A factor of three increase is representative of the permeability improvement of RO membranes in the past several decades20 and represents a useful measure of how RO systems would perform given enhanced permeability.Moreover, in order to quantify the effects of feed water concentration, we consider two different saline water sources: seawater (42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm) and brackish water (2
000 ppm) and brackish water (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm). Because conventional seawater RO (SWRO) plants operate differently from conventional brackish water (BWRO) plants, we examine the benefits from UPMs relative to typical operational conditions for both feed waters achievable today with TFC membranes. The reference conditions for each feed water type are summarized in Table 1.
000 ppm). Because conventional seawater RO (SWRO) plants operate differently from conventional brackish water (BWRO) plants, we examine the benefits from UPMs relative to typical operational conditions for both feed waters achievable today with TFC membranes. The reference conditions for each feed water type are summarized in Table 1.
| Reference parameter | SWRO | BWRO |
|---|---|---|
| Feed salinity (ppm) | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Inlet pressure (bar) | 70 | 12 (First stage) |
| Membrane elements per vessel | 8 | 7 |
| Feed flowrate per vessel (m3 day−1) | 300 | 140 |
| Permeate recovery | 42% | 65% (First stage) |
| Water permeability (L (m2 h bar)−1) | 1.0 | 1.5 |
| Source: | Dow Water21 | Sessions et al.22 |
In RO, feed water enters pressure vessels containing several cylindrical spiral-wound membrane elements connected in series. The feed water travels parallel to the membrane surface, and water molecules selectively permeate radially across the membrane while most undesired substances remain in the feed channel. For conventional RO systems and new membrane classes alike, empirical studies and molecular dynamics simulations have shown that the local permeate flux J (units: L h−1) obeys:10,14,15,23
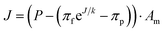 | (1) |
As the feed salinity increases in the streamwise direction as water is removed through the membrane, the net driving pressure and the local permeate flux both decline. In order for the permeate flux to remain positive throughout the RO vessel, the feed pressure must be greater than the osmotic pressure difference at any streamwise position. The profile of local permeate flux, feed flowrate, feed pressure and bulk salinity (J(z), Q(z), P(z), cb(z)) over the length of the RO vessel are governed by the differential equations for local permeate flux, conservation of water, conservation of salt, and pressure loss as well as the inlet conditions.
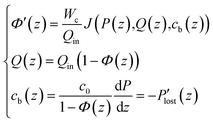 | (2) |
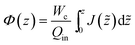 | (3) |
| Symbol | Quantity | Units |
|---|---|---|
| A m | Water permeability | L (m2 h bar)−1 |
| Q in | Feed flowrate | m3 day−1 |
| Q out | Permeate flowrate | m3 day−1 |
| RR | Recovery ratio | % |
| P in | Inlet pressure | bar |
| P lost | Pressure loss across RO vessel | bar |
| E | Specific power consumption per unit of permeate | kWh m−3 |
| J | Permeate flux at position z | m s−1 |
| k | Mass transfer coefficient | m s−1 |
| L | Pressure vessel length | m |
| c b | Bulk salinity at position z | mol L−1 |
| R 0 | Salt rejection | % |
| T | Temperature | K |
| R | Universal gas constant | J (K mol)−1 |
| ξ | Pressure recovery efficiency | % |
| η | Pump efficiency | % |
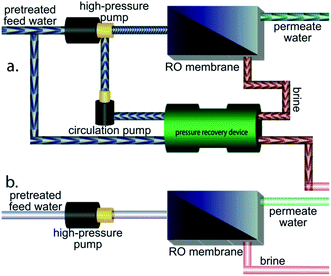
Systems-level quantities were calculated by considering the typical RO process diagram shown in Fig. 3. SWRO systems employ isobaric pressure recovery devices (PRDs) to pressurize the feed using mechanical energy salvaged from the brine (Fig. 3a), while BWRO typically do not28 (Fig. 3b). The total permeate production per vessel is calculated as
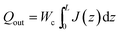 | (4) |
The energy consumption per m3 of permeate arises both from a minimum dictated by thermodynamics and from entropy generated throughout the RO process29 and is calculated as:
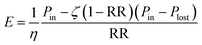 | (5) |
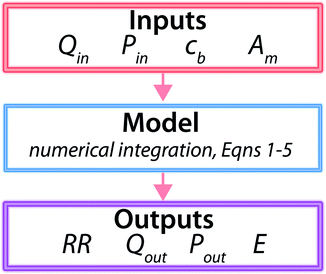
The methodology described above is summarized schematically in Fig. 4. Using this methodology, we calculate how inlet pressure and number of RO vessels would evolve as a function of membrane permeability while all other parameters are held fixed at the reference values typical of each feed water concentration today. Since RO pressure vessels operate in parallel, the number of required pressure vessels for a given total capacity scales inversely with Qout. The variable and fixed parameters for each case are summarized in Table 3.
| Scenario | P in | Q out | RR | L |
|---|---|---|---|---|
| #1 | f(Am) | Fixed | Fixed | Fixed |
| #2 | Fixed | f(Am) | Fixed | Fixed |
3 Results
3.1 Seawater RO
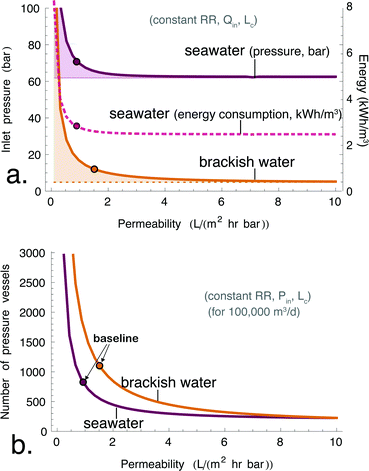
We first consider the impact of UPMs on energy consumption in SWRO. Consistent with prior work, we find that the opportunity for lower energy consumption in SWRO is limited by thermodynamics.16–18 Lower energy consumption (for a given recovery ratio, membrane area and feed flowrate) would be obtained by reducing the inlet pressure, and the achievable pressure reduction as a function of membrane permeability is shown in Fig. 5a. The feed inlet pressure for SWRO (purple line) declines asymptotically to the outlet brine osmotic pressure. This limit28 corresponds to the osmotic pressure of the brine, and it represents a fundamental constraint on the energy efficiency of desalination that is entirely independent of membrane performance. Fig. 5a shows that tripling Am from 1 to 3 L (m2 h bar)−1 would reduce the inlet pressure from 70 bar to 63 bar. This 10% reduction in inlet pressure translates to a 15% reduction in specific energy consumption. However, the figure also shows that any further improvements in membrane permeability beyond 3 L (m2 h bar)−1 would have essentially no effect on energy consumption, since 63 bar is already within 1% of the osmotic limit for SWRO at the chosen recovery ratio.We now turn to the effect of permeability on the equipment requirements for SWRO. In this case, the increase in Am serves to increase the permeate flux, while the higher feed velocity mitigates the effect of concentration polarization since the mass transfer coefficient increases monotonically with fluid velocity. We have plotted the total number of pressure vessels needed for a 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 day−1 RO plant as a function of the permeability of the membranes in Fig. 5. Fig. 5b indicates that tripling Am would allow SWRO plants to produce the same total output (at the same inlet pressure and recovery ratio) with 55% fewer pressure vessels. However, more energy is dissipated by viscous losses at high feed velocity, so the specific energy consumption would also increase by 6% at this higher throughput. Alternatively, by operating at lower pressure instead, SWRO plants could maintain the same energy consumption while reducing the number of pressure vessels by 44% (not shown in figure).
000 m3 day−1 RO plant as a function of the permeability of the membranes in Fig. 5. Fig. 5b indicates that tripling Am would allow SWRO plants to produce the same total output (at the same inlet pressure and recovery ratio) with 55% fewer pressure vessels. However, more energy is dissipated by viscous losses at high feed velocity, so the specific energy consumption would also increase by 6% at this higher throughput. Alternatively, by operating at lower pressure instead, SWRO plants could maintain the same energy consumption while reducing the number of pressure vessels by 44% (not shown in figure).
3.2 Brackish water RO
We now turn to the potential operational impacts of UPMs on BWRO. Fig. 5 reveals a result that is largely unaddressed in the literature, namely that inlet pressure leaves much more room for reduction in the case of BWRO compared with SWRO. Fig. 5a indicates that the inlet pressure required to achieve 65% recovery in BWRO rapidly drops for increasing Am. Because the osmotic limit for BWRO is only a fraction of that of SWRO, a tripling in membrane permeability would achieve a much greater reduction in inlet pressure, namely down to 6.4 bar from 12 bar in the case of TFC membranes (a 46% reduction in pressure and energy consumption). For even more permeable membranes, the pressure essentially reaches the asymptotic limit when Am > 5 L (m2 h bar)−1. Thus, UPMs could nearly halve the energy consumption of the RO stage for brackish water.The reduction in the number of pressure vessels is also greater for BWRO than for SWRO. Fig. 5b indicates that tripling Am would allow for 63% fewer pressure vessels for a given plant capacity by increasing the feed flowrate per vessel from 139 m3 day−1 to 378 m3 day−1. Furthermore, the increase in feed flowrate involves approximately no energy penalty, since viscous losses represent a negligible component of the overall energy consumption in a BWRO system.
3.3 Concentration polarization
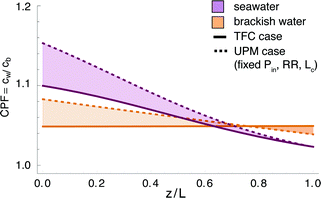
The effect of concentration polarization is to impede the flux across the membrane (our model accounts for this effect) and to increase the likelihood of membrane scaling (which our model does not account for). Scaling has been observed to occur when the concentration polarization factor (CPF), or ratio of membrane surface salinity to bulk salinity, exceeds 1.20 for SWRO.32 The detailed effects of scaling and fouling are beyond the scope of this paper but are relevant to the design constraints of an RO plant. We have computed the CPF for each scenario investigated as a function of z in Fig. 6. We also report the maximum CPF for each system in the ESI.†Fig. 6 shows that the maximum CPF is higher with UPMs than with TFC membranes, which is consistent with the fact that the former allow for higher transmembrane flux. The CPF begins with high values in the front of the RO vessel, where the permeate flux is highest, and decays to unity towards the end of the vessel. In the reference case, corresponding to conventional TFC membrane operation, the CPF profile is comparatively flat in all three scenarios since the permeate flux is relatively modest. In contrast, the UPM system (with Pin, RR and L fixed and a larger value of Qin) exhibits greater CP at the front of the vessel (consistent with higher membrane permeability) but decays more steeply to unity along the vessel length. In the SWRO scenario, the CPF in the second half of the vessel is actually lower than in the reference case. Despite the marginally higher CPF values for UPMs, the CPF remains below 1.20 in all three scenarios.
4 Implications
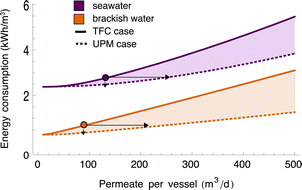
The preceding sections quantified the extent to which UPMs would reduce the energy and pressure vessel requirements for SWRO and BWRO by operating at lower pressure or higher flowrate. However, each improvement (e.g. reducing Pin) was calculated by holding other quantities fixed (e.g. RR and Qin). Since the various improvements described above cannot be attained simultaneously, the advent of UPMs would require new and existing RO plants to reach a compromise between energy and pressure vessel savings.Fig. 7 represents graphically the tradeoff between the energy and pressure vessel savings from UPMs. Energy consumption and permeate production per vessel are represented on independent axes for a fixed recovery ratio and membrane area. For each scenario, the operating regimes achievable using UPMs (dashed lines) can be compared with those achievable with TFC membranes (solid lines). The figure indicates RO plants could adopt any combination of energy savings (up to 15% for SWRO and 46% for BWRO) and pressure vessel savings (up to 44% for SWRO and 63% for BWRO) along the dashed line, with the energy savings becoming smaller for a greater reduction in the number of pressure vessels.
We have shown that the impacts of UPMs depend heavily on the feed water type as well as which parameter (pressure or flowrate) is being optimized. We now briefly turn to the potential implications of these operational impacts in order to evaluate our original hypothesis, i.e. that a tripling in membrane permeability would result in significant gains for RO.
The potential implications of lower pressure operation or greater permeate production can be estimated with reasonable confidence. We emphasized above that the energy savings from UPMs in SWRO would be limited to about 15%. In practice, this limitation is due to the fact that current SWRO plants operate near the lowest allowable pressure at the expense of low permeate production per vessel. SWRO plants are optimized to operate in this manner because the minimum pressure required to extract permeate water from seawater is already quite high (60–70 bar) owing to the high salinity of seawater. Since pre- and post-treatment account for another ∼1 kWh m−3, a 15% reduction in the energy consumption of the RO stage would only result in a ∼10% reduction in the total energy cost of SWRO. Although a 10% savings may seem limited, it may still represent an important improvement given the high energy footprint of SWRO. Assuming an electricity price of 0.10 $ per kWh, reducing the total energy consumption of SWRO from 3.8 kWh to 3.5 kWh would result in a cost savings of about 0.03 $ per m3.
When it comes to capital costs, our analysis allows us to posit certain qualitative trends. According to Global Water Intelligence, the levelized capital cost for a typical 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 day−1 SWRO plant today is about 0.20 $ per m3 (excluding land), and 20% of this cost is due to membranes, pressure vessels and piping.33 Thus, if UPMs were to cost the same per unit area as current membranes and if they were to reduce the number of required pressure vessels by 44% thanks to a tripling in water permeability, the membranes would save on the order of 0.02 $ per m3 in capital costs. For this estimate, we assume that the portion of capital costs due to membranes, pressure vessels and piping scales linearly with the number of pressure vessels and that the remainder of the capital cost (including intake, pretreatment, pumps, etc.) is unaffected by the number of pressure vessels. As a fraction of the overall cost of SWRO, the energy or pressure vessel savings are relatively small: they would only reduce the overall cost of SWRO by about 3–4%. Returning to our starting hypothesis, this implies that a tripling in membrane permeability would result in significant performance improvements at the RO stage but with cost savings that only range in the single digits for SWRO. Applications of SWRO that are space-constrained (e.g., ship-board systems) might also find a 44% reduction in pressure vessels attractive from the perspective of a reduced physical footprint.
000 m3 day−1 SWRO plant today is about 0.20 $ per m3 (excluding land), and 20% of this cost is due to membranes, pressure vessels and piping.33 Thus, if UPMs were to cost the same per unit area as current membranes and if they were to reduce the number of required pressure vessels by 44% thanks to a tripling in water permeability, the membranes would save on the order of 0.02 $ per m3 in capital costs. For this estimate, we assume that the portion of capital costs due to membranes, pressure vessels and piping scales linearly with the number of pressure vessels and that the remainder of the capital cost (including intake, pretreatment, pumps, etc.) is unaffected by the number of pressure vessels. As a fraction of the overall cost of SWRO, the energy or pressure vessel savings are relatively small: they would only reduce the overall cost of SWRO by about 3–4%. Returning to our starting hypothesis, this implies that a tripling in membrane permeability would result in significant performance improvements at the RO stage but with cost savings that only range in the single digits for SWRO. Applications of SWRO that are space-constrained (e.g., ship-board systems) might also find a 44% reduction in pressure vessels attractive from the perspective of a reduced physical footprint.
The benefits are more significant for BWRO. We found that BWRO systems would see a 46% reduction in energy consumption using UPMs. This is because the energy consumption in existing BWRO plants is typically much greater today than would be strictly required by thermodynamics since economics favor maximizing recovery and minimizing plant size at the expense of suboptimal energy consumption.34 Thus, UPMs could reduce the energy footprint of BWRO while keeping capital costs and permeate recovery unchanged. Moreover, we also found that BWRO plants using UPMs could alternatively benefit from 63% fewer pressure vessels for a given plant capacity, which would allow for more compact plants with identical pretreatment, posttreatment, pumps and ancillary processes but with proportionally smaller capital expenses for pressure vessels, membranes and piping. Given the same assumptions as in the SWRO case above,35 BWRO plants with lower inlet pressure and BWRO plants with fewer vessels would both save around 0.03 $ per m3 (9% of costs). Thus, UPMs are projected to have a greater impact on the cost of BWRO than of SWRO.
We note that throughout this paper, we kept the membrane's salt rejection fixed at 99.8% in order to properly investigate the effect of water permeability in isolation from the separate issue of salt rejection performance and fouling potential. We restricted the scope of this paper to steady-state desalination without time-dependent effects such as gradual fouling or mineral scaling on the membrane surface, because fouling resistance represents a qualitatively different axis for membrane improvement than high permeability.
5 Conclusion
We have shown that the development of ultra-permeable membranes could help to reduce the energy consumption and the pressure vessel requirements of RO desalination. However, the benefits of UPMs for reducing energy consumption are limited to ∼15% in the case of SWRO. We also showed that membranes with 3× higher permeability could in principle reduce the number of pressure vessels by 44% for seawater RO plants and 63% in brackish water RO plants without affecting energy consumption or permeate recovery. Such membranes could also reduce the energy consumption of SWRO and BWRO by 15% and 46% respectively at the same permeate production per vessel as is typical today.For even greater permeabilities beyond 3–4.5 L (m2 h bar)−1, the incremental energy savings become negligible but capital requirements could continue to decrease thanks to fewer pressure vessels. Despite concerns expressed in the literature, we find that concentration polarization does not nullify the benefits of UPMs, although it does mitigate them relative to what would be expected in the absence of CP. As membrane permeability increases, so too will typical cross-flow velocities and mass transfer coefficients, and permeate flux will increase monotonically – although less than linearly – with membrane permeability. Although novel system designs may be required to fully take advantage of greatly increased feed flowrates, our results suggest that advances in membrane science will continue to make desalination increasingly competitive as an option for fresh water supply in coming decades.
Acknowledgements
We thank Rick Stover, Erik Nottleson, Eric Lam, IDE Technologies and Dianne Wiley for discussions, Felice Frankel for sharing visual communication insights and Jason Hill for helping with graphic design. Funding for this work came from the NSF Graduate Research Fellowship Program, the MIT Energy Initiative Seed Grant Program, the Fulbright International Science and Technology Award Program, the International Desalination Association, the Channabasappa Memorial Scholarship, the MIT Martin Family Sustainability Fellowship Program and a generous gift by the Douglas C. Spreng Fund.References
- F. Devoto, E. Duflo, P. Dupas, W. Pariente and V. Pons, National Bureau of Economic Research, Working Paper 16933, 2011.
- R. Baker, Membrane Technology and Applications, Wiley, 2nd edn, 2004 Search PubMed.
- N. Voutchkov, IDA conference, November, 2010, pp. 2–3 Search PubMed.
- J. MacHarg and T. Seacord, Desalination & Water Reuse, 2008 Search PubMed.
- P. Dickie, WWF, 2007.
- A. Gorenflo, J. A. Redondo and F. Reverberi, Desalination, 2005, 178, 247–260 CrossRef CAS PubMed.
- L. Addams, G. Boccaletti, M. Kerlin and M. Stuchtey, Charting Our Water Future: Economic Frameworks to Inform Decision-making, W. R. Group and McKinsey and Company, 2009 Search PubMed.
- S. T. Oyama and S. M. Stagg-Williams, Inorganic, Polymeric and Composite Membranes, Elsevier, 2011 Search PubMed.
- S. C. O'Hern, C. A. Stewart, M. S. H. Boutilier, J.-C. Idrobo, S. Bhaviripudi, S. K. Das, J. Kong, T. Laoui, M. Atieh and R. Karnik, ACS Nano, 2012, 6, 10130–10138 CrossRef CAS PubMed.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- F. Fornasiero, H. G. Park, J. K. Holt, M. Stadermann, C. P. Grigoropoulos, A. Noy and O. Bakajin, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17250–17255 CrossRef CAS PubMed.
- H. Y. Yang, Z. J. Han, S. F. Yu, K. L. Pey, K. Ostrikov and R. Karnik, Nat. Commun., 2013, 4, 2220 Search PubMed.
- C. Y. Tang, Y. Zhao, R. Wang, C. Hélix-Nielsen and A. G. Fane, Desalination, 2013, 308, 34–40 CrossRef CAS PubMed.
- S. Lin and M. J. Buehler, Nanoscale, 2013, 5, 11801–11807 RSC.
- K. P. Lee, T. C. Arnot and D. Mattia, Science, 2011, 370, 1–22 CAS.
- L. Song, J. Y. Hu, S. L. Ong, W. J. Ng, M. Elimelech and M. Wilf, J. Membr. Sci., 2003, 214, 239–244 CrossRef CAS.
- A. Zhu, A. Rahardianto, P. D. Christofides and Y. Cohen, Desalin. Water Treat., 2010, 15, 256–266 CrossRef CAS.
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CrossRef CAS PubMed.
- Z. Dorsey, WateReuse Association Desalination Committee, 2011.
- J. Johnson and M. Busch, Desalin. Water Treat., 2010, 15, 236–248 CrossRef.
- Dow Water Process Solutions, http://www.dowwaterandprocess.com.
- B. Sessions, W.-Y. Shih, J. MacHarg, S. Dundorf and J. A. Arroyo, Texas Water Development Board, Report 0804830845, 2011.
- D. Konatham, J. Yu, T. A. Ho and A. Striolo, Langmuir, 2013, 29, 11884–11897 CrossRef CAS PubMed.
- S. S. Sablani, M. Goosen, R. Al-Belushi and M. Wilf, Desalination, 2001, 141, 269–289 CrossRef CAS.
- K. Spiegler and O. Kedem, Desalination, 1966, 1, 311–326 CrossRef CAS.
- P. Brian, Ind. Eng. Chem. Fundam., 1965, 4, 439–445 CAS.
- E. Hoek, A. S. Kim and M. Elimelech, Environ. Eng. Sci., 2002, 19, 357–372 CrossRef CAS.
- A. Zhu, P. D. Christofides and Y. Cohen, J. Am. Chem. Soc., 2009, 48, 6010–6021 CAS.
- K. H. Mistry, R. K. McGovern, G. P. Thiel, E. K. Summers, S. M. Zubair and J. H. Lienhard, Entropy, 2011, 13, 1829–1864 CrossRef CAS.
- M. E. Williams, A review of reverse osmosis theory, 2003 Search PubMed.
- J. C. van Dijk, Drinking water treatment technology, 2007 Search PubMed.
- C. Bartels, R. Franks and K. Andes, Singapore International Water Week, Singapore, 2010 Search PubMed.
- http://www.Desaldata.com, Global Water Intelligence, 2013 Search PubMed.
- F. Banat, From Red Sea to Dead Sea – Water and Energy Conference, Geneva, 2007 Search PubMed.
- Z. Amjad, Reverse osmosis, Chapman & Hall, 1993 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details regarding RO dynamics and methods employed in this work. See DOI: 10.1039/c3ee43221a |
| This journal is © The Royal Society of Chemistry 2014 |