Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental and computational studies on the formation of cyanate from early metal terminal nitrido ligands and carbon monoxide†
Anthony F.
Cozzolino
,
Jared S.
Silvia
,
Nazario
Lopez
and
Christopher C.
Cummins
*
Department of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA. E-mail: ccummins@mit.edu
First published on 3rd February 2014
Abstract
An important challenge in the artificial fixation of N2 is to find atom efficient transformations that yield value-added products. Here we explore the coordination complex mediated conversion of ubiquitous species, CO and N2, into isocyanate. We have conceptually split the process into three steps: (1) the six-electron splitting of dinitrogen into terminal metal nitrido ligands, (2) the reduction of the complex by two electrons with CO to form an isocyanate linkage, and (3) the one electron reduction of the metal isocyanate complex to regenerate the starting metal complex and release the product. These steps are explored separately in an attempt to understand the limitations of each step and what is required of a coordination complex in order to facilitate a catalytic cycle. The possibility of this cyanate cycle was explored with both Mo and V complexes which have previously been shown to perform select steps in the sequence. Experimental results demonstrate the feasibility of some of the steps and DFT calculations suggest that, although the reduction of the terminal metal nitride complex by carbon monoxide should be thermodynamically favorable, there is a large kinetic barrier associated with the change in spin state which can be avoided in the case of the V complexes by an initial binding of the CO to the metal center followed by rearrangement. This mandates certain minimal design principles for the metal complex: the metal center should be sterically accessible for CO binding and the ligands should not readily succumb to CO insertion reactions.
Introduction
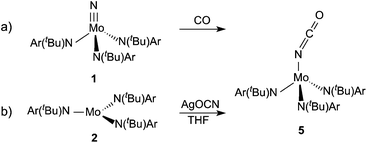
The fixation of N2 directly into value added chemicals is an exciting, yet challenging problem. Recently, we reported the transfer of an N2-derived terminal nitrido ligand, N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mo(N[tBu]Ar)3 (1, Ar = 3,5-Me2C6H3), into organic nitriles with concomitant regeneration of the starting material, Mo(N[tBu]Ar)3 (2).1 In a related approach, the terminal nitride ligand in 1 was converted to cyanide, where the carbon atom source was the methylene carbon of methoxymethyl chloride.2 While both of these studies demonstrated the functionalization of N2 derived N, neither represents a particularly atom-efficient set of transformations. A more appealing transformation is depicted in Fig. 1: the reduction of an N2-derived metal nitride (Fig. 1, Step 1, a six electron process) by carbon monoxide, which acts as a two electron reductant, to produce an isocyanate linkage (Fig. 1, Step 2) that, in turn, can be reduced off the metal center with input of one electron (Fig. 1, Step 3) to give the overall reaction presented in eqn (1). Ideally, this transformation can be driven either electrochemically or chemically as illustrated in eqn (1) or (2). Here it can be seen that the formation of the salt is much more enthalpically favorable than the formation of isocyanic acid, however the formation of the isocyanic acid is thermodynamically spontaneous in the gas phase at 298.15 K.
Mo(N[tBu]Ar)3 (1, Ar = 3,5-Me2C6H3), into organic nitriles with concomitant regeneration of the starting material, Mo(N[tBu]Ar)3 (2).1 In a related approach, the terminal nitride ligand in 1 was converted to cyanide, where the carbon atom source was the methylene carbon of methoxymethyl chloride.2 While both of these studies demonstrated the functionalization of N2 derived N, neither represents a particularly atom-efficient set of transformations. A more appealing transformation is depicted in Fig. 1: the reduction of an N2-derived metal nitride (Fig. 1, Step 1, a six electron process) by carbon monoxide, which acts as a two electron reductant, to produce an isocyanate linkage (Fig. 1, Step 2) that, in turn, can be reduced off the metal center with input of one electron (Fig. 1, Step 3) to give the overall reaction presented in eqn (1). Ideally, this transformation can be driven either electrochemically or chemically as illustrated in eqn (1) or (2). Here it can be seen that the formation of the salt is much more enthalpically favorable than the formation of isocyanic acid, however the formation of the isocyanic acid is thermodynamically spontaneous in the gas phase at 298.15 K.| CO + 1/2N2 + e− → OCN− | (1) |
K(s) + CO(g) + 1/2N2(g) → KOCN(s) ΔH0 = −73.4 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,4 3,4 | (2) |
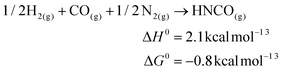 | (3) |
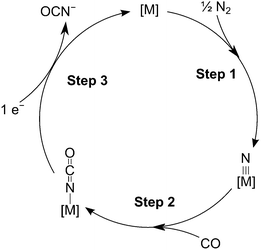 | ||
| Fig. 1 Proposed reaction cycle for coordination complex [M] mediated isocyanate formation from CO, N2 and an electron source. | ||
Isocyanate salts, specifically the sodium and potassium salts are of commercial importance. Collectively, the worldwide demand for cyanate salts is 8000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tonnes per annum.5 The salts are prepared industrially through the treatment of sodium carbonate with urea, effectively requiring two moles of NH3 for each mole of cyanate that is produced, and takes place at temperatures in excess of 400 °C.5 The cyanate salts find application from steel hardening to fine chemical and pharmaceutical synthesis, and are still used in the agrochemical industry in developing nations where there is an increase in new production.5
000 tonnes per annum.5 The salts are prepared industrially through the treatment of sodium carbonate with urea, effectively requiring two moles of NH3 for each mole of cyanate that is produced, and takes place at temperatures in excess of 400 °C.5 The cyanate salts find application from steel hardening to fine chemical and pharmaceutical synthesis, and are still used in the agrochemical industry in developing nations where there is an increase in new production.5
Evidence for Step 2 from the cycle in Fig. 1 has been observed with two different terminal vanadium nitrides, [N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) V(N[tBu]Ar)3]− (3)6 and N
V(N[tBu]Ar)3]− (3)6 and N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) V(nacnac)(N[p-tol]2) (4, nacnac = Ar′NC(CH3)CHC(CH3)NAr′), Ar′ = 2,6-iPr2C6H3).7 In the case of 3, the isocyanate is spontaneously lost as the cyanate salt liberating V(N[tBu]Ar)3 (Fig. 2a). In the case of 4, the isocyanate complex is cleanly formed, but Step 3, the reduction of the complex to liberate the isocyanate, was not demonstrated (Fig. 2b). A third example of Step 2, which remains a relatively rare transformation, involves the reduction of a ruthenium bound nitrido ligand to an isocyanate accompanied by addition of a carbonyl ligand (Fig. 2c).8 An additional example has a molybdenum(II) dicarbonyl form an isocyanate concomitant with N2O cleavage.9 In all these examples, however, the nitrogen source is an azide or N2O. Two examples of (μ2,η1,η2-N2)Hf2 complexes show N2 cleavage that is facilitated by reduction with CO to form an equivalent of isocyanate for each mole of N2 (Fig. 2d).10,11 We were, therefore, curious if a similar transformation could be realized with dinitrogen-derived metal nitride ligands. This would entail either starting from a system that is already known to cleave dinitrogen, or preparing a new system capable of all three steps.
V(nacnac)(N[p-tol]2) (4, nacnac = Ar′NC(CH3)CHC(CH3)NAr′), Ar′ = 2,6-iPr2C6H3).7 In the case of 3, the isocyanate is spontaneously lost as the cyanate salt liberating V(N[tBu]Ar)3 (Fig. 2a). In the case of 4, the isocyanate complex is cleanly formed, but Step 3, the reduction of the complex to liberate the isocyanate, was not demonstrated (Fig. 2b). A third example of Step 2, which remains a relatively rare transformation, involves the reduction of a ruthenium bound nitrido ligand to an isocyanate accompanied by addition of a carbonyl ligand (Fig. 2c).8 An additional example has a molybdenum(II) dicarbonyl form an isocyanate concomitant with N2O cleavage.9 In all these examples, however, the nitrogen source is an azide or N2O. Two examples of (μ2,η1,η2-N2)Hf2 complexes show N2 cleavage that is facilitated by reduction with CO to form an equivalent of isocyanate for each mole of N2 (Fig. 2d).10,11 We were, therefore, curious if a similar transformation could be realized with dinitrogen-derived metal nitride ligands. This would entail either starting from a system that is already known to cleave dinitrogen, or preparing a new system capable of all three steps.
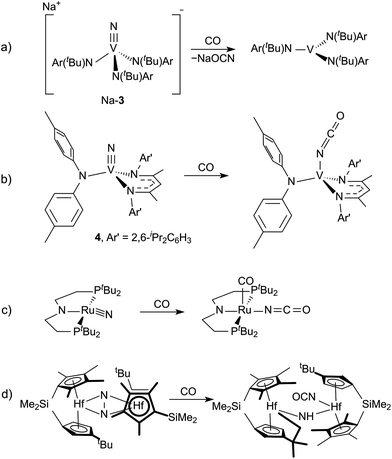 | ||
| Fig. 2 Examples of isocyanate formation from the reduction of N2-derived complexes by CO.6–8,11 | ||
The present work outlines our efforts towards the formation of an isocyanate moiety from the direct reduction of early transition metal (Mo or V) nitrido complexes with carbon monoxide. Initially, the reduction of a dinitrogen-derived molybdenum(VI) nitride containing complex (1) by CO is explored under a variety of experimental conditions. DFT calculations are used to find molybdenum(VI) nitride complexes (9 and 11) with more favorable enthalpies for reduction by CO. Driven by a further lack of observed reactivity, a related vanadium(II) complex (13) is prepared for the purpose of six electron reduction of dinitrogen, with the expectation of a more reactive nitrido ligand. Characterization data are presented for a bimetallic dinitrogen complex of the new vanadium system (14). DFT calculations are presented with the aim of elucidating the differences in CO reactivity between 1 and an isoelectronic vanadium complex (4) by way of acquiring design principles for future studies of this nature. Finally, the characterization of the independently synthesized thermochromic OCN–Mo(N[tBu]Ar)3 (5) is presented and the origin of the phenomenon elucidated.
Results and discussion
Treatment of N2-derived 1 with CO
We first probed the possibility of the direct conversion of a terminal nitride ligand to an isocyanate ligand by carbon monoxide treatment with 1 (Scheme 1a); the latter is obtained directly from the facile cleavage of dinitrogen by 2.12 The treatment of 1 with carbon monoxide was screened under a variety of conditions including: 1 and 14 atm CO over 1 dissolved in pentane or THF, under reducing (Na{Hg}) conditions, and under UV (254 and 300 nm) irradiation. Isocyanate formation was monitored by IR absorbance; an OCN stretching frequency of 2225 cm−1 was monitored as determined by independent synthesis of the desired product (see below). None of the above reaction conditions led to the appearance of a band that could be assigned to isocyanate formation and no changes were observed by 1H NMR spectroscopy. In light of the recent results demonstrating CO assisted N2 cleavage with Me2Si(η5-C5Me4)(η5-C5H3-3-tBu)Hf,11,13 the bridging dinitrogen complex (μ-N2)[Mo(N[tBu]Ar)3]2 (6)14 was also treated with CO, however only the previously reported carbonyl complex OC–Mo(N[tBu]Ar)3 was observed in the reaction mixture.15DFT calculations were performed on a model system, N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mo(NMe2)3 (1-mod),16 in order to estimate the thermodynamic driving force for eqn (4) starting from nitride 1. The calculated entropy for eqn (4), corrected for the basis set superposition error (BSSE, ∼1 kcal mol−1), is 0.5 kcal mol−1 and the Gibbs free energy at 298.15 K is 11.5 kcal mol−1 with a GGA only functional (PW91)17 and ΔH298.15 = −8.8 kcal mol−1 and ΔG298.15 = 5.3 kcal mol−1 when exchange is included using a hybrid functional (B3PW: exchange B88,18 correlation PW91,17 30% HF19). The electronic energy calculated for eqn (4) using the full model of 1 is −8.6 kcal mol−1 (PW91) which is more favorable than for the model 1-mod (0.1 kcal mol−1, PW91). Accordingly, low temperatures and high CO pressures should favor the formation of isocyanate complex 5.
Mo(NMe2)3 (1-mod),16 in order to estimate the thermodynamic driving force for eqn (4) starting from nitride 1. The calculated entropy for eqn (4), corrected for the basis set superposition error (BSSE, ∼1 kcal mol−1), is 0.5 kcal mol−1 and the Gibbs free energy at 298.15 K is 11.5 kcal mol−1 with a GGA only functional (PW91)17 and ΔH298.15 = −8.8 kcal mol−1 and ΔG298.15 = 5.3 kcal mol−1 when exchange is included using a hybrid functional (B3PW: exchange B88,18 correlation PW91,17 30% HF19). The electronic energy calculated for eqn (4) using the full model of 1 is −8.6 kcal mol−1 (PW91) which is more favorable than for the model 1-mod (0.1 kcal mol−1, PW91). Accordingly, low temperatures and high CO pressures should favor the formation of isocyanate complex 5.
N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) [M] + CO → OCN–[M] [M] + CO → OCN–[M] | (4) |
Preparation and characterization of OCNMo(N[tBu]Ar)3, 5
In order to determine if 5 is stable towards CO loss and establish the precise spectral signatures of 5, a sample of 5 was independently prepared by the treatment of 2 with a stoichiometric amount of AgOCN in THF (Scheme 1b). Following filtration and solvent removal, the product was isolated in 77% yield as analytically pure crystals grown from diethyl ether–pentane solutions at −35 °C. 1H NMR spectroscopy in C6D6 revealed four broad resonances ranging from 28 to −10 ppm. Evans method solution magnetic susceptibility measurements gave a μeff of 2.33μB, which is lower than the spin-only value for an S = 1 system implying a degree of spin–orbit coupling. This value is lower than the magnetic susceptibility determined by variable-temperature SQUID magnetometry measurements (μeff of 2.66μB, see below), however differences between solution and the solid state such as this have been previously observed with Mo complexes in similar ligand fields.20,21 DFT calculations of the paramagnetic NMR shifts22,23 for triplet 5 are in good agreement (slope = 0.74, correlation (r2) = 0.997) with the observed resonances (Table 1). The assignments are further confirmed by linewidth calculations which correlated well (r2 = 0.999, slope = 0.57) with the experimental linewidths (Table 1) and indicate that the observed linewidths are dominated by the dipolar contribution—in other words the linewidths in this case are a function of the hydrogen atom distances from the metal center.23 The infrared spectrum of complex 5 displayed an intense absorbance at 2225 cm−1 that can be attributed to the isocyanate and is consistent with the calculated vibrational frequency (2266 cm−1).| Position | Experimental | DFT calculated |
|---|---|---|
| t Bu | 27.16 [80] | 36.2 [238] |
| MeAr | −2.20 [11] | −2.5 [46] |
| o-Ar | −2.90 [155] | −4.7 [421] |
| p-Ar | −7.84 [13] | −13.0 [50] |
Stability and reactivity of 5
To determine the thermal stability of isocyanate 5, a sample was sealed in a glass NMR tube and monitored by 1H NMR spectroscopy as a function of time. No change was observed after 144 h at 21 °C, however above 60 °C isobutylene formation could be observed after 8 h which is indicative of tert-butyl radical ejection, or cation ejection together with proton transfer, from one of the anilide ligands.21,24 At 90 °C the process was accelerated and complete depletion of 5 was observed within 5 h concomitant with the appearance of new products that were not characterized.The photolytic stability of isocyanate 5 was probed since the photolysis of metal azide complexes is an established route to prepare the metal nitride complexes.25,26 Furthermore, the reductive decarbonylation of a niobium isocyanate complex was shown to yield an anionic niobium nitride complex that is isoelectronic with 1.27 In benzene and borosilicate glass, a sample of 5 was irradiated for 12 h with broadband visible light with a maximum at 419 nm. Under these conditions only residual 5 and the products associated with thermal decomposition were observed as a result of the heating of the sample induced by the lamps. A sample in pentane and quartz, irradiated at 254 nm for 6 h, was found to slowly decarbonylate to produce 1 and CO in addition to the products of thermal degradation. While the formation of small amounts of 1 could be confirmed by 1H NMR spectroscopy, the formation of CO was confirmed by trapping the CO with Cp*RuCl(PCy3) to form Cp*RuCl(PCy3)(CO) and measuring the conversion by analyzing the 31P NMR spectrum as was previously reported.28 A conversion of only 3% was determined from this NMR experiment.
When treated with KC8 in THF under an Ar atmosphere, isocyanate 5 does not decarbonylate,6 but rather generates complex 2 and releases the cyanate anion. The potassium cyanate was quantified by recovering the pentane insoluble portion of the reaction mixture, dissolving it in water and precipitating the cyanate as AgOCN in 60% yield. The clean reduction of 5 represents an important step (Step 3) if the overall transformation envisioned in eqn (1) or (2) is to be realized.
During the manipulation of 5 it was noted that, upon cooling, solid samples of 5 underwent a reversible thermochromic transformation and the origin of this effect is described in detail in a later section.
Attempted preparation of 5 from 1 and oxalyl chloride
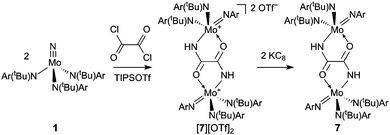
In an effort to realize the formation of isocyanate 5 from nitride 1via an alternative route, 1 was treated with 0.5 equivalents of oxalyl chloride in the presence of triisopropylsilyl triflate (TIPSOTf) (Scheme 2). The reaction proceeded upon warming in a dichloromethane solution. 1H NMR spectroscopy of the recovered product revealed the loss of a tert-butyl group and 19F NMR spectroscopy showed the presence of a triflate group. IR data were consistent with incorporation of the oxalyl group (vC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, 1613 cm−1) and also contained a new NH stretch at 3361 cm−1. Reduction of the material with KC8 in THF led to a dark blue, thermally sensitive solution. When the THF solution was stored at −35 °C no decomposition was observed and after 36 h a mixture of dark blue and colorless crystals had formed. The structure of the blue crystals was elucidated by X-ray diffraction and is shown in Fig. 3. The structure is consistent with the spectroscopic data for [7][OTf]2 with the exception of the triflate signal, which is absent as a result of loss of triflate as the coproduct KOTf upon reduction. The structure in Fig. 3 illustrates that the oxalyl moiety becomes incorporated into an oxamidide ligand which bridges the two Mo centers and is the twice-protonated variant of the ligand that is formed when either [Me2Si(η5-C5Me4)(η5-C5H3-3-tBu)Hf]2(μ2,η2,η2-N2) or [(η5-C5Me4H)2Hf]2(μ2,η2,η2-N2) is treated with two equivalents of CO.11,13 Additionally, one of the anilide ligands has been transformed to an imide ligand, presumably as a result of effective tert-butyl cation dissociation. The tert-butyl cation can serve as a proton source with concomitant formation of isobutene.21,24 In this case, the proton was located in the electron density difference map on the nitrogen of the oxamidide ligand, thereby completing the mass and charge balance.
O, 1613 cm−1) and also contained a new NH stretch at 3361 cm−1. Reduction of the material with KC8 in THF led to a dark blue, thermally sensitive solution. When the THF solution was stored at −35 °C no decomposition was observed and after 36 h a mixture of dark blue and colorless crystals had formed. The structure of the blue crystals was elucidated by X-ray diffraction and is shown in Fig. 3. The structure is consistent with the spectroscopic data for [7][OTf]2 with the exception of the triflate signal, which is absent as a result of loss of triflate as the coproduct KOTf upon reduction. The structure in Fig. 3 illustrates that the oxalyl moiety becomes incorporated into an oxamidide ligand which bridges the two Mo centers and is the twice-protonated variant of the ligand that is formed when either [Me2Si(η5-C5Me4)(η5-C5H3-3-tBu)Hf]2(μ2,η2,η2-N2) or [(η5-C5Me4H)2Hf]2(μ2,η2,η2-N2) is treated with two equivalents of CO.11,13 Additionally, one of the anilide ligands has been transformed to an imide ligand, presumably as a result of effective tert-butyl cation dissociation. The tert-butyl cation can serve as a proton source with concomitant formation of isobutene.21,24 In this case, the proton was located in the electron density difference map on the nitrogen of the oxamidide ligand, thereby completing the mass and charge balance.
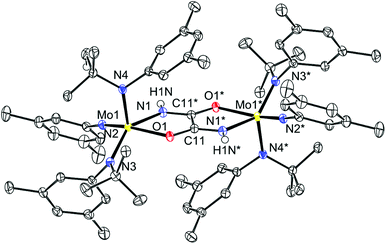 | ||
| Fig. 3 Thermal ellipsoid plot (50% probability) of 7 (where the two halves of the molecule are related by an inversion center) with modelled hydrogen atoms and all THF molecules omitted for clarity. | ||
Treatment of Mo![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) N containing complexes with CO
N containing complexes with CO
In an effort to make the reduction potential of the MoVI center more accessible, we employed an analogue with a more electronegative ligand set. The monofluorinated variant, Mo(N[R]ArF)3 (8, R = C(CD3)2CH3, ArF = 4-C6H4F), had been previously prepared and was known to cleave N2 to give the terminal nitride, N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mo(N[R]ArF)3 (9).16 DFT calculations predicted that the reduction of 9 by CO to give the isocyanate linkage (eqn (4)) should be more favorable than for nitride 1 by 22 kcal mol−1, enough to overcome the predicted entropy that was calculated with model complex 1-mod, 11.0 kcal mol−1 at 298.15 K. Cyclic voltammetry (Fig. S8†) showed an anodic shift in the reduction potential by 0.2 V. The treatment of nitride 9 with CO under the same set of conditions that were screened with 1, however, resulted in no discernable reaction.
Mo(N[R]ArF)3 (9).16 DFT calculations predicted that the reduction of 9 by CO to give the isocyanate linkage (eqn (4)) should be more favorable than for nitride 1 by 22 kcal mol−1, enough to overcome the predicted entropy that was calculated with model complex 1-mod, 11.0 kcal mol−1 at 298.15 K. Cyclic voltammetry (Fig. S8†) showed an anodic shift in the reduction potential by 0.2 V. The treatment of nitride 9 with CO under the same set of conditions that were screened with 1, however, resulted in no discernable reaction.
We had in hand a MoIV species, Cl2Mo(N[R]ArMeL)2 (10, R = C(CD3)2CH3, ArMeL = 2-NMe2-5-MeC6H3), that could potentially be treated with an azide source to yield a new terminal nitride. We postulated that the energetic cost of breaking the strong Mo![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond in the conversion of the terminal nitride to the isocyanate could be offset by the formation of a Mo–Naniline dative bond. DFT calculations were performed on the reaction of N(N3)Mo(N[R]ArMeL)2 (see below) with CO to give OCN(N3)Mo(N[R]ArMeL)2 according to eqn (4) which accordingly was estimated to be thermodynamically favorable by 21.2 kcal mol−1 according to the electronic energies. This is significantly more favorable than the conversion of nitride 1 to isocyanate 5 is predicted to be. In fact, this energy is more comparable to that calculated, using the same method, for Mindiola's recently reported reaction of the terminal V
N triple bond in the conversion of the terminal nitride to the isocyanate could be offset by the formation of a Mo–Naniline dative bond. DFT calculations were performed on the reaction of N(N3)Mo(N[R]ArMeL)2 (see below) with CO to give OCN(N3)Mo(N[R]ArMeL)2 according to eqn (4) which accordingly was estimated to be thermodynamically favorable by 21.2 kcal mol−1 according to the electronic energies. This is significantly more favorable than the conversion of nitride 1 to isocyanate 5 is predicted to be. In fact, this energy is more comparable to that calculated, using the same method, for Mindiola's recently reported reaction of the terminal V![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond in 4 with CO to form an isocyanate linkage (−41.9 kcal mol−1).7 With this motivation, we set about preparing such a terminal nitride.
N triple bond in 4 with CO to form an isocyanate linkage (−41.9 kcal mol−1).7 With this motivation, we set about preparing such a terminal nitride.
Compound 10 was prepared by treatment of MoCl3(THF)3 with LiN[R]ArMeL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 in Et2O with a 2
29 in Et2O with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometry. The initial MoIII center is oxidized over the course of reaction to MoIV. The source of the chlorine is presumably MoCl3(THF)3
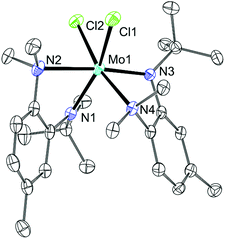
3 stoichiometry. The initial MoIII center is oxidized over the course of reaction to MoIV. The source of the chlorine is presumably MoCl3(THF)3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 which is present in excess under the optimized conditions. Recrystallization from Et2O gave an analytically pure material which had an Evans method magnetic susceptibility of μeff = 2.31 μB which is lower than the S = 1 spin-only value 2.83 μB. As in the case of 5, this value is anomalously low and is likely not representative of the actual g value. In the absence of variable temperature solid-state data, this value is taken as being indicative of a paramagnetic system as opposed to a thermally populated S = 0 system. Diffraction quality crystals were also obtained from Et2O and the asymmetric unit is shown in Fig. 4. The Mo center is six-coordinate with a pseudo-octahedral environment. The coordination sphere contains two Mo–Nanilide (2.009(2) and 2.033(2) Å), two Mo–Naniline (2.364(2) and 2.393(2) Å) and two Mo–Cl (2.3950(8) and 2.4216(8) Å) bonds arranged such that one Nanilide is trans to one Naniline and the other is trans to a Cl as represented in Fig. 4.
30 which is present in excess under the optimized conditions. Recrystallization from Et2O gave an analytically pure material which had an Evans method magnetic susceptibility of μeff = 2.31 μB which is lower than the S = 1 spin-only value 2.83 μB. As in the case of 5, this value is anomalously low and is likely not representative of the actual g value. In the absence of variable temperature solid-state data, this value is taken as being indicative of a paramagnetic system as opposed to a thermally populated S = 0 system. Diffraction quality crystals were also obtained from Et2O and the asymmetric unit is shown in Fig. 4. The Mo center is six-coordinate with a pseudo-octahedral environment. The coordination sphere contains two Mo–Nanilide (2.009(2) and 2.033(2) Å), two Mo–Naniline (2.364(2) and 2.393(2) Å) and two Mo–Cl (2.3950(8) and 2.4216(8) Å) bonds arranged such that one Nanilide is trans to one Naniline and the other is trans to a Cl as represented in Fig. 4.
Treatment of 10 with excess NaN3 resulted in the formation of a diamagnetic product with a single azide stretch (2061 cm−1) in the IR spectrum, formulated as N(N3)Mo(N[R]ArMeL)2 (11). Suitable crystals were grown from pentane and the crystal structure (Fig. 5) revealed the hemilabile nature of the amino-anilide ligand. Upon formation of the azide–nitride product, one of the XL-type ligands31 remains bidentate, while the other dissociates at the aniline-N leaving a pentacoordinate Mo center with a pseudo square-pyramidal geometry composed of one nitrido nitrogen (1.654(2) Å) two anilide nitrogens (2.011(2) and 2.036(2) Å), one azide nitrogen (2.119(2) Å) and one aniline nitrogen (2.362(2) Å). It is noteworthy that if reduction from MoVI to MoIV by CO can take place, then the cost of breaking the Mo![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond can be offset, not only by the formation of the stable isocyanate linkage, but also by the formation of the additional Mo–Naniline dative bond as observed in 10. Treatment of this new terminal nitride complex with CO did not, however, result in any reaction. In a following section, we turn to DFT in order to contrast the possible mechanistic differences between the terminal nitrides probed in this study and the neutral VV system, 4, that was previously shown to be successfully reduced by CO (Fig. 2b)7 in order to account for the lack of reaction in the above systems.
N triple bond can be offset, not only by the formation of the stable isocyanate linkage, but also by the formation of the additional Mo–Naniline dative bond as observed in 10. Treatment of this new terminal nitride complex with CO did not, however, result in any reaction. In a following section, we turn to DFT in order to contrast the possible mechanistic differences between the terminal nitrides probed in this study and the neutral VV system, 4, that was previously shown to be successfully reduced by CO (Fig. 2b)7 in order to account for the lack of reaction in the above systems.
Design of a new VII system for N2 activation
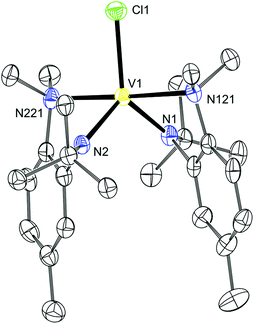
In the previous section, the reaction of CO with a MoVI nitride (Fig. 1, Step 2) was focused on due to the precedent for N2 cleavage by MoIII centers, specifically with 2 and 8.12 An alternative approach is to use systems in which the nitride-to-isocyanate transformation has more precedent. Since two of the examples of Step 2 involve a vanadium supported nitride,6,7 we sought to prepare a low-valent V complex with the requisite number of electrons such that two equivalents can reduce N2 by 6 electrons.32–35 There is precedent for N2 activation by low valent VII complexes included in the work from the groups of Gambarotta,32–34 Cloke,36 and Mindiola.35 A VII complex had been previously prepared in the Cummins group with a similar ligand set to [N[R]ArMeL],37 the N2 chemistry of which was not explored. We sought to prepare the related low valent vanadium complex supported by the monoanionic bidentate ligand [N[R]ArMeL]−.To prepare a pure material, a VIII species was first prepared which was subsequently reduced to the desired VII species. A sample of ClV(N[R]ArMeL)2 (12) was prepared by treating VCl3(THF)3 with two equivalents of the ligand in a frozen Et2O slurry. The purified material had a room temperature magnetic susceptibility, μeff, of 2.89 μB which compares well with the spin-only value of 2.83 μB for an S = 1 system.
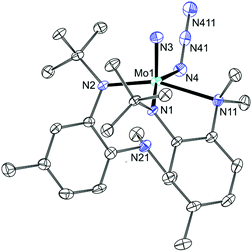
The desired product had paramagnetically broadened 1H and 2H NMR spectra which could be fully assigned with the aid of DFT calculations.22,23Table 2 shows the assignment of the 1H and 2H NMR spectra of 12. The strong correlation between the calculated and experimental values indicates that the relative distribution of unpaired electron density is correctly calculated by DFT in this case, although the non-unity slope would indicate that the absolute value of the unpaired electron density at each hydrogen is systematically in error. An X-ray diffraction quality crystal of 12 was grown from Et2O and the asymmetric unit is displayed in Fig. 6. Here it can be seen that the vanadium(III) ion is pentacoordinate with one Cl (2.338(1) Å), two Naniline (2.259(3) and 2.269(3) Å) and two Nanilide (1.944(3) 1.949(3) Å) atoms completing the coordination sphere.
| Position | 12 (Exp.) | 12 (DFT) | 13 (Exp.) | 13 (DFT) |
|---|---|---|---|---|
| t Bu | 9.15 | 10.32 | 38 | 61 |
| NMe2 | −5.16 | −7.26 | 68/105 | 100/193 |
| MeAr | 4.71 | 3.99 | 1.62 | 0.59 |
| H(3-Ar) | −10.83 | −25.67 | −11.1 | −12.6 |
| H(5-Ar) | −17.32 | −31.49 | −14.8 | −18.3 |
| H(6-Ar) | 0.98 | −6.20 | 13.1 | 8.2 |
| Correlation (r2) | 0.96 | 0.98 | ||
| Slope | 0.60 | 0.57 |
Ultimately, the desired product, 13, could be obtained in pure form upon sodium amalgam reduction of 12. It should be noted that the product can also be obtained using Na and catalytic amounts of naphthalene in THF. Evans method room temperature magnetic susceptibility measurements of 13 revealed a susceptibility that was lower than the spin-only value (3.55 vs. 3.87 μB for S = 3/2). Again, the proton NMR resonances could be confidently assigned by correlating their chemical shifts with the DFT predicted resonances. Here the two aniline methyl groups are inequivalent, unlike in 12, an observation which suggests a tighter binding of the bidentate ligand.
Initial attempts to prepare 13 involved the treatment of the VII salt VCl2(TMEDA)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 with two equivalents of LiN[R]ArMeL in Et2O. 2H NMR spectroscopy revealed the presence of a single paramagnetic species in the mixture that could be crystallized out as diffraction quality crystals. Single crystal analysis revealed that the desired product, V(N[R]ArMeL)2 (13) had cocrystallized with half of an equivalent of the starting material (Fig. 7). The crystal structure of 13 (from 13·1/2
38 with two equivalents of LiN[R]ArMeL in Et2O. 2H NMR spectroscopy revealed the presence of a single paramagnetic species in the mixture that could be crystallized out as diffraction quality crystals. Single crystal analysis revealed that the desired product, V(N[R]ArMeL)2 (13) had cocrystallized with half of an equivalent of the starting material (Fig. 7). The crystal structure of 13 (from 13·1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VCl2(TMEDA)2, Fig. 7) reveals a pseudotetrahedral coordination environment with inequivalent V–N distances (2.028(2)/2.032(2) or 2.218(2)/2.200(2) Å for Nanilide or Naniline, respectively). These values are slightly shorter and longer, respectively, than the distances determined for 12. The angle between the N2V planes is 68.68(5)° which is much more acute than in an idealized tetrahedral geometry (90°) and reflects the restraint imposed by the acute bite angle (∼78°) of the ortho-aminoanilide ligand.
VCl2(TMEDA)2, Fig. 7) reveals a pseudotetrahedral coordination environment with inequivalent V–N distances (2.028(2)/2.032(2) or 2.218(2)/2.200(2) Å for Nanilide or Naniline, respectively). These values are slightly shorter and longer, respectively, than the distances determined for 12. The angle between the N2V planes is 68.68(5)° which is much more acute than in an idealized tetrahedral geometry (90°) and reflects the restraint imposed by the acute bite angle (∼78°) of the ortho-aminoanilide ligand.
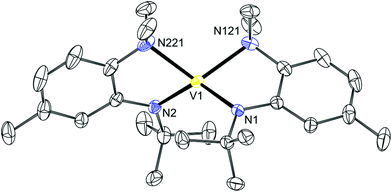 | ||
| Fig. 7 Thermal ellipsoid plot (50% probability) of 13 with hydrogen atoms, solvent of crystallization and disordered VCl2(TMEDA)2 omitted for clarity. | ||
Although the reactions to produce 13 were initially performed under Ar, no reaction with N2 was observed, even under elevated pressures (up to 14 atm) or in the presence of a reducing agent such as KC8. There is precedent for heterobimetallic N2 activation and in some cases N2 cleavage when 2 is employed as a co-reagent.39–41 An immediate color change was observed when a solution of 13 was treated with a solution of 2 under an atmosphere of N2. It has been proposed that the formation of a reduced 2 (“2−”) leads to the facile reaction of 2 with N2 as evidenced by the reaction of 2 with N2 in the presence of Na.39 It is conceivable that a similar phenomenon is occurring here. 1H and 2H NMR studies revealed a new series of paramagnetically broadened resonances and an Evans method magnetic susceptibility measurement revealed a room temperature susceptibility of 2.81 μB for the structural formula (Ar[tBu]N)3Mo(μ-N2)V(N[R]ArMeL)2 (14) (cf. 2.83 μB for spin-only S = 1). Prolonged drying under vacuum at room temperature resulted in loss of N2. Crystallization from tetramethylsilane (TMS) yielded a solid sample of the desired material. The difficulties in manipulating this material, related to easy loss of N2 and general sensitivity, resulted in only a reasonable elemental analysis of 14 (0.95% error in hydrogen). The infrared absorption spectrum of 14 features a band at 1646 cm−1 that is not present in the infrared absorption spectra of either 2 or 13, and which we tentatively assign to the vN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching mode. This frequency lies between that of [(N2)Mo(N[tBu]Ar)3]− (1761 cm−1)39 and those of the heterobimetallic systems (Ar[tBu]N)3Mo(μ-N2)Nb(N[Np]Ar)3 (1564 cm−1, Np = neopentyl),40 (Ar[tBu]N)3Mo(μ-N2)Ti(N[tBu]Ar)3 (1575 cm−1)39 and (Ar[1-Ad]N)3Mo(μ-N2)U(N[tBu]Ar)3 (1568 cm−1, 1-Ad = 1-adamantyl),41 and it is on par with (Ar[tBu]N)3Mo(μ-N2)SiMe3 (1650 cm−1)39 and (μ-N2)[Mo(N[tBu]Ar)3]2 (1630 cm−1).20
N stretching mode. This frequency lies between that of [(N2)Mo(N[tBu]Ar)3]− (1761 cm−1)39 and those of the heterobimetallic systems (Ar[tBu]N)3Mo(μ-N2)Nb(N[Np]Ar)3 (1564 cm−1, Np = neopentyl),40 (Ar[tBu]N)3Mo(μ-N2)Ti(N[tBu]Ar)3 (1575 cm−1)39 and (Ar[1-Ad]N)3Mo(μ-N2)U(N[tBu]Ar)3 (1568 cm−1, 1-Ad = 1-adamantyl),41 and it is on par with (Ar[tBu]N)3Mo(μ-N2)SiMe3 (1650 cm−1)39 and (μ-N2)[Mo(N[tBu]Ar)3]2 (1630 cm−1).20
The single crystal structure of 14 was obtained from crystals grown in tetramethylsilane. The structure, which is shown in Fig. 8, confirms the bimetallic bridging-N2 nature of the complex. The Mo–N bond is 1.802(3) Å and is shorter than the Mo–N interatomic distance in both [(N2)Mo(N[tBu]Ar)3]− and (μ-N2)[Mo(N[tBu]Ar)3]2 (1.84(1) and 1.868(1) Å, respectively),39 but longer than those in (Ar[tBu]N)3Mo(μ-N2)SiMe3 (1.753(2) Å) and (Ar[tBu]N)3Mo(μ-N2)Ti(N[tBu]Ar)3 (1.787(3) Å).39 The N–N bond is longer than in [(N2)Mo(N[tBu]Ar)3]− (1.210(5) vs. 1.17(1) Å) which is consistent with the lower energy vibrational mode in 14 that is indicative of a weaker bond. Despite the apparent degree of N2 activation, and the presence of the requisite number of electrons for N2 cleavage, neither thermal nor photochemical cleavage14,42 could be realized. Heating a toluene solution of 14 to 90 °C or irradiating a pentane solution with an emission maximum of 254 nm or with an emission maximum of 419 nm both resulted in the loss of N2 and liberation of the starting complexes 2 and 13. Furthermore, treatment of 14 with the strong reductant KC8 resulted in the liberation of 13 and the generation of K[(N2)Mo(N[tBu]Ar)3]. In an effort to access the desired isocyanate directly, 14 was treated with excess CO, resulting in the displacement of N2; here the product of the reaction of tricoordinate molybdenum complex 2 with CO can be observed by 1H NMR spectroscopy.15
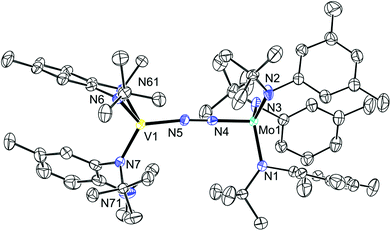 | ||
| Fig. 8 Thermal ellipsoid plot (50% probability) of 14 with hydrogen atoms and minor disordered component omitted for clarity. | ||
DFT investigations of step 2
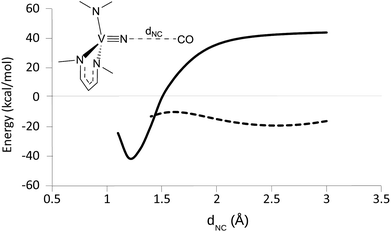
In order to probe the mechanism of CO reduction of 1 to give 5, a potential energy surface (PES) was constructed where the NC distance (dNC) was varied in both the triplet and the singlet state (Fig. 9). In order to accomplish this in a computationally efficient manner, the aryl and tBu groups of 1 were replaced with methyl groups (N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mo(NMe2)3, 1-mod). The overall reaction electronic energy difference was slightly less favorable with this substitution than with the full ligand set (see Table 3). The singlet and triplet surfaces crossed in the vicinity of 1.4 Å, the triplet being more stable at shorter distances and the singlet at longer distances (Fig. 9). A minimum energy crossing point calculation was attempted in order to determine the crossing point of the two surfaces, but no solution was obtained. Instead, the barrier to the reaction was estimated to be 19 kcal mol−1 from the crossing point on the PESs. In an attempt to obtain the same set of surfaces for a truncated model of 4, N
Mo(NMe2)3, 1-mod). The overall reaction electronic energy difference was slightly less favorable with this substitution than with the full ligand set (see Table 3). The singlet and triplet surfaces crossed in the vicinity of 1.4 Å, the triplet being more stable at shorter distances and the singlet at longer distances (Fig. 9). A minimum energy crossing point calculation was attempted in order to determine the crossing point of the two surfaces, but no solution was obtained. Instead, the barrier to the reaction was estimated to be 19 kcal mol−1 from the crossing point on the PESs. In an attempt to obtain the same set of surfaces for a truncated model of 4, N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) V(nacnac′)(NMe2) (4-mod, nacnac′ = MeN(CH)3NMe), it was found that while the triplet surface followed the same general trend, the singlet surface appeared to be negative at all points up to and including the singlet/triplet surface crossing (Fig. 10).
V(nacnac′)(NMe2) (4-mod, nacnac′ = MeN(CH)3NMe), it was found that while the triplet surface followed the same general trend, the singlet surface appeared to be negative at all points up to and including the singlet/triplet surface crossing (Fig. 10).
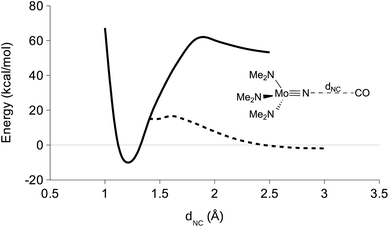 | ||
| Fig. 9 DFT derived triplet (solid line) and singlet (hashed line) PES for varying the NC distance in CO + nitride 1-mod. Only the parameter (dNC) was fixed. | ||
 | ||
| Fig. 10 DFT derived triplet (solid line) and singlet (hashed line) PES for varying the NC distance in CO + nitride 4-mod. Only the parameter (dNC) was fixed. | ||
| Nitrido complex | ΔE | ΔH298.15 | ΔS298.15 | ΔG298.15 |
|---|---|---|---|---|
| 1 [Mo] | −8.6 | |||
| 9 [Mo] | −30.7 | |||
| 1-mod [Mo] | 0.1 | −0.5 | −11.0 | 11.5 |
| 11 [Mo] | −24.3 | |||
| 4 [V] | −41.9 | |||
| 4-mod [V] | −39.2 | −38.8 | −11.0 | −26.8 |
Inspection of the geometries at various points reveals that the CO molecule favorably binds to the V center as a first step in the reaction.7 An isomerization to the isocyanate ensues with an activation energy of 10.9 kcal mol−1, estimated from the singlet PES, before crossing onto the triplet surface of the final product. Interestingly, a similar pathway was proposed for the extrusion of N2 from the azido precursor to 4, analogous to the reverse of this reaction.7 This analysis suggests that a thermodynamic driving force is insufficient for the forward reaction to take place and that an accessible metal site might be key to reducing the activation barrier for the formation of the isocyanate in these cases. From a practical point of view, caution must be used when choosing a ligand to support this type of unsaturated metal site because CO insertion into the metal–ligand bonds can easily become a competitive reaction.43
Thermochromism of solid-state 5
During the manipulation of 5 it was noted that upon cooling, solid samples underwent a reversible thermochromic transformation as shown in Fig. 11. In order to determine the origin of this property a variety of variable temperature studies were performed. SQUID magnetometry was performed to determine if the thermochromism was the result of a change in spin state (triplet to singlet). The data, shown in Fig. 12, were collected at two different field strengths. Although no change in magnetic behavior was observed in the temperature regime where the thermochromism was observed, a decay in magnetic moment was observed below 50 K attributable to either antiferromagnetic coupling between two metal centers or to a zero-field splitting (ZFS). The data were fit to an S = 1 spin Hamiltonian for a single metal center (see Fig. 12) from which the following parameters were extracted: g = 1.88 cm−1 and D = 37 cm−1. A ZFS value of this magnitude is suggestive of a large anisotropy as indeed would be expected for the geometry of 5, in fact similar ZFS values (g = 1.69 cm−1 and D = 42 cm−1) were found for μ-N2 complex 6 which has a geometry between tetrahedral and trigonal-monopyramidal at each of the molybdenum centers.14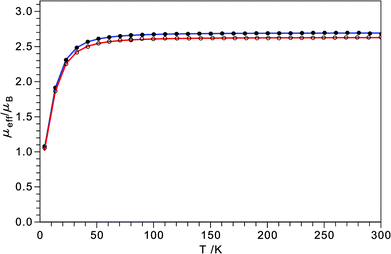 | ||
Fig. 12 SQUID magnetometry of 5 as a function of temperature at applied fields of 0.5 (open circles) and 1 T (closed circles). Red and blue lines represent fits at 0.5 and 1 T from a spin Hamiltonian (H = D[Sz2 − 1/3S(S + 1) + E/D(Sx2 − Sy2)] + gβ ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) · ·![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) )44,45 for an S = 1 state with g = 1.88 and D = 36.6 cm−1 (solid blue). )44,45 for an S = 1 state with g = 1.88 and D = 36.6 cm−1 (solid blue). | ||
In order better to understand the origin of the solid-state thermochromism, variable temperature visible absorption spectra of 5 were obtained from 22 to −170 °C as a KBr diluted solid mixture that was pressed into an optically transparent pellet. These spectra are displayed in Fig. 13 and are compared with the room temperature solution absorption spectrum where it can be noted that the profile of the solid-state absorption spectrum at 22 °C is consistent with that of the solution spectrum. The only changes that are observed upon lowering the temperature are a narrowing of the absorption envelopes for the peaks centered at 480 and 680 nm. As the changes are quite subtle, a difference absorption spectrum, where the spectrum at 22 °C is used as the zero, is provided in Fig. 14. Here the effect of the narrowing of the bands is much more apparent with the two isosbestic points (630 and 715 nm) separating regions of increasing (670 nm) and decreasing (550 and 790 nm) absorption intensity. The narrowing of the bands and resulting changes in absorption can be attributed to a loss of thermally induced vibrational motion. TD-DFT calculations were performed on 5 and the calculated spectrum, upon application of a Lorentzian function (Fig. S21†), had features consistent with both the solution and solid-state spectra of 5. The absorption bands at 480 nm and 680 nm can be attributed to transitions from the HOMO or HOMO−1 to the LUMO or a combination of the LUMO+1 and LUMO+2. While these are predominantly d–d transitions, the near-degenerate set of HOMO and HOMO−1 both have significant overlap with the π orbitals of the isocyanate group.
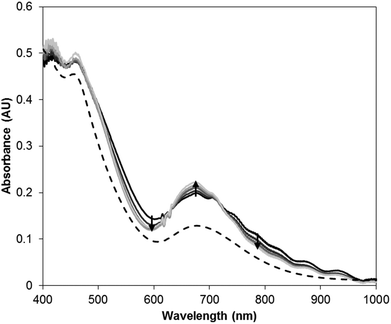 | ||
| Fig. 13 Visible absorption spectra of 5. Solution spectrum (hashed line) in diethyl ether at 22 °C. Solid state spectra in KBr window at 22, −40, −100, −140 and −170 °C. | ||
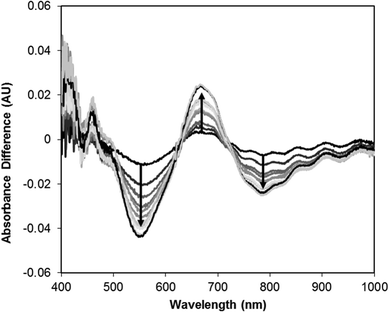 | ||
| Fig. 14 Solid state difference absorption spectra of 5 relative to spectrum at 22 °C. Solid state spectra in KBr window at 0, −40, −60, −80, −100, −110, −120, −130, −140, −160 and −170 °C. | ||
X-ray diffraction quality crystals of 5 were grown from pentane–THF solutions at −30 °C. Attempts to obtain a data set at −177 °C resulted in the crystal fracturing. A DSC scan (Fig. 15) of 5 reveals a reversible solid–solid phase transition at −128 °C (onset) with an enthalpy of transition of −4.3 kJ mol−1 when cooling from the β-modification (β-5) to the α modification (α-5). There is a 20° hysteresis in the phase change temperature; the phase transition in the reverse direction occurs at −108 °C (onset) with an enthalpy of transition of 4.0 kJ mol−1. No shattering of the single crystals occurred at −100 °C allowing a data set to be acquired of the high-temperature phase, β-5. The asymmetric unit for β-5 is shown in Fig. 16a. The geometry around Mo is typical for a MoIV species with similar ligand sets.2,46,47 It should be noted that the thermal ellipsoids on the tBu and isocyanate groups are quite large; attempts to model these groups as disordered over two positions did not lead to an improved model suggesting that these groups may be somewhat dynamic at this temperature.
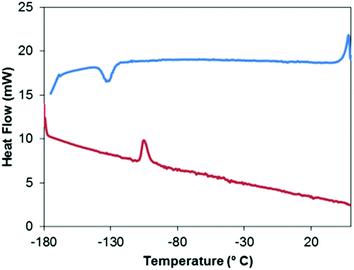 | ||
| Fig. 15 Differential scanning calorimetric curve of 5. Increasing temperature denoted with red and decreasing temperature denoted with blue. | ||
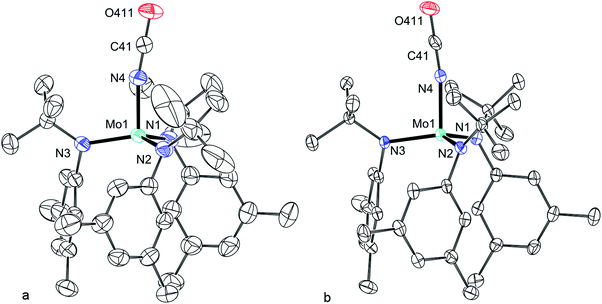 | ||
| Fig. 16 Thermal ellipsoid plot (50% probability) of (a) β-5 (collected at 177 K) and (b) α-5 (collected at 100 K) with hydrogen atoms and minor disordered component omitted for clarity. | ||
The lower temperature phase, α-5, was structurally investigated by slowly cooling a crystal of β-5, that was heavily coated in oil, through the phase change. Although some fracturing of the crystal occurred upon phase change, a sufficiently large portion of the crystal remained intact to allow for the collection of a data set. Both α-5 and β-5 crystallize in the same space group (P21/c). Overall, there is a 2.9% decrease in the volume of the unit cell that results from the a and c axes shortening by 5.3% and 3.2% respectively, the b axis lengthening by 6.2% and the β angle becoming more obtuse by 1.8%. Inspection of the single molecule in the asymmetric unit of α-5 (Fig. 16b) reveals that the thermal motion of the isocyanate and tBu groups have decreased as a result of the conformation becoming locked as compared to β-5. Beyond this, the major structural differences are the Nanilide–Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C dihedral angles and the Mo–N
C dihedral angles and the Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C angle which are the result of a change in the isocyanate position. Further subtle changes are observed in the Mo coordination sphere but the majority of the structural parameters are identical between the two phases within 3σ. Considering the progressive change in the absorption spectrum as a function of temperature, it seems reasonable that the thermal motion decreased as the temperature was lowered and then, upon reaching the phase change temperature, the thermal motion was reduced to the point where a void was created; the potential solvent accessible void in β-5 is 102.7 Å3. The phase change occurs in response to this. In fact, the percent filled space increases from 63.1% to 65.5% from β-5 to α-5 and the potential solvent accessible void becomes zero. The hysteresis in the phase change temperature is consistent with the packing having to change in order to accommodate the density decrease associated with the increasing thermal motion. This type of phase change is consistent with that of D-amphetamine sulfate which proceeds through a similar order–disorder mechanism.48
C angle which are the result of a change in the isocyanate position. Further subtle changes are observed in the Mo coordination sphere but the majority of the structural parameters are identical between the two phases within 3σ. Considering the progressive change in the absorption spectrum as a function of temperature, it seems reasonable that the thermal motion decreased as the temperature was lowered and then, upon reaching the phase change temperature, the thermal motion was reduced to the point where a void was created; the potential solvent accessible void in β-5 is 102.7 Å3. The phase change occurs in response to this. In fact, the percent filled space increases from 63.1% to 65.5% from β-5 to α-5 and the potential solvent accessible void becomes zero. The hysteresis in the phase change temperature is consistent with the packing having to change in order to accommodate the density decrease associated with the increasing thermal motion. This type of phase change is consistent with that of D-amphetamine sulfate which proceeds through a similar order–disorder mechanism.48
The optimized geometry of 5 using single molecules from α-5 or β-5 as a starting point led to the same minimum energy structure in both cases. The bond distances and angles around Mo are well reproduced with the exception of the Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C angle which is calculated to be linear. The difference in electronic energies for the two single point calculations, where the Mo–N
C angle which is calculated to be linear. The difference in electronic energies for the two single point calculations, where the Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C angle is fixed in at the crystallographically refined angle or at the linear angle, is only 0.4 kcal mol−1 suggesting that the observed angle in the crystal structure is simply the result of crystal packing.
C angle is fixed in at the crystallographically refined angle or at the linear angle, is only 0.4 kcal mol−1 suggesting that the observed angle in the crystal structure is simply the result of crystal packing.
Based on the above data, the origin of the thermochromism in isocyanate complex 5 is the result of restricted vibrational motion in a denser low-temperature phase leading to a narrowing of the absorption envelopes.
Experimental
General considerations
Unless otherwise stated, all manipulations were carried out either in a Vacuum Atmospheres model MO-40M glovebox under an atmosphere of N2 or using standard Schlenk techniques. All solvents were degassed and dried using a solvent-purification system provided by Glass Contour. After purification, all solvents were stored under an atmosphere of N2 over 4 Å molecular sieves. Deuterated benzene, deuterated toluene and deuterated chloroform (Cambridge Isotope Labs) were dried by stirring over CaH2 for 24 h and was subsequently vacuum-transferred onto 4 Å molecular sieves. MoCl3(THF)3,30 (Et2O)Li[N(CCH3(CD3)2)ArMeL],29 Cp*RuCl(PCy3)49 and compounds 1,12,14816 and 916 were prepared according to literature methods. All other reagents were used as supplied by the vendor without further purification. Celite 435 (EMD Chemicals), alumina (Aldrich) and 4 Å molecular sieves were dried prior to use by heating at 200 °C for 48 h under dynamic vacuum. All glassware was oven dried at 220 °C prior to use. All photochemical reactions were performed in a Rayonet Photochemical Reactor (RPR-200, Southern New England Ultra Violet Company) using either 16 RPR-2540 or 16 RPR-4190 lamps. NMR spectra were obtained on either a Varian 500 Inova spectrometer equipped with an Oxford Instruments Ltd. superconducting magnet, a Bruker 400-AVANCE spectrometer equipped with a Magnex Scientific superconducting magnet, or a Varian Mercury 300 spectrometer equipped with an Oxford Instruments Ltd. superconducting magnet. Proton NMR spectra were referenced to residual C6D5H (7.16 ppm) or residual CHCl3 (7.26 ppm). 19F NMR spectra were referenced externally to Et2O·BF3 (153.35 ppm) that had been previously referenced to CFCl3. 2H NMR spectra were referenced to the naturally abundant 2H signals in the solvent. IR spectra were collected on a Bruker Tensor 37 FT-IR spectrophotometer or a Bruker Alpha FTIR spectrometer fitted with a diamond ATR and stored in an N2 purged glovebox. Elemental analysis was performed by Midwest Microlab, Indianapolis, IN.Synthesis
Photolysis of OCNMo(N[tBu]Ar)3 (5)
A 0.1211 g (0.1818 mmol) sample of 5 was dissolved in 50 mL of pentane and placed in a quartz reaction flask. The quartz reaction flask was attached through a bridge to a flask containing 0.0741 g (0.0140 mmol) of Cp*RuCl(PCy3). The apparatus was degassed with three freeze–pump–thaw cycles and left under static vacuum. The portion of the apparatus containing 5 was irradiated (16 bulbs at 254 nm) for 20 hours while the portion of the apparatus containing the Cp*RuCl(PCy3) was kept outside of the irradiation chamber. After 20 h, the portion of the apparatus containing the Cp*RuCl(PCy3) was cooled with a liquid nitrogen bath causing all the volatiles from the reaction flask to be transferred. The flask was isolated and allowed to warm to 20 °C with stirring. After achieving this temperature, the solvent was removed under dynamic vacuum.Crystallography
Crystals were mounted on MiTGen mounts using Paratone-N oil (Hampton). The structure of β-5 was determined at 177 K. All other structures were collected at 100 K. Preliminary frames were obtained in order to determine the unit cell. Diffraction data (φ- and ω-scans) were collected on either a Siemens Platform three-circle diffractometer coupled to a Bruker-AXS Smart Apex CCD detector with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å), performing ω- and φ-scans or a Bruker-AXS X8 Kappa Duo diffractometer coupled to a Smart APEX II CCD detector with Mo Kα radiation (λ = 0.71073 Å) from a IμS microfocus source. Absorption and other corrections were applied using SADABS. The structures were solved by direct methods using SHELXS and refined against F2 on all data by full-matrix least squares as implemented in SHELXL-97. All non-hydrogen atoms of the framework were refined anisotropically. Hydrogen atoms pertaining to the ligand were included in the model at geometrically calculated positions using a riding model.SQUID magnetometry
DC-SQUID data were obtained on a sample packed in a cellulose capsule. Data was collected from 2 K to 300 K at field strengths of 0.5 and 1 T. The data were corrected for the magnetic susceptibility of the sample holder and the diamagnetic contribution from the sample. The data were fit to a spin Hamiltonian using Julx.45Calculations
Calculations were performed using the ORCA 2.9 quantum chemistry program package from the development team at the Max Planck Institute for Bioinorganic Chemistry.51 For geometry optimizations the LDA and GGA functionals employed were those of Perdew and Wang (PW-LDA, PW91).17 In all cases where a crystal structure was determined, the coordination geometry was reproduced by this method within 0.1 Å for bond distances, 1° for bond angles and 2° for dihedral angles. The one exception was in the calculated geometry of 5 where the Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond angle deviates from the crystal structure and was determined to be the result of packing effects in the crystal structure (see Discussion in text). For structures of 12 and 13, only the hydrogen atomic coordinates were optimized. In the case of thermodynamic calculations, the hybrid functional (30% HF)19 of Becke (B88)18 was used for exchange and that of Perdew and Wang (PW91)17 for the correlation. In addition, all calculations were carried out using the Zero-Order Regular Approximation (ZORA),52,53 in conjunction with the SARC-TZV(2pf) basis set for the transition metal atoms, the SARC-TZV basis set for the hydrogen atoms, and SARC-TZV(p) set for all other atoms.54 Spin-restricted and unrestricted Kohn–Sham determinants were chosen to describe the closed shell and open shell wavefunctions respectively, employing the RI approximation and the tight SCF convergence criteria provided by ORCA.
C bond angle deviates from the crystal structure and was determined to be the result of packing effects in the crystal structure (see Discussion in text). For structures of 12 and 13, only the hydrogen atomic coordinates were optimized. In the case of thermodynamic calculations, the hybrid functional (30% HF)19 of Becke (B88)18 was used for exchange and that of Perdew and Wang (PW91)17 for the correlation. In addition, all calculations were carried out using the Zero-Order Regular Approximation (ZORA),52,53 in conjunction with the SARC-TZV(2pf) basis set for the transition metal atoms, the SARC-TZV basis set for the hydrogen atoms, and SARC-TZV(p) set for all other atoms.54 Spin-restricted and unrestricted Kohn–Sham determinants were chosen to describe the closed shell and open shell wavefunctions respectively, employing the RI approximation and the tight SCF convergence criteria provided by ORCA.
NMR calculations were performed with the EPR and NMR modules and the analysis to find the observed shift, δ was performed as outlined by Bagno using eqn (5), where δo is determined according to eqn (6), δFC is determined from eqn (7) and δPC is considered to be negligible as it only is appreciable within a few angstroms of the paramagnetic center.22,23 In eqn (6), the orbital component, σorb, of the diamagnetic shielding was determined by performing an NMR calculation on the paramagnetic complex and the overall chemical shift, δorb was determined using TMS as the reference material, σorb, and assuming that the diamagnetic shielding can be approximated by the chemical shift. The Fermi contact term, δFC, was calculated by performing an EPR calculation on the paramagnetic complex and extracting the isotropic hyperfine coupling constant, A, in frequency units and applying it to eqn (7), where γI is magnetogyric ratio of element I, giso is the isotropic g-factor, k is the Boltzmann constant, T is temperature, S is the spin and μB represents the Bohr magneton. Linewidths were calculated according to the Solomon–Bloembergen equation using a rotational correlation time of 5 × 10−11 s estimated from the Debye equation (τr = ηVm/kT) with a molecular volume estimated from the crystallographic structure and an electronic relaxation correlation time (τS) of 5 × 10−12 s. The spin density was assumed to reside on the metal atom, consistent with the calculated spin density.
| δ = δo + δFC + δPC | (5) |
| δorb = σref − σorb ≈ δo | (6) |
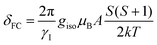 | (7) |
TDDFT was used to calculate the 100 lowest energy singlet and triplet excitations. The potential energy surfaces were constructed by allowing all parameters to relax as a single parameter (the NC distance for reactions according to eqn (4) and the Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond angle for the PES for the Mo–N
C bond angle for the PES for the Mo–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond angle in 5) was varied.
C bond angle in 5) was varied.
Conclusions
We have explored an atom efficient cycle for the conversion of ubiquitous small molecules, CO and N2, into the industrially relevant cyanate ion. A variety of Mo and V complexes were investigated with regard to their ability to mediate the various steps in this cycle. Three-coordinate Mo complexes, which had been shown previously to split N2 and form terminal nitrido complexes, were found to be unreactive towards the two-electron reductant CO, despite the transformation being predicted to be thermodynamically favorable by DFT calculations in one of the cases. A new Mo–nitride complex was prepared (with azide as the nitrogen source) that was similarly found not to be reactive with CO, despite indications once more from quantum chemical calculations that isocyanate formation would be favorable. DFT calculations were used to rationalize the difference between these systems and systems that are known to participate in nitride–CO coupling to isocyanate. It was found that the CO reduction of the vanadium nitride model complex proceeded through a metal carbonyl intermediate which isomerized to give the isocyanate. In this way, a large reaction barrier was avoided. One possible approach, then, is to design systems that maintain an accessible metal center having CO affinity in order to mediate the reaction. This will have to be balanced with a choice of ligands that do not favor CO insertion into the metal–ligand bond. Additionally, the origin of the thermochromism of a molybdenum isocyanate complex was elucidated and was found to be the result of restricted vibrational motion in a denser low-temperature phase leading to narrow absorption envelopes.Acknowledgements
This material is based upon work supported by the National Science Foundation under CHE-1111357 as well as the National Science and Engineering Research Council of Canada (NSERC-PDF – AFC).Notes and references
- J. J. Curley, E. L. Sceats and C. C. Cummins, J. Am. Chem. Soc., 2006, 128, 14036–14037 CrossRef CAS PubMed
.
- J. J. Curley, A. F. Cozzolino and C. C. Cummins, Dalton Trans., 2011, 40, 2429–2432 RSC
.
- M. W. Chase Jr., J. Phys. Chem. Ref. Data Monogr., 1998, 9, 1–1951 Search PubMed
.
- C. E. Vanderzee and R. A. Myers, J. Phys. Chem., 1961, 65, 153–158 CrossRef CAS
.
-
P. M. Schalke, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2000, pp. 669–672 Search PubMed
.
- J. S. Silvia and C. C. Cummins, J. Am. Chem. Soc., 2009, 131, 446–447 CrossRef CAS PubMed
.
- B. L. Tran, M. Pink, X. Gao, H. Park and D. J. Mindiola, J. Am. Chem. Soc., 2010, 132, 1458–1459 CrossRef CAS PubMed
.
- B. Askevold, J. T. Nieto, S. Tussupbayev, M. Diefenbach, E. Herdtweck, M. C. Holthausen and S. Schneider, Nat. Chem., 2011, 3, 532–537 CrossRef CAS PubMed
.
- J. P. Reeds, B. L. Yonke, P. Y. Zavalij and L. R. Sita, J. Am. Chem. Soc., 2011, 133, 18602–18605 CrossRef CAS PubMed
.
- D. J. Knobloch, E. Lobkovsky and P. J. Chirik, Nat. Chem., 2009, 2, 30–35 CrossRef PubMed
.
- D. J. Knobloch, E. Lobkovsky and P. J. Chirik, J. Am. Chem. Soc., 2010, 132, 15340–15350 CrossRef CAS PubMed
.
- C. E. Laplaza and C. C. Cummins, Science, 1995, 268, 861–863 CAS
.
- D. J. Knobloch, E. Lobkovsky and P. J. Chirik, J. Am. Chem. Soc., 2010, 132, 10553–10564 CrossRef CAS PubMed
.
- J. J. Curley, T. R. Cook, S. Y. Reece, P. Müller and C. C. Cummins, J. Am. Chem. Soc., 2008, 130, 9394–9405 CrossRef CAS PubMed
.
- J. C. Peters, A. L. Odom and C. C. Cummins, Chem. Commun., 1997, 1995–1996 RSC
.
- M. J. A. Johnson, P. M. Lee, A. L. Odom, W. M. Davis and C. C. Cummins, Angew. Chem., Int. Ed., 1997, 36, 87–91 CrossRef CAS
.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244–13249 CrossRef
.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed
.
- C. E. Laplaza, M. J. A. Johnson, J. C. Peters, A. L. Odom, E. Kim, C. C. Cummins, G. N. George and I. J. Pickering, J. Am. Chem. Soc., 1996, 118, 8623–8638 CrossRef CAS
.
- A. R. Johnson, W. M. Davis, C. C. Cummins, S. Serron, S. P. Nolan, D. G. Musaev and K. Morokuma, J. Am. Chem. Soc., 1998, 120, 2071–2085 CrossRef CAS
.
- F. Rastrelli and A. Bagno, Magn. Reson. Chem., 2010, 48(Suppl 1), S132–S141 CrossRef CAS PubMed
.
- F. Rastrelli and A. Bagno, Chem.–Eur. J., 2009, 15, 7990–8004 CrossRef CAS PubMed
.
- J. C. Peters, L. M. Baraldo, T. A. Baker, A. R. Johnson and C. C. Cummins, J. Organomet. Chem., 1999, 591, 24–35 CrossRef CAS
.
- R. A. Eikey and M. M. Abu-Omar, Coord. Chem. Rev., 2003, 243, 83–124 CrossRef CAS
.
- J. Strähle, Z. Anorg. Allg. Chem., 2007, 633, 1757–1761 CrossRef
.
- A. L. Odom, C. C. Cummins and M. G. Fickes, Chem. Commun., 1997, 1993–1994 Search PubMed
.
- J. S. Silvia and C. C. Cummins, J. Am. Chem. Soc., 2010, 132, 2169–2171 CrossRef CAS PubMed
.
- A. R. Fox, J. S. Silvia, E. M. Townsend and C. C. Cummins, C. R. Chim., 2010, 13, 781–789 CrossRef CAS PubMed
.
- F. Stoffelbach, D. Saurenz and R. Poli, Eur. J. Inorg. Chem., 2001, 2001, 2699–2703 CrossRef
.
- M. L. H. Green, J. Organomet. Chem., 1995, 500, 127–148 CrossRef CAS
.
- P. Berno, S. Hao, R. K. Minhas and S. Gambarotta, J. Am. Chem. Soc., 1994, 116, 7417–7418 CrossRef CAS
.
- J. J. H. Edema, A. Meetsma and S. Gambarotta, J. Am. Chem. Soc., 1989, 111, 6878–6880 CrossRef CAS
.
- I. Vidyaratne, P. Crewdson, E. Lefebvre and S. Gambarotta, Inorg. Chem., 2007, 46, 8836–8842 CrossRef CAS PubMed
.
- B. L. Tran, B. Pinter, A. J. Nichols, F. T. Konopka, R. Thompson, C.-H. Chen, J. Krzystek, A. Ozarowski, J. Telser, M.-H. Baik, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13035–13045 CrossRef CAS PubMed
.
- G. K. B. Clentsmith, V. M. E. Bates, P. B. Hitchcock and F. G. N. Cloke, J. Am. Chem. Soc., 1999, 121, 10444–10445 CrossRef CAS
.
-
M. J. A. Johnson, Synthesis and Reactivity of Early Transition Metal Complexes Supported by Sterically Demanding Amido Ligands, PhD, Massachusetts Institute of Technology, 1998, p. 240 Search PubMed
.
- J. J. H. Edema, W. Stauthamer, F. Van Bolhuis, S. Gambarotta, W. J. J. Smeets and A. L. Spek, Inorg. Chem., 1990, 29, 1302–1306 CrossRef CAS
.
- J. C. Peters, J.-P. F. Cherry, J. C. Thomas, L. Baraldo, D. J. Mindiola, W. M. Davis and C. C. Cummins, J. Am. Chem. Soc., 1999, 121, 10053–10067 CrossRef CAS
.
- J. S. Figueroa, N. A. Piro, C. R. Clough and C. C. Cummins, J. Am. Chem. Soc., 2006, 128, 940–950 CrossRef CAS PubMed
.
- A. L. Odom, P. L. Arnold and C. C. Cummins, J. Am. Chem. Soc., 1998, 120, 5836–5837 CrossRef CAS
.
- A. S. Huss, J. J. Curley, C. C. Cummins and D. A. Blank, J. Phys. Chem. B, 2013, 117, 1429–1436 CrossRef CAS PubMed
.
- M. H. Chisholm, C. E. Hammond and J. C. Huffman, Organometallics, 1987, 6, 210–211 CrossRef CAS
.
-
O. Kahn, in Molecular Magnetism, VCH Publishers Inc., Weinheim, Germany, 1993, p. 17 Search PubMed
.
-
E. Bill, JulX: A Program for the Simulation and Analysis of Magnetic Susceptibility Data. V. 1.4, MPI for Chemical Energy Conversion, Mülheim an der Ruhr, 2008 Search PubMed
.
- M. Temprado, J. E. McDonough, A. Mendiratta, Y.-C. Tsai, G. C. Fortman, C. C. Cummins, E. V. Rybak-Akimova and C. D. Hoff, Inorg. Chem., 2008, 47, 9380–9389 CrossRef CAS PubMed
.
- A. Fürstner, C. Mathes and C. W. Lehmann, J. Am. Chem. Soc., 1999, 121, 9453–9454 CrossRef
.
- K. Pogorzelec-Glaser, J. Kaszyńska, A. Rachocki, J. Tritt-Goc, N. Piślewski and A. Pietraszko, New J. Chem., 2009, 33, 1894 RSC
.
- B. K. Campion, R. H. Heyn and T. D. Tilley, J. Chem. Soc., Chem. Commun., 1988, 278 RSC
.
- F. A. Miller and C. H. Wilkins, Anal. Chem., 1952, 24, 1253–1294 CrossRef CAS
.
-
F. Neese, ORCA – an ab initio, Density Functional and Semiempirical program package, Version 2.9.0, MPI for Bioinorganic Chemistry, Mülheim an der Ruhr, 2013 Search PubMed
.
- E. van Lenthe, J. Baerends Evert and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS PubMed
.
- J. L. Heully, I. Lindgren, E. Lindroth, S. Lundqvist and A. M. Maartensson-Pendrill, J. Phys. B: At. Mol. Phys., 1986, 19, 2799–2815 CrossRef CAS
.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: For spectra, tables of crystallographic data and tables of DFT optimized coordinates. CCDC 961016–961023. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3dt52738g |
| This journal is © The Royal Society of Chemistry 2014 |