Optical activity in the scattering of structured light
Received
6th August 2014
, Accepted 7th October 2014
First published on 7th October 2014
Abstract
We observe that optical activity in light scattering can be probed using types of illuminating light other than single plane (or quasi plane) waves and that this introduces new possibilities for the study of molecules and atoms. We demonstrate this explicitly for natural Rayleigh optical activity which, we suggest, could be exploited as a new form of spectroscopy for chiral molecules through the use of illuminating light comprised of two plane waves that are counter propagating.
1 Introduction
It is now well established in theory that a difference in response to left- and right-handed circular polarisations, or optical activity, in the scattering of light is exhibited naturally by chiral molecules1–5 and can be induced additionally in all molecules and atoms by an applied static magnetic5,6 or electric5,7 field. The phenomenon permits the extraction of information about molecules and atoms that is not readily obtainable through optical rotation or circular dichroism, owing to the subtly different physical mechanism and greater geometrical freedom involved.4,5
Many manifestations of optical activity in light scattering have now been observed in experiment.5,8–12 Natural Raman optical activity in particular has been developed into an incisive spectroscopic tool which has been employed to study large biological molecules and even intact viruses.5,8,11,12 Owing primarily to the smallness of the effects involved, there remains much to be pursued, however. Natural Rayleigh optical activity for example has thus far resisted attempts to observe it in experiment,5,13 in spite of potential applications such as the robust assignment of the absolute configurations of small chiral molecules.14
To the best of our knowledge, the theoretical and experimental approaches undertaken to date towards the phenomenon have been concerned with the illumination of molecules or atoms by single plane (or quasi plane) waves.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–12,14 We observe, however, that optical activity in light scattering can also be probed, in general, using other types of illuminating light and that this introduces new possibilities for the study of molecules and atoms. In the present paper, we demonstrate this explicitly for natural Rayleigh optical activity which, we suggest, could be exploited as a new form of spectroscopy for chiral molecules through the use of illuminating light comprised of two plane waves that are counter propagating.
1–12,14 We observe, however, that optical activity in light scattering can also be probed, in general, using other types of illuminating light and that this introduces new possibilities for the study of molecules and atoms. In the present paper, we demonstrate this explicitly for natural Rayleigh optical activity which, we suggest, could be exploited as a new form of spectroscopy for chiral molecules through the use of illuminating light comprised of two plane waves that are counter propagating.
In what follows, we work within the classical domain and consider ourselves to be in an inertial frame of reference. We adopt a right-handed Cartesian coordinate system; x, y, z. A double appearance of an index taken from the start of the roman alphabet; a, b, c,…, implies summation over x, y and z. The international system of units is respected, with ε0 and μ0 the electric and magnetic constants and 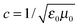 the speed of light in vacuum. Complex quantities are indicated as such using a tilde. Unit vectors are indicated as such using a circumflex.
the speed of light in vacuum. Complex quantities are indicated as such using a tilde. Unit vectors are indicated as such using a circumflex.
2 Natural Rayleigh optical activity
Consider a collection of N ≫ 1 chiral molecules located at fixed positions Rn (n = 1,…, N). Neglecting interactions between them and assuming an absence of applied static electric and magnetic fields, we take the molecules to be randomly orientated but otherwise identical. We suppose, however, that they are illuminated by weak, monochromatic, off-resonance light of angular frequency ω = ck, the length scale 2π/k associated with which is significantly larger than each molecule. The electric field E = E(r,t) and magnetic flux density B = B(r,t) comprising the illuminating light evolve in space r and time t as
E = ℜ[Ẽ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], |
| | B = ℜ[![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], | (1) |
with the function ℜ yielding the real part of its argument and the complex quantities Ẽ = Ẽ(r) and ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) =
= ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) (r) satisfying
(r) satisfying
∇·![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) = 0, = 0, |
∇ × Ẽ = iω![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) , , |
| | ∇ × ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) = −ε0μ0iωẼ, = −ε0μ0iωẼ, | (2) |
with ∇ the gradient operator with respect to r, as follows from the charge-free Maxwell equations:15 we regard the illuminating light as being an externally imposed influence acting upon the molecules that is (otherwise) freely propagating.
The illuminating light induces oscillations in the charge and current distributions of the molecules. In particular, the components μ(n)a = μ(n)a(t), Θ(n)ab = Θ(n)ab(t) and m′(n)a = m′(n)a(t) of the induced electric dipole, electric quadrupole and magnetic dipole moments of the nth molecule are, in a standard notation,5
μ(n)a ≈ ℜ[![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) (n)a (n)a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], |
Θ(n)ab ≈ ℜ[![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (n)ab (n)ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], |
| | m′(n)a ≈ ℜ[![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) ′(n)a ′(n)a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], | (3) |
with the complex quantities
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) (n)a
(n)a,
![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (n)ab
(n)ab and
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif)
′
(n)a related to the illuminating light as
| | 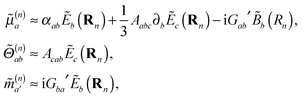 | (4) |
for
ω lying in the visible or near infrared say, with
αab =
αba =
αab(
fω),
Aabc =
Aacb =
Aabc(
fω),
Gab′ =
Gab′(
fω) molecular polarisabilities. These oscillations generate Rayleigh
scattered light in turn,
4,5 the electric field
Es =
Es(
r,
t) and magnetic flux density
Bs =
Bs(
r,
t) of which at a position
R of fixed magnitude |
R| ≫ |
Rn|, 2π/
k are
Es ≈ ℜ[Ẽs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], |
| | Bs ≈ ℜ[![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) s s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)], exp(−iωt)], | (5) |
with the components
Ẽsa and
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) sa
sa of the complex quantities
Ẽs =
Ẽs(
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
) and
![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) s
s =
![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) s
s(
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
) related to the oscillations in the charge and current distributions of the molecules as
5| | 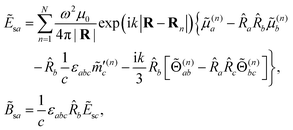 | (6) |
for
εabc the rotational Levi-Civita pseudotensor defined such that
εxyz = 1. The intensity
I =
I(
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
) of the scattered light seen at
R follows from Poynting's vector as
| | 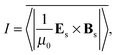 | (7) |
with an overbar indicating a cycle average and angular brackets indicating an isotropic rotational average,
4,5 to account for the random orientations of the molecules. Making no assumptions beyond those described above whilst rejecting ‘
A2’, ‘
AG′’ and ‘
G′
2’ contributions, which are anticipated to be some three orders of magnitude smaller than the smallest contributions thus retained,
5 we find that we can express
I in terms of six properties
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
,
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
,
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
,
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
,
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif)
and
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
of the molecules and six related properties
W,
Tab,
H,
S,
Nab and
Xab of the illuminating light:
| | 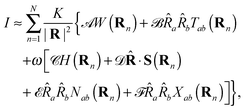 | (8) |
with
K =
μ02cω4/2880π
2. Both
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
and
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
are equal for opposite molecular enantiomers and are thus insensitive to the chirality of the molecules, whilst
W and
Tab pertain to the energy and linear momentum of the illuminating light.
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
,
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
,
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif)
and
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
, however, each assume equal magnitudes but opposite signs for opposite molecular enantiomers and so
are sensitive to the chirality of the molecules, whilst
H,
S and
Nab pertain to the helicity, spin and
ab infra zilches of the illuminating light, these being manifestly intrinsic rotation angular momenta.
16–21 Explicit expressions for these and
Xab are given in Appendix A.
Our calculation differs from those that have been performed previously1–5 in that the illuminating light here need not be comprised of a single plane wave of angular frequency ω but rather can be constructed from any superposition of such waves. Moreover, the molecules need not be distributed homogeneously and could instead be confined within a plane, for example. It should be noted, however, that (8) is not appropriate when the direction ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) of observation coincides with the direction of propagation of a plane-wave component of the illuminating light, which will then interfere with the scattered light as Rayleigh scattering is a coherent process.4,5 Moreover, having been derived specifically for illuminating light that is (otherwise) freely propagating in accord with the charge-free Maxwell equations, (8) is not appropriate for illuminating light the electric field of which possesses a non-vanishing irrotational component, such as may be found in the near field of a radiating structure, for example. We have refrained from exhibiting a generalised structure factor (inter-molecule cross terms4) in (8) as it makes no contribution in the examples that follow and in most other geometries besides.
of observation coincides with the direction of propagation of a plane-wave component of the illuminating light, which will then interfere with the scattered light as Rayleigh scattering is a coherent process.4,5 Moreover, having been derived specifically for illuminating light that is (otherwise) freely propagating in accord with the charge-free Maxwell equations, (8) is not appropriate for illuminating light the electric field of which possesses a non-vanishing irrotational component, such as may be found in the near field of a radiating structure, for example. We have refrained from exhibiting a generalised structure factor (inter-molecule cross terms4) in (8) as it makes no contribution in the examples that follow and in most other geometries besides.
Our general result (8) reveals in particular that natural Rayleigh optical activity, as manifest in I, can be utilised to extract information about the chirality of the molecules using essentially any type of illuminating light possessing non-vanishing helicity, spin and/or ab infra zilches.16–21 A single circularly polarised plane wave is, perhaps, the most obvious example of such light and is examined in Section 3. It is not the only one, however:22 as we will demonstrate in Sections 4–6, types of illuminating light comprised of two plane waves that are counter propagating can carry these angular momenta in novel ways and thus enable new possibilities. In identifying these, we were guided by symmetry considerations. In particular, it is necessary for the illuminating light together with the direction of observation to be of chiral character in order that I itself be capable of distinguishing between opposite molecular enantiomers, as is inherent, of course, in (8).
3 Example zero: circularly polarised illuminating light
As a check on the validity of (8) and for comparison in what follows, let us begin now by following previous approaches1–5 and considering illuminating light comprised of a single circularly polarised plane wave of amplitude E0 propagating in the z direction as
Ẽ(0)± = E0(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ± iŷ) ± iŷ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz), exp(ikz), |
| | ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) (0)± = E0(∓i (0)± = E0(∓i![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + ŷ) + ŷ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz)/c, exp(ikz)/c, | (9) |
with ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , ŷ (and ẑ) unit vectors in the x, y (and z) directions and where the upper and lower signs yield left- and right-handed circular polarisation in the optics convention,15 which we adopt. This is both the prototypical type of light possessing non-vanishing helicity, spin and ab infra zilches17,18 and the prototypical type of chiral light:5 as time passes, E and B rotate with a phase that varies in z such that they trace out cylindrical helices, the chiralities of which differ for the upper and lower signs in (9). Accordingly
, ŷ (and ẑ) unit vectors in the x, y (and z) directions and where the upper and lower signs yield left- and right-handed circular polarisation in the optics convention,15 which we adopt. This is both the prototypical type of light possessing non-vanishing helicity, spin and ab infra zilches17,18 and the prototypical type of chiral light:5 as time passes, E and B rotate with a phase that varies in z such that they trace out cylindrical helices, the chiralities of which differ for the upper and lower signs in (9). Accordingly
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·S(0)± = ± ·S(0)± = ±![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) zε0E02/ω, zε0E02/ω, |
| | ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) a a![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) bX(0)ab± = 0, bX(0)ab± = 0, | (10) |
where the upper and lower signs correspond to those in (9). Taking the molecules to be homogeneously distributed around the origin, we find then that| | 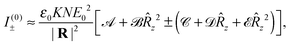 | (11) |
where the upper and lower signs again correspond to those in (9). Natural Rayleigh optical activity, as manifest in I(0)±, is thus attributable to the non-vanishing helicity, spin and ab infra zilches possessed by the illuminating light: I(0)± differs for left- and right-handed circular polarisations because H(0)±, S(0)± and N(0)ab± do. For right-angled observation in particular, with ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) say;
say;| | 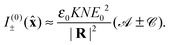 | (12) |
This situation is depicted in Fig. 1.
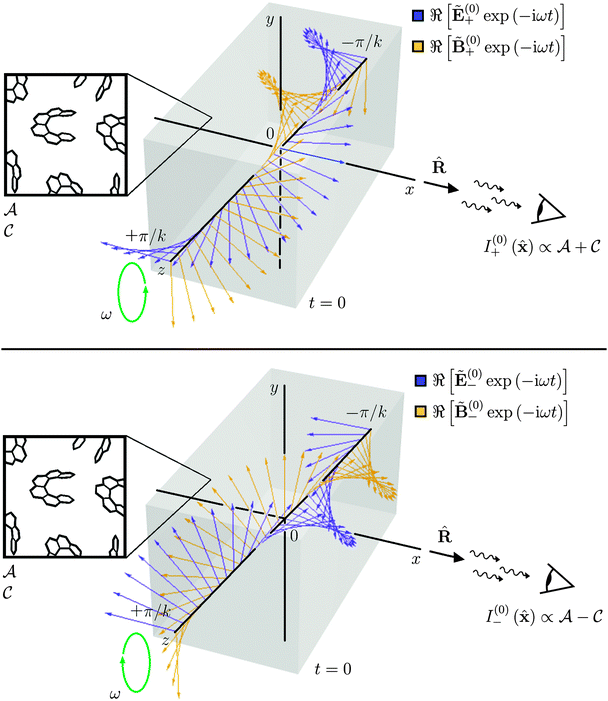 |
| | Fig. 1 Illuminating light comprised of a single circularly polarised plane wave is scattered differently by the molecules depending upon whether it is left- or right-handed. | |
This phenomenon is neatly quantified by the circular intensity difference Δ(0) = Δ(0)(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ) defined as‡
) defined as‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2
| | 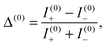 | (13) |
which has equal magnitudes but opposite signs for opposite molecular enantiomers. Without loss of generality, we take
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
= sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
+ cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕẑ
ϕẑ and find that
| | 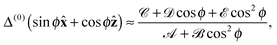 | (14) |
which is the anticipated result.
3 For right-angled observation in particular,
2,4,5 with
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
=
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
;
| | 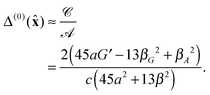 | (15) |
Owing primarily to the contribution made in the denominator by
a2,
Δ(0) is rather small and, to the best of our knowledge, has not yet been observed in experiment for chiral molecules:
5,13 calculated magnitudes of
Δ(0) typically lie between 10
−6 and 10
−4.
14 We note, however, that experimental results have been reported for large biological structures.
23
4 Example one: superchiral illuminating light
Following a procedure recently suggested24 and demonstrated25 for luminescence-detected circular dichroism, we observe here the possibility of using so-called superchiral illuminating light, rather than illuminating light comprised of a single circularly polarised plane wave, to ensure that a larger fraction of I is sensitive to the chirality of the molecules, albeit at the expense of an overall reduction in I. We associate with this illuminating light, a quantity analogous to Δ(0)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) that can be made larger in magnitude and may, therefore, be more amenable to observation in experiment.
) that can be made larger in magnitude and may, therefore, be more amenable to observation in experiment.
Consider then a superposition of two circularly polarised plane waves of opposite handedness, the first of which has amplitude 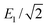 and propagates in the z direction whilst the second has amplitude
and propagates in the z direction whilst the second has amplitude 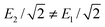 and propagates in the −z direction as
and propagates in the −z direction as
| | 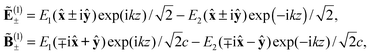 | (16) |
where the upper and lower signs distinguish the cases in which the first wave is left- or right-handed. This illuminating light is manifestly chiral as, at any given
t,
E and
B twist helically in
z, the sense of twist depending on sgn(
E1 −
E2) whilst differing for the upper and lower signs in
(16). As time passes, these helical patterns themselves rotate rigidly about the
z axis, with the sense of rotation differing for the upper and lower signs in
(16). In the vicinity of the
z = 0 plane,
E twists
unusually fast in
z, doing so at the cost of a reduced magnitude: a superoscillatory phenomenon.
26 In contrast,
B twists rather slowly in the vicinity of
z = 0, but is of relatively large magnitude. The effect becomes more pronounced as |
E1 −
E2| → 0.
Let us suppose then that the molecules are distributed homogeneously in the z = 0 plane around the origin. Adopting a right-angled observation geometry with ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , we find that
, we find that
| | 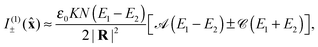 | (17) |
where the upper and lower signs correspond to those in
(16). Comparing
(17) with
(12), we see that the chirally insensitive
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
contribution to
I(1)±(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) is reduced relative to the chirally sensitive
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
contribution, albeit at the expense of an overall reduction in
I(1)±(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
). This occurs because the chirally insensitive
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
contribution to
I(1)±(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) is driven by
E alone through
![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif)
whilst the chirally sensitive
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
contribution is driven instead by both
E and
B through
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif)
: in the latter case, the unusually high degree of twisting exhibited by
E in the vicinity of the
z = 0 plane, where the molecules reside, together with the relatively large magnitude of
Bcompensates somewhat for the small magnitude of
E there. The situation is depicted in
Fig. 2.
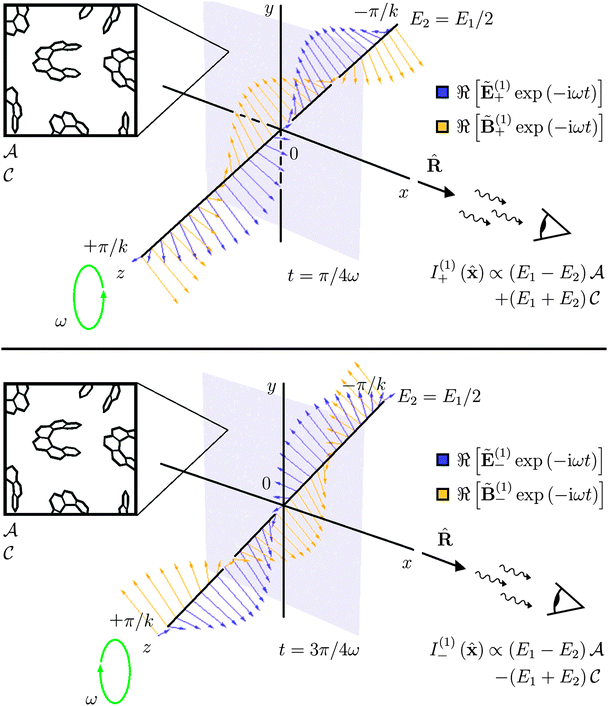 |
| | Fig. 2 Superchiral illuminating light can be employed to ensure that a larger fraction of the intensity of the scattered light is sensitive to the chirality of the molecules, as compared to illuminating light comprised of a single circularly polarised plane wave. | |
We quantify this phenomenon through a generalised intensity difference χ(1) defined as
| | 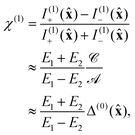 | (18) |
which has equal magnitudes but opposite signs for opposite molecular enantiomers. This
χ(1) should be equal to or greater in magnitude than
Δ(0)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) and diverges, in fact, as |
E1 −
E2| → 0 (and
I(1)±(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) → 0). In reality, such enhancements of
χ(1) relative to
Δ(0) are limited by contributions to the
m′
(n)a induced by
B, which we have omitted explicitly from our analysis. Nevertheless, gains up to three orders of magnitude may be possible.
4,5,24,25
5 Example two: σ–σ illuminating light
We observe now the possibility of using so-called σ–σ illuminating light, rather than illuminating light comprised of a single circularly polarised plane wave, to remove isotropic contributions to I whilst retaining both chirally insensitive and chirally sensitive anisotropic contributions. We associate with this illuminating light, a quantity analogous to Δ(0)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) that is significantly larger in magnitude whilst offering different and perhaps more desirable information about the chirality of the molecules. This quantity may, therefore, be more suitable for observation in experiment. σ–σ light is employed for example in the laser cooling of atoms.27
) that is significantly larger in magnitude whilst offering different and perhaps more desirable information about the chirality of the molecules. This quantity may, therefore, be more suitable for observation in experiment. σ–σ light is employed for example in the laser cooling of atoms.27
Consider then a superposition of two circularly polarised plane waves of the same handedness and equal amplitude 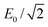 , the first of which propagates in the z direction whilst the second propagates in the −z direction as
, the first of which propagates in the z direction whilst the second propagates in the −z direction as
| | 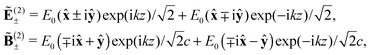 | (19) |
where the upper and lower signs distinguish the cases in which the waves are left- or right-handed. This illuminating light is manifestly chiral, as
E and
B oscillate linearly and parallel to each other at each
z whilst the plane in which they oscillate twists helically in
z, the sense of twist differing for the upper and lower signs in
(19) whilst
E lags or leads
B by a quarter cycle. In the
z = 0 plane,
E and
B lie parallel to the
x axis.
Let us suppose then that the molecules are distributed homogeneously in the z = 0 plane around the origin. Adopting a right-angled observation geometry with ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , we find that
, we find that
| | 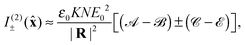 | (20) |
where the upper and lower signs correspond to those in
(19). Evidently,
I(2)±(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) contains
no isotropic contributions, either chirally insensitive:
a2, or chirally sensitive:
aG′. It
does, however, possess non-vanishing anisotropic contributions, both chirally insensitive:
β2, and chirally sensitive:
βG2 and
βA2. This may be understood simply by recalling that an oscillating electric dipole moment radiates no energy on axis and so an isotropically polarisable molecular species would, to the order of present interest, exhibit no scattering in the direction
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
=
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
of observation as the latter lies parallel to the (electric-dipole-inducing)
E vectors in the
z = 0 plane where the molecules reside. The situation is depicted in
Fig. 3.
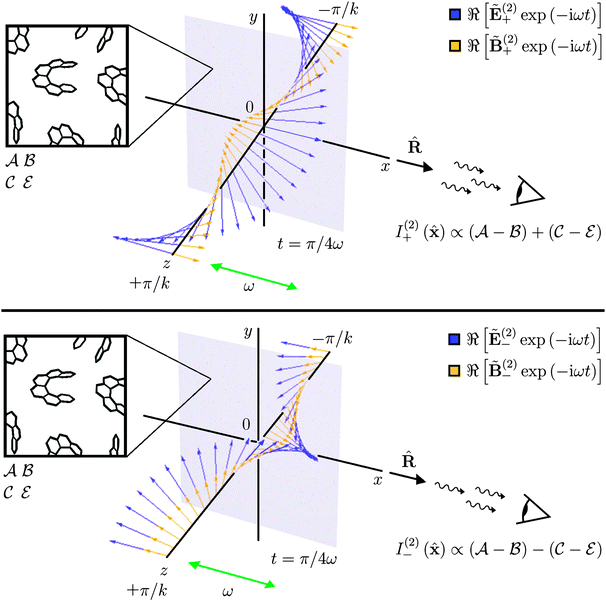 |
| | Fig. 3 σ–σ illuminating light can be employed to ensure that the intensity of the scattered light contains no isotropic contributions whilst still being sensitive to the chirality of the molecules. | |
We quantify this phenomenon through a generalised intensity difference Λ(2) defined as
| | 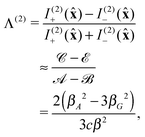 | (21) |
which has equal magnitudes but opposite signs for opposite molecular enantiomers. This
Λ(2) should be larger than
Δ(0)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) by around two orders of magnitude
14 owing to the absence of a contribution from
a2 in the denominator. Moreover,
Λ(2)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) offers different and perhaps more desirable information about the chirality of the molecules than
Δ(0)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) as its numerator is comprised solely of the quantities
βG2 and
βA2 of particular interest. We note that
Λ(2) is −1 times the familiar depolarised right-angled circular intensity difference.
4,5 The latter, however, requires analysed measurements of the intensities of scattered light polarised perpendicular to the scattering plane and is prone to spurious effects,
13 owing to the relatively large intensities of scattered light polarised parallel to the scattering plane. In contrast,
Λ(2) requires measurement only of
unanalysed scattered intensities and should, therefore, be robust in this regard. Theoretical predictions of the variation of the familiar depolarised right-angled circular intensity difference (and hence,
Λ(2)) with frequency for various molecules can be seen in the work of Züber, Wipf and Beratan.
14
6 Example three: lin ⊥ lin illuminating light
We observe finally the novel possibility of using so-called lin ⊥ lin illuminating light which is essentially achiral, rather than illuminating light comprised of a single circularly polarised plane wave, to extract information about the chirality of the molecules through I. We associate with this illuminating light a quantity analogous to Δ(0)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) that is impervious to spurious contributions attributable to circular dichroism whilst being of a different form. Lin ⊥ lin light is employed for example in the laser cooling of atoms.27
) that is impervious to spurious contributions attributable to circular dichroism whilst being of a different form. Lin ⊥ lin light is employed for example in the laser cooling of atoms.27
Consider then a superposition of two linearly polarised plane waves of equal amplitude E0, the first of which is polarised along the x axis and propagates in the z direction whilst the second is polarised along the y axis and propagates in the −z direction as
Ẽ(3) = E0i![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz) − E0ŷ exp(ikz) − E0ŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ikz), exp(−ikz), |
| | ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) (3) = E0iŷ (3) = E0iŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz)/c − E0 exp(ikz)/c − E0![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ikz)/c. exp(−ikz)/c. | (22) |
It should be noted that we only have one form of illuminating light here, in contrast to examples zero, one and two where there were two forms of illuminating light which we distinguished using plus and minus signs. In the
z = 0 plane,
E and
B rotate in opposite directions which is, by itself, an essentially achiral configuration. The combination of
E,
Band the direction of observation
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
, however,
is chiral in general. In particular, a parity inversion of the illuminating light and the direction of observation
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
=
ŷ through the origin yields a new configuration not superposable upon the old. An essentially equivalent transformation is invoked, however, by leaving the illuminating light unaltered and changing the direction of observation from
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
=
ŷ to
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif)
=
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
. This is depicted in
Fig. 4.
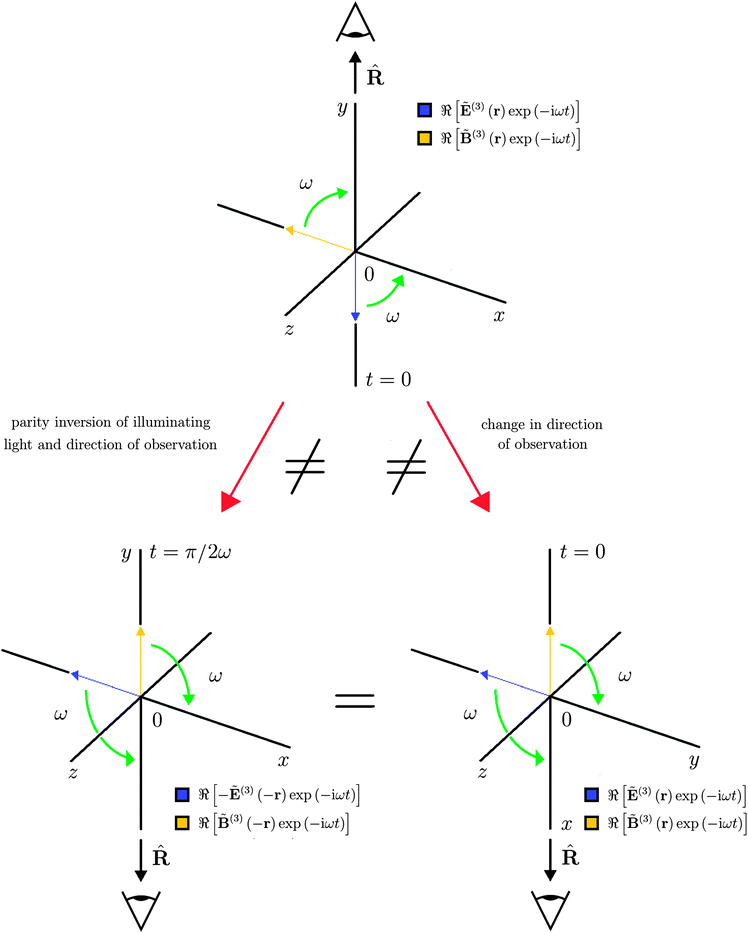 |
| | Fig. 4 A parity inversion of the lin ⊥ lin illuminating light and the direction of observation ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = ŷ through the origin can be mimicked in the z = 0 plane by leaving the light unaltered and changing the direction of observation from = ŷ through the origin can be mimicked in the z = 0 plane by leaving the light unaltered and changing the direction of observation from ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = ŷ to = ŷ to ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = = ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) . . | |
Let us suppose then that the molecules are distributed homogeneously in the z = 0 plane around the origin. We then find that
| | 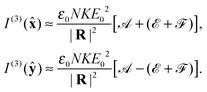 | (23) |
Evidently, information about the chirality of the molecules can be extracted simply by contrasting
I(3)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) and
I(3)(
ŷ). This is of course possible owing to the equivalence described above. The situation is depicted in
Fig. 5.
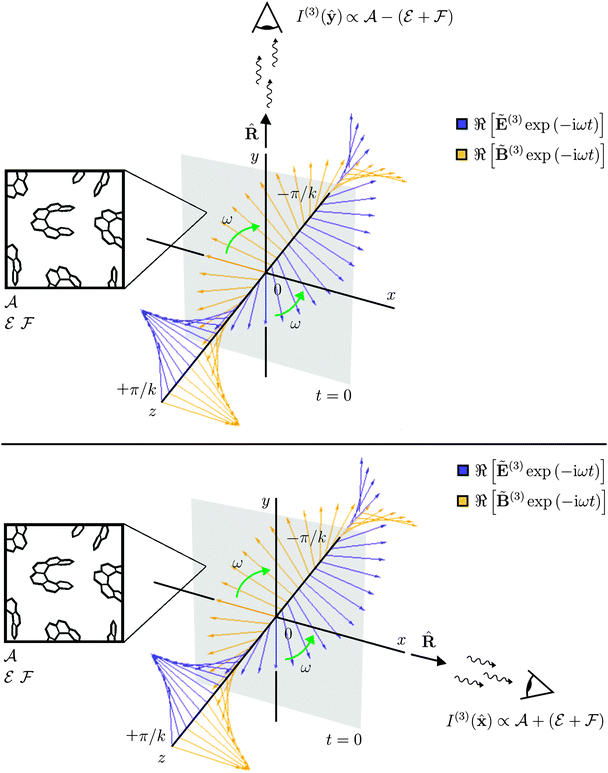 |
| | Fig. 5 Lin ⊥ lin illuminating light, which is by itself essentially achiral, can be employed to probe the chirality of the molecules by making explicit use of the degree of freedom that is the direction in which the intensity of scattered light is observed. | |
We quantify this phenomenon through a generalised intensity difference ϒ(3) defined as
| | 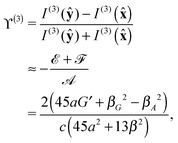 | (24) |
which has equal magnitudes but opposite signs for opposite molecular enantiomers. This
ϒ(3) is of a different character, of course, to
Δ(0),
χ(1) and
Λ(2) as it is dependent upon scattered intensities associated with one form of illuminating light rather than two. It should be comparable in magnitude to
Δ(0)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
)
14 but offers somewhat different information about the chirality of the molecules: the contributions made by
βG2 and
βA2 to
ϒ(3) are of opposite sign to those in
Δ(0)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
) and the former is 13 times smaller. Although we have assumed the illuminating light to be off resonance, there will always exist in reality some absorption of the illuminating light by the molecules. Owing to circular dichroism: the differential absorption of left- and right-handed circularly polarised light,
Δ(0)(
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
),
χ(1) and
Λ(2) will therefore suffer from spurious contributions attributable not to light scattering but rather, to luminescence. By its very nature,
ϒ(3), however, is impervious to such contributions. Moreover, lin ⊥ lin illuminating light will be absorbed at the same rate by opposite molecular enantiomers, as it is essentially achiral.
7 Discussion
We have demonstrated that natural Rayleigh optical activity can be probed using illuminating light comprised of two plane waves that are counter propagating and that this permits new possibilities for the study of molecular chirality. Exploitation of these possibilities requires, however, that the scattering molecules be confined to a plane, in which case their number and hence, the scattered intensity, is necessarily reduced relative to that attainable in a fully homogeneous sample. It is unclear to us at present whether this limitation can be overcome simply. In experiment, such confinement might be realised by depositing the molecules onto a surface.30 Of course, additional effects associated with the surface, such as reflection and refraction of the illuminating light and molecular orientation,31 would then have to be considered with care.
For our two-plane-wave examples, we restricted our attention to right-angled observation which is particularly well suited to experiment as it ‘avoids’ the illuminating light as much as possible. Nevertheless, more information about the chirality of the molecules may be extracted by exploring other scattering geometries, as has been suggested for illuminating light comprised of single circularly polarised plane waves.3 Our approach has been centred upon the unanalysed scattered intensity as this is, perhaps, the most readily measurable property of the scattered light. The polarisation properties of the scattered light remain to be explored, however, and may yield additional possibilities. Finally, we highlight the fact that analogous approaches to those undertaken in the present paper can be pursued for other manifestations of optical activity in light scattering. We shall return to these tasks elsewhere.
Appendix A: definitions
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ,
, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,
, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pertain to the molecules as
pertain to the molecules as
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 2(45a2 + 13β2), = 2(45a2 + 13β2), |
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 2(45a2 + β2), = 2(45a2 + β2), |
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) = 4(45aG′ − 13βG2 + βA2)/c, = 4(45aG′ − 13βG2 + βA2)/c, |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 8(−45aG′ + 5βG2 + 3βA2)/c, = 8(−45aG′ + 5βG2 + 3βA2)/c, |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 4(−45aG′ − βG2 − 3βA2)/c, = 4(−45aG′ − βG2 − 3βA2)/c, |
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = 16βA2/c, = 16βA2/c, | (25) |
for
| β2 = (3αabαab − αaaαbb)/2, |
| βG2 = (3αabGab′ − αaaGbb′)/2, |
| | | βA2 = ωεabcαadAbcd/2. | (26) |
a2 and β2 do not distinguish between opposite molecular enantiomers and are strictly positive. They can be measured through a combination of optical refraction and depolarised Rayleigh scattering experiments.3–5β2 is typically an order of magnitude smaller than a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and vanishes entirely for an isotropic molecule.4,5aG′, βG2 and βA2do distinguish between opposite molecular enantiomers however, by taking on equal magnitudes but opposite signs.§aG′ can be measured through a combination of optical refraction and optical rotation experiments.3–5 In contrast, βG2 and βA2cannot be readily measured by other means and they are, therefore, quantities of particular interest.5,14aG′/c, βG2/c and βA2/c are typically three to five orders of magnitude smaller than a2.4,5
14 and vanishes entirely for an isotropic molecule.4,5aG′, βG2 and βA2do distinguish between opposite molecular enantiomers however, by taking on equal magnitudes but opposite signs.§aG′ can be measured through a combination of optical refraction and optical rotation experiments.3–5 In contrast, βG2 and βA2cannot be readily measured by other means and they are, therefore, quantities of particular interest.5,14aG′/c, βG2/c and βA2/c are typically three to five orders of magnitude smaller than a2.4,5
W = W(r), Tab = Tab(r), H = H(r), S = S(r), Nab = Nab(r) and Xab = Xab(r) pertain to the illuminating light as
| | 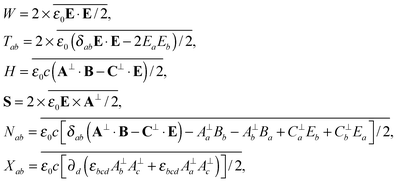 | (27) |
with
δab the Kronecker delta and
A⊥ =
A⊥(
r,
t) and
C⊥ =
C⊥(
r,
t) the transverse, gauge-invariant pieces of potentials defined generally for the charge-free Maxwell equations such that
E = −∂
A⊥/∂
t = −
ε0μ0 ∇ ×
C⊥ and
B = ∇ ×
A⊥ = −∂
C⊥/∂
t.
28,29W,
Tab and
S can be identified as being (twice the cycle-averaged forms of the electric pieces of) an energy density,
15 a linear momentum flux density
15 and a spin density
16 of the illuminating light whereas
H and
Nab can be identified as being (the cycle-averaged forms of) a helicity density
¶![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17,32
17,32 and an
ab infra zilch density
18 of the same. Whereas the energy and linear momentum of light are rather well established, the helicity, spin and
ab infra zilches of light have only recently been scrutinised: they are manifestly intrinsic angular momenta associated with various rotational symmetries inherent in the charge-free Maxwell equations.
16–21Xab is unfamiliar to us and vanishes, in fact, for illuminating light comprised of a single plane wave. It is non vanishing in general, however. We could have incorporated
Xab into part of
Nab whilst retained the interpretation of the latter as being the (cycle-averaged form) of an
ab infra zilch density, as
Xab is a total divergence which vanishes when integrated over all space. Indeed, the identification of
W,
Tab,
H,
S,
Nab and
Xab in
(8) is neither fundamental nor unique. Nevertheless, it provides us with a simple physical picture.
Acknowledgements
This work was supported by the Carnegie Trust for the Universities of Scotland and the Engineering and Physical Sciences Research Council (EPSRC) grant number EP/I012451/1; “Challenges in Orbital Angular Momentum”. We thank Laurence D Barron for his helpful correspondences and Václav Potoček for his assistance in producing the figures.
References
- P. W. Atkins and L. D. Barron, Rayleigh scattering of polarized photons by molecules, Mol. Phys., 1969, 16, 453–466 CrossRef CAS.
- L. D. Barron and A. D. Buckingham, Rayleigh and Raman scattering from optically active molecules, Mol. Phys., 1971, 20, 1111–1119 CrossRef CAS.
- D. L. Andrews, Rayleigh and Raman optical activity: An analysis of the dependence on scattering angle, J. Chem. Phys., 1980, 72, 4141–4144 CrossRef CAS PubMed.
-
D. P. Craig and T. Thirunamachandran, Molecular Quantum Electrodynamics: An Introduction to Radiation Molecule Interactions, Dover, New York, 1998 Search PubMed.
-
L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 2004 Search PubMed.
- L. D. Barron and A. D. Buckingham, Rayleigh and Raman scattering by molecules in magnetic fields, Mol. Phys., 1972, 23, 145–150 CrossRef CAS.
- A. D. Buckingham and R. E. Raab, Electric-field-induced differential scattering of right and left circularly polarized light, Proc. R. Soc. London, Ser. A, 1975, 345, 365–377 CrossRef.
- L. D. Barron, M. P. Bogaard and A. D. Buckingham, Raman scattering of circularly polarized light by optically active molecules, J. Am. Chem. Soc., 1973, 95, 603–605 CrossRef CAS.
- L. D. Barron, Magnetic vibrational optical activity in the resonance Raman spectrum of ferrocytochrome c, Nature, 1975, 257, 372–374 CrossRef CAS.
- A. D. Buckingham and R. A. Shatwell, Linear electro-optic effect in gases, Phys. Rev. Lett., 1980, 45, 21–25 CrossRef CAS.
- L. D. Barron, F. Zhu, L. Hecht, G. E. Tranter and N. W. Isaacs, Raman optical activity: An incisive probe of molecular chirality and biomolecular structure, J. Mol. Struct., 2007, 834, 7–16 CrossRef PubMed.
- L. D. Barron and A. D. Buckingham, Vibrational optical activity, Chem. Phys. Lett., 2010, 492, 199–213 CrossRef CAS PubMed.
- Private communication with Laurence D Barron.
- G. Züber, P. Wipf and D. N. Beratan, Exploring the optical activity tensor by anisotropic Rayleigh optical activity scattering, ChemPhysChem, 2008, 9, 265–271 CrossRef PubMed.
-
J. D. Jackson, Classical Electrodynamics, Wiley, New York, 1999 Search PubMed.
- S. M. Barnett, Rotation of electromagnetic fields and the nature of optical angular momentum, J. Mod. Opt., 2010, 57, 1339–1343 CrossRef PubMed.
- S. M. Barnett, R. P. Cameron and A. M. Yao, Duplex symmetry and its relation to the conservation of optical helicity, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 013845 CrossRef.
- R. P. Cameron, S. M. Barnett and A. M. Yao, Optical helicity, optical spin and related quantities in electromagnetic theory, New J. Phys., 2012, 14, 053050 CrossRef.
- S. J. van Enk and G. Nienhuis, Spin and orbital angular momentum of photons, Europhys. Lett., 1994, 25, 497–501 CrossRef.
- S. J. van Enk and G. Nienhuis, Commutation rules and eigenvalues of spin and orbital angular momentum of radiation fields, J. Mod. Opt., 1994, 41, 963–977 CrossRef.
- R. P. Cameron and S. M. Barnett, Electric-magnetic symmetry and Noether's theorem, New J. Phys., 2012, 14, 123019 CrossRef.
- R. P. Cameron, S. M. Barnett and A. M. Yao, Optical helicity of interfering waves, J. Mod. Opt., 2014, 61, 25–31 CrossRef.
- M. F. Maestre, C. Bustamante, T. L. Hayes, J. A. Subirana and I. Tinoco, Differential scattering of circularly polarized light by the helical sperm head of the octopus Eledone cirrhosa, Nature, 1982, 298, 773–774 CrossRef CAS.
- Y. Tang and A. E. Cohen, Optical chirality and its interaction with matter, Phys. Rev. Lett., 2010, 104, 163901 CrossRef.
- Y. Tang and A. E. Cohen, Enhanced enantioselectivity in excitation of chiral molecules by superchiral light, Science, 2011, 332, 333–336 CrossRef CAS PubMed.
- Y. Aharonov, F. Colombo, I. Sabadini and J. Tollaksen, Some mathematical properties of superoscillations, J. Phys. A: Math. Theor., 2011, 44, 365304 CrossRef.
- J. Dalibard and C. Cohen-Tannoudji, Laser cooling below the Doppler limit by polarization gradients: simple theoretical models, J. Opt. Soc. Am. B, 1989, 6, 2023–2045 CrossRef CAS.
-
H. Bateman, The Mathematical Analysis of Electrical and Optical Wave-Motion on the Basis of Maxwell's Equations, Cambridge University Press, Cambridge, 1915 Search PubMed.
- R. P. Cameron, On the ‘second potential’ in electrodynamics, J. Opt., 2014, 16, 015708 CrossRef.
- S. Guy, L. Guy, A. Bensalah-Ledoux, A. Pereira, V. Grenard, O. Cosso and T. Vautey, Pure organic thin films with high isotropic optical activity synthesised by UV pulsed laser deposition, J. Mater. Chem., 2009, 19, 7093–7097 RSC.
- L. Hecht and L. D. Barron, Rayleigh and Raman optical activity from chiral surfaces, Chem. Phys. Lett., 1994, 225, 525–530 CrossRef CAS.
- D. J. Candlin, Analysis of the new conservation law in electromagnetic theory, II Nuovo Cimento, 1965, 37, 1390–1395 CrossRef.
Footnotes |
| † In experiment, single beams of light that resemble plane waves. |
| ‡ Δ(0) differs in sign from the circular intensity difference introduced in ref. 2. |
| § βG2 and βA2 can be positive or negative, in spite of the misleading but standard notation.14 |
| ¶ For strictly monochromatic light, this helicity density is time independent and cycle averaging is, therefore, inconsequential. |
|
| This journal is © the Owner Societies 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–12,14 We observe, however, that optical activity in light scattering can also be probed, in general, using other types of illuminating light and that this introduces new possibilities for the study of molecules and atoms. In the present paper, we demonstrate this explicitly for natural Rayleigh optical activity which, we suggest, could be exploited as a new form of spectroscopy for chiral molecules through the use of illuminating light comprised of two plane waves that are counter propagating.
1–12,14 We observe, however, that optical activity in light scattering can also be probed, in general, using other types of illuminating light and that this introduces new possibilities for the study of molecules and atoms. In the present paper, we demonstrate this explicitly for natural Rayleigh optical activity which, we suggest, could be exploited as a new form of spectroscopy for chiral molecules through the use of illuminating light comprised of two plane waves that are counter propagating. the speed of light in vacuum. Complex quantities are indicated as such using a tilde. Unit vectors are indicated as such using a circumflex.
the speed of light in vacuum. Complex quantities are indicated as such using a tilde. Unit vectors are indicated as such using a circumflex.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) =
= ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) (r) satisfying
(r) satisfying![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) = 0,
= 0,![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) ,
,![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) = −ε0μ0iωẼ,
= −ε0μ0iωẼ,![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) (n)a
(n)a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (n)ab
(n)ab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) ′(n)a
′(n)a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) (n)a,
(n)a, ![[capital Theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e134.gif) (n)ab and
(n)ab and ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) ′(n)a related to the illuminating light as
′(n)a related to the illuminating light as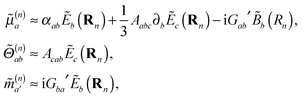
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) s
s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iωt)],
exp(−iωt)],![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) sa of the complex quantities Ẽs = Ẽs(
sa of the complex quantities Ẽs = Ẽs(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ) and
) and ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) s =
s = ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) s(
s(![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ) related to the oscillations in the charge and current distributions of the molecules as5
) related to the oscillations in the charge and current distributions of the molecules as5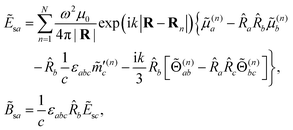
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ) of the scattered light seen at R follows from Poynting's vector as
) of the scattered light seen at R follows from Poynting's vector as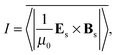
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ,
, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,
, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ,
, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) of the molecules and six related properties W, Tab, H, S, Nab and Xab of the illuminating light:
of the molecules and six related properties W, Tab, H, S, Nab and Xab of the illuminating light: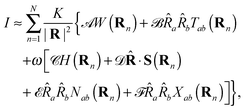
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and
and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) are equal for opposite molecular enantiomers and are thus insensitive to the chirality of the molecules, whilst W and Tab pertain to the energy and linear momentum of the illuminating light.
are equal for opposite molecular enantiomers and are thus insensitive to the chirality of the molecules, whilst W and Tab pertain to the energy and linear momentum of the illuminating light. ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ,
, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , however, each assume equal magnitudes but opposite signs for opposite molecular enantiomers and so are sensitive to the chirality of the molecules, whilst H, S and Nab pertain to the helicity, spin and ab infra zilches of the illuminating light, these being manifestly intrinsic rotation angular momenta.16–21 Explicit expressions for these and Xab are given in Appendix A.
, however, each assume equal magnitudes but opposite signs for opposite molecular enantiomers and so are sensitive to the chirality of the molecules, whilst H, S and Nab pertain to the helicity, spin and ab infra zilches of the illuminating light, these being manifestly intrinsic rotation angular momenta.16–21 Explicit expressions for these and Xab are given in Appendix A.
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) of observation coincides with the direction of propagation of a plane-wave component of the illuminating light, which will then interfere with the scattered light as Rayleigh scattering is a coherent process.4,5 Moreover, having been derived specifically for illuminating light that is (otherwise) freely propagating in accord with the charge-free Maxwell equations, (8) is not appropriate for illuminating light the electric field of which possesses a non-vanishing irrotational component, such as may be found in the near field of a radiating structure, for example. We have refrained from exhibiting a generalised structure factor (inter-molecule cross terms4) in (8) as it makes no contribution in the examples that follow and in most other geometries besides.
of observation coincides with the direction of propagation of a plane-wave component of the illuminating light, which will then interfere with the scattered light as Rayleigh scattering is a coherent process.4,5 Moreover, having been derived specifically for illuminating light that is (otherwise) freely propagating in accord with the charge-free Maxwell equations, (8) is not appropriate for illuminating light the electric field of which possesses a non-vanishing irrotational component, such as may be found in the near field of a radiating structure, for example. We have refrained from exhibiting a generalised structure factor (inter-molecule cross terms4) in (8) as it makes no contribution in the examples that follow and in most other geometries besides.![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ± iŷ)
± iŷ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz),
exp(ikz),![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) (0)± = E0(∓i
(0)± = E0(∓i![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + ŷ)
+ ŷ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz)/c,
exp(ikz)/c,![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , ŷ (and ẑ) unit vectors in the x, y (and z) directions and where the upper and lower signs yield left- and right-handed circular polarisation in the optics convention,15 which we adopt. This is both the prototypical type of light possessing non-vanishing helicity, spin and ab infra zilches17,18 and the prototypical type of chiral light:5 as time passes, E and B rotate with a phase that varies in z such that they trace out cylindrical helices, the chiralities of which differ for the upper and lower signs in (9). Accordingly
, ŷ (and ẑ) unit vectors in the x, y (and z) directions and where the upper and lower signs yield left- and right-handed circular polarisation in the optics convention,15 which we adopt. This is both the prototypical type of light possessing non-vanishing helicity, spin and ab infra zilches17,18 and the prototypical type of chiral light:5 as time passes, E and B rotate with a phase that varies in z such that they trace out cylindrical helices, the chiralities of which differ for the upper and lower signs in (9). Accordingly![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) a
a![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) bT(0)ab± =
bT(0)ab± = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) z2ε0E02,
z2ε0E02,![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ·S(0)± = ±
·S(0)± = ±![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) zε0E02/ω,
zε0E02/ω,![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) a
a![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) bN(0)ab± = ±
bN(0)ab± = ±![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) z2ε0E02/ω,
z2ε0E02/ω,![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) a
a![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) bX(0)ab± = 0,
bX(0)ab± = 0,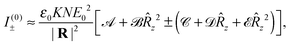
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) say;
say;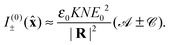

![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) ) defined as‡
) defined as‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2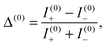
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = sin
= sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + cos
+ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕẑ and find that
ϕẑ and find that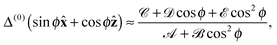
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ;
;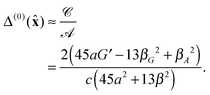
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) that can be made larger in magnitude and may, therefore, be more amenable to observation in experiment.
) that can be made larger in magnitude and may, therefore, be more amenable to observation in experiment.
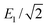 and propagates in the z direction whilst the second has amplitude
and propagates in the z direction whilst the second has amplitude 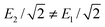 and propagates in the −z direction as
and propagates in the −z direction as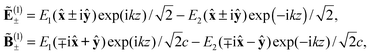
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , we find that
, we find that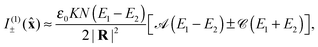
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) contribution to I(1)±(
contribution to I(1)±(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) is reduced relative to the chirally sensitive
) is reduced relative to the chirally sensitive ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) contribution, albeit at the expense of an overall reduction in I(1)±(
contribution, albeit at the expense of an overall reduction in I(1)±(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ). This occurs because the chirally insensitive
). This occurs because the chirally insensitive ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) contribution to I(1)±(
contribution to I(1)±(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) is driven by E alone through
) is driven by E alone through ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) whilst the chirally sensitive
whilst the chirally sensitive ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) contribution is driven instead by both E and B through
contribution is driven instead by both E and B through ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) : in the latter case, the unusually high degree of twisting exhibited by E in the vicinity of the z = 0 plane, where the molecules reside, together with the relatively large magnitude of Bcompensates somewhat for the small magnitude of E there. The situation is depicted in Fig. 2.
: in the latter case, the unusually high degree of twisting exhibited by E in the vicinity of the z = 0 plane, where the molecules reside, together with the relatively large magnitude of Bcompensates somewhat for the small magnitude of E there. The situation is depicted in Fig. 2.
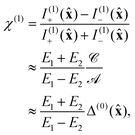
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) and diverges, in fact, as |E1 − E2| → 0 (and I(1)±(
) and diverges, in fact, as |E1 − E2| → 0 (and I(1)±(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) → 0). In reality, such enhancements of χ(1) relative to Δ(0) are limited by contributions to the m′(n)a induced by B, which we have omitted explicitly from our analysis. Nevertheless, gains up to three orders of magnitude may be possible.4,5,24,25
) → 0). In reality, such enhancements of χ(1) relative to Δ(0) are limited by contributions to the m′(n)a induced by B, which we have omitted explicitly from our analysis. Nevertheless, gains up to three orders of magnitude may be possible.4,5,24,25
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) that is significantly larger in magnitude whilst offering different and perhaps more desirable information about the chirality of the molecules. This quantity may, therefore, be more suitable for observation in experiment. σ–σ light is employed for example in the laser cooling of atoms.27
) that is significantly larger in magnitude whilst offering different and perhaps more desirable information about the chirality of the molecules. This quantity may, therefore, be more suitable for observation in experiment. σ–σ light is employed for example in the laser cooling of atoms.27
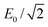 , the first of which propagates in the z direction whilst the second propagates in the −z direction as
, the first of which propagates in the z direction whilst the second propagates in the −z direction as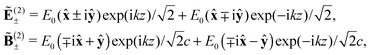
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , we find that
, we find that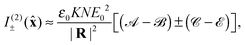
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) contains no isotropic contributions, either chirally insensitive: a2, or chirally sensitive: aG′. It does, however, possess non-vanishing anisotropic contributions, both chirally insensitive: β2, and chirally sensitive: βG2 and βA2. This may be understood simply by recalling that an oscillating electric dipole moment radiates no energy on axis and so an isotropically polarisable molecular species would, to the order of present interest, exhibit no scattering in the direction
) contains no isotropic contributions, either chirally insensitive: a2, or chirally sensitive: aG′. It does, however, possess non-vanishing anisotropic contributions, both chirally insensitive: β2, and chirally sensitive: βG2 and βA2. This may be understood simply by recalling that an oscillating electric dipole moment radiates no energy on axis and so an isotropically polarisable molecular species would, to the order of present interest, exhibit no scattering in the direction ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) of observation as the latter lies parallel to the (electric-dipole-inducing) E vectors in the z = 0 plane where the molecules reside. The situation is depicted in Fig. 3.
of observation as the latter lies parallel to the (electric-dipole-inducing) E vectors in the z = 0 plane where the molecules reside. The situation is depicted in Fig. 3.

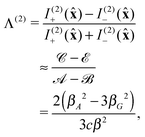
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) by around two orders of magnitude14 owing to the absence of a contribution from a2 in the denominator. Moreover, Λ(2)(
) by around two orders of magnitude14 owing to the absence of a contribution from a2 in the denominator. Moreover, Λ(2)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) offers different and perhaps more desirable information about the chirality of the molecules than Δ(0)(
) offers different and perhaps more desirable information about the chirality of the molecules than Δ(0)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) as its numerator is comprised solely of the quantities βG2 and βA2 of particular interest. We note that Λ(2) is −1 times the familiar depolarised right-angled circular intensity difference.4,5 The latter, however, requires analysed measurements of the intensities of scattered light polarised perpendicular to the scattering plane and is prone to spurious effects,13 owing to the relatively large intensities of scattered light polarised parallel to the scattering plane. In contrast, Λ(2) requires measurement only of unanalysed scattered intensities and should, therefore, be robust in this regard. Theoretical predictions of the variation of the familiar depolarised right-angled circular intensity difference (and hence, Λ(2)) with frequency for various molecules can be seen in the work of Züber, Wipf and Beratan.14
) as its numerator is comprised solely of the quantities βG2 and βA2 of particular interest. We note that Λ(2) is −1 times the familiar depolarised right-angled circular intensity difference.4,5 The latter, however, requires analysed measurements of the intensities of scattered light polarised perpendicular to the scattering plane and is prone to spurious effects,13 owing to the relatively large intensities of scattered light polarised parallel to the scattering plane. In contrast, Λ(2) requires measurement only of unanalysed scattered intensities and should, therefore, be robust in this regard. Theoretical predictions of the variation of the familiar depolarised right-angled circular intensity difference (and hence, Λ(2)) with frequency for various molecules can be seen in the work of Züber, Wipf and Beratan.14
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) that is impervious to spurious contributions attributable to circular dichroism whilst being of a different form. Lin ⊥ lin light is employed for example in the laser cooling of atoms.27
) that is impervious to spurious contributions attributable to circular dichroism whilst being of a different form. Lin ⊥ lin light is employed for example in the laser cooling of atoms.27
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz) − E0ŷ
exp(ikz) − E0ŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ikz),
exp(−ikz),![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) (3) = E0iŷ
(3) = E0iŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ikz)/c − E0
exp(ikz)/c − E0![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ikz)/c.
exp(−ikz)/c.![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) , however, is chiral in general. In particular, a parity inversion of the illuminating light and the direction of observation
, however, is chiral in general. In particular, a parity inversion of the illuminating light and the direction of observation ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = ŷ through the origin yields a new configuration not superposable upon the old. An essentially equivalent transformation is invoked, however, by leaving the illuminating light unaltered and changing the direction of observation from
= ŷ through the origin yields a new configuration not superposable upon the old. An essentially equivalent transformation is invoked, however, by leaving the illuminating light unaltered and changing the direction of observation from ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) = ŷ to
= ŷ to ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) =
= ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) . This is depicted in Fig. 4.
. This is depicted in Fig. 4.
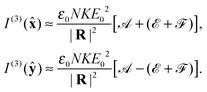
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) and I(3)(ŷ). This is of course possible owing to the equivalence described above. The situation is depicted in Fig. 5.
) and I(3)(ŷ). This is of course possible owing to the equivalence described above. The situation is depicted in Fig. 5.
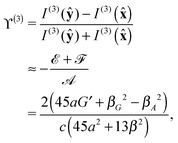
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) )14 but offers somewhat different information about the chirality of the molecules: the contributions made by βG2 and βA2 to ϒ(3) are of opposite sign to those in Δ(0)(
)14 but offers somewhat different information about the chirality of the molecules: the contributions made by βG2 and βA2 to ϒ(3) are of opposite sign to those in Δ(0)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ) and the former is 13 times smaller. Although we have assumed the illuminating light to be off resonance, there will always exist in reality some absorption of the illuminating light by the molecules. Owing to circular dichroism: the differential absorption of left- and right-handed circularly polarised light, Δ(0)(
) and the former is 13 times smaller. Although we have assumed the illuminating light to be off resonance, there will always exist in reality some absorption of the illuminating light by the molecules. Owing to circular dichroism: the differential absorption of left- and right-handed circularly polarised light, Δ(0)(![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ), χ(1) and Λ(2) will therefore suffer from spurious contributions attributable not to light scattering but rather, to luminescence. By its very nature, ϒ(3), however, is impervious to such contributions. Moreover, lin ⊥ lin illuminating light will be absorbed at the same rate by opposite molecular enantiomers, as it is essentially achiral.
), χ(1) and Λ(2) will therefore suffer from spurious contributions attributable not to light scattering but rather, to luminescence. By its very nature, ϒ(3), however, is impervious to such contributions. Moreover, lin ⊥ lin illuminating light will be absorbed at the same rate by opposite molecular enantiomers, as it is essentially achiral.
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ,
, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) ,
, ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) pertain to the molecules as
pertain to the molecules as![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 2(45a2 + 13β2),
= 2(45a2 + 13β2),![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = 2(45a2 + β2),
= 2(45a2 + β2),![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) = 4(45aG′ − 13βG2 + βA2)/c,
= 4(45aG′ − 13βG2 + βA2)/c,![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 8(−45aG′ + 5βG2 + 3βA2)/c,
= 8(−45aG′ + 5βG2 + 3βA2)/c,![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 4(−45aG′ − βG2 − 3βA2)/c,
= 4(−45aG′ − βG2 − 3βA2)/c,![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = 16βA2/c,
= 16βA2/c,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and vanishes entirely for an isotropic molecule.4,5aG′, βG2 and βA2do distinguish between opposite molecular enantiomers however, by taking on equal magnitudes but opposite signs.§aG′ can be measured through a combination of optical refraction and optical rotation experiments.3–5 In contrast, βG2 and βA2cannot be readily measured by other means and they are, therefore, quantities of particular interest.5,14aG′/c, βG2/c and βA2/c are typically three to five orders of magnitude smaller than a2.4,5
14 and vanishes entirely for an isotropic molecule.4,5aG′, βG2 and βA2do distinguish between opposite molecular enantiomers however, by taking on equal magnitudes but opposite signs.§aG′ can be measured through a combination of optical refraction and optical rotation experiments.3–5 In contrast, βG2 and βA2cannot be readily measured by other means and they are, therefore, quantities of particular interest.5,14aG′/c, βG2/c and βA2/c are typically three to five orders of magnitude smaller than a2.4,5
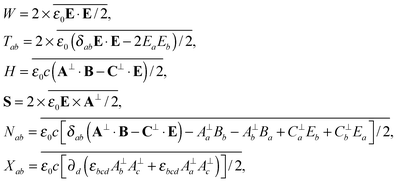
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17,32 and an ab infra zilch density18 of the same. Whereas the energy and linear momentum of light are rather well established, the helicity, spin and ab infra zilches of light have only recently been scrutinised: they are manifestly intrinsic angular momenta associated with various rotational symmetries inherent in the charge-free Maxwell equations.16–21Xab is unfamiliar to us and vanishes, in fact, for illuminating light comprised of a single plane wave. It is non vanishing in general, however. We could have incorporated Xab into part of Nab whilst retained the interpretation of the latter as being the (cycle-averaged form) of an ab infra zilch density, as Xab is a total divergence which vanishes when integrated over all space. Indeed, the identification of W, Tab, H, S, Nab and Xab in (8) is neither fundamental nor unique. Nevertheless, it provides us with a simple physical picture.
17,32 and an ab infra zilch density18 of the same. Whereas the energy and linear momentum of light are rather well established, the helicity, spin and ab infra zilches of light have only recently been scrutinised: they are manifestly intrinsic angular momenta associated with various rotational symmetries inherent in the charge-free Maxwell equations.16–21Xab is unfamiliar to us and vanishes, in fact, for illuminating light comprised of a single plane wave. It is non vanishing in general, however. We could have incorporated Xab into part of Nab whilst retained the interpretation of the latter as being the (cycle-averaged form) of an ab infra zilch density, as Xab is a total divergence which vanishes when integrated over all space. Indeed, the identification of W, Tab, H, S, Nab and Xab in (8) is neither fundamental nor unique. Nevertheless, it provides us with a simple physical picture.



