Nanoscale control of graphene electrodes

Abstract

Single layer graphene nano-gaps are fabricated by applying the method of feedback-controlled electroburning to notched ribbon devices, which are plasma etched from CVD grown graphene that is wet-transferred onto pre-patterned metal electrodes. Electrical and structural characterizations show that nanometer size gaps form at the center of the notch. We have processed a total number of 1079 devices using this method with a fabrication yield of 71%. Our results demonstrate precise control over the size and position of the nano-gaps, and open up the possibility of graphene electrodes for large-scale integrated molecular devices.

---

Integrated circuits where each functional unit is formed by only a single molecule will be the ultimate form of electronic device scaling.¹ Experimental demonstrations of molecular device functionality include rectifiers,^2,3 switches⁴ and transistors,^5,6 and effects of quantum interference have been observed in charge transport through single molecules.⁷ To harness the full potential of individual molecules, technological progress towards robust and identical three-terminal devices is necessary, including alternative electrode materials that are stable at room temperature. Graphene is a promising candidate for the replacement of metal electrodes because of the high-temperature stability of the covalent bond-structure (the strongest C–C bond is the three fold coordinated sp² bond in graphene), the ability to anchor diverse molecules covalently or using π–π stacking and the reduced screening of the gate-field due to the extreme thinness of the electrodes (a single atomic layer). Wafer-scale growth⁸ and integration of graphene with conventional silicon electronics⁹ have recently been demonstrated.

Recent studies have reported two distinct approaches towards the fabrication of graphene-based molecular junctions based on electroburning^10,11 and plasma etching.¹² The former approach relies on the current induced breakdown of graphene. The size of the nano-gaps can be controlled by either varying the partial pressure of oxygen¹¹ or by feedback-controlled electroburning,¹⁰ a method similar to feedback-controlled electromigration.^13,14 The feedback allows for precise control over the gap size which is typically 1–2 nanometers. Although the fabrication yield of electroburning is high (92%¹⁰ to 95%¹¹), the position of nano-gaps fabricated is not well controlled due to the random nature of the electroburning process. The latter approach is based on plasma etching of chemical vapour deposition (CVD) grown graphene point contacts. Over-etching the lithographically defined pattern produces nano-gaps that are less than or equal to nanometer. The use of large area CVD graphene enables the fabrication of nano-gaps arrays on a wafer scale with precise control over the position of the nano-gaps, however the yield of the plasma etched devices is only 33%. In this letter we present a method of fabricating arrays of single layer graphene nano-gaps that combines these two approaches and provides a viable route for achieving high-yield fabrication on a wafer scale.

The nano-gap fabrication strategy comprises a lithography process where the minimum feature size is 200 nm followed by a feedback-controlled electroburning process which results in 0.5–2.5 nm sized gaps. We have processed a total number of 1079 devices resulting in 776 nano-gaps. In this paper we characterized the devices before and after the electroburning process and studied the geometry of individual nano-gaps using atomic force microscopy (AFM). We have further investigated the nano-gap formation by modelling the current density in our device geometry.

We fabricated the graphene devices using a passive-first active-last process flow, where the graphene is transferred onto a pre-patterned silicon chip as illustrated in Fig. 1(a–d). This passive-first active-last fabrication process enables integration of graphene into conventional silicon logic circuits.⁹ Single layer graphene (SLG) was prepared using a 1% CH₄:Ar gas mixture at atmospheric pressure on liquid copper in a CVD furnace at 1090 °C. This method produces large area single layer graphene.¹⁵ PMMA was spun across the SLG/copper stack before etching the copper away with a 0.1 M solution of ammonium persulfate. The PMMA/graphene stack was rinsed in DI water before being transferred onto the pre-patterned 1 × 1 cm² Si/SiO₂ chip (Fig. 1(a and b)). Each chip contains 540 pairs of Cr/Au electrodes that were patterned using electron beam lithography and metal evaporation. After the SLG is transferred onto the metal electrodes it is patterned into notched ribbons by exposing a negative resist using electron beam lithography followed by oxygen plasma etching (Fig. 1(c and d)). Before electroburning the devices were annealed at 350 °C for 1 hour in an Ar atmosphere to remove residual resist.

Fig. 1 (a–d) Schematics for the process flow of our device fabrication. (e) Scanning electron micrograph of a single layer graphene (SLG) notched ribbon between two Cr/Au contacts. (f) Current–voltage (I–V) traces recorded during the feedback-controlled electroburning. The feedback conditions used were ΔI_set = 6, 9, 12 and 15 μA for V_th ≥ 1.9, 1.6, 1.3 and 1.0 V respectively.

Fig. 1(e) shows a scanning electron micrograph of a SLG notched ribbon between two Cr/Au electrodes. The feedback-controlled electroburning is performed in air at room temperature using an automated probestation. A voltage (V) applied across the devices is ramped up at a rate of 0.75 V s⁻¹, while the current (I) is recorded with a 200 μs sampling rate. When the feedback condition, which is set at a drop ΔI_set of the current within the past 15 mV, is met the voltage is ramped down to zero at a rate of 225 V s⁻¹. After each voltage ramp the resistance of the SLG device is measured and the process is repeated until the low-bias resistance exceeds R_set. To prevent the SLG device from electroburning too abruptly at the initial voltage ramps we adjust the feedback condition for each voltage ramp depending on the threshold voltage V_th at which the previous current drop occurred.

A typical evolution of the current–voltage (I–V) traces is shown in Fig. 1(f). The first voltage ramp (red trace in Fig. 1(f)) shows a distinct region of negative differential conductance (NDC). Regions of NDC or ‘kinks’ in the I–V characteristics of single layer graphene devices are a characteristic feature of bipolar transport in single layer graphene.¹⁶ Typically, graphene on SiO₂ is p-doped, with holes being the majority carriers throughout the entire channel. When the source–drain voltage V is increased, the current starts to saturate as the electrochemical potential at the drain end of the channel moves towards the Dirac point. At a particular voltage V_‘kink’, the electrochemical potential at the drain end corresponds to the Dirac point resulting in a pinch-off at the drain contact. By increasing V beyond V_‘kink’ the pinch-off is moved through the channel until the entire channel switches to electron carriers and the current will increase again. The value for V_‘kink’ is dependent on the relative position of the Fermi level from the Dirac point for the graphene electrodes, and is therefore dependent on the doping level. We observe a shift of V_‘kink’ towards lower source–drain voltages with each electroburning voltage ramp event. We attribute this to the removal of residual resist from current annealing.¹⁷ The removal of residual resist shifts the Fermi level closer towards the Dirac point which corresponds to the shift of V_‘kink’ towards lower voltages. This increase in conductance has previously been observed in electroburning of few-layer graphene flakes and is attributed to the removal of residual resist by Joule heating of the graphene. From the AFM image of the device in Fig. 3, it can be observed that close to the notched region, the graphene is much cleaner compared to regions further away. This is an indication of residual resist removal from current annealing during our electroburning process.

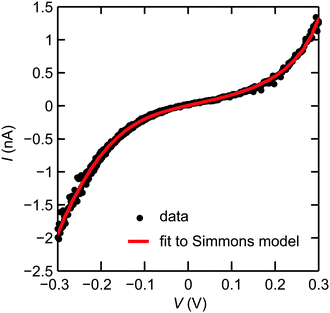
The geometry of the nano-gaps is characterized by measuring the current–voltage curves using the same setup used for the feedback controlled electroburning. Fig. 2 shows a typical I–V trace of a SLG nano-gap after completion of the electroburning process, i.e. after the low-bias resistance becomes larger than R_set. The non-ohmic I–V traces measured after the electroburning process are characteristic of transport through a single tunnel junction. The size of the tunnel-barrier can be estimated by fitting the I–V traces to the Simmons model using the barrier height, width and asymmetry as fitting parameters.^10,18,19 The controllability and reproducibility of the nano-gap fabrication process were investigated by fitting 307 devices to the Simmons model. The average gap-size of 140 devices that underwent the electroburning process with a stop condition R_crit = 300 MΩ is d = 1.42 ± 0.56 nm. For the 167 devices that were processed with a stop condition R_crit = 500 MΩ, the gap-size is d = 1.39 ± 0.46 nm. 94.8% of 307 devices fitted return a gap size within the range of 0.5–2.5 nm, which make these graphene nano-gaps appealing for contacting single molecules in molecular devices. The average fitted barrier heights is 0.24 ± 0.11 eV. Similar barrier heights have previously been observed in electroburned few-layer graphene nano-gaps¹⁰ and in electromigrated metal electrodes.¹⁹

Fig. 2 Typical I–V trace of a SLG nano-gap. The I–V trace was fitted to the Simmons model for tunnelling through a trapezoidal barrier with the fitting parameters: barrier height ϕ = 0.26 eV; barrier width (gap-size) d = 1.50 ± 0.03 nm; and barrier asymmetry α = −0.89 ± 0.05. A fit to the Simmons model of 328 devices yields an average gap-size of 0.5–2.5 for 96.5%.

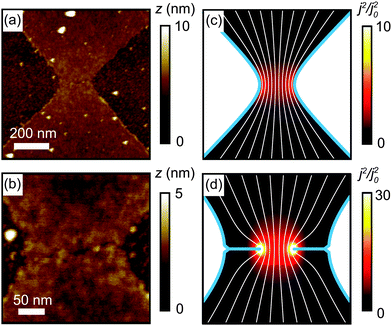Fig. 3 (a, b) AFM images of a typical graphene nano-gap after the electroburning process. Light areas are graphene and dark areas are the SiO₂ substrate. A gap can be discerned in the narrowest part of the notch. Close to the notch, the graphene is free of residual resist due to current annealing. Height profiles alongside and across the nano-gap are shown in the ESI.† (c) Calculated current density profile for a pristine device. The thick solid lines indicate the edges of the device, the narrow stream lines illustrate the current flow. (d) Calculated current density profile in the case of a partially formed nano-gap. The current flows around the cracks extending inwards from the notch apex resulting in a ‘hotspot’ at the crack-tip.

To further investigate the formation of the nano-gaps, we performed AFM on several devices after the electroburning process. Fig. 3(a and b) shows an AFM image of an electroburned nano-gap. The AFM images show that the nano-gap forms at the narrowest part of the notch. The formation of the nano-gap at the narrowest part of the notch can be understood from the fact that the current density, and therefore the Joule heating, will be largest at the this point. We determine the breakdown current as the current at which the feedback condition is met for the first voltage ramp. The breakdown current for the device shown in Fig. 3(a and b) is 310 μA, which corresponds to a current density j = 4.7 × 10⁸ A cm⁻² assuming a van der Waals thickness of 0.355 nm as sheet thickness. Breakdown current densities of j ≈ 5 × 10⁸ A cm⁻² have previously been reported for mechanically exfoliated SLG.²⁰ For 1079 devices we found an average breakdown current of 324 ± 163 μA. Previous studies have suggested that the electroburning process relies on a thermally activated reaction between carbon atoms and oxygen, based on the fact that the nano-gap formation in graphene flakes takes places furthest from the metal electrodes, where the temperature due to Joule heating is highest. Our observation that the nano-gaps form at the point where the current density, and therefore the Joule heating, is maximum verifies this interpretation. The formation of the nano-gaps is expected to be mediated by the breaking of carbon bonds at the graphene edges because of the higher reactivity of the edge-carbon atoms due to incomplete sp²-hybridization.^21,22 We observe that the formation of the nano-gap proceeds via a crack developing across the narrowest region of the notch instead of a gradual narrowing of the entire notch region.

We have investigated the nano-gap formation by calculating the current density profile in the graphene notch. To calculate the current density (j(r) = ∇ρ(r), where ρ(r) is the charge density) as function of position r, the Laplace equation ∇²ρ(r) = 0 was solved using conformal mapping (see ESI†). The current density is highest at the apex of the notch (see Fig. 3(c)), which is where experimentally observe the formation of the nano-gap. Fig. 3(d) shows the current flow around a crack extending from the apex of each notch, which was calculated using a Schwarz transformation.²³ Since the current is forced to flow around the cracks, the current density is highest at the crack-tip. Once a crack forms at the apex of the notch, it is therefore expected to propagate through the material, rather than becoming wider, in accordance with our observations. Our calculations and experimental findings demonstrate the ability to lithographically control the position of the nano-gaps, which allows for the precise alignment of the nano-gaps with other lithographically defined structures.

Table 1 gives an overview of the success rate of the electroburning process for a total number of 1079 devices on 5 chips. We identified three ways in which the electroburning process can fail: (i) the current required to start the electroburning process is larger than the maximum current supplied by our voltage source; (ii) the feedback-control did not ramp the voltage back to zero fast enough, resulting in a nano-gap with an infinite resistance (>100 GΩ); (iii) the feedback-control is too sensitive and ramps the voltage before electroburning occurs. Whereas the second and third failures are intrinsic to the feedback-controlled electroburning process, the first failure occurs if the lithographically defined notch is too wide. Because the first failure is not intrinsic to the electroburning process and could be overcome by using a different voltage source, we define the yield of the electroburning process by only considering those devices where the threshold current is within the range of our setup. Using this definition, we find that the yield of the electroburning process is 85%. The total fabrication yield is 71%.

Table 1 Fabrication yield of the feedback-controlled electroburning process

	# of devices
Devices before electroburning	1079
Threshold current too high	167
Feedback not fast enough	67
Feedback too sensitive	69
Nano-gaps after electroburning	776

---

In this work, we have demonstrated the large scale fabrication of CVD graphene nano-gaps with a yield of 71%, through a combined approach of conventional lithographically defined plasma etching and feedback-controlled electroburning. AFM images display a nano-gap located at the narrowest part of the graphene notched ribbon. Fits of (I–V) data of 307 devices to the Simmons model yield a gap size of 0.5–2.5 nm for 94.8% of the devices. The ability to controllably fabricate and position nanogaps of 0.5–2.5 nm makes this technique an attractive technique for contacting single molecules with lithographically aligned gates. Our use of CVD graphene means that this technique can be scaled up using wafer-scale grown graphene. The passive-first-active-last process adopted in this technique enables integration into conventional silicon logic circuits. This scalable approach paves the way towards employing graphene electrodes for large-scale integrated molecular circuits.

Acknowledgements

C.S.L. thanks Agency for Science Technology and Research (A*STAR) for support. J.A.M. received funding from the Royal Society Newton International Fellowship scheme. J.H.W. thanks the Royal Society for support. This work is supported by the EPSRC Platform Grant Molecular Quantum Devices (EP/J015067/1). We thank Junfeng Wang and Dr Lapo Bogani for the help with the AFM imaging and the useful discussions.

References

1. S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410.
2. A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283.
3. R. M. Metzger, B. Chen, U. Höpfner, M. V. Lakshmikantham, D. Vuillaume, T. Kawai, X. Wu, H. Tachibana, T. V. Hughes, H. Sakurai, J. W. Baldwin, C. Hosch, M. P. Cava, L. Brehmer and G. J. Ashwell, J. Am. Chem. Soc., 1997, 119, 10455–10466.
4. A. S. Blum, J. G. Kushmerick, D. P. Long, C. H. Patterson, J. C. Yang, J. C. Henderson, Y. Yao, J. M. Tour, R. Shashidhar and B. R. Ratna, Nat. Mater., 2005, 4, 167–172.
5. P. L. McEuen, H. Park, J. Park, A. K. L. Lim, E. H. Anderson and A. P. Alivisatos, Nature, 2000, 407, 57–60.
6. S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, J.-L. Brédas, N. Stuhr-Hansen, P. Hedegård and T. Bjørnholm, Nature, 2003, 425, 698–701.
7. C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305–309.
8. J. H. Lee, E. K. Lee, W. J. Joo, Y. Jang, B. S. Kim, J. Y. Lim, S. H. Choi, S. J. Ahn, J. R. Ahn, M. H. Park, C. W. Yang, B. L. Choi, S. W. Hwang and D. Whang, Science, 2014, 344, 286–289.
9. S.-J. Han, A. V. Garcia, S. Oida, K. A. Jenkins and W. Haensch, Nat. Commun., 2014, 5, 3086,  DOI:10.1038/ncomms4086.
10. F. Prins, A. Barreiro, J. W. Ruitenberg, J. S. Seldenthuis, N. Aliaga-Alcalde, L. M. K. Vandersypen and H. S. J. van der Zant, Nano Lett., 2011, 11, 4607–4611.
11. C. Nef, L. Posa, P. Makk, W. Fu, A. Halbritter, C. Schönenberger and M. Calame, Nanoscale, 2014, 6, 7249–7254.
12. Y. Cao, S. Dong, S. Liu, L. He, L. Gan, X. Yu, M. L. Steigerwald, X. Wu, Z. Liu and X. Guo, Angew. Chem., 2012, 124, 12394–12398.
13. D. R. Strachan, D. E. Smith, D. E. Johnston, T. H. Park, M. J. Therien, D. A. Bonnell and A. Johnson, Appl. Phys. Lett., 2005, 86, 043109.
14. F. Prins, T. Hayashi, B. J. A. de Vos van Steenwijk, B. Gao, E. A. Osorio, K. Muraki and H. S. J. van der Zant, Appl. Phys. Lett., 2009, 94, 123108.
15. Y. A. Wu, Y. Fan, S. Speller, G. L. Creeth, J. T. Sadowski, K. He, A. W. Robertson, C. S. Allen and J. H. Warner, ACS Nano, 2012, 6, 5010–5017.
16. I. Meric, M. Y. Han, A. F. Young, B. Ozyilmaz, P. Kim and K. L. Shepard, Nat. Nanotechnol., 2008, 3, 654–659.
17. J. Moser, A. Barreiro and A. Bachtold, Appl. Phys. Lett., 2007, 91, 163513.
18. J. G. Simmons, J. Appl. Phys., 1963, 34, 1793.
19. A. Mangin, A. Anthore, M. L. Della Rocca, E. Boulat and P. Lafarge, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235432.
20. B. Standley, W. Bao, H. Zhang, J. Bruck, C. N. Lau and M. Bockrath, Nano Lett., 2008, 8, 3345–3349.
21. J. H. Warner, M. H. Rümmeli, L. Ge, T. Gemming, B. Montanari, N. M. Harrison, B. Büchner and G. A. D. Briggs, Nat. Nanotechnol., 2009, 4, 500–504.
22. C. Jin, H. Lan, L. Peng, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 205501.
23. K. W. Lodge and G. A. D. Briggs, J. Mater. Sci., 1983, 18, 2354–2360.

---

Footnote

† Electronic supplementary information (ESI) available: Description of the conformal mapping technique used to calculated the current density profiles in Fig. 3. See DOI: 10.1039/c4cp03257h

---