Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing mixed metal halide ammines for ammonia storage using density functional theory and genetic algorithms†
Peter Bjerre
Jensen
ab,
Steen
Lysgaard
a,
Ulrich J.
Quaade
c and
Tejs
Vegge
*a
aDepartment of Energy Conversion and Storage, Technical University of Denmark, Frederiksborgvej 399, DK-4000 Roskilde, Denmark. E-mail: teve@dtu.dk; Fax: +45 4677 5858; Tel: +45 4677 5818
bCenter for Atomic-scale Materials Design, Technical University of Denmark, Fysikvej 311, DK-2800 Kgs. Lyngby, Denmark. E-mail: pbjen@dtu.dk
cAmminex Emmisions Technology A/S, Gladsaxevej 363, DK-2860 Søborg, Denmark. E-mail: ujq@amminex.com
First published on 5th August 2014
Abstract
Metal halide ammines have great potential as a future, high-density energy carrier in vehicles. So far known materials, e.g. Mg(NH3)6Cl2 and Sr(NH3)8Cl2, are not suitable for automotive, fuel cell applications, because the release of ammonia is a multi-step reaction, requiring too much heat to be supplied, making the total efficiency lower. Here, we apply density functional theory (DFT) calculations to predict new mixed metal halide ammines with improved storage capacities and the ability to release the stored ammonia in one step, at temperatures suitable for system integration with polymer electrolyte membrane fuel cells (PEMFC). We use genetic algorithms (GAs) to search for materials containing up to three different metals (alkaline-earth, 3d and 4d) and two different halides (Cl, Br and I) – almost 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 combinations, and have identified novel mixtures, with significantly improved storage capacities. The size of the search space and the chosen fitness function make it possible to verify that the found candidates are the best possible candidates in the search space, proving that the GA implementation is ideal for this kind of computational materials design, requiring calculations on less than two percent of the candidates to identify the global optimum.
000 combinations, and have identified novel mixtures, with significantly improved storage capacities. The size of the search space and the chosen fitness function make it possible to verify that the found candidates are the best possible candidates in the search space, proving that the GA implementation is ideal for this kind of computational materials design, requiring calculations on less than two percent of the candidates to identify the global optimum.
1. Introduction
Ammonia is one of the most important chemicals produced, making it possible for the world's population to grow dramatically, because of its use in fertilizers.1 There is, however, also an interest in using ammonia as a future energy carrier in vehicles2–6 and as an ammonia reservoir for the selective catalytic reduction (SCR) of NOx gases in diesel cars and trucks;7 a segment in rapid growth, in e.g. Asia that has large, unresolved challenges for urban pollution.8 The toxicity of ammonia is, however, a major drawback, making handling and storing difficult. It has been shown that storing ammonia in metal halide ammines can be both safe, by lowering the vapor pressure significantly, and inexpensive.2,9 One of the most studied metal ammines is Mg(NH3)6Cl2,9,10 which has a high hydrogen density, displays good kinetics,11,12 but has an unpractical multi-step release occurring at too high temperatures (450 K, 585 K and 680 K).9,10 Also Sr(NH3)8Cl2 displays a high energy density, but depending on the reaction conditions a mono- or diammine is generally too stable, making the practically available ammonia density at least 12.5% lower.13 Because of this, new materials with high storage capacities, releasing all ammonia, preferably in one step, are needed.For energy storage for transportation usage, it is possible to burn the stored ammonia in an internal combustion engine,14 but this will not reduce the pollution and climate challenges. The energy should therefore be extracted using a fuel cell, which can either run directly on ammonia in a high temperature SOFC,15 in a direct ammonia fuel cell (DAFC) operating at intermediate temperatures,16 or decomposed, and the hydrogen can then be used in a low-17 or high temperature PEMFC,18 which is a much more mature fuel cell technology. If the ammonia is decomposed and used in the PEMFC, there will be energy losses in form of waste heat from both processes – this waste heat can be used to release the stored ammonia making the total system efficiency higher.2 Ultimately the success of energy storage materials depends on the usable energy density, therefore we search for materials releasing all the stored ammonia in one step, with the highest possible weight percent.
Here, we use computational methods to search for new materials because the potential phase space of mixed metal halide ammines is very large, thus experimentally testing all compounds is not practically feasible. We use van der Waal's corrected density functional theory (DFT) calculations (vdW-DF)19–21 to obtain predictive accuracy on the formation enthalpies. DFT is however still a relatively computationally expensive method, which sets a limit on how many structures can be studied, and in how great detail each structure can be studied. Therefore, we are employing a template based screening, where the calculations are performed on structures in known crystal symmetries, which will allow us to investigate electronic trends, selecting materials with improved characteristics, which can then undergo a more detailed computational and experimental investigation. The applied structural templates for the DFT calculations must capture the local coordination well in order to be able describe relative energy differences in the range of only a few kJ mol−1, as discussed previously for related coordination complexes.22,23
It has been shown that it is possible to form multiple stable mixtures, e.g. of alkaline-earth chlorides and bromides, both mixing the halides and the metals, resulting in new stable materials with changed ab- and desorption characteristics, which are not simply the average of the pure metal ammines in the mixture.24 In this work, we identify a number of new, promising mixed metal halide ammines combining a range of different metals and halides for applications as energy carrier in the transportation sector, which first of all requires that the ammonia/energy density is high to be competitive with existing liquid fuels. Furthermore, the elements used should be earth abundant, and thereby also cheaper, and the possible toxicity should be manageable – both during normal operation and in case of traffic accidents. From a practical point of view, a material releasing all stored ammonia in one step is preferred in order to be able to release the stored ammonia fast and in a steady stream when needed. A one-step release in a predefined temperature interval is thus the target of the screening and an analysis of possible intermediate phases is therefore also performed before selecting the most promising candidates. We use the magnesium chloride system9,10 as a model, since a one-step release is more probable in mixed metal halide hexa ammines than octa ammines.
We study materials with a maximum of three different metals in a unit cell containing four metals in total. The allowed metals are alkaline-earth (except Ra) and the 3d and 4d transition metals (except Tc). Because large quantities of materials are needed for automotive applications, earth abundant and non-expensive materials are needed; we have therefore introduced a maximum limit of 25% of expensive metals, defined as Nb, Sc, Ag, Pd, Rh, Ru and Be.25 On the halide side, we allow a maximum of two different of the halides Cl, Br and I at a time, since it is practically difficult to synthesize compounds with multiple halides.26 Fluorides are excluded from the search given the very limited commercial interest due to their toxicity.27
Since the screening is based on template structures, atomic permutations within a specific stoichiometry are not considered explicitly, and structures with the same composition are treated as identical. For a given crystal structure of a mixed metal halide ammine, this is not necessarily correct, but sufficient to investigate e.g. electronic trends systematically. In total, this results in a search space containing almost 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible mixtures resulting in 54
000 possible mixtures resulting in 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible structures to test, as both the energy of the hexa ammine and the empty salt have to be calculated. This large, but not intangible number of combinations of metals and halides, is ideal for testing our genetic algorithm (GA),28–35 an evolutionary guided search technique, which we have earlier successfully implemented to predict the optimal structure of nano particles,36 since it enables an absolute validation of the ability of the algorithm to identify the most fit materials combinations. The proposed algorithm implementation is part of the Atomic Simulation Environment (ASE), which is freely available at http://https://wiki.fysik.dtu.dk/ase/.
000 possible structures to test, as both the energy of the hexa ammine and the empty salt have to be calculated. This large, but not intangible number of combinations of metals and halides, is ideal for testing our genetic algorithm (GA),28–35 an evolutionary guided search technique, which we have earlier successfully implemented to predict the optimal structure of nano particles,36 since it enables an absolute validation of the ability of the algorithm to identify the most fit materials combinations. The proposed algorithm implementation is part of the Atomic Simulation Environment (ASE), which is freely available at http://https://wiki.fysik.dtu.dk/ase/.
2. Methods
2.1 Calculation details
We use DFT calculations19,20 to determine the thermodynamic properties of the observed mixed metal halide ammines. The calculations are performed within the ASE framework37 using the Grid-based Projector Augmented Wave method (GPAW);38 a real space implementation of the PAW method.39 We use the PBE (Perdew, Burke and Ernzerhof) exchange–correlation functional40 for structural optimizations of reference structures, which gives good geometries,41 and use the computationally more expensive vdW-DF functional21 for single point energy calculations on the optimized structures. The vdW-DF functional accounts for dispersion and van der Waal's forces, which are essential to describe the metal halide ammines, containing a large amount of hydrogen bond donors (N–H) and acceptors (X−). The Brillouin-zone is sampled using a Monkhorst–Pack grid42 with at least 25 k-points Å−1 in each direction, the grid spacing is 0.18 Å and all crystal reference structures are allowed to relax the atomic coordinates by a quasi-Newton type optimization algorithm43 using the calculated DFT forces. The energy of NH3(g) is calculated by placing a molecule in a cube with a side length of 8 Å and using the same grid spacing as above.The data set of pure metal halide reference energies is calculated by substituting the metals and halides into the optimized experimental magnesium chloride structures and subsequently the cell is allowed to relax hydrostatically, thereby keeping the symmetry. The enthalpies of desorption for the mixed ammines are calculated as the difference between the absolute electronic energies of the mixed hexa ammines and the salts including the gas-phase energy of the released ammonia molecules. The desorption temperatures are determined using a standard entropy value of 230 J (mol K NH3)−1 which is a representative average value observed for the pure metal halide ammines,44 and the van't Hoff equation to calculate the temperature at which the equilibrium pressure, peq, reaches 105 Pa (1 bar) for a given reaction, e.g. a full one step release from a mixed metal halide ammine: Sr2Mg2(NH3)24Cl8(s) → Sr2Mg2Cl8(s) + 24NH3(g).
The GA implementation described in the following is closely coupled to the Computational Materials Repository (CMR),45 an open source database implementation for electronic structure calculations. All structures are stored and retrieved from the database during the genetic algorithm run. This has several advantages including easy monitoring and post-processing of the data, reuse of already calculated data (both from the current and old GA runs) and easy sharing among colleagues. All of this can be done both from a web interface or locally using scripting.
2.2 Genetic algorithm setup
Genetic algorithms are evolutionary guided searches that work by breeding on a population of individuals to create new and hopefully better offspring; the best, or most ‘fit’, of these will then be mated with each other. This is parallel to natural evolution, and has been proven to be useful for search and optimization in many different scientific disciplines.29 Brute force screening is often the only alternative, but for large search spaces it is not possible to calculate the fitness of all individuals. The search space investigated in this work with around 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures is on the verge of what can be done with the currently available computational power, requiring millions of CPU hours – however, the ultimate goal is to investigate lower dopant concentrations, which require bigger unit cells, thereby increasing both the total number of combinations and the computational time needed to calculate the fitness of each individual. Just doubling the unit cell to eight metal atoms, increases the search space drastically, making it unfeasible to tackle with brute force screening.
000 structures is on the verge of what can be done with the currently available computational power, requiring millions of CPU hours – however, the ultimate goal is to investigate lower dopant concentrations, which require bigger unit cells, thereby increasing both the total number of combinations and the computational time needed to calculate the fitness of each individual. Just doubling the unit cell to eight metal atoms, increases the search space drastically, making it unfeasible to tackle with brute force screening.
The efficiency and success of a GA run depends explicitly on the choice of fitness function and crossover/permutation operators. Multiple aspects can be included in the fitness function, but it is challenging to determine the relative weights of different components. Because of this, a better choice is often to choose a single parameter as the fitness function, and then set up extra rules, which determines if a new trial structure is accepted for further progress. It is important to notice that such rules do not guide the search directly, because the selection of parent structures for a new generation is solely dependent on the fitness where only the individuals with highest fitness are selected; however the rules determines where not to search. In addition to these rules determining what is accepted, one can post-process the datasets generated, and rank the evaluated structures according to other criteria, e.g. price or expected desorption temperatures, which might be relevant for specific applications. This can be useful for identifying the scientific optimal mixtures, and then afterwards determine which of these would have commercial interest. Here, we apply a simple fitness function, which is simply the weight percent of hydrogen in the material (wH) combined with selection rules setting the relevant formation enthalpy and stabilities (see below), because these are ultimately the most important factors in determining whether a material is interesting for use as an energy carrier in the transportation sector. This wH-fitness also give us the opportunity, to validate the GA predictions and test whether structures potentially could be better than those found by the algorithm, as the maximum wH value can be calculated easily.
We have chosen two criteria for determining whether a structure is accepted in the population – namely that it should be stable against decomposition into the simple metal halides salts and ammines (e.g. Mg3Be(NH3)4xCl8 → 3Mg(NH3)xCl2 + Be(NH3)xCl2, for x = 0, 6) and have an acceptable ammonia desorption temperature. Given the use of predefined template structures, we also include marginally unstable mixtures (up to 0.5 eV per formula unit containing one metal atom) in order not to exclude candidates that may potentially display stability following full relaxation of all structures. For ΔH, we have chosen an interval from 35 to 55 kJ (mol NH3)−1 per released ammonia molecule, which corresponds to a release temperature of approximately 260 to 410 degrees Kelvin, by using the van't Hoff equation and the representative entropy value of 230 J (mol K NH3)−1. Small variations in the reaction entropies for different metal halides are observed,44 so the estimated release temperatures have higher uncertainty than the reaction enthalpies. Calculating the reaction entropy changes for all the mixtures is, however, not computationally feasible in a screening study of this size, so one have to remember this uncertainty, which we do by screening a relatively broad temperature interval. The chosen temperature range is suitable for system integration with both low- and high temperature PEMFC16 and is generally chosen to be sufficiently broad to avoid de-selection of potential candidate materials. For offspring creation, we allow a slightly broader region, by allowing parents with ΔH outside the interval, with an exponentially decreasing probability, since chemically closely related structures can have correlated binding characteristics, and thereby a child of parents on the border of the interval, might likely end up being inside the interval. Parents outside the region are selected with an exponentially decreasing probability fitted to be 25% for being 3 kJ (mol NH3)−1 and 1% for being 10 kJ (mol NH3)−1 off, respectively.
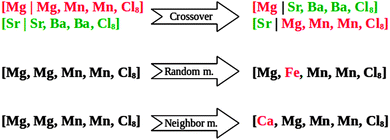
The initialization of the algorithm is done by generating 15 random mixed metal halide ammines (individuals) from the defined phase space. This population size is chosen so that it is large enough to ensure that the algorithm does not end up in a local, pre-converged optimum. On the other hand the population size should not be too large, as this would result in wasting time by testing too many structures. As a general rule of thumb, the population size, S, should be in the range log2(N) < S < 2log2(N), where N is the total number of combinations in the search space.46 The following generations are created by selecting some of the best known candidates from the current population, as parents and using the standard operators of GAs, namely crossover and mutation (Fig. 1).29 The crossover is picking a random point at the atoms list, which is specifying the constituents of the two parents, and taking the part before the cut from the first parent and the last part from the other parent.
We apply the following mutation operators:
(1) Random mutation: picking one element and substituting it to another chosen randomly.
(2) Neighbor mutation: one random element is exchanged for one of its neighbors in the periodic table (up, down, left or right).
(3) Complete mutation: to prevent the algorithm from getting stuck in local minima, we also use a complete mutation random operator, which generates a new structure without using any information from the current population (similar to creating the structures in the initial population).
As a further precaution, to ensure not ending up in a pre-converged state, parents are not only selected from the current population, but a small number of parents are selected with a probability dependent on their fitness, no matter if they are part of the current population or not. More specifically, three out of 15 individuals are selected from all tested structures with a probability equal to
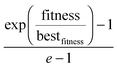 | (1) |
This type of coordination compounds often display correlations between different mixtures and local operators (crossover and the neighbor mutation) are therefore expected to be more important for the efficiency of the search than random operators. We therefore employ a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between them, indicating that local operators are used three times more frequently than random operators. Within the local operators, twice as many crossovers as neighbor mutations, and within the random operators we use the random mutation three times more than the complete mutation operator. To determine when the algorithm is converged, i.e. when it is not expected that further progress would create better offspring, the algorithm keeps track of whether new stable individuals, with ΔH in the specified interval, are entering the population; more specifically the convergence criteria is set to be that the five best structures remain unchanged for five generations.
1 ratio between them, indicating that local operators are used three times more frequently than random operators. Within the local operators, twice as many crossovers as neighbor mutations, and within the random operators we use the random mutation three times more than the complete mutation operator. To determine when the algorithm is converged, i.e. when it is not expected that further progress would create better offspring, the algorithm keeps track of whether new stable individuals, with ΔH in the specified interval, are entering the population; more specifically the convergence criteria is set to be that the five best structures remain unchanged for five generations.
2.3 Template based screening
As mentioned in the introduction, magnesium chloride can store six ammonia molecules per metal atom, corresponding to 9.2% stored hydrogen by weight (wH). Here, we focus on the metal halide hexa ammines although certain metal halides are known to form octa ammines.13,44 This is done because metal halides forming octa ammines are generally heavier and more prone to multi-step release, and multiple metal halides are known to form hexa ammines and share simple crystal symmetries, e.g. MgCl2, NiCl2, FeBr2 and CrI2,10,47 with potential of having a high weight percent. Since all the stored ammonia in Mg(NH3)6Cl2 is not accessible at relevant temperatures, we direct the search towards a one step release at an acceptable temperature between 260 and 410 degrees Kelvin. Using the template structure for all candidates provides an estimate of how the mixed systems will behave and especially the relative stabilities and desorption enthalpies are expected to be correctly determined. A range of the generated structures will exist in other crystal structures, but we expect that the error would be comparable in the salt and the hexa ammine, resulting in an unchanged ΔH, which is one of the important selection criteria.All single metal halides, i.e. consisting of only one metal atom and one halide in the ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
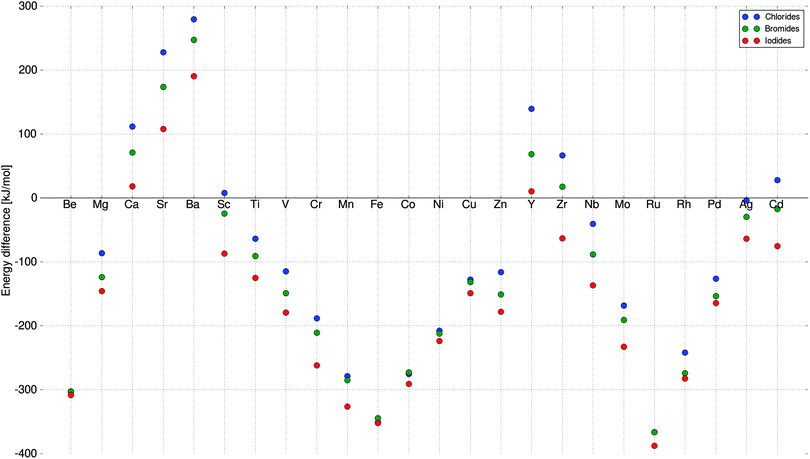
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, are calculated as reference structures for the GA search. This is done for completeness although it is known that not all can form stable hexa ammines, e.g. TiCl2, where only a tetra ammine has been observed48 and SrCl2 since strontium is big enough to coordinate eight ammonia molecules.13 The last fact is taken into account in our screening, when determining the stability of the mixed hexa ammine, where it is possible that mixtures split up to a mixture of single metal hexa and octa ammines. To determine whether it would split up to some octa ammine, we have also calculated all pure reference structures in the strontium octa ammine structure, and thereby determined whether the system prefers to be an octa ammine or a hexa ammine and two free ammonia molecules in the gas phase (Fig. 2). The octa ammine is actually only preferred for a small number of the investigated metals, where mainly alkaline-earth metals containing e.g. Ca, Sr or Ba would split up to some octa ammine and some pure salt, resulting in that the stability of e.g. SrMg(NH3)12Cl4 would be calculated relative to (3Sr(NH3)8Cl2 + SrCl2)/4 and Mg(NH3)6Cl2. The decomposition energy is always calculated relative to the most favorable way of splitting up the constituents, which especially is relevant when the mixture contains both different anions and cations.
2, are calculated as reference structures for the GA search. This is done for completeness although it is known that not all can form stable hexa ammines, e.g. TiCl2, where only a tetra ammine has been observed48 and SrCl2 since strontium is big enough to coordinate eight ammonia molecules.13 The last fact is taken into account in our screening, when determining the stability of the mixed hexa ammine, where it is possible that mixtures split up to a mixture of single metal hexa and octa ammines. To determine whether it would split up to some octa ammine, we have also calculated all pure reference structures in the strontium octa ammine structure, and thereby determined whether the system prefers to be an octa ammine or a hexa ammine and two free ammonia molecules in the gas phase (Fig. 2). The octa ammine is actually only preferred for a small number of the investigated metals, where mainly alkaline-earth metals containing e.g. Ca, Sr or Ba would split up to some octa ammine and some pure salt, resulting in that the stability of e.g. SrMg(NH3)12Cl4 would be calculated relative to (3Sr(NH3)8Cl2 + SrCl2)/4 and Mg(NH3)6Cl2. The decomposition energy is always calculated relative to the most favorable way of splitting up the constituents, which especially is relevant when the mixture contains both different anions and cations.
Another advantage of using the magnesium system is that the hexa ammine crystallizes in the relatively simple K2PtCl6 cubic structure, containing four metal atoms per unit cell,49,50 which makes it ideal for this screening. The magnesium chloride salt crystallizes in the trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 space group (# 164), normally referred to as the layered CdCl2 structure.51 After the GA run, a stability check is also performed on the mono- and diammines of the best compounds to determine whether the release of ammonia is a one step reaction. Here, we define that the mono ammine is observed if the desorption enthalpy for going from the hexa ammine to the mono ammine is more than 2 kJ (mol NH3)−1 lower than for going directly to the salt; the same considerations holds for determining the existence of a diammine. The presence of intermediate ammine phases lower the amount of available hydrogen and the fitness is lowered accordingly. The structure used in order to determine the existence of the mono ammine phase is similar to the one proposed in ref. 10, which, when minimized, has orthorhombic Pbnm symmetry (space group # 62). The diammine is based on the magnesium structure,52 which when relaxed has an orthorhombic Ccme symmetry (space group # 64).
m1 space group (# 164), normally referred to as the layered CdCl2 structure.51 After the GA run, a stability check is also performed on the mono- and diammines of the best compounds to determine whether the release of ammonia is a one step reaction. Here, we define that the mono ammine is observed if the desorption enthalpy for going from the hexa ammine to the mono ammine is more than 2 kJ (mol NH3)−1 lower than for going directly to the salt; the same considerations holds for determining the existence of a diammine. The presence of intermediate ammine phases lower the amount of available hydrogen and the fitness is lowered accordingly. The structure used in order to determine the existence of the mono ammine phase is similar to the one proposed in ref. 10, which, when minimized, has orthorhombic Pbnm symmetry (space group # 62). The diammine is based on the magnesium structure,52 which when relaxed has an orthorhombic Ccme symmetry (space group # 64).
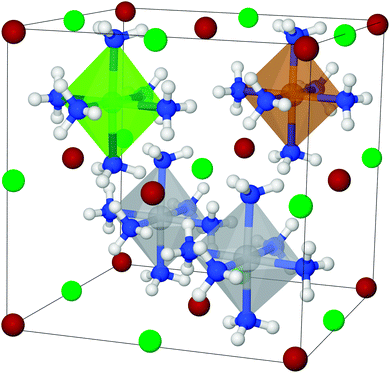
To set up a new mixed structure (example shown in Fig. 3), the atoms are substituted into the template structures, and the following parameters are set: the volume is set as the average volume of the constituents, and the metal to nitrogen distances are set for each metal, using the values calculated for the pure reference structures (for details, see Section 2.1). The chosen structures are therefore not necessarily the thermodynamic ground state structures, since it is simply not feasible to make computationally intense structural optimizations of all the structures during a GA run, and as explained previously, it is expected that the template structures will give reasonable estimates of desorption enthalpies.
3. Results and discussion
3.1 Visiting relevant parts of the search space
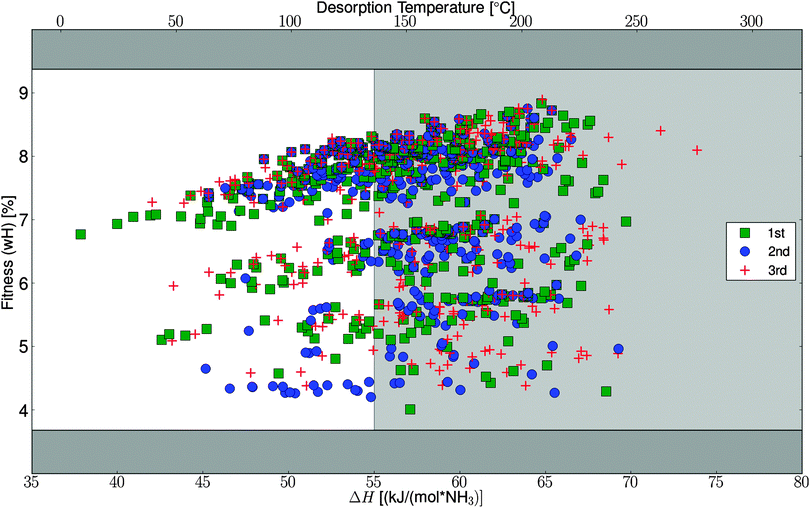
To test the efficiency of the GA search, the algorithm was started three times with the specified parameters, starting from three randomly chosen and thereby different initial populations (for details, see Table S1, ESI†). The algorithm progresses very similarly for the three different runs and ends up finding optimal mixtures with similar fitness and composition (Fig. 4). In Fig. 5, the fitness (wH) for all the potentially stable mixtures that are tested by the algorithm are plotted against the desorption enthalpies. As can be seen from the figure, the full interval of allowed desorption enthalpies does not appear to be sampled equally, which might be due to the fact that light mixtures, with high fitness, simply bind the ammonia harder. It should be stressed that the full interval is allowed in the algorithm runs, it is simply an observation that the generated mixtures have ΔH values in the high end of the interval.3.2 Optimal identified structures
Several materials have been found with a high fitness (hydrogen weight percent, wH) as can be seen in Table 1 showing the top ten structures for the three different runs. As explained in Section 2.2, the structures allowed in the population all satisfy the requirements of having acceptable desorption enthalpies and being stable or marginally unstable against decomposition. The structures which are strictly stable against all decomposition reactions are highlighted in the table, as they naturally are the most interesting structures. As can be seen, the algorithm is able to find the same relevant structures, from three random start populations, with the selected parameters proving that the concept, in this case can be used without rerunning the algorithm, however for other systems this should be tested (pure TiCl2, which was found only the 2nd run, does not form hexa ammines as described earlier).| 1st run | 2nd run | 3rd run | |||
|---|---|---|---|---|---|
| Structure | Fitness (wH) | Structure | Fitness (wH) | Structure | Fitness (wH) |
| TiScTiCaCl8 | 8.31 | TiTiCuMgCl8 | 8.28 | CaTiTiScCl8 | 8.31 |
| TiTiCuMgCl8 | 8.28 | ScTiTiTiCl8 | 8.24 | CuTiTiMgCl8 | 8.28 |
| TiTiTiScCl8 | 8.24 | TiTiTiTiCl8 | 8.21 | ScNiCaCaCl8 | 8.28 |
| TiScTiVCl8 | 8.21 | ScTiTiVCl8 | 8.21 | TiTiTiScCl8 | 8.24 |
| TiScTiCrCl8 | 8.20 | ScTiTiCrCl8 | 8.20 | CaTiCuCaCl8 | 8.21 |
| TiTiTiVCl8 | 8.18 | TiTiVTiCl8 | 8.18 | TiTiVScCl8 | 8.21 |
| TiTiTiCrCl8 | 8.17 | TiTiTiCrCl8 | 8.17 | CrTiTiScCl8 | 8.20 |
| ScCuCuMgCl8 | 8.17 | ScCuCuMgCl8 | 8.17 | VTiTiTiCl8 | 8.18 |
| VTiTiVCl8 | 8.15 | TiVVTiCl8 | 8.15 | CrTiTiTiCl8 | 8.17 |
| VTiTiCrCl8 | 8.14 | TiVTiCrCl8 | 8.14 | ScCuCuMgCl8 | 8.17 |
As can be seen in Table 1, there is a high dominance of titanium rich structures, which is not surprising because it is one of the lightest elements in the search space, and apparently the mixtures have a relatively low ΔH resulting in acceptable release temperatures. The top four stable candidates, Ti2CuMgCl8, Ti2ScVCl8, Ti3VCl8 and ScCu2MgCl8, have predicted release temperatures of 136, 130, 130 and 130 °C respectively, and furthermore both the ammines and the salts are stable against decomposition. Especially Ti2CuMgCl8 and ScCu2MgCl8 are predicted to be very stable compared to having the pure metal halide ammines and salts separated (for details, see Table S2, ESI†).
3.3 Genetic algorithm performance
We have made a more detailed analysis of the convergence of the algorithm, which will be described in this section. In general it is found that the chosen convergence criteria and suggested operators are ideal for this kind of template based screening. The general suggestion from the analysis is that rerunning the algorithm multiple times, to ensure finding the global optimum, is preferred over changing the convergence criteria or increasing the populations size – this is further favored in our setup where we reuse data from earlier algorithm runs as described in Section 2.1. The importance of reusing data has been observed already from the 2nd run where 21% of the calculations are skipped, and for the 3rd run 34% was reused; these numbers is only counting reuse from the original part of the first run, not including the extra convergence test. These numbers support the general suggestion about rerunning instead of changing the convergence criteria or increasing the populations size.As mentioned, the algorithm succeeds in finding the same optimal structures, from three random start populations, which is very interesting. In general, the algorithm needs approximately ten generations before it ends up in the area with the optimal elements and high fitness, no matter where it starts (Fig. 4). After this initial narrowing, the algorithm only makes slight improvements from generation to generation, where more and more optimal candidates are seen, but the maximum is not changing much. The observed jumps in the fitness function in the first part of the search, can also be seen in Fig. 5, where the searched parts of space are organized in almost horizontal bands, in between which not much have been tested. These bands represent use of different halides or mixtures thereof.
To test the chosen convergence criteria, i.e. that the five best structures are constant for five generations, the first run was continued until a new structure entered the population (Fig. 4). The original run fulfilled the convergence criteria after generation number 22, and almost 50% longer run time was necessary to find a new candidate in generation 31. As a result, we conclude that our convergence criteria are well chosen, and it is generally better to rerun the algorithm for different starting populations, to ensure that the algorithm searches in a different parts of the search space. The extra candidate found in the extension of the first run was TiCaCuCaCl8 which entered as the 4th best structure with fitness, wH = 8.21, however the hexa ammine is slightly unstable with a decomposition energy of 27 kJ mol−1 per formula unit containing one metal atom. A possible explanation for not observing the calcium containing structures in all the different runs, is that calcium structures in general have too high ΔH values, and therefore have a very low probability of being selected for offspring creation. Furthermore, the decomposition energy is calculated relative to the calcium chloride octa ammine, which is known to be more stable than a hexa ammine (Fig. 2), requiring the mixed hexa ammine to be very stable.
Different kinds of operators are available for generating new offspring and we tested whether all the used operators are relevant and equally important for finding the optimal solution (Fig. 6). The crossover operator behaves as expected, where it initially has a relatively low success rate, because the components it mixes are not the optimal one; in the middle it has a maximum, where it directs the search by combining better and better building blocks, and later on the success rate drops again. The chemical neighbor operator does generally have a high success rate and seems to be very important, to guide the search. The mutation operator has the lowest success rate, which probably is because the fitness function is the weight percent, which gets harder and harder to optimize, when substituting in a random element. If one would continue with this fitness function it might be suggested to lower the rate of random mutations as a function of time, however, if other fitness functions are used this is probably not advisable. In our earlier work with use of GAs36 we argued that dynamically operators are more efficient for optimization of nano particles, but this does not seem to be important for the template based screening performed here.
 | ||
| Fig. 6 Operator success during the three algorithm runs. Success is defined as generating an individual with higher fitness, which furthermore obeys the additional rules on ΔH and stability. | ||
3.4 Global optimum
A validation of the method and the results can be performed because the weight percent is chosen as the fitness, since it is possible to determine which structures in the search space have a higher weight percent and could potentially have acceptable stabilities and release temperatures. It turns out that only 253 structures in the search space would have a higher weight percent than the best candidate, Ti2CuMgCl8, found by all of the three runs, and 83 of these have already been tested by the three runs, leaving us with 170 candidates. Because it is this very limited number of structures, we manually tested all of these candidates. None of these structures were found to have acceptable ΔH and fulfill the stability criteria. This demonstrates that the global optimum structure was found by the algorithm in all three GA runs, thereby proving that the suggested algorithm is very efficient.Only ∼400 out of the ∼27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures were tested on average for a genetic algorithm run in this search space. The top-down validation approach is naturally only possible in this special case because of the simple fitness function. The goal of a screening is often to find multiple candidates, which would favor the use of the genetic algorithm; in this specific example it would require 253 calculations to get the best, 337 to get top two, 372 to get top three and 401 to get top four, which is more than the average length of one run, which in all cases find the top four candidates. Furthermore, the GA would also find stable structures, with lower, but still high wH, which is a lot better than the top-down approach leaving us with only one to four stable structures.
000 structures were tested on average for a genetic algorithm run in this search space. The top-down validation approach is naturally only possible in this special case because of the simple fitness function. The goal of a screening is often to find multiple candidates, which would favor the use of the genetic algorithm; in this specific example it would require 253 calculations to get the best, 337 to get top two, 372 to get top three and 401 to get top four, which is more than the average length of one run, which in all cases find the top four candidates. Furthermore, the GA would also find stable structures, with lower, but still high wH, which is a lot better than the top-down approach leaving us with only one to four stable structures.
3.5 Check on possible intermediate ammine phases
For the best candidates in Table 1, we also tested whether a mono- or diammine would be observed, as this might result in a multi-step release, possibly lowering the available energy density (details in Table S2, ESI†). As a result of this analysis some of the suggested candidates are found not to be interesting, due to slightly unstable mixed phases. However, intermediate ammine phases are not expected for the three out of the four best materials, Ti2ScVCl8, Ti3VCl8 and ScCu2MgCl8, further verifying, that they are indeed interesting candidates for new improved materials. From these extra checks it was found that Ti2CuMgCl8, would have a stable diammine, lowering the practical amount of ammonia, and releasing the last two ammonia molecules at high temperatures (>200 °C). Again, it must be stressed that we are doing template based screening and it could still be interesting to test all compounds for completeness. When disregarding the unstable mixtures, we are left with compounds which are titanium-rich. It has been shown that similar mixtures are synthesizable, e.g. TiMgCl4,53 and pure titanium(II) chloride has been observed in the MgCl2 structure,54 which indicates that the suggested materials can be synthesized, and the templates used should give accurate energies.4. Conclusion
By using genetic algorithms combined with vdW-DF density functional theory calculations, we have identified a number of new, mixed metal hexa ammines with hydrogen storage capacities in excess of 8 wt% and excellent desorption characteristics, releasing all the ammonia in one step at temperatures relevant for HT-PEMFC applications. The most promising candidates are currently investigated further, both computationally and experimentally. The developed methods, which have been shown to be able to find the global optimum, testing a very limited number of structures (less than two percent of the total number of combinations), are easy transferable to other searches, with different search parameters, possibly including more intermediate phases, which we are currently investigating.Acknowledgements
The authors would like to acknowledge the Danish National Advanced Technology Foundation (DNATF) grant 078-2011-1, the Danish Center for Scientific Computing, the Center for Atomic-scale Materials Design (CAMD) and the Catalysis for Sustainable Energy (CASE) initiative. CASE is funded by the Danish Ministry of Science, Technology and Innovation.References
- V. Smil, Nature, 1999, 400, 415 CrossRef CAS PubMed.
- A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18, 2304–2310 RSC.
- C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Catal. Today, 2006, 111, 140–144 CrossRef CAS PubMed.
- D. Chakraborty, H. N. Petersen, C. Elkjær, A. Cagulada and T. Johannessen, Fuel Cells Bull., 2009, 2009, 12–15 CrossRef.
- R. Lan, J. T. S. Irvine and S. Tao, Int. J. Hydrogen Energy, 2012, 37, 1482–1494 CrossRef CAS PubMed.
- F. Schüth, R. Palkovits, R. Schlögl and D. S. Su, Energy Environ. Sci., 2012, 5, 6278–6289 Search PubMed.
- T. D. Elmøe, R. Z. Sørensen, U. Quaade, C. H. Christensen, J. K. Nørskov and T. Johannessen, Chem. Eng. Sci., 2006, 61, 2618–2625 CrossRef PubMed.
- U. S. Energy Information Administration, International Energy Outlook 2013, 2013.
- C. H. Christensen, R. Z. Sørensen, T. Johannessen, U. J. Quaade, K. Honkala, T. D. Elmøe, R. Køhler and J. K. Nørskov, J. Mater. Chem., 2005, 15, 4106–4108 RSC.
- R. Z. Sorensen, J. S. Hummelshoj, A. Klerke, J. B. Reves, T. Vegge, J. K. Norskov, C. H. Christensen, R. Z. Sørensen, J. S. Hummelshøj and J. K. Nørskov, J. Am. Chem. Soc., 2008, 130, 8660–8668 CrossRef PubMed.
- H. S. Jacobsen, H. A. Hansen, J. W. Andreasen, Q. Shi, A. Andreasen, R. Feidenhans'l, M. M. Nielsen, K. Ståhl and T. Vegge, Chem. Phys. Lett., 2007, 441, 255–260 CrossRef CAS PubMed.
- A. Tekin, J. S. Hummelshøj, H. S. Jacobsen, D. Sveinbjörnsson, D. Blanchard, J. K. Nørskov and T. Vegge, Energy Environ. Sci., 2010, 3, 448 CAS.
- S. Lysgaard, A. L. Ammitzbøll, R. E. Johnsen, P. Norby, U. J. Quaade and T. Vegge, Int. J. Hydrogen Energy, 2012, 37, 18927–18936 CrossRef CAS PubMed.
- C. Zamfirescu and I. Dincer, Fuel Process. Technol., 2009, 90, 729–737 CrossRef CAS PubMed.
- G. G. M. Fournier, I. W. Cumming and K. Hellgardt, J. Power Sources, 2006, 162, 198–206 CrossRef CAS PubMed.
- T. Vegge, R. Z. Sørensen, A. Klerke, J. S. Hummelshøj, T. Johannessen, J. K. Nørskov and C. H. Christensen, in Solid state hydrogen storage: Materials and chemistry, ed. G. Walker, British Welding Research Association, 2008, pp. 533–568 Search PubMed.
- B. McNicol, D. Rand and K. Williams, J. Power Sources, 2001, 100, 47–59 CrossRef CAS.
- Q. Li, R. He, J. O. Jensen and N. J. Bjerrum, Chem. Mater., 2003, 15, 4896–4915 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- J. Voss, J. S. Hummelshøj, Z. Lodziana and T. Vegge, J. Phys.: Condens. Matter, 2009, 21, 012203 CrossRef CAS PubMed.
- J. S. Hummelshøj, D. D. Landis, J. Voss, T. Jiang, A. Tekin, N. Bork, M. Dułak, J. J. Mortensen, L. Adamska, J. Andersin, J. D. Baran, G. D. Barmparis, F. Bell, a. L. Bezanilla, J. Bjork, M. E. Björketun, F. Bleken, F. Buchter, M. Bürkle, P. D. Burton, B. B. Buus, A. Calborean, F. Calle-Vallejo, S. Casolo, B. D. Chandler, D. H. Chi, I. Czekaj, S. Datta, A. Datye, A. DeLaRiva, V. Despoja, S. Dobrin, M. Engelund, L. Ferrighi, P. Frondelius, Q. Fu, A. Fuentes, J. Fürst, A. García-Fuente, J. Gavnholt, R. Goeke, S. Gudmundsdottir, K. D. Hammond, H. a. Hansen, D. Hibbitts, E. Hobi, J. G. Howalt, S. L. Hruby, A. Huth, L. Isaeva, J. Jelic, I. J. T. Jensen, K. a. Kacprzak, A. Kelkkanen, D. Kelsey, D. S. Kesanakurthi, J. Kleis, P. J. Klüpfel, I. Konstantinov, R. Korytar, P. Koskinen, C. Krishna, E. Kunkes, a. H. Larsen, J. M. G. Lastra, H. Lin, O. Lopez-Acevedo, M. Mantega, J. I. Martínez, I. N. Mesa, D. J. Mowbray, J. S. G. Mýrdal, Y. Natanzon, A. Nistor, T. Olsen, H. Park, L. S. Pedroza, V. Petzold, C. Plaisance, J. a. Rasmussen, H. Ren, M. Rizzi, a. S. Ronco, C. Rostgaard, S. Saadi, L. a. Salguero, E. J. G. Santos, a. L. Schoenhalz, J. Shen, M. Smedemand, O. J. Stausholm-Møller, M. Stibius, M. Strange, H. B. Su, B. Temel, A. Toftelund, V. Tripkovic, M. Vanin, V. Viswanathan, A. Vojvodic, S. Wang, J. Wellendorff, K. S. Thygesen, J. Rossmeisl, T. Bligaard, K. W. Jacobsen, J. K. Nørskov and T. Vegge, J. Chem. Phys., 2009, 131, 014101 CrossRef PubMed.
- C. Y. Liu and K. I. Aika, Ind. Eng. Chem. Res., 2004, 43, 7484–7491 CrossRef CAS.
- http://www.chemicool.com, 2013.
- S. Hodorowicz, E. Hodorowicz and H. Eick, J. Solid State Chem., 1983, 50, 180–188 CrossRef CAS.
- O. Barbier, L. Arreola-Mendoza and L. M. Del Razo, Chem.-Biol. Interact., 2010, 188, 319–333 CrossRef CAS PubMed.
- J. H. Holland, Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor, 1975 Search PubMed.
- S. Forrest, Science, 1993, 261, 872–878 CAS.
- G. Jóhannesson, T. Bligaard, A. Ruban, H. Skriver, K. Jacobsen and J. Nørskov, Phys. Rev. Lett., 2002, 88, 255506 CrossRef.
- T. Bligaard, G. H. Jóhannesson, A. V. Ruban, H. L. Skriver, K. W. Jacobsen and J. K. Nørskov, Appl. Phys. Lett., 2003, 83, 4527–4529 CrossRef CAS PubMed.
- L. B. Vilhelmsen, K. S. Walton and D. S. Sholl, J. Am. Chem. Soc., 2012, 134, 12807–12816 CrossRef CAS PubMed.
- L. B. Vilhelmsen and D. S. Sholl, J. Phys. Chem. Lett., 2012, 3, 3702–3706 CAS.
- D. Teng, L. B. Vilhelmsen and D. S. Sholl, Surf. Sci., 2014, 628, 98–103 CrossRef CAS PubMed.
- L. B. Vilhelmsen and B. Hammer, J. Chem. Phys., 2014, 141, 044711 CrossRef PubMed.
- S. Lysgaard, D. D. Landis, T. Bligaard and T. Vegge, Top. Catal., 2014, 57, 33–39 CrossRef CAS PubMed.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- P. Maragakis, S. A. Andreev, Y. Brumer, D. R. Reichman and E. Kaxiras, J. Chem. Phys., 2002, 117, 4651–4658 CrossRef CAS PubMed.
- E. Lepinasse and B. Spinner, Int. J. Refrig., 1994, 17, 309–322 CrossRef CAS.
- D. D. Landis, J. S. Hummelshoj, S. Nestorov, J. Greeley, M. Dulak, T. Bligaard, J. K. Norskov and K. W. Jacobsen, Comput. Sci. Eng., 2012, 14, 51–57 CrossRef.
- J. T. Alander, Proceedings Computer Systems and Software Engineering, IEEE Comput. Soc. Press, 1992, pp. 65–70 Search PubMed.
- R. Essmann, G. Kreiner, A. Niemann, D. Rechenbach, A. Schmieding, T. Sichla, U. Zachwieja and H. Jacobs, Z. Anorg. Allg. Chem., 1996, 622, 1161–1166 CrossRef CAS PubMed.
- W. C. Schumb and R. F. Sundström, J. Am. Chem. Soc., 1933, 55, 596–604 CrossRef CAS.
- I. Olovsson, Acta Crystallogr., 1965, 18, 889–893 CrossRef CAS.
- I. Hwang and T. Drews, J. Am. Chem. Soc., 2000, 8486–8489 CrossRef CAS.
- I. Bassi, F. Polato, M. Calcaterra and J. Bart, Z. Kristallogr., 1982, 159, 297–302 CAS.
- A. Leineweber, M. W. Friedriszik and H. Jacobs, J. Solid State Chem., 1999, 147, 229–234 CrossRef CAS.
- A. Fuwa and S. Takaya, JOM, 2005, 56–60 CrossRef CAS PubMed.
- G. Meyer, T. Gloger and J. Beekhuizen, Z. Anorg. Allg. Chem., 2009, 635, 1497–1509 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp03133d |
| This journal is © the Owner Societies 2014 |