Evaluation of composite schemes for CCSDT(Q) calculations of interaction energies of noncovalent complexes

Abstract

Recently, it has become possible to apply higher-order coupled-cluster methods to polyatomic systems including molecular noncovalent complexes. Due to the steep scaling of the complexity of these calculations, the size of the basis set becomes a critical factor and larger systems can be calculated only in small basis sets. To obtain the most accurate results, it is necessary to use composite schemes where the higher-order terms are added to a baseline calculation for which a larger basis set can be used. In this work, we have examined the accuracy of composite schemes where CCSDT(Q) correction calculated in a smaller basis set is added to CCSD(T), CCSD[T] and CCSDT calculations. As a benchmark, we have used CCSDT(Q)/aug-cc-pVTZ interaction energies calculated in a set of 18 small noncovalent complexes. We have found that the differences between the studied schemes are small and that it is safe to make the correction in a single step starting from the CCSD(T) baseline. The basis set dependence of the correction is strongly affected by the nature of the interaction. For dispersion-bound complexes, the correction calculated in a basis set as small as 6-31G**(0.25,0.15) improves the results consistently. On the other hand, description of polar complexes and especially hydrogen bonds is more difficult and the CCSDT(Q) correction has an incorrect sign until a rather large basis set is used; even the aug-cc-pVDZ result is not reliable in rare cases.

---

Introduction

Noncovalent interactions play a crucial role in various areas of chemistry. Intermolecular interactions determine the structure and properties of molecular assemblies and they are equally important for the structure of large molecules. In biomolecules, the prominent examples are the DNA double helix structure and the secondary and tertiary structure of proteins. Since direct experimental measurement of noncovalent interactions is difficult, theoretical methods are often used as the main tool for their study.

Reliable interaction energies for different types of noncovalent complexes (e.g. hydrogen-bonded or dispersion-dominated) are only obtained if the most accurate wave-function based methods are applied.¹ Among them, the coupled-cluster theory plays a dominant role because it offers a systematic way of improving the results by adding higher-order excitation operators. However, these improvements come at the cost of increasing the complexity of the calculations. To achieve reliable, quantitative results for all kinds of noncovalent interactions, it is necessary to include the triple excitations. This can be done rigorously at the CCSDT level² but the steep scaling and the iterative nature of the method limit its use only to small systems. The computational cost can be lowered when the triples are treated in an approximate way. The currently most employed coupled-cluster method is the noniterative CCSD(T) approach³ (where the triples are added perturbatively after an iterative CCSD calculation), often called the “gold standard” of computational chemistry. Other comparable approaches are the perturbative CCSD[T]⁴ and approximate iterative CCSDT-n (n = 1, 1b, 2, 3, 4)^4–6 methods. The advantage of all these approaches lies in their relatively low computational cost while the accuracy remains acceptably high.

The approximate nature of these widely used methods naturally raises the question on their accuracy, not only with respect to the complete CCSDT calculations but also to methods covering also higher-order excitations. A comparison with the most accurate benchmarks (up to full configuration interaction) in the smallest systems¹ indicates that the inclusion of quadruples is needed to achieve the accuracy comparable to e.g. spectroscopic measurements. Here, the cheaper, perturbative CCSDT(Q) method⁷ closely reproduces full CCSDTQ⁸ calculations. Nevertheless, even the CCSDT(Q) calculations are extremely demanding and can be applied only to small systems.

Several published studies have reported the interaction energies in noncovalent complexes at a level of theory beyond the CCSD(T). We mention the work of Pittner and Hobza,⁹ where hydrogen-bonded and stacked complexes were studied at the CCSDT level; later Hopkins and Tschumper¹⁰ employed the CCSD(TQ) method for calculations of dispersion-bound and stacked systems. A few years ago, small model noncovalent complexes were examined in our laboratory at the CCSDT(Q) and CCSDTQ levels of theory in order to assess the performance of the CCSD[T] and CCSD(T) methods.¹¹ Later, we developed a data set of 24 small model complexes for which we reported calculations at the CCSDT(Q) level.¹² We also examined the convergence of the interaction energies in the coupled cluster series using the FCI, CCSDTQP and CCSDTQ(P) data as a benchmark.¹

The major restraint in all higher-order calculations (in real-world systems such as complexes of molecules) is the limited size of the basis set that has to be used because of the steep scaling of the methods. A solution presents itself immediately – the interaction energies could be evaluated using a composite scheme where the energies at the CCSD(T), CCSD[T] and possibly CCSDT level are obtained using a larger basis set and the additional contributions are calculated using smaller basis sets.

Such schemes are widely used in computational thermochemistry^13–17 and have also been used for noncovalent interactions. Adding a higher-order correction to standard CCSD(T)/CBS results is the most obvious solution but more complex incremental schemes can be used as well. For example, Harding and Klopper in 2013 studied the lithium–thiophene complex,¹⁸ improving the baseline fc-CCSD(F12)/cc-pVQZ-F12 (cc-pCVQZ-F12) calculations with contributions of perturbative triples using the cc-pwCVTZ (and aTZ, aug-pCVTZ) basis set, iterative triples (a(D+d)Z and aug-pCVDZ basis sets) and perturbative quadruples (a plain cc-pVDZ basis set). Small hydrogen bonded complexes were studied by Boese up to the CCSDTQ level,¹⁹ decreasing the basis set at each level (and employing extrapolation to a complete basis set where possible).

However, the accuracy of these composite schemes has not been studied yet in the specific context of noncovalent interactions. There are also questions regarding the design of the scheme, e.g. which steps to be included. This is complicated by the fact that some of the calculations, including the common starting point, CCSD(T), are approximate methods that, to some extent, rely on error cancellation. In this work we investigate several possible incremental schemes in order to find the one most suitable for the description of larger noncovalent complexes. The goal is to add the contributions up to the CCSDT(Q) level using basis sets that would make the scheme applicable to larger systems. As a benchmark, we use full CCSDT(Q) calculations in the largest basis set applicable to our small model systems. For clarity, we do not include the extrapolation to the complete basis set limit in this study as it would be included at the lowest level, e.g. CCSD(T), not affecting the higher-order contributions that are subject of this study. We do not go beyond the CCSDT(Q) level for two reasons: firstly, it has been shown that it closely reproduces full CCSDTQ calculations and its accuracy is in most cases sufficient. Secondly, while it would be possible to add another incremental step, the difference between CCSDT(Q) and CCSDTQ, in larger systems it would be limited to such a small basis set that the uncertainty in this term would be larger than its actual magnitude.

Computational details

In order to determine the most efficient way of including the contributions of higher excitations within the coupled cluster theory, we chose 18 weakly interacting model complexes. These complexes are fairly small, allowing us to calculate the contribution of higher excitations to the interaction energies in a larger basis set. They cover diverse types of interactions: six of them feature a hydrogen or a lithium bond, six are electrostatically bound and six complexes are stabilized mainly by London dispersion. The optimized structures of all the model complexes are displayed in Fig. 1.

Fig. 1 Dispersion bound, electrostatically stabilized and hydrogen- and lithium-bonded complexes studied in this work.

The geometries of the complexes were taken from earlier studies where available. For the water dimer, the ammonia dimer, and the methane dimer we used the CCSD(T)/CBS geometries from ref. 20. The FH⋯F⁻ and the neon dimer complex were optimized at the same level. The geometry of the LiH dimer was taken from ref. 21. The remaining complexes were optimized at the QCISD/6-31++G(d,p) level of theory in the Gaussian09²² package.

The interaction energies were calculated at the CCSD(T) (coupled-cluster with singles, doubles and perturbative triples), CCSD[T] (coupled-cluster with singles, doubles and perturbative triples), CCSDT (coupled-cluster with singles, doubles and triples) and the CCSDT(Q) (coupled-cluster with singles, doubles, triples and perturbative quadruples) levels of theory, in Dunning's correlation consistent basis sets aug-cc-pVDZ and aug-cc-pVTZ²³ (abbreviated as aDZ and aTZ in this work) and the 6-31G**(0.25,0.15) basis set. The 6-31G**(0.25,0.15) basis set is a modified version of the 6-31G** basis set where the exponents of the polarization functions of second-period elements and hydrogens are changed to 0.25 and 0.15, respectively. For the lithium atom we maintain the original value of the exponent, 0.20. This basis set is known to perform well for calculations of weakly interacting systems, as has been shown in several studies involving hydrogen-bonded and stacked complexes.^24–26 For the validation of the CCSDT(Q)/aTZ benchmark, CCSDT(Q)/aQZ calculations were carried out for the smallest systems and the correlation energy was extrapolated to the complete basis set limit.²⁷

The Boys and Bernardi²⁸ counterpoise correction was used to remove the basis set superposition error. All electrons were correlated in all calculations (it improves the interaction energies even when polarized-core basis sets are not used). Spherical d-functions were used. The calculations were performed using the CFOUR²⁹ quantum chemistry software package, coupled with the MRCC³⁰ program by M. Kállay.

The error of the composite calculations in comparison with the benchmark is evaluated as a mean unsigned error (MUE). To make it possible to compare the results obtained for different complexes in which the magnitude of the interaction correlation energy varies, this error is furthermore expressed in relative terms, in percent of the absolute value of the interaction correlation energy (this quantity is denoted as relative error). The average relative error is reported for the whole set of model systems and for distinct groups of complexes.

Results and discussion

In all of the following tables, we report only the contribution of correlation to the interaction energy (correlation interaction energy) instead of the complete interaction energies. The analysis of our data and relative errors is thus independent of the total interaction energies, which enables us to focus on the differences at various correlation levels.

The starting point for our composite schemes is a CCSD(T), CCSD[T] or CCSDT calculation in the aTZ basis set. In practical applications, extrapolation to the complete basis set limit will be used at this level; in this work, it is omitted for clarity as it does not make any difference in the discussion of higher-order contributions. The benchmark for our composite calculations are then CCSDT(Q)/aTZ calculations. To test the quality of this benchmark, the three smallest model complexes were calculated also in a larger basis set, aQZ, and extrapolated to the CBS limit. The results, plotted in Fig. 2, indicate that the results obtained with aTZ are not fully converged (especially in the case of LiH dimer) but no qualitative change occurs when the basis set is enlarged (unlike the large changes that occur in basis sets smaller than aTZ). These calculations suggest that our benchmark is robust enough for the purpose of testing composite schemes based on smaller basis sets.

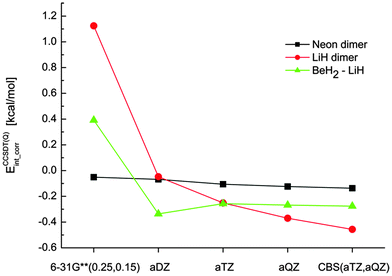Fig. 2 The correlation interaction energies [kcal mol⁻¹] obtained at the CCSDT(Q) level of theory using several basis sets.

In the first three schemes, the correction from the baseline method to CCSDT(Q) is done in one step and the schemes differ only in the baseline methods:

E^Int = E^Int_CCSDT/aTZ + ΔE^Int_{CCSDT(Q)/small BS} (1)

E^Int = E^Int_CCSD(T)/aTZ + ΔE^Int_{CCSDT(Q)/small BS} (2)

E^Int = E^Int_CCSD[T]/aTZ + ΔE^Int_{CCSDT(Q)/small BS} (3)

where ΔE^Int_CCSDT(Q) is the higher-order correction and “small BS” stands for the basis set used for its evaluation. Here, the 6-31G**(0.25,0.15) and aDZ basis sets are used. In addition to these schemes, it is possible to calculate the correction in a stepwise manner, calculating CCSDT in a larger (aDZ) basis set and adding the contributions of quadruples from a CCSDT(Q) calculation in a smaller basis set, 6-31G**(0.25,0.15):

E^Int = E^Int_CCSD(T)/aTZ + ΔE^Int_CCSDT/aTZ + ΔE^Int_{CCSDT(Q)/6-31G**(0.25,0.15)} (4)

The correlation interaction energies of dispersion-bound complexes, electrostatically stabilized, lithium and hydrogen-bonded complexes, are summarized in Tables S1–S3 in the ESI.† There, we present the correlation interaction energies at various levels of theory up to the CCSDT(Q) method obtained with the use of the 6-31G**(0.15,0.25), aDZ and aTZ basis sets, respectively.

First we look at the interaction energies obtained without using the composite schemes. The accuracy of the correlation interaction energies of dispersion-bound complexes obtained with the CCSD[T] and CCSD(T) methods is very similar. When the smallest 6-31G**(0.25,0.15) basis set is used, the CCSD[T] method yields slightly better results. In the group of electrostatically stabilized complexes the situation is similar, the data resulting from the use of both methods with perturbative triples exhibit comparable relative errors relative to the CCSDT(Q) benchmark. Again the CCSD[T] method performs slightly better in combination with the 6-31G**(0.25,0.15) and the aDZ basis sets. This is the behavior we discussed in our previous work on this topic.¹¹ For hydrogen-bonded and lithium-bonded complexes, we observe that the data obtained with 6-31G**(0.25,0.15) are closer to the benchmark than those obtained using the aDZ basis set. Also, the CCSD(T) method yields in this case more accurate correlation interaction energies than CCSD[T]. Overall, all the considered methods covering the triples yield very similar results, which justifies the inclusion of all of them as a starting point for the composite calculations. It should also be noted that the CCSDT[Q] method, an alternative perturbative description of the quadruples, yields rather bad results and is inferior even to plain CCSDT calculations. This confirms our previous findings¹ and we will not discuss this method further.

The results obtained with the composite calculations are presented in Table 1 together with the relative errors evaluated with respect to the CCSDT(Q)/aTZ benchmark data. The average relative errors are listed in Table 2. The fundamental point is whether the composite schemes using such a small basis set bring any improvement over the baseline data, as this is often questioned in discussions. The average relative errors of the baseline CCSD[T], CCSD(T) and CCSDT data were thus added to Table 2 as well. For all the schemes discussed here, the average errors with respect to the benchmark are smaller than the errors of the baseline data alone. This means that adding the CCSDT(Q) correction in a basis set as small as 6-31G**(0.25,0.15) generally improves the interaction energies towards the benchmark. However, this does not necessarily apply for each of the complexes individually; these cases and the trends observed are discussed below.

Table 1 The correlation interaction energies [kcal mol⁻¹] obtained using three composite schemes (the first row) and the corresponding relative errors with respect to the CCSDT(Q) benchmark (see Tables S1–S3, ESI) in % (the second row) together with the RMS error and the maximum unsigned error for each scheme

	6-31G** as small BS			ADZ as small BS			6-31G**+aDZ
	1	2	3	1	2	3	4
Li2⋯H2	−0.123	−0.121	−0.117	−0.123	−0.123	−0.122	−0.122
	0.291	1.446	5.018	0.163	0.276	0.423	0.404
BH3⋯H2	−0.180	−0.179	−0.179	−0.180	−0.181	−0.180	−0.181
	0.203	0.644	0.854	0.154	0.047	0.190	0.002
BeH2⋯H2	−0.179	−0.178	−0.178	−0.179	−0.179	−0.178	−0.179
	0.090	0.564	0.673	0.096	0.015	0.142	0.022
CH4 dimer	−0.985	−0.988	−0.983	−0.987	−0.990	−0.987	−0.988
	0.516	0.265	0.695	0.305	0.010	0.365	0.221
LiH⋯H2	−0.321	−0.319	−0.318	−0.321	−0.321	−0.321	−0.321
	0.086	0.818	1.018	0.091	0.121	0.278	0.117
NH3 dimer	−1.544	−1.550	−1.541	−1.551	−1.557	−1.550	−1.550
	0.856	0.508	1.038	0.399	0.010	0.507	0.466
H2O dimer	−1.153	−1.141	−1.159	−1.158	−1.155	−1.155	−1.150
	0.856	1.851	0.363	0.429	0.642	0.643	1.069
BeH2⋯LiH	−0.256	−0.254	−0.252	−0.256	−0.254	−0.253	−0.253
	0.374	1.145	1.861	0.180	1.179	1.456	1.372
LiH dimer	−0.249	−0.250	−0.247	−0.247	−0.246	−0.245	−0.248
	0.705	0.488	1.721	1.716	2.163	2.299	1.152
H^−⋯LiH	1.087	1.087	1.092	1.087	1.092	1.093	1.092
	0.253	0.200	0.658	0.241	0.674	0.776	0.687
LiH⋯Li^+	0.287	0.289	0.289	0.286	0.288	0.288	0.289
	0.043	0.736	0.834	0.067	0.586	0.584	0.696
HF dimer	−0.580	−0.556	−0.597	−0.577	−0.566	−0.578	−0.569
	0.115	4.290	2.901	0.649	2.479	0.469	1.945
Ne dimer	−0.106	−0.105	−0.105	−0.106	−0.105	−0.106	−0.105
	0.433	0.848	0.829	0.170	0.782	0.104	1.046
HCN⋯HF	−1.253	−1.257	−1.268	−1.256	−1.259	−1.282	−1.256
	1.198	0.874	0.006	0.955	0.681	1.146	0.923
F^−⋯HF	5.002	5.158	4.944	5.067	5.168	5.046	5.103
	1.309	1.770	2.470	0.024	1.964	0.447	0.680
HCN⋯Li^+	1.876	1.865	1.931	1.851	1.858	1.871	1.883
	0.823	0.221	3.759	0.512	0.160	0.537	1.176
C2H2⋯Li^+	1.540	1.554	1.560	1.527	1.543	1.550	1.556
	0.790	1.711	2.108	0.064	1.015	1.453	1.869
C2H2⋯H^−	−0.660	−0.673	−0.649	−0.705	−0.705	−0.705	−0.660
	7.876	6.044	9.494	1.630	1.596	1.557	7.842
RMS error	0.022	0.026	0.039	0.005	0.024	0.010	0.019
Max. error	0.066	0.090	0.125	0.012	0.016	0.023	0.056

---

Table 2 Average relative errors (%) of the correlation interaction energies with respect to the CCSDT(Q)/aTZ benchmark. The errors of the baseline CCSDT, CCSD(T) and CCSD[T] data are evaluated from calculations done in the aTZ basis set

	6-31G** as small BS			aDZ as small BS			Combination	CCSDT	CCSD(T)	CCSD[T]
	1	2	3	1	2	3
All	0.93	1.36	2.02	0.44	0.80	0.74	1.20	1.42	3.78	4.13
Neutral	0.48	1.15	1.41	0.44	0.70	0.67	0.73	0.82	3.47	3.70
Charged	1.85	1.78	3.22	0.42	1.00	0.89	2.16	2.63	4.40	5.00

---

The average relative errors (plotted in Fig. 3) are the first tool for assessing the accuracy of the different schemes. As expected, the schemes using the largest basis set, aDZ, for the evaluation of the ΔCCSDT(Q) contribution produce the most accurate data. The average MUE is below 10 cal mol⁻¹ for all three schemes, that is, below 0.8%. It is surprising that among the three schemes, the first one (based on the CCSDT calculations) exhibits the highest accuracy with the average MUE error being below 3.5 cal mol⁻¹ (0.4%). However, the applications of this scheme are limited because obtaining accurate CCSDT energy to start with is significantly more difficult than calculating the triples perturbatively. Even if we assume that this baseline energy is extrapolated to CBS, the error introduced by the limitations on the basis set size in CCSDT calculation (in contrast to e.g. CCSD(T)) would be larger than the improvement in the accuracy of the contribution of quadruples. Surprisingly, scheme 3 (using the CCSD[T] baseline) produces on average more accurate correlation interaction energies than scheme 2 (based on the golden standard CCSD(T) calculations), the absolute errors being 6.89 vs. 9.96 cal mol⁻¹ (0.74% vs. 0.80%). This is a consequence of a more favorable error compensation in CCSD[T] interaction energies obtained with small basis sets, which we have described in our recent study.¹¹

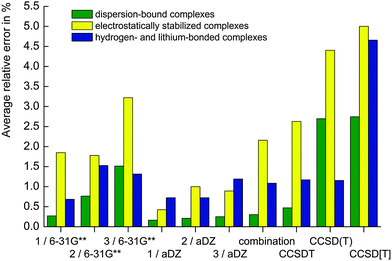Fig. 3 Average relative errors (in %) evaluated for all the schemes for different types of noncovalent complexes. The 6-31G** notation means that the 6-31G**(0.25,0.15) basis set was used.

The schemes using the smaller 6-31G**(0.25,0.15) basis set produce data with only slightly higher absolute errors: the highest error is observed for scheme 2, 13.74 cal mol⁻¹, it is 3.8 cal mol⁻¹ higher than the error in scheme 2 using the aDZ basis set despite the fact that the basis set is much smaller. For example, in the case of the BeH₂–LiH complex, there are 73 basis functions in the aDZ basis set and only 43 in the 6-31G**(0.25,0.15) basis set. Having in mind the scaling of the calculations, it is clear that the 6-31G**(0.25,0.15) basis set is applicable to much larger systems than aDZ. Again, the most accurate scheme is the first one with the average error of 11.2 cal mol⁻¹ (0.9%). The highest absolute error is observed for scheme 3 – 20.63 cal mol⁻¹ (2%). Scheme 4 uses both aDZ and 6-31G**(0.15,0.26) basis sets in a stepwise manner for the evaluation of the ΔCCSDT and ΔCCSDT(Q) corrections. The baseline interaction correlation energy is calculated using the CCSD(T)/aTZ method and we can thus compare it directly with the similarly constructed scheme 2. As expected, its accuracy lies between scheme 2/aDZ and scheme 2/6-31G**(0.25,0.15), the average MUE error for all complexes being 11.33 cal mol⁻¹ (1.2%). However, for neutral complexes, there is a substantial improvement and the two-step scheme yields an average error very close to the one-step correction in the larger basis set.

While all the composite schemes improve the correlation interaction energies when the average is evaluated over the whole set, inspection into the individual complexes shows that there are cases where adding the CCSDT(Q) correction leads to a worse result. This happens most often in the group of hydrogen- and lithium-bonded complexes. The baseline correlation interaction energies of the NH₃ dimer, the H₂O dimer, the LiH dimer, the HF dimer and the HCN–HF complex calculated without further corrections exhibit smaller errors with respect to the CCSDT(Q) benchmark than some of the composite results. The only scheme that consistently improves over the baseline in all the complexes is scheme 3/aDZ. Among the rest of the schemes, the ones that use the larger aDZ basis set perform the best, the exceptions being scheme 1/aDZ for the LiH dimer and scheme 2/aDZ for the HF dimer. Also the scheme 4 exhibits only one problematic case, the H₂O dimer. The schemes using the 6-31G**(0.15,0.25) basis set for the calculation of the Δ(Q) contribution yield even less reliable data.

The performance of the composite schemes in the group of electrostatically stabilized complexes is slightly better, with the problematic cases being the acetylene–Li⁺, acetylene–H⁻ and the LiH–Li⁺ complexes. There are 2 schemes that improve the correlation interaction energies of all the complexes: 2/aDZ and 3/6-31G**(0.25,0.15). The most problematic complex from this point of view is the acetylene molecule interacting with the lithium cation, where the schemes 2/6-31G**(0.15,0.25), 3/aDZ and scheme 4 produce less accurate data with respect to the benchmark compared to the baseline calculations alone.

The correlation interaction energies of dispersion-bound complexes show improvement towards the benchmark data upon applying the Δ(Q) correction within all the presented composite schemes. There is only one exception – the neon dimer – where the improvement is observed only for the 2/aDZ and 3/aDZ schemes. Here, the problem stems from the fact that the effective size of the basis set in an atomic complex is smaller than in molecular ones where the mixing of basis functions on all the atoms allows for better description of the wavefunction.

The difference between polar (hydrogen-bonded and charged) and nonpolar (dispersion-bound) complexes is probably caused not by the different nature of the electron correlation but by the limitations of the description of more polarized wavefunctions in the small basis sets.

Another line can be drawn between larger systems (seven species in a set having both interacting molecules containing more than four valence electrons) and smaller ones. The conclusions drawn from inspecting these groups of complexes separately are in accord with the conclusions valid for the whole set. The schemes using the aDZ basis set give more reliable results and should be used if possible. From these the 1/aDZ and 3/aDZ are the most effective.

Overall, the most successful composite schemes are the ones using the aDZ basis set for the calculation of the Δ(Q) correction to the correlation interaction energies. For the dispersion-bound complexes, the 2/aDZ and 3/aDZ schemes show the most accurate results. In the group of electrostatically stabilized complexes it is the 2/aDZ scheme that gives the most accurate data with respect to the benchmark. Finally the 3/aDZ scheme describes the correlation interaction energies of the hydrogen- and lithium-bonded complexes with the highest accuracy.

These results suggest that in specific cases, such as dispersion-dominated systems, it is possible to improve the interaction energies using a higher-order correction calculated in a rather small basis set, which opens up the possibility of applying such calculations to somewhat larger systems. On the other hand, if general applicability is sought, a larger basis set has to be used to avoid the deterioration of the baseline results in some polar complexes. In light of the findings presented here, we started to work on improving the ΔCCSDT(Q) term in the A24 data set. In the original work, the calculations were performed in the 6-31G**(0.25,0.15) basis set; these results will be updated to at least aDZ.

Conclusions

We have examined several approaches to adding the contribution of quadruple excitations calculated in a small basis set to CCSDT, CCSD(T) and CCSD[T] calculations. Overall, such corrections improve the results towards benchmark CCSDT(Q) calculations in a large basis set. Of course, the larger the basis set, the better the results, but even the most economic correction calculated in the 6-31G**(0.25,0.15) basis set is beneficial. A closer look at different classes of the complexes shows that dispersion-dominated ones are consistently described well even when a higher-order correction is calculated in a small basis set. On the other hand, more polar systems such as hydrogen bonds can only be described reliably when larger basis sets are used and in some cases, even the aDZ basis set is not sufficient. This situation is analogous to the composite CCSD(T)/CBS calculations where it was shown that for hydrogen bonds, the CCSD(T) contribution has to be calculated in a basis set larger than aDZ in order to achieve improvement over uncorrected MP2 results.³¹ Therefore, special care must be taken and the nature of the interaction has to be considered if a calculation of the ΔCCSDT(Q) correction is attempted in larger systems where the size of the basis set is the limiting factor.

Another important conclusion is that the choice of the baseline method does not affect the results significantly. It is thus possible to start with more efficient methods such as CCSD(T), avoiding the expensive CCSDT calculation in a large basis set.

Acknowledgements

This work was part of the Research Project RVO: 61388963 of the Institute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic. This work was also supported by the Czech Science Foundation [P208/12/G016] and the operational program Research and Development for Innovations of the European Social Fund (CZ 1.05/2.1.00/03/0058).

References

1. L. Šimová, J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 3420.
2. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041.
3. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
4. M. Urban, J. Noga, S. J. Cole and R. J. Bartlett, J. Chem. Phys., 1985, 83, 4041.
5. Y. S. Lee, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1984, 81, 5906.
6. J. Noga, R. J. Bartlett and M. Urban, Chem. Phys. Lett., 1987, 134, 126.
7. S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1998, 108, 9221.
8. Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 054101.
9. J. Pittner and P. Hobza, Chem. Phys. Lett., 2004, 390, 496.
10. B. W. Hopkins and G. S. Tschumper, J. Phys. Chem. A, 2004, 108, 2941.
11. J. Řezáč, L. Šimová and P. Hobza, J. Chem. Theory Comput., 2013, 9, 364.
12. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151.
13. A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kállay and J. Gauss, J. Chem. Phys., 2004, 120, 4129.
14. A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108.
15. A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114.
16. N. J. De Yonker, T. R. Cundari and A. K. Wilson, J. Chem. Phys., 2006, 124, 114104.
17. G. A. Petersson, in Computational Thermochemistry, ed. K. K. Irikura, D. J. Frurip, ACS Symposium Series No. 677, 1998, p. 237.
18. M. E. Harding and W. Klopper, ChemPhysChem, 2013, 14, 708.
19. A. D. Boese, J. Chem. Theory Comput., 2013, 9, 4403.
20. J. Černý, M. Pitoňák, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 12, 3924.
21. S. A. C. McDowell, J. Comput. Chem., 2003, 24, 1201.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
23. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007.
24. L. M. J. Kroon-Batenburg and F. B. van Duijneveldt, J. Mol. Struct., 1985, 121, 185.
25. P. Hobza and J. Šponer, Chem. Rev., 1999, 99, 3247.
26. D. Svozil, P. Hobza and J. Šponer, J. Phys. Chem., 2010, 114, 1191.
27. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639.
28. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
29. CFOUR, a quantum chemical program package written by J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay. With contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf, P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, J. Olsen), and ECP routines by A. V. Mitin, C. van Wüllen, For the current version, see http://www.cfour.de (accessed Sep 2012).
30. MRCC, a string-based quantum chemical program suite written by M. Kállay. See also M. Kállay and P. R. Surján, J. Chem. Phys., 2001, 115, 2945 , as well as http://www.mrcc.hu (accessed Sep 2012).
31. M. Marshall, L. Burns and D. C. Sherrill, J. Chem. Phys., 2011, 135, 194102.

---

Footnote

† Electronic supplementary information (ESI) available: Correlation interaction energies used to construct the composite results (Tables S1–S3) and the optimized geometries of the complexes used in this work. See DOI: 10.1039/c4cp02617a

---