Ultrafast photo-induced ligand solvolysis of cis-[Ru(bipyridine)₂(nicotinamide)₂]²⁺: experimental and theoretical insight into its photoactivation mechanism

Abstract

Mechanistic insight into the photo-induced solvent substitution reaction of cis-[Ru(bipyridine)₂(nicotinamide)₂]²⁺ (1) is presented. Complex 1 is a photoactive species, designed to display high cytotoxicity following irradiation, for potential use in photodynamic therapy (photochemotherapy). In Ru(II) complexes of this type, efficient population of a dissociative triplet metal-centred (³MC) state is key to generating high quantum yields of a penta-coordinate intermediate (PCI) species, which in turn may form the target species: a mono-aqua photoproduct [Ru(bipyridine)₂(nicotinamide)(H₂O)]²⁺ (2). Following irradiation of 1, a thorough kinetic picture is derived from ultrafast UV/Vis transient absorption spectroscopy measurements, using a ‘target analysis’ approach, and provides both timescales and quantum yields for the key processes involved. We show that photoactivation of 1 to 2 occurs with a quantum yield ≥0.36, all within a timeframe of ∼400 ps. Characterization of the excited states involved, particularly the nature of the PCI and how it undergoes a geometry relaxation to accommodate the water ligand, which is a keystone in the efficiency of the photoactivation of 1, is accomplished through state-of-the-art computation including complete active space self-consistent field methods and time-dependent density functional theory. Importantly, the conclusions here provide a detailed understanding of the initial stages involved in this photoactivation and the foundation required for designing more efficacious photochemotherapy drugs of this type.

---

1. Introduction

The unique photochemical properties of ruthenium-pyridyl complexes have been exploited for a plethora of technological and medicinal applications, such as: light-harvesting,^1,2 light-emitting devices,^3–5 fluorescence imaging^6,7 and cytotoxic action.^7,8 One of the more novel uses of these complexes is as photoactivatable prodrugs, where light induces formation of an active species from a stable, inert precursor molecule; a technique known by the term photodynamic therapy (PDT),⁹ or more generally as photochemotherapy. PDT has the obvious benefit of spatial control, limiting the possible side effects to the immediate area of tissue,^10,11 and also has the potential to generate unique reactive species that might otherwise be biologically incompatible i.e. caged delivery.^12–14

Several novel transition metal complexes with charge-transfer transitions have been shown to be photoactive including complexes of iron,¹⁵ osmium,¹⁶ rhodium,¹⁷ platinum¹⁸ and ruthenium.^19–21 For all these complexes, there is only a limited understanding of the photochemistry and photophysics that underpins their transformation from the inert to the active species. Perhaps the most heavily studied inorganic chromophores are polypyridyl complexes of ruthenium(II), of which, the archetypal tris-(2,2′-bipyridine)ruthenium(II), or [Ru(bpy)₃]²⁺, is a member.²² Numerous experimental and computational studies of [Ru(bpy)₃]²⁺ have revealed that its photophysics hinges around a manifold of near-degenerate metal-to-ligand charge-transfer triplet states (³MLCT) formed by ultrafast intersystem crossing (ISC) from the initially photo-populated (singlet) ¹MLCT state.^23–25 The ‘averaged’ ³MLCT state therefore involves electron transfer from a metal d-orbital to the π* orbital of one of the bipyridine (bpy) ligands and is formally termed [Ru^III(bpy)₂(bpy⁻)]²⁺. At a similar energy to this ³MLCT state, lies the lowest energy triplet metal-centred (³MC, d–d ligand field) state, the accessibility of which is dependent on solvent and temperature.²⁶ The ³MC state is known to exhibit significant distortions of the geometry relative to the ground state or that of the MLCT states,²⁷ and therefore an increased ligand labilization. For fully bidentate-chelated complexes such as [Ru(bpy)₃]²⁺, this dissociation channel is not usually a high yielding relaxation pathway^28,29 and such complexes primarily decay radiatively back to the ground state from the ³MLCT and/or ³MC states.²⁵ When one of the bpy ligands is replaced, for example, by two monodentate pyridines (or related aromatic heterocycles, L) to form a complex of the class [Ru(bpy)₂(L′)(L′′)]²⁺, a solvent substitution reaction may ensue, depending on the nature of the solvent.³⁰ As such, the replacement of an L ligand with a solvent molecule (solvolysis), following photodetachment, may provide a further excited state deactivation mode. The relative ordering of the energies of the ³MLCT and ³MC states becomes variable depending on the polar and steric effects of the substituent ligand, L.²⁶ It has been postulated that in order to create complexes with high photoproduct quantum yields (i.e. those which undergo ligand dissociation), the ³MC state must be made the lowest energy excited state or thermally accessible from the ³MLCT state.²⁶

To date, limited time-resolved spectroscopic and computational studies have been conducted on photoactivatable complexes of this type.^19,31–34 Such investigations may provide fundamental understanding of the mode(s) of activation, highlighting inefficiencies in the photoreaction of these complexes and so aid the design of more efficacious complexes, ultimately delivering improved healthcare technologies. Turro and co-workers have studied the ultrafast dynamics of the bipyridyl ruthenium acetonitrile complex cis-[Ru(bpy)₂(CH₃CN)₂]²⁺ following photoexcitation at 310 nm, in both water and acetonitrile solutions.³² For aqueous transient UV/Vis absorption experiments at early times (<10 ps), typical absorption features of the ³MLCT excited state and an absorption, assigned to a penta-coordinated Ru(II) intermediate (PCI), i.e. [Ru(bpy)₂(CH₃CN)]²⁺, were observed. Due to the near simultaneous appearance of these features, and the relatively slow decay (∼50 ps) of the ³MLCT signature, the authors proposed a kinetic picture of direct formation of the PCI from the initially populated singlet states (MLCT and/or ππ* ligand centred). The PCI may then recombine with its original partner ligand or, especially in the case of aqueous solutions, undergo solvolysis. Importantly, Turro and co-workers observed an absorption peak at 458 nm, appearing after 10 ps, which they assigned to the monoaqua complex, i.e., [Ru(bpy)₂(CH₃CN)(H₂O)]²⁺.³²

More recently, Lamberti and co-workers have carried out a combined experimental and theoretical study, using transient X-ray and visible absorption spectroscopies, and time-dependent density functional theory calculations to unravel the ³MLCT excited state structure of cis-[Ru(bpy)₂(py)₂]²⁺ (py = pyridine).³⁴ Their results showed that there is little reorganization of the geometry from the ground state to the ³MLCT state; only a small shortening of the Ru–N(bpy) bonds. Calculations of the ³MC state, however, showed a significant lengthening of one of the Ru–N(py) bonds and minimal re-optimizations of the bpy ligands. The transient X-ray absorption data provided experimental verification of the ³MLCT structure, but experimental determination of the ³MC geometries remains a challenge. The small intensity and energy differences in the transient visible absorptions between the ground state and mono-aquated photoproduct, cis-[Ru(bpy)₂(py)(H₂O)]²⁺, made accurate determination of the dissociation time of the pyridine ligand difficult, with an estimated dissociation time of <3 ns after excitation.

Depending on the size of the labile ligands and the nature of the extended solvent structure, it can be expected that there will be an ensemble of PCI species with their geminate partners having various degrees of separation.³⁵ These nascent photodetached ligands and partnering PCI complexes, surrounded by a solvation shell, can be classed as caged species and may either geminately reform the original complex or undergo (some degree) of diffusional separation, with the relative propensities for these processes depending on the exact nature of the system. In systems that undergo separation (or where the ligand is initially ejected through the solvation shell, e.g. smaller ligands), photodetached ligands may in principle still re-encounter the PCI complex, but after a longer diffusional period, to afford diffusive recombination. To date, no work has placed an emphasis on understanding the structural changes surrounding the PCI of a [Ru(bpy)₂(L′)(L′′)]²⁺ type complex during ligand solvolysis and the impact of caging on the degree of solvolysis (i.e. the quantum yield for formation of the mono-aquated species), which will undoubtedly contribute to its efficacy as a pro-drug.

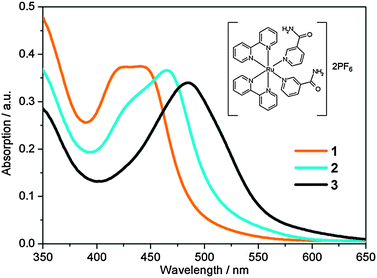
To this end, in this work we have investigated the structural and photochemical properties of the novel ruthenium complex, cis-[Ru(bpy)₂(NA)₂]²⁺ (1) (bpy = 2,2′-bipyridine and NA = nicotinamide, pyridine-3-carboxamide), the structure of which is shown in Fig. 1 inset and is termed 1 hereon. Following activation with light, this complex has potential for biological activity through both the release of nicotinamide and the generation of the chemically active Ru centre.^21,36–38 Given the high levels of cytotoxicity shown in similar Ru(II) anticancer complexes in the recent literature,^7,21,38–421 is likely to provide high cytotoxicity once activated. In aqueous solution, upon irradiation with UV or blue light, 1 undergoes solvolysis to form the mono-aquated photoproduct [Ru(bpy)₂(NA)(H₂O)]²⁺ (2). Continued irradiation (ca. 1 h) leads to the formation of the bis-aquated photoproduct [Ru(bpy)₂(H₂O)₂]²⁺ (3). Here we report the first detailed investigation into the excited state dynamics of the transformation of 1 to 2 (the transformation of 2 to 3 is much slower and beyond the time-window of our experiment) using a combination of ultrafast UV/Vis transient absorption spectroscopy (TAS) in conjunction with detailed theoretical calculations using density functional theory and its time-dependent analogue, in addition to the complete active space self-consistent field method.

Fig. 1 Static UV/Vis absorption spectra of [Ru(bpy)₂(NA)₂]²⁺ (1, orange), [Ru(bpy)₂(NA)(H₂O)]²⁺ (2, cyan) and [Ru(bpy)₂(H₂O)₂]²⁺ (3, black). Irradiation of 1 with 465 nm for 50 s yields 2. Further irradiation of 2 for 1 h 50 min yields 3. Molecular structure of 1 is shown inset.

2. Methods

2.1. Synthesis and characterization

NA was purchased from Sigma Aldrich and used as received. [Ru(bpy)₂Cl₂] was prepared following the literature procedure outlined in ref. 43. 1·(PF₆)₂, was synthesized in an analogous manner to other ruthenium(II) complexes of the type [Ru(bpy)₂(L)₂](PF₆)₂.¹⁴ [Ru(bpy)₂Cl₂] (104 mg, 0.2 mmol) was added to 10 mL degassed water and the solution was heated in the dark at 353 K for 15 min. NA (122 mg, 1 mmol) was added and the solution was heated for a further 2 h. The resulting dark red solution was allowed to cool, and any insoluble material was removed by filtration. NH₄PF₆ (163 mg, 1 mmol) was added to give an orange precipitate. The solution was cooled for 2 h (ca. 277 K) and filtered under suction. The precipitate was washed with 40 mL cold water and 40 mL diethyl ether. Yield 48.5%. ¹H NMR (300 MHz, dimethylsulfoxide-d₆)δ ppm: 7.50 (m, 4H), 7.76 (br s, 2H, NH), 7.90 (t, 2H, J = 6.5 Hz), 7.99 (d, 2H, J = 5.6 Hz), 8.03 (t, 2H, J = 8.0 Hz), 8.21 (br s, 2H, NH), 8.24 (t, 2H, J = 7.8 Hz), 8.36 (d, 2H, J = 8.1 Hz), 8.54 (d, 2H, J = 5.6 Hz), 8.60 (d, 2H, J = 8.1 Hz), 8.66 (m, 2H), 9.07 (d, 2H, J = 5.5 Hz). ESI-MS (methanol): 329.0 m/z ([M-2(PF₆)]²⁺, calculated 329.1 m/z). Anal. calcd for C₃₂H₂₈F₁₂N₈O₂P₂Ru: C: 40.56%, H: 2.98%, N: 11.82%. Found: C: 40.25%, H: 2.91%, N: 11.48%.

2.2. Ultrafast transient UV/Vis absorption spectroscopy

The UV/Vis TAS setup has been described previously.⁴⁴ Femtosecond laser pulses are produced by a commercial Ti-Sapphire regenerative amplified laser system (Spectra-Physics, Spitfire XP), which outputs 40 fs, 3 mJ pulses centred at 800 nm with a 1 kHz repetition rate. The beam is split into three parts of equal intensity. Two of these 1 W beams are used in the transient absorption setup: one beam is split into 95% and 5% parts for harmonic generation (not used in these experiments) and white light continuum (WLC) generation, respectively; the second beam is used to pump an optical parametric amplifier (OPA) (Light Conversion, TOPAS-C (UV-VIS)). The OPA provides the pump source with tuneable wavelengths in the range 240–1160 nm and typical powers of 8–90 μJ per pulse. A neutral density filter in the pump path provides variable pump fluences. The WLC probe is generated, by focusing the weak 800 nm beam into a 1 mm thick calcium fluoride (CaF₂) window. A variable aperture and a neutral density filter control the focusing and power of the 800 nm beam. A piezo actuator continuously translates the CaF₂ window vertically, in order to prevent WLC instabilities and damage to the CaF₂.⁴⁵ The WLC is recollimated using a spherical mirror (f = 50 mm) and is passed through a colour filter (Hoya CM-500) to remove the 800 nm fundamental and to reduce the intensity of the red component of the WLC. The usable WLC probe, spanning a range of 340–700 nm, is focused into the sample by a second spherical mirror (f = 200 mm). A hollow gold retroreflector (Edmund Optics) mounted on a motorized translation stage (Physik-Instrumente, M-505.4DG) in the pre-WLC path creates a variable pump–probe time delay ranging from femtoseconds (fs) to picoseconds (ps). Use of optics on flip mounts and prepositioned magnetic bases gives extra delay lines for select longer, nanosecond (ns) pump–probe time delays.

The pump beam is focused 10 mm behind the sample by a CaF₂ lens (f = 500 mm) to ensure that the diameter of the pump at the sample is greater than that of the probe. The pump and probe beams intersect the sample (see below) with a crossing angle of ∼4°. Rotation of a λ/2 waveplate in the pre-WLC path allows control of the polarization of the WLC; this is set at magic angle (54.7°)⁴⁶ relative to the pump polarization. Probe pulses at each pump–probe time delay are recorded using a fibre-coupled spectrometer (Avantes, AvaSpec-ULS1650F). The spectrometer captures at 1 kHz with 1000 shots per frame-grab. A mechanical chopper in the pump beam blocks every-other pulse so that the detector records ‘sample-pumped’ and ‘sample-not-pumped’ spectra sequentially. Data acquisition and the calculation of difference spectra, as well as control of the translation stage, are performed using a purpose built LabVIEW program.

Sample, at room temperature (295 K), is delivered using a 1 mm path length flow through quartz cuvette (Starna UK) and a PTFE tubing peristaltic pump (Masterflex). A homebuilt shutter based around the design in ref. 47 is used to block both pump and probe beams when not recording data to reduce sample degradation. This is also controlled through the LabVIEW program.

2.3. Theoretical calculations

The ground state geometries of complexes 1, 2 and the [Ru(bpy)₂(NA)]²⁺ PCI were optimized using density functional theory (DFT). Analytical Hessian evaluation confirmed the nature of the optimized geometries as minima. Several different functionals and basis sets were compared (PBE0,⁴⁸ M06L,⁴⁹ CAM-B3LYP⁵⁰ and B3LYP^51,52). In particular, regarding basis sets the use of non-, quasi-, and fully relativistic effective core potentials (ECPs) was investigated in conjunction with the cc-pVTZ valence basis on the metal and non-metals, respectively.⁵³ It was found that such basis-set effects on geometry and electronic spectroscopy (vide infra) were relatively minor compared to the choice of functional. As such, a non-relativistic SDD 28 electron (1s²2s²2p⁶3s²3p⁶3d¹⁰) ECP was used for the Ru centre, while the cc-pVTZ basis set⁵⁴ was selected for the remaining C, N, O and H atoms. The electronic spectroscopy (singlet and triplet excitations) of 1, 2 and the PCI was subsequently modelled with time-dependent density functional theory (TD-DFT), using the same basis set. For the functional, by far the best comparison with experimental UV/Vis spectra was found to be the B3LYP functional. A polarizable continuum model (PCM) was used to model the effects of solvation in H₂O.

To investigate the excited state reaction pathways in the PCI species, which determine the subsequent relaxation mechanism following light absorption, complete active space self-consistent field (CASSCF) calculations were performed. An active space was chosen consisting of the five 4d orbitals of the Ru centre, plus a corresponding set with an extra radial node in the Ru–N internuclear region to allow for dynamic electron correlation in the dative bonds.^55–57 Alternative schemes including quasi-natural orbital approaches, such as those discussed in ref. 58 and 59, were also performed at selected geometries to ensure the active space description was balanced and stable. Generally, these two schemes gave very similar results although the quasi-natural orbital approach was more problematic both in terms of convergence and characterization of the metal centred components, due to initial strong orbital mixing. Given the size of the systems under investigation, and the associated computational expense, the basis sets used for CASSCF calculations were a non-relativistic SDD 28 electron (1s²2s²2p⁶3s²3p⁶3d¹⁰) ECP basis for the ruthenium; the 4-31G basis for carbon, oxygen, and nitrogen; and the STO-3G basis for hydrogen. This basis was calibrated (at the ground state geometry of the PCI) against a larger basis consisting of the same metal centred part, plus the 6-31G(d) basis for the non-metals. Geometrical effects in using the larger basis were very small. For calculations in the singlet and triplet manifolds many-electron configuration state function (CSF) bases were used, corresponding to 〈Ŝ_z〉 = 0, 〈Ŝ²〉 = 0 and 〈Ŝ_z〉 = 1, 〈Ŝ²〉 = 2, respectively. For calculations of singlet/triplet interactions a Slater determinant many-electron basis with 〈Ŝ_z〉 = 0 was used. The orbital rotation derivatives were neglected in solving the coupled-perturbed multi-configurational self-consistent field (MCSCF) equations in geometry optimizations involving state-averaged orbitals. Gaussian09⁶⁰ was used for DFT and TD-DFT calculations, while Gaussian03⁶¹ was used for CASSCF calculations.

3. Results and discussion

3.1. Static UV/Vis absorption spectra

UV/Vis absorption spectra of 1 in aqueous solution (40 μM) before, and following excitation at 465 nm using a 50 mW blue LED, are shown in Fig. 1. Complex 1 has a broad visible absorption maximum, λ_max = 420–450 nm. Following 50 seconds of irradiation, the ground state absorption of 1 decayed and only the absorption of 2 was present with λ_max = 465 nm. The identity of the mono-aqua adduct 2 was confirmed by MS data shown in the ESI† (Fig. S1). Furthermore, HPLC analysis indicated that only one isomer of 2 was present after irradiation, in-line with previous literature, which reported that only the cis-2, and not trans-2, isomer will be generated.³⁰ We discuss the lack of isomerisation (and its origins) further in Section 3.6. A further 1 h 50 min of irradiation was required to convert the entire sample to the bis-aqua complex, 3, further red-shifting the λ_max to 483 nm. Power dependence studies of a similar complex (cis-[Ru(bpy)₂(CH₃CN)₂]²⁺) and the times of conversion indicated that the stepwise ligand exchange has two separate photochemical mechanisms.³²

In order to benchmark our complementary TD-DFT calculations against experiments, the calculated UV/Vis absorption spectra for complexes 1 and 2, using the TD-B3LYP method, are presented in Fig. 2a and b, respectively. As alluded to in Section 2.3, the B3LYP functional together with an SDD 28 electron ECP (Ru) and a cc-pVTZ (H, C, O and N) basis set, was selected based on the best comparison with experimental findings. For complex 1, Fig. 2a shows very good agreement between the calculated spectra and the experimental spectrum. The TD-B3LYP calculations on 1 were performed both on the isolated gas phase species, as well as in the presence of an H₂O PCM, in an attempt to capture some affects (if any) of solvation on the singlet electronic transitions. The results of both of these calculations are given in Fig. 2a, and show that for 1, negligible changes to the energies of singlet electronic excitations are observed between the gas phase and H₂O PCM TD-B3LYP calculations, although an overall enhancement in the transition dipole moments (TDMs) for the dominant ‘bright’ transitions is observed (cf. oscillator strengths, f, given in Table 1), the strongest of which belong to excitations of ¹MLCT states at 428 and 408 nm.

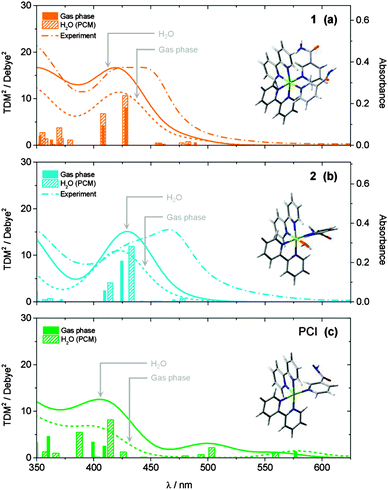Fig. 2 Calculated static UV/Vis absorption spectra for (a) 1, (b) 2 and (c) PCI, both in the gas phase (dotted lines) and with an H₂O PCM (solid lines). Calculated ground state structures shown inset. Spectra were calculated at the TD-B3LYP level of theory using a 28 electron SDD ECP for Ru and a cc-pVTZ basis set for C, O, N and H atoms. Calculated spectra were generated by convolution of the calculated squared transition dipole moments (TDM²) for singlet excitations with Gaussian functions (50 nm FWHM). Experimentally measured spectra for 1 and 2 from Fig. 1 are shown in panels (a) and (b), respectively, for comparison (dashed lines).

Table 1 Calculated vertical excitation energies (ΔE), transition wavelengths and associated oscillator strengths (f) for significant triplet and singlet electronic excitation transitions in complexes 1 and 2, using TD-B3LYP with an SDD 28 electron ECP (Ru) and cc-pVTZ (H, C, O and N) basis set. Major molecular orbital transitions and their relative contributions (%) to a given state are also provided (L = LUMO and H = HOMO) together with vertical energy differences (δE) between significant states in 1 (see Fig. 7 for orbital transitions in 1). Central wavelengths for the experimentally observed absorption bands of 1 and 2, assigned predominantly to the ‘bright’ ¹MLCT state(s), are also given (cf.Fig. 1)

State/parameter			TD-B3LYP/cc-pVTZ-SDD (+H2O PCM)^b			Experiment
Character	Transition^a	%^a	ΔE/eV	λ/nm	f	λ/nm
a Major orbital transition associated with electronic excitation. b All values in parentheses are for TD-B3LYP/cc-pVTZ-SDD calculation results including an H2O PCM.
cis-[Ru(bpy)2(NA)2]^2+ (1)
^3MLCT	L + 1 ← H − 2 (L + 1 ← H − 2)	56 (56)	2.64 (2.66)	470 (465)	—
^3MLCT	L ← H − 2 (L ← H − 2)	64 (64)	2.71 (2.73)	458 (454)	—
^1MLCT	L ← H − 2 (L ← H − 2)	65 (66)	2.90 (2.90)	428 (428)	0.0891 (0.1175)	∼435
^3MC	L + 10 ← H (L + 10 ← H)	58 (52)	2.94 (3.00)	422 (413)	—
^1MLCT	L + 1 ← H − 2 (L + 1 ← H − 2)	62 (62)	3.04 (3.04)	408 (408)	0.0487 (0.0782)
^1MC	L + 10 ← H (L + 10 ← H)	48 (48)	3.56 (3.61)	348 (343)	0.0024 (0.0077)
	δE [^1MLCT − ^3MLCT]		0.19 (0.17)
	δE [^3MC − ^3MLCT]		0.23 (0.27)
cis-[Ru(bpy)2(NA)(H2O)]^2+ (2)
^3MLCT	L ← H − 2 (L ← H − 2)	38 (41)	2.47 (2.46)	501 (502)	—
^3MLCT	L + 1 ← H − 1 (L + 1 ← H − 2)	61 (49)	2.53 (2.51)	490 (494)	—
^1MLCT	L ← H − 2 (L ← H − 2)	51 (49)	2.92 (2.86)	425 (433)	0.0974 (0.1294)	∼470
^1MLCT	L + 1 ← H − 1 (L + 1 ← H − 2)	42 (47)	3.03 (2.99)	409 (414)	0.0282 (0.0464)

---

Results of analogous calculations for the mono-aqua photoproduct complex 2 are also presented in Fig. 2b. These generate a UV/Vis absorption spectrum which is blue shifted by ∼30 nm relative to experiment, for both the gas phase and H₂O PCM, although in good qualitative agreement with the experimentally observed profile. Once again, the major absorption signatures arise from bright ¹MLCT transitions, as with complex 1 (see Table 1 and ESI,† Fig. S2, for orbital transitions). Most notably, experimental findings clearly show an absorption red shift of ∼30 nm upon evolution from the starting complex 1 to photoproduct 2. Computationally, this red shift is only qualitatively captured upon inclusion of the H₂O PCM, while gas phase calculations predicted that 1 and 2 absorb at similar wavelengths. However, even with the inclusion of the H₂O PCM, the calculations only predict a red shift of ∼5–10 nm between 1 and 2 at this level of theory (N.B. similar shifts were observed with other functionals, e.g. PBE0). There may be several reasons for this discrepancy. (i) This may be a direct effect of solvation, and more in-depth solvation models (such as hybrid QM/MM methods^62,63), although beyond the scope of the present work, may be necessary to capture this behaviour fully. (ii) The TD-B3LYP calculations predict a number of singlet electronic states to lie below the bright ¹MLCT states (in both 1 and 2), which have minimal transition strengths from the equilibrium ground states of 1 and 2. Vibronic coupling however, may lend transition strength to excitations through thermal population of low frequency vibrations modes in the ground state, which are not captured in these vertical excitation calculations. (iii) Finally, for both 1 and 2, the bright ¹MLCT states will be strongly spin–orbit coupled with the analogous ³MLCT states, which lie lower in energy (see Table 1); this assumption is reinforced by the fact that in [Ru(bpy)₃]²⁺, ISC between the ¹MLCT and ³MLCT states is observed to occur within ∼100 fs.^24,64–67 This spin–orbit coupling will lend transition strength for direct excitation to these (formally forbidden) ³MLCT states, and may also be responsible for contributing to the observed differences between the experimental and computational UV/Vis spectra.

3.2. Ultrafast transient UV/Vis absorption spectra

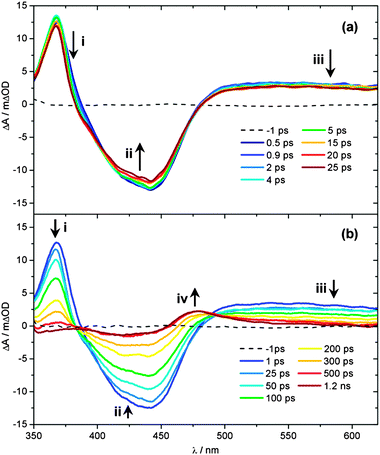
Ultrafast UV/Vis TAS was used to follow the dynamics of an 890 μM aqueous solution of 1 flowing through a flow cell, following excitation with a 340 nm, 650 μW pump pulse. Fig. 3 shows TAS at pump–probe time delays ranging from t = −1 ps to 1.2 ns. We begin by focusing on the spectra recorded at early pump–probe delays shown in Fig. 3a (t < 25 ps). Inspection of these spectra shows that several distinct regions can be identified immediately following excitation, related to the spectral location. A strong bleach signal is observed, centred on 420 nm (feature ii), which closely matches the spectral profile of the steady state absorption of 1 (Fig. 1, orange line). As such, feature ii is assigned to the ground state bleach (GSB) signal of 1. Relative to the absorption profile of 1 in Fig. 1, a narrowing of the GSB feature ii is also observed at the ‘wings’ of the bleach (∼400 and ∼475 nm). This is due to overlap with positive ΔOD signal either side of this feature, where ΔOD denotes the change in the optical density (absorbance). The strongest of these adjacent features, labelled i in Fig. 3a, is centred at ∼370 nm. UV/Vis spectroelectrochemistry measurements of [Ru(bpy)₃]^2+ 68 and related complexes with functionalized bpy derivatives⁶⁷ indicate that feature i can be assigned to an excited state absorption (ESA) of the ³MLCT excited state, and specifically corresponds to an absorption from the bpy anion (bpy⁻) present within the formally charge-separated character of the ³MLCT state (i.e. [Ru^III(bpy)(bpy⁻)(NA)₂]²⁺).⁶⁹ Further comparison with earlier literature also indicates that there should be a second (less strong) ESA absorption signal associated with the ³MLCT state within the region ∼450–550 nm.⁷⁰ Between 450–500 nm any such signal will be strongly convoluted with the GSB feature ii. At λ > 500 nm however, a broad plateau of transient absorption signal is observed. We therefore suggest that the absorption between 500–550 nm is primarily due to the ESA of the ³MLCT state.

Fig. 3 UV/Vis TAS of 890 μM aqueous solution of 1 over pump–probe delay ranges (a) t = −1 to 25 ps and (b) t = −1 ps to 1.2 ns, following photoexcitation at 340 nm. Growth/decay features i–iv highlighted indicate the spectral location assigned to the ³MLCT ESA, GSB of 1, absorption of the PCI and, finally, photoproduct 2, respectively. See main text for further details.

At much longer wavelengths (λ > 550 nm), another absorbing species must be contributing to this plateau of transient absorption signal, labelled feature iii. Once again, comparison with earlier studies can prove instructive here. Very recently, further UV/Vis TAS measurements on [Ru(bpy)₃]²⁺ and its methylated derivatives by Hauser and co-workers,⁷¹ have suggested that absorption in this region of the TAS is due to ESA of the ³MC state. In these bidentate-ligand chelated complexes, at larger Ru–N(bpy) bond distances the ³MC surface will exhibit notable bound character, as complete Ru–N(bpy) bond fission is necessarily aborted (see Fig. 4 in ref. 71), enabling population to become trapped transiently in the ³MC state, prior to population transfer back to the ground state. This behaviour will extend the lifetime of population in the ³MC state and make it spectroscopically detectable in the TAS measurements. However, the analogous ³MC state in 1 will be purely repulsive with respect to bond fission, meaning that any population transferred to the ³MC state will undergo rapid (ultrafast) dissociation into a PCI complex and NA ligand, rather than being transiently trapped on this surface. Calculated profiles of the ³MC state along the Ru–N(py) dissociation coordinate in the related cis-[Ru(bpy)₂(py)₂]²⁺ complex support this picture.³¹ Such a scenario would make it unlikely that any fleeting population in the ³MC state is observable in 1. In earlier TAS work on cis-[Ru(bpy)₂(CH₃CN)₂]²⁺ by Turro and co-workers, a similar signal was instead assigned to absorption of a PCI complex, although limited justification was provided for this assignment.³² To add weight to this postulate here, we have also performed TD-B3LYP calculations in an attempt to predict the absorption profile of the PCI complex, the results of which are shown in Fig. 2c. Unlike complex 1 and the mono-aquated photoproduct 2 (Fig. 2a and b, respectively), the calculated absorption profiles for the PCI (in the gas phase and H₂O PCM) indeed qualitatively suggest that: (i) its absorption cross-section is weaker than 1 and 2; and (ii) it should absorb weakly into the ‘red end’ of our experimental detection window in the TAS (λ > 550 nm). Given this, we are therefore inclined to assign feature iii to absorbance of the PCI complex, [Ru(bpy)₂(NA)]²⁺, in concord to earlier work by Turro and co-workers.³² The presence of feature iii in the TAS at the earliest pump–probe delays (t = 0.5 ps) also confirms that any Ru–NA bond fission occurs on a sub-picosecond timeframe.

Having assigned the main features in Fig. 3a, we now consider any observed temporal evolution at early time-delays (t < 25 ps). In general, all three labelled features in Fig. 3a begin to deplete within the first 25 ps. Perhaps most significant though is the evolution of the ³MLCT ESA feature i, which both begins to deplete, spectrally narrow and blue-shift over this timeframe. Such behaviour can be broadly attributed to vibrational cooling of the nascent ³MLCT state occurring over the timescale of a few picoseconds and we return to consider this behaviour in greater detail below. Similar depletion of the signal associated with the PCI feature iii may also indicate rapid cooling of any nascent PCI species, or alternatively may be due to a structural rearrangement of the PCI after it is formed – we examine this further in Section 3.6. Finally, the apparent depletion of the GSB feature ii is most likely attributable to the vibrational cooling dynamics in the spectrally overlapped ³MLCT ESA signal, rather than any rapid repopulation of the ground state of 1.

Fig. 3b follows the dynamics of these features to longer time delays (25 ps < t < 1.2 ns). The GSB feature ii recovers whilst the ³MLCT ESA feature i and the PCI feature iii concomitantly decay over the following few hundred picoseconds and a new absorption feature centred at 475 nm (labelled feature iv) emerges at t > 300 ps, reaching a maximum intensity after ∼500 ps. The growth of feature iv results in a quasi-isosbestic point at 490 nm as this new feature rises and the ³MLCT ESA and PCI absorption features at λ > 500 nm decay over this time window. We attribute this absorption to mono-aquation of the PCI and the formation of photoproduct 2, as the location of feature iv is concordant with the static UV/Vis absorption spectrum of 2 in Fig. 1 (cyan line). The formation of a photoproduct is in-line with the fact that the GSB feature ii never fully recovers back to a baseline signal of ΔOD = 0, confirming that some portion of initially photo-excited population in 1 never returns to the ground state. Further confirmation of the assignment of feature iv to the formation of 2 can be seen when TAS measurements on 1 are recorded from an acetone solution (ESI,† Fig. S3); acetone is a weakly coordinating ligand compared to H₂O. In this comparative data set (i) no obvious transient absorption signal of a ligand substituted photo-product is present within our probe window of 340–700 nm and (ii) the GSB feature fully recovers to a baseline of ΔOD = 0, suggesting an absence of any significant photoproduct yield (even if its absorption signature were to lie outside our probe window).

In earlier ultrafast transient absorption studies of related Ru(II) complexes, a more quantitative insight into the timescales for ³MLCT state decay (and vibrational cooling), GSB recovery, decay of the PCI species and the formation of the mono-aquated photoproduct was attempted by integrating ‘slices’ through different spectral regions of the recorded TAS and then fitting the decay/growth of these traces to either mono- or bi-exponential functions.³² However, given that many of the spectral signatures for each of these individual species are heavily convoluted within the recorded TAS (vide supra), such an analysis can return misleading timescales and quantum yields (ϕ) for the dissociation dynamics (e.g.Fig. 1 clearly shows that the spectral signatures for 1 and 2 are strongly overlapped). In an attempt to circumvent this issue, we elect instead to perform a ‘target analysis’ of the TAS by fitting each of the time-resolved spectra with appropriate basis functions (associated with each of the absorption/bleach features) using the spectral analysis package KOALA (see ESI,† Section S5 for further details).⁷² Integration of each of these fitted basis functions as a function of time then returns kinetic traces that solely correlate to the population dynamics of individual species involved in the dissociation of 1.

Representative fit examples, obtained for time-resolved spectra recorded at t = 1 ps and 1 ns, are given in Fig. 4a and b, respectively. The static UV/Vis absorption spectra recorded for 1 and 2 in Fig. 1 are used as basis functions for modelling the evolution of the GSB of 1 and the formation of photoproduct 2 (orange and cyan lines, respectively). For the ³MLCT component, two Gaussians are used to approximate the ESA profile (blue line), with their precise locations, relative amplitudes and widths based on the known spectral profile of the bpy⁻ absorption of similar complexes.^67–70

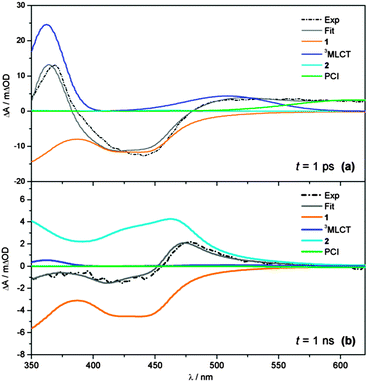Fig. 4 Representative fits (grey) to transient absorption spectra (black dashed) at (a) t = 1 ps and (b) t = 1 ns, showing the individual basis functions used in the ‘target analysis’ of the TAS in Fig. 2. Basis functions have been assigned to the ³MLCT ESA (blue), PCI complex (green), GSB recovery of 1 (orange) and formation of the photoproduct 2 (cyan). Static UV/Vis absorption spectra in Fig. 1 are used as basis functions for 1 and 2 – see text for further details.

Finally, the spectral profile of the PCI species present at long wavelengths is modelled with a broad Gaussian function (green line). In the case of the PCI, we acknowledge that, like 1 and 2, TD-B3LYP calculations predict this species should also absorb in the blue end of our detection window (λ < 450 nm), albeit less strongly (see Fig. 2c). However, attempts to include this behaviour make the target analysis far more cumbersome, due to the multiple absorbing species in this spectral region. To make the analysis feasible, we therefore elect to only model the PCI absorption at λ > 550 nm. The representative fits in Fig. 4 serve to highlight the convoluted nature of the final TAS. This is particularly clear at longer time-delays (Fig. 4b, t = 1 ns) where the remaining GSB signal for 1 and the photoproduct 2 are directly overlapped at λ < 450 nm, and the sum of the basis function profiles generated in the fit (grey line) replicates the experimental spectrum (black dashed line) exceptionally well.

3.3. Kinetic model for dissociation of cis-[Ru(bpy)₂(NA)₂]²⁺

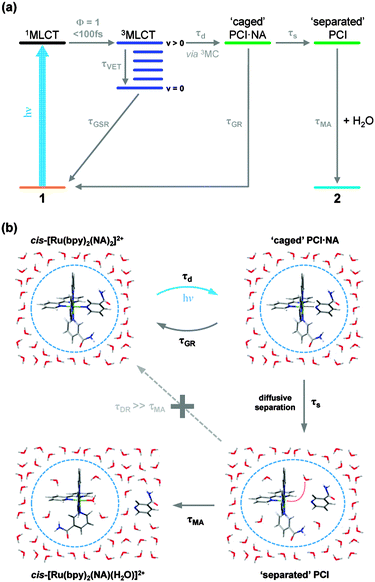
Integration of the fitted basis functions from the target analysis for the ³MLCT ESA, GSB recovery of 1, the PCI and the growth of photoproduct 2 are presented in Fig. 5a–d. Before proceeding with any fitting of these traces, we first establish a full kinetic model for the dissociation of 1 by considering the dynamical pathways that give rise to Ru–NA bond fission, as well as any (dominant) competing relaxation processes. We herein discuss these with reference to the scheme in Fig. 6a.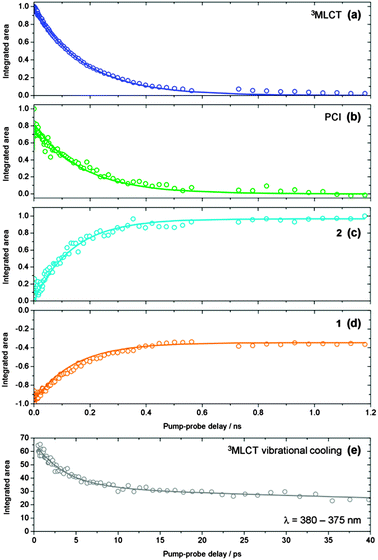

Fig. 5 (a–d) Kinetic traces for the time-dependent evolution of the ³MLCT state population (blue), PCI (green), photoproduct 2 (cyan) and GSB recovery of 1 (orange), obtained by integration of the basis functions (see Fig. 4) used in the ‘target analysis’ of the TAS in Fig. 3. Kinetic fits to these traces, in accordance with the scheme in Fig. 6a, are shown by the solid lines – see main text for details. (e) Kinetic trace reflecting the vibrational cooling of the ³MLCT state at t < 25 ps (grey squares), obtained by integration of the ‘red edge’ of the ³MLCT feature i in Fig. 3a over a range λ = 375–380 nm. The solid grey line represents a fit to the trace with a bi-exponential decay function.

Fig. 6 (a) Kinetic scheme illustrating the major pathways and associated time constants (τ), used to model the photodissociation dynamics of 1 in H₂O. The individual steps involved in this kinetic scheme are discussed further in the main text (Section 3.3). (b) Pictorial schematic of the post-dissociation processes involving the PCI and formation of the photoproduct 2.

The predominant models for photo-induced ligand exchange/dissociation in similar Ru(II) complexes in the literature, propose extremely efficient traversal of excited state flux from the vertical Franck–Condon excitation region of the ¹MLCT state(s) to the PCI via³MLCT state(s) and a dissociative ³MC state. Following ISC and geometry rearrangements, the PCI can then accommodate the addition of an H₂O molecule to yield 2. To help construct such a model for 1, and to gain some insight into the relative energies of the ¹MLCT, ³MLCT and ³MC states postulated to drive ligand dissociation, we once again turn to our complementary TD-DFT calculations. The results of these TD-B3LYP calculations are summarized in Table 1 and show an optically bright ¹MLCT centred around 2.90 eV (428 nm), in both the gas phase and with an H₂O PCM. This state is the central component of the ‘triply degenerate’ state (split by only ∼0.15 eV) that one would expect in a d⁶ metal complex with metal–π interactions. Analysis of the (dominant) orbital transition associated with this state confirms it to be of MLCT type, with the relevant orbital transition shown in Fig. 7a (LUMO ← HOMO − 2). A higher energy, but more weakly absorbing, ¹MLCT component is identified to lie at 3.04 eV (408 nm), with the associated orbital transition for this state shown in Fig. 7b (LUMO + 1 ← HOMO − 2); for both of these ¹MLCT states the associated orbital transitions further highlight their formally charge separated [Ru^III(bpy)(bpy⁻)(NA)₂]²⁺ character (vide supra). Based on the oscillator strengths, f, returned by the TD-B3LYP calculations, the absorption of photons with energy around 2.90 eV or higher, viz. λ_excitation = 340 nm (4.76 eV), will most likely result in the initial population of highly electronically excited ¹MLCT states, rather than ¹MC states (see Table 1), followed by ultrafast internal conversion to the lower energy ¹MLCT states. We note for completeness that the TAS pump wavelength of 340 nm is selected since it lies outside our probe window and thus avoids contaminating part of our TAS spectra.

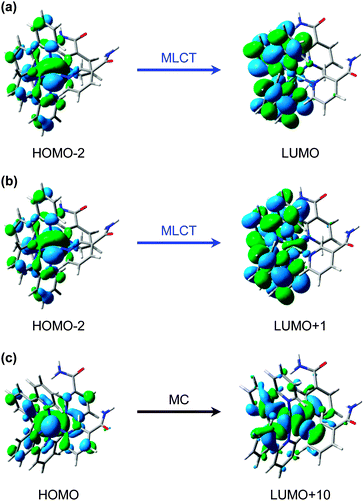Fig. 7 Calculated (major) orbital transitions associated with (a, b) the ¹MLCT/³MLCT states and (c) ¹MC/³MC states for complex 1 using the TD-B3LYP method – see Table 1.

The associated ³MLCT state (of analogous LUMO ← HOMO − 2 character) is calculated to lie at ∼2.70 eV (∼458 nm); ∼0.2 eV lower in energy than ¹MLCT (see Table 1). Similarly, the ³MLCT state dominated by the LUMO + 1 ← HOMO − 2 transition lies lower in energy again at ∼2.65 eV (∼468 nm). The high-density of states will promote very efficient vibronic coupling via multiple Jahn–Teller (JT) and pseudo-JT type couplings between these ¹MLCT and ³MLCT potential energy surfaces.⁵⁷ For the archetypal complex, [Ru(bpy)₃]²⁺, ¹MLCT → ³MLCT ISC is reported to: (i) possess a (near) unity quantum yield (ϕ ∼ 1);⁷³ and (ii) be ultrafast (∼100 fs^24,64–67), leading to a non-thermally equilibrated (vibrationally excited/hot) ³MLCT state, henceforth termed ³MLCT_v>0 in Fig. 6a.⁷⁴ McGarvey and co-workers⁷⁵ found there to be remarkably little difference in ¹MLCT → ³MLCT_v>0 coupling within the [Ru(bpy)₃]²⁺ complex and other similar complexes, where similar sub-picosecond population of ³MLCT_v>0 state(s) is also observed. Such behaviour is also consistent with observations from our TAS spectra of 1 in Fig. 3, which indicate that population is present in the ³MLCT state at our earliest recorded time-delay (t = 0.5 ps), and confirms that ¹MLCT → ³MLCT_v>0 ISC occurs on a sub-500 fs timeframe.

Once populated, intramolecular and/or intermolecular (solute–solvent mediated) vibrational relaxation (collectively termed vibrational energy transfer (VET)⁷⁶) of ³MLCT_v>0 may subsequently occur with a lifetime τ_VET, leading to the formation of a vibrationally-cold ³MLCT state, termed ³MLCT_v=0, as indicated in the schematic in Fig. 6a. Once again, this is consistent with our observations for band narrowing of the ³MLCT ESA feature i at t < 25 ps in Fig. 3a. Integrating the signal on the ‘red edge’ (λ = 375–380 nm) of the ³MLCT ESA feature i in Fig. 3a yields the kinetic trace in Fig. 5e, which when fitted to a bi-exponential decay returns a time-constant of 3.6 ps for τ_VET (see Table 2). Once cooled, the population located in ³MLCT_v=0 may then undergo relaxation (via either ISC or phosphorescence) back to the singlet electronic ground state of 1 (ground state recovery, GSR) with a time constant τ_GSR, which based on observations in Fig. 3b and the kinetic trace for ³MLCT in Fig. 5a, must occur over a longer timeframe of hundreds of picoseconds.

Table 2 Time constants (τ) and quantum yields (ϕ) extracted for the dissociation of 1 in both H₂O. Values for τ are extracted from kinetic fits to the traces in Fig. 5, in accordance with the kinetic model presented in Fig. 6. See main text for further details

Parameter	Value
τ d	0.4 ps
τ VET	3.6 ps
τ GSR	180 ps
τ GR	263 ps
τ s	377 ps
τ MA	<1 ps
ϕ d	0.89
ϕ ^3MLCTv=0	0.11
ϕ GR	0.53
ϕ 2	0.36
ϕ 1	0.64

---

In addition to the VET and recovery of the ground state of 1 from the ³MLCT state, population in this state must also couple onto a neighbouring dissociative ³MC surface to drive Ru–NA bond fission.³⁰ Our TD-B3LYP calculations in Table 1 predict the lowest energy of these ³MC states to lie between ∼2.9–3.0 eV (425–413 nm), ∼0.25 eV higher in energy than the lower lying ³MLCT (LUMO ← HOMO − 2) state in the vertical Franck–Condon region. The dominant orbital transition associated with this ³MC state (LUMO + 10 ← HOMO, see Fig. 7c) populates an anti-bonding MC orbital which has strong 4d_x²−y² character and is dissociative with respect to both of the Ru–NA dative bonds (as well as the equatorial Ru–N(bpy) bonds). For completeness, the analogous ¹MC state is calculated to lie at ∼3.6 eV (∼345 nm). We recall that, as with the ³MLCT ESA feature i in Fig. 3, a transient absorption signature for the nascent PCI species, formed as a result of Ru–NA dissociation, is also observed at the earliest time-delay of t = 0.5 ps in the TAS, indicating that Ru–NA bond fission must also occur on a sub-500 fs timeframe, with a time-constant τ_d. Based on simple kinetics grounds, if coupling onto the ³MC surface were barrierless (i.e. accessible from both the ³MLCT_v>0 and ³MLCT_v=0 levels), the observed lifetime of the ³MLCT state should in turn be solely defined by the rapid dissociation lifetime τ_d. However, this picture is clearly not consistent with general observations from Fig. 3 and the kinetic trace for ³MLCT in Fig. 5a, which decays over hundreds of picoseconds, rather than a sub-500 fs timeframe. Given this, we invoke a simple model where a barrier to dissociation (coupling onto the ³MC state) can only be surmounted from a vibrationally hot ³MLCT_v>0 state; the presence of a barrier to coupling between ³MLCT and ³MC states is generally supported by the fact that our TD-B3LYP calculations predict the ³MC to lie above the ³MLCT in the vertical Franck–Condon region.²⁵ Within this model, VET out of the ³MLCT_v>0 level over τ_VET = 3.6 ps acts as a ‘time dependent switch’, preventing population transfer between ³MLCT and ³MC states as the process becomes energetically inaccessible (a barriered process) after population is funnelled into ³MLCT_v=0. Fig. 6a therefore shows that population subsequently trapped in ³MLCT_v=0 following VET may then only undergo relaxation back to the ground state of 1.²⁷

Immediately after dissociation, the size of both the PCI complex and NA ligand will mean that they undergo strong caging within the solvation shell, and can be viewed as ‘loosely associated’, as illustrated pictorially in Fig. 6b. These nascent caged photoproducts, henceforth labelled PCI·NA (Fig. 6), may then geminately reform the initial complex 1 with a time-constant τ_GR, or alternatively undergo some degree of diffusional separation on a timescale τ_s. The later of these processes will yield the formation of a PCI complex that may then accept a free H₂O solvent molecule into its now open coordination site, simply termed ‘separated’ PCI in Fig. 6, and undergo mono-aquation to form the final photoproduct 2 on a timescale τ_MA.

The above kinetic picture of dissociation is broadly consistent with phenomenological models used to treat VET, bond fission, caging and diffusional separation/escape dynamics observed in ultrafast photodissociation studies of smaller organic species.^77,78 However, before proceeding further we first briefly justify some of the inherent assumptions surrounding the aforementioned picture, for the dissociation of 1 in H₂O. (i) After dissociation the ‘caged’ PCI·NA pair are in close proximity and as a result we make the assumption that direct formation of 2 from this species will be strongly hindered on steric grounds – hence this pathway is absent in Fig. 6. (ii) After some degree of diffusional separation, the ‘separated’ PCI and NA species may in principle re-encounter one another, leading to a ‘diffusive recombination’ pathway for the reformation of 1, rather than the production of 2. However, given the vast excess of H₂O solvent molecules, and their relative lability compared to the bulkier PCI and NA, we propose that τ_MA will strongly out-compete any timescale for diffusive recombination, τ_DR (i.e. τ_DR ≫ τ_MA). As such, τ_DR is neglected in our kinetic model for the dissociation of 1 in H₂O in Fig. 6a, and is represented as a kinetically inactive channel for the post-dissociation processes illustrated in Fig. 6b, which we justify further below.

3.4. Kinetic analysis

Using this kinetic model for the photodissociation of 1 in H₂O, full kinetic fits to the traces were performed. These traces, presented in Fig. 5a–d, were simultaneously fit to the analytical solutions for the time-dependent populations of each of these species within our model in Fig. 6a; these first-order differential kinetic equations are detailed in the ESI† online (Section S5). We note that during this fitting procedure, the τ_VET timescale of 3.6 ps, extracted earlier from Fig. 5e, is held fixed. Given that our kinetic model in Fig. 6a displays branched kinetic pathways, fixing τ_VET helps to make the fitting procedure more reliable (and less cumbersome). The results of these fits are presented as solid lines through the data sets in Fig. 5a–d, and the time-constants returned are collated in Table 2.

For the case of the ³MLCT feature in Fig. 5a, this trace is fitted to both the kinetic equations for ³MLCT_v>0 and ³MLCT_v=0, given that they will both contribute to this feature. Similarly, the PCI feature in Fig. 4b is fitted with the equations for both the ‘caged’ PCI·NA and ‘separated’ PCI species in our model, as they will both possess the same spectral signature. In this case though, the amplitude of the ‘separated’ PCI component required to fit this trace is found to be negligible. This is in-line with the time-constants returned by the kinetic fits, which indicate that the steady-state population of the ‘separated’ PCI complex will be minimal, as it is rapidly consumed to generate the mono-aquated photoproduct 2, with a timescale of τ_MA < 1 ps.

More generally the results of this analysis confirm that Ru–NA bond fission, via coupling from ³MLCT_v>0 onto the dissociative ³MC state, does indeed occur on a sub-picosecond timeframe (τ_d = 0.4 ps). After dissociation into ‘caged’ PCI·NA species, geminate reformation of 1 or diffusive separation, forming ‘separated’ PCI complexes, occur. Both are strongly competitive processes, taking place on the order of a few hundred picoseconds (τ_GR = 263 ps and τ_s = 377 ps). For the fraction of PCI·NA that do go on to form ‘separated’ PCI complexes, the PCI may then rapidly accommodate an H₂O solvent molecule into the now open coordination site (τ_MA < 1 ps), and our analysis indicates that it is the diffusional separation/reorganization process from ‘caged’ PCI·NA to ‘separated’ PCI that acts as the rate limiting step to the formation of photoproduct 2 (i.e. τ_MA ≪ τ_s) – hence the observed build-up of 2 over hundreds of picoseconds in the TAS. Moreover, the hundreds of picoseconds timeframe extracted for diffusive separation, further serves to confirm our assertion from Section 3.3 that diffusive recombination, τ_DR, of the separated PCI and NA in aqueous solution (which is also a diffusion limited process) must also occur over a similar timeframe post-separation, and as such can be negated from our kinetic model in Fig. 6, as τ_MA ≪ τ_DR. In tandem with these dissociative pathways, a fraction of the population initially present in ³MLCT_v>0 will be vibrationally quenched into a cold ³MLCT_v=0 state (τ_VET = 3.6 ps), and from here undergo relaxation back to the ground state of 1 with a time constant of τ_GSR = 180 ps.

3.5. Quantum yields

In the above kinetic analysis, we have assumed that all population initially imparted to the optically bright ¹MLCT state by the excitation pulse is transferred through ISC to the ³MLCT surface.⁷³ In assuming this initial ¹MLCT → ³MLCT_v>0 ISC quantum yield to be unity (ϕ = 1), subsequently we can extract values for ϕ for all of the remaining processes within our kinetic model in Fig. 6, which are also collated in Table 2.

Based on our model in Fig. 6a, the quantum yield for dissociation (ϕ_d) can be determined by the relative magnitudes of the rate constants for VET (k_VET) and dissociation (k_d), where the rate constant k is related to the lifetime τ through k = 1/τ. Formally, ϕ_d = k_d/(k_d + k_VET) and returns a value of ϕ_d = 0.89 for the photodissociation of 1 in H₂O. Meanwhile, the remaining fraction of population (ϕ_³MLCTv=0 = 1 − ϕ_d) will be funnelled into vibrationally cold ³MLCT_v=0. In deriving these values for ϕ_d and ϕ_³MLCTv=0, an assumption is made that the timescale for VET remains constant for the duration of the vibrational cooling process in ³MLCT. However, this is an over simplification and, in reality, the initial VET rate around the hot ³MLCT_v>0 levels is likely to be much more rapid than the value for τ_VET reported in Table 2, due to the comparatively high density of vibrational levels and the smaller energy spacing (cf. closer to ³MLCT_v=0). As vibrational energy is quenched away from ³MLCT_v>0, relaxation will populate lower vibrational levels where the density of states is reduced and the inter-state spacing is increased, leading to a reduction in the VET rate as ³MLCT_v=0 is approached. VET out of these lower vibrational levels will therefore act as a rate-limiting step in vibrational cooling,^76–78 and our value for τ_VET in H₂O most likely reflects these later stages of this process. Taking this into consideration, the value we extract for ϕ_d from this ‘zero-order’ model should be considered as an absolute upper limit for the fraction of population evolving towards dissociation. Even so, the value for ϕ_d derived here is still instructive and leads to a general conclusion that ϕ_d ≥ ϕ_³MLCTv=0 for 1 – such a conclusion is broadly supported by previous work on other related Ru(II) systems,^31–34 which also suggest ϕ_d will be large. Given this, it is striking that the relative intensity of the ³MLCT ESA features in the TAS are comparable to, or greater than, the spectral signature for the PCI complex formed through Ru–NA dissociation (cf. feature ivs. feature iii in Fig. 3a). This generally suggests that the ESA cross-section from the ³MLCT state is significantly greater than the absorption cross-section of the PCI species. Similar findings can also be seen in the TAS for 1 in acetone (ESI,† Fig. S3), and are qualitatively supported by the predicted weak absorption intensity of the PCI complex at λ > 550 nm by the TD-B3LYP calculations in Fig. 2c.

After dissociation, some fraction of the ‘caged’ PCI·NA pair will geminately reform 1 (ϕ_GR), the quantum yield for which is determined according to ϕ_GR = [k_GR/(k_GR + k_s)] × ϕ_d. This returns a value of ϕ_GR = 0.53. The remaining fraction of the PCI·NA pair will also undergo a degree of diffusional rearrangement into ‘separated’ PCI and NA. In H₂O, the portion of PCI·NA that diffusively separates will rapidly form 2, with a quantum yield of ϕ₂ = 0.36 (defined as ϕ₂ = ϕ_d − ϕ_GR). Knowing this, and based on our above discussion that ϕ_d must be taken as an absolute upper limit, we can state more definitively that 0.36 ≤ ϕ_d ≤ 0.89 must be true. Consistent with ϕ₂, the quantum yield for the ground state recovery of 1 (ϕ₁) will be defined as ϕ₁ = 1 − ϕ₂ = ϕ_GR + ϕ_³MLCTv=0 = 0.64. These values for ϕ₁ and ϕ₂ are in excellent agreement with the percentage recovery of the GSB determined through our target analysis (see Fig. 5d), which recovers by ∼65%. We draw attention to the fact that had ϕ₁ and ϕ₂ simply been estimated through inspection of the percentage recovery of GSB feature ii in the TAS in Fig. 3b, the returned quantum yields would have been incorrect (cf. ϕ₂ ∼ 0.1), due to the strong spectral overlap of the signatures for 1 and 2 in the TAS. This emphasizes that, where possible, target analysis is a vital tool for extracting reliable kinetic information and quantum yields from UV/Vis TAS.

3.6. Formation and relaxation dynamics of the intermediate [Ru(bpy)₂(NA)]²⁺

The methodologies used here are not sensitive to tracing the precise pathways for the formation of the ‘caged’ PCI·NA pair from the ³MLCT state of 1, after flux leaves the vertical Franck–Condon region. After population leaves the ³MLCT state, not only do we lose our optical handle on any population which may be transiently present in the ³MC surface (recall the discussion in Section 3.2), but identifying precise geometries where strong electronic state couplings occur along the Ru–NA dissociation coordinate with theoretical calculations, such as CASSCF methods, becomes problematic due to active space impurities incurred by mixing with the large number of near-degenerate states. However, the schematic potential energy profiles in Fig. 8a depict a qualitative picture of the Ru–NA bond fission in 1, and the involvement of the MLCT and MC states (based on earlier calculated potentials in related systems^64,73). Coupling between the ³MLCT state and the ³MC state most likely involves motion along anti-symmetric Ru–N stretch vibrations, which is then energetically stabilized by the distorted ³MC state geometry,²⁷as previously described for related complexes.³⁴ Moreover, our above kinetic analysis and quantum yields indicate very efficient mixing of the ³MLCT_v>0 and ³MC states (vide supra), and find that crossing between these states must take place on a timescale of <400 fs (cf. τ_d in Table 2).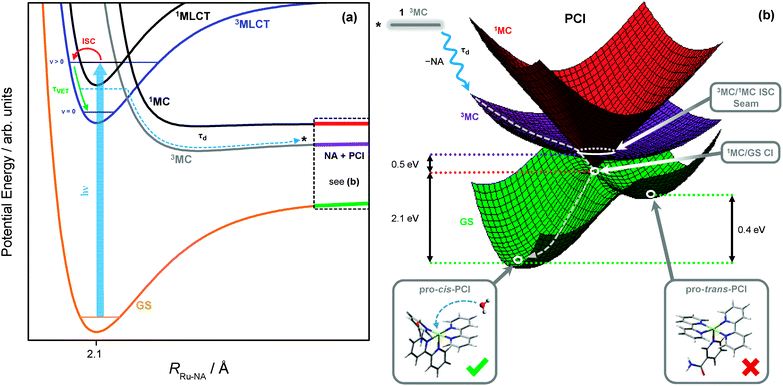

Fig. 8 (a) Schematic potential energy profiles of the ¹MLCT, ³MLCT, ³MC, ¹MC and singlet ground state (GS) along the Ru–NA bond dissociation coordinate in 1, including the major relaxation channels after excitation (hν) to the ‘bright’ ¹MLCT state. (b) Schematic potential energy surfaces for the significant electronic states in the PCI complex. From the top left, downwards: excited state population from the ³MC of 1 (black) may land on the ³MC PCI (purple) following NA ligand elimination; displacement through the ³MC/¹MC ISC seam minimum (Fig. 9a) to the ¹MC PCI (red); and then through the ¹MC/GS CI minimum (Fig. 9b) leading to the GS of the PCI (green). On the GS, two possible isomers of PCI exist, labelled pro-cis and pro-trans (see ESI,† Table S6, for enlarged structures), into which a solvent molecule may be accommodated to complete the formation of 2.

As with simpler d⁶ metal systems, the ³MC state, which involves a singly occupied 4d_x²−y² orbital (see Fig. 7c), will become strongly stabilised upon Ru–NA dissociation and at infinite separation will transform into the lowest energy excited ³MC state of the PCI complex – see ref. 79 and 80 for a more expanded discussion of this behaviour. In the immediate wake of NA loss from the ³MC state of 1, the PCI complex present within the PCI·NA pair will therefore be formed in its lowest energy electronically excited ³MC state (involving singly occupied 4d_x²−y² and 4d_yz orbitals), consistent with the thesis in previous literature.^79–82 Thus, in order to gain a greater understanding of how these electronically excited ³MC PCI species relax to their electronic ground state (GS) before generating 2, we close by discussing the results of complementary CASSCF calculations aimed at identifying regions of strong electronic state coupling (either via internal conversion or ISC) within the excited state potential energy landscape of the PCI species. The findings from these calculations are summarized by the schematic potential energy surfaces for the PCI complex in Fig. 8b.

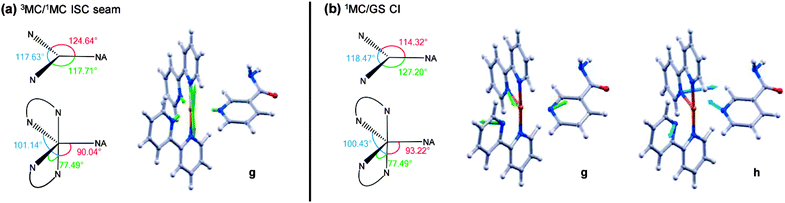
These calculations locate a region in nuclear co-ordinate space for strong ISC between the electronically excited ³MC and ¹MC states (of the same character) in the PCI. The geometry presented in Fig. 9a is a minimum energy crossing point (MECP) on the 3N − 7 (where N is the number of atoms)⁸³ dimensional seam of electronic state degeneracy⁸⁴ between the ³MC and ¹MC surfaces (³MC/¹MC ISC seam), involving predominantly population of the 4d_x²−y² orbital. Due to the presence of a seam around the ISC minimum, ³MC → ¹MC population transfer via ISC is expected to be extremely efficient in the PCI. This MECP geometry has a combination of both trigonal bipyramid (TBP) and square pyramidal (SP) character around the Ru(II) metal centre, and also shows the vibrational motion responsible for lifting the degeneracy between the ³MC and ¹MC surfaces (labelled g in Fig. 9a). This vibration corresponds to a contraction/expansion of all Ru–N bonds in the PCI, with the most pronounced motion lying along the axial Ru–N(bpy) coordinate.

Fig. 9 (a) MECP of the CASSCF calculated ³MC/¹MC ISC seam. Equatorial and axial angles of this geometry as well as the gradient difference motion (g) are presented. (b) MECP of the CASSCF calculated ¹MC/GS CI, of quasi-JT type, and branching space. Equatorial and axial angles of this geometry as well as the gradient difference (g) and derivative coupling motions (h) are presented.

Further to the ³MC/¹MC ISC seam, a conical intersection (CI)⁸⁴ geometry, of quasi-TBP nature, subsequently connects the ¹MC surface with the electronic GS of the PCI, the calculated MECP of which is shown in Fig. 9b (¹MC/GS CI). Minimal distortion away from the (higher energy) MECP geometry of ³MC/¹MC ISC seam is subsequently required to access the MECP geometry of the ¹MC/GS CI, which is pseudo-JT like due to the degeneracy imposed by partial occupancy of both the 4d_xy and 4d_x²−y² orbitals.⁸⁵ As can be seen in Fig. 9b, the MECP structure is ‘skewed’ from a pure TBP in that the axial–equatorial angles between bpy ligands differs from 90° with one angle at approximately 77°, and the other at approximately 100° – hence the structural designation of quasi-TBP. The equatorial–axial angle to the NA ligand is around 90°, and the equatorial–equatorial angles are all close to 120°. Further analysis of the CASSCF calculations indicate that the topography of this ¹MC/GS CI is of ‘peaked’ type in the terminology of Ruedenberg and co-workers⁸⁶ (as one would anticipate for a pseudo-JT type CI⁸⁴), and is calculated to lie around 0.5 eV below the MECP of the ³MC/¹MC ISC seam discussed above (see Fig. 8b). The two nuclear motions that remove the degeneracy between the ¹MC state and GS, termed the gradient difference (g) and derivative coupling (h), are also presented in Fig. 9b, where the latter is typically responsible for enabling population transfer through the CI.⁸⁴ Both of these motions lie in the equatorial plane, and evolution along a linear combination of these vibrational modes will lead to the creation of a PCI structure with an open coordination site on the electronic GS (i.e. quasi-SP). We note that the ¹MC/GS CI and associated connected minima identified in the PCI are very similar to those identified in related species (see, for example, ref. 55, 58 and 59), for both open- and closed-shell transition metal complexes, that undergo ligand photodissociation and subsequent non-adiabatic relaxation in their associated PCI complexes.

Depending on how population evolves through the ¹MC/GS CI, two different minima may be accessed on the electronic GS of the PCI, corresponding to two different structural isomers. The lowest energy of these GS isomers is calculated to be around 2.1 eV below the MECP of the ¹MC/GS CI. In Fig. 8b this minimum is labelled pro-cis-PCI, together with its calculated structure, given that insertion of an H₂O solvent molecule into its free coordinate site will give rise to the cis isomer of 2. Alternatively, rearrangement of the bpy ligands upon evolution through the CI could yield the pro-trans-PCI to enable subsequent formation of trans-2 mono-aquated photoproducts; the pro-trans-PCI is calculated to lie ∼0.4 eV above the pro-cis-PCI species using B3LYP/cc-pVTZ-SDD. Note that, isomerisation as a result of excited state PCI relaxation has been reported previously for other metal complexes.^58,59 Here though, we only observe experimental evidence for the formation of the cis isomer of 2, suggesting that the pro-trans-PCI structure is never accessed. Unlike the pro-cis-PCI, the pro-trans-PCI clearly exhibits much greater deviation from a true SP geometry due to steric distortion of the two bpy ligands induced by the adjacent NA (see structures in Fig. 8b), hence why the pro-cis-PCI lies lower in energy. This may be a contributing factor in the sole formation of pro-cis-PCI. Perhaps more importantly though, the electronic state relaxation of the PCI will occur within the ‘caged’ PCI·NA pair, and the close proximity of the neighbouring NA partner will aid to prevent isomerisation to the pro-trans-PCI structure on steric grounds as flux relaxes through the ¹MC/GS CI.

The electronic state relaxation scheme presented for the PCI complex from these CASSCF calculations implies that during this process, a structural evolution from quasi-SP → quasi-TBP → quasi-SP must occur. Following dissociation in simpler systems, this rearrangement process was observed to be ultrafast (sub-200 fs).^80,82 This is also likely to be the case here, meaning that any spectral signature for this process will be too fast to observe in our current TAS measurements. However, after relaxation to the GS, the nascent pro-cis-PCI will necessarily be formed vibrationally hot. Experimentally, we noted in Section 3.2 that the early time TAS in Fig. 3a (t < 25 ps) display some rapid depletion of the PCI feature iii, on the order of ∼10 ps. These earlier time dynamics may, in part, be due to relaxation of a vibrationally hot pro-cis-PCI in the GS, undergoing vibrational cooling through VET to the solvent.⁷⁶ Therefore, our combined experimental and computational findings lead us to broadly conclude that after Ru–NA bond fission in 1, electronically excited PCI complexes in the nascent PCI·NA pair can relax via an efficient sequential ³MC →¹MC → GS coupling process, mediated by appropriate ³MC/¹MC ISC and ¹MC/GS CI seams, on a sub-500 fs timescale, followed by vibrational relaxation of the pro-cis-PCI on the order of ≤10 ps, after which diffusional separation can occur and enable the formation of photoproduct 2.

4. Conclusions

One of the primary aims of the study presented here has been to increase our understanding of the key mechanistic pathways of photoactivation of a potential prodrug. Specifically, a synergy between experiment and theory has revealed that cis-[Ru(bpy)₂(NA)₂]²⁺ (1) has several efficient excited state pathways that are pivotal in the control of the branched kinetics that ultimately dictate the quantum yield for forming the reactive photoproduct, [Ru(bpy)₂(NA)(H₂O)]²⁺ (2). The ability of target analysis to decipher accurate timescales and quantum yields from congested transient absorption spectra is critical to these investigations. In identifying these important ‘crossroads’, we can propose the following arguments, which afford the relatively high reported quantum yield of 2, ϕ₂ = 0.36: (i) complete conversion of the initial excited ¹MLCT state population to the vibrationally excited ³MLCT with a lifetime of <100 fs; (ii) efficient traversal of flux from the vibrationally excited ³MLCT state to the dissociative ³MC state, and subsequent dissociation with the quantum yield 0.36 ≤ ϕ_d ≤ 0.89, occurs on a <400 fs timescale; (iii) the nascent photodetached ligand may be viewed as part of a ‘caged’ product pair within the solvation shell, PCI·NA; and (iv) the nascent PCI·NA pair may either geminately reform 1 or undergo a degree of diffusional separation, both of which are kinetically competitive processes, where the later subsequently enables ultrafast (sub-1 ps) solvent substitution to finally form 2.

The results presented here provide an excellent basis for understanding the initial stages involved in photoactivation of potential metal complex prodrugs and how we can tailor molecular properties to improve their performance. One clear notion is that bulkier ligands will suffer severe caging in the immediate wake of dissociation, which will, in turn, significantly dictate the formation of the target species 2. The quantum yield for forming the target product will ultimately be governed by a combination of (i) the quantum yield for dissociation and (ii) the relative rates of diffusive separation versus geminate recombination for the nascent caged product pair. This work serves to highlight the significance of structure–dynamics–function relationships, with particular emphasis here, on the design of more efficacious photo chemotherapeutic agents.

Acknowledgements

G.M.R. and V.G.S. are grateful to Prof. Mike Ashfold, Dr Dan Murdock and Dr Michael Grubb (Bristol) for enlightening conversations. S.E.G, M.D.H. and G.M.R. thank the EPSRC for doctoral/postdoctoral funding. G.M.R. also thanks the Ramsay Memorial Fellowship Trust for a Ramsay Memorial Fellowship. M.J.P. and R.G.M. thank the European Research Council for funding under the European Union's Seventh Framework Programme (FP7/2007–2013)/ERC Grant No. 258990. M.J.P. and J.M.Z. also thank the EPSRC for funding (EP/J006602). N.A.S. and P.J.S. thank the EPSRC (EP/G006792/1), the ERC (award no. 247450). V.G.S. thanks the EPSRC for equipment grants (EP/H003401 and EP/J007153), and the Royal Society for a University Research Fellowship. Finally we thank the National Cancer Institute (http://www.cancer.gov) for use of the image of a breast cancer cell as a background to our graphical abstract.

Notes and references

1. M. Grätzel, Inorg. Chem., 2005, 44, 6841.
2. P. D. Frischmann, K. Mahata and F. Wurthner, Chem. Soc. Rev., 2013, 42, 1847.
3. H. Rudmann and M. F. Rubner, J. Appl. Phys., 2001, 90, 4338.
4. E. Holder, B. M. W. Langeveld and U. S. Schubert, Adv. Mater., 2005, 17, 1109.
5. H. Rudmann, S. Shimada and M. F. Rubner, J. Am. Chem. Soc., 2002, 124, 4918.
6. V. Fernandez-Moreira, F. L. Thorp-Greenwood and M. P. Coogan, Chem. Commun., 2010, 46, 186.
7. M. R. Gill and J. A. Thomas, Chem. Soc. Rev., 2012, 41, 3179.
8. A. Yadav, T. Janaratne, A. Krishnan, S. S. Singhal, S. Yadav, A. S. Dayoub, D. L. Hawkins, S. Awasthi and F. M. MacDonnell, Mol. Cancer Ther., 2013, 12, 643.
9. T. J. Dougherty, in Photodynamic Therapy: Methods and Protocols, ed. C. J. Gomer, Humana Press Inc, Totowa, 2010, vol. 635, p. 1.
10. P. Mroz, A. Yaroslavsky, G. B. Kharkwal and M. R. Hamblin, Cancers, 2011, 3, 2516.
11. P. Agostinis, K. Berg, K. A. Cengel, T. H. Foster, A. W. Girotti, S. O. Gollnick, S. M. Hahn, M. R. Hamblin, A. Juzeniene, D. Kessel, M. Korbelik, J. Moan, P. Mroz, D. Nowis, J. Piette, B. C. Wilson and J. Golab, Ca-Cancer J. Clin., 2011, 61, 250.
12. K. L. Ciesienski, L. M. Hyman, D. T. Yang, K. L. Haas, M. G. Dickens, R. J. Holbrook and K. J. Franz, Eur. J. Inorg. Chem., 2010, 2224.
13. M. A. Sgambellone, A. David, R. N. Garner, K. R. Dunbar and C. Turro, J. Am. Chem. Soc., 2013, 135, 11274.
14. L. Zayat, C. Calero, P. Alborés, L. Baraldo and R. Etchenique, J. Am. Chem. Soc., 2003, 125, 882.
15. M. Roy, B. V. S. K. Chakravarthi, C. Jayabaskaran, A. A. Karande and A. R. Chakravarty, Dalton Trans., 2011, 40, 4855.
16. Y. Sun, L. E. Joyce, N. M. Dickson and C. Turro, Chem. Commun., 2010, 46, 6759.
17. D. A. Lutterman, P. K. L. Fu and C. Turro, J. Am. Chem. Soc., 2005, 128, 738.
18. F. S. Mackay, J. A. Woods, P. Heringova, J. Kasparkova, A. M. Pizarro, S. A. Moggach, S. Parsons, V. Brabec and P. J. Sadler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20743.
19. S. Betanzos-Lara, L. Salassa, A. Habtemariam, O. Novakova, A. M. Pizarro, G. J. Clarkson, B. Liskova, V. Brabec and P. J. Sadler, Organometallics, 2012, 31, 3466.
20. A. Gabrielsson, S. Záliš, P. Matousek, M. Towrie and A. Vlček, Inorg. Chem., 2004, 43, 7380.
21. T. N. Singh and C. Turro, Inorg. Chem., 2004, 43, 7260.
22. R. J. Watts, J. Chem. Educ., 1983, 60, 834.
23. J. Van Houten and R. J. Watts, J. Am. Chem. Soc., 1976, 98, 4853.
24. N. H. Damrauer, G. Cerullo, A. Yeh, T. R. Boussie, C. V. Shank and J. K. McCusker, Science, 1997, 275, 54.
25. B. Durham, J. V. Caspar, J. K. Nagle and T. J. Meyer, J. Am. Chem. Soc., 1982, 104, 4803.
26. P. S. Wagenknecht and P. C. Ford, Coord. Chem. Rev., 2011, 255, 591.
27. A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. Belser and A. von Zelewsky, Coord. Chem. Rev., 1988, 84, 85.
28. B. Durham, J. L. Walsh, C. L. Carter and T. J. Meyer, Inorg. Chem., 1980, 19, 860.
29. J. Van Houten and R. J. Watts, Inorg. Chem., 1978, 17, 3381.
30. D. V. Pinnick and B. Durham, Inorg. Chem., 1984, 23, 1440.
31. L. Salassa, C. Garino, G. Salassa, R. Gobetto and C. Nervi, J. Am. Chem. Soc., 2008, 130, 9590.
32. Y. Liu, D. B. Turner, T. N. Singh, A. M. Angeles-Boza, A. Chouai, K. R. Dunbar and C. Turro, J. Am. Chem. Soc., 2009, 131, 26.
33. L. Salassa, E. Borfecchia, T. Ruiu, C. Garino, D. Gianolio, R. Gobetto, P. J. Sadler, M. Cammarata, M. Wulff and C. Lamberti, Inorg. Chem., 2010, 49, 11240.
34. E. Borfecchia, C. Garino, L. Salassa, T. Ruiu, D. Gianolio, X. Zhang, K. Attenkofer, L. X. Chen, R. Gobetto, P. J. Sadler and C. Lamberti, Dalton Trans., 2013, 42, 6564.
35. A. L. Harris, J. K. Brown and C. B. Harris, Annu. Rev. Phys. Chem., 1988, 39, 341.
36. P. C. A. Bruijnincx and P. J. Sadler, Curr. Opin. Chem. Biol., 2008, 12, 197.
37. J. M. Kelly, D. J. McConnell, C. OhUigin, A. B. Tossi, A. K.-D. Mesmaeker, A. Masschelein and J. Nasielski, J. Chem. Soc., Chem. Commun., 1987, 1821.
38. O. Novakova, J. Kasparkova, O. Vrana, P. M. van Vliet, J. Reedijk and V. Brabec, Biochemistry, 1995, 34, 12369.
39. E. Wachter, D. K. Heidary, B. S. Howerton, S. Parkin and E. C. Glazer, Chem. Commun., 2012, 48, 9649.
40. B. S. Howerton, D. K. Heidary and E. C. Glazer, J. Am. Chem. Soc., 2012, 134, 8324.
41. Y. Sun, L. E. Joyce, N. M. Dickson and C. Turro, Chem. Commun., 2010, 46, 2426.
42. L. Salassa, T. Ruiu, C. Garino, A. M. Pizarro, F. Bardelli, D. Gianolio, A. Westendorf, P. J. Bednarski, C. Lamberti, R. Gobetto and P. J. Sadler, Organometallics, 2010, 29, 6703.
43. B. P. Sullivan, D. J. Salmon and T. J. Meyer, Inorg. Chem., 1978, 17, 3334.
44. S. E. Greenough, M. D. Horbury, J. O. Thompson, G. M. Roberts, T. N. Karsili, B. Marchetti, D. Townsend and V. G. Stavros, Phys. Chem. Chem. Phys., 2014, 16, 16187.
45. A. Maciejewski, R. Naskrecki, M. Lorenc, M. Ziolek, J. Karolczak, J. Kubicki, M. Matysiak and M. Szymanski, J. Mol. Struct., 2000, 555, 1.
46. J. R. Lakowicz, in Principles of Fluorescence Spectroscopy, ed. J. R. Lakowicz, Springer, USA, 2006, ch. 10, p. 353.
47. L. P. Maguire, S. Szilagyi and R. E. Scholten, Rev. Sci. Instrum., 2004, 75, 3077.
48. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
49. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
50. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51.
51. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
52. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
53. R. G. McKinlay and M. J. Paterson, J. Phys. Chem. A, 2012, 116, 9295.
54. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
55. M. J. Paterson, L. Blancafort, S. Wilsey and M. A. Robb, J. Phys. Chem. A, 2002, 106, 11431.
56. G. A. Worth, G. Welch and M. J. Paterson, Mol. Phys., 2006, 104, 1095.
57. R. G. Mckinlay, J. M. Żurek and M. J. Paterson, Adv. Inorg. Chem., 2010, 62, 351.
58. J. M. Żurek and M. J. Paterson, J. Phys. Chem. A, 2012, 116, 5375.
59. J. M. Żurek and M. J. Paterson, J. Chem. Phys., 2012, 137, 034308.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
61. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford, CT, 2004.
62. C. Bo and F. Maseras, Dalton Trans., 2008, 2911.
63. L.-P. Wang and T. Van Voorhis, J. Chem. Theory Comput., 2012, 8, 610.
64. A. C. Bhasikuttan, M. Suzuki, S. Nakashima and T. Okada, J. Am. Chem. Soc., 2002, 124, 8398.
65. S. Yoon, P. Kukura, C. M. Stuart and R. A. Mathies, Mol. Phys., 2006, 104, 1275.
66. A. Cannizzo, F. van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2006, 45, 3174.
67. N. H. Damrauer and J. K. McCusker, J. Phys. Chem. A, 1999, 103, 8440.
68. G. A. Heath, L. J. Yellowlees and P. S. Braterman, J. Chem. Soc., Chem. Commun., 1981, 287.
69. J. K. McCusker, Acc. Chem. Res., 2003, 36, 876.
70. For related complexes in ref. 67 to 69 oxidation of Ru(II) to Ru(III) adds a red shift of the first MLCT of ∼50 nm.
71. Q. Sun, S. Mosquera-Vazquez, L. M. Lawson Daku, L. Guénée, H. A. Goodwin, E. Vauthey and A. Hauser, J. Am. Chem. Soc., 2013, 135, 13660.
72. M. P. Grubb, A. J. Orr-Ewing and M. N. R. Ashfold, Rev. Sci. Instrum., 2014, 85, 064104.
73. J. N. Demas and D. G. Taylor, Inorg. Chem., 1979, 18, 3177.
74. S. Wallin, J. Davidsson, J. Modin and L. Hammarström, J. Phys. Chem. A, 2005, 109, 4697.
75. W. Henry, C. G. Coates, C. Brady, K. L. Ronayne, P. Matousek, M. Towrie, S. W. Botchway, A. W. Parker, J. G. Vos, W. R. Browne and J. J. McGarvey, J. Phys. Chem. A, 2008, 112, 4537.
76. J. C. Owrutsky, D. Raftery and R. M. Hochstrasser, Annu. Rev. Phys. Chem., 1994, 45, 519.
77. S. J. Harris, D. Murdock, Y. Zhang, T. A. A. Oliver, M. P. Grubb, A. J. Orr-Ewing, G. M. Greetham, I. P. Clark, M. Towrie, S. E. Bradforth and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2013, 15, 6567.
78. T. N. V. Karsili, A. M. Wenge, S. J. Harris, D. Murdock, J. N. Harvey, R. N. Dixon and M. N. R. Ashfold, Chem. Sci., 2013, 4, 2434.
79. C. Pollak, A. Rosa and E. J. Baerends, J. Am. Chem. Soc., 1997, 119, 7324.
80. M. J. Paterson, P. A. Hunt, M. A. Robb and O. Takahashi, J. Phys. Chem. A, 2002, 106, 10494.
81. J. K. Burdett, J. M. Grzybowski, R. N. Perutz, M. Poliakoff, J. J. Turner and R. F. Turner, Inorg. Chem., 1978, 17, 147.
82. S. A. Trushin, W. Fuss, W. E. Schmid and K. L. Kompa, J. Phys. Chem. A, 1998, 102, 4129.
83. Two surfaces of the same spin intersect in a space of dimension 3N − 8, with the gradient difference and derivative coupling vectors lifting the degeneracy at first order. By symmetry the derivative coupling is the zero vector if the states have different spin symmetries.
84. D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985.
85. R. G. McKinlay and M. J. Paterson, in The Jahn–Teller Effect, ed. H. Köppel, D. R. Yarkony and H. Barentzen, Springer, Berlin Heidelberg, 2009, ch. 11, vol. 97, p. 311.
86. G. J. Atchity, S. S. Xantheas and K. Ruedenberg, J. Chem. Phys., 1991, 95, 1862.

---

Footnotes

† Electronic supplementary information (ESI) available: Electrospray ionization mass spectrum, calculated molecular orbitals for the [Ru(bpy)₂(NA)(H₂O)]²⁺ photoproduct, ultrafast and static transient UV/Vis absorption spectra of [Ru(bpy)₂(NA)₂]²⁺ in acetone, further kinetic analysis details and enlarged figures of complex structures. See DOI: 10.1039/c4cp02359e

‡ These authors contributed equally.

§ Current address: School of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK.

---