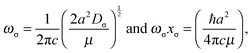A reduced radial potential energy function for the halogen bond and the hydrogen bond in complexes B⋯XY and B⋯HX, where X and Y are halogen atoms
Received
3rd April 2014
, Accepted 1st May 2014
First published on 2nd May 2014
Abstract
It is shown by considering 76 halogen- and hydrogen-bonded complexes B⋯XY and B⋯HX (where B is a Lewis base N2, CO, C2H2, C2H4, H2S, HCN, H2O, PH3 or NH3 and X, Y are F, Cl, Br or I) that the intermolecular stretching force constants kσ (determined from experimental centrifugal distortion constants via a simple model) and the intermolecular dissociation energies Dσ (calculated at the CCSD(T)(F12*)/cc-pVDZ-F12 level of theory) are related by Dσ = Cσkσ, where Cσ = 1.50(3) × 103 m2 mol−1. This suggests that one-dimensional functions implying direct proportionality of Dσ and kσ, (e.g. a Morse or Rydberg function) might serve as reduced radial potential energy functions for such complexes.
1. Introduction
During the last decade there has been a rapid growth of interest in the halogen bond across the disciplines of Chemistry, Materials Science and Biology,1 especially in its parallels with the hydrogen bond.2 The halogen bond3 is represented conventionally by the three centred dots in B⋯X–R, where the halogen atom X of the molecule X–R interacts with a nucleophilic acceptor atom/centre Z of a simple Lewis base B or of a much larger molecule. There has naturally followed discussion of both the radial and angular potential energy functions associated with such interactions.4,5 This article is concerned with the characteristics of the one-dimensional function that describes the variation of the energy with the intermolecular distance r(Z⋯X), that is the intermolecular radial potential energy function. Attention will be focussed initially on several series of halogen-bonded complexes B⋯XY, where B is one of the Lewis bases N2, CO, C2H2, C2H4, H2S, HCN, H2O, PH3 and NH3 and XY is one of the dihalogen molecules F2, ClF, Cl2, BrCl, Br2 and ICl. Thereafter, the corresponding series of hydrogen-bonded complexes B⋯HX, where X = F, Cl, Br or I, will be discussed.
Two important characteristics of such a one-dimensional radial potential energy function are the intermolecular dissociation energy Dσ and the intermolecular quadratic stretching force constant kσ, both of which provide a measure of the strength of the (generally weak) interaction of B and XY. Dσ is the energy required to take the complex from the equilibrium distance re along r to infinite separation, while kσ is the curvature of the function at re and provides a measure of the restoring force per unit infinitesimal displacement from re along the same path.
In this article, a direct proportionality of Dσ and kσ is established for many complexes of the halogen-bonded type B⋯XY and the hydrogen-bonded type B⋯HX. The values of Dσ were obtained by means of ab initio calculations at the explicitly correlated level of theory CCSD(T)(F12*)/cc-pVDZ-F12, after correction for basis set superposition error, while the kσ values were those established from the rotational spectra of B⋯XY or B⋯HX through interpretation of experimental zero-point centrifugal distortion constants in terms of a simple model. The kσ are therefore zero-point, rather than equilibrium, values and are also subject to errors introduced by the assumption of rigid subunits B and XY (or HX). The fact that the equation Dσ = Cσkσ describes, with the same constant of proportionality Cσ, the behaviour of a large number of complexes B⋯XY and B⋯HX suggests that, for example, a reduced Morse function V(r) = Dσ[1 − e−a(r−re)]2, with a = (2Cσ)−½, or a reduced Rydberg function V(r) = −Dσ[1 + b(r − re)]e−b(r−re), with b = Cσ−½, could be useful to describe the radial intermolecular potential energy functions in such molecules.
2. Methods
2.1
k
σ values from centrifugal distortion constants
In the quadratic approximation and with the assumption of rigid subunits B and XY unperturbed by the weak interaction, Millen6 showed that the quartic centrifugal distortion constant DJ for a linear or symmetric top complex B⋯XY (or B⋯HX) is simply related to the intermolecular stretching force constant by the expression| | | kσ = (16π2μB3/DJ)[1 − B/BB − B/BXY], | (1) |
in which B, BB and BXY are strictly the equilibrium rotational constants of the complex, B and XY, respectively, and μ = mBmXY/(mB + mXY) is the reduced mass for the intermolecular motion in question. When B⋯XY is an asymmetric-top molecule of C2v symmetry, in which XY lies along the C2 axis, the corresponding centrifugal distortion constant ΔJ, obtained by fitting the rotational transitions by means of a Hamiltonian that employs the Watson A reduction in the Ir representation, is given by| | | kσ = (8π2μ/ΔJ)[B3(1 − b) + C3(1 − c)], | (2) |
in which b = (B/BB) + (B/BXY) and c = (C/BB) + (C/BXY), and B and C are equilibrium rotational constants of the complex. When ΔJ is used, eqn (2) holds whether the C2v molecule B⋯XY is planar, as in C2H2⋯XY, or non-planar, as in C2H4⋯XY where XY is perpendicular to the plane containing the ethene nuclei. Identical equations, with XY replaced by HX, apply to the corresponding members of the series of hydrogen-bonded complexes B⋯HX.
Equilibrium values of the spectroscopic constants required for use in eqn (1) and (2) to obtain kσ have not been determined experimentally for complexes of the type considered here and in general only zero-point quantities are available. To allow progress, we invoke a type of ‘effective’ rigid-rotor approximation, namely the use of zero-point centrifugal distortion constants and rotational constants in these equations in place of their equilibrium counterparts. The utility of this approximation can be judged, in general, by the conclusions presented in this article and, in particular, by reference in Section 4 to the examples of the simple linear complexes OC⋯HX and OC⋯XY, for which tests of the approximation are available.
Values of kσ calculated by means of the appropriate eqn (1) or (2) for a wide range of complexes B⋯XY,7–52 where the Lewis base B is one of N2, CO, C2H2, C2H4, H2S, HCN, H2O, PH3 and NH3 and XY is one of the dihalogen molecules F2, ClF, Cl2, BrCl, Br2 and ICl are given in Tables 1 and 2, while Table 3 collects together the values of kσ for the corresponding set of hydrogen-bonded complexes B⋯HX.53–86 All complexes considered here, except for those involving H2O and H2S, are either linear molecules, symmetric-top molecules or have C2v symmetry, so that eqn (1) and (2) are strictly applicable at equilibrium. All complexes of H2O with either HX or XY are effectively planar, that is although the equilibrium geometry has a pyramidal conformation at O (Cs symmetry) there is rapid inversion in the zero-point state between the two equivalent conformers and the vibrational wavefunctions have C2v symmetry. Eqn (2) is then a reasonable approximation. Complexes H2S⋯HX/XY, on the other hand, all have Cs symmetry and are non-inverting in the zero-point state. They have a right-angled geometry in which HX or XY lies along an axis that passes through the H2S centre of mass and is very nearly perpendicular to the H2S plane. Nevertheless, eqn (2) is probably an acceptable approximation for the H2S complexes.
Table 1 Some observed and calculated properties of halogen-bonded complexes B⋯X2 involving non-polar dihalogen molecules X2a
| Lewis base B |
Dihalogen molecules X2 |
| Difluorine F2 |
Dichlorine Cl2 |
Dibromine Br2 |
|
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯Xi)/Å |
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯Xi)/Å |
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯Xi)/Å |
|
Values of kσ are either taken directly from the reference having the number indicated in columns 3, 7 or 11, as appropriate, or are recalculated from the centrifugal distortion constant DJ or ΔJ given therein by using eqn (1) or (2). The quoted error is that transmitted by the error in the distortion constant. Dσ and r(Z⋯Xi) are equilibrium values calculated ab initio at the CCSD(T)(F12*)/cc-pVDZ-F12 level of theory (see text). r(Z⋯Xi) is the distance from the acceptor atom/centre Z in the Lewis base B to the inner halogen atom Xi.
|
| OC |
— |
— |
— |
— |
3.68(1) |
12
|
5.19 |
3.145 |
5.03(2) |
20
|
7.26 |
3.111 |
| C2H2 |
— |
— |
— |
— |
5.61(1) |
13
|
7.45 |
3.146 |
7.80(3) |
21
|
10.69 |
3.106 |
| C2H4 |
— |
— |
— |
— |
5.88(2) |
14
|
8.61 |
3.092 |
8.8(2) |
22
|
12.93 |
3.004 |
| H2S |
2.34(1) |
7
|
3.43 |
3.143 |
6.23(2) |
15
|
8.53 |
3.246 |
9.8(2) |
23
|
13.68 |
3.131 |
| H3P |
— |
— |
— |
— |
5.58(2) |
16
|
8.34 |
3.222 |
9.79(3) |
24
|
15.07 |
3.013 |
| HCN |
2.62(1) |
8
|
4.15 |
2.811 |
6.55(2) |
17
|
9.71 |
2.921 |
— |
— |
— |
— |
| H2O |
3.66(1) |
9 and 10
|
4.63 |
2.696 |
7.98(3) |
18
|
10.66 |
2.808 |
9.9(2) |
25
|
14.64 |
2.804 |
| H3N |
4.67(1) |
11
|
6.59 |
2.679 |
12.73(2) |
19
|
17.85 |
2.681 |
18.5(4) |
26
|
27.36 |
2.601 |
Table 2 Some observed and calculated properties of halogen-bonded complexes B⋯XY involving polar dihalogen molecules XYa
| Lewis base B |
Dihalogen molecules XY |
| Chlorine monofluoride ClF |
Bromine monochloride BrCl |
Iodine monochloride ICl |
|
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯X)/Å |
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯X)/Å |
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯X)/Å |
|
Values of kσ are either taken directly from the reference having the number indicated in columns 3, 7 or 11, as appropriate, or are recalculated from the centrifugal distortion constant DJ or ΔJ given therein by using eqn (1) or (2). The quoted error is that transmitted by the error in the distortion constant. Dσ and r(Z⋯X) are equilibrium values calculated ab initio at the CCSD(T)(F12*)/cc-pVDZ-F12 level of theory (see text). r(Z⋯X) is the distance from the acceptor atom/centre Z in the Lewis base B to the inner halogen atom X.
|
|
|
| N2 |
5.00(3) |
27
|
6.28 |
2.918 |
4.40(2) |
35
|
5.63 |
3.106 |
5.37(2) |
44
|
7.08 |
3.187 |
| OC |
7.04(2) |
28
|
10.56 |
2.772 |
6.27(5) |
36
|
9.20 |
3.006 |
8.00(3) |
45
|
12.73 |
3.003 |
| C2H2 |
10.01(2) |
29
|
13.68 |
2.859 |
9.48(6) |
37
|
12.92 |
3.038 |
12.12(8) |
46
|
17.22 |
3.090 |
| C2H4 |
11.01(3) |
30
|
17.01 |
2.730 |
10.54(1) |
38
|
15.74 |
2.927 |
14.0(1) |
47
|
21.49 |
2.958 |
| H2S |
13.40(3) |
31
|
18.13 |
2.835 |
12.07(10) |
39
|
16.65 |
3.057 |
16.55(5) |
48
|
22.65 |
3.120 |
| H3P |
— |
— |
— |
— |
11.56(7) |
40
|
19.30 |
2.878 |
20.7(1) |
49
|
28.88 |
2.898 |
| HCN |
12.33(5) |
32
|
18.42 |
2.639 |
11.09(10) |
41
|
16.83 |
2.826 |
14.5(1) |
50
|
23.66 |
2.840 |
| H2O |
14.24(3) |
33
|
20.14 |
2.544 |
12.08(2) |
42
|
18.05 |
2.735 |
15.9(2) |
51
|
24.65 |
2.776 |
| H3N |
34.3(5) |
34
|
40.43 |
2.304 |
26.7(3) |
43
|
34.01 |
2.532 |
30.4(3) |
52
|
46.75 |
2.599 |
Table 3 Some observed and calculated properties of hydrogen-bonded complexes B⋯HXa
| Lewis base B |
Hydrogen halide molecules HX |
| Hydrogen fluoride HF |
Hydrogen chloride HCl |
|
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯H)/Å |
k
σ/(N m−1) |
Ref. |
D
σ/(kJ mol−1) |
r(Z⋯H)/Å |
|
Values of kσ are either taken directly from the reference having the number indicated in columns 3 or 7, as appropriate, or are recalculated from the centrifugal distortion constant DJ or ΔJ given therein by using eqn (1) or (2). The quoted error is that transmitted by the error in the distortion constant. Dσ and r(Z⋯H) are equilibrium values calculated ab initio at the CCSD(T)(F12*)/cc-pVDZ-F12 level of theory (see text). r(Z⋯H) is the distance from the acceptor atom/centre Z of the Lewis base B to the hydrogen atom H.
|
|
|
| N2 |
5.13(3) |
53
|
9.26 |
2.099 |
2.55(1) |
62 and 63
|
5.12 |
2.400 |
| OC |
8.48(9) |
54
|
14.21 |
2.103 |
3.88(1) |
64
|
7.78 |
2.393 |
| C2H2 |
— |
— |
— |
— |
6.4(3) |
65
|
11.03 |
2.378 |
| C2H4 |
— |
— |
— |
— |
5.88(16) |
66
|
11.32 |
2.396 |
| H2S |
12.0(2) |
55 and 56
|
20.36 |
2.284 |
6.81(1) |
67
|
12.73 |
2.480 |
| H3P |
10.94(4) |
57
|
19.38 |
2.354 |
6.01(2) |
68
|
11.89 |
2.569 |
| HCN |
18.26(5) |
58
|
30.33 |
1.859 |
9.25(4) |
69
|
18.33 |
2.092 |
| H2O |
24.51(2) |
59 and 60
|
35.34 |
1.721 |
12.72(12) |
70
|
21.34 |
1.912 |
| H3N |
32.8 |
61
|
50.98 |
1.703 |
18.2(3) |
71
|
32.72 |
1.820 |
|
|
|
|
Hydrogen bromide HBr |
Hydrogen iodide HI |
| N2 |
1.92(1) |
72
|
3.98 |
2.503 |
— |
— |
— |
— |
| OC |
2.99(1) |
73
|
6.08 |
2.489 |
1.713(1) |
81
|
4.02 |
2.675 |
| C2H2 |
5.39(2) |
74
|
9.24 |
2.440 |
— |
— |
— |
— |
| C2H4 |
5.21(2) |
75
|
9.65 |
2.456 |
— |
— |
— |
— |
| H2S |
5.86(2) |
76
|
11.01 |
2.526 |
4.02(1) |
82
|
7.78 |
2.670 |
| H3P |
5.05(1) |
77
|
10.19 |
2.618 |
3.409(2) |
83
|
7.17 |
2.778 |
| HCN |
7.64(2) |
78
|
14.92 |
2.161 |
4.44(1) |
84
|
10.42 |
2.319 |
| H2O |
10.06(15) |
79
|
17.53 |
1.969 |
6.64(1) |
85
|
12.06 |
2.117 |
| H3N |
13.4(3) |
80
|
28.60 |
1.800 |
7.18(6) |
86
|
19.82 |
1.926 |
2.2 Calculation of Dσ values
Values of the energy change, Dσ, accompanying the dissociation B⋯XY = B + XY of each of the complexes B⋯XY into the components B and XY, all in their (hypothetical) equilibrium electronic ground states, were calculated at the explicitly correlated level87 CCSD(T)(F12*)/cc-pVDZ-F12 by using the ab initio program MOLPRO.88 This involved geometry optimisations of B⋯XY, B and XY. Corrections for basis set superposition error (BSSE) were applied using the Boys–Bernardi89 method. An advantage of using basis functions of the type cc-pVDZ-F12, that is functions optimised for use at the explicitly correlated level of theory, is that the BSSE corrections are relatively small, typically a few percent of Dσ. The basis functions for Br and I were of the type cc-pVDZ-F12-PP, where PP indicates that a pseudo-potential is used for core electrons, and were provided by J. G. Hill of the University of Sheffield prior to their public release.90 For some complexes B⋯XY it was possible to conduct calculations at the CCSD(T)(F12*)/cc-pVTZ-F12 level. This increased Dσ by approximately 5% in each case. Unfortunately, for a few complexes in the series B⋯BrCl, B⋯Br2 and B⋯ICl, use of the cc-pVTZ-F12 basis functions would have proved too demanding of computer time. Therefore, in view of the systematic nature of the present investigation, it was decided to employ the highest level of theory that could be applied uniformly to all complexes considered, namely the level CCSD(T)(F12*)/cc-pVDZ-F12. Values of Dσ so calculated for halogen-bonded complexes are included in Tables 1 and 2 while those calculated by the same approach for the hydrogen-bonded analogues B⋯HX are in Table 3. The atoms/points Z⋯X–Y and Z⋯H–X are required by symmetry to be collinear for all B⋯XY and B⋯HX except those involving H2O and H2S. It has been shown, however, that the deviation from collinearity will be negligible for H2O and H2S complexes involving both types of non-covalent interaction31,70 and therefore collinearity was enforced for these complexes during the geometry optimisations.
3. Results
3.1 Halogen-bonded complexes B⋯XY
Fig. 1 shows the calculated values of Dσ plotted as the ordinate against the experimental values of kσ along the abscissa for the series of complexes B⋯Cl2 and B⋯Br2 in which B is CO, C2H2, C2H4, H2S, HCN, H2O, PH3 and NH3. Also included on the same graph are B⋯F2 for B = H2S, H2O, HCN and NH3, which are the only difluorine complexes known in the gas phase for the B listed and for which experimental kσ are available. The point (0, 0) has been included under the reasonable assumption that when there is no interaction between a pair of molecules forming a complex both measures of the binding strength become zero. The points in Fig. 1 fall on a straight line through the origin, indicating direct proportionality of Dσ and kσ. The equation for the line obtained by means of linear regression is| | | Dσ/(kJ mol−1) = 1.47(3){kσ/(N m−1)} − 0.21(21) | (3) |
 |
| | Fig. 1 A plot of Dσversus kσ for complexes of the type B⋯X2, where B is one of the series of Lewis bases CO, C2H2, C2H4, H2S, H2O, PH3 or NH3 and X2 is one of the nonpolar dihalogen molecules F2, Cl2 or Br2. The continuous line represents the straight line fitted to the points (including the origin) by linear regression and is given as eqn (3) in the text. | |
The choice of B⋯X2 molecules for the initial demonstration of the direct proportionality of Dσ and kσ was dictated by the fact that in general the nonpolar molecules X2 form weaker complexes than do their polar counterparts ClF, BrCl and ICl. Given the limitations of the model (see Section 2.1) for the experimental determination of kσ from the centrifugal distortion constants DJ and ΔJ, especially the assumption of monomer geometries unchanged on complex formation, it is likely that the model will better apply to the B⋯X2 than to those involving the polar dihalogens. Fig. 2 shows the points (kσ, Dσ) for B⋯XY, when XY includes all dihalogen molecules, both polar and nonpolar. The continuous straight line in Fig. 2 corresponds to that defined in eqn (3), i.e. that fitted to the points for B⋯X2 only. Note that the scatter from the straight line of eqn (3) tends to increase as the binding strength increases. The points with largest deviation correspond to those for complexes of H3N with each of BrCl and ICl. For H3N⋯ClF there is experimental evidence from the nuclear quadrupole coupling constants for a significant charge redistribution (and probably geometrical rearrangement) on complex formation34 and therefore the point (kσ, Dσ) for this complex was excluded from the graph. When all the points shown in Fig. 2 are fitted by means of linear regression, the result is
| | | Dσ/(kJ mol−1) = 1.45(3){kσ/(N m−1)} − 0.06(35), | (4) |
that is, a straight line through the origin and of slope within experimental error of that obtained (
eqn (3)) when only homonuclear dihalogen molecules act as the halogen-bond donor. Proportionality of
kσ and
Dσ for several H
3N⋯XY complexes was also noted by Hill and Xu.
91
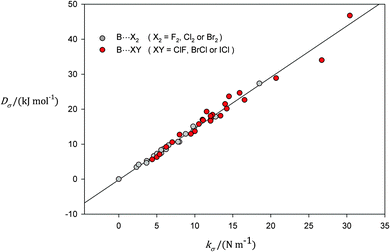 |
| | Fig. 2 A plot of Dσ against kσ for complexes of the type B⋯X2 and B⋯XY, where B is one of the Lewis bases N2, CO, C2H2, C2H4, H2S, H2O, PH3 or NH3, X2 is one of the nonpolar dihalogen molecules F2, Cl2 or Br2, and XY is one of the polar dihalogens ClF, BrCl or ICl. The continuous line is that represented by eqn (3) and shown in Fig. 1, that is the straight line fitted to the points arising from B⋯X2 complexes only. | |
3.2 Hydrogen-bonded complexes B⋯HX
It is of interest to apply the same approach to hydrogen-bonded complexes B⋯HX, where B is again one of the same series of simple Lewis bases N2, CO, C2H2, C2H4, H2S, H2O, PH3 and NH3 used in the discussion of the halogen-bonded complexes in Section 3.1 and X is F, Cl, Br or I. Experimental values of kσ obtained as before from centrifugal distortion constants and Dσ values calculated at the CCSD(T)(F12*)/cc-pVDZ level of theory are set out in Table 3. Fig. 3, in which Dσ is plotted versus kσ for all members of the hydrogen-bonded series B⋯HX except H3N⋯HBr and H3N⋯HI, again reveals a reasonable straight line, with the following equation fitted by linear regression:| | | Dσ/(kJ mol−1) = 1.53(3){kσ/(N m−1)} − 1.8(3) | (5) |
We note that the slope is just within experimental error of that obtained for the halogen-bonded series B⋯XY, but that the line does not pass as precisely through the origin. The reason for excluding H3N⋯HBr and H3N⋯HI is that these are the most likely to suffer from a significant contribution of H4N+⋯X− to a valence bond description of the complex in view of the increased ease of dissociation HX = H+ + X− along the series X = F, Cl, Br and I.
 |
| | Fig. 3 A plot of Dσ against kσ for hydrogen-bonded complexes of the type B⋯HX, where B is one of the Lewis bases N2, CO, C2H2, C2H4, H2S, H2O, PH3 or NH3 and X is F, Cl, Br or I. The continuous line is that represented by eqn (5), that is the straight line fitted to the points (including the origin) by linear regression. | |
4. Discussion
It has been shown that it is possible to express the intermolecular dissociation energy Dσ in terms of the intermolecular stretching force constant kσ for a wide range of simple bimolecular halogen- and hydrogen-bonded complexes B⋯XY and B⋯HX, where XY is a homo- or hetero-dihalogen molecule and X is a halogen atom, by means of the expressionwhere the constant Cσ = 1.50(3) × 103 m2 mol−1 = 2.49(5) × 10−21 m2 It is not obvious why Cσ should have the same value for the hydrogen- and halogen-bonded series; it could be a coincidence. The fact that these two series of halogen- and hydrogen-bonded complexes obey eqn (6) does suggest, however, that empirical radial potential energy functions leading to a direct proportionality between kσ and Dσ might be used to calculate the energy levels associated with the intermolecular stretching vibration in such molecules. In order to derive eqn (1) and (2) for use in the determination of kσ, it was necessary to assume that the motion associated with kσ involved only a change in the intermolecular distance r between the two rigid, unperturbed components while maintaining the angular geometry. Two examples of simple functions92 that imply a relation of the type in eqn (6) are the Morse function| | | V(r) = Dσ[1 − e−a(r−re)]2, | (7) |
and the Rydberg function| | | V(r) = −Dσ[1 + b(r − re)]e−b(r−re). | (8) |
The quadratic force constant kσ is related to V(r) by  so that differentiation of eqn (7) and (8) leads to the expressions Dσ = kσ/2a2 and Dσ = kσ/b2, respectively, and hence to the identifications a = (2Cσ)−½ and b = Cσ−½ respectively. Given values of a or b, the term values G(v), as wavenumbers, for the intermolecular stretching vibration (as defined above) for any of the complexes B⋯XY or B⋯HX considered here can then be estimated by means of the usual expression
so that differentiation of eqn (7) and (8) leads to the expressions Dσ = kσ/2a2 and Dσ = kσ/b2, respectively, and hence to the identifications a = (2Cσ)−½ and b = Cσ−½ respectively. Given values of a or b, the term values G(v), as wavenumbers, for the intermolecular stretching vibration (as defined above) for any of the complexes B⋯XY or B⋯HX considered here can then be estimated by means of the usual expression
| | | G(v) = ωσ(v + 1/2) − ωσxσ(v + 1/2)2, | (9) |
in which
92
For the Morse function, ωσ and ωσxσ can then be related to the constant a in the exponential term (and thence to Cσ) by differentiation to give
| | 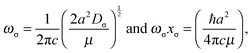 | (10) |
For the Rydberg function the corresponding expressions in terms of its constant b are
| |  | (11) |
The quantities ωσ and ωσxσ have proved difficult to obtain experimentally, but Bevan, Lucchese and co-workers93–95 have determined accurate values of both for the complexes 16O12C⋯H19F, 16O12C⋯H35Cl, OC⋯35Cl2 and 16O12C⋯79Br35Cl with the aid of morphed potential energy functions for these molecules. Their values for the pairs of quantities [ωσ and ωσxσ] are [107.99(2) and 3.79 cm−1], [62.88(3) and 1.61 cm−1], [56.43(4) and 2.91 cm−1] and [58(3) and 1.87 cm−1], respectively. Those calculated from the Morse function by means of eqn (10) when Cσ = 1.50(3) × 103 m2 mol−1 = 2.49(5) × 10−21 m2 is used are [117(2) and 2.9(1) cm−1], [74.8(15) and 2.15(9) cm−1], [54.2(10) and 1.69(7) cm−1], and [68.0(14) and 1.51(6) cm−1], respectively. The agreement between the morphed values of Bevan, Lucchese et al. and those generated by eqn (10) is satisfactory, but the former are more accurate. Values of ωσxσ implied by the Rydberg function are smaller by the factor of 0.917 than those predicted by the Morse function.
The morphed potential energy functions for OC⋯HF, OC⋯HCl, OC⋯Cl2 and OC⋯BrCl reported in ref. 93–95 allow a severe test of the use of zero-point spectroscopic constants in eqn (1) and (2) in the absence of equilibrium values, as advertised in Section 2.1. The six-dimensional morphing described in ref. 93 leads to the prediction ωσ = 107.99(2) cm−1 for the (experimentally unknown) equilibrium wavenumber associated with the intermolecular stretching mode σ of the isotopologue 16O12C⋯H19F, which implies the value kσ = 8.017(2) N m−1 for the equilibrium quadratic force constant of that mode. By comparison, use of the centrifugal distortion constant DJ of 16O12C⋯H19F in eqn (1) in place of the unavailable equilibrium values gives kσ = 8.48(9) N m−1 (see Table 3), thereby providing some confidence in the approximations alluded to. This confidence is reinforced by the similar quality of agreement found between the values kσ = 3.668(3), 3.751(5) and 4.5(4) implied by the ωσ from morphed potential energy functions94,95 of 16O12C⋯H35Cl, 16O12C⋯35Cl2 and 16O12C⋯79Br35Cl, respectively, and those 3.88(1), 3.68(1) and 4.40(2) N m−1 calculated from zero-point DJ values viaeqn (1) (see Tables 1–3, respectively).
Finally, it has been shown96 that kσ values for complexes B⋯HX can be predicted with the aid of eqn (12)
where
c′ is a constant, from numerical nucleophilicities
NB assigned to the Lewis bases B and numerical electrophilicities
EHX assigned to the acids HX. A similar expression
97 holds when the Lewis acids are dihalogen molecules. In view of the direct proportionality
Dσ =
Cσkσ established here, it follows that it is also possible to use
Dσ values in a similar manner to establish nucleophilicities for Lewis bases B and electrophilicities for Lewis acids HX or XY.
Acknowledgements
I am pleased to acknowledge generous advice about ab initio calculations from Dr David Tew (University of Bristol) and Dr Grant Hill (University of Sheffield). I am grateful to the latter for making available the cc-pVDZ-PP-F12 basis functions for bromine and iodine in advance of their publication.
References
-
Halogen Bonding, Fundamentals and Applications, ed. P. Metrangolo and G. Resnati, Structure and Bonding, Springer-Verlag, Berlin, 2008, vol. 126 Search PubMed.
- A. C. Legon, Phys. Chem. Chem. Phys., 2010, 12, 7736–7747 RSC.
- Definition of the halogen bond (IUPAC Recommendations 2013), G. R. Desiraju, P. Shing Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. A. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- M. Carter, A. K. Rappé and P. Shing Ho, J. Chem. Theory Comput., 2012, 8, 2461–2473 CrossRef CAS.
-
A. C. Legon, in Halogen Bonding, Fundamentals and Applications, ed. P. Metrangolo and G. Resnati, Structure and Bonding, Springer-Verlag, Berlin, 2008, ch. 2, vol. 126, pp. 17–64 Search PubMed.
- D. J. Millen, Can. J. Chem., 1985, 63, 1477–1479 CrossRef CAS PubMed.
- G. Cotti, C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1997, 264, 513–521 CrossRef.
- S. A. Cooke, G. Cotti, C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1996, 262, 308–314 CrossRef CAS.
- S. A. Cooke, G. Cotti, J. H. Holloway and A. C. Legon, Angew. Chem., Int. Ed. Engl., 1997, 36, 129–130 CrossRef CAS.
- S. A. Cooke, G. Cotti, C. M. Evans, J. H. Holloway, Z. Kisiel, A. C. Legon and J. M. A. Thumwood, Chem. – Eur. J., 2001, 7, 2295–2305 CrossRef CAS.
- H. I. Bloemink, K. Hinds, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1995, 245, 598–604 CrossRef CAS.
- W. Jäger, Y. Xu and M. C. L. Gerry, J. Phys. Chem., 1993, 97, 3685–3689 CrossRef.
- H. I. Bloemink, S. A. Cooke, K. Hinds, A. C. Legon and J. C. Thorn, J. Chem. Soc., Faraday Trans., 1995, 91, 1891–1900 RSC.
- H. I. Bloemink, K. Hinds, A. C. Legon and J. C. Thorn, Chem. – Eur. J., 1995, 1, 17–25 CrossRef CAS.
- H. I. Bloemink, S. J. Dolling, K. Hinds and A. C. Legon, J. Chem. Soc., Faraday Trans., 1995, 91, 2059–2066 RSC.
- A. C. Legon and H. E. Warner, J. Chem. Phys., 1993, 98, 3827–3832 CrossRef CAS PubMed.
- A. C. Legon and J. C. Thorn, J. Chem. Soc., Faraday Trans., 1993, 89, 4157–4162 RSC.
- J. B. Davey, A. C. Legon and J. M. A. Thumwood, J. Chem. Phys., 2001, 114, 6190–6202 CrossRef CAS PubMed.
- A. C. Legon, D. G. Lister and J. C. Thorn, J. Chem. Soc., Faraday Trans., 1994, 90, 3205–3212 RSC.
- E. R. Waclawik, J. M. A. Thumwood, D. G. Lister, P. W. Fowler and A. C. Legon, Mol. Phys., 1999, 97, 159–166 CrossRef CAS.
- J. B. Davey and A. C. Legon, Chem. Phys. Lett., 2001, 350, 39–50 CrossRef CAS.
- A. C. Legon and J. M. A. Thumwood, Phys. Chem. Chem. Phys., 2001, 3, 1397–1402 RSC.
- A. C. Legon and J. M. A. Thumwood, Phys. Chem. Chem. Phys., 2001, 3, 2758–2764 RSC.
- E. R. Waclawik and A. C. Legon, Chem. – Eur. J., 2000, 6, 3968–3975 CrossRef CAS.
- A. C. Legon, J. M. A. Thumwood and E. R. Waclawik, Chem. – Eur. J., 2002, 8, 940–950 CrossRef CAS.
- H. I. Bloemink and A. C. Legon, J. Chem. Phys., 1995, 103, 876–882 CrossRef CAS PubMed.
- S. A. Cooke, G. Cotti, K. Hinds, J. H. Holloway, A. C. Legon and D. G. Lister, J. Chem. Soc., Faraday Trans., 1996, 92, 2671–2676 RSC.
- K. Hinds, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1995, 242, 407–414 CrossRef CAS.
- K. Hinds, J. H. Holloway and A. C. Legon, J. Chem. Soc., Faraday Trans., 1996, 92, 1291–1296 RSC.
- H. I. Bloemink, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1996, 250, 567–575 CrossRef CAS.
- H. I. Bloemink, K. Hinds, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1995, 242, 113–120 CrossRef CAS.
- K. Hinds, A. C. Legon and J. H. Holloway, Mol. Phys., 1996, 88, 673–682 CrossRef CAS.
- S. A. Cooke, G. Cotti, C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Commun., 1996, 2327–2328 RSC.
- H. I. Bloemink, C. M. Evans, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1996, 248, 260–268 CrossRef CAS.
- A. C. Legon and P. Ottaviani, Phys. Chem. Chem. Phys., 2002, 4, 441–444 RSC.
- S. Blanco, A. C. Legon and J. C. Thorn, J. Chem. Soc., Faraday Trans., 1994, 90, 1365–1371 RSC.
- H. I. Bloemink, K. Hinds, A. C. Legon and J. C. Thorn, J. Chem. Soc., Chem. Commun., 1994, 1229–1230 RSC.
- H. I. Bloemink, K. Hinds, A. C. Legon and J. C. Thorn, Angew. Chem., Int. Ed. Engl., 1994, 33, 1512–1513 CrossRef.
- H. I. Bloemink and A. C. Legon, Chem. – Eur. J., 1996, 2, 265–270 CrossRef CAS.
- A. C. Legon, J. M. A. Thumwood and E. R. Waclawik, J. Chem. Phys., 2000, 113, 5278–5286 CrossRef CAS PubMed.
- K. Hinds and A. C. Legon, Chem. Phys. Lett., 1995, 240, 467–473 CrossRef CAS.
- J. B. Davey and A. C. Legon, Phys. Chem. Chem. Phys., 2001, 3, 3006–3011 RSC.
- H. I. Bloemink, A. C. Legon and J. C. Thorn, J. Chem. Soc., Faraday Trans., 1995, 91, 781–787 RSC.
- J. B. Davey, A. C. Legon and E. R. Waclawik, J. Mol. Struct., 2000, 500, 391–402 CrossRef.
- J. B. Davey, A. C. Legon and E. R. Waclawik, Phys. Chem. Chem. Phys., 1999, 1, 3097–3102 RSC.
- J. B. Davey and A. C. Legon, Phys. Chem. Chem. Phys., 1999, 1, 3721–3726 RSC.
- J. M. A. Thumwood and A. C. Legon, Chem. Phys. Lett., 1999, 310, 88–96 CrossRef CAS.
- A. C. Legon and E. R. Waclawik, Chem. Phys. Lett., 1999, 312, 385–393 CrossRef CAS.
- J. B. Davey, A. C. Legon and E. R. Waclawik, Phys. Chem. Chem. Phys., 2000, 2, 2265–2269 RSC.
- W. A. Herrebout, A. C. Legon and E. R. Waclawik, Phys. Chem. Chem. Phys., 1999, 1, 4961–4966 RSC.
- J. B. Davey, A. C. Legon and E. R. Waclawik, Phys. Chem. Chem. Phys., 2000, 2, 1659–1665 RSC.
- E. R. Waclawik and A. C. Legon, Phys. Chem. Chem. Phys., 1999, 1, 4695–4700 RSC.
- P. D. Soper, A. C. Legon, W. G. Read and W. H. Flygare, J. Chem. Phys., 1982, 76, 292–300 CrossRef CAS PubMed.
- A. C. Legon, P. D. Soper and W. H. Flygare, J. Chem. Phys., 1981, 74, 4944–4950 CrossRef CAS PubMed.
- R. Viswanathan and T. R. Dyke, J. Chem. Phys, 1982, 77, 1166–1174 CrossRef CAS PubMed.
- L. C. Willoughby, A. J. Fillery-Travis and A. C. Legon, J. Chem. Phys., 1984, 81, 20–26 CrossRef CAS PubMed.
- A. C. Legon and L. C. Willoughby, Chem. Phys., 1983, 74, 127–136 CrossRef CAS.
- A. C. Legon, D. J. Millen and L. C. Willoughby, Proc. R. Soc. London, Ser. A, 1985, 401, 327–347 CrossRef CAS.
- Z. Kisiel, A. C. Legon and D. J. Millen, Proc. R. Soc. London, Ser. A, 1982, 381, 419–442 CrossRef CAS.
- S. P. Belov, V. M. Demkin, N. F. Zobov, E. N. Karyakin, A. F. Krupnov, I. N. Kozin, O. L. Polyansky and M. Yu. Tretyakov, J. Mol. Spectrosc., 2007, 241, 124–135 CrossRef CAS PubMed.
-
B. J. Howard and P.R. R. Langridge-Smith, private communication.
- R. S. Altman, M. D. Marshall and W. Klempere, J. Chem. Phys., 1983, 79, 57–61 CrossRef CAS PubMed.
- Z. Kisiel, L. Pszczólkowski, P. W. Fowler and A. C. Legon, Chem. Phys. Lett., 1997, 276, 202–209 CrossRef CAS.
- P. D. Soper, A. C. Legon and W. H. Flygare, J. Chem. Phys., 1981, 74, 2138–2142 CrossRef CAS PubMed.
- A. C. Legon, P. D. Aldrich and W. H. Flygare, J. Chem. Phys., 1981, 75, 625–630 CrossRef CAS PubMed.
- P. D. Aldrich, A. C. Legon and W. H. Flygare, J. Chem. Phys., 1981, 75, 2126–2134 CrossRef CAS PubMed.
- E. J. Goodwin and A. C. Legon, J. Chem. Soc., Faraday Trans. 2, 1984, 80, 51–65 RSC.
- A. C. Legon, J. M. A. Thumwood, E. R. Waclawik and L. C. Willoughby, Phys. Chem. Chem. Phys., 2000, 2, 4918–4924 RSC.
- A. C. Legon, E. J. Campbell and W. H. Flygare, J. Chem. Phys., 1982, 76, 2267–2274 CrossRef CAS PubMed.
- Z. Kisiel, B. A. Pietrewicz, P. W. Fowler, A. C. Legon and E. Steiner, J. Phys. Chem., 2000, 104, 6970–6978 CrossRef CAS.
- N. W. Howard and A. C. Legon, J. Chem. Phys., 1988, 88, 4694–4701 CrossRef CAS PubMed.
- N. W. Howard and A. C. Legon, J. Chem. Phys., 1989, 90, 672–678 CrossRef CAS PubMed.
- M. R. Keenan, T. K. Minton, A. C. Legon, T. J. Balle and W. H. Flygare, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 5583–5587 CrossRef CAS.
- G. C. Cole, J. B. Davey, A. C. Legon and A. F. Lyndon, Mol. Phys., 2003, 101, 603–612 CrossRef CAS.
- P. W. Fowler, A. C. Legon, J. M. A. Thumwood and E. R. Waclawik, Coord. Chem. Rev., 2000, 197, 231–247 CrossRef CAS.
- A. I. Jaman and A. C. Legon, J. Mol. Struct., 1986, 145, 261–276 CrossRef CAS.
- L. C. Willoughby and A. C. Legon, J. Phys. Chem., 1983, 87, 2085–2090 CrossRef CAS.
- E. J. Campbell, A. C. Legon and W. H. Flygare, J. Chem. Phys., 1983, 78, 3494–3500 CrossRef CAS PubMed.
- A. C. Legon and A. P. Suckley, Chem. Phys. Lett., 1988, 150, 153–158 CrossRef CAS.
- N. W. Howard and A. C. Legon, J. Chem. Phys., 1987, 86, 6722–6730 CrossRef CAS PubMed.
- Z. Wang, R. R. Lucchese, J. W. Bevan, A. P. Suckley, C. A. Rego and A. C. Legon, J. Chem. Phys., 1993, 98, 1761–1767 CrossRef CAS PubMed.
-
A. P. Suckley, PhD thesis, University of Exeter, 1991.
- N. W. Howard, A. C. Legon and G. J. Luscombe, J. Chem. Soc., Faraday Trans., 1991, 87, 507–512 RSC.
- P. W. Fowler, A. C. Legon and S. A. Peebles, Chem. Phys. Lett., 1994, 226, 501–508 CrossRef CAS.
- A. McIntosh, T. Walther, R. R. Lucchese, J. W. Bevan, R. D. Suenram and A. C. Legon, Chem. Phys. Lett., 1999, 314, 57–64 CrossRef CAS.
- A. C. Legon and D. Stephenson, J. Chem. Soc., Faraday Trans., 1992, 88, 761–762 RSC.
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
-
H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, MOLPRO, version 2012.1, a package of ab initio programs. See http://www.molpro.net Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
-
K. A. Peterson and J. G. Hill, in preparation.
- J. G. Hill and X. Hu, Chem. – Eur. J., 2013, 19, 3620–3628 CrossRef CAS PubMed.
- See, e.g., G. W. King, Spectroscopy and Molecular Structure, Holt, Rinehart and Winston, New York, 1964, p. 164 Search PubMed.
- L. A. Rivera-Rivera, Z. Wang, B. A. McElmurry, R. R. Lucchese, J. W. Bevan and G. Kanschat, Chem. Phys., 2011, 390, 42–50 CrossRef CAS PubMed.
- S. D. Springer, L. A. Rivera-Rivera, K. W. Scott, B. A. McElmurry, Z. Wang, I. I. Leonov, R. R. Lucchese, A. C. Legon and J. W. Bevan, J. Phys. Chem. A, 2012, 116, 1213–1223 CrossRef CAS PubMed.
- L. A Rivera-Rivera, K. W. Scott, B. A. McElmurry, R. R. Lucchese and J. W. Bevan, Chem. Phys., 2013, 425, 162–169 CrossRef PubMed.
- A. C. Legon and D. J. Millen, J. Am. Chem. Soc., 1987, 109, 356–358 CrossRef CAS.
- A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714 CrossRef.
|
| This journal is © the Owner Societies 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article


 so that differentiation of eqn (7) and (8) leads to the expressions Dσ = kσ/2a2 and Dσ = kσ/b2, respectively, and hence to the identifications a = (2Cσ)−½ and b = Cσ−½ respectively. Given values of a or b, the term values G(v), as wavenumbers, for the intermolecular stretching vibration (as defined above) for any of the complexes B⋯XY or B⋯HX considered here can then be estimated by means of the usual expression
so that differentiation of eqn (7) and (8) leads to the expressions Dσ = kσ/2a2 and Dσ = kσ/b2, respectively, and hence to the identifications a = (2Cσ)−½ and b = Cσ−½ respectively. Given values of a or b, the term values G(v), as wavenumbers, for the intermolecular stretching vibration (as defined above) for any of the complexes B⋯XY or B⋯HX considered here can then be estimated by means of the usual expression