A DFT and ONIOM study of C–H hydroxylation catalyzed by nitrobenzene 1,2-dioxygenase

Abstract

A detailed description of the mechanism of C–H hydroxylation by Rieske non-heme iron dioxygenases remains elusive, as the nature of the oxidizing species is not definitively known. DFT calculations on cluster models of nitrobenzene 1,2-dioxygenase were done to explore possible mechanisms arising from oxidation by either the experimentally observed Fe^III–OOH complex or the putative high-valent HO–Fe^V=O intermediate formed through a heterolytic O–O bond cleavage. Hydrogen abstraction by HO–Fe^V=O, followed by oxygen rebound, was found to be consistent with experimental studies. The findings from the quantum mechanical cluster approach were verified by accounting for the effect of the protein environment on transition state geometries and reaction barriers through ONIOM calculations.

---

Introduction

Monooxygenation is among the wide range of reactions catalyzed by Rieske non-heme iron dioxygenases (RDOs),^1,2 which include aromatic cis-dihydroxylation, desaturation, sulfoxidation, O- and N-dealkylation and amine oxidation.^3–6 The reactivity of RDOs toward stable aromatic compounds has made them important to the development of biodegradation measures for recalcitrant environmental pollutants.⁷ The challenges of selective functionalization of alkanes in the chemical industry have also driven research on biomimetic iron catalysts, which benefit from an understanding of the mechanism of these enzymes.⁸ The active site of RDOs is a high-spin mononuclear Fe^II bound to two histidines and a bidentate aspartate residue, forming the recurring 2-His-1-carboxylate facial triad motif of non-heme iron-containing oxygenases. Two external electrons supplied by NAD(P)H are transferred to the active site during the catalytic cycle via a Rieske [2Fe–2S] cluster located within 12 Å of Fe^II in an adjacent α subunit. Formation of the reduced enzyme–substrate complex induces conformational changes that allow O₂ binding and activation.^1,2

A ferric (hydro)peroxo complex is believed to be a key reaction intermediate based on extensive studies on naphthalene 1,2-dioxygenase (NDO), including crystallographic data,⁹ single turnover¹⁰ and peroxide shunt experiments,¹¹ and theoretical calculations.¹² However, there is no consensus on whether this species reacts directly with the substrate or initially undergoes O–O bond cleavage to form a high-valent iron–oxo intermediate. It was recently found that a high-spin (S = 5/2) biomimetic complex, [Fe^III(OOH)(TMC)]²⁺ [TMC = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane], is capable of C–H hydroxylation of alkylaromatics.¹³ The low-spin (S = 1/2) Fe^III–OOH intermediate of the non-heme antitumor drug bleomycin (activated BLM) is also believed to initiate DNA cleavage by directly abstracting hydrogen.¹⁴ In both cases, O–O bond cleavage prior to H abstraction was found to have a higher activation energy.

On the other hand, hydroxylation catalyzed by enzymes such as 2-oxo acid dioxygenases and aromatic amino acid hydroxylases, which also have a 2-His-1-carboxylate facial triad motif, involves electron donation from a cofactor or cosubstrate allowing the formation of an Fe^IV=O intermediate.^1,15 Direct spectroscopic evidence of this species has been reported for taurine-α-ketoglutarate dioxygenase,¹⁶ tyrosine hydroxylase¹⁷ and phenylalanine hydroxylase.¹⁸ In contrast, only one electron is provided by the Rieske center in RDOs,^10,19 which would lead to a HO–Fe^V=O species as in heme enzymes and methane monooxygenase.¹⁵ However, the non-heme ligands in RDOs do not stabilize high oxidation states (through spin delocalization and ligand oxidation) as well as porphyrin and thiolate ligands do for heme enzymes.²⁰ This is supported by cluster model calculations showing that O–O bond cleavage in high-spin Fe^III–OOH is endothermic with a prohibitively high energy barrier (26.5 kcal mol⁻¹).¹² Nevertheless, experimental studies of monooxygenase reactions of RDOs suggest the involvement of a HO–Fe^V=O intermediate. The latter is capable of solvent exchange which would explain the ¹⁸O-labeled products obtained from toluene dioxygenase (TDO)-catalyzed oxidation of indan.²¹ As in the case of a Fe^III–OOH oxidant,^13,14 H abstraction by HO–Fe^V=O would lead to the formation of radical intermediates, which were inferred from the rearranged products observed in the reactions of NDO with norcarane and bicyclohexane¹⁹ and TDO with indene.^21,22

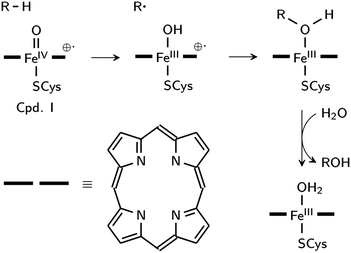
Aliphatic hydroxylation catalyzed by cytochrome P450 enzymes, which share the chemistry of RDOs (with the exception of cis-dihyroxylation),²³ proceeds through a rebound mechanism. The reactive intermediate is [(Por˙)Fe^IV=O]⁺¹, also known as compound I (Cpd I), where the oxidizing species is formally Fe^V=O. Hydrogen is initially abstracted by the oxo ligand, and in the rebound step, the resulting hydroxyl group recombines with the radical carbon to yield the alcohol product (Scheme 1).²⁴ Low-spin biomimetic non-heme iron complexes catalyze substrate hydroxylation in a similar manner,²⁵ with HO–Fe^V=O as the proposed reactive species.^26–29 HO–Fe^V=O has been detected in a Fe–^Me,HPytacn [^Me,HPytacn = 1-(2′-pyridylmethyl)-4,7-dimethyl-1,4,7-triazacyclononane] complex using variable-temperature mass spectrometry.²⁶ The O–O bond cleavage is facilitated by solvent water as evidenced by incorporation of ¹⁸O from H₂¹⁸O in the product.^26,27 Previous calculations on the Fe–TPA [TPA = tris(2-pyridylmethyl)amine] complex show that this mechanism is energetically feasible due to the weak O–O bond of low-spin Fe^III–OOH.³⁰ The Fe–Pytacn and Fe–TPA complexes can be considered as functional models of RDOs unlike the Fe–TMC complex since these contain two cis-exchangeable sites.²⁵

Scheme 1 Mechanism of aliphatic hydroxylation catalyzed by cytochrome P450.

The present work examines the C–H hydroxylation of 2-nitrotoluene (2NT) catalyzed by nitrobenzene 1,2-dioxygenase (NBDO), a member of the naphthalene family of RDOs that include NDO.³¹ This reaction, along with the competing aromatic cis-dihydroxylation, is an important biodegradation pathway of nitroaromatic pollutants. cis-Dihydroxylation has been shown to involve oxidation by HO–Fe^V=O, in which the hydroxo group initially attacks the aromatic ring followed by the oxo ligand.³² Direct oxidation by Fe^III–OOH and reaction through a HO–Fe^V=O intermediate were investigated using density functional theory (DFT) calculations on cluster models. Quantum mechanics/molecular mechanics (QM/MM) calculations, specifically the ONIOM (Our own N-layered Integrated molecular Orbital and molecular Mechanics) method, were then performed with the most plausible mechanism to elucidate the effect of the protein environment on geometry, electronic structure and energetics.

Computational methods

Preparation of the initial structure of the NBDO–2NT complex, as well as details of the molecular dynamics (MD) simulation, are discussed in the ESI.† The root-mean-square deviation (RMSD) with respect to the crystal structure (Fig. S1, ESI†) and hydrogen bonding interactions formed during simulation (Table S1, ESI†) are also reported.

DFT calculations on cluster models

A cluster model consisting of mononuclear Fe, the sidechains of histidine and aspartate residues (imidazole and acetate, respectively), and a hydroperoxo ligand (M1 model) was derived from the initial structure and used to explore the possible mechanisms of C–H hydroxylation. Geometries were optimized using the B3LYP hybrid density functional^33–36 and the double-ζ-quality LACVP* basis set, which incorporates the effective core potential of Hay and Wadt³⁷ for Fe, and a 6-31G* basis set for the other atoms. The solvent effects were included using the Polarizable Continuum Model (PCM)^38,39 with a dielectric constant of ε = 5.62 (corresponding to chlorobenzene) to mimic the hydrophobic environment of the substrate pocket in RDOs.⁴⁰ Stationary points were confirmed by frequency analysis and the validity of transition states was established by intrinsic reaction coordinate (IRC) calculations at the same level. Single-point energies were determined using the LACV3P+* basis set for Fe and 6-311+G* for the rest of the atoms. The larger basis set gives the correct ground state and inclusion of polarization functions was shown to be important when dealing with O–O bonds.⁴¹ Spin contamination in the doublet state was corrected using the spin projection scheme,^42,43 although the difference from uncorrected values is less than 0.5 kcal mol⁻¹. These methods have been found to give satisfactory results for both heme and non-heme iron systems.^41,44,45

The O–O bond cleavage and H abstraction steps were also modeled with the inclusion of carboxamide (M2 model) to represent Asn-258, which positions the substrate for oxidation through the H bonding interaction with the nitro O atom.³¹ Optimization of M2 model geometries was performed with the C_β atoms of the ligands frozen to reproduce positions in the crystal structure and to prevent carboxamide from forming artificial hydrogen bonds with active site ligands. DFT calculations were done using Gaussian 09.⁴⁶ Molecular orbitals of the reactant complex and the H abstraction transition state were analyzed using QMForge.⁴⁷

ONIOM calculations on the enzymatic model

The lowest energy structure from the 2.5 ns molecular dynamics simulation, in which the initial methyl H–O bond is 2.50 Å, was chosen as the starting point for the ONIOM calculations. The residues located outside the 20 Å radius of the active site region were removed to reduce the system size. Solvent waters within this region were also kept as they may play a role in the O–O bond cleavage step. The truncated protein was capped with acetyl and N-methyl amide groups and neutralized with counterions. The final structure used to model the reaction is illustrated in Fig. 1 and consists of 9522 atoms.

Fig. 1 Truncated enzyme model. The QM region composed of Fe–OOH, His-206, His-211 and Asp-360 sidechains, and 2NT is shown as sticks.

The QM region composed of Fe, the hydroperoxo ligand, the sidechains of His-206, His-211 and Asp-360, and 2NT (49 atoms) was treated at the B3LYP/LACVP* level while the MM region was described using the AMBER ff99SB force field.⁴⁸ The active site ligands were truncated at the C_α–C_β bond and hydrogen link atoms were added to saturate the dangling bonds of the QM atoms at the QM/MM boundary. The charge of the link atom is equal to the total charge of the atoms left out (N, H, CA, HA, C, and O) while the charge of C_α was adjusted so that the total charge of the backbone atoms is zero. This was done to maintain integer charges for the QM (+1) and MM (0) regions.⁴⁹

The ONIOM energy is expressed as

E_ONIOM = E_MM(QM,MM) + E_QM(QM) − E_MM(QM) (1)

where E_MM(QM,MM) is the MM energy of the entire system, and E_QM(QM) and E_MM(QM) are the QM and MM energies of the QM region, respectively.⁵⁰ Geometry optimization was performed using both mechanical (ME) and electronic (EE) embedding schemes of ONIOM, with only residues within 8 Å of the QM region allowed to move. This section includes the 17 residues of the catalytic domain and the Rieske cluster in the adjacent α subunit. The nature of the stationary points obtained from both ONIOM-ME and ONIOM-EE optimizations was confirmed by frequency calculations. Final energies are calculated using the LACV3P+* basis set and corrected with zero-point energies obtained at the LACVP* level. Dispersion-corrected B3LYP energies (B3LYP-D2⁵¹) and single-point energies calculated using the B97-D functional,⁵¹ which is specifically parameterized to treat dispersion, are also reported. ONIOM calculations were done using Gaussian 09.⁴⁶

Results and discussion

Possible oxidizing species

The crystal structure of the NDO–O₂–indole complex shows side-on binding of O₂ with Fe–O bond distances of 1.7 and 2.0 Å.⁹ The presumed reactive species is the protonated Fe^III–OOH (1),^11,12 for which the calculated ground state is a sextet as magnetic circular dichroism data for NDO confirm.² No ⁴1 was found while the doublet state is 14.4 kcal mol⁻¹ higher in energy. The end-on adduct (1′) is lower in energy by 1.0 kcal mol⁻¹ and it has been observed in a high-spin biomimetic non-heme complex⁵² unlike 1. ⁴1′ and ²1′ lie 4.4 and 17.2 kcal mol⁻¹, respectively, above the ground state.

Oxidation of the methyl sidechain of 2NT can proceed through either direct reaction with Fe^III–OOH (1 or 1′) or via a HO–Fe^V=O intermediate (2) (Fig. 2). The latter is formed through heterolytic O–O bond cleavage, which requires 27.8 kcal mol⁻¹ in the sextet ground state. However, 2 has a quartet ground state, as verified by CCSD(T) calculations on model Fe^V=O complexes showing preference for the high-spin state when a π-donor ligand such as OH is cis to Fe^V=O.⁴² The sextet state, which is 3.2 kcal mol⁻¹ higher in energy, can be considered as an excited state Fe^IV–O˙ species⁵³ based on the spin densities of Fe (3.06) and the oxo ligand (1.01). The doublet state, on the other hand, lies 20.4 kcal mol⁻¹ above the ground state.

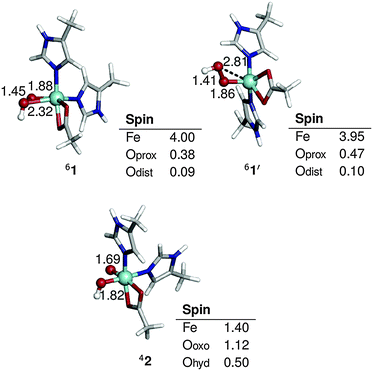Fig. 2 Optimized geometries and spin populations for side-on (1) and end-on (1′) S = 5/2 Fe^III–OOH and S = 3/2 HO–Fe^V=O (2). Distances are given in Å.

O–O bond homolysis, which yields Fe^IV=O and OH˙, was not considered as it would be inconsistent with the regio- and stereospecific products observed in monooxygenase reactions catalyzed by RDOs.^3,21,22,54 Solvent exchange, as inferred from the ¹⁸O-labeled products, would also not be possible with this intermediate. The failure of scavengers to inhibit monohydroxylation confirms that the hydroxyl radical is not involved in the enzymatic reaction.²¹

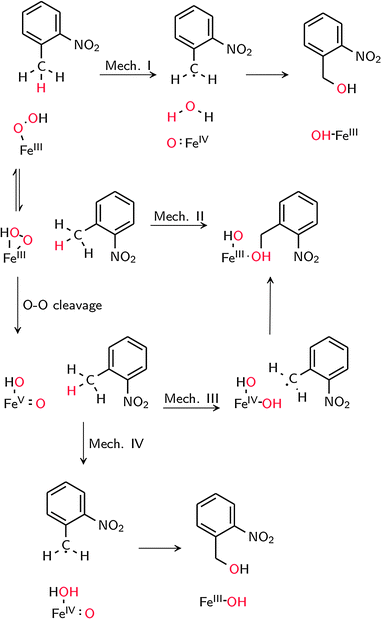
The possible reaction mechanisms for oxidation by 1′ (mechanism I), 1 (mechanism II) and 2 (mechanisms III and IV) are summarized in Scheme 2. Optimized M1 geometries for the H abstraction transition state in mechanisms I–III are shown in Fig. 3 while those for the other stationary points and for mechanism IV can be found in the ESI† (Fig. S2–S5). Potential energy surfaces (PES) of mechanisms I–III at different spin states are illustrated in Fig. 4–6. The energies were calculated relative to separated reactants as it was not possible to optimize an appropriate geometry of the reactant complex due to the tendency of the substrate to either form a spurious hydrogen bond with the hydroperoxo ligand or dissociate completely.

Scheme 2 Possible mechanisms for C–H hydroxylation.

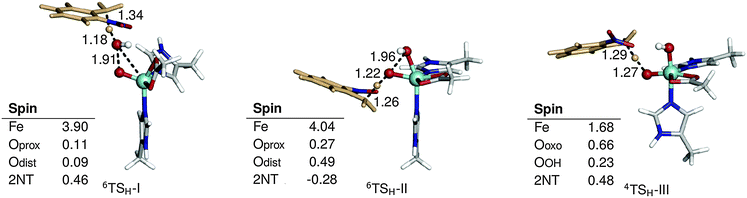Fig. 3 Optimized geometries and spin populations for H abstraction transition states (TS_H) in mechanisms I–III. Distances are given in Å.

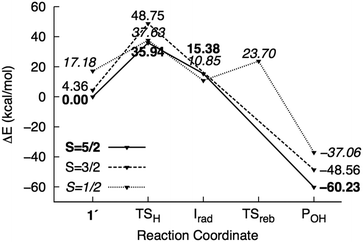Fig. 4 Potential energy surface of mechanism I calculated using the M1 model. Energies are reported relative to ⁶1′ + 2NT.

Fig. 5 Potential energy surface of mechanism II calculated using the M1 model. Energies are reported relative to ⁶1 + 2NT.

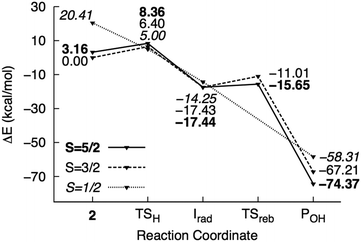Fig. 6 Potential energy surface of mechanism III calculated using the M1 model. Energies are reported relative to ⁴2 + 2NT.

Concerted O–O bond cleavage and H abstraction by Fe^III–OOH

H abstraction by the distal O atom (O_dist) of 1′ (mechanism I) requires 35.9 kcal mol⁻¹ in the sextet ground state. Activation energies in the quartet and doublet states are 44.4 and 20.4 kcal mol⁻¹, respectively (Fig. 4). ⁶TS_H-I is characterized as a late transition state (Wiberg bond index r_C–H = 0.38), as verified by the significant spin density on 2NT (0.46). Moreover, the spin density on O_distH (0.09) is consistent with the fact that H₂O is nearly formed in the transition state. On the other hand, the decreased total spin density of Fe–O_prox (from 4.42 to 4.01) and shortening of the bond from 1.86 to 1.75 Å indicate oxidation to Fe^IV=O (Fig. 3). Formation of the radical ⁶I_rad-I is an endothermic process (15.4 kcal mol⁻¹). ⁶I_rad-I is a shoulder-type energy minimum that transforms to the product ⁶P_OH-I in a barrierless process. This involves the transfer of the abstracted H to O_prox upon recombination of O_distH˙ and the methyl C radical. ⁶P_OH-I is located outside the first coordination shell of the metal center (d_Fe–O = 3.6 Å) and is exothermic by −60.2 kcal mol⁻¹. The doublet state follows the same mechanism with the exception of a barrier (12.8 kcal mol⁻¹) for the rebound step (²TS_reb-I). On the other hand, no intermediate was found in the quartet state as H abstraction leads directly to the alcohol product.

Direct reaction with 1 (mechanism II) involves concerted O–O bond cleavage and H abstraction by the proximal O atom (O_prox), with an activation energy of 23.9 kcal mol⁻¹ in the sextet state. The transition states in the quartet and doublet states lie at higher energies compared to ⁶TS_H-II, and the corresponding barriers are 32.6 and 22.1 kcal mol⁻¹, respectively (Fig. 5). ⁶TS_H-II can be characterized as central (r_C–H= 0.46) with a nearly linear O–O–H angle (172°). O–O bond cleavage is reflected in the increased spin density of O_distH from 0.09 to 0.48. However, the negligible change in the Fe spin density (∼4) suggests that the metal center is not involved in the reaction. 2NT, on the other hand, has a negative spin density of −0.28 indicating the transfer of an α-spin electron to the O–O σ* orbital (Fig. 3). No intermediate is formed as oxygen rebound occurs spontaneously after additional electron donation from 2NT completes O–O bond cleavage. ⁶P_OH-II is coordinated to the ferric center (d_Fe–O = 2.3 Å) and is 3.0 kcal mol⁻¹ higher in energy than ⁶P_OH-I.

Stepwise mechanism via a HO–Fe^V=O intermediate

H abstraction by the oxo ligand of 2 (mechanism III) has a barrier of 6.4 kcal mol⁻¹ in the ground state. However, the energy of the doublet transition state is slightly lower by 1.4 kcal mol⁻¹ (Fig. 6). ⁴TS_H-III is central as in mechanism II with r_C–H = 0.47. Spin densities on 2NT (0.48) and Fe (1.68) indicate radical formation and reduction, respectively (Fig. 3). H abstraction yields S = 1 Fe^IV–OH ferromagnetically coupled to the nitrobenzyl radical giving a total spin of S = 3/2 in an exothermic process (−17.4 kcal mol⁻¹). However, the sextet state, wherein S = 2 Fe^IV–OH is ferromagnetically coupled to the radical, is isoenergetic. ⁶I_rad-III is achieved through a spin flip to an unoccupied α-spin MO.⁵⁵ On the other hand, ²I_rad-III is 3.2 kcal mol⁻¹ higher in energy. The rebound step involving C–O bond formation has an early transition state (d_C–O = 2.7–2.8 Å) with a low energy barrier in the sextet (1.8 kcal mol⁻¹) and a higher one (6.4 kcal mol⁻¹) in the quartet state. As in previous mechanisms, alcohol formation is exothermic (−77.5 and −67.2 kcal mol⁻¹ for the sextet and quartet states, respectively) and the product is still bound to the active site (d_Fe–O = 2.2 Å). There is no barrier to the rebound step in the doublet state and the resulting alcohol product lies 16.0 kcal mol⁻¹ above ⁶P_OH-III.

H abstraction by the OH ligand of 2 (mechanism IV) was also investigated and found to be similar to mechanism I, in which the abstracted H atom is transferred from the bound H₂O to the oxo ligand in the rebound step (Fig. S5, ESI†). However, the barrier to H abstraction in the quartet state was found to be much higher at 12.8 kcal mol⁻¹. While the activation energy is low in the sextet state (3.0 kcal mol⁻¹), the rebound step requires 13.3 kcal mol⁻¹ and the alcohol product is dissociated from the active site.

Although the fact that only one electron is provided by the Rieske center in RDOs implies that the oxidant is most likely either 1(1′) or 2,^10,11,19 H abstraction by HO–Fe^IV=O was also examined for comparison with 2. Calculations at the quintet (ground) state show that HO–Fe^IV=O is less oxidizing than 2, with an activation energy of 21.0 kcal mol⁻¹ for H abstraction by the oxo ligand.

Comparison of different mechanisms and experimental evidence

To summarize, the sextet PES is the lowest energy pathway for mechanisms I, II and IV while in the case of mechanism III, the sextet and quartet PES are close in energy. The reactant complexes and H abstraction transition states were then recalculated using the M2 model (Fig. S6, ESI†) and activation energies are summarized in Table 1. Mechanism I has the highest barrier, which is in contrast to the similarly high-spin Fe–TMC complex with a reported activation enthalpy of only 16.1 kcal mol⁻¹ (B3LYP/6-311+G**). The high reduction potential of the complex was attributed to minimal ligand charge donation and lowered energy of the redox-active molecular orbital (RAMO) resulting from a configuration interaction with the hydroperoxo σ* orbital.¹³ In comparison, the RAMO of 1′, which is a β-spin d_x²−y²–σ* bonding orbital (Fig. 7), is increased in energy, presumably due to antibonding interactions with the π orbital of the acetate ligand, which contributes 6.0%. The activation energy for O–O bond homolysis in 1′ is 29.8 kcal mol⁻¹, which indicates that oxidation of Fe and formation of O_distH˙ dominate contributions to the barrier for mechanism I.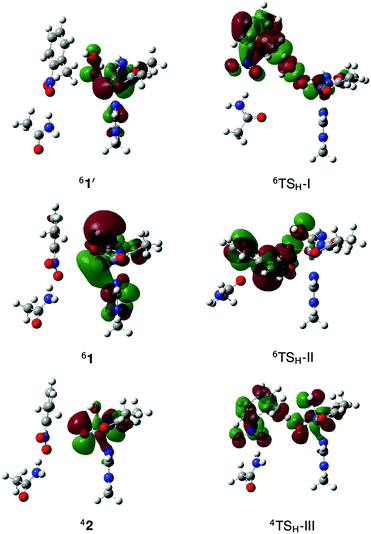

Table 1 Activation energies (kcal mol⁻¹) for H abstraction and O–O bond cleavage calculated using the M2 model (which includes Asn-258 sidechain)

Transition state	ΔE^‡
a Relative to ^42. b Relative to ^61.
^6TSH-I	37.40
^6TSH-II	27.93
^6TSO–O	29.55
^6TSH-III	14.92^a (32.89^b)
^4TSH-III	13.19 (31.16^b)
^6TSH-IV	11.40^a (29.37^b)

---

Fig. 7 Redox-active molecular orbitals of the reactant complex (1′, 1 or 2) and the H abstraction transition state (TS_H) in mechanisms I–III.

The activation energy for mechanism II is lower than that for mechanism I by about 10 kcal mol⁻¹. Unlike the latter, O–O bond cleavage is heterolytic and Fe remains in the ferric state throughout the process. Thus, Fe is not involved in the redox reaction and the electrons that must be transferred to the O–O σ* orbital for bond cleavage instead comes from the substrate. This preserves favorable exchange interactions in the metal center.⁵⁶ Moreover, the large O_prox character of the O–O σ* orbital (18.9%) makes it a better electrophile⁵⁵ than the RAMO involved in mechanism I (2.4% contribution from O_distH) (Fig. 7). While direct reaction with 1 has been implicated in the cis-dihydroxylation of naphthalene,¹² aliphatic hydroxylation through this concerted mechanism has no precedent.

Mechanisms III and IV have the lowest activation energies. However, the rebound barrier for mechanism IV is more than 10 kcal mol⁻¹ higher than that for mechanism III as this involves concerted O–H bond breaking and C–O bond formation. In the case of mechanism III, the H abstraction barrier is lower in the quartet state by 1.7 kcal mol⁻¹. 2 is a better electrophile as indicated by the large coefficient of the oxo ligand in the RAMO (39.7%),⁵⁵ which is a β-spin d_xy–π* antibonding orbital (Fig. 7). The stepwise mechanism (TS_H-III) allows the substrate to attack sideways since the RAMO is a Fe–O π* orbital (Fig. 7). In contrast, the concerted mechanism requires the C–H bond of the substrate to be linearly aligned with the O–O bond for good overlap between the substrate π orbital and the Fe–O σ* (TS_H-I) or O–O σ* (TS_H-II) orbital (Fig. 7).

Radical clock experiments on the monooxygenase reaction of NDO with norcarane and bicyclohexane yield a significant fraction of the radical rearrangement product, with a radical lifetime of the order 10 ns.¹⁹ Further evidence of a radical intermediate is inferred from the TDO-catalyzed oxidation of deuterated indene to inden-1-ol. Deuterium was found in either the C1 or C3 position, which is consistent with the formation of an allylic or benzylic radical intermediate that can have different resonance forms.^21,22 Mechanism III is thus the most consistent with experimental studies. Although the activation energy for direct reaction with 1 (mechanism II) is slightly lower by 1.6 kcal mol⁻¹ compared to formation of 2, the mechanism does not involve a radical intermediate, contrary to experiment. On the other hand, the radical intermediate in mechanism I forms the alcohol product in a barrierless process, which would not allow rearrangement to occur. Moreover, the formation of the radical itself is endothermic and requires a high activation energy. Finally, mechanism IV has a large rebound barrier and the alcohol product is dissociated from the active site (as in mechanism I), which is not consistent with the proposed catalytic cycle wherein the product is not released until the ferric active site is reduced back to Fe^II.^10,11

The involvement of 2 as the oxidant is also in agreement with the recent theoretical study on aromatic cis-dihydroxylation of nitrobenzene and 2NT by NBDO.³² It was found that substrate oxidation by 1 has a higher barrier than formation of 2 and do not lead to cis-diol formation. Initial attack of the hydroxo ligand of 2 on the ring has an activation energy of 2.4 kcal mol⁻¹ (S = 5/2) at the B97-D/LACV3P+* level for both substrates. The corresponding barrier for H abstraction by 2 (⁶TS_H-III) is higher at 6.1 kcal mol⁻¹.

Effect of the protein environment

C–H hydroxylation via mechanism III was further studied using the ONIOM method to incorporate steric and electronic effects from the protein environment. Energies in the sextet and quartet states were calculated using the ME and EE schemes and compared in Table 2, with higher values from the latter due to polarization of the QM region induced by H bonding interactions with the MM environment.

Table 2 Relative energies (kcal mol⁻¹) for O–O bond cleavage and C–H hydroxylation calculated using ONIOM(B3LYP/LACVP*:AMBER) geometries

	ONIOM		Protein effect^b
	ME	EE^a	E MM(QM,MM) − EMM(QM)	E QM(QM)^c	E(M2 model)^c	E QM(QM) − E(M2 model)
a B3LYP-D2 energies in square brackets, B97-D energies in parenthesis. b Based on decomposition of ONIOM-EE energies into QM and MM contributions. c Without zero-point energy correction.
S = 5/2
1	0.00	0.00 [0.00] (0.00)	0.00	0.00	0.00	0.00
TSO–O	22.46	24.79 [23.60] (13.37)	−2.76	29.47	29.55	−0.08
2	12.52	14.67 [12.63] (1.65)	−3.00	19.54	21.72	−2.18
TSH	16.66	25.54 [20.74] (6.82)	−2.66	33.48	32.89	0.59
Irad	−10.63	3.31 [0.28] (−9.46)	−1.09	7.45	7.17	0.28
TSreb	−10.77	11.07 [7.58] (−3.07)	−0.90	14.07	8.69	5.38
POH	−64.59	−44.90 [−50.24] (−44.67)	−0.33	−46.18	−56.36	10.17
S = 3/2
2	8.42	11.12 [7.97] (0.43)	−1.76	13.51	17.97	−4.47
TSH	15.65	24.55 [18.62] (7.92)	−0.68	29.23	31.16	−1.93
Irad	−4.98	3.48 [−0.88] (−4.31)	0.47	3.86	8.17	−4.31
TSreb	−0.73	13.95 [9.29] (3.55)	−0.10	14.92	11.57	3.36
POH	−53.69	−32.94 [−39.36] (34.64)	−0.36	−35.09	−48.11	13.02

---

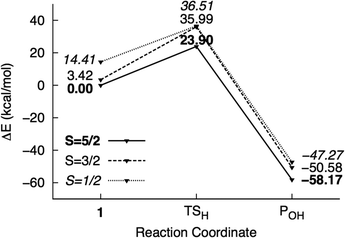
Heterolytic O–O bond cleavage (TS_O–O) is the rate-limiting step and has activation energies of 22.5 and 24.8 kcal mol⁻¹ in the ME and EE schemes, respectively. The barrier was recalculated in the ONIOM-ME scheme using different initial structures and results are summarized in Table S2 (ESI†). The values ranged from 22.5 to 25.7 kcal mol⁻¹, suggesting that some protein conformations are more favorable toward O–O bond cleavage than others. It has been previously shown through free-energy perturbation corrections to ONIOM calculations on isopenicillin N synthase that dynamical contributions, specifically statistical effects due to fluctuations about the average protein geometry, lower the O–O bond heterolysis barrier obtained from the static method by about 3 kcal mol⁻¹.⁵⁷ Thus, it is possible that the barrier is overestimated in the present study due to negligence of geometric polarization of the MM region. ONIOM-ME and ONIOM-EE geometries for the stationary points in the O–O bond cleavage step are similar. The spin population of 1 is also comparable in both schemes, but ONIOM-EE predicts a more significant electron transfer from Fe to the antibonding O–O σ* orbital at the transition state. There is also a difference of about 0.1 in the spin density of the oxo ligand in ⁴2 (Fig. S7, ESI†).

Concerted O–O bond cleavage and H abstraction by 1 was also investigated given that the activation energy obtained using the M2 model was lower compared to that for formation of 2. To locate the transition state, O–O–H and O–H–C angles were incrementally brought to 170° and 175°, respectively, to position the substrate for overlap between its π orbital and the O–O σ* orbital (see TS_H-II, Fig. 7). A potential energy scan was then generated along the H_2NT–O_prox reaction coordinate. The highest point (d_H–O = 1.2 Å, d_O–O = 1.8 Å) has an energy of 40.5 kcal mol⁻¹ at the ONIOM-ME(B3LYP/LACVP*:AMBER) level (Fig. S8, ESI†) and optimization after release of restraints led to the TS_O–O geometry. The calculations were repeated for two other structures from the simulation but the transition state was also not located. Moreover, the energy was already over 40 kcal mol⁻¹ at d_H–O = 1.9 Å. Steric hindrance from second-shell ligands, particularly Val-207 (Fig. S9, ESI†), prevents the substrate from relaxing to the transition state geometry TS_H-II (Fig. 3) and leads to a repulsive MM energy contribution (∼5 kcal mol⁻¹ in the first structure calculated).

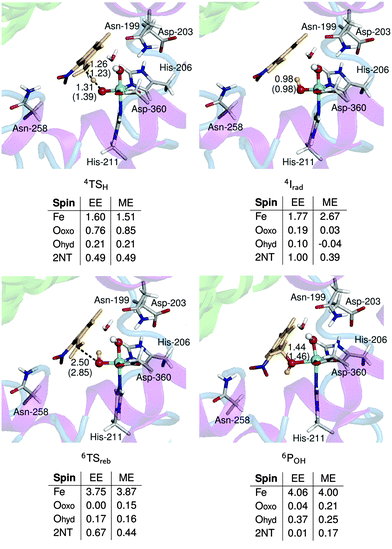
H abstraction by 2 (TS_H) in the ONIOM-ME PES has a lower energy in the quartet state, corresponding to a barrier of 7.2 kcal mol⁻¹. ⁴TS_H was obtained using three other structures from the simulation and results calculated by the ONIOM-ME method are summarized in Table S3 (ESI†). C–H and O–H bond distances and spin densities did not vary significantly (with the exception of one structure) and activation energies were within 1–2 kcal mol⁻¹. I_rad is much more stable in the sextet state by 5.6 kcal mol⁻¹. The rebound step to form P_OH is essentially barrierless in the sextet PES. On the other hand, the ONIOM-EE activation energy for H abstraction is higher at 13.4 kcal mol⁻¹ due to the change in the charge distribution of the substrate as it reacts with 2, which is unaccounted for in the ONIOM-ME method. Another notable difference from the ONIOM-ME method is that formation of I_rad is much more endothermic, with the quartet and sextet states becoming nearly isoenergetic. The rebound barrier in the sextet PES also increased to 7.8 kcal mol⁻¹.

The ONIOM-ME method fails to give a correct description of the electronic structure of the stationary points along this reaction. This can be most clearly seen by comparing the spin population of ⁴I_rad from the two methods (Fig. 8). A β-spin electron is transferred from the substrate to the active site during H abstraction and the ONIOM-EE method consistently yields a spin density of 1.0 on 2NT. In contrast, incomplete electron transfer was obtained from the ONIOM-ME method, as indicated by the smaller spin density on 2NT (0.39). Moreover, the spin density became more localized on Fe, as the value increased from 1.5 in ⁴TS_H to 2.7 in ⁴I_rad. Based on ONIOM-EE calculations, the spin-flip in I_rad to the sextet state results in a spin density of 3.3 on Fe. This increased to 3.8 in ⁶TS_reb while the spin density of 2NT decreased to 0.7. In ⁶P_OH, the ONIOM-ME method shows a residual spin density on the oxo ligand and 2NT, unlike in the ONIOM-EE method, where the spin density is concentrated on Fe and the hydroxo ligand. The Fe–O bond lengths are comparable in the two methods except in the case of ⁶I_rad, where bonds are 0.4–0.9 Å longer in the ONIOM-ME geometries. The ONIOM-ME method also predicts earlier transition states, as can be seen from the relatively long H–O (1.39 Å) and C–O (2.85 Å) bonds in ⁴TS_H and ⁶TS_reb, respectively.

Fig. 8 Optimized geometries and spin populations of stationary points in the C–H hydroxylation step calculated using mechanical (ME) and electronic (EE) embedding schemes. Distances (Å) in parenthesis are obtained using the ME scheme. Residues and a water molecule forming hydrogen bonds with the QM region are also shown.

A comparison between the QM energy (E_QM(QM)) and the energy calculated using the cluster model (M2) gives a qualitative idea of the effect of the protein environment on the geometry and the electronic structure of the active site (high-level effect). The protein effect on the energetics of the reaction can also be evaluated in terms of E_MM(QM,MM) − E_MM(QM), which includes the non-bonded interactions between the QM and MM regions (low-level effect).⁵⁸ The decomposition of ONIOM-EE energies into high- and low-level effects is summarized in Table 2.

The high-level effect for TS_O–O is negligible but it stabilizes ⁴2 by about 4 kcal mol⁻¹. The spin density of ⁴2 in the two models is similar but ONIOM-EE shows a slightly larger (∼3°) O–Fe–O angle. On the other hand, the low-level effect for TS_O–O is 3 kcal mol⁻¹ while that for ⁴2 is 2 kcal mol⁻¹. Thus, the protein environment makes heterolytic O–O bond cleavage slightly more favorable.

QM energies of ⁴TS_H and ⁴I_rad are about 2 and 4 kcal mol⁻¹ lower than those in the M2 model, while QM energies are higher for ⁶TS_reb and ⁶P_OH by about 5 and 10 kcal mol⁻¹. For ⁶TS_reb, the difference can be attributed to the much earlier transition state predicted by the M2 model based on the longer C–O bond length (by 0.7 Å) and the higher spin density on 2NT (0.81 compared to 0.67 in ONIOM-EE) (Fig. S10, ESI†). In the case of ⁶P_OH, the difference in energy is possibly an artifact of including Asn-258 (which moved closer to the active site, see Fig. S10, ESI†) in the M2 model since the geometry and spin population are similar for the two models. In contrast to the O–O bond cleavage step, the low-level effects for the C–H hydroxylation step only ranged from −0.9 (⁶TS_reb) to 0.5 (⁴I_rad) kcal mol⁻¹ since the substrate essentially remained in the same position during the reaction.

Effect of dispersion interactions

The effect of dispersion interactions on ONIOM-EE energies was also investigated in light of its possible importance in obtaining accurate activation energies for enzymatic reactions, as shown in a QM/MM study of H abstraction by P450_cam.⁵⁹Table 2 includes dispersion-corrected ONIOM-EE energies calculated using B3LYP-D2, which was used by Lonsdale et al.,⁵⁹ and B97-D, which was used in the study on cis-dihydroxylation by NBDO mentioned above.³² A comparison of the energy profiles for the overall reaction is shown in Fig. 9. It can be seen that the O–O bond cleavage barrier is lowered by dispersion, and in the case of B97-D, the barrier is only 13.4 kcal mol⁻¹. This is slightly lower than those reported by Pabis et al.³² (14.6–16.7 kcal mol⁻¹), which were obtained using various cluster models of NBDO. Formation of ground state 2 is also essentially thermoneutral (0.4 kcal mol⁻¹) using the B97-D functional. The H abstraction barrier in the quartet state decreased to 10.7 kcal mol⁻¹ and the resulting ⁴I_rad is stabilized when the D2 correction is added to B3LYP energies. In contrast, the B97-D functional yields a slightly lower energy for ⁶TS_H, resulting in a barrier of only 6.4 kcal mol⁻¹ relative to ⁴2. ⁶I_rad is also more stable than the corresponding quartet state by 5.2 kcal mol⁻¹, which would be consistent with the notion that a higher number of identical-spin unpaired electrons results in more favorable exchange interactions.⁵⁶ On the other hand, all methods consistently indicate that the rebound step is more favorable in the sextet PES, with B97-D giving the lowest barrier (6.4 kcal mol⁻¹) and B3LYP-D2 giving the most exothermic reaction energy (−50.5 kcal mol⁻¹).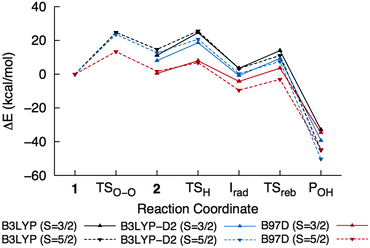

Fig. 9 ONIOM-EE energy profiles for the overall reaction calculated using different functionals. The values are listed in Table 2.

Possible role of other residues in the substrate pocket

The substrate pocket of NBDO is composed of mostly hydrophobic residues, some of which have been shown to influence stereo- or regioselectivity. In particular, Asn-258 may be crucial to aromatic cis-dihydroxylation of mononitrotoluenes by suitably positioning the ring for oxygen attack through hydrogen bonding.⁶⁰ This is indicated by the predominance of the competing reaction, C–H hydroxylation, in the N258V mutant of NBDO⁶⁰ and in NDO,³¹ which has valine at the equivalent position. On the other hand, there is no experimental evidence for the direct involvement of neighbouring residues in the reaction itself. Several hydrogen bonding interactions with the active site were observed during simulation and have also been reported in a recent MD study of NBDO.⁶¹ These include interactions between (a) the substrate and Asn-258, (b) His-206 and Asp-203, which bridges the active site and the adjacent Rieske cluster, (c) the hydroperoxo ligand and a water molecule, (d) the same water molecule and Asn-199, which is believed to be connected to a water channel facilitating proton transfer,⁹ (e) the hydroperoxo ligand and Asn-199 and (f) Asp-203 and Asn-199 (Fig. 8, Table S1, ESI†).

ONIOM-EE geometries of ⁶TS_O–O and ⁴TS_H obtained with the QM region consisting only of Fe, the hydroperoxo ligand, the sidechains of His-206, His-211 and Asp-360, and 2NT were re-optimized with inclusion of these residues to investigate the effect on energy, geometry and electronic structure. In the case of O–O bond cleavage, the barrier increased with inclusion of other residues in the QM region although the difference is less than 1 kcal mol⁻¹ (Table 3). On the other hand, the H atom abstraction barrier decreased by about 1 kcal mol⁻¹ with addition of Asn-258 in the QM region (Table 4). However, ⁶TS_O–O and ⁴TS_H geometries and spin densities did not change significantly with the QM region.

Table 3 O–O bond cleavage transition state (⁶TS_O–O) calculated using the ONIOM-EE method with different QM regions

QM region	Atoms	ΔE^‡^a (kcal mol^−1)	O–O bond distance (Å)	Spin densities
				Fe	Oprox	Odist
a Without zero-point correction. b Fe–OOH + His-206 + His-211 + Asp-360 + 2NT.
Core^b	49	26.71	1.88	3.70	0.49	0.31
+ H2O	52	26.93	1.88	3.70	0.50	0.32
+ Asp-203	55	27.02	1.88	3.69	0.49	0.32
+ H2O + Asp-203	58	27.28	1.88	3.69	0.51	0.31
+ H2O + Asp-203 + Asn-199	66	27.19	1.88	3.69	0.52	0.30

---

Table 4 H abstraction transition state (⁴TS_H) calculated using the ONIOM-EE method with different QM regions

QM region	Atoms	ΔE^‡^a (kcal mol^−1)	Bond distances (Å)		Spin densities
			C–H	O–H	Fe	Ooxo	Ohyd	2NT
a Without zero-point correction. b Fe–OOH + His-206 + His-211 + Asp-360 + 2NT.
Core^b	49	16.81	1.26	1.31	1.60	0.76	0.21	0.49
+ Asp-203	55	16.91	1.26	1.30	1.59	0.74	0.21	0.48
+ Asn-258	57	15.68	1.25	1.32	1.59	0.77	0.21	0.49
+ Asn-199	57	17.49	1.27	1.30	1.61	0.75	0.20	0.49

---

Conclusions

DFT calculations on cluster models of nitrobenzene 1,2-dioxygenase reveal the mechanistic differences between C–H hydroxylation by Fe^III–OOH and HO–Fe^V=O. Direct reaction with Fe^III–OOH involves concerted H abstraction and O–O bond cleavage to form the alcohol product. On the other hand, H abstraction by HO–Fe^V=O, which is formed through O–O bond heterolysis in Fe^III–OOH, leads to a radical intermediate. The latter mechanism is consistent with deuterium labeling studies and radical clock experiments on other Rieske non-heme iron dioxygenases. However, the activation energy for formation of the HO–Fe^V=O oxidant calculated using cluster models is higher compared to that for direct reaction with Fe^III–OOH. ONIOM calculations gave a better description of the energetics of the two possible mechanisms through explicit inclusion of the steric effects of the protein environment. The concerted mechanism with Fe^III–OOH requires the C–H bond to be aligned with the O–O bond for good orbital overlap, but formation of this transition state was hindered by the surrounding residues. In comparison, H abstraction by HO–Fe^V=O involves a sideways attack of the substrate, which was slightly stabilized by the protein environment. Formation of HO–Fe^V=O also became more favorable and it is possible that dispersion and free-energy perturbation corrections would lower the calculated activation energy further. On the other hand, no evidence was found to indicate the involvement of other residues in the substrate pocket on the reaction itself. Inclusion of Asn-199, Asp-203 and Asn-258, which form hydrogen bonding interactions with the active site, in the QM region of the ONIOM model also did not affect O–O bond cleavage and H abstraction barriers and transition state geometries significantly. The results of the study can provide an insight into the nature of the oxidant and the mechanism of aliphatic hydroxylation in Rieske non-heme iron dioxygenases in general.

Acknowledgements

This work was supported by the grants FP7-264329 from the 7th Framework Programme, Marie Curie Action ITN “CSI:Environment” and PSRP-025/2010 from the Polish-Swiss Research Program. Access to computing facilities at the Lodz University of Technology Computer Center (under the PLATON project) is gratefully acknowledged.

Notes and references

1. P. C. A. Bruijnincx, G. van Koten and R. J. M. K. Gebbink, Chem. Soc. Rev., 2008, 37, 2716–2744.
2. T. Ohta, S. Chakrabarty, J. D. Lipscomb and E. I. Solomon, J. Am. Chem. Soc., 2008, 130, 1601–1610.
3. D. T. Gibson, S. M. Resnick, K. Lee, J. M. Brand, D. S. Torok, L. P. Wackett, M. J. Schocken and B. E. Haigler, J. Bacteriol., 1995, 177, 2615–2621.
4. J. Lee and H. Zhao, Angew. Chem., Int. Ed., 2006, 45, 622–625.
5. D. R. Boyd, N. D. Sharma, B. E. Byrne, S. A. Haughey, M. A. Kennedy and C. C. R. Allen, Org. Biomol. Chem., 2004, 2, 2530–2537.
6. S. M. Resnick, K. Lee and D. T. Gibson, J. Ind. Microbiol. Biotechnol., 1996, 17, 438–457.
7. L. P. Wackett, Enzyme Microb. Technol., 2002, 31, 577–587.
8. M. Bordeaux, A. Galarneau and J. Drone, Angew. Chem., Int. Ed., 2012, 51, 10712–10723.
9. A. Karlsson, J. V. Parales, R. E. Parales, D. T. Gibson, H. Eklund and S. Ramaswamy, Science, 2003, 299, 1039–1042.
10. M. D. Wolfe, J. V. Parales, D. T. Gibson and J. D. Lipscomb, J. Biol. Chem., 2001, 276, 1945–1953.
11. M. D. Wolfe and J. D. Lipscomb, J. Biol. Chem., 2003, 278, 829–835.
12. A. Bassan, M. R. A. Blomberg and P. E. M. Siegbahn, JBIC, J. Biol. Inorg. Chem., 2004, 9, 439–452.
13. L. V. Liu, S. Hong, J. Cho, W. Nam and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 3286–3299.
14. M. S. Chow, L. V. Liu and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13241–13245.
15. E. G. Kovaleva and J. D. Lipscomb, Nat. Chem. Biol., 2008, 4, 186–193.
16. J. C. Price, E. W. Barr, B. Tirupati, J. M. Bollinger, Jr. and C. Krebs, Biochemistry, 2003, 42, 7497–7508.
17. B. E. Eser, E. W. Barr, P. A. Frantom, L. Saleh, J. M. Bollinger, Jr., C. Krebs and P. F. Fitzpatrick, J. Am. Chem. Soc., 2007, 129, 11334–11335.
18. A. J. Panay, M. Lee, C. Krebs, J. M. Bollinger, Jr. and P. F. Fitzpatrick, Biochemistry, 2011, 50, 1928–1933.
19. S. Chakrabarty, R. N. Austin, D. Deng, J. T. Groves and J. D. Lipscomb, J. Am. Chem. Soc., 2007, 129, 3514–3515.
20. A. Decker and E. I. Solomon, Curr. Opin. Chem. Biol., 2005, 9, 152–163.
21. L. P. Wackett, L. D. Kwart and D. T. Gibson, Biochemistry, 1988, 27, 1360–1367.
22. D. R. Boyd, N. D. Sharma, N. I. Bowers, R. Boyle, J. S. Harrison, K. Lee, T. D. H. Bugg and D. T. Gibson, Org. Biomol. Chem., 2003, 1, 1298–1307.
23. B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980.
24. D. Kumar, S. P. de Visser, P. K. Sharma, S. Cohen and S. Shaik, J. Am. Chem. Soc., 2004, 126, 1907–1920.
25. I. Prat, A. Company, V. Postils, X. Ribas, L. Que, Jr., J. M. Luis and M. Costas, Chem. – Eur. J., 2013, 19, 6724–6738.
26. I. Prat, J. S. Mathieson, M. Güell, X. Ribas, J. M. Luis, L. Cronin and M. Costas, Nat. Chem., 2011, 3, 788–793.
27. K. Chen and L. Que, Jr., J. Am. Chem. Soc., 2001, 123, 6327–6337.
28. Y. He, J. D. Gorden and C. R. Goldsmith, Inorg. Chem., 2011, 50, 12651–12660.
29. J. England, R. Gondhia, L. Bigorra-Lopez, A. R. Petersen, A. J. P. White and G. J. P. Britovsek, Dalton Trans., 2009, 5319–5334.
30. A. Bassan, M. R. A. Blomberg, P. E. M. Siegbahn and L. Que, Jr., J. Am. Chem. Soc., 2002, 124, 11056–11063.
31. R. Friemann, M. M. Ivkovic-Jensen, D. J. Lessner, C.-L. Yu, D. T. Gibson, R. E. Parales, H. Eklund and S. Ramaswamy, J. Mol. Biol., 2005, 348, 1139–1151.
32. A. Pabis, I. Geronimo and P. Paneth, J. Phys. Chem. B, 2014, 118, 3245–3256.
33. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
34. A. D. Becke, J. Chem. Phys., 1992, 97, 9173–9177.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
36. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
37. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
38. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
39. B. Mennucci, E. Cancès and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506–10517.
40. D. J. Heyes, M. Sakuma, S. P. de Visser and N. S. Scrutton, J. Biol. Chem., 2009, 284, 3762–3767.
41. E. Derat, D. Kumar, H. Hirao and S. Shaik, J. Am. Chem. Soc., 2006, 128, 473–484.
42. H. Chen, W. Lai, J. Yao and S. Shaik, J. Chem. Theory Comput., 2011, 7, 3049–3053.
43. K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, Chem. Phys. Lett., 1988, 149, 537–542.
44. S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542.
45. S. P. de Visser, J. Am. Chem. Soc., 2006, 128, 9813–9824.
46. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revisions A.02 and D.01), Gaussian, Inc., Wallingford CT, 2009.
47. A. L. Tenderholt, QMForge Version 2.1, Stanford University, Stanford, CA, 2007.
48. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725.
49. M. Lundberg, T. Kawatsu, T. Vreven, M. J. Frisch and K. Morokuma, J. Chem. Theory Comput., 2009, 5, 222–234.
50. T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, Jr., K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826.
51. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
52. F. Li, K. K. Meier, M. A. Cranswick, M. Chakrabarti, K. M. V. Heuvelen, E. Münck and L. Que, Jr., J. Am. Chem. Soc., 2011, 133, 7256–7259.
53. A. Miłaczewska, E. Broclawik and T. Borowski, Chem. – Eur. J., 2013, 19, 771–781.
54. K. Lee and D. T. Gibson, Appl. Environ. Microbiol., 1996, 62, 3101–3106.
55. M. L. Neidig, A. Decker, O. W. Choroba, F. Huang, M. Kavana, G. R. Moran, J. B. Spencer and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12966–12973.
56. D. Usharani, D. Janardanan, C. Li and S. Shaik, Acc. Chem. Res., 2013, 46, 471–482.
57. T. Kawatsu, M. Lundberg and K. Morokuma, J. Chem. Theory Comput., 2011, 7, 390–401.
58. M. Lundberg and K. Morokuma, J. Phys. Chem. B, 2007, 111, 9380–9389.
59. R. Lonsdale, J. N. Harvey and A. J. Mulholland, J. Chem. Theory Comput., 2012, 8, 4637–4645.
60. K.-S. Ju and R. E. Parales, Appl. Environ. Microbiol., 2006, 72, 1817–1824.
61. A. Pabis, I. Geronimo, D. M. York and P. Paneth, J. Chem. Theory Comput., 2014 DOI:10.1021/ct500205z.

---

Footnote

† Electronic supplementary information (ESI) available: Protein structure preparation, MD simulation methodology and analysis, figures of optimized stationary points and additional ONIOM calculations using other initial structures from the simulation. See DOI: 10.1039/c4cp01030b

---