Open Access Article
Open Access ArticleWater and small organic molecules as probes for geometric confinement in well-ordered mesoporous carbon materials
Yeping
Xu
a,
Tobias
Watermann
b,
Hans-Heinrich
Limbach
c,
Torsten
Gutmann
a,
Daniel
Sebastiani
b and
Gerd
Buntkowsky
*a
aEduard-Zintl-Institut für Anorganische und Physikalische Chemie, Technische Universität Darmstadt, Alarich-Weiss-Str. 8, D-64287 Darmstadt, Germany. E-mail: gerd.buntkowsky@chemie.tu-darmstadt.de
bInstitut für Chemie, Martin-Luther-Universität Halle-Wittenberg, von-Danckelmann-Platz 4, 06120 Halle, Germany
cInstitut für Physikalische und Theoretische Chemie, Freie Universität Berlin, Takustr.3, D-14195 Berlin, Germany
First published on 25th March 2014
Abstract
Mesoporous carbon materials were synthesized employing polymers and silica gels as structure directing templates. The basic physico-chemical properties of the synthetic mesoporous materials were characterized by 1H and 13C MAS solid-state NMR, X-ray diffraction, transmission electron microscopy (TEM) and nitrogen adsorption measurements. The confinement effects on small guest molecules such as water, benzene and pyridine and their interactions with the pore surface were probed by a combination of variable temperature 1H-MAS NMR and quantum chemical calculations of the magnetic shielding effect of the surface on the solvent molecules. The interactions of the guest molecules depend strongly on the carbonization temperature and the pathway of the synthesis. All the guest-molecules, water, benzene and pyridine, exhibited high-field shifts by the interaction with the surface of carbon materials. The geometric confinement imposed by the surface causes a strong depression of the melting point of the surface phase of water and benzene. The theoretical calculation of 1H NICS maps shows that the observed proton chemical shifts towards high-field values can be explained as the result of electronic ring currents localized in aromatic groups on the surface. The dependence on the distance between the proton and the aromatic surface can be exploited to estimate the average diameter of the confinement structures.
Introduction
Porous carbon materials are widely used in industry for adsorption, separation and catalysis.1,2 Due to the binding versatility of the carbon atom, these materials exhibit an unprecedented wealth of morphologies. They depend not only on the starting material but also on the conditions of preparation, such as the carbonization temperature which strongly influences the amount of oxygen-containing surface functional groups. Activated carbon is a material with high porosity, broad pore size range and localized microcrystalline structure.3 The broad pore size distribution4–8 results in a fairly large number of different local structures and thus different microenvironments for the molecules adsorbed on the surface. This difficult to control nature of activated carbon gave rise to develop well-ordered mesoporous carbon materials with regular properties. The well-ordered mesoporous carbon (CMK-1) was firstly synthesized by using ordered silica as a template in 1999.9 It has a narrow distribution of pore sizes and an ordered pore structure which simplify the surface and pore conditions.In the last two decades, several systems of activated carbon,10–14 carbon nanotubes15–18 and graphite19–21 have been studied by X-ray11,17,18,22–24 and neutron diffraction25 as well as thermal analysis.26,27 Most of these studies focused on activated carbon28–30 and carbon black31 which lack a regular pore structure, and detailed solid-state NMR studies have been very rare up to now.30,32,33 This fact motivates us to investigate well-ordered carbon materials employing a combination of solid-state NMR, quantum chemical calculations and thermodynamic methods.
Quantum chemical calculations of the chemical shifts are indispensable for the structural interpretation of NMR-data. Within electronic structure theory, NMR chemical shifts arise from quantum-mechanically induced electronic ring currents. There are two main contributors to a given NMR chemical shift: the intramolecular electrons and the electrons from other molecules. The intramolecular contribution depends on the molecular geometry (bond lengths and angles), whereas the intermolecular part is a function of the relative position and orientation of the considered nuclear spin relative to the molecular fragment or the other molecule which creates these ring currents. This second contribution can be modeled quantum-chemically by means of the so-called nucleus independent chemical shift (NICS) maps.34–43
In the present work we are studying hexagonally ordered mesoporous carbon with a narrow pore size distribution, both experimentally and theoretically, employing guest molecules with characteristic interactions. In the first step, three types of carbon materials are synthesized and their basic properties are characterized by TEM, BET and solid-state NMR. In the second step, small molecules such as water, benzene and pyridine are employed as probes for the surface properties. These systems are characterized employing solid-state NMR experiments at variable temperature. Finally, the interpretation of experimental results is approved by employing theoretical calculations of NICS maps.
Theoretical section
NICS fields
The values of NICS fields at a particular coordinate quantify the relative offset in terms of the NMR chemical shift that a given nuclear spin would experience if it is located at this coordinate. It can be seen as an additive displacement of the actual NMR chemical shift value, which is independent of the species of the nucleus. In other words, the NMR resonance of a proton (or carbon) atom with a NMR chemical shift of X ppm, located in a region with a NICS value of −2 ppm, will appear in the spectrum at X − 2 ppm. It should be noted that these NICS fields are computed in all points of space, and not only at the coordinates of actual atoms/spins.Formally, the induced magnetic field Bind is well defined at any given point R in space without the need for the actual nucleus at that position. Bind(R) is obtained from a DFT response calculation. The chemical shielding σ(R) is then calculated by
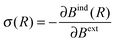 | (1) |
| δ(R) = −⅓Tr[σ(R)] | (2) |
Unlike in the case of regular NMR chemical shifts, there is no need for a reference atom per molecule for converting the nuclear shielding into chemical shift values (e.g. TMS). The value of the NICS maps gives the change in the chemical shift for arbitrary protons, e.g. two protons with chemical shifts of 5 and 6 ppm in a NICS map region with −2 ppm will be modified to 3 and 4 ppm, respectively.
Computational details
Calculations of the optimized geometries and nucleus independent chemical shift (NICS) maps have been performed using the CPMD program package. The response calculations were performed using the density functional perturbation (DFPT)44,45 module. The BLYP exchange and correlation functional46,47 with additional van der Waals correction and pseudopotentials of Martins–Trouiller type were used employing a plane-wave cutoff of 100 Ry.48,49 The visualizations of the NICS maps have been performed using the JMOL program as well as the GIMP image manipulation package for post-processing purposes.Experimental section
Synthesis of mesoporous carbon
Three different types of mesoporous carbon materials were synthesized for this study. The first two mesoporous carbon materials with ordered pore sizes were directly prepared using Pluronic F-127 as the template, employing a method derived from the procedure described in ref. 50. In a 200 ml polypropylene bottle (PP bottle), 6.61 g of resorcinol was added to a solution composed of 17.4 g of distilled water, 23 g of ethanol and 0.6 ml of hydrochloric acid (5.0 mol l−1). 3.78 g of Pluronic F-127 was added. After stirring for one hour, 10 g of formaldehyde was added to the pellucid solution and continued to stir for 2 hours at 333 K in the sealed PP bottle. To stabilize the gel, the entire system was warmed at 363 K and opened to air for 5 h. The resulting gel was heated under N2 gas in a home-built tubular oven starting at a carbonization temperature of 300 °C. This temperature was raised in steps of 100 °C every 30 minutes until the final carbonization temperatures of 600 °C or 800 °C were reached. At these temperatures the materials were tempered for 4 hours. According to the final carbonization temperature the materials are denoted as C600 and C800.The third porous carbon material was synthesized in replica from silica gel and carbonized at 800 °C similar to the description in ref. 51. In this preparation, 1.8 g of sucrose was added into a silica solution containing 4.2 g of tetraethyl orthosilicate (TEOS) in the ratio TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH
EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl = 1
HCl = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 at 60 °C to form a carbon/silica gel. The composite was carbonized at 800 °C under argon for 4 hours. The silica was removed from the composite by HF solution. This porous carbon material is denoted as C_SiO2.
0.01 at 60 °C to form a carbon/silica gel. The composite was carbonized at 800 °C under argon for 4 hours. The silica was removed from the composite by HF solution. This porous carbon material is denoted as C_SiO2.
Characterization of ordered carbon materials
The pore textures were investigated through physical adsorption of nitrogen at 77 K on an automatic volumetric sorption analyzer, Quantachrome Nova 1200. The surface area was calculated by the Brunauer–Emmett–Teller (BET)52 method in the relative pressure range from 0.05 to 0.2. The pore size distributions were calculated by the Barrett–Joyner–Halenda (BJH) method53,54 from desorption branch.TEM was carried out using a Tecnai F20 (FEI Company, Oregon, USA) equipped with a field emission gun. Images were taken at an accelerating voltage of 160 kV.
All NMR experiments were performed on a 14 T Varian Infinity plus solid state NMR spectrometer equipped with 4 mm and 3.2 mm probes, respectively, corresponding to a frequency of 600.0 MHz for 1H and 150.9 MHz for 13C. All 1H MAS spectra were recorded at 10 kHz spinning with the spin-echo pulse sequence with a repetition delay of 3 s. 16 scans were performed for the proton spectra of host materials, and 4 scans for the spectra when guest molecules were added.
1H and 13C signals were referenced employing the proton, respectively carbon, signals of the trimethylsilyl group of TSP (trimethylsilyl-propionate) set as 0 ppm.
Adsorption of small molecules
To investigate the behavior of small guest molecules in these ordered carbon materials, water as well as benzene and pyridine were chosen as probes. In these adsorption studies, defined amounts of the liquid guest compounds were directly added to the NMR rotor containing weighted amounts of the carbon materials.To determine the adsorption state of the guest molecules (monolayer or multilayer), the total area of the adsorbate Stotal area is needed, which is calculated from:
 | (3) |
Results and discussion
N2 isotherms and pore size distributions of the carbon materials
The N2 isotherms and pore size distributions are shown in Fig. 1. Structural information on the mesoporous materials is collected in Table 1. According to the IUPAC convention,58 both the C600 and C800 materials possess type IV isotherms with type H2 hysteresis loops. Their pore size distribution plots calculated from the desorption branch using the BJH method practically coincide. The similar pore structure characteristics of these two materials show that the difference in carbonization temperature has no influence on the textural structures or pore morphologies.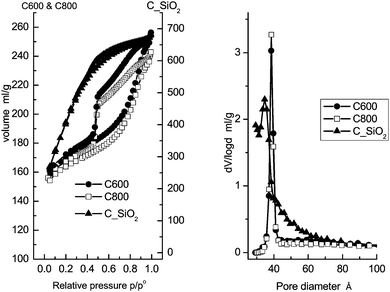 | ||
| Fig. 1 N2 isotherms (left) and pore size distributions (right) of the mesoporous carbon materials, C600, C800 and C_SiO2. | ||
| S BET (m2 g−1) | Total pore volume (ml g−1) | Pore size (BJH) (nm) | |
|---|---|---|---|
| C600 | 526 | 0.39 | 3.85 |
| C800 | 507 | 0.37 | 3.85 |
| C_SiO2 | 1556 | 1.05 | 3.57 |
In contrast, the C_SiO2 material possesses a type I isotherm according to the IUPAC convention.58 Moreover, the pore size distribution is broader compared to the C600 and C800 materials, which is attributed to the absence of the surfactant as a structural template during preparation.
Both the C600 and C800 materials have similar specific surface areas and pore volumes as well as the same narrowly centered pore diameter of 3.85 nm. The C_SiO2 material has nearly three times larger specific surface area above 1500 m2 g−1, owing to the large number of micropores. Finally, a wider pore size distribution with a slightly smaller median of 3.57 nm is found.
TEM of mesoporous carbon
High resolution TEM images and the corresponding hexagonal diffraction pattern of C600 (Fig. 2) reveal the highly ordered structure of the material. The hexagonal structure of the material is confirmed by the electron diffraction image.The TEM image of C800 (not shown) shows similarity compared to that of C600 which corroborates the results of the adsorption measurements shown above. In contrast, TEM images of C_SiO2 related carbon materials (see ref. 51) showed an amorphous structure with a worm-like pore system. Thus, for C_SiO2 in this work, for which no TEM data were available, similar pore structure properties are expected.
NMR experiments of bulk materials
The 1H spin-echo MAS and the single-pulse 13C MAS NMR spectra of the three samples are shown in Fig. 3. All proton spectra showed a very low signal to noise ratio, which indicates that the three materials are all proton-poor. In all spectra a broad signal in the region at 7 ppm is visible indicating the aromatic character of these protons. This hypothesis is also corroborated by the 13C MAS NMR spectra which display weak signals in the range of sp2 carbons.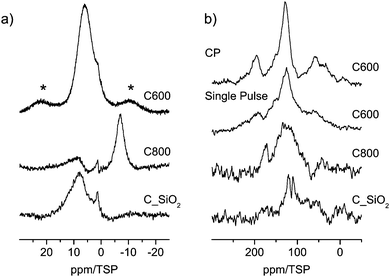 | ||
| Fig. 3 (a) 1H MAS NMR spectra (asterisks mark spinning sidebands) and (b) 13C (right) MAS NMR spectra of carbon materials (see discussion in the text). | ||
Next to these aromatic signals in the 1H spin-echo MAS a second high-field shifted signal is visible which dominates in the spectrum of C800 at −7 ppm. For organic compounds this unusual chemical shift value is a clear indication of the presence of interactions with the inside of aromatic rings (see the discussion below).
No signal could be obtained by CPMAS from the two samples carbonized at 800 °C (C800 and C_SiO2). This is a clear indication of the low concentration of protons in these systems, which prevents cross polarization. In contrast, a CP-MAS signal is found for the C600 sample after 20k scans, which shows that the concentration of protons in C600 is higher than those in the other two samples. A comparison of this signal to the signal of the single pulse spectrum (Fig. 3, right panel) shows that both experiments reveal the same line shape. This is a clear indication that no local areas containing only carbon are present in the sample and thus the material is well ordered.
Water adsorption in neat carbon materials
Fig. 4 displays the 1H MAS-NMR spectra of water adsorbed on the surface of C600 as a function of various amounts of water. The sample containing no water displays only a very weak broad proton background signal centered on the aromatic region. This signal is clearly separated from the signal of the adsorbed water. With 1 μl of water loading, three high-field shifted signals appear at 1.1, 0.8 and 0.4 ppm. The absence of a bulk-water peak at ca. 5 ppm shows that all water molecules are in contact with the carbon surface. The high-field shifts are attributed to the aromatic structure of the carbon material surface where ring currents from the surface shield the external magnetic field. This situation is similar to results found for monomeric water molecules dissolved in deuterated benzene, where a chemical shift of 0.4 ppm was observed.59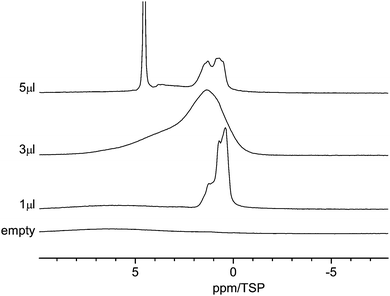 | ||
| Fig. 4 Room temperature 1H MAS NMR spectra of water in C600 for various amounts of water between 1 μl and 5 μl. | ||
Since the pore size distribution is narrowly centered at 3.8 nm, as shown above, a pore size effect as the origin of the three different signals can be ruled out. Thus, one can conclude that all water molecules are adsorbed at primary and secondary sites60,61 and the three signals are an indication of the diversity of the surface functional group.
Upon increasing the water content to 3 μl, the signal becomes strongly broadened and now consists mainly of two broad lines centered at ca. 1.5 ppm and 4 ppm. The line at 1.5 ppm has a shoulder at 1 ppm. While the high-field shift of the first line is again indicative of surface water, the more low-field shifted line at 4 ppm for small water clusters (H2O)n, n = 2 to 4, exhibiting a similar number of free and hydrogen bonded OH groups.62 The strong line broadening is a clear indication of dynamic processes inside these water clusters or phases, e.g. hydrogen bonding and proton exchange. The strong line broadening is a clear indication of dynamic processes inside these water phases which cause the exchange of proton or water molecules.
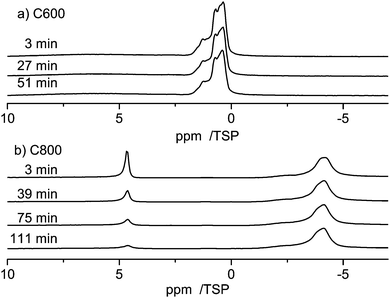
As shown in Fig. 5 the line shape of the spectra changes as a function of time. Shortly (3 min) after water is injected into the pores the low-field phase contains a strong contribution centered at ca. 5 ppm. 39 min after the injection the relative intensity of this component decreased and the line shifted towards a slightly higher field. This development of the line shape continues until the final line shape is obtained in the spectrum at 111 min. Since the chemical shift of ca. 5 ppm is indicative of bulk water one can conclude that after 3 min part of the water is still in the form of small droplets, and not the whole surface is wetted completely with hydrogen bonded water molecules. The water from these small droplets then continues to wet the surface, which causes the shift to a higher field and the intensity changes.
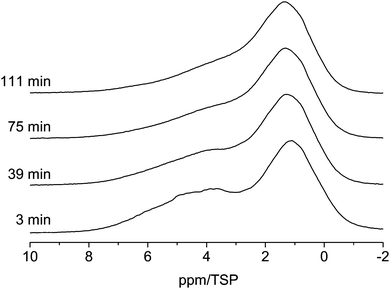 | ||
| Fig. 5 Evolution of the 1H MAS NMR spectra of the C600 sample containing 3 μl of water (room temperature, spin-echo spectrum, 10 kHz spinning speed). | ||
With 5 μl of water content, the spectrum changes considerably. It now shows a strong narrow peak at 4.8 ppm, two additional and relatively narrow peaks at 1 ppm and 1.5 ppm, and a weaker broad peak between 2 ppm and 4 ppm. The peak at 4.8 ppm can be attributed to the confined bulk water phase. The value is similar to the one of 5.2 ppm found for larger water clusters in benzene.59 The broad peak is typical again for small water clusters (H2O)n, n = 2 to 4, which are located in different slowly exchanging environments.62 The two relatively narrow lines at 1 ppm and 1.5 ppm are from water molecules which are not hydrogen bonded to other water molecules. Since the preparation time of the sample was long enough to ensure an equilibrium distribution of water inside the pores, this is indicative of the presence of special water adsorption sites in micropores or similarly separated positions.
Fig. 6 shows the 1H MAS NMR spectra of the C800 sample as a function of water loading. There are clear differences compared to the C600 material. With 1 μl of water loading, the water signal is strongly shifted to high field and two lines centered at −3 ppm and −4 ppm are observable. This shift is a clear indication of the surface effect of the aromatic rings. Similar high-field shifts were calculated by Marques63 and some of us43 for carbon nanotubes. Increasing the water content to 3 μl causes a shift of the high-field signal at −4 ppm to −2 ppm. In addition a new line at 5 ppm appears. This is an indication of the presence of large water clusters in the sample, which exhibit a bulk-like chemical shift. Upon further increase of the water content the high-field shifted part of the spectrum remains constant and only the intensity of the bulk-like water in the sample increases. In particular both lines stay well separated, which means that there is no exchange between bulk-like water and the strong surface interacting water.
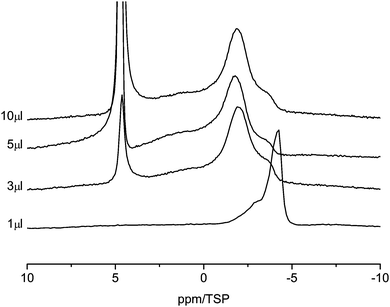 | ||
| Fig. 6 1H MAS NMR spectra of water in C800 sample (room temperature, spin-echo spectrum, 10 kHz spinning speed). | ||
Fig. 7 compares the evolution of the spectra when water is entering the pores of the carbon materials, C600 and C800. For both samples the first spectrum was recorded 3 minutes after injection of water into the carbon material. While the bulk water peak disappears very fast in the case of the C600 sample (in less than 3 minutes), showing a fast intake of the water into the pores, there is a much slower dynamics in the case of the C800 sample, where it takes more than two hours to adsorb the major amount of water onto the pores.
This result is again a clear indication of the strong hydrophobicity of the C800 sample, where the low density of terminal oxygen containing groups causes a stronger aromaticity of the material.
The difference in the NMR chemical shift value of monomeric water in C600 (0.4 ppm) and in C800 (−4 ppm) can be explained by a lower degree of aromaticity in the C600 pore walls, which results in the absence of magnetic shielding effects with respect to water molecules confined inside. This would yield proton NMR resonances of about the value of a monomeric water molecule in vacuo (of precisely +0.4 ppm).64 In turn, a stronger aromatic character of the C800 sample can shift the proton NMR signal by several ppm further down to −4 ppm, in good agreement with our quantum-chemical calculations (see below, Fig. 12).
Water adsorption in C_SiO2
The RT 1H MAS NMR spectra of the C_SiO2 sample containing 1 μl of water are shown at the top of Fig. 8 (marked as “Fresh”). Directly after filling the pores the signal has its main intensity at 3.3 ppm. After 40 minutes the main intensity is shifted to 2.9 ppm. This shift is accompanied by a line narrowing. The line-shape after two hours coincides with the one after 40 minutes.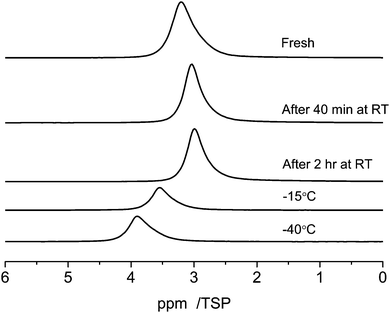 | ||
| Fig. 8 Temperature dependent 1H MAS-NMR spectra at 10 kHz spinning speed of 1 μl of water in C_SiO2 depending on the evolution time at room temperature and on the sample temperature. | ||
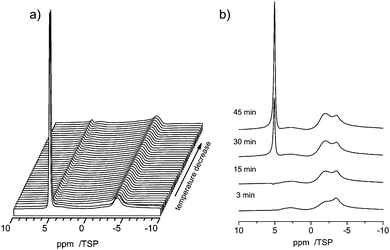
Cooling the sample to −15 °C causes a low field shift of the signal to 3.6 ppm and a further cooling to −40 °C increases the low-field shift of the signal to 3.8 ppm. This temperature dependent shift is most probably the result of a complex interplay of the relatively broad distribution of pore-diameters of the C_SiO2 sample, which was already visible in the BJH-results (Fig. 1) and in different silanol group densities on the pore surfaces: (i) porous media in general cause a strong reduction of the melting, respectively glass-transition temperatures, of fluids inside the pores; (ii) the surface induced chemical shifts of the carbon part of the pore surfaces are also expected to depend on the pore diameter; (iii) the density of silanol-groups and thus the number of possible water–silanol hydrogen bonds changes the observed chemical shift. Since all three effects can influence the chemical shift of the water inside the pores a detailed theoretical modeling of the pore surfaces and the water inside the pores is necessary to model the experiments in Fig. 8.
The freezing process of water and non-freezable water
Due to the capillary effect65 the freezing process and the melting process can exhibit a temperature hysteresis, which is visible in DSC.66 Moreover the interaction with the surface can lead to the formation of non-freezable water phases, similar to the situation found in silica pores67 or water–protein solutions.68To search for such a hysteresis or the presence of non-freezable water we recorded the 1H MAS NMR spectra for decreasing and increasing temperatures. Upon lowering the temperature a disappearance of the signal from bulk water is observed in the temperature range of −14.5 to −15.8 °C (Fig. 9a). This disappearance is caused by the formation of ice inside the pores, which has a very broad NMR-line, which disappears in the baseline of the spectrum.69
Upon further lowering the temperature (not shown) the peak at −3.8 ppm almost remains constant during the entire temperature range down to −50 °C. The latter is a clear indication that the interactions with the surface cause the formation of a phase of non-freezable surface water. Moreover, also a strong temperature hysteresis is observed. Upon increasing the temperature the reappearance of the signal from bulk water occurs at a temperature close to 0 °C, as shown in Fig. 9b.
Benzene in C600
The interaction of guest molecules with pore surfaces depends strongly on the type of the guest molecules.70 As shown in the previous paragraphs, in the case of water as the guest, the molecule can act both as a donor or an acceptor of a hydrogen bond. Thus, the interactions among the molecules and of the molecules and the surface are dominated by hydrogen bonding interactions, in particular with silanol groups in the case of silica supports. In the case of an aromatic guest molecule like benzene, however, the main intermolecular interaction is the π–π stacking interaction.28,71 Owing to these various types of possible interactions, different guest molecules can probe the properties of the material surfaces. For benzene in C600 one can assume that the main interaction is with the graphitic parts of the carbon surface, which also has an aromatic structure. In addition, there may also be weak hydrogen bonding like interactions of the silanol groups with the ring center of the benzene molecules.Fig. 10 shows the 1H NMR spectra of various amounts of benzene (2 μl, 7 μl, 12 μl) adsorbed on C600. As the lowest filling volume, a value of 2 μl was chosen. Comparing the total area of 2 μl of monolayered benzene (5.7 m2, respectively 14.5 m2, depending on the cross-sectional area used for the benzene) with the specific area of 24 mg of C600 (12.6 m2) calculated from BET it can be considered that just a monolayer is formed by this adsorption. At this filling level a relatively broad signal in the range from 6 ppm to 3 ppm is visible in the spectrum. Compared to the standard value for bulk benzene (7.3 ppm), this corresponds to a high-field shift of 1–4 ppm of the benzene molecules inside the pores. This observation clearly shows that the benzene molecule experiences a similar ring current effect from the carbon surface as the water molecules discussed above. To explain the equivalence of the ring current for all protons a rotation of the benzene molecules parallel to the graphite layer is assumed. Such rotation is well known for bulk benzene72 and benzene in other porous media,73 and was discussed by Ueno et al.30 who calculated the motion of benzene molecules over the microporous activated carbon.
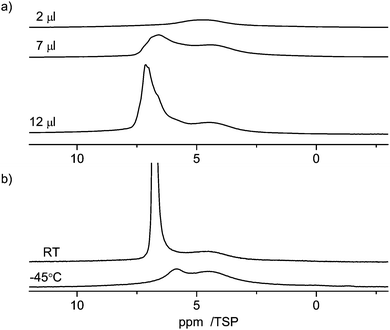 | ||
| Fig. 10 1H MAS NMR spectra at 10 kHz spinning speed of benzene in C600 (a) at room temperature (RT) with different loadings between 2 and 12 μl, and (b) at variable temperature. | ||
The large line width of the signal may result from two different effects: (i) inhomogeneities of the carbon surface which yield a distribution of chemical shifts and (ii) interactions of the benzene with the surface which lead to a partial anisotropy of the motion of the benzene molecules that creates intramolecular residual dipolar couplings among the protons of the benzene molecule.
When the amount of benzene is increased to 7 μl or 12 μl a strong asymmetric signal of bulk benzene at ca. 7 ppm is observed in addition to the broad monolayer signal at 1–4 ppm. Both signals are broad, which indicates an exchange effect with an intermediate rate between bulk and surface species.
At −45 °C (note: melting point of bulk benzene is 5 °C), the intensity of the signal from surface benzene molecules is kept the same and the intensity of bulk benzene large-scale dropped and shifted to a higher field as seen in Fig. 10. This spectrum also shows a broad signal at 4.4 ppm indicating the presence of non-freezable species on the surface. The mechanism of the freezing process of benzene in carbon pores seems to be similar to the freezing–melting process of benzene inside the silica material as measured by 2H NMR.73 The benzene molecules were almost divided into two groups during the freezing–melting process: the ordered molecules on the surface and the amorphous ones in the pore center. Herein, the interaction of benzene with the carbon surface is stronger than that of benzene with silica since silica materials are strongly hydrophilic. Therefore, it is reasonable that the surface layer of benzene molecules is better ordered on the carbon surface according to the surface properties.
Pyridine in C600
Pyridine, which is similar in structure to benzene, has two different possibilities to interact with the surface. On the one hand, owing to its aromatic character it can form π–π stacking interactions with the surface, which cause it to lie flat on the aromatic carbon surfaces. On the other hand, pyridine is an acceptor for hydrogen bonding and can form hydrogen bonds with surface hydrogen donors.74,75Fig. 11 shows the 1H NMR spectra of various amounts of pyridine (1 μl, 3 μl, 6 μl and 10 μl) adsorbed on C600. As the lowest filling volume, a value of 1 μl was chosen. Comparing the total area of 1 μl of monolayered pyridine (1.9 m2, mentioned above) with the specific area of 27 mg of C600 (14 m2) calculated from BET it can be assumed that just a monolayer is formed by this adsorption.
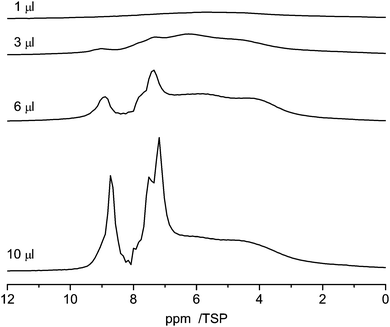 | ||
| Fig. 11 1H NMR spectra recorded at 10 kHz spinning speed of pyridine in C600 for different loadings between 1 μl and 10 μl. | ||
With 1 μl of loading, the spectrum of pyridine adsorbed on C600 (Fig. 11) shows one broad signal including the signals from all non-equivalent protons. This observation is very similar to the former one where benzene was adsorbed. This behavior is also supported by previous simulations.28 In addition the reduced motion of the pyridine caused by hydrogen bonding interactions contributes to the large chemical shift distribution of the protons from 10 ppm to 2 ppm.
With increasing loading of the sample two signal groups in the aromatic region between 7 and 9 ppm appear which are assigned to bulk pyridine which is present next to the adsorbed pyridine.
Aromaticity of carbon materials
To characterize the aromaticity of the mesoporous carbon surface, the chemical shift difference Δδ between the molecule in the bulk phase δbulk and the molecule adsorbed on the carbon material δC can be used as an indication as shown in ref. 10.The results regarding water and benzene are summarized in Table 2. The largest Δδ value is found for water molecules in the C800 sample. This observation refers to the large graphitic surface unit and a low concentration of surface functional groups in the C800 sample. Both of them result in stronger ring current effects which increase the aromaticity.
| Sample | Guest molecule | δ bulk | δ C | Δδ | Average |
|---|---|---|---|---|---|
| a Δδ = δbulk − δC is an indication of aromaticity of the mesoporous carbon surface.10δbulk is the proton chemical shift of the guest molecule in the bulk phase. δC is the proton chemical shift of the guest molecule in carbon materials. | |||||
| C600 | Water | 4.7 | 1.1 | 3.6 | 3.9 |
| 0.8 | 3.9 | ||||
| 0.4 | 4.3 | ||||
| C800 | Water | 4.7 | −2.8 | 7.5 | 8.1 |
| −4.0 | 8.7 | ||||
| C_SiO2 | Water | 4.7 | 3.0 | 1.7 | 1.7 |
| C600 | Benzene | 6.9 | 4.4 | 2.1 | 2.1 |
In the C600 material, the protons in benzene had a less high-field shift, 2.1 ppm, compared to that of the proton in the surface water molecule (3.9 ppm). This could be caused by the difference in the distance of the protons in the two molecules, which means that the water molecule is closer to the surface than the benzene molecule. A detailed analysis of this result would necessitate molecular dynamics simulations, which are beyond the scope of the present paper.
Computational results
We calculated 1H Nucleus Independent Chemical Shift (NICS) maps for hexabenzocoronene, an aromatic graphene like structure, as an example of structures that might be found in an aromatic amorphous carbon. One calculation (Fig. 12, left) has been performed in a large cell to avoid artifacts stemming from the periodic boundary conditions that are employed during the calculations. This situation resembles an isolated structure. The second calculation (Fig. 12, right) used a smaller periodicity of 1.5 nm perpendicular to the surface, resembling an infinite stack of molecules. This situation would be closer to the structures found in an aromatic confinement, resulting in an increased high-field shift between the molecules compared to the isolated case. The NICS maps show a strong influence of the aromatic structure, namely a high-field shift of >−1 ppm between the stacked molecules and up to −4 ppm in 2 Å distance to the molecule.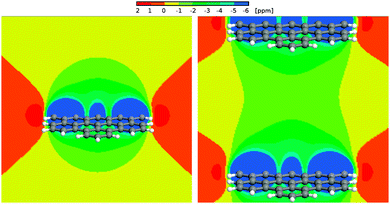 | ||
| Fig. 12 Left panel: 1H NICS maps of a hexabenzocoronene molecule. Right panel: 1H NICS maps of a periodic stack of hexabenzocoronene molecules with an intermolecular distance of 15 Å. | ||
Bulk water exhibits a 1H chemical shift of 4.8 ppm. It was shown before that this value strongly decreases in the proximity of the surface of, e.g., a silica confinement.76,77 For the extreme case of an isolated water molecule, water vapor, experiments show proton chemical shifts of ca. 1.0 ppm.78 In the proximity of the aromatic surface this would then, depending on the actual distance to the surface, be high-field shifted by 2–4 ppm. Even in the center between the periodic surfaces, a shift by more than −1 ppm can be observed. This results in (isolated) water proton chemical shifts of −0.5 (center) to −2.5 ppm (2 Å to the wall) depending on the distance to the surface, and δ < 0.5 ppm even in the center between two aromatic molecules.
Summary and conclusion
Mesoporous carbon materials were synthesized employing polymers and silica gels as structure directing templates. Their basic properties were probed by electron microscopy, nitrogen adsorption, and 1H and 13C MAS solid-state NMR spectroscopy. They were used as host-materials for the investigation of carbon–guest molecule interactions. For this, small guest molecules, such as water, benzene and pyridine, were adsorbed inside the pores and their properties monitored by solid state MAS NMR spectroscopy. The interactions of the guest molecules were found to be strongly dependent on the carbonization temperature and the pathway of the synthesis. In particular the interaction of water with the inner pore surface was very interesting. At low water concentrations a layer of non-freezable water was formed. All water molecules in this layer exhibited relatively high chemical shift values, indicating that basically all water molecules are bound at the primary and secondary adsorption sites60,61 of the carbon materials. Similar results were found for the proton shifts of benzene and pyridine molecules, which revealed that they are adsorbed on the carbon surface mainly via π–π-stacking interactions, which cause them to lay flat on the surface. The pore structure strongly influences the surface properties of carbon materials when the materials were carbonized at the same temperature by comparison of the adsorption properties of water in the C800 and C_SiO2 samples. For the carbon materials prepared by the same method, the surface properties depend on the carbonization temperature, although they have the same pore size distributions. The theoretical calculation shows that the high-field shift of the proton over the aromatic surface depends on the distance between the proton and the surface.Acknowledgements
We thank Dr Christoph Boettcher from the Forschungszentrum für Elektronenmikroskopie, FU Berlin, for the TEM-measurements. Financial support from the Deutsche Forschungsgemeinschaft in the research group FOR 1583 contracts Bu-911/18-1 and Se-1008/8-1 is gratefully acknowledged.References
- J. Lee, J. Kim and T. Hyeon, Adv. Mater., 2006, 18, 2073–2094 CrossRef CAS PubMed.
- R. Ryoo, S. H. Joo, M. Kruk and M. Jaroniec, Adv. Mater., 2001, 13, 677–681 CrossRef CAS.
- A. Dandekar, R. T. K. Baker and M. A. Vannice, Carbon, 1998, 36, 1821–1831 CrossRef CAS.
- V. M. Gun'ko, V. V. Turov, O. P. Kozynchenko, D. Palijczuk, R. Szmigielski, S. V. Kerus, M. V. Borysenko, E. M. Pakhlov and P. P. Gorbik, Appl. Surf. Sci., 2008, 254, 3220–3231 CrossRef CAS PubMed.
- R. Leboda, V. V. Turov, W. Tomaszewski, V. M. Gun'ko and J. Skubiszewska-Zieba, Carbon, 2002, 40, 389–396 CrossRef CAS.
- V. V. Turov, V. M. Gun'ko, R. Leboda, T. J. Bandosz, J. Skubiszewska-Zieba, D. Palijczuk, W. Tomaszewski and S. Zietek, J. Colloid Interface Sci., 2002, 253, 23–34 CrossRef CAS PubMed.
- N. S. Polyakov, M. M. Dubinin, L. I. Kataeva and G. A. Petuhova, Pure Appl. Chem., 1993, 65, 2189–2192 CrossRef CAS.
- V. M. Gun'ko, O. P. Kozynchenko, V. V. Turov, S. R. Tennison, V. I. Zarko, Y. M. Nychiporuk, T. V. Kulik, B. B. Palyanytsya, V. D. Osovskii, Y. Ptushinskii and A. V. Turov, Colloids Surf., A, 2008, 317, 377–387 CrossRef CAS PubMed.
- R. Ryoo, S. H. Joo and S. Jun, J. Phys. Chem. B, 1999, 103, 7743–7746 CrossRef CAS.
- V. V. Turov and R. Leboda, Adsorpt. Sci. Technol., 1998, 16, 837–855 CAS.
- R. K. Harris, T. V. Thompson, P. Forshaw, N. Foley, K. M. Thomas, P. R. Norman and C. Pottage, Carbon, 1996, 34, 1275–1279 CrossRef CAS.
- R. S. Vartapetyan, A. M. Voloshchuk, M. M. Dubinin, J. Karger and H. Pfeifer, Bull. Acad. Sci. USSR, Div. Chem. Sci. (Engl. Transl.), 1985, 34, 2241–2245 CrossRef.
- R. K. Harris, T. V. Thompson, P. R. Norman and C. Pottage, J. Chem. Soc., Faraday Trans., 1996, 92, 2615–2618 RSC.
- F. Cosnier, A. Celzard, G. Furdin, D. Begin, J. F. Mareche and O. Barres, Carbon, 2005, 43, 2554–2563 CrossRef CAS PubMed.
- P. Kim and S. Agnihotri, J. Colloid Interface Sci., 2008, 325, 64–73 CrossRef CAS PubMed.
- M. Sliwinska-Bartkowiak, M. Jazdzewska, L. L. Huang and K. E. Gubbins, Phys. Chem. Chem. Phys., 2008, 10, 4909–4919 RSC.
- S. H. Mao, A. Kleinhammes and Y. Wu, Chem. Phys. Lett., 2006, 421, 513–517 CrossRef CAS PubMed.
- S. Ghosh, K. V. Ramanathan and A. K. Sood, Europhys. Lett., 2004, 65, 678–684 CrossRef CAS.
- P. Cabrera-Sanfelix and G. R. Darling, J. Phys. Chem. C, 2007, 111, 18258–18263 CAS.
- B. Collignon, P. N. M. Hoang, S. Picaud and J. C. Rayez, Chem. Phys. Lett., 2005, 406, 430–435 CrossRef CAS PubMed.
- S. Picaud, B. Collignon, P. N. M. Hoang and J. C. Rayez, Phys. Chem. Chem. Phys., 2008, 10, 6998–7009 RSC.
- E. V. Khozina, R. S. Vartapetyan and D. S. Idiyatullin, Russ. Chem. Bull., 2002, 51, 2036–2043 CrossRef CAS.
- R. K. Harris, T. V. Thompson, P. R. Norman, C. Pottage and A. N. Trethewey, J. Chem. Soc., Faraday Trans., 1995, 91, 1795–1799 RSC.
- L. M. Dickinson, R. K. Harris, J. A. Shaw, M. Chinn and P. R. Norman, Magn. Reson. Chem., 2000, 38, 918–924 CrossRef CAS.
- M. C. Bellissent-Funel, J. Phys.: Condens. Matter, 2001, 13, 9165–9177 CrossRef CAS.
- M. R. Smith, S. W. Hedges, R. LaCount, D. Kern, N. Shah, G. P. Huffman and B. Bockrath, Carbon, 2003, 41, 1221–1230 CrossRef CAS.
- B. B. Marosfoi, A. Szabo, G. Marosi, D. Tabuani, G. Camino and S. Pagliari, J. Therm. Anal. Calorim., 2006, 86, 669–673 CrossRef CAS PubMed.
- Y. Ueno, Y. Muramatsu, M. M. Grush and R. C. C. Perera, J. Phys. Chem. B, 2000, 104, 7154–7162 CrossRef CAS.
- P. Kowalczyk, E. A. Ustinov, A. P. Terzyk, P. A. Gauden, K. Kaneko and G. Rychlicki, Carbon, 2004, 42, 851–864 CrossRef CAS PubMed.
- Y. Ueno and Y. Muramatsu, Carbon, 2000, 38, 1939–1942 CrossRef CAS.
- G. R. Birkett and D. D. Do, J. Phys. Chem. C, 2007, 111, 5735–5742 CAS.
- T. Yamaguchi, H. Hashi and S. Kittaka, J. Mol. Liq., 2006, 129, 57–62 CrossRef CAS PubMed.
- C. B. Minella, I. Lindemann, P. Nolis, A. Kiessling, M. D. Baro, M. Klose, L. Giebeler, B. Rellinghaus, J. Eckert, L. Schultz and O. Gutfleisch, Int. J. Hydrogen Energy, 2013, 38, 8829–8837 CrossRef PubMed.
- P. V. Schleyer, C. Maerker, A. Dransfeld, H. J. Jiao and N. J. R. V. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS.
- P. V. Schleyer, H. J. Jiao, N. J. R. V. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670 CrossRef CAS.
- Z. F. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- B. Kirchner and D. Sebastiani, J. Phys. Chem. A, 2004, 108, 11728–11732 CrossRef CAS.
- C. Corminboeuf, T. Heine, G. Seifert, P. V. Schleyer and J. Weber, Phys. Chem. Chem. Phys., 2004, 6, 273–276 RSC.
- P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223 RSC.
- S. Pelloni and P. Lazzeretti, J. Phys. Chem. A, 2011, 115, 4553–4557 CrossRef CAS PubMed.
- D. Moran, F. Stahl, H. F. Bettinger, H. F. Schaefer and P. V. Schleyer, J. Am. Chem. Soc., 2003, 125, 6746–6752 CrossRef CAS PubMed.
- D. Sebastiani, ChemPhysChem, 2006, 7, 164–175 CrossRef CAS PubMed.
- D. Sebastiani and K. N. Kudin, ACS Nano, 2008, 2, 661–668 CrossRef CAS PubMed.
- A. Putrino, D. Sebastiani and M. Parrinello, J. Chem. Phys., 2000, 113, 7102–7109 CrossRef CAS PubMed.
- D. Sebastiani and M. Parrinello, J. Phys. Chem. A, 2001, 105, 1951–1958 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS.
- S. Tanaka, N. Nishiyama, Y. Egashira and K. Ueyama, Chem. Commun., 2005, 2125–2127 RSC.
- Q. Y. Hu, J. B. Pang, N. Jiang, J. E. Hampsey and Y. F. Lu, Microporous Mesoporous Mater., 2005, 81, 149–154 CrossRef CAS PubMed.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619 CrossRef CAS.
- L. G. Joyner, E. P. Barrett and R. Skold, J. Am. Chem. Soc., 1951, 73, 3155–3158 CrossRef CAS.
- E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef CAS.
- A. S. Lekomtsev and I. V. Chernyshev, J. Struct. Chem., 2003, 44, 852–858 CrossRef CAS.
- H. H. Hsing and W. H. Wade, J. Colloid Interface Sci., 1974, 47, 490–498 CrossRef CAS.
- S. Suzuki, H. Onishi, K. Fukui and Y. Iwasawa, Chem. Phys. Lett., 1999, 304, 225–230 CrossRef CAS.
- K. S. W. Sing, Pure Appl. Chem., 1982, 54, 2201–2218 CrossRef.
- M. Nakahara and C. Wakai, Chem. Lett., 1992, 809–812 CrossRef CAS.
- S. Y. Qi, K. J. Hay and M. J. Rood, J. Environ. Eng., 1998, 124, 1130–1134 CrossRef CAS.
- N. J. Foley, K. M. Thomas, P. L. Forshaw, D. Stanton and P. R. Norman, Langmuir, 1997, 13, 2083–2089 CrossRef CAS.
- H. H. Limbach, P. M. Tolstoy, N. Pérez-Hernández, J. Guo, I. G. Shenderovich and G. S. Denisov, Isr. J. Chem., 2009, 49, 199–216 CrossRef CAS.
- M. A. L. Marques, M. d'Avezac and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125433 CrossRef.
- H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512–7515 CrossRef CAS.
- H. Schubert, Kapillarität in porösen Feststoffsystemen, Springer-Verlag GmbH, 1982 Search PubMed.
- W. F. H. G. W. H. Höhne, H.-J. Flammersheim, Differential Scanning Calorimetry, Springer-Verlag, 2003 Search PubMed.
- G. Buntkowsky, H. Breitzke, A. Adamczyk, F. Roelofs, T. Emmler, E. Gedat, B. Grünberg, Y. Xu, H. H. Limbach, I. Shenderovich, A. Vyalikh and G. H. Findenegg, Phys. Chem. Chem. Phys., 2007, 9, 4843–4853 RSC.
- J. Bodurka, A. Gutsze, G. Buntkowsky and H.-H. Limbach, Z. Phys. Chem., 1995, 190, 99 CrossRef CAS.
- D. R. Kinney, I. S. Chuang and G. E. Maciel, J. Am. Chem. Soc., 1993, 115, 6786–6794 CrossRef CAS.
- M. Werner, N. Rothermel, H. Breitzke, T. Gutmann and G. Buntkowsky, Isr. J. Chem., 2014, 54, 60–73 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS PubMed.
- J. H. Ok, R. R. Vold, R. L. Vold and M. C. Etter, J. Phys. Chem., 1989, 93, 7618 CrossRef CAS.
- E. Gedat, A. Schreiber, J. Albrecht, T. Emmler, I. Shenderovich, G. H. Findenegg, H. H. Limbach and G. Buntkowsky, J. Phys. Chem. B, 2002, 106, 1977–1984 CrossRef CAS.
- E. Gedat, A. Schreiber, G. Findenegg, I. Shenderovich, H.-H. Limbach and G. Buntkowsky, Magn. Reson. Chem., 2001, 39, S149–S157 CrossRef CAS PubMed.
- I. Shenderovich, G. Buntkowsky, A. Schreiber, E. Gedat, S. Sharif, J. Albrecht, N. S. Golubev, G. H. Findenegg and H. H. Limbach, J. Phys. Chem. B, 2003, 107, 11924–11939 CrossRef CAS.
- B. Gruenberg, T. Emmler, E. Gedat, I. Shenderovich, G. H. Findenegg, H. H. Limbach and G. Buntkowsky, Chem. – Eur. J., 2004, 10, 5689–5696 CrossRef CAS PubMed.
- X. Y. Guo, T. Watermann, S. Keane, C. Allolio and D. Sebastiani, Z. Phys. Chem., 2012, 226, 1415–1424 CrossRef CAS.
- J. C. Hindman, J. Chem. Phys., 1966, 44, 4582–4592 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2014 |