Dissolution of NaCl nanocrystals: an ab initio molecular dynamics study

Abstract

The dissolution of NaCl has been systematically investigated by employing ab initio molecular dynamics (AIMD) on different NaCl nanocrystals as well as on a surface system immersed in water. We discovered a complex dissolution process simultaneously involving multiple ions initiated at the corner sites of the crystal. Our simulations indicated a difference in the dissolution rates of sodium and chlorine. While sodiums readily became partially solvated, chlorines more frequently transitioned into the fully solvated state leading to an overall greater dissolution rate for Cl. We determined that this difference arises due to faster water mediated elongations of individual ionic bonds to Na, but a significantly slower process for the last bond in comparison to Cl. In an attempt to investigate this phenomenon further, we performed metadynamics based free energy simulations on a surface slab presenting corner sites similar to those in cubic crystals, aiming to extract the dissolution free energy profile of corner ions. In qualitative agreement with the nanocrystal simulations, this revealed a shallower first free energy minimum for Na, but no statistically significant difference in the corresponding barriers and inconclusive results for the latter stage. Finally, simulations of smaller NaCl crystals illustrated how dissolution proceeds beyond the point of crystal lattice collapse, highlighting the strength of solvated ion interactions.

---

1 Introduction

The dissolution of alkali halides, e.g. ordinary salt (NaCl), is one of the most fundamental chemical processes playing a vital role in, for instance, atmospheric chemistry.¹ Specifically, NaCl dissolution has been linked to the generation of chlorine, which can subsequently oxidise volatile organic compounds to form ozone in the troposphere.^1,2 Of even higher importance are the dissolved ion solutions, demonstrated, for example, by the fact that important biological processes, such as protein folding,³ occur in electrolyte solutions with aqueous sodium and chlorine as the main ionic constituents. While the dissolution process of NaCl has been well characterized at the macroscopic level, represented by quantities such as solubility and dissolution enthalpy, the exact molecular dissolution mechanism and the kinetics involved in this process remain unsolved. Understanding of the microscopic phenomena in NaCl dissolution would not only provide insight into the dissolution of other ionic solids, but it would also have a profound impact on our understanding of the water–ion interaction – key in a vast range of applications.

The solid–liquid interface between NaCl and water has been tackled with a variety of experimental techniques. Surface probing methods, such as atomic force microscopy (AFM), have been utilized to study wetting phenomena on NaCl surfaces and nanocrystals under a range of relative humidities below the deliquescence limit. The subjects explored include water orientation and step movements on the surface, tribological properties and dissolution.^4–10 Recent advances in frequency-modulation AFM have enabled the atomic scale imaging of hydrated ionic surfaces, e.g. calcite, in true liquid environments.^11–15 Additionally, similar studies on the NaCl–water interface have been conducted employing X-ray, infra-red, transmission electron microscopy, and mobility analysing techniques.^16–22 These studies provide valuable insight into the interfacial boundary, revealing, for instance, that dissolution is initiated at the sites of least coordination, i.e. corner sites or edge sites in case no corner sites are present. However, the resolution of the employed methods is insufficient to shed light on the elementary dissolution stages of individual ions.

On the other hand, atomistic computer simulations provide a natural means to study the molecular level events in dissolution. To this end, the effective potential governing the dissociation of a NaCl ion pair has been well characterized employing both forcefield-based (classical) and ab initio molecular dynamics (AIMD) as well as Monte Carlo simulations.^23–30 These studies reveal standard classical models to be over bonding compared to ab initio methods, even though the use of inter ionic distance as the reaction coordinate has been questioned due to neglect of solvent effects.^31,32 Moreover, the solvation structure of individual ions, either as cluster calculations of the form X(H₂O)_n, where X = Na or Cl, or as bulk water calculations, has been widely studied with ab initio simulations.^23,33–42 The results show excellent correspondence with experimental results obtained from neutron diffraction or X-ray photoabsorption spectroscopy measurements (see discussion in ref. 33). Recently, free energy sampling methods were used to examine the initial dissolution steps of Na and Cl on a defected NaCl(001) surface system indicating a clear difference between ions and between ab initio and classical models.⁴³ The dissolution of NaCl nanocrystals has also been explored, to some extent, with forcefield-based methods;^44–48 however, there is a definite demand for a more rigorous AIMD examination.

In this study, we present a systematic characterization of the initial steps of NaCl dissolution with ab initio molecular dynamics employing three NaCl nanocrystals of growing size together with a NaCl surface slab presenting corner ions similar to those in cubic crystals. Due to the inherently long time scales involved in ionic crystal dissolution being far beyond the reach of current AIMD simulations, we limit ourselves to the study of the dissolution initiating steps and discuss their significance for further stages of the process. We focus on analysing how corner ions of the largest crystal dissolve and describe the observed difference in the dissolution behaviour of Na and Cl based on water mediated bonding. Furthermore, to provide an energetic basis for the asymmetry, we perform metadynamics simulations on the surface slab to extract the free energy profile related to the dissolution process. Lastly, we employ smaller crystals to shed light on the overall dissociation process having progressed beyond the solvation of individual corner ions.

2 Computational details

2.1 Dissolution of NaCl nanocrystals

The hybrid Gaussian and plane waves (GPW) method was employed for the reported AIMD simulations as implemented in the CP2K/Quickstep⁴⁹ code. The exchange–correlation (XC) interaction of electrons was represented by the PBE⁵⁰ functional, while long range diffusive interactions were accounted for using the empirical van der Waals corrections of Grimme.⁵¹ These corrections have been shown to improve the structure, diffusivity, and density of water indicating their significance in condensed phase simulations,^52–54 granted no improvement is observed in the overstructuring of water with the PBE functional.⁵⁵ Electrons in the outermost electron shells of atoms were explicitly treated as valence electrons. The wave functions of valence electrons were expanded in terms of Gaussian functions by utilizing short-range, molecularly optimized, polarized, double ζ basis sets (MOLOPT-SR-DZVP).⁵⁶ This basis set has been demonstrated to produce accurate results compared to traditional, larger, polarized basis sets for a variety of molecules while being computationally efficient for condensed phase calculations.⁵⁶ The core electrons were represented with norm conserving Goedecker–Teter–Hutter (GTH)^57–59 pseudopotentials. The auxiliary plane wave basis set was truncated with a 280 Ry energy cutoff.

For sodium, various pseudopotential and plane wave cutoff combinations were tested prior to selecting the aforementioned combination by using a model system with a NaCl ion pair in vacuum. Due to some overlap of the 2s and 2p electrons with the 3s electron, a pseudopotential treatment of these semi-core electrons introduces the problem of nonlinear core correlation affecting, especially, the exchange–correlation energy.⁶⁰ This problem is often circumvented by treating the 2s and 2p electrons explicitly as valence electrons;⁶¹ however, it was noted that a much higher, 600 Ry, plane wave cutoff was necessary to reproduce the proper vibrational motion of the ion pair when describing Na with more valence electrons. Instead, a smoothing operator was used to smooth the electron density on the XC grid improving the accuracy of XC energy evaluation at the ionic cores.⁴⁹ Consequently, we find that both valence electron representations produce the same vibrational motion with a sufficient plane wave cutoff energy. Furthermore, increasing cutoff beyond 280 Ry with the one valence electron representation had no effect on the dynamics of the ion pair.

The ionic cores were propagated with ab initio molecular dynamics based on the Born–Oppenheimer⁶² assumption, within the canonical (NVT) ensemble at a constant temperature of 348.15 K. This temperature was chosen to reduce the effects of overstructuring present in DFT water,^63–65 especially, when employing the PBE functional.^33,52 Three linked Nose–Hoover thermostats^66,67 with a time constant of 200 fs⁻¹ were employed to maintain a constant temperature. The equations of motion were solved using the velocity Verlet algorithm⁶⁸ with a 1.0 fs time step. To facilitate this time step, water hydrogens were replaced by deuteriums also minimizing the effects of quantum hydrogen motion;⁶⁹ although, herein deuteriums will be referred to as hydrogens and deuterated water as water. Periodic boundary conditions were applied in all directions using cubic symmetry.

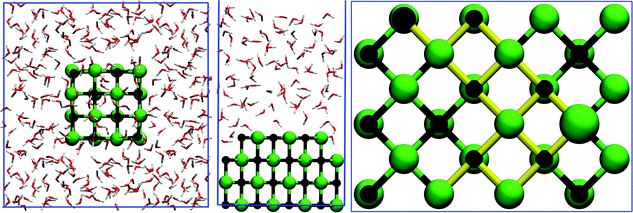
NaCl dissolution was studied using three different sized nanocrystals, where the number of ions on the edge of the cubic lattice was incrementally raised from two to four. These crystals are denoted small (8 ions), medium (27 ions), and large (64 ions) in the order of growing crystal size. Of these crystals, the medium crystal is charged due to an uneven number of ions in the lattice. In this study, only the negatively charged species, presenting chlorines at each corner site, was investigated. The crystals were constructed with the experimental lattice constant of 5.64 Å⁷⁰ as we obtained a calculated lattice constant within 2% of this value with the computational setup described earlier. The crystals were solvated by covering all facets with approximately 8.5 Å thick water layers corresponding to 229, 349, or 475 water molecules inside the simulation supercell, as shown in Fig. 1 for the largest system. The corresponding box vectors of the cubic simulation cells are 19.8 Å, 22.5 Å, and 25.5 Å. The systems were simulated for a total of 78, 100, and 160 ps, respectively.

Fig. 1 Initial configurations of the largest NaCl crystal (left) and the NaCl(001) surface system (side view in middle, top view at right) solvated in water. The black and green spheres correspond to Na and Cl, respectively. The size of ions has been increased for clarity. The vacuum layer above water in the surface system is not shown. The zigzag shaped top layer is indicated with yellow bonds while the size of corner-like ions within this layer has been further increased.

2.2 Solvation barrier calculations on the NaCl surface

To assess the energy barriers related to corner ion dissolution in a larger system, we employed a NaCl(001) surface slab with three complete and a zigzag shaped top layer inside a (4 × 3) supercell, as depicted in Fig. 1, similar to the set up of Michaelides et al.⁴³ The top layer presents both corner Cl and Na sites which closely resemble those of cubic crystals despite being slightly more stable due to higher coordination. The NaCl surface was covered by 95 water molecules corresponding to a 15 Å thick water layer with an additional 20 Å of vacuum placed on top of water, resulting in a final simulation cell of size 15.9 Å × 11.9 Å × 50.0 Å. Contrary to the nanocrystal simulations, both the valence and semi-core electrons of sodium were treated explicitly with basis functions. Accordingly, the plane wave cutoff energy was increased to 600 Ry to avoid introducing artefacts in the dynamics of ions (see discussion in Section 2.1 for details). The remaining computational parameters are identical to those employed in simulating NaCl nanocrystals.

Metadynamics⁷¹ was used to compute the free energy profile of corner ion dissolution by biasing two collective variables (CV), specifically, the height of the corner ion above the surface and the coordination number of the ion with respect to counter ions in the uppermost complete surface layer. Repulsive Gaussian potentials of 0.0002 a.u. height and 0.15 a.u. width were added in case either of the CVs had diffused over 0.225 a.u. and 100 AIMD steps had passed since the addition of the previous Gaussian. A new Gaussian was immediately spawned had 200 steps elapsed with no addition. Furthermore, the height CV in the Cl simulation was restrained to values below 7.25 Å using a harmonic potential with a 0.015 a.u. spring constant, since the ion was observed to irreversibly escape into water without the restraint. The validity of the present metadynamics setup has been established elsewhere.⁴³

Independent metadynamics simulations starting from the same configuration were initiated to study the dissolution of corner Na and Cl ions. The initial configuration was created by simulating the surface system for 15 ps with unbiased AIMD during which no ions were observed to dissolve. The length of the metadynamics runs were approximately 169 and 173 ps, respectively.

3 Results and discussion

3.1 Largest crystal

3.1.1 Distribution of ions. We begin by describing the initial dissolution steps of the largest NaCl crystal. To analyse the dissolution process, we compute the radial number density of ions with respect to the center of mass of the crystal by averaging the trajectory in 10 ps time intervals employing a bin width of 0.1 Å. In Fig. 2, number densities are plotted at different time windows of the dissolution process, where the legend entries correspond to the last frame of each averaging window. The ions closest to the center of mass, the core ions, have been omitted from this analysis as dissolution has not progressed to them in the simulated time frame. Initially, three distinct maxima can be distinguished from the 10 ps graphs, each corresponding to ions at different sites of the cubic crystal. The outermost maxima between 6.8–8.0 Å correspond to the corner ions of the crystal, while the maxima at 5.6–6.8 Å represent the ions adjacent to corner ions. We shall refer to these adjacent ions as edge ions. The remaining maxima stem from ions located next to edge ions on crystal facets, which in the following will be called facet ions.

Fig. 2 Averaged number densities of Na (top) and Cl (bottom) ions in select 10 ps long intervals of the trajectory. The legend entries correspond to the last frames of the respective averaging blocks. The insets show a magnification of the interval between 8 and 16 Å.

The number density graphs suggest a difference in the dissolution rates of Na and Cl. The peak initially representing corner sodiums has already flattened at 10 ps extending to values up to 11 Å, demonstrating that the ions are loosely bound to edge ions. In contrast, the corresponding Cl maximum remains distinct up to 90 ps. In spite of this, there is a positive chlorine density beyond a distance of 11 Å, approximately 40 ps sooner than for sodiums, see insets in Fig. 2. According to the trajectory, this density arises from solvated ions with no ionic bonds to the crystal, implying that this distance may be used to characterize dissolved corner ions. The heights of corner ion and counter edge ion peaks, e.g. corner Cl and edge Na, exhibit a correlation. As corner ions begin dissolving, the maximum corresponding to edge ions immediately starts flattening. Indeed, this is a clear indication that NaCl crystal dissolution is initiated at corner sites, where ions are the least coordinated, followed by edge ions, leading to an overall dissolution process progressing inwards from corners. Once again, we find evidence of differing dissolution rates exhibited by the faster flattening of the edge Na maximum compared to Cl. Furthermore, after 130 ps, the Na peak position begins shifting, indicating that each edge Na is dislodged from their original coordination sites. The dissolution of edge ions, in turn, initiates the dissolution process of facet ions seen as broadening of the corresponding maxima at the latter stages of the trajectory.

To assess the exact number of ions at different dissolution stages, we integrate the number density functions of Fig. 2 in five distance intervals 3.8–5.6, 5.6–6.8, 6.8–8.0, 8.0–11.0, and >11.0 Å. These intervals were chosen based on the original density maxima positions, as well as the different dissolution configurations observed whilst examining the number density graphs. The integrated ion counts at the corresponding time intervals are shown in Table 1. Additionally, to aid in distinguishing ions transitioning between dissolution stages, in Fig. 3, we plot the time evolution of the combined coordination number of ions originating from different crystal sites, which is normalized by the initial value of the quantity. With this normalization, the graph describes the portion of ionic bonds, on average, each ion loses to adjacent counter ions compared to the initial configuration where corner, edge, and facet ions are connected by 3, 4, or 5 bonds, respectively. As before, we have excluded core ions from both analyses.

Table 1 The number of sodium and chlorine ions within indicated distances (in Å) from the center of mass of the NaCl crystal at different time intervals of the trajectory. The values were obtained by integrating the respective number density graphs of Fig. 2

Time (ps)	Na					Cl
	3.8–5.6	5.6–6.8	6.8–8.0	8.0–11.0	>11.0	3.8–5.6	5.6–6.8	6.8–8.0	8.0–11.0	>11.0
10	12.0	10.8	3.0	2.1	—	12.0	10.9	4.7	0.4	—
50	12.1	11.3	2.8	1.8	—	12.0	10.9	3.8	1.3	—
90	12.0	8.4	4.9	2.7	—	12.0	9.3	4.0	1.7	1.0
130	11.5	5.7	7.2	2.6	1.0	11.1	8.4	2.8	4.4	1.2
160	10.6	4.5	8.3	3.0	1.6	10.8	5.9	4.0	5.2	2.1

---

Fig. 3 The combined coordination numbers of sodiums (top) and chlorines (bottom) originating from different sites of the crystal as a function of time. The graphs have been normalized by the initial value. See text for the definitions of the different crystal sites.

Together, the integrated ion count and combined coordination number clarify the observed difference in the dissolution rates of Na and Cl. The immediate flattening of the corner Na peak around 7.5 Å in Fig. 2 can be attributed to the partial solvation of two ions, based on the positive ion count at 8.0–11.0 Å. Moreover, this is seen as a sharp drop from 1.0 to 0.6 in the combined coordination number of corner sodiums, which corresponds to each ion losing, on average, 1.2 ionic bonds to edge ions. This transition is reversible, demonstrated by the increase in coordination at 35 ps. In contrast to Na, it takes roughly 40 ps for the first chlorine to transition into this state with no return events observed. Moreover, the stepped form of the graph linked with the steadily growing number of Cl beyond 8.0 Å suggests that the dissolution of corner chlorines primarily occurs ion-by-ion, whereas most corner sodiums immediately transit to a partially solvated state. Despite the faster initial solvation rate of Na, at the end of the trajectory we find more chlorines in the fully solvated state at a distance beyond 11 Å. Also, in total they have lost a larger portion of ionic bonds than sodiums, demonstrating corner chlorines to dissolve at a greater overall rate than Na. Consequently, edge sodiums begin dissolving prior to chlorines and, as expected, at a faster initial, but slower total rate, illustrated by the rate of change in the number of ions between 6.8–8.0 and 8.0–11.0 Å, which correspond to the partially and fully solvated states for edge ions, respectively. These analyses also reveal that the effect of dissolution is, in this time scale, modest on facet ions as only a small portion of ions have begun transitioning into solvated configurations.

The discovered dissolution mechanism simultaneously involving multiple ions results in significant deformations of the overall crystal structure, as illustrated in a series of snapshots in Fig. 4. Although the core structure remains unaffected, water incursion softens the corners of the crystal leaving most solvated ions close to the remaining crystal. These ions interact with adjacent ions complicating their dissolution process compared to the solvation of corner ions. Furthermore, as the total dissolution rate of Na and Cl differs, the process progresses differently at sodium and chlorine terminated corners. Indeed, this difference is clearly seen in Fig. 4 as more chlorines are fully solvated, which is reflected in our earlier discussion of number densities.

Fig. 4 A series of snapshots of the largest NaCl crystal at 10, 90, 130, and 160 ps (from left to right) of the AIMD simulation illustrating the effect of dissolution on the crystal. Sodiums and chlorines are represented by the black and green spheres, respectively. For clarity, water molecules have been omitted. The bonds between ions have been coloured based on the ion–ion distance. In the CIP configuration, the bond is black-green, while in the SSIP configuration, the bond is yellow. See text for definitions of these configurations.

3.1.2 Water mediated corner ion solvation. Here, we present a more detailed analysis of the solvation of corner ions aiming to understand the difference observed between dissolving Na and Cl, and to provide a molecular level description of corner ion dissolution. To this end, we analyse the elementary steps of dissolution and the role of water molecules in this process. We adopt the nomenclature widely used in describing the dissolution configurations of individual NaCl pairs, namely, the contact ion pair (CIP), solvent-separated ion pair (SSIP), and dissociating ion pair (DIP) configurations. Herein, we define the configurations based on ion–ion distance r according to CIP r ≤ 3.6 Å, SSIP 3.6 Å < r ≤ 6.0 Å, and DIP 6.0 Å < r ≤ 8.0 Å. These boundary values are in agreement with the reported range of transition states between the respective configurations 3.4–3.7, 5.8–6.0, and 8.0–8.5 Å.^23,24,37 Beyond 8.0 Å there is no bonding characteristic between ions, thus, an ion is considered to be dissociated only if the distance to the nearest ion exceeds this value, although the DIP configuration is at best very weakly bonded.^24,37 To provide a link to our earlier analysis of ion distributions, we note that the previously discussed solvated ions are factually characterized by configurations where some or all ionic bonds to the particular ions have elongated beyond the maximum distance of the CIP configuration.

In order to determine how water participates in the cleavage of ionic bonds, we employ the two definitions of Fig. 5 to describe ion pairs bridged by either one or two water molecules, denoted by W₁ and W₂ configurations, respectively. For two ions to be bridged by the same water molecule, the separation of Na and water oxygen has to be below 3.2 Å, while the separation of Cl and either of the water hydrogens below 2.8 Å. In the W₂ configuration, the same distances are used for determining the water molecules solvating each ion; additionally, the shortest O–H distance between unshared waters is computed, excluding hydrogen bonded with Cl, and given it is below 2.4 Å, the ions are considered bridged by two water molecules. These cutoffs were determined from the first intermolecular minima of the respective radial distribution functions (RDF), exhibiting excellent correspondence with previously reported values of 3.2 (Na–O), 2.9 (Cl–H),³³ and 2.5 Å (O–H).⁶⁴

Fig. 5 Distance definitions for single water (left), W₁, and two water (right), W₂, bridging. In the W₂ configuration, the hydrogen bond distance between unshared water molecules is computed for each O–H combination and the smallest value is compared to the cutoff. The hydrogen bonding with Cl is excluded from this calculation. The distance cutoffs were determined from the first minima of the respective intermolecular radial distribution functions.

The probability of single and two water bridging in different bonding configurations is presented in Table 2, calculated based on corner-edge ion pairs. As expected, the values separately calculated for sodiums and chlorines are in agreement with one another. Table 2 reveals the water bridging probability to be dependant on ionic separation. For W₁ bridging, we find that the probability reaches a maximum of approximately 70% in the SSIP configuration, with a bridging probability less than a third of this value in the CIP region and non-existent bridging beyond the SSIP configuration. The relatively low degree of single water bridging in CIP is consistent with water molecules mainly residing atop individual ions, instead of in-between ion pairs that is necessary for simultaneously bonding with adjacent ions. Moreover, this implies that the initial elongation of ionic bonds to corner ions requires the formation of single water bridges. On the other hand, W₂ bridging probability peaks in the DIP state with a value of around 60%, roughly doubling from configuration to configuration. Thus, single water bridging must change to two water bridging to facilitate the SSIP–DIP transition for an ion pair.

Table 2 The probability of single, W₁, and two water, W₂, bridging between corner and edge ion pairs in different bonding configurations for corner sodiums and chlorines. Standard deviations are given in parentheses. See text for definitions of bonding configurations

Configuration	Na			Cl
	W1	W2	Either	W1	W2	Either
CIP	0.20 (0.07)	0.27 (0.15)	0.41 (0.14)	0.23 (0.15)	0.25 (0.13)	0.40 (0.15)
SSIP	0.65 (0.18)	0.42 (0.21)	0.88 (0.05)	0.68 (0.18)	0.41 (0.20)	0.85 (0.13)
DIP	0.01 (0.02)	0.53 (0.31)	0.54 (0.28)	0.01 (0.01)	0.70 (0.13)	0.70 (0.12)

---

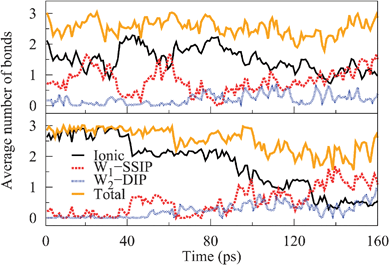
The high degree of water bridging in the SSIP and DIP configurations allows us to define two ions to be W₁–SSIP or W₂–DIP bonded in the case that their separation is within previously stated values for the respective configuration and the ions are W₁ or W₂ bridged, respectively. In Fig. 6, we present the number of different bonds to corner ions as a function of time averaged in 1 ps intervals and normalized by the number of ions. These graphs reveal the origin of the asymmetry observed for dissolving Na and Cl. Specifically, one or more ionic bonds to sodiums readily become elongated by single water bridging, whereas for chlorines this is less probable, proving the faster initial solvation rate of sodiums. Based on our earlier coordination number analysis, the drops in the number of ionic bonds to chlorines implies that each bond to a Cl elongates roughly simultaneously instead of a single bond elongating to each Cl. This decrease naturally correlates with a growth in the number of W₁–SSIP bonds, as illustrated, for instance, at 40 ps. For chlorines in the SSIP configuration, the dissolution process continues by the sequential elongation of W₁–SSIP bonds to W₂–DIP bonds, as seen e.g. at around 65 ps in Fig. 6. Importantly, the absolute number of bonds to chlorines decreases over time, which is indicative of some bonds being severed entirely or, equivalently, of some chlorines becoming fully dissociated. Furthermore, as the number of ionic bonds approaches zero, we may conclude that each chlorine is in fact fully solvated at the end of the trajectory. In contrast, most sodiums remain connected to the crystal in a partially solvated state throughout the trajectory – as the total number of bonds remains relatively constant, with each ion on average being bound by at least one ionic bond. Thus, the transition between partially and fully solvated states, which is characterized by no ionic bonds, occurs more rapidly for chlorines. Given that the overall dissolution rate of chlorines is greater, this step controls the kinetics of the dissolution process. We note that the slight variances introduced are a consequence of our definition of W₁–SSIP and W₂–DIP bonds, as the probability of finding water molecules in the correct orientation is not unity in the respective configurations.

Fig. 6 The average number of ionic, W₁–SSIP, and W₂–DIP bonds to corner sodiums (top) and chlorines (bottom) as a function of time. Also presented is the total number of bonds obtained by summing the individual graphs. The graphs have been averaged over an interval of 1 ps and normalized by the number of ions.

The differing transition rates of Na and Cl into the partially and fully solvated states would suggest an asymmetry in the energy barriers for transitions between configurations and the underlying effective potential at different corner sites. Particularly, they indicate the barrier for single CIP–SSIP transitions to be higher for Cl than Na, as demonstrated by the slower rate of transition into the partially solvated configuration. Furthermore, as most sodiums retain their last ionic bond, the barrier for the elongation of this bond ought to be higher than for earlier ones. The observed return events from SSIP to CIP for Na also suggest the return barrier to be smaller than the barrier for the final elongation. In contrast, we anticipate the reverse to hold for chlorines as full solvation is achieved, with greater probability once the first bond elongates. To provide insight into this matter, we next explore the subject fully, by presenting the results of free energy simulations of corner ion dissolution on a NaCl surface system.

3.2 Surface

We model the corner site of the cubic NaCl crystal with a more stable NaCl(001) surface, presenting a zigzag shaped top layer (see Fig. 1) in an attempt to quantify an energetic cause for the observed difference in the dissolution rates of corner chlorine and sodium. The free energy profiles of corner ion dissolution obtained by biasing the system with metadynamics are presented as a function of height from the surface in Fig. 7. The free energy profiles reveal the first minimum at 2.9 Å to be 3 kJ mol⁻¹ deeper for Cl compared to Na. A second energy minimum is located at approximately 4.0–5.0 Å with a transition state residing between the first two minima at a height of 3.7 Å. Analysis of the transition state shows that in this state only the bond between the corner ion and the ion directly beneath it has elongated; thus, this state corresponds to the transition state of the CIP–SSIP transition of the particular ion pair. The barrier heights relative to the CIP minimum are 6 kJ mol⁻¹ and 7 kJ mol⁻¹ for Na and Cl, respectively. This difference between barrier heights is below the error limit of metadynamics and arises from the limited number of samplings of the transition state, so that quantitatively the barriers for both ions are identical. Nevertheless, the initial dissolution properties of the ions can be compared based on the differences of the first free energy minimum; for both ions, the minimum is nearly filled despite the numerical noise. The validity of the present results is confirmed by comparison with an ab initio potential mean force (PMF) study of a NaCl ion pair dissociating in water, which reports a 5.9 kJ mol⁻¹ barrier height,²³ showing excellent agreement with the obtained barriers. On the other hand, the values significantly differ from the respective values of 29 kJ mol⁻¹ and 13 kJ mol⁻¹ obtained by Michaelides et al.,⁴³ employing the same NaCl surface slab. We note that the magnitudes of these values might be sensitive to the exact DFT setup, accounting for the difference from our results. Additionally, the computed barrier heights are about half of the those obtained from classical PMF simulations with various forcefields conforming with earlier comparisons of ab initio and classical data.^23,37

Fig. 7 The dissolution free energy profiles of corner Na and Cl as a function of ion height from the surface obtained with metadynamics. The tails of the free energy plots are dashed denoting their uncertainty, as the sampling in this region is insufficient to determine an estimate of the final solvation barrier.

Despite the barrier difference being small and assuming it to be accurate, transition state theory predicts the rate of elongations for the first ionic bond to be approximately 1.4 times larger for sodium than for chlorine given identical pre-exponential factors. Factually, we observed the difference to be more profound than that predicted based on our unbiased AIMD simulation of the NaCl crystal. More importantly, there is a substantial difference in the depths of the first minima, indicating that initially chlorine is more tightly bound to surface in comparison to Na, which further verifies the faster initial solvation of sodiums. We acknowledge that a proper kinetic study would provide a more comprehensive perspective on this matter, however, this is beyond the scope of this paper.

Due to the generality of the chosen biasing collective variables, the broad second minimum corresponds to many locally different bonding geometries. In the most sampled geometries, the corner ion resides in an elevated position with respect to the original corner site forming an elongated bond to the topmost complete surface layer facilitated by water bridging. There is more variance in the bonding between the corner ion and neighbouring counter ions within the zigzag shaped layer as the ion may either form an elongated and a normal length bond, or two elongated bonds to these ions. Here, the elongated bonds correspond to the W₁–SSIP bond. In addition to the mentioned geometries, irrelevant configurations to the dissolution process exist in the same minimum represented, for instance, by the artificial minimum at 5.0 Å of the Na free energy graph, where the ion has diffused to an entirely different site atop the complete layer. As the height of the ion increases to values beyond the second minimum, the ion is fully solvated with distances to closest counter ions being in the SSIP–DIP region. We find that the fully solvated Na and Cl are coordinated, on average, by 5.0 and 5.2 water molecules, respectively, which conform reasonably well with prior experimental and ab initio results.^33,40

While the various configurations where the ion remains at the corner site prove that dissolution can occur via many paths, they provide little insight into the underlying free energy surface since there are no unique minima beyond the first transition state. Therefore, no conclusive remarks can be drawn from either the barriers for the reverse SSIP–CIP transition of the first bond or the case of full solvation. This effectively prohibits us from further discussing the asymmetry observed in the dissolution kinetics of corner Na and Cl in the largest NaCl crystal.

3.3 Smaller crystals

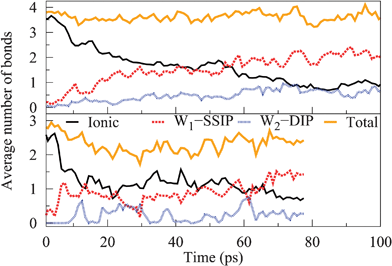
In the following, we move on to discuss the dissolution of smaller NaCl crystals to gain insight into the dissolution process beyond corner ion solvation. Both smaller NaCl crystals are treated together as they dissolve with a similar mechanism. We employ the same bonding characteristic analysis used in context of the largest crystal to describe the dissolution process of these crystals; however, here we apply the analysis collectively to all ions, as separate plots for Na and Cl are identical in shape with only the absolute values differing in the medium sized system due to an uneven number of ions. The average number of ionic, W₁–SSIP, and W₂–DIP bonds between ions are presented as a function of time for both systems in Fig. 8.

Fig. 8 The average number of ionic, W₁–SSIP, and W₂–DIP bonds between ions in the medium (top) and small (bottom) sized systems as a function of time. Also presented is the total number of bonds obtained by summing the individual graphs. The graphs for the smallest system terminate earlier due to a shorter simulation time scale.

Dissolution proceeds rapidly for both crystals denoted by the decrease in the number of ionic bonds stabilising at a level of approximately one bond for each ion and eventually slowly tending towards zero. Indeed, this indicates that neither crystal dissociates ion-by-ion; instead, in both cases the mechanism is best described as the total collapse of the cubic crystal structure. As expected, the degree of ionic bonding declines over a longer time period for the larger crystal due to size effects. Nevertheless, the high number of W₁–SSIP bonds, combined with only minor variances in the total number of bonds, indicates that most solvated ions remain connected through water mediated bonding. Specifically, the ions adopt a cluster arrangement where the degree of ionic bonding decreases out from the center of the cluster, as shown in Fig. 9 for the medium sized system.

Fig. 9 A representative snapshot of the medium sized NaCl cluster at 39.5 ps of the trajectory illustrating the ordering of ions after the crystal structure has collapsed. The bond and ion colouring schemes of Fig. 4 apply to this figure. Water molecules have been omitted to aid visualization.

The presence of a cluster of solvated ions causes the stabilisation in the number of ionic bonds, visible in Fig. 8, because total dissociation requires water molecules to break various ion arrangements, such as chains, rings, and their water bridged equivalents. This effect appears to be quite long term compared to the initial dissolution rate, suggesting that the local ordering of partially solvated ions may slow down dissolution, for instance, at the corner sites of larger crystals. Similar to the largest crystal, ions farthest from the core, the least coordinated, are the first to become fully solvated. Closer inspection of the trajectory reveals an additional contribution to the overall dissolution mechanism. Once enough water has penetrated the structure, the cluster starts degrading into smaller subclusters of ions with fewer bonds connecting each substructure. Consequently, we expect dissolution to proceed simultaneously through the full solvation of individual, less coordinated ions and the formation of increasingly many subclusters, ultimately resulting in total dissociation. This discussion applies to both smaller crystals although the ion cluster in the smallest system is naturally less complex than the one shown in Fig. 9 for the medium crystal. Here, we observe no difference between dissolving Na and Cl apart from more chlorines residing farther away from cluster cores. In the case of the medium crystal this is most likely a consequence of having only chlorines present at corner sites.

3.4 Microscopic crystals

In order to apply the observations of nanosized NaCl dissolution studied here to crystals of any size, in a related study⁷² we have characterized the ionic dissolution barriers of Na and Cl originating from different surface sites on a surface slab using AIMD and a constraint approach. These barriers are then used to develop a full kinetic Monte Carlo dissolution model that can be scaled up to almost any size and time. Here, we present a brief comparison of the results to demonstrate the connection of the modelling approaches at different scales.

As expected, it was determined that dissolution barriers decreased with the coordination of the ion in order of flat, edge, and corner sites with barriers of approximately 71, 23, and 13 kJ mol⁻¹, respectively. In accordance with the results of this study, a 3 kJ mol⁻¹ larger overall dissolution barrier was obtained for corner Na, with similar differences on other surface sites. Moreover, the constructed kinetic model predicted dissolution to proceed mainly through the rounding of corners, as indicated by our AIMD simulation of the largest crystal.

4 Conclusions

In summary, we have performed extensive ab initio molecular dynamics simulations on different NaCl systems in water, aiming to describe the initial dissolution mechanism of nanosized NaCl. As expected, we found that dissolution is initiated at corner sites. Importantly, our investigations revealed a difference in the dissolution rates of Cl and Na. Whereas sodiums were frequently witnessed moving between fully bound and partially solvated configurations, in the end more chlorines were found in the fully solvated state despite initially being more strongly bound. The origin of this behaviour was determined to be the greater probability of water mediated elongation of the last ionic bond connecting Cl to Na, which also was deduced to control the total dissolution rate. Metadynamics based free energy investigations on a NaCl surface system agreed with this behaviour, revealing a shallower first free energy minimum for corner Na with the energy barriers being identical within error limits. Due to problems with constructing unique reaction coordinates, we were unable to obtain a reliable energetic contribution for the rate determining step. The observation that chlorines dissolve at a higher overall rate is in accordance with the results of Michaelides et al.,⁴³ who report the final dissolution barrier of Na to be twice the Cl barrier, despite also showing a similar asymmetry for the initial barrier in contradiction with our results. Furthermore, the greater solvation free energy of Na^73,74 and the resulting more tightly bound solvation shell⁷⁵ support the faster initial solvation of sodiums. On the molecular level, we suggest that this behaviour manifests through the easier hydrogen-first movement of water molecules in between ion pairs necessary for bond cleavage, especially near multiple negative ions present at corner sites.

Following the initial dissolution of corner ions, we found a significant concentration of partially solvated ions at sites of subsequent dissolution, resulting in complex solvation processes simultaneously involving several ions. The importance of hydrated ion interactions was further highlighted in simulating smaller NaCl crystals, where the ordering of partially solvated ions hindered dissociation, despite a rapid collapse of the crystal lattice. We propose that experimental techniques with picosecond temporal resolution, such as ultrafast X-ray absorption spectroscopy,⁷⁶ should be able to detect these local ion clusters, providing a tool to pinpoint sites of dissolution in more macroscopic crystals. The absence of a clear ion-by-ion dissolution mechanism contradicts earlier classical simulations⁴⁶ that showed a sequential dissolution process of alternating Cl and Na. We believe this difference in mechanisms to be a direct consequence of the higher solvation barriers obtained using forcefields that have not been parametrized with ion interactions in mind. This causes an over-stabilization of the ionic crystal structure (see discussion in ref. 23 and 43). Additionally, it is our belief that the dissolution mechanism characterized herein might also be of importance in the dissolution of other ionic solids, where water mediated bonds are of comparable strength to ionic bonds.

Much remains to be resolved regarding the dissolution of crystalline NaCl. The underlying cause for the observed asymmetry for dissolving Na and Cl needs to be characterized more rigorously by devising a more appropriate sample system, with sufficient control on the process so the appropriate free energy landscape can be extracted. Ultimately, higher level quantum calculations might be required to fully explore this matter, as the solvation properties of ions³³ and, especially, the characteristics of liquid water have been shown to greatly depend on the choice of exchange–correlation functional (cf.ref. 64). Recently, Zhang et al.⁷⁷ have compared Cl solvation using a hybrid (PBE0) and a semilocal (PBE) functional; whereas the hybrid functional improved the energy gap between the ion HOMO and the valence band maximum of water, only minor changes in structural properties were observed. Similar studies with liquid water have shown that while the use of hybrid or van der Waals functionals generally betters the description of water, full agreement with experimental data in key structural properties, such as RDFs, is nonetheless not achieved, and the improvement is relatively minor when compared to simulations using temperature scaling to reduce the overstructuring of water.^65,78–80 These results indicate that while the present model might not be able to reproduce the dissolution mechanism in exact detail, it can be employed to accurately study ionic crystal dissolution, as the expected deviations are not significant. Nevertheless, there is a clear need for increased simulation lengths, as well as system sizes beyond scales currently attainable with ab initio techniques, thus, demanding classical molecular dynamics simulations with a forcefield that can accurately reproduce the interactions involved in ionic dissolution. In light of this, the recent forcefield implementation of Tazi et al.,⁸¹ which has specifically been derived for aqueous ionic systems, might present an interesting avenue for further research.

Acknowledgements

This research has been supported by the Academy of Finland through its Centres of Excellence Program project no. 251748 and through project no. 140115. Computational resources provided by CSC IT Centre for Science, Finland, are gratefully acknowledged.

References

1. B. J. Finlayson-Pitts, Chem. Rev., 2003, 103, 4801–4822.
2. W. R. Simpson, R. von Glasow, K. Riedel, P. Anderson, P. Ariya, J. Bottenheim, J. Burrows, L. J. Carpenter, U. Frieß, M. E. Goodsite, D. Heard, M. Hutterli, H. W. Jacobi, L. Kaleschke, B. Neff, J. Plane, U. Platt, A. Richter, H. Roscoe, R. Sander, P. Shepson, J. Sodeau, A. Steffen, T. Wagner and E. Wolff, Atmos. Chem. Phys., 2007, 7, 4375–4418.
3. L. M. Pegram, T. Wendorff, R. Erdmann, I. Shkel, D. Bellissimo, D. J. Felitsky and M. T. Record, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7716–7721.
4. S. Garcia-Manyes, A. Verdaguer, P. Gorostiza and F. Sanz, J. Chem. Phys., 2004, 120, 2963–2971.
5. M. Luna, F. Rieutord, N. A. Melman, Q. Dai and M. Salmeron, J. Phys. Chem. A, 1998, 102, 6793–6800.
6. S. Rozhok, P. Sun, R. Piner, M. Lieberman and C. A. Mirkin, J. Phys. Chem. B, 2004, 108, 7814–7819.
7. H. Shindo, M. Ohashi, O. Tateishi and A. Seo, J. Chem. Soc., Faraday Trans., 1997, 93, 1169–1174.
8. A. Verdaguer, G. M. Sacha, H. Bluhm and M. Salmeron, Chem. Rev., 2006, 106, 1478–1510.
9. A. Verdaguer, G. M. Sacha, M. Luna, D. F. Ogletree and M. Salmeron, J. Chem. Phys., 2005, 123, 124703.
10. L. Xu, H. Bluhm and M. Salmeron, Surf. Sci., 1998, 407, 251–255.
11. T. Fukuma, K. Kobayashi, K. Matsushige and H. Yamada, Appl. Phys. Lett., 2005, 87, 034101.
12. S. Rode, N. Oyabu, K. Kobayashi, H. Yamada and A. Kuhnle, Langmuir, 2009, 25, 2850–2853.
13. T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101.
14. H. Imada, K. Kimura and H. Onishi, Langmuir, 2013, 29, 10744–10751.
15. N. Kobayashi, S. Itakura, H. Asakawa and T. Fukuma, J. Phys. Chem. C, 2013, 117, 24388–24396.
16. J. Arsic, D. M. Kaminski, N. Radenovic, P. Poodt, W. S. Graswinckel, H. M. Cuppen and E. Vlieg, J. Chem. Phys., 2004, 120, 9720–9724.
17. G. E. Ewing, Chem. Rev., 2006, 106, 1511–1526.
18. M. C. Foster and G. E. Ewing, J. Chem. Phys., 2000, 112, 6817–6826.
19. U. Malaske, H. Pfnur, M. Bassler, M. Weiss and E. Umbach, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 13115–13120.
20. S. J. Peters and G. E. Ewing, J. Phys. Chem. B, 1997, 101, 10880–10886.
21. G. Biskos, A. Malinowski, L. M. Russell, P. R. Buseck and S. T. Martin, Aerosol Sci. Technol., 2006, 40, 97–106.
22. M. E. Wise, S. T. Martin, L. M. Russell and P. R. Buseck, Aerosol Sci. Technol., 2008, 42, 281–294.
23. J. Timko, D. Bucher and S. Kuyucak, J. Chem. Phys., 2010, 132, 114510.
24. M. K. Ghosh, S. Re, M. Feig, Y. Sugita and C. H. Choi, J. Phys. Chem. B, 2012, 117, 289–295.
25. A. Kovalenko and F. Hirata, J. Chem. Phys., 2000, 112, 10391–10402.
26. J. Marti and F. S. Csajka, J. Chem. Phys., 2000, 113, 1154–1161.
27. Z. S. Zidi, Chem. Phys., 2005, 123, 064309.
28. D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757.
29. P. Jungwirth, J. Phys. Chem. A, 1999, 104, 145–148.
30. E. Guardia, R. Rey and J. A. Padro, Chem. Phys., 1991, 155, 187–195.
31. P. L. Geissler, C. Dellago and D. Chandler, J. Phys. Chem. B, 1999, 103, 3706–3710.
32. A. J. Ballard and C. Dellago, J. Phys. Chem. B, 2012, 116, 13490–13497.
33. A. Bankura, V. Carnevale and M. L. Klein, J. Chem. Phys., 2013, 138, 014501.
34. C. Krekeler, B. Hess and L. D. Site, J. Chem. Phys., 2006, 125, 054305.
35. L. Ge, L. Bernasconi and P. Hunt, Phys. Chem. Chem. Phys., 2013, 15, 13169–13183.
36. L. X. Dang, G. K. Schenter, V.-A. Glezakou and J. L. Fulton, J. Phys. Chem. B, 2006, 110, 23644–23654.
37. I. V. Khavrutskii, J. Dzubiella and J. A. McCammon, J. Chem. Phys., 2008, 128, 044106.
38. D. J. Miller and J. M. Lisy, J. Am. Chem. Soc., 2008, 130, 15393–15404.
39. S. Obst and H. Bradaczek, J. Phys. Chem., 1996, 100, 15677–15687.
40. S. Varma and S. B. Rempe, Biophys. Chem., 2006, 124, 192–199.
41. D. Feller, E. D. Glendening, D. E. Woon and M. W. Feyereisen, J. Chem. Phys., 1995, 103, 3526.
42. J. Zhou, X. Lu, Y. Wang and J. Shi, Fluid Phase Equilib., 2002, 194–197, 257–270.
43. L.-M. Liu, A. Laio and A. Michaelides, Phys. Chem. Chem. Phys., 2011, 13, 13162–13166.
44. H. Ohtaki, N. Fukushima, E. Hayakawa and I. Okada, Pure Appl. Chem., 1988, 60, 1321–1324.
45. H. Ohtaki and N. Fukushima, Pure Appl. Chem., 1989, 61, 179–185.
46. Y. Yang, S. Meng and E. G. Wang, J. Phys.: Condens. Matter, 2006, 18, 10165.
47. R. Bahadur, L. M. Russell, S. Alavi, S. T. Martin and P. R. Buseck, J. Chem. Phys., 2006, 124, 154713.
48. A. Y. Zasetsky, J. J. Sloan and I. M. Svishchev, J. Phys. Chem. A, 2008, 112, 3114–3118.
49. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
51. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
52. J. Schmidt, J. VandeVondele, I. F. W. Kuo, D. Sebastiani, J. I. Siepmann, J. Hutter and C. J. Mundy, J. Phys. Chem. B, 2009, 113, 11959–11964.
53. I. C. Lin, A. P. Seitsonen, M. D. Coutinho-Neto, I. Tavernelli and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 1127–1131.
54. R. Jonchiere, A. P. Seitsonen, G. Ferlat, A. M. Saitta and R. Vuilleumier, J. Chem. Phys., 2011, 135, 154503.
55. I. C. Lin, A. P. Seitsonen, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2012, 8, 3902–3910.
56. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
57. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
58. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
59. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
60. S. G. Louie, S. Froyen and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 1738–1742.
61. L.-M. Liu, M. Krack and A. Michaelides, J. Chem. Phys., 2009, 130, 234702.
62. M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484.
63. J. VandeVondele, F. Mohamed, M. Krack, J. Hutter, M. Sprik and M. Parrinello, J. Chem. Phys., 2005, 122, 014515.
64. H.-S. Lee and M. E. Tuckerman, J. Chem. Phys., 2006, 125, 154507.
65. T. Todorova, A. P. Seitsonen, J. Hutter, I. F. W. Kuo and C. J. Mundy, J. Phys. Chem. B, 2005, 110, 3685–3691.
66. S. Nose, J. Chem. Phys., 1984, 81, 511–519.
67. S. Nose, Mol. Phys., 1984, 52, 255–268.
68. W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649.
69. J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 017801.
70. CRC Handbook of Chemistry and Physics, ed. D. R. Lide and H. P. R. Frederikse, CRC Press, Inc., 75th edn, 1994.
71. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
72. J.-C. Chen, B. Reischl, N. Holmberg, A. Foster and K. Laasonen, 2014, unpublished manuscript.
73. Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999.
74. G. Hummer, L. R. Pratt and A. E. García, J. Phys. Chem., 1996, 100, 1206–1215.
75. K. D. Collins, G. W. Neilson and J. E. Enderby, Biophys. Chem., 2007, 128, 95–104.
76. C. Bressler and M. Chergui, Chem. Rev., 2004, 104, 1781–1812.
77. C. Zhang, T. A. Pham, F. Gygi and G. Galli, J. Chem. Phys., 2013, 138, 181102.
78. M. Guidon, F. Schiffmann, J. Hutter and J. VandeVondele, J. Chem. Phys., 2008, 128, 214104.
79. C. Zhang, D. Donadio, F. Gygi and G. Galli, J. Chem. Theory Comput., 2011, 7, 1443–1449.
80. C. Zhang, J. Wu, G. Galli and F. Gygi, J. Chem. Theory Comput., 2011, 7, 3054–3061.
81. S. Tazi, J. J. Molina, B. Rotenberg, P. Turq, R. Vuilleumier and M. Salanne, J. Chem. Phys., 2012, 136, 114507.

---