Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Central-transition double-quantum sideband NMR spectroscopy of half-integer quadrupolar nuclei: estimating internuclear distances and probing clusters within multi-spin networks†
Andreas
Brinkmann
*a and
Mattias
Edén
b
aMeasurement Science and Standards, National Research Council Canada, 1200 Montreal Road, M-40, Ottawa, Ontario K1A 0R6, Canada. E-mail: Andreas.Brinkmann@nrc-cnrc.gc.ca
bPhysical Chemistry Division, Department of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, 106 91 Stockholm, Sweden
First published on 21st February 2014
Abstract
We introduce a strategy to estimate the size of clusters of recoupled homonuclear half-integer quadrupolar nuclei under magic-angle spinning (MAS) conditions, by combining double-quantum (2Q) sideband NMR experiments with an approximate numerical analysis based on the summation of all spin-pairs present over a given radius of the structure. The experiment relies solely on the evolution of homonuclear 2Q coherences (2QC) among the central-transitions (CT) of half-integer spins and is suitable for probing clusters in network structures, such as those encountered in large groups of oxide-based materials. Experimental 11B, 23Na and 27Al NMR results are presented on bis(catecholato)diboron, Na2SO4 and Al2O3, respectively; in each case, the growth of the spin-cluster size was monitored from a series of experiments that employed progressively lengthened 2QC excitation intervals. Our new approach is the first option for probing larger constellations of half-integer spins; it provides similar information as the “multiple-quantum spin counting” experiment, which is well-established for spin-1/2 applications but has hitherto not been demonstrated for half-integer spins undergoing MAS. We also discuss various options for determining the internuclear distance within a (nearly) isolated pair of half-integer spins by comparing the experimental 2Q sideband NMR spectra with results from numerical simulations involving various degrees of approximation.
1 Introduction
Precise interatomic-distance information constitutes the core of a detailed understanding of a given molecular structure, and is generally best determined by diffraction methods. However, whenever the possibility of obtaining large and well-ordered crystals is not feasible, either because the structure lacks long-range order or feature dynamics within its sub-units, solid state nuclear magnetic resonance (NMR) spectroscopy offers an attractive alternative. The power of high-resolution magic-angle spinning (MAS) NMR that utilizes distance-dependent through-space dipolar interactions restored by “dipolar recoupling” techniques1–5 is well documented for providing highly accurate information about selected internuclear distances4,6 and dihedral angles7–12 in well-defined clusters of spin-1/2 nuclei—primarily involving 1H, 13C and 15N in bio-molecules. This is generally arranged by site-specific isotopic labeling, which is feasible thanks to the combination of well-established synthetic routes and the low natural abundance of 13C and 15N. Recent progress in dipolar recoupling NMR methodology is gradually also permitting the simultaneous accurate extraction of increased numbers of internuclear distances in uniformly (13C, 15N)-enriched biological macromolecules.4Yet, comparatively few distance-determinations involving homonuclear (i.e., of the same species) spins-1/2 are demonstrated in the large groups of inorganic network structures, e.g., minerals, ceramics, glasses and porous materials, where the nature of the structures implies very large networks of mutually coupled spins. Further, the state-of-affairs is much worse when considering even semi-quantitative internuclear distance-estimates between half-integer spin quadrupolar nuclei,13–15 despite a strong impetus for exploiting them for structural studies by NMR, stemming from their dominating abundance in inorganic materials.14,16 Owing to their multi Zeeman-level character and the presence of strong quadrupolar interactions, the development of homonuclear dipolar recoupling methodology targeting half-integer spins is a complex task, as reviewed in ref. 14 and 15. Yet, during the past decade, several alternatives have been proposed.15,17–31 However, these recoupling techniques, including dipolar self-recoupling under MAS32,33 and experimentation on non-spinning samples,34–36 have predominantly been applied for gaining qualitative information about connectivities, proximities, and distributions of homonuclear spins, or relative orientations of NMR interaction tensors,15,17–19,22–28,30,31,37–44 whereas present reports on direct internuclear distance-estimates remains very sparse.20,21,45,46 Furthermore, recent work exploits homonuclear through-bond (“J”) interactions among half-integer spins to gain information about site-connectivities in inorganic structures.47–49
All existing strategies to directly measure internuclear distances via their associated dipolar interactions within homonuclear pairs of half-integer spins undergoing MAS, have relied on double-quantum (2Q) dipolar recoupling radio-frequency (rf) pulse sequences. The magnetization may either (i) be allowed to evolve under their resulting effective dipolar Hamiltonian,20,21 or be converted into 2Q coherences (2QC) among the central transitions (CTs) of the two spins, onwards referred to as “2QCT”. The latter option has involved either (ii) monitoring of the 2QCT generation (which is directly dependent on the dipolar interaction-strength) for prolonged excitation intervals (τexc),45 or (iii) using 2Q–1Q 2D correlation spectroscopy, which results in an internuclear distance-sensitive spinning sideband manifold if the t1-evolution is sampled faster than at completed rotational periods.46 Strategy (iii) was introduced by Spiess and co-workers as a general means of determining NMR interaction-parameters in systems involving at least one spin-1/2.6,50–54 All three approaches to interatomic distance-measurements have been applied extensively in the area of spins-1/2, which possesses a very substantial arsenal of 2Q-recoupling schemes (reviewed in ref. 1–4), whereas much fewer such options exist for half-integer spins.15,19,22,24,26–31
In ref. 46, we introduced CT 2Q sideband NMR spectroscopy to the realm of half-integer spins: we demonstrated its potential by employing a simple analysis for extracting the internuclear distance in the pair of 11B spins in bis(catecholato)-diboron (with a relative uncertainty of 2%), in excellent accordance with the value obtained by single crystal X-ray diffraction (XRD).55 Herein, we refine and justify this distance-estimate by accounting for effects from longer-range intermolecular dipolar interactions, by employing numerically exact simulations involving up to four coupled 11B (spin I = 3/2).
Yet, isolated pairs of quadrupolar spins are rarely encountered in inorganic systems. We therefore also explore the CT 2Q NMR sideband technique further in the context of the densely coupled networks of 23Na (I = 3/2) and 27Al (I = 5/2) in anhydrous sodium sulfate (Na2SO4) and α-Al2O3, respectively. We demonstrate that a recently introduced general strategy for modeling the NMR spectrum from a multi-spin system—that approximates the intractable exact calculation of the large spin-system by a summation of the responses from each spin-pair in the structure over a given radius56—successfully reproduces the experimental 2QCT spinning sideband manifold from each of the two model structures. The sideband envelope depends on the product of the dipolar coupling constant (bjk) and the 2QC reconversion interval (τrec) employed following the 2QCT evolution.6,50–54 Hence, given that a series of experiments is recorded for increasing τexc = τrec, and the known atomic coordinates of the structure are used to calculate the 2D NMR spectrum for each τexc-value, our new method constitutes an alternative to existing “spin-counting” NMR techniques57–64 for determining the relationship between the cluster-size of mutually interacting spins and the recoupling interval τexc.
2 Double-quantum sideband NMR spectroscopy
2.1 Experimental protocol
Fig. 1 displays the rf pulse scheme for the CT 2Q sideband NMR experiment. It starts by enhancing the spectral signal-to-noise ratio by increasing the population-difference across the CT:39 here, we employ a smoothly attenuated single frequency sweep,46,65 but any alternative technique is equally applicable, e.g., those of ref. 66–69. The longitudinal magnetization is subsequently converted into 2QCT, in this work by repeating a R212R2−12 2Q-recoupling sequence26m times to arrange a 2QC excitation interval of τexc = 4mτr, where the sample rotational period τr relates to the angular spinning frequency ωr as τr = 2π/ωr. This pulse scheme conforms to the R-symmetry class,2,3,70 and requires that the spin-I CT nutation frequency ωCTnut = (I + 1/2)|γI|B1/2 equals ωCTnut = ωr/2, where γI is the spin gyromagnetic ratio and B1 the rf amplitude. All recoupling pulses are sandwiched between two CT-selective π/2-pulses, each of duration τsel90, as discussed in detail in ref. 26, 27 and 29. While we recommend using the R212R2−12 scheme for 2QCT-excitation in samples displaying relatively low resonance-frequency dispersions,27,29 the CT 2Q sideband experiment may utilize any 2QCT generator for half-integer spins,22,24,27–31 or supercycles thereof. The pulse trains described in ref. 27, 29 and 30 are beneficial for cases featuring large frequency-spreads among the recoupled spin sites. Next follows a Hahn spin-echo of duration T, timed such that T + 2τsel90 = pτr, where p is any even integer; the phase-cycling71 of the CT-selective π-pulse should retain solely the ±2QCT → ∓2QCT pathways to block 2QC involving the satellite transitions (STs),24 as indicated in Fig. 1c.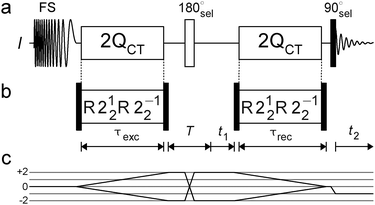 | ||
| Fig. 1 (a) General radiofrequency pulse sequence to record two-dimensional homonuclear double-quantum correlation spectra on half-integer quadrupolar nuclei for the purpose of 2QCT sideband spectroscopy. The block labeled “2QCT” represents any pulse sequence generating central transition 2Q coherences. A frequency sweep (FS) may be used to enhance the central transition population difference. (b) The pulse sequence R212R2−12 (ref. 26) is specifically used in this work for 2QCT excitation. The subscript “sel” indicates central-transition-selective pulses. (c) Coherence transfer pathway diagram71 for the I-spins. | ||
In the absence of t1-evolution, the 2QCT coherences are transferred directly into detectable CT single-quantum coherences (1QC) by repeating the π/2-sandwiched R212R2−12 sequence for a reconversion interval τrec, followed by a CT-selective π/2-pulse (Fig. 1a). While one may arrange that τexc ≠ τrec,72 herein we employ equal excitation and reconversion segments throughout all our experiments. However, when t1 > 0, the incrementation of the evolution interval has strong bearings on the 2Q–1Q 2D NMR spectrum. When internuclear proximity-information is desired, t1 is normally sampled at integer multiples of τr,24,26–28,30,39,41,56 which ensures that the rotor position is identical at the start of each τexc and τrec event, thereby forcing all spinning sidebands to fold onto each respective centerband (“isotropic”) frequency: the 2D spectral coordinates then reveals all unique 2QCT frequencies ω2Qjk along the indirect (vertical) dimension, correlated with their respective CT 1QC frequencies ωj and ωk that appear along the direct (horizontal) spectral dimension.
However, if the t1-incrementation is performed in steps smaller than τr, a spinning sideband formation occurs along the indirect spectral dimension. It typically originates from two distinct mechanisms: (i) Rotor-modulation, stemming from 2QCT-evolution under anisotropic interactions, produces sidebands at positions shifted by pωr (p is any integer) from the centerband frequency. They are well-known and become significant in all MAS NMR experimentation when the magnitude(s) of the anisotropic interaction(s) exceed the spinning frequency. (ii) Rotor-encoded spinning sidebands, on the other hand, only appear at odd integer multiples of ωr, and arise if the spatial sample position is different at the start of each 2QC excitation and reconversion segment.6,50–54 These sideband-intensities are essentially independent on the relative sizes of the MAS frequency and the chemical shift and quadrupolar anisotropies active during the evolution interval t1, provided that rotor-modulated contributions are eliminated by employing fast MAS. However, the precise appearance of the rotor-encoded sideband-envelope depends on the product bjkτexc = bjkτrec, which provides a route to measure the dipolar coupling constant bjk,6,50–54 related as rjk−3 to the internuclear separation rjk between spins j and k. We exploit this feature to estimate internuclear distances between half-integer spins,46 as explored further herein. There are two options for implementing the t1-sampling in Fig. 1a, which have bearings both on the experimental time and the precise numerical protocol to extract information from the rotor-encoded sidebands:
(1) The protocol in Fig. 1a is used to record a complete 2Q–1Q 2D NMR spectrum by sampling the evolution period over a ms-range, i.e., over many rotational periods of the sample. This is required to achieve sufficient signal-resolution in the presence of several distinct spin-pairs in the structure.
(2) The evolution interval is only sampled over the first rotational period, i.e., at N time-points tj1 = jτr/N, with j = 0, 1,…, N − 1, which in practice is implemented as an array of N 1D NMR experiments. This approach is only beneficial when the sample produces one unique 2QCT frequency, but is then highly advantageous for reducing the experimental time (as well as that for the numerical simulations discussed below), as the 2QCT spinning sideband manifold results directly on Fourier transformation (with respect to t1) of the “pseudo-2D” data-set {S(tj1, t2 = 0)}; these values are in practice obtained by integrating the total intensity along the ω2 spectral dimension for each consecutive tj1-value. Similar approaches have been utilized both for numerical simulations of MAS NMR experiments (e.g., see ref. 73), and in several experimental NMR protocols, such as for spin-counting57–64 and molecular torsion-angle determinations.7
Implementation (1) was used for the bis(catecholato)-diboron sample and protocol (2) was employed for the samples Na2SO4 and α-Al2O3. The 2QCT sideband manifold along the ω1 dimension will be depicted by a “stick-spectrum”, where the height of each stick reflects the respective integrated sideband intensity, plotted against the sideband order k.
2.2 Strategies for extracting inter-atomic distances and spin-cluster sizes
(A) The rare case when the internuclear separation within an isolated pair of half-integer spins is to be determined. Such spin systems may feature one internuclear distance rjk that is much shorter than all others; a typical scenario is a spin-pair within a molecular unit where the crystal structure involves an ordered arrangement of such units. This case may be handled by directly fitting the experimental data to numerically exact spin-pair simulations.46 Even for structures built from separate molecular units, truly isolated spin-pairs are extremely rare due to intermolecular dipolar interactions. This will be expanded on in Section 4.1, where we explore the consequences of including longer-range intermolecular couplings, and hence the deviation from a truly “isolated” 11B–11B pair, for determining of the B–B interatomic distance in the bis(catecholato)-diboron molecule.
In scenario (B) of a large continuous spin network, for which the CT 2Q sideband NMR experiment will create a significant number of recoupled spin-pairs, the size of such a spin-I cluster grows for increasing τexc. Then a large number of distinct spin-pairs associated with a spread in rjk-values contributes to the sideband pattern of the CT 2Q experiment. The measurement of a “single distance” is then not a well-defined concept for such cases, and one must simultaneously determine the large number of distances associated with the entire set of individual spin-pairs. Accurate numerical simulations cannot address this task due to the substantial time required to calculate the NMR spectrum from even a few dipolar coupled I = 3/2 spins, and the prohibitive scaling of the computation time for higher-spin numbers. Numerically exact simulations accounting for more than four coupled spins-3/2 appears presently intractable by using standard computer resources, at least if employed for the purpose of iterative fitting to experimental data. Hence, one must resort to approximating the complex spin dynamics, as well as lower the ambition level from extracting multiple internuclear distances to just defining the spin cluster size. Here we employ the strategy of ref. 56, which amounts to first calculating the NMR spectrum from each unique spin-pair in the structure over given radius R—onwards denoted the “cut-off distance”—followed by summation over all contributing spectra. Note that whereas each spin-pair is treated numerically exact, the procedure ignores all cross-couplings between spins of distinct pairs and their mutual interferences. Despite invoking a crude approximation that may not in general be justified rigorously, this strategy allowed for the successful determination of the absolute orientations of all 23Na quadrupolar tensors in Na2SO3;56 further validation of the approach is gained from the results presented in Section 4.1.
For each pair jk of unique crystallographic sites, all dipolar coupling constants and their accompanying orientations are extracted from the (known) crystal structure: firstly, the primitive unit cell is build from its corresponding asymmetric unit. Secondly, the central unit cell is extended into an odd order supercell, e.g. 3 × 3 × 3 or 5 × 5 × 5. Finally, all dipolar interactions from crystallographic sites in the central unit cell to sites in the same, as well as to surrounding, unit cells are located and sorted according to the relative absolute values of their dipolar coupling constants, i.e., by the corresponding internuclear distances. In the analysis below, dipolar interactions are considered up to the cut-off distance R. The corresponding minimum dipolar coupling constant is denoted by b(R) = −(μ0/4π)γI2ℏR−3. Dipolar interactions that are related by translational symmetry are considered equivalent. Each of the inequivalent dipolar couplings is a member of one set of M(bjk) symmetry-related couplings, where M(bjk) is referred to as the dipolar multiplicity:56 all dipolar interactions within this set are associated with the same magnitude of bjk, but differ in their orientations in the crystal structure. Concrete examples of this approach are provided in Sections 4.1–4.3 for the samples used in this study.
Next, the NMR spectrum for each dipolar vector is calculated: it may represent either the entire 2Q–1Q 2D correlation NMR spectrum or its ω1-projection, depending on which underlying t1-sampling approach is used (Section 2.1). This computation also involves all relevant chemical shift and quadrupolar interaction parameters, whose values must be a priori known. In general, all M(bjk) members that feature a fixed value of the dipolar coupling constant bjk may be divided into N(bjk) subsets. The NMR spectrum generated from each subset is distinct from that of any other subset, meaning that there are N(bjk) unique (i.e., distinct) spectra. In contrast, all dipolar coupling orientations within a given subset produce identical NMR spectra, owing to additional symmetries in the NMR responses.38,56 Then explicit simulations must only be performed for one sole dipolar vector orientation from each of the N(bjk) subsets. The resulting set of dipolar coupling parameters is denoted {(bjk, ΩDDjk,i)}, with the index i running over all distinct subsets; i = 1,…, N(bjk). The corresponding individual simulated spectra are labeled Sjk(ω1, ω2; τexc, bjk, ΩDDjk,i). With this approach the computation time reduces by the factor M(bjk)/N(bjk).56
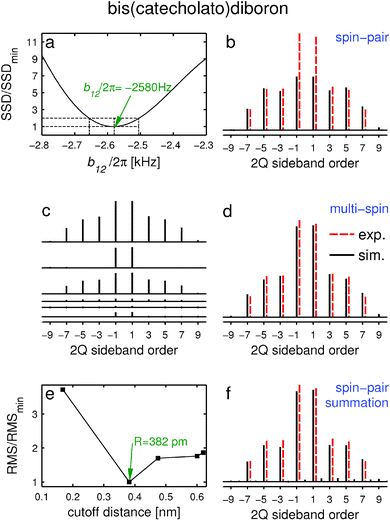
The NMR spectrum SRsum(ω1, ω2; τexc) that is representative of the entire spin system—the latter being defined by the τexc-dictated radius R—is constructed by summing all individual contributions Sjk(ω1, ω2; τexc, bjk, ΩDDjk,i), while considering their respective dipolar multiplicities:56
 | (1) |
3 Materials and methods
3.1 Solid-state NMR experiments
All experiments were performed at a static magnetic field of B0 = 11.75 T using a Bruker Avance-III spectrometer. The sample of bis(catecholato)diboron was studied at a 11B Larmor frequency (−γIB0) of −160.5 MHz in a Varian 3.2 mm double-resonance standard-bore Varian MAS probehead.46 The powder of bis(catecholato)diboron was purchased from Sigma-Aldrich and was spun at 25 kHz. This corresponds to an rf field of 6.25 kHz during dipolar recoupling, i.e., to a CT nutation frequency equal to half the MAS frequency,26 as for the HORROR condition.20,21,74 The CT selective 90° and 180° pulses operated at 9.0 kHz rf field amplitude. Complete 2D nutation experiments were performed to calibrate all rf amplitudes. To enhance the CT population difference, a single-frequency sweep (SFS)46 of 2 ms duration was performed at the same rf field-strength, by using an rf frequency offset and a sweep bandwidth of 500 kHz and 800 kHz, respectively, where the beginning and end of the sweep-pulse shape were attenuated by a sin2 and cos2 function, respectively. The States-TPPI scheme was employed to obtain 2D pure absorption lineshapes and for distinguishing positive and negative 2Q coherences.75,76The experiments on the Na2SO4 sample were performed on a 3.2 mm double-resonance standard-bore Varian MAS probehead at a 23Na Larmor frequency of −132.3 MHz and a spinning frequency of 20 kHz. The rf field during the 2QCT-recoupling was set to 5 kHz. The CT selective 90° and 180° pulses operated at 7.151 kHz. The CT population was enhanced by a SFS of 2 ms duration at the same rf field strength, 550 kHz rf offset and 900 kHz bandwidth, where the beginning and the end of the sweep where attenuated, as described above.
Prior to the NMR experiments, the sample of Al2O3 was heated to 1360 °C for 96 h to ensure a phase-pure α-Al2O3 specimen, which was confirmed by a directly excited 27Al MAS NMR spectrum. The NMR experiments were performed on a 4 mm double-resonance standard-bore Varian MAS probehead at a 27Al Larmor frequency of −130.3 MHz and a spinning frequency of 10 kHz. The rf field during the 2QCT-recoupling was set to 1.674 kHz. The CT selective 90° and 180° pulses operated at 980 Hz. The CT population was enhanced by a SFS of 2 ms duration at 2.577 kHz rf field strength, 500 kHz rf offset and 800 kHz bandwidth, as described above.
3.2 Numerical spin dynamics simulations
The numerical simulations of the 11B, 27Al and 23Na 2QCT sideband patterns were performed by using either the SIMPSON package (version 3.0.1)77 or software developed in Stockholm.27,41,56 The simulations invoked the experimental parameters listed in Section 3.1. All pulses were explicitly accounted for, except for the CT population enhancement and the 90° read pulse. Both the initial density operator and the detection operator represented CT z-magnetization. The CT 2QC were selected by nulling all other elements in the density matrix before and after the 180° spin-echo pulse. The CT 2Q sideband amplitudes were simulated by incrementing t1 in N steps of duration τr/N, with N equal to 35, 35 and 16 for the simulations involving 11B, 27Al and 23Na, respectively. The results of the separately calculated time-dependent signal amplitudes of the +2QC and −2QC were combined to form “cosine” and “sine” NMR signal components required by the procedure of States et al.75 The resulting complex t1-signal was subjected to a complex Fourier transformation to obtain the integrated CT 2Q spinning sideband amplitudes. Powder averaging was accomplished using a set of 6044 triplets of Euler angles selected according to the ZCW scheme.78–80 In all cases, we used the respective experimentally estimated values of the quadrupolar coupling constant and asymmetry parameter listed in Table 1. In case of bis(catecholato)diboron, the parameters of the CSA tensor and the orientation of the quadrupolar tensor as calculated by GIPAW-DFT were employed in the numerical simulations. Both for α-Al2O3 and Na2SO4 the experimentally estimated value of the anisotropic chemical shift and asymmetry parameter were used together with the corresponding tensor orientations obtained by GIPAW-DFT calculations.| Sample | Experiment | DFT calculations | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C Q [MHz] | η Q | δ iso [ppm] | δ aniso [ppm] | η | Ref. | C Q [MHz] | η Q | Ω QPM [°] | σ iso [ppm] | δ aniso [ppm] | η | Ω CSAPM [°] | Ref. | |
| C12H8B2O4 | 2.71 | 0.745 | 28.6 | — | — | 46 | 3.18 | 0.77 | {38.7, 86.2, −135.0} | −67.1 | −22.6 | 0.67 | {−38.9, 95.0, 49.1} | 46 |
| Na2SO4 | 2.6 | 0.6 | −8.5 | −18.9 | 0.0 | 37 and 98 | −3.20 | 0.60 | {−31.4, 66.5, −166.4} | −562.3 | −10.8 | 0.78 | {−61.5, 86.1, −2.1} | This work |
| α-Al2O3 | 2.40 | 0.0 | 18.8 | 17.3 | 0.0 | 99 | 2.29 | 0.0 | {0, 0, 0} | 538.1 | 7.90 | 0.0 | {0, 0, 0} | This work |
3.3 Quantum chemical calculations
For the GIPAW-DFT calculations of the quadrupolar and chemical shift tensors CASTEP81 and CASTEP-NMR82–84 (version 4.4) were used together with Accelrys' Materials Studio. The generalized gradient approximation with the Perdew–Burke–Ernzerhof exchange correlation functional85 and “on-the-fly” pseudo-potentials were chosen. In all cases the plane wave cutoff energy was selected to be 550 eV. In case of bis(catecholato)diboron the k-point grid was set to 5 × 2 × 4. Starting from the structure determined by single-crystal XRD,55 initially, only the proton positions were optimized, whereupon the NMR parameters were calculated.46 In case of Na2SO4 the conventional orthorhombic unit cell of the single-crystal structure86 was converted to the primitive unit cell prior to the DFT calculations employing a 5 × 5 × 5 k-point grid. For α-Al2O3 the conventional hexagonal unit cell of the structure determined by single-crystal XRD87 was converted to the primitive unit cell prior to the DFT calculations with a 6 × 6 × 6 k-point grid.4 Results
4.1 The 11B–11B pair in bis(catecholato)diboron (I = 3/2)
We recently demonstrated that CT 2Q sideband NMR spectroscopy allowed for accurately determining the internuclear distance in the pair of directly bonded boron atoms in bis(catecholato)diboron by iterative fitting of numerically exact 11B–11B two-spin simulations to experimental results, i.e., using approach (A) in Section 2.2.1.46Nevertheless, despite a favorable accuracy and precision in the estimated distance, these two-spin simulations deviated systematically in their lowest-order (±1) sideband amplitudes relative to their experimental counterparts, despite that all higher-order sideband amplitudes agreed well.46 Here we analyze the source of these discrepancies further by employing numerically exact multi-spin simulations (comprising up to 4 spins) to account for the contributions from weaker intermolecular 11B–11B dipolar couplings between neighboring molecules, whose inclusion will be shown to provide excellent agreement with the experimental sideband patterns. Indeed, Holland et al. reported similar effects of intensified low-order sideband amplitudes in the context of 1H NMR, and attributed them to the presence of distributions of dipolar-coupling strengths.88 We further demonstrate that the relatively effortless summation of sideband NMR spectra from a larger set of spin-pairs (i.e., strategy (B) in Section 2.2.1) reproduce the results from the rigorous multi-spin analysis. Noteworthy, the estimated internuclear distance of the directly bonded B–B pair remains largely unaffected by the approach for numerical analysis.
Fig. 2a shows the structure of a single bis(catecholato)diboron molecule together with the principal axis systems of the 11B chemical shift and quadrupolar tensors as obtained by GIPAW-DFT calculations.46Fig. 2b displays the nearest neighboring molecules in the crystal structure, where the four boron sites in closest spatial contact are labeled by 1–4. From the XRD structure55 the internuclear distances are determined to rXRD12 = 168 pm, rXRD23 = rXRD14 = 382 pm and rXRD13 = rXRD24 = 475 pm. The corresponding 11B–11B dipolar coupling constants are given by bXRD12/2π = −2619 Hz, bXRD23/2π = −222 Hz and bXRD13/2π = −116 Hz. Note that the intramolecular coupling constant of the directly bonded (1,2) boron sites is ≈12 times larger than the second largest intermolecular counterpart. In ref. 46 we therefore analyzed the experimental CT 2Q spinning sideband amplitudes by solely employing spin-pair simulations.
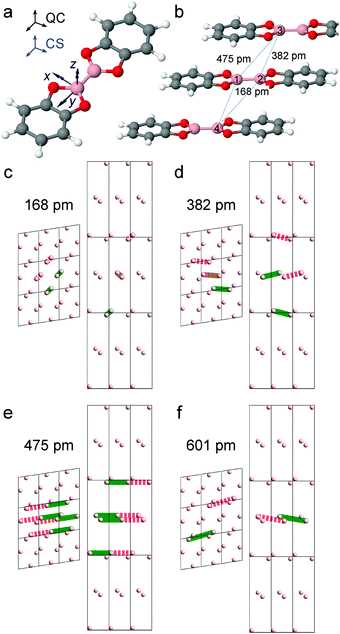 | ||
| Fig. 2 (a) Molecular structure of bis(catecholato)diboron.55 The principal axis systems of the 11B quadrupole coupling (QC) and chemical shift tensors (CS) as determined by CASTEP calculations are indicated. (b) Stacking of molecules in the bis(catecholato)diboron crystal structure. Selected intra- and intermolecular B–B distances are indicated, with the distinct boron sites labeled. (c)–(f) 11B–11B dipolar coupling network in the crystal structure of bis(catecholato)diboron. Contacts drawn with a solid line contribute to the multiplicity of a particular coupling, whereas dashed lines indicate equivalent couplings that do not contribute to the multiplicity. The individual 11B–11B dipolar coupling constants are given by (c) −2619 Hz, (d) −222 Hz, (e) −116 Hz, and (f) −57 Hz. | ||
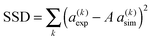 | (2) |
 | ||
| Fig. 3 The three rows show the result of using the spin-pair, multi-spin, and spin-pair summation approaches to analyze the experimental 11B CT 2Q spinning sideband amplitudes obtained in bis(catecholato)diboron for τexc = 480 μs. Experimental and simulated CT 2Q spinning sideband amplitudes are depicted for comparison as dashed as solid sticks, respectively, in the right column. (a) Normalized sum-squared deviation (SSD) of experimental and spin-pair simulated CT 2Q spinning sideband amplitudes against the 11B–11B dipolar coupling constant. The 95% confidence interval is indicated. (b) The best-fit numerical spin-pair simulations depicted as solid lines are for a 11B–11B dipolar coupling constant of b12/2π = −2580 Hz. (c) Individual multi-spin simulated CT 2Q spinning sideband amplitude patterns for the different 11B multiple spin-systems shown in Fig. 2. The spin systems are given with their respective contribution from bottom to top by: 5.1% (4–1/2–3); 5.1% (4–2/1–3); 2.5% (1–2); 20.5% (4–1–2/1–2–3); 20.5% (4–1–3/4–2–3); 41.2% (4–1–2–3). (d) The simulations shown as solid lines correspond to the sum of multi-spin contributions in (c). (e) Normalized root-mean-square (RMS) deviation between experimental CT 2Q spinning sideband amplitudes and summed spin-pair simulations plotted against the cut-off distance R. (f) The solid sticks represent the sum of numerical simulations for B–B distances out to R = 381.9 pm, corresponding to the minimum of the RMS deviation in (e). | ||
Fig. 3a plots the ratio SSD/SSDmin against the dipolar coupling constant b12/2π, where SSDmin represents the deviation obtained for the best fit. The 95% confidence interval, indicated in the figure, was determined by the set of dipolar couplings that obey SSD ≤ SSDmin{1 + F0.051,6/6}, where Fα(p1, p2) is the upper α probability point of the F distribution with p1 and p2 degrees of freedom.89,90 The resulting 95% confidence interval for the 11B–11B dipolar coupling constant is −2580 ± 75 Hz, corresponding to a solid-state NMR determined distance of 168.6 (+1.7, −1.6) pm. In ref. 46, we also showed that varying the 11B quadrupolar coupling constant in the range of (−3.5, −2.1) MHz had a very weak effect on the sideband amplitudes. This generally also applies to the orientations of the quadrupolar interaction, as well as to the magnitude and orientation of the CSA tensor. After accounting for the potential contributions from these interactions, our analysis amounted in a reliable estimate of the 11B–11B dipolar coupling constant as −2580 (+140, −120) Hz, i.e., corresponding to a B–B distance of (168.6 ± 3) pm, with relative uncertainties of about ±5% and ±2% in the dipolar coupling constant and the internuclear distance, respectively.
The observed dipolar coupling constant is about 1.5% smaller than that calculated from the XRD structure, and the corresponding NMR determined distance is only about 0.5% larger than that obtained from XRD. This small discrepancy can be attributed to the thermal motion of the boron positions: for the case of glycine, Ishii et al. calculated by molecular dynamics simulations that direct bond distances between non-proton nuclei measured by NMR at 273 K are typically 1.9–2.9% longer than the distances estimated by diffraction techniques.91 Furthermore, the anisotropy of the J-coupling (ΔJ) has the same symmetry under sample rotation and rf pulses as the direct dipolar interaction. Hence, in principle, only the effective spin–spin interaction Deff = b12/2π − ΔJ/3 can be determined with the CT 2Q sideband experiment.92 However, DFT calculations (not shown here), indicate that ΔJ is in the order of 13–17 Hz for the 11B–11B pair in bis-catecholato-diboron. Consequently, its potential bearings on the estimation of the dipolar coupling is negligible compared to the effects from thermal motions.
Fig. 3c shows the calculated CT 2Q sideband amplitude patterns obtained from the various 11B multiple-spin systems by employing numerically exact simulations; each is scaled by the corresponding probability of finding that particular constellation of coupled 11B sites (see Table S1 in the ESI†). Fig. 3d contrasts their sum (solid sticks) with the experimental amplitudes (dashed sticks): an excellent agreement is observed. We stress that the present summation procedure is only required due to the presence of the 10B isotope in the sample; it must not be confused with the analogous spin-pair summation protocol described in Section 2.2.2 and utilized in Section 4.1.3, as well as for the 100% abundant 27Al and 23Na nuclides below.
Fig. 3e shows the RMS deviation between the experimental 2QCT-sideband amplitudes and the sum of two-spin simulations according to eqn (1), plotted against R. The RMS calculation accounted for all odd sideband orders k = ±1, ±3, ±5, ±7, ±9, with each RMS value normalized with respect to its minimum (RMSmin) found at R = 382 pm; Fig. 3f contrasts the respective sideband pattern obtained by summing all two-spin simulations (solid sticks) with the corresponding experimental result (dashed sticks). The very good agreement observed between the simulation and experiment is only marginally worse than that by using numerically exact multi-spin simulations in Fig. 3d. This validates the approach leading to eqn (1), i.e. that the spin dynamics of a large number of mutually dipolar-coupled spins may in these applications be reasonably well approximated by a sum over pair-wise responses.
4.2 The 23Na (I = 3/2) network in Na2SO4
We next consider application of CT 2Q sideband NMR spectroscopy to the dipolar-coupled network of 23Na spins (I = 3/2) in Na2SO4, which involves one crystallographically unique Na site. Fig. 4a illustrates the single-crystal XRD-derived structure,86 also indicating the directions of the principal axes of the 23Na chemical shift and quadrupolar tensors, as obtained by GIPAW-DFT calculations. Fig. 4b–e convey the spatial relationship between the various equivalent and inequivalent 23Na–23Na pairs. Table S2 in the ESI† summarizes all inequivalent 23Na–23Na dipolar interactions, the corresponding multiplicities, and vector directions over a cut-off radius of R = 590 pm.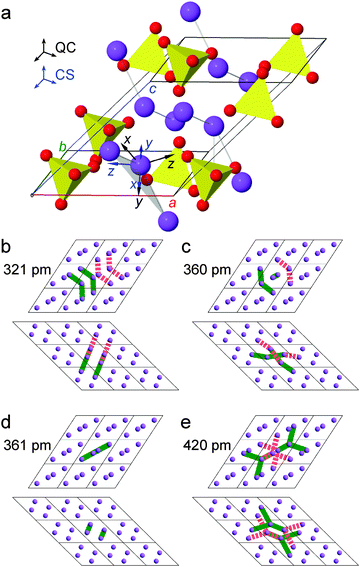 | ||
| Fig. 4 (a) Crystal structure of Na2SO4 determined by XRD.86 The principal axis systems of the 23Na quadrupole coupling (QC) and chemical shift (CS) tensors as determined by CASTEP calculations are indicated. (b)–(e) 23Na–23Na dipolar coupling network in the crystal structure of Na2SO4. Contacts depicted as solid lines contribute to the multiplicity of a particular coupling, whereas contacts shown by dashed lines are equivalent couplings that do not contribute to the multiplicity. The individual 23Na–23Na dipolar coupling constants are given by (b) −254 Hz, (c) −181 Hz, (d) −180 Hz, and (e) −113.5 Hz. | ||
Fig. 5 plots the experimental 23Na 2QCT-filtered (2QFCT) efficiencies against the excitation interval τexc. The results were obtained at a spinning frequency of 20 kHz, an external field of 11.75 T and two distinct rf carrier frequency positions (relative to the center of mass of the 23Na powder lineshape); this produced resonance offsets of 0 Hz and 1080 Hz, and the associated maximum 2QFCT efficiencies of 15.9% and 23.4%, respectively. However, regardless of the precise value of the resonance offset, an optimum signal intensity was observed at τexc = τmaxexc = 0.8 ms.
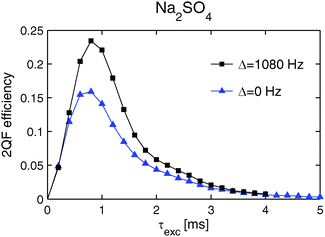 | ||
Fig. 5 Experimental 23Na 2QCT-filtered efficiencies plotted against τexc. They were obtained from Na2SO4 by using the pulse sequence shown in Fig. 1 at a spinning frequency of 20 kHz, an external field of 11.75 T, and two distinct rf offsets:  0 Hz and ■ 1080 Hz. 0 Hz and ■ 1080 Hz. | ||
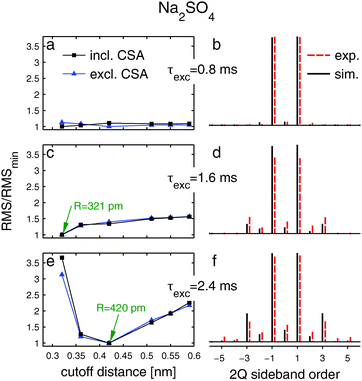
The left panel of Fig. 6 shows RMS deviations between experimental 2QCT-sideband amplitudes and those calculated by summing over simulated two-spin responses [eqn (1)], plotted against the cut-off distance R, and with 2QCT excitation periods increasing from top to bottom; each curve is normalized with respect to its respective minimum. The RMS deviations were determined both by including (squares) and omitting (triangles) CSA in the calculations. The right panel contrasts the experimental CT 2Q sideband amplitude manifold (dashed sticks) with the best-fit simulation incorporating CSA (solid sticks).
At the shortest 2QCT excitation interval of τexc = 0.8 ms, solely the lowest order (±1) sidebands are present in the manifold (Fig. 6b) that depends marginally on the cut-off distance (Fig. 6a); this feature precludes the probing of long-range Na–Na internuclear distances. The middle row of Fig. 6 displays the results for τexc = 1.6 ms. The experimental 2QCT-sideband pattern now comprises sidebands up to orders ±3 and the RMS deviation varies significantly when R changes; it minimizes at R = 321 pm, regardless of whether CSA was accounted for in the simulations. The latter applies throughout all cases examined in the present work. The results of lengthening the excitation period further (τexc = 2.4 ms) are shown in Fig. 6e and f that reveal 2QCT-sideband patterns incorporating orders ±5 and also the most pronounced sensitivity of the RMS deviation when the cut-off distance alters. As expected, the best-fit simulation is obtained at an expanded radius (R = 420 pm) relative to that at the shorter τexc values. The simulated and experimental 2QCT-sideband patterns agree very well. Hence, this choice of 2QCT excitation time is preferable to probe longer-range structural fragments in the 23Na nuclear spin network of Na2SO4.
As opposed to the confined 11B spin system in bis(catecholato)diboron, the macroscopic network of 23Na spins in Na2SO4 precludes the determination of individual internuclear distances. Structural analyses must rather aim at validating if the atomic coordinates (and its associated set of dipolar interactions) of a proposed structural model may reproduce the experimental results. At a selected 2QCT excitation interval, the experiment provides the number Nspins of interacting spins within the macroscopically large spin ensemble. For a finite-sized cluster in a structure, Nspins corresponds to its number of spins. The value of Nspins may then be estimated by locating the R-value that minimizes the RMS deviation between the experimental 2QCT sideband manifold and the sum over all simulated spin-pair responses therein. Table 2 lists the cluster-size (Nspins) of the Na2SO4 structure assessed at each excitation period; Nspins increases from 12 to 22 when τexc increases from 1.6 ms to 2.4 ms.
| Sample | τ exc [ms] | R [pm] | N pairs | N spins |
|---|---|---|---|---|
| C12H8B2O4 | 0.48 | 382 | 8 | 12 |
| Na2SO4 | 1.6 | 321 | 8 | 12 |
| 2.4 | 420 | 31 | 22 | |
| α-Al2O3 | 0.4 | 266 | 2 | 4 |
| 0.8 | 279 | 14 | 16 | |
| 1.0 | 350 | 50 | 34 |
We note that Duer37 used a related approach to analyze the 23Na–23Na dipolar coupling-network in Na2SO4, by modeling the experimental triple-quantum MAS (3QMAS)93 NMR spectrum via numerical simulations that also accounted for multiple homonuclear couplings. This experiment produces a sideband manifold stemming from the rotor-modulated evolution of (single-spin) 3QC under the, by slow-MAS incompletely averaged, homonuclear 23Na–23Na couplings, which in the absence of explicit homonuclear dipolar-recoupling were truncated to solely comprise the mutually commuting IjzIkz operators of the dipolar Hamiltonians in the analysis.37 By including the homonuclear couplings to the five nearest neighbors, Duer successfully reproduced the isotropic projection of the 3QMAS experiment by exploiting the known dipolar coupling-constants and orientations in the crystal structure of Na2SO4. This approach differs to ours, both concerning the origin of the sideband-formation, as well as in the numerical analysis, where we include the full form of the (high-field) dipolar Hamiltonian, yet assuming a set of mutually non-interacting spin-pairs.
4.3 The 27Al (I = 5/2) network in α-Al2O3
We further evaluated the CT 2Q sideband NMR experimentation and its accompanying “spin-counting” analysis in the context of the 27Al spins (I = 5/2) in α-Al2O3, which involves one crystallographically unique Al site coordinated by oxygen atoms. Fig. 7a reveals a very densely populated network of Al, stemming from the presence of face-shared AlO6 octahedra. The GIPAW-DFT-derived principal axis systems of the 27Al chemical shift and quadrupolar tensors are shown in Fig. 7a and b. A selection of inequivalent Al–Al pairs is shown in Fig. 7c–f, while all coupling constants, multiplicities and dipolar vector orientations out to R = 591 pm are listed in Table S2 in the ESI.†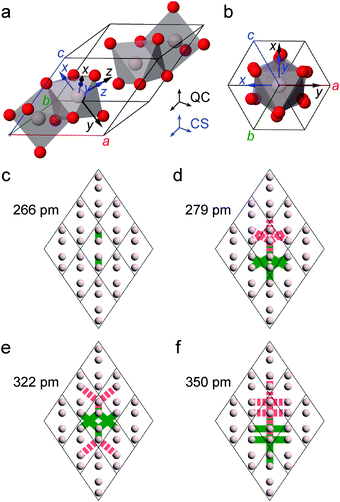 | ||
| Fig. 7 (a, b) Crystal structure of α-Al2O3 determined by XRD.87 The principal axis systems of the 27Al quadrupole coupling and chemical shift tensors as determined by CASTEP calculations are indicated. (c)–(f) 27Al–27Al dipolar coupling network in the crystal structure of α-Al2O3. The line styles are explained in the caption of Fig. 4. The individual 27Al–27Al dipolar coupling constants are given by (c) −436 Hz, (d) −375 Hz, (e) −245 Hz, and (f) −191 Hz. | ||
Fig. 8 plots experimental 27Al 2QFCT efficiencies against increasing τexc-values, as obtained from α-Al2O3 at a magnetic field of 11.75 T and 10 kHz MAS frequency. A maximum 2QFCT efficiency of 7% was obtained around τexc = 0.4 ms, which is considerably lower than the 23Na 2QFCT efficiency in Na2SO4. While these signal losses stem partially from a more rapid 27Al relaxation during rf application compared to that for 23Na in Na2SO4, they primarily originate from a significantly higher CT-magnetization leakage out to the satellite transitions for a spin-5/2 compared to the spin-3/2 case, as discussed in ref. 15 and 28. Furthermore, for a fixed dipolar-coupling constant, the 2QC buildup rate is higher for a I = 5/2 pair compared to that of two spins-3/2 (vide infra);28 together with the overall stronger 27Al–27Al dipolar coupling constants in the α-Al2O3 structure (see Table S2, ESI†), this accounts for the nearly doubled 2QC generation rate; compare the results of Fig. 5 and 8.
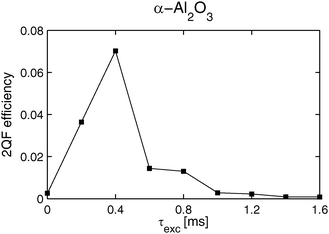 | ||
| Fig. 8 Experimental 27Al 2QCT-filtered efficiencies obtained from α-Al2O3 and plotted against τexc. The pulse sequence shown in Fig. 1 was employed at a spinning frequency of 10 kHz and an external field of 11.75 T. | ||
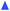
Fig. 9 displays the experimental and simulated 2QCT-sideband spectra for increasing 2QCT excitation periods. At the shortest value τexc = τmaxexc = 0.4 ms where the 2QFCT efficiency is optimized (Fig. 9a and b), the experimental 2QCT-sideband spectrum reveals only the ±1 sideband orders. The best-fit spin-pair sum was obtained from the set of couplings over R = 266 pm, corresponding to only two Al–Al pairs and a cluster of four 27Al sites (i.e., Nspins = 4); see Table 2. On the other hand, at τexc = 0.8 ms (Fig. 9c), the sideband manifold comprises both ±1 and ±3 sideband orders. Now only a fair agreement is observed for the “best-fit” NMR sideband pattern, which resulted by summing the simulated responses from all pairs over R = 279 pm (Npairs = 14), and translating into a cluster comprising 16 unique 27Al sites. At the longest 2QCT excitation period τexc = 1.0 ms (Fig. 9f), the experimental 2QCT-sideband pattern includes all sideband orders up to ±5, although the amplitudes of the highest order are very weak. The experimental result is well-reproduced by a sum over 50 spin-pairs within R = 350 pm, corresponding to a cluster comprising 34 spins (Table 2).
5 Discussion
Here we discuss the prospects of applying each of strategies (A) and (B) of Section 2.2 for analyzing dipolar-coupled spin networks and estimating internuclear distances.5.1 Estimating internuclear distances
The results for the 11B spin-3/2 pair in bis(catecholato)diboron demonstrates that CT 2Q spectroscopy is an excellent method to accurately determine internuclear distances within (isolated) pairs of half-integer quadrupolar nuclei. The sensitivity of the method increases with the number of 2QCT sideband orders that are considered in the analysis. Given that the number of spinning sidebands with significant intensity depends on the product bjkτexc, the excitation period may be progressively increased to ensure that a sufficiently large sideband manifold is available for the estimation of weak dipolar coupling constants, whereas the upper limit of the τexc is only limited by signal-damping effects from relaxation. For a truly isolated spin-pair, the dipolar coupling constant is then readily extracted through effortless two-spin simulations: the calculated 2QCT sideband manifold that most faithfully reproduces the experimental spectrum is located, while accounting for all sideband orders in the iterative fitting.Despite that truly isolated half-integer spin-pairs are very rare, spin-pair approximations still provide reliable results provided that the targeted dipolar coupling constant is much larger (≳10 times) than those of the other couplings in the system: for example, the directly bonded B–B pair in the bis(catecholato)diboron molecule represents a very strong 11B–11B dipolar coupling that is ≈12 times larger than its second-largest counterpart. The longer-range intermolecular interactions manifest themselves primarily in the ±1 sideband amplitudes that become overemphasized relative to those of the higher-orders; such effects account for most of the deviations between experimental results and those obtained by spin-pair simulations. Yet, an accurate estimate of the large dipolar coupling is still feasible by simply omitting the lowest-order sidebands in the RMS calculation and only evaluating all higher order (±3, ±5,…) sideband amplitudes. This effectively amounts to ignoring all weaker dipolar interactions; see Fig. 3 and discussions thereof.
5.2 Probing spin-cluster sizes
We next consider the more common scenario of macroscopically large quadrupolar-spin systems encountered in inorganic materials, which implies the absence of well-defined “clusters”. Here, analysis of the 2QCT experiment via strategy (B) of Section 2.2 provides information about the number of unique spin sites that contributes to the experimental sideband pattern, the number of which increases with the 2QCT preparation period. As may be verified both from the CT 2Q NMR results of the Na2SO4 and α-Al2O3 structures in Fig. 6 and 9, there are no 2QCT sideband intensities beyond the lowest (±1) order at τexc ≈ τmaxexc, i.e., when the selected excitation period optimizes the total 2QCT signal amplitude. For such cases, the number of contributing spins is necessarily small and also most difficult to determine, because the discrimination between simulations with distinct cut-off radii is poor.For increasing τexc, the best-fit R-value grows and thereby also its associated number of contributing spins. The number of spinning sidebands of significant amplitude is proportional to the product of the 2QCT excitation interval and the effective dipolar interaction of the multi-spin system, i.e., a fictive dipolar coupling constant that approximates the net effect from all spin-pairs in the system;34–36,72,94–96 it is dictated by the magnitudes and numbers of all contributing dipolar interactions over a certain R-value. Hence, for progressively increased excitation intervals, inspection of the sideband intensity-distributions at the corresponding ratios of τexc/τmaxexc gives direct qualitative information about the magnitude of the effective dipolar coupling constant of the probed spin network. For increasing τexc/τmaxexc ratio, Table 2 reveals that the observed number of interacting spins grows significantly faster in the α-Al2O3 structure relative to its Na2SO4 counterpart, in full accordance with the known higher packing density of Al in α-Al2O3 compared to that of Na in Na2SO4.
Thus far, the prevailing approach to estimate spin-cluster sizes—“multiple-quantum spin counting”57–64—relies on high-order multiple-quantum coherences (MQC) excitation in stationary or rotating powders comprising multi-spin-1/2 systems. The highest generated MQC order provides a (directly determined) lower bound of M interacting spins present in the “real” cluster. However, only one such attempt at using MQC excitation to count the number of half-integer spins is hitherto reported, then restricted to low-resolution applications in stationary powders.64 Our proposed strategy of comparing experimental 2QCT-sideband intensities with approximative spin-pair summations constitutes the first general means for estimating the size of a cluster of half-integers spins under MAS conditions. The spin-pair summation strategy is not necessarily restricted to quadrupolar nuclei;56 we are currently exploring its prospects for spin-1/2 applications.
The main limitation of the present spin-pair summation strategy is its time-consuming numerical analysis.56 Yet, despite its feature of providing the spin-cluster sizes indirectly through an (approximate) numerical approach, it exhibits a decisive advantage relative to MQ spin counting in that it avoids the cumbersome high-order MQC excitation. Also noteworthy is that techniques for producing high-order multiple-quantum coherences solely involving the central transitions of half-integer spins remain to be developed. The current spin-1/2 MQC-excitation strategy is also prone to underestimating the size of large spin-systems due to the impact of NMR relaxation and pulse imperfections, particularly in rotating solids where the progressive high-order MQC generation is slow. Furthermore, also MQ spin-counting data-analyses often resorts to indirect estimates of the “real” spin-cluster size by fitting the experimental MQC amplitude envelope to a Gaussian decay;57,58 this procedure may be associated with non-negligible uncertainties, as discussed further in ref. 58 and 63.
6 Conclusions
In this contribution, we consolidated the application of CT 2Q sideband NMR spectroscopy for estimating internuclear distances within (nearly) isolated pairs of half-integer spin quadrupolar nuclei, and demonstrated that this experimental approach may be combined with numerical analyses to probe multiple-spin effects and estimate the sizes of local clusters of mutually dipolar-coupled quadrupolar nuclei in network structures.All these aspects were first explored for the case of bis(catecholato)diboron, where each molecule involves one pair of directly bonded boron atoms, while the intermolecular B–B distances are sufficiently long to ensure a nearly isolated 11B–11B spin pair in each molecule. Since the largest coupling is an order of magnitude stronger than its second largest counterpart, we demonstrated the feasibility of determining its magnitude by fitting results from two-spin simulations employing variable dipolar couplings to the experimental results. Considering only the higher odd-order (±3, ±5,…) 2QCT sidebands in the numerical fitting, the B–B internuclear distance was determined as (168.6 ± 3) pm, i.e., with an uncertainty of ±2%. However, the strong amplitudes of the lowest order (±1) sidebands cannot be reproduced by single spin-pair simulations; they were shown to stem from the longer range intermolecular 11B–11B dipolar interactions. We presented two approaches to account for their contributions, both of which successfully reproduced the entire experimental manifold of 2QCT sidebands: (i) performing computationally expensive multi-spin simulations, or (ii) apply the spin-pair summation approach in ref. 56, in which the complete calculated NMR spectrum is obtained by summation of individual simulations for spin-pairs found within a certain cut-off distance.
Besides justifying the approximative numerical spin-pair simulation protocol by rigorous multi-spin 11B–11B simulations for the case of bis(catecholato)diboron, we further successfully demonstrated it by 23Na and 27Al NMR on the macroscopic networks of Na2SO4 and Al2O3, respectively. For progressively lengthened 2QCT excitation intervals, each respective 23Na and 27Al cluster size may be extracted by locating its corresponding cut-off distance, thereby allowing the monitoring of a growing number of interacting nuclear spins. Altogether, this analysis yields similar information as the MQ spin-counting experiment,57–64 but without the cumbersome need to excite high-order MQC, which for MAS applications is hitherto only demonstrated for spin-1/2 systems.59–63 However, we emphasize that the MQ spin-counting technique provides direct estimates of spin-cluster sizes, whereas the 2QCT sideband experiment requires a priori knowledge about the atomic coordinates of the structure for determining the number of interacting spins for the given 2QCT excitation interval.
The approach of analyzing experimental CT 2Q sideband data by comparison with sums of numerically simulated spin-pair responses may in its present form only be used for discriminating between various proposed structural models through the adherence of their corresponding numerically simulated sideband patterns to the experimental results. Nevertheless, this protocol makes an important dent towards elucidating the dependence of the quadrupolar-spin dynamics on a potentially wide range of structural parameters, such as the positions and local geometries of the quadrupolar spin-sites. As already demonstrated in the context of 2Q–1Q correlation spectroscopy, a spin-pair summation analysis allows for determining the absolute orientations of the electric field gradient (EFG) tensor at each quadrupolar spin-site:56 hence, the encoding of distance-information in the sidebands from the closely related CT 2Q sideband protocol may be linked to the EFG tensor orientations of the recoupled spins.
Our method prepares the grounds for “ab initio distance-measurements” by numerical fitting of experimental CT 2Q spinning sideband data from disordered structures, where direct information about the coordinates of the quadrupolar sites is intractable by other means; for many structures, this technique may constitute the sole option for obtaining (semi-) quantitative information about internuclear distances and spin-cluster sizes. The strategy of analyzing results from 2Q sideband experiments with a spin-pair summation numerical protocol is generally applicable: we are currently exploring it for spins-1/2 applications to oxide-based inorganic network structures.
Acknowledgements
The authors would like to thank Igor Moudrakovski, Victor Terskikh and Chris Ratcliffe for helpful discussions. Access to CASTEP was provided by the National Ultrahigh-Field NMR Facility for Solids (Ottawa, Canada), a national research facility funded by the Canada Foundation for Innovation, the Ontario Innovation Trust, Recherche Québec, the National Research Council Canada, and Bruker BioSpin and managed by the University of Ottawa (http://www.nmr900.ca). This work was supported by the National Research Council Canada (NRC), the Swedish Research Council (contract VR-NT 2010-4943) and the Faculty of Sciences at Stockholm University.References
- S. Dusold and A. Sebald, Annu. Rep. NMR Spectrosc., 2000, 41, 185–264 CrossRef CAS.
- M. H. Levitt, Encyclopedia of Nuclear Magnetic Resonance, Wiley, Chichester, England, 2002, vol. 9, pp. 165–196 Search PubMed.
- M. Edén, eMagRes, 2013, 2, 351–364 Search PubMed.
- V. Ladizhansky, Solid State Nucl. Magn. Reson., 2009, 36, 119–128 CrossRef CAS PubMed.
- N. C. Nielsen, L. A. Strassø and A. B. Nielsen, Solid-State NMR, Springer-Verlag, Berlin/Heidelberg, 2012, vol. 306, pp. 1-45 Search PubMed.
- I. Schnell, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 45, 145–207 CrossRef CAS PubMed.
- X. Feng, Y. K. Lee, D. Sandström, M. Edén, H. Maisel, A. Sebald and M. H. Levitt, Chem. Phys. Lett., 1996, 257, 314–320 CrossRef CAS.
- X. Feng, M. Edén, A. Brinkmann, H. Luthman, L. Eriksson, A. Gräslund, O. N. Antzutkin and M. H. Levitt, J. Am. Chem. Soc., 1997, 119, 12006–12007 CrossRef CAS.
- M. Hong, J. D. Gross and R. G. Griffin, J. Phys. Chem. B, 1997, 101, 5869–5874 CrossRef CAS.
- M. Edén, A. Brinkmann, H. Luthman, L. Eriksson and M. H. Levitt, J. Magn. Reson., 2000, 144, 266–279 CrossRef PubMed.
- J. C. C. Chan and R. Tycko, J. Am. Chem. Soc., 2003, 125, 11828–11829 CrossRef CAS PubMed.
- V. Ladizhansky, C. P. Jaroniec, A. Diehl, H. Oschkinat and R. G. Griffin, J. Am. Chem. Soc., 2003, 125, 6827–6833 CrossRef CAS PubMed.
- A. Jerschow, Prog. Nucl. Magn. Reson. Spectrosc., 2005, 46, 63–78 CrossRef CAS PubMed.
- S. E. Ashbrook and M. J. Duer, Concepts Magn. Reson., Part A, 2006, 28, 183–248 CrossRef.
- M. Edén, Solid State Nucl. Magn. Reson., 2009, 36, 1–10 CrossRef PubMed.
- J. V. Hanna and M. E. Smith, Solid State Nucl. Magn. Reson., 2010, 38, 1–18 CrossRef CAS PubMed.
- P. Hartmann, C. Jäger and J. W. Zwanziger, Solid State Nucl. Magn. Reson., 1999, 13, 245–254 CrossRef CAS.
- M. Nijman, M. Ernst, A. P. M. Kentgens and B. H. Meier, Mol. Phys., 2000, 98, 161–178 CrossRef CAS.
- M. Baldus, D. Rovnyak and R. G. Griffin, J. Chem. Phys., 2000, 112, 5902–5909 CrossRef CAS PubMed.
- S. Wi, H. Heise and A. Pines, J. Am. Chem. Soc., 2002, 124, 10652–10653 CrossRef CAS PubMed.
- S. Wi, J. W. Logan, D. Sakellariou, J. D. Walls and A. Pines, J. Chem. Phys., 2002, 117, 7024–7033 CrossRef CAS PubMed.
- A. J. Painter and M. J. Duer, J. Chem. Phys., 2002, 116, 710–722 CrossRef CAS PubMed.
- T. G. Ajithkumar and A. P. M. Kentgens, J. Am. Chem. Soc., 2003, 125, 2398–2399 CrossRef CAS PubMed.
- G. Mali, G. Fink and F. Taulelle, J. Chem. Phys., 2004, 120, 2835–2845 CrossRef CAS PubMed.
- M. Edén, H. Annersten and Å. Zazzi, Chem. Phys. Lett., 2005, 410, 24–30 CrossRef PubMed.
- M. Edén, D. Zhou and J. Yu, Chem. Phys. Lett., 2006, 431, 397–403 CrossRef PubMed.
- A. Y. H. Lo and M. Edén, Phys. Chem. Chem. Phys., 2008, 10, 6635–6644 RSC.
- A. Brinkmann, A. P. M. Kentgens, T. Anupõld and A. Samoson, J. Chem. Phys., 2008, 129, 174507 CrossRef PubMed.
- M. Edén and A. Y. H. Lo, J. Magn. Reson., 2009, 200, 267–279 CrossRef PubMed.
- Q. Wang, B. Hu, O. Lafon, J. Trébosc, F. Deng and J. P. Amoureux, J. Magn. Reson., 2009, 200, 251–260 CrossRef CAS PubMed.
- D. Iuga, J. Magn. Reson., 2011, 208, 225–234 CrossRef CAS PubMed.
- M. Edén and L. Frydman, J. Phys. Chem. B, 2003, 107, 14598–14611 CrossRef.
- M. Edén, J. Grinshtein and L. Frydman, J. Am. Chem. Soc., 2002, 124, 9708–9709 CrossRef PubMed.
- E. Ratai, M. Janssen and H. Eckert, Solid State Ionics, 1998, 105, 25–37 CrossRef CAS.
- B. A. Gee, Magn. Reson. Chem., 2004, 42, 30–38 CrossRef CAS PubMed.
- J. D. Epping, W. Strojek and H. Eckert, Phys. Chem. Chem. Phys., 2005, 7, 2384–2389 RSC.
- M. J. Duer, Chem. Phys. Lett., 1997, 277, 167–174 CrossRef CAS.
- N. G. Dowell, S. E. Ashbrook, J. McManus and S. Wimperis, J. Am. Chem. Soc., 2001, 123, 8135–8136 CrossRef CAS.
- G. Mali and V. Kaučič, J. Magn. Reson., 2004, 171, 48–56 CrossRef CAS PubMed.
- I. Hung, A. P. Howes, T. Anupõld, A. Samoson, D. Massiot, M. E. Smith, S. P. Brown and R. Dupree, Chem. Phys. Lett., 2006, 432, 152–156 CrossRef CAS PubMed.
- M. Edén, J. Magn. Reson., 2010, 204, 99–110 CrossRef PubMed.
- A. Jaworski, B. Stevensson, B. Pahari, K. Okhotnikov and M. Edén, Phys. Chem. Chem. Phys., 2012, 14, 15866–15878 RSC.
- F. A. Perras, I. Korobkov and D. L. Bryce, Phys. Chem. Chem. Phys., 2012, 14, 4677–4681 RSC.
- F. A. Perras, I. Korobkov and D. L. Bryce, CrystEngComm, 2013, 15, 8727–8738 RSC.
- G. Mali, V. Kaučič and F. Taulelle, J. Chem. Phys., 2008, 128, 204503 CrossRef PubMed.
- A. Brinkmann and M. Edén, Can. J. Chem., 2011, 89, 892–899 CrossRef CAS.
- N. S. Barrow, J. R. Yates, S. A. Feller, D. Holland, S. E. Ashbrook, P. Hodgkinson and S. P. Brown, Phys. Chem. Chem. Phys., 2011, 13, 5778–5789 RSC.
- F. A. Perras and D. L. Bryce, J. Chem. Phys., 2013, 138, 174202 CrossRef PubMed.
- F. A. Perras and D. L. Bryce, J. Am. Chem. Soc., 2013, 135, 12596–12599 CrossRef CAS PubMed.
- H. Geen, J. J. Titman, J. Gottwald and H. W. Spiess, J. Magn. Reson., Ser. A, 1995, 114, 264–267 CrossRef CAS.
- J. Gottwald, D. E. Demco, R. Graf and H. W. Spiess, Chem. Phys. Lett., 1995, 243, 314–323 CrossRef CAS.
- R. Graf, D. E. Demco, J. Gottwald, S. Hafner and H. W. Spiess, J. Chem. Phys., 1997, 106, 885–895 CrossRef CAS PubMed.
- U. Friedrich, I. Schnell, S. P. Brown, A. Lupulescu, D. E. Demco and H. W. Spiess, Mol. Phys., 1998, 95, 1209–1227 CrossRef CAS.
- A. Lupulescu, S. P. Brown and H. W. Spiess, J. Magn. Reson., 2002, 154, 101–129 CrossRef CAS PubMed.
- W. Clegg, M. R. J. Elsegood, F. J. Lawlor, N. C. Norman, N. L. Pickett, E. G. Robins, A. J. Scott, P. Nguyen, N. J. Taylor and T. B. Marder, Inorg. Chem., 1998, 37, 5289–5293 CrossRef CAS.
- M. Edén, Chem. Phys. Lett., 2009, 470, 318–324 CrossRef PubMed.
- J. Baum, M. Munowitz, A. N. Garroway and A. Pines, J. Chem. Phys., 1985, 83, 2015–2025 CrossRef CAS PubMed.
- S. Lacelle, S. Hwang and B. C. Gerstein, J. Chem. Phys., 1993, 99, 8407–8413 CrossRef CAS PubMed.
- H. Geen, R. Graf, A. S. D. Heindrichs, B. S. Hickman, I. Schnell, H. W. Spiess and J. J. Titman, J. Magn. Reson., 1999, 138, 167–172 CrossRef CAS PubMed.
- N. A. Oyler and R. Tycko, J. Phys. Chem. B, 2002, 106, 8382–8389 CrossRef CAS.
- M. Edén, Chem. Phys. Lett., 2002, 366, 469–476 CrossRef.
- P. E. Kristiansen, M. Carravetta, J. D. van Beek, W. C. Lai and M. H. Levitt, J. Chem. Phys., 2006, 124, 234510 CrossRef PubMed.
- G. Teymoori, B. Pahari, E. Viswanathan and M. Edén, J. Magn. Reson., 2013, 236, 31–40 CrossRef CAS PubMed.
- A. J. Dodd and E. R. H. van Eck, Solid State Nucl. Magn. Reson., 2004, 26, 121–131 CrossRef CAS PubMed.
- J. Haase, M. S. Conradi, C. P. Grey and A. J. Vega, J. Magn. Reson., Ser. A, 1994, 109, 90–97 CrossRef CAS.
- A. P. M. Kentgens and R. Verhagen, Chem. Phys. Lett., 1999, 300, 435–443 CrossRef CAS.
- R. Siegel, T. T. Nakashima and R. E. Wasylishen, Chem. Phys. Lett., 2004, 388, 441–445 CrossRef CAS PubMed.
- P. K. Madhu, A. Goldbourt, L. Frydman and S. Vega, Chem. Phys. Lett., 1999, 307, 41–47 CrossRef CAS.
- Z. Yao, H.-T. Kwak, D. Sakellariou, L. Emsley and P. J. Grandinetti, Chem. Phys. Lett., 2000, 327, 85–90 CrossRef CAS.
- M. Carravetta, M. Edén, X. Zhao, A. Brinkmann and M. H. Levitt, Chem. Phys. Lett., 2000, 321, 205–215 CrossRef CAS.
- G. Bodenhausen, H. Kogler and R. R. Ernst, J. Magn. Reson., 1984, 58, 370–388 CAS.
- A. Brinkmann, M. Edén and M. H. Levitt, J. Chem. Phys., 2000, 112, 8539–8554 CrossRef CAS PubMed.
- M. Edén, Concepts Magn. Reson., Part A, 2003, 18A, 1–23 CrossRef.
- N. C. Nielsen, H. Bildsøe, H. J. Jakobsen and M. H. Levitt, J. Chem. Phys., 1994, 101, 1805–1812 CrossRef CAS PubMed.
- D. States, R. A. Haberkorn and D. J. Ruben, J. Magn. Reson., 1982, 48, 286–292 CAS.
- D. Marion, M. Ikura, R. Tschudin and A. Bax, J. Magn. Reson., 1989, 85, 393–399 CAS.
- M. Bak and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330 CrossRef CAS PubMed.
- S. K. Zaremba, SIAM Rev., 1968, 10, 303–314 CrossRef.
- H. Conroy, J. Chem. Phys., 1967, 47, 5307–5318 CrossRef PubMed.
- V. B. Cheng, H. H. Suzukawa Jr. and M. Wolfsberg, J. Chem. Phys., 1973, 59, 3992–3999 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CrossRef CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef.
- M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- F. C. Hawthorne and R. B. Ferguson, Can. Mineral., 1975, 13, 181–187 Search PubMed.
- D. S. J. Lewis and H. D. Flack, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1982, 38, 733–739 CrossRef.
- G. P. Holland, B. R. Cherry and T. M. Alam, J. Magn. Reson., 2004, 167, 161–167 CrossRef CAS PubMed.
- G. A. F. Seber and C. J. Wild, Nonlinear Regression, Wiley-Interscience, Hoboken, USA, 2003 Search PubMed.
- E. M. L. Beale, J. R. Stat. Soc. Ser. B, 1960, 22, 41–88 Search PubMed.
- Y. Ishii, T. Terao and S. Hayashi, J. Chem. Phys., 1997, 107, 2760–2774 CrossRef CAS PubMed.
- R. E. Wasylishen, Indirect Nuclear Spin–Spin Coupling Tensors, eMagRes, 2007 DOI:10.1002/9780470034590.emrstm0237.
- L. Frydman and J. S. Harwood, J. Am. Chem. Soc., 1995, 117, 5367–5368 CrossRef CAS.
- C. Filip, S. Hafner, I. Schnell, D. E. Demco and H. W. Spiess, J. Chem. Phys., 1999, 110, 423–440 CrossRef CAS PubMed.
- V. E. Zorin, S. P. Brown and P. Hodgkinson, Mol. Phys., 2006, 104, 293–304 CrossRef CAS.
- J. S. auf der Günne, J. Magn. Reson., 2006, 180, 186–196 CrossRef PubMed.
- R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59–84 CrossRef CAS.
- G. E. Hubert Koller, A. P. M. Kentgens and J. Sauer, J. Phys. Chem., 1994, 98, 1544–1551 CrossRef.
- T. Vosegaard and H. J. Jakobsen, J. Magn. Reson., 1997, 128, 135–137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp00029c |
| This journal is © the Owner Societies 2014 |