Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coherent analysis of disordered mesoporous adsorbents using small angle X-ray scattering and physisorption experiments†
Daniela
Stoeckel
ab,
Dirk
Wallacher
c,
Gerald A.
Zickler
d,
Jan
Perlich
e,
Ulrich
Tallarek
b and
Bernd M.
Smarsly
*a
aInstitute of Physical Chemistry, Justus-Liebig-Universität Giessen, Heinrich-Buff-Ring 58, 35392 Giessen, Germany. E-mail: bernd.smarsly@phys.chemie.uni-giessen.de; Fax: +49-641-9934509; Tel: +49-641-9934590
bDepartment of Chemistry, Philipps-Universität Marburg, Hans-Meerwein-Strasse, 35032 Marburg, Germany
cBerlin Neutron Scattering Center (BENSC), Helmholtz Zentrum Berlin für Materialien und Energie GmbH, Hahn-Meitner-Platz 1, 14109 Berlin, Germany
dInstitute of Mechanics, Montanuniversität Leoben, Franz-Josef-Strasse 18, 8700 Leoben, Austria
eDeutsches Elektronen-Synchrotron, Notkestraße 85, 22607 Hamburg, Germany
First published on 26th February 2014
Abstract
Characterization of mesoporous adsorbents is traditionally performed in terms of the pore size distribution with bulk methods like physisorption and mercury intrusion. But their application relies on assumptions regarding the basic pore geometry. Although novel tools have enabled the quantitative interpretation of physisorption data for adsorbents having a well-defined pore structure the analysis of disordered mesoporosity still remains challenging. Here we show that small angle X-ray scattering (SAXS) combined with chord length distribution (CLD) analysis presents a precise and convenient approach to determine the structural properties of two-phase (solid–void) systems of mesopores. Characteristic wall (solid) and pore (void) sizes as well as surface areas are extracted without the need to assume a certain pore shape. The mesoporous structure of modern, commercially available fully porous and core–shell adsorbent particles is examined by SAXS/CLD analysis. Mean pore size and surface area are compared with results obtained from nitrogen physisorption data and show excellent agreement.
1. Introduction
Particulate mesoporous adsorbents are intensively used as supports in heterogeneous catalysis and chemical separations, and the specific physical characteristics of an adsorbent impact its performance in a particular application. Some characteristics influence the preparation of the packed beds used as supports. These parameters (e.g., the surface roughness of the particles and particle size distribution) address the morphology and homogeneity of a bed.1,2 Other parameters like particle porosity, particle types (fully porous, nonporous, or core–shell design), and chemical surface modification influence the interaction between analytes and the stationary phase and the intraparticle transport (e.g., diffusion coefficient).3,4 Whereas the inherent heterogeneity of the packed bed dominates the separation efficiency,5,6 differences in the intraparticle mesopore space are important for the selectivity of a chromatographic process or a catalytic reaction.Substantial progress has been made in the development of silica-based mesoporous particles for their application in high performance liquid chromatography (HPLC) over the last few years.7,8 Worth mentioning is the reintroduction of core–shell particles9 into the HPLC field and the advent of sub-2 μm fully porous particles.10 Since the mesopores of silica-based adsorbents provide the area of contact between analytes and the stationary phase their shape, size distribution, and accessibility are substantial for the diffusion properties, and because the total surface area is directly coupled with the pore size the accurate determination of the pore size distribution (PSD) is a prerequisite. The evaluation of mesoporous adsorbents has relied mainly on techniques such as inverse size-exclusion chromatography (ISEC),11 mercury intrusion porosimetry (MIP), and physisorption12 using gases such as nitrogen or argon.13 However, data analysis is limited by the fact that the mesopores usually neither feature a defined pore shape nor a narrow PSD.14 Obviously, the precise determination of these parameters is fundamental, if the mesopore space characteristics are correlated with the overall transport properties.
Novel data analysis tools (e.g., the nonlocal density function theory, NLDFT)15,16 have enabled the improved quantitative interpretation of physisorption data for materials with well-defined pore hierarchy.17 Despite this progress, the interpretation of physisorption data for disordered mesoporosity, which is inherent to most, if not all chromatographic materials, still poses a challenge.12 Thus, as long as a detailed three-dimensional model of the materials' mesopore network is lacking, it is important to verify physisorption results with an additional method to avoid misleading data evaluation because of an inappropriate pore model. This strategy will eventually ensure the consistent use of physisorption results and open up further possibilities for the investigation of gas sorption mechanisms in disordered structures. Additional independent techniques are needed in order to validate theoretical approaches behind current physisorption analysis.18
In this context, small angle X-ray scattering (SAXS) is a method for the characterization of materials at the nanometer scale.19–22 SAXS offers the opportunity to obtain deeper insight into mesoporosity even for materials without defined mesopore shape and PSD.23 The characterization of pore structure over length scales covering several orders of magnitude is possible in a single experiment. Whereas a concise analysis of the SAXS data for ordered mesoporous materials is achieved by using evaluation procedures based on regular arrays of mesopores,22–27 a SAXS study of disordered mesopore systems is less straightforward. The concept of chord length distributions (CLD), already applied in the 1960s,28 offers a general strategy to interpret the SAXS data of two-phase (solid–void) systems with sharp or diffuse phase boundaries, as is the case for mesoporous oxides.29–32
A CLD is basically a statistical distribution of the linear surface-to-surface distances. Applied to data obtained from a SAXS experiment, this routine provides a suitable tool to extract the relevant material information, such as the average pore size, pore geometry, and the prevalent length scales.22 CLD analysis is useful for the characterization of materials lacking a high degree of mesoscopic order.23 Its main advantage lies in the fact that the evaluation can be performed without need to assume a certain pore shape. This feature allows the determination of average pore size independent of simplifications regarding pore geometry and enables a comparison with parameters derived from physisorption data.22 Such an approach has already successfully been applied to characterize various porous materials of different chemical nature30,33,34 including porous silica.35–38 However, thorough studies of disordered mesoporous silicas by the SAXS/CLD approach in combination with physisorption analysis are still rare,18,27,39,40 especially studies where the results from small angle scattering (SAS)/CLD (e.g., mean pore size, surface area and the potential presence of microporosity) are compared with NLDFT interpretation of physisorption data.41
Recently, the interparticle macropore space morphology of packed beds prepared from small mesoporous adsorbents (fully porous and core–shell particles) became accessible through 3D imaging methods like confocal laser scanning microscopy1,42,43 and was subsequently analyzed using the CLD method. Elucidating the intraparticle mesopore space morphology is thus the next logical step in characterizing the structural details of packed beds of adsorbent particles, which will allow us to connect specific pore-morphological features with variations in the observed chromatographic performance, like it has been demonstrated for the interparticle macropore space of chromatographic beds.1,5,44–46
In this work, the mesoporous structure of the following (commercially available) mesoporous adsorbent particles is investigated as representative chromatographic adsorbents with reproducible characteristics: fully porous Atlantis, Luna, and Zorbax particles on the one hand, and core–shell Halo, Kinetex, and Poroshell particles on the other hand. All samples were evaluated by SAXS using synchrotron radiation at HASYLAB (DESY, Hamburg). SAXS data were compared with results from conventional nitrogen physisorption analysis based on NLDFT and BJH evaluation. In addition, scanning electron microscopy (SEM) pictures of the particles were recorded to qualitatively discuss their structural properties.
2. Experimental section
2.1 Materials
The studied particulate materials are commercially available chromatographic adsorbents used as obtained from the manufacturer: 3.5 μm Atlantis particles were purchased from Waters Corporation (Milford, MA); 3 μm Luna and 2.6 μm Kinetex were provided by Phenomenex (Aschaffenburg, Germany); 3.5 μm Zorbax and 2.5 μm Poroshell particles were a gift from Agilent Technologies (Waldbronn, Germany); 2.7 μm Halo particles came from Advanced Materials Technologies (Wilmington, DE).2.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), λ being the wavelength and 2θ the scattering angle. To avoid air scattering, a vacuum flight tube was inserted between the sample and the detector. The transmission of a sample was analyzed using an ionization chamber before the adsorption cell for monitoring the primary synchrotron X-ray flux and a photodiode mounted in the beamstop for measuring the transmitted photons. An exposure time of 60 s yielded a scattering pattern with excellent measuring statistics. The scattering patterns were corrected for background scattering, electronic noise, transmission, and polarization using the data reduction program FIT2D.49 All the specimens showed isotropic scattering patterns, which were azimuthally averaged for equal radial distances from the central beam.
θ), λ being the wavelength and 2θ the scattering angle. To avoid air scattering, a vacuum flight tube was inserted between the sample and the detector. The transmission of a sample was analyzed using an ionization chamber before the adsorption cell for monitoring the primary synchrotron X-ray flux and a photodiode mounted in the beamstop for measuring the transmitted photons. An exposure time of 60 s yielded a scattering pattern with excellent measuring statistics. The scattering patterns were corrected for background scattering, electronic noise, transmission, and polarization using the data reduction program FIT2D.49 All the specimens showed isotropic scattering patterns, which were azimuthally averaged for equal radial distances from the central beam.
For the SAXS experiments a special apparatus was designed. The specimen chamber was made of aluminum and the cell windows were equipped with Kapton foils. The chamber was temperature-controlled by Peltier devices and connected to a vacuum pump. Further details of the setup can be found elsewhere.50,51 Before starting with an experiment the powder was dried at 423 K and a pressure of <10−5 mbar for at least 1 h. Sample powders were afterwards carefully filled and compacted into the cell of 0.3 mm thickness and 3 mm diameter and mounted on the sample holder. The whole setup was evacuated at a pressure of <10−3 mbar. The cell was temperature-controlled and set to 300 K.
The mesoporous adsorbents used in chromatography are materials with a correlative disorder: the resulting CLD is a unimodal distribution or a superposition of the unimodal distributions of void space and the wall phase.52,53 Its statistical mode describes the typical correlation length in the material. Size and shape of a CLD are influenced by the volume ratio, surface area, anisotropy, and heterogeneity of the underlying morphological element. Chords that stretch from pore to pore provide a tail to the distribution. Structural heterogeneities of the materials contribute to widen the CLD.
The CLD g(r) is related to the autocorrelation function γ(r) by
| g(r) = lPγ′′(r), r > 0, | (1) |
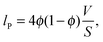 | (2) |
 | (3) |
 | (4) |
 | (5) |
Provided that the SAXS data cover a sufficiently large span of the scattering vector, the CLD can be applied for complete characterization of the porous structure. In particular, sub-structures having different orders of characteristic lengths can be determined in a complex pore system, e.g., micropores and mesopores. To accomplish the requirements of an ideal two-phase system, expressed in the fulfillment of Porod's law54 (s−4 asymptote at large values of s), a constant background was subtracted from the acquired data. The corrected SAXS data were evaluated by calculating the CLD in a parameterized form.30
3. Results and discussion
3.1 SEM image analysis
The width of the particle size distribution is the most notable difference between core–shell and fully porous particles besides the evident differences in their intraparticle morphology. As a consequence of their manufacturing process55 the fully porous particles show a large size variation with a relative standard deviation of 15.0–16.7%, in contrast to core–shell particles (3.4–9.3%). The fully porous particles are commonly produced from silica sols forming silica hydrogel beads in a Stöber like synthesis,56 which are afterwards subject to calcination. In comparison, the core–shell particles are manufactured by starting with monosized, nonporous silica spheres and subsequent coating of the solid cores with a porous shell (Fig. 2). For the shell preparation different manufacturing techniques are used, i.e., the coacervation method or the multilayering process.57Another parameter that can be assessed from the SEM image analysis is the particles' surface roughness (Fig. 3). The roughness of the particles has a major influence in the slurry packing process for HPLC columns, since it contributes to shear stress of the particles within the column wall and influences particle–particle interaction. Both factors regulate the bed morphology, the former the morphology near the wall, the latter the morphology in the bulk.7,58 Regarding the particles under study, there is a significant qualitative difference in surface roughness. The fully porous particles are mostly very smooth (Atlantis and Luna), whereas the manufacturing process of the core–shell particles results in at least slightly rough particle surfaces. Halo and Zorbax particles show the roughest surfaces in this study. A summary of the results extracted from SEM analysis can be found in Table 1.
| Chromatographic adsorbent | Particle type | Particle size (manufacturer data) (μm) | Particle size (measured, mean) (μm) | RSD (%) | Surface roughness |
|---|---|---|---|---|---|
| Atlantis | Fully porous | 3.5 | 3.64 | 16.7 | Very smooth |
| Luna | Fully porous | 3.0 | 3.37 | 15.0 | Very smooth |
| Zorbax | Fully porous | 3.5 | 3.45 | 15.9 | Rough |
| Halo | Core–shell | 2.7 | 2.67 | 3.4 | Very rough |
| Kinetex | Core–shell | 2.6 | 2.51 | 3.9 | Smooth |
| Poroshell | Core–shell | 2.7 | 2.61 | 9.3 | Rough |
3.2 Nitrogen physisorption
Nitrogen physisorption data were recorded to derive parameters related to the mesoporosity of the adsorbents such as the surface area and mesopore volume (Fig. 4). For data evaluation the NLDFT method was chosen and utilized to calculate the PSD for all materials under study. A cylindrical mesopore shape was assumed with respect to the synthesis55,57,59 and the complementary analysis of similar systems.60–62 In addition, sorption data were evaluated by the classical BET approach to specific surface areas. Table 2 summarizes these results as obtained with the Quantachrome software, including specific surface area, specific pore volume, and intraparticle porosity of the materials, as well as the average pore size estimated with the BJH approach (using the desorption branch) and the mode of the PSD determined with the NLDFT method (using both adsorption and desorption branches of N2 isotherms). Total mesopore volume was estimated from nitrogen adsorbed at P/P0 = 0.98. The isotherm shape (Fig. 4) is typical of mesoporous adsorbents and shows a marked hysteresis loop (type IV isotherms).63 No microporosity was indicated from the sorption analysis. Regardless, the curve of the PSD for pores <40 Å seems to be at unrealistically small values, a problem that has been found before for materials with small or negligible microporosity and is possibly a consequence of the inappropriate fitting of the isotherm in this area. | ||
| Fig. 4 Nitrogen physisorption isotherms of the fully porous (a) and core–shell particles (b). Lines connecting the data points serve as a guide to the eye. | ||
| Physisorption | SAXS | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Chromatographic adsorbent | Average pore diameter (BJH)a (Å) | Pore diameter (mode) (NLDFT-ads) (Å) | Pore diameter (mode) (NLDFT-des) (Å) | Surface area (BET) (m2 g−1) | Total mesopore volume (cm3 g−1) | Porosity ϕ (from total pore volume) | l v (Å) | l w (Å) | Surface area (m2 g−1) |
| a The BJH pore diameter was calculated from the desorption branch. | |||||||||
| Atlantis | 111.2 | 104.9 | 104.9 | 232 | 0.64 | 0.59 | 114.2 | 80.5 | 225 |
| Luna | 93.8 | 91.0 | 81.5 | 210 | 0.49 | 0.52 | 94.7 | 87.1 | 208 |
| Zorbax | 90.0 | 70.3 | 81.5 | 112 | 0.25 | 0.36 | 91.1 | 164.1 | 111 |
| Halo | 83.1 | 73.1 | 94.2 | 127 | 0.26 | 0.37 | 82.2 | 141.3 | 128 |
| Kinetex | 110.5 | 94.2 | 121.2 | 97 | 0.27 | 0.37 | 109.6 | 185.4 | 98 |
| Poroshell | 116.9 | 91.0 | 104.9 | 77 | 0.22 | 0.33 | 115.5 | 233.7 | 78 |
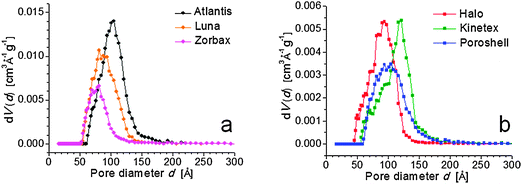
The average mesopore size of the studied adsorbents varies between 80 and 120 Å. The PSD determined by the NLDFT approach covers an overall range of ca. 50–150 Å (Fig. 5) and no significant difference is noticeable for the two particle types (fully porous and core–shell). As a consequence, the mesopore size is not affected by the inclusion of a solid core in the particle structure. Surface area and pore volume, by contrast, are expected to change with the particle architecture unless the shell structure of the core–shell particles significantly differs from the structure of the fully porous particles. As can be inferred from Fig. 2, only the porous shell contributes to the surface and pore volume. The solid core accounts for the specific mass of a material and in this way affects specific pore volume data. Thus, from a chromatographer's viewpoint, only the characteristic of the porous shell is relevant. Especially the PSD (e.g., by its width) is important for the effective diffusivity of analytes in the particles, which usually dominates intraparticle mass transfer resistance in chromatographic practice.3,4,64,65 For the two particle types under study (fully porous and core–shell) no major difference regarding their PSDs was observed. According to the NLDFT results, the width of a PSD varies slightly for each particle brand.
In contrast, the surface areas and total pore volumes follow a clear trend (Table 2). Values of both parameters are significantly higher, up to 230 m2 g−1 and 0.65 cm3 g−1, for the fully porous than for the core–shell particles, which reach ∼100 m2 g−1 and 0.25 cm3 g−1. The larger overall pore volume is also reflected in the cumulative pore volume of the particles displayed in Fig. 6. But particles within the two groups also show distinct differences. For example, the Zorbax particles are just as porous as the core–shell materials and among the core–shell particles the surface area varies significantly.
Pore diameters obtained with NLDFT and BJH methods agree well. For example, 111 Å (BJH model, desorption branch, average pore size) and 105/105 Å (NLDFT, adsorption/desorption branch, mode of PSD) are found as mesopore size for the Atlantis particles, and for the Halo particles the values are 83 Å and 73/94 Å, respectively. This latter difference appears to be large, but the PSD's mode derived by the NLDFT approach only refers to the local maximum of the curve. It should be noted that local maxima (spikes) are observed in the differential PSD (Fig. 5); however, they are caused by the mathematical evaluation procedure (the first derivative of the cumulative pore volume vs. pore size) and the limited number of data points; they have no physical meaning. A reasonable agreement is observed when the shape of the NLDFT derived PSDs is compared (see ESI,† Fig. S1). Therefore, the comparison of cumulative pore volume plots can be more appropriate in a discussion of PSDs, because they are not affected by mathematical differentiation. For all materials we did not observe significant differences in the shape of the PSDs derived from the NLDFT method using the adsorption or the desorption branch, which is an indication of the lack of pore blocking effects in the mesoporous structures. The PSD derived from the BJH approach often showed an unrealistically small peak, for that reason regarding the PSD we prefer the NLDFT evaluation.17
The physisorption data also confirm the predictable geometric effect that a smaller pore size considerably increases the surface area (if the total pore volume remains constant), as can be seen for the Halo and Kinetex particles. While their total pore volume is nearly identical, the BET surface area increases by 30 m2 g−1 for the Halo particles due to a decrease in the pore size from 111 to 83 Å. Mesopore diameters of most commercial fully porous HPLC silicas usually are between 60 and 150 Å, with surface areas in the range of 120–450 m2 g−1. Pore volumes of porous particles are typically between 0.5 and 1.2 cm3 g−1.66 All of the studied fully porous particles fall into this conventional mesoporosity regime.
3.3 SAXS experiments
To obtain a quantitative description of the mesopore space without assuming a specific pore model, the CLD concept was applied to the SAXS data. Evaluation of CLD g(r) from the SAXS data is based on the parameterization (“fitting”) of the experimental scattering data by means of analytical basis functions.30 Model functions are created which are successively adjusted to fit experimental data by application of standard fitting and regularization methods. From the fitting parameters, various structural parameters can be derived, especially the Porod length lp.22The SAXS patterns of the mesoporous silicas are depicted in Fig. 7. In the double-logarithmic plot it can be seen that the curves follow Porod's law, i.e., the intensity I(s) is proportional to s−4 for larger values of s. Slight deviations from ideal Porod behavior were addressed using a background correction tool. The data showed a constant additive background resulting from three-dimensional electron density fluctuations, a reasonable assumption for amorphous silica. After correction, Porod plots for all samples reached a plateau with the data points fluctuating only slightly around the Porod constant, providing a sufficiently high quality of the data. The complete fitting process is illustrated in Fig. 8.
 | ||
| Fig. 7 Double-logarithmic plot of the SAXS patterns of the fully porous (a) and core–shell particles (b). For better visualization curves were slightly shifted with respect to each other. | ||
The I(s) curves themselves do not display any distinct features. None of the scattering curves shows a pronounced interference maximum; this is indicative of a random mesopore structure of the adsorbents. The sole conclusion that can be drawn from the SAXS pattern is that the weak scattering intensity for s > 0.35 nm−1 also points to the absence of a larger number of micropores (as micropores are expected to generate SAXS intensity for scattering vectors larger than ∼0.4 nm−1).33 The CLD concept applied to such SAXS data reveals structural features, as seen in Fig. 9, although care has to be taken when interpreting the CLDs: maxima and minima visible in a CLD do not necessarily directly reveal the corresponding sizes of the pores and pore walls.
 | ||
| Fig. 9 Chord length distributions g(r) (panels a and b) and the representation g(r)r (panels c and d) for fully porous (a, c) and core–shell particles (b, d) calculated from SAXS data shown in Fig. 7. | ||
In general, the CLD is a superposition of the distributions of the pores (void) and the walls (solid). Their apparent first maximum for r < 10 nm (Fig. 9) therefore might be interpreted as corresponding to the average diameter of the pores, respectively, pore walls. The subsequent minima and maxima between 10 and 25 nm possibly reflect chords penetrating two (or more) interfaces, thus corresponding to “pore(s) plus pore wall”, respectively. Such an assignment is speculative for disordered pore systems and should be validated using independent methods, e.g., high-resolution TEM measurements.
The slight dip at r < 2 nm is an artifact that arises from the background correction, as can be seen in the g(r)r plots (Fig. 9c and d). The g(r)r plot points out the most prominent pore size (respectively wall size) of a system. In addition, the representation as g(r)r helps to visualize which pore size actually contributes to the inner surface of the porous sample. All CLDs show their most relevant contributions at lengths between 2 and 20 nm.
For Atlantis and Luna as well as the Poroshell particles no distinct minima can be observed in the CLD, whereas CLDs of Zorbax, Halo, and Kinetex show slight oscillations. A pronounced oscillation indicates a higher order in the system and, in the extreme case, results in a Bragg peak in the SAXS pattern. Yet, none of the samples shows such a Bragg peak, but the SAXS pattern of the Zorbax particles includes at least a slight shoulder due to a preferred average distance between the mesopores (Fig. 7, s ∼ 0.07 nm−1).
More information can be obtained from the CLDs' first moment, the Porod length lP. Using lP and eqn (5), the average pore size lv and the average wall thickness lw of the porous samples can be calculated (Table 1). The porosity ϕ in this equation corresponds to the total mesopore volume measured by physisorption at P/P0 = 0.98. (This value can only be used if all pores of the studied material are accessible, an assumption that requires further verification and is still matter of current research (e.g., using in-situ sorption/SAXS experiments).) The resulting pore sizes lv are in very good agreement with the average pore size value found by nitrogen physisorption NLDFT analysis. In accordance with this calculation the Poroshell particles have the largest average pore size and wall thickness, which is also reflected by their CLD. The first peak maximum for this particle type is located at a higher r-value than for any other of the studied samples. Though, for a more systematic quantitative interpretation of the CLD knowledge about the pore (wall) morphology is required.
As mentioned before, the CLD derived from the SAXS pattern contains characteristic lengths of the pore wall (solid phase) and the pores (void space). Thus, it is not possible to determine the PSDs of the samples directly from their CLDs without further assumptions or information. The bimodal characteristics of the CLD are strongly pronounced for Halo and Kinetex and less for Zorbax and Poroshell. For Atlantis and Luna relatively narrow maxima in the CLD can be found. This could be due to the fact that the calculated pore size lv and wall thickness lw are very similar (the difference lv–lw is only 10–30 Å). The maximum in the CLD is noticeably broader for the Zorbax and the core–shell particles, whose lv–lw difference is between 60 and 120 Å.
Additionally, with eqn (2) the surface area per weight unit of a material can be estimated. After solving the equation for S one arrives at
 | (6) |
In eqn (6), V stands for the total irradiated sample volume (sum of pore volume and volume of the solid silica walls) per weight unit. ϕ stands for the porosity measured by physisorption, as mentioned before. Surface areas obtained with eqn (6) perfectly match the surface areas derived from physisorption analysis, as summarized in Table 2. SAXS and CLD approaches do not rely on an accessibility of the pores, in contrast to nitrogen sorption analysis, this indicates that the number of inaccessible pores should be negligible.
The CLD at small r (<2 nm) is controlled by the general structure of the solid–void interface (edges, curvature, vertices) and the presence of small structural features, especially micropores. Hence, an interesting parameter of the CLDs is their g(0) values. In contrast to, e.g., porous carbons,26g(0) of the studied particles is close to zero. g(0) is an indicator of the degree of angularity in the samples. As reported by Ciccariello et al.67–70 a value of g(0) > 0 hints towards angular structures. A sphere's CLD is characterized by g(0) = 0, which is also the case for polydisperse spheres. In conclusion, narrow slit pores and a larger microporosity, found in the aforementioned porous carbons, cannot be identified for the investigated porous silicas. This agrees with the nitrogen physisorption analysis and provides further evidence for the absence of microporosity in these materials.
4. Conclusions
We applied state-of-the-art nitrogen physisorption with NLDFT analysis and the SAXS/CLD approach to the pore space characterization of mesoporous chromatographic adsorbents, i.e., fully porous and core–shell particles. The particles feature a disordered mesoporosity without defined pore shape and size. The main purpose of this study was to demonstrate a correlation between two important quantitative parameters (surface area and mean pore size), as obtained with independent methods of pore size evaluation based on SAXS and nitrogen physisorption experiments. Our results confirm that both approaches provide similar data, regardless of the methods' different underlying concepts.While the evaluation of the SAXS data using the CLD approach does not require assumptions about the geometrical shape of the pores and walls, it does not allow a simple interpretation of the CLDs' maximum. The mesopore volume obtained from nitrogen adsorption experiments is required for quantitative interpretation of the CLDs, providing the mean mesopore size and specific surface area. Using the Porod length in addition to the pore size, even the wall size can be derived from SAXS data (which cannot be obtained by sorption or mercury intrusion analysis). Our results will be helpful to users of physisorption analysis, which depends on the evaluation method (BJH or NLDFT), selected pore geometry and the chosen isotherm branch. For the adsorbents studied in this work the NLDFT analysis with a cylindrical pore model was found to be most suitable. The presented analysis is not limited to these adsorbents, which are ideally suited to study disordered mesoporous systems due to their reproducible characteristics. The employed particles exemplarily illustrate the diversity of issues that have to be addressed.
Acknowledgements
Parts of this research were carried out at the light source DORIS III at DESY, Hamburg, a member of the Helmholtz Association (HGF). We would like to thank Christoph Weidmann for help in the SAXS measurements at HASYLAB beamline BW 4. This project was supported by the Laboratory of Materials Research (LaMa) at Justus-Liebig-Universität Giessen and by the Deutsche Forschungsgemeinschaft DFG (Bonn, Germany) under grant TA 268/5.References
- S. Bruns, D. Stoeckel, B. M. Smarsly and U. Tallarek, J. Chromatogr. A, 2012, 1268, 53 CrossRef CAS PubMed.
- A. Daneyko, A. Höltzel, S. Khirevich and U. Tallarek, Anal. Chem., 2011, 83, 3903 CrossRef CAS PubMed.
- U. Tallarek, F. J. Vergeldt and H. Van As, J. Phys. Chem. B, 1999, 103, 7654 CrossRef CAS.
- U. Tallarek, E. Rapp, A. Seidel-Morgenstern and H. Van As, J. Phys. Chem. B, 2002, 106, 12709 CrossRef CAS.
- S. Bruns, J. P. Grinias, L. E. Blue, J. W. Jorgenson and U. Tallarek, Anal. Chem., 2012, 84, 4496 CrossRef CAS PubMed.
- S. Khirevich, A. Höltzel, A. Seidel-Morgenstern and U. Tallarek, Anal. Chem., 2009, 81, 7057 CrossRef CAS PubMed.
- G. Guiochon and F. Gritti, J. Chromatogr. A, 2011, 1218, 1915 CrossRef CAS PubMed.
- K. K. Unger and A. I. Liapis, J. Sep. Sci., 2012, 35, 1201 CrossRef CAS PubMed.
- J. J. De Stefano, T. J. Langlois and J. J. Kirkland, J. Chromatogr. Sci., 2008, 46, 254 CAS.
- J. W. Thompson, J. S. Mellors, J. W. Eschelbach and J. W. Jorgenson, LCGC North Am., 2006, 24, 16 CAS.
- Y. Yao and A. M. Lenhoff, J. Chromatogr. A, 2004, 1037, 273 CrossRef CAS PubMed.
- M. Thommes, Chem. Ing. Tech., 2010, 82, 1059 CrossRef CAS.
- P. J. Branton, P. G. Hall, K. S. W. Sing, H. Reicher, F. Schüth and K. K. Unger, J. Chem. Soc., Faraday Trans., 1994, 90, 2965 RSC.
- L. Hagel, M. Ostberg and T. Andersson, J. Chromatogr. A, 1996, 743, 33 CrossRef CAS.
- A. V. Neimark and P. I. Ravikovitch, Microporous Mesoporous Mater., 2001, 44, 697 CrossRef.
- P. I. Ravikovitch and A. V. Neimark, Colloids Surf., A, 2001, 187, 11 CrossRef.
- M. Thommes, B. M. Smarsly, M. Groenewolt, P. I. Ravikovitch and A. V. Neimark, Langmuir, 2006, 22, 756 CrossRef CAS PubMed.
- W. Gille, D. Enke, F. Janowski and T. Hahn, J. Porous Mater., 2003, 10, 179 CrossRef CAS.
- A. Guinier and G. Fournet, Small-Angle Scattering of X-Rays, John Wiley & Sons, New York, 1955, ch. 2 Search PubMed.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Plenum Press, New York, 1987, ch. 2 Search PubMed.
- O. Glatter and O. Kratky, Small Angle X-ray Scattering, Academic Press, London, 1982, ch. 1 Search PubMed.
- B. Smarsly, M. Groenewolt and M. Antonietti, Prog. Colloid Polym. Sci., 2005, 130, 105 CAS.
- B. M. Smarsly, H. Kaper, S. Mascotto and C. Weidmann, Chem. Ing. Tech., 2010, 82, 823 CrossRef CAS.
- S. Förster, A. Timmann, M. Konrad, C. Schellbach, A. Meyer, S. S. Funari, H. Nakamura, P. Mulvaney and R. Knott, J. Phys. Chem. B, 2005, 109, 1347 CrossRef PubMed.
- W. Ruland and B. Smarsly, J. Appl. Crystallogr., 2005, 38, 78 CrossRef.
- W. Ruland and B. Smarsly, J. Appl. Crystallogr., 2007, 40, 409 CrossRef CAS.
- B. Smarsly, C. Göltner, M. Antonietti, W. Ruland and E. Hoinkis, J. Phys. Chem. B, 2001, 105, 831 CrossRef CAS.
- J. Méring and D. J. Tchoubar, J. Appl. Crystallogr., 1968, 1, 153 CrossRef.
- C. Burger and W. Ruland, Acta Crystallogr., Sect. A: Found. Crystallogr., 2001, 57, 482 CrossRef CAS PubMed.
- B. Smarsly, M. Antonietti and T. Wolff, J. Chem. Phys., 2002, 116, 2618 CrossRef CAS PubMed.
- R. Perret and W. J. Ruland, J. Appl. Crystallogr., 1970, 3, 525 CrossRef CAS.
- S. Torquato and B. Lu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 2950 CrossRef.
- S. Mascotto, D. Wallacher, A. Kuschel, S. Polarz, G. A. Zickler, A. Timmann and B. M. Smarsly, Langmuir, 2010, 26, 6583 CrossRef CAS PubMed.
- W. Gille and A. Braun, J. Non-Cryst. Solids, 2003, 321, 89 CrossRef CAS.
- B. Smarsly, C. Göltner, M. Antonietti, W. Ruland and E. Hoinkis, J. Phys. Chem. B, 2001, 105, 831 CrossRef CAS.
- C. G. Göltner, B. Smarsly, B. Berton and M. Antonietti, Chem. Mater., 2001, 13, 1617 CrossRef.
- S. Mascotto, D. Wallacher, A. Brandt, T. Hauss, M. Thommes, G. A. Zickler, S. S. Funari, A. Timmann and B. M. Smarsly, Langmuir, 2009, 25, 12670 CrossRef CAS PubMed.
- D. Enke, F. Janowski, W. Gille and W. Schwieger, Colloids Surf., A, 2001, 187–188, 131 CrossRef CAS.
- W. Gille, D. Enke and F. Janowski, J. Porous Mater., 2002, 9, 221 CrossRef CAS.
- W. Gille, O. Kabisch, S. Reichl, D. Enke, D. Fürst and F. Janowski, Microporous Mesoporous Mater., 2002, 54, 145 CrossRef CAS.
- B. Smarsly, M. Thommes, P. I. Ravikovitch and A. V. Neimark, Adsorption, 2005, 11, 653 CrossRef PubMed.
- S. Bruns and U. Tallarek, J. Chromatogr. A, 2011, 1218, 1849 CrossRef CAS PubMed.
- S. Bruns, A. Höltzel and U. Tallarek, LCGC North Am., 2013, 31, 486 CAS.
- S. Bruns, T. Hara, B. M. Smarsly and U. Tallarek, J. Chromatogr. A, 2011, 1218, 5187 CrossRef CAS PubMed.
- K. Hormann and U. Tallarek, J. Chromatogr. A, 2013, 1312, 26 CrossRef CAS PubMed.
- S. Bruns, E. G. Franklin, J. P. Grinias, J. M. Godinho, J. W. Jorgenson and U. Tallarek, J. Chromatogr. A, 2013, 1318, 189 CrossRef CAS PubMed.
- S. V. Roth, R. Döhrmann, M. Dommach, M. Kuhlmann, I. Kröger, R. Gehrke, H. Walter, C. Schroer, B. Lengeler and P. Müller-Buschbaum, Rev. Sci. Instrum., 2006, 77, 085106 CrossRef PubMed.
- T. C. Huang, H. Toraya, T. N. Blanton and Y. Wu, J. Appl. Crystallogr., 1993, 26, 180 CrossRef CAS.
- A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Häusermann, High Pressure Res., 1996, 14, 235 CrossRef.
- G. A. Zickler, S. Jähnert, S. S. Funari, G. H. Findenegg and O. Paris, J. Appl. Crystallogr., 2007, 40, s522 CrossRef CAS.
- G. A. Zickler, S. Jähnert, W. Wagermaier, S. S. Funari, G. H. Findenegg and O. Paris, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 184109 CrossRef.
- P. Levitz and D. J. Tchoubar, J. Phys. I, 1992, 2, 771 CrossRef CAS.
- P. Levitz, Adv. Colloid Interface Sci., 1998, 76–77, 71 CrossRef CAS.
- G. Porod, in Small Angle X-ray Scattering, ed. O. Glatter and O. Kratky, Academic Press, London, 1982, pp. 17–51 Search PubMed.
- K. K. Unger, D. Kumar, M. Grün, G. Büchel, S. Lüdtke, Th. Adam, K. Schumacher and S. Renker, J. Chromatogr. A, 2000, 892, 47 CrossRef CAS.
- W. Stoeber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62 CrossRef CAS.
- J. J. Kirkland, F. A. Truszkowski, C. H. Dilks Jr. and G. S. Engel, J. Chromatogr. A, 2000, 890, 3 CrossRef CAS.
- F. Gritti, T. Farkas, J. Heng and G. Guiochon, J. Chromatogr. A, 2011, 1218, 8209 CrossRef CAS PubMed.
- Z. A. ALOthman, Materials, 2012, 5, 2874 CrossRef CAS.
- L. D. Gelb and K. E. Gubbins, Langmuir, 1999, 15, 305 CrossRef CAS.
- B. Smarsly, S. Polarz and M. Antonietti, J. Phys. Chem. B, 2001, 105, 10473 CrossRef CAS.
- F. Gritti, I. Leonardis, J. Abia and G. Guiochon, J. Chromatogr. A, 2010, 1217, 3819 CrossRef CAS PubMed.
- S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area and Porosity, Academic Press, London, 2nd edn, 1982, ch. 3 Search PubMed.
- F. Gritti and G. Guiochon, Anal. Chem., 2006, 78, 5329 CrossRef CAS PubMed.
- F. Gritti and G. Guiochon, Anal. Chem., 2009, 81, 2723 CrossRef CAS PubMed.
- I. Rustanmov, T. Farcas, F. Ahmed, F. Chan, R. LoBrutto, H. M. McNair and Y. V. Kazakevich, J. Chromatogr. A, 2001, 913, 49 CrossRef.
- S. Ciccariello, G. Cocco, A. Benedetti and S. Enzo, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6474 CrossRef CAS.
- S. Ciccariello and A. Benedetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 6384 CrossRef CAS.
- S. Ciccariello, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 398 CrossRef.
- S. Ciccariello and R. Sobry, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 60 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp55072a |
| This journal is © the Owner Societies 2014 |