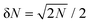A cell-model study on counterion fluctuations in macroionic systems: effect of non-extensiveness in entropy
Yiing-Rei
Chen
a and
Chi-Lun
Lee
*b
aDepartment of Physics, National Taiwan Normal University, Taipei 11677, Taiwan
bDepartment of Physics, National Central University, Jhongli 32001, Taiwan. E-mail: chilun@ncu.edu.tw
First published on 21st October 2013
Abstract
Rigorously speaking, entropy is slightly non-extensive, and this non-extensiveness, which characterizes the degree of fluctuations, can contribute to effective interactions between mesoscopic objects. In this paper, we consider a pair of macroions, each accompanied by 1000 counterions, and with a cell-model description we demonstrate that the slow variation of non-extensiveness in counterion entropy over macroionic distance leads to an effective long-range attraction between the macroions. With the aid of Monte Carlo simulation and a Bragg–Williams theory including counterion number fluctuations, we find the depth of attraction in free energy to be approximately 0.2kBT. The observation in our cell-model study provides an insight for further understanding of effective interactions in real macroionic systems.
1 Introduction
The phenomenon of the so-called “like-charge attraction” has been observed in systems of colloidal particles1–7 and other macroionic systems8–12 in low ionic strength, and has been under debate for decades.13–25 It was first observed in a solution that is confined between glass walls with a narrow separation,1–3 and in metastable colloidal crystals4 as well. While like-charge attractions have not been observed in bulk colloidal solutions in earlier works, quite recent experiments6,7 did show effective attractions between colloidal pairs in the bulk. For example, Tata et al. used a confocal laser scanning microscope and found like-charge attraction between colloidal particles deep in the solution6 (up to 150 micrometers.) In their experiment, stable colloidal pairs can be observed for up to 7 seconds. On the other hand, due to its long-range nature, currently this effective interaction might be hardly resolved via direct-force measurements using optical tweezers, since the gradient of energy in the scale of thermal magnitude over a few micrometers is in the order of femtonewtons, while the resolution of current optical tweezer measurements is in piconewtons.Such like-charge attraction exists peculiarly when the counterions are monovalent, and its range is often in the order of the macroionic size, far beyond the range van der Walls interaction can account for. This relatively long-range attraction among macroions is generally believed to result from an electrostatic origin. While no definite answer is given, mechanisms of the attractive force among these mesoscopic objects have been proposed by the Sogami–Ise theory,13,15 the collective fluctuations of counterions,26–28 possible charge inversions in colloids,17 and even hydrodynamic effects of the confining glass plates.19 For colloids at the air–water interface it has also been demonstrated that the seemingly attractive force could arise from electrostatic interactions, either the meta-stabilization of the system due to competitions among various sources of repulsion among and within colloidal clusters,29 or the pairwise attractions among in-plane dipoles that are created from surface heterogeneity.30
In this work we introduce a new mechanism that gives rise to an effective like-charge attraction between macroions under the cell-model description. We choose to study a system of two macroions, each accompanied by a large number of counterions, and we focus on the impact of counterion entropy for cases where the two macroionic clouds do not overlap. To start our discussion, we first demonstrate in Section 2 via a very simple ideal-gas model that entropy does increase upon joining particles over two compartments. This entropy increase, or the “non-extensive entropy” as we name it, arises from particle number fluctuations over partitioned volumes. In Section 3 we proceed to extend from the ideal gas scenario to an analogous two-macroion system, where electrostatic interactions must be considered. While counterion number fluctuations always exist, the degree of fluctuations varies over the macroionic separation distance. We study this behavior with the aid of Monte Carlo simulations in Section 4, and derive in Section 5 the corresponding non-extensive entropy using a Bragg–Williams (BW) theory that includes counterion number fluctuations.
Our result from computer simulations reveals a very long-range decay in counterion number fluctuation, which suggests an entropic mechanism that drives the two macroions to approach each other. The features extracted from the simulation result are then used in our BW theory, where we derive the thermodynamic quantities needed to confirm the dominant role of this entropic attraction. Note that our mechanism works in the regime where the cells do not overlap, such that other entropic interactions such as the DLVO osmotic repulsive force31 becomes insignificant.
2 Non-extensiveness in entropy: an ideal-gas scenario
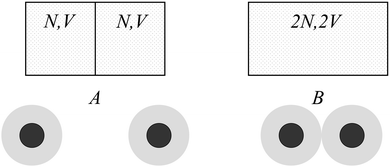
The existence of a non-extensive term in entropy can be demonstrated via a simple ideal-gas lattice model as depicted in Fig. 1. Consider N identical particles distributed among V lattice sites in each of the two compartments. We assume no pairwise interaction and allow multiple occupancies at each lattice site. Originally, there exists a partition between the two compartments, as particles cannot move across this partition. Thus the original total entropy of the system is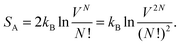 | (1) |
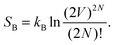 | (2) |
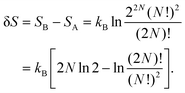 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N! ≈ N
N! ≈ N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N − N, eqn (3) becomes
N − N, eqn (3) becomesδS ≈ kB{2N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 − [2N 2 − [2N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2N) + 2N] + 2(N (2N) + 2N] + 2(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N − N)} = 0. N − N)} = 0. | (4) |
On the other hand, a more accurate estimate can be obtained if one would care for a better-off description of Stirling's approximation:32
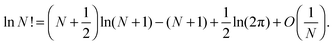 | (5) |
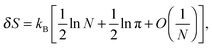 | (6) |
The existence of non-extensiveness in entropy can be understood from the number fluctuations of particles over two sides. For example, one can distribute 100 particles in a merged box such that there are half on each side. On the other hand, one can also distribute in a way that 49 particles are on the left and 51 on the right. The combinations of these distributions with unequal amount of particles give rise to the difference in entropy between the bisected and merged conditions as depicted in Fig. 1.
The contribution of δS is often neglected in the consideration of bulk thermodynamics since it is relatively tiny compared with bulk terms. As examples, δS ≈ 5.2kB for N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and δS ≈ 4.0kB for N = 1000. However, such entropy difference can be relevant if one aims to study the effective interaction between a pair of ‘big’ (mesoscopic) objects. The dependence of δS on N is shown in Fig. 2 for the simple ideal-gas model introduced in this section, while the numerical values of δS are computed viaeqn (3) directly. The linear increase over ln
000 and δS ≈ 4.0kB for N = 1000. However, such entropy difference can be relevant if one aims to study the effective interaction between a pair of ‘big’ (mesoscopic) objects. The dependence of δS on N is shown in Fig. 2 for the simple ideal-gas model introduced in this section, while the numerical values of δS are computed viaeqn (3) directly. The linear increase over ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N can be understood from the refined approximation in eqn (6). Meanwhile, the non-extensiveness of δS is shown in the inset, as δS/(NkB) exhibits a monotonic decrease over N.
N can be understood from the refined approximation in eqn (6). Meanwhile, the non-extensiveness of δS is shown in the inset, as δS/(NkB) exhibits a monotonic decrease over N.
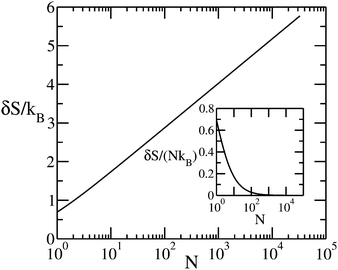 | ||
| Fig. 2 The “non-extensive entropy” δS versus N plot for an ideal gas. The non-extensive entropy, as given in eqn (3), is defined as the entropy increase when joining together identical particles from the two volumes, as illustrated in Fig. 1. The entropy increase results from counterion number fluctuations over the two sides. The non-extensive entropy per particle δS/(NkB) is shown in the inset. | ||
3 Analogy in a system with two macroions
For a solution of charged colloidal particles, there are approximately ten thousand neutralizing counterions surrounding each host colloidal particle. In the salt-free case, the sparse dehydrated water ions contribute to a Debye screening length of the order of one micrometer. Thus counterions form micrometer-sized clouds about colloidal particles in such case. The average distance among neighboring counterions is of several tens of nanometers, which is significantly larger than the Bjerrum length lB (≈7 Å in aqueous solutions). Therefore the pairwise electrostatic interactions of counterions are individually rather weak, and the ideal-gas approximation in entropy for the DLVO or Debye–Hückel theory stays quite legitimate. Nevertheless, since extensiveness in entropy is naturally adopted in the DLVO theory,34 it neglects possible effects due to local counterion density fluctuations.To study the effect of counterion fluctuations, we first make a crude analogy between a system of two macroions and the ideal-gas scenario introduced in the previous section. In the two-macroion system, each macroion is dressed with a net charge of −Ne on its surface and charge-compensated by +N monovalent cations that form a neighboring cloud of volume V. While the clouds sit far apart, it can be compared to the ideal-gas case where the partition exists between the two compartments; while the clouds meet, it can be compared to the case where the partition is removed, as illustrated in Fig. 1.
The analogy we have made, between the system of two macroions with counterions and the ideal-gas scenario, is based on the assumption that the counterions cannot transfer from one cell to the other when the macroions are far apart, as if there exists a partition in between. As the macroions get closer, the counterion clouds eventually meet, as if the partition is removed. In reality counterions do transfer between clouds even when the clouds are held apart. In addition, the electrostatic interaction certainly plays a role in the change of such non-extensive entropy, in the sense that it would suppress large number fluctuations in counterions. With this consideration, the macroionic distance d becomes a crucial parameter since it mediates the degree of suppression over counterion number fluctuations. It is therefore important to further study the non-extensive contribution in entropy in the macroionic system by considering electrostatic interactions. We shall show in the following sections that when macroions sit far apart, the counterion number fluctuations get more suppressed due to the penalty in electrostatic energy, and this suppression leads to a smaller total entropy.
4 Monte Carlo simulations
For the purpose as explained, we perform Monte Carlo simulations over a system of two macroions using the cell model,33 where each cell represents a counterion cloud as illustrated in Fig. 1. For simplicity we use dimensionless variables, by setting R1 = 1 for the radius of the non-penetrable macroions, and R2 = 2 for the radius of the concentric sphere that defines the outer boundary and confines the counterions. The reason that we choose the thickness of the counterion cloud to be R is in view of the fact that it matches the scale of the Debye–Hückel screening length in a salt-free solution with dissociated water ions only. We consider a total of 2N monovalent counterions, while each macroion is dressed by a net charge −N uniformly distributed over its surface. The dimensionless temperature, which tells the thermal fluctuation in measures of electrostatic strength, is defined by t ≡ R/lB. In our simulations we use t = 100 and N = 1000, which correspond to a Bjerrum length close to that in a typical aqueous solution.The counterions are approximated as point-like particles, and the energy Hamiltonian is equal to the summation of electrostatic interactions among all charge species. In each trial the system updates the position (x, y, z) of a randomly picked counterion to a neighboring point (x′, y′, z′), while x′∈(x − δ, x + δ), y′∈(y − δ, y + δ), and z′∈(z − δ, z + δ) with uniform probability distribution, while we set δ = 0.01. The success rate of the update is judged by the requirement that the chosen counterion stays inside the cell, as well as the Metropolis algorithm, which weighs the change in energy including both intra- and inter-cell electrostatic interactions.
Since in real macroionic systems the number of counterions inside a cell is not strictly conserved, to enable number fluctuations in the simplest manner, we consider beyond the usual cell-model description an additional “jumping” algorithm that allows the chosen counterion to switch to the other cell. This jumping algorithm is performed with a probability p = 0.1, i.e., on average, one jump occurs in every ten trial updates, and the algorithm is executed regardless of the macroionic separation distance d. When it occurs, the chosen counterion jumps to the same relative position on the other cell. For each parameter setting, we acquire averaged quantities we need from 1010 Monte Carlo simulation steps.
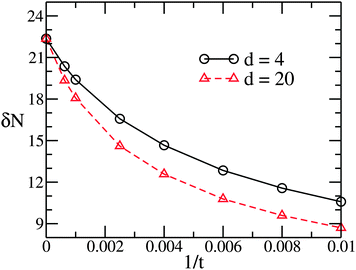
From our simulation result, we first find in Fig. 3 that the observed δN is smaller than that in the ideal-gas case, the latter corresponding to the high-temperature limit t−1 = 0. For example, in case N = 1000 the quantity δN drops from its ideal-gas value 22.36 to 10.60 at t = 100 for the case d = 4, whereas the ideal-gas result is evaluated using the formula 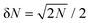 . A similar trend is observed at the far-separation case d = 20 as well. This deficit arises simply from the fact that configurations of large number fluctuations lead to stronger violation of charge neutrality within each cell, and therefore are energetically unfavored at lower temperature.
. A similar trend is observed at the far-separation case d = 20 as well. This deficit arises simply from the fact that configurations of large number fluctuations lead to stronger violation of charge neutrality within each cell, and therefore are energetically unfavored at lower temperature.
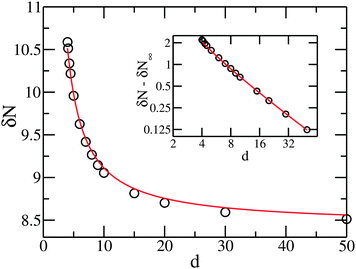
Fig. 3 and 4 also indicate that the number fluctuation decreases with increasing separation d, but still stays at the same order of magnitude in the far-separation case d = 20. Therefore, rigorously speaking, the bisected-cell scenario in our arguments in Section 2 cannot be compared directly to the far-separation case in macroions. Nevertheless, the decrease in δN over d, as shown in Fig. 4, suggests that the counterion number fluctuation gets more suppressed as the separation distance between cells increases.
The mechanism that leads to the trend of δN is mostly guided by the Coulomb penalty, and illustrated as follows by the two extreme cases. As two macroions get close enough to each other, so their counterion clouds merge, there exist more available counterion distribution configurations that satisfy the overall charge neutral condition without a huge energy penalty. On the other hand, when the two macroions are far apart, the number fluctuation, and therefore the number of available configurations are suppressed, since it's the charge neutral condition over each macroion that the system has to satisfy.
To derive a crude estimate for the non-extensive entropy δS as introduced in eqn (3) for our macroionic system with rather loosened constraints, we first denote ΩN−δN′,N−δN′ for the number of configurations to distribute N − δN′ counterions in the left cell and N + δN′ in the right. Using the ideal-gas approximation, one has
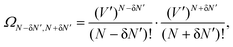 | (7) |
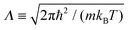 is the thermal wavelength. And δS can be approximated as
is the thermal wavelength. And δS can be approximated as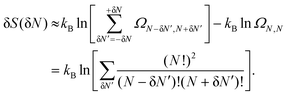 | (8) |
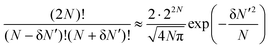 | (9) |
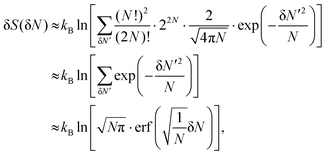 | (10) |
| δS(δN = 10.60) − δS(δN = 8.70) ≈ 0.186kB, | (11) |
Most important of all, as shown in Fig. 4 for distances up to d = 50, the decay of δN, and therefore the non-extensive part in entropy δS, is indeed long-range. The inset of Fig. 4 shows the logarithmic plot, where the d > 8 data form a straight line and a power law of d−1. Note that in this inset plot, the asymptotic number fluctuation δN∞, simulated with d = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, is subtracted from δN.
000, is subtracted from δN.
This entropic trend, while it has never been investigated in previous studies, implies a very long-range effective interaction, and therefore may serve as a candidate of the so-called “like-charge attraction” among colloids and other macroionic systems. However, we should use caution here and point out that, the resolution of total electrostatic energy in our simulations is no better than the magnitude of the thermal energy. Therefore, a free energy that can make a distinction between the short- (d = 4) and long-distance (d = 20) cases with a resolution less than kBT, is needed to confirm the dominant contribution from our entropic mechanism. This is what we will provide, via a BW partition function, in the next section.
5 A Bragg–Williams theory with counterion number fluctuation
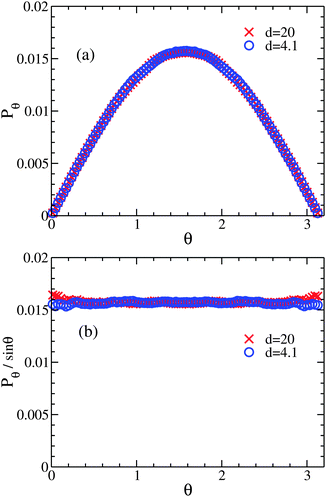
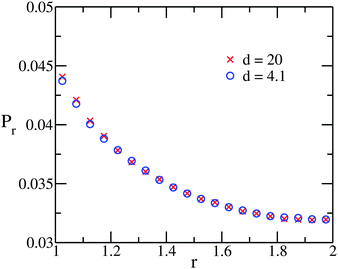
We shall now proceed, with the thermodynamic quantities extracted from our simulation data, to construct a theoretical partition function model within the mean-field scheme. Note that in our theory we improve from the DLVO mean-field-type scheme by allowing extra number fluctuation between the counterion clouds. To do this, we first point out a few features observed from further examination of the counterion distribution. Fig. 5 shows Pθ, the probability distribution of counterions over polar angle θ, where the north pole is defined by the line connecting the centers of the two cells. Note that, as long as the counterion clouds do not overlap (d > 4), Pθ exhibits an approximately sinusoidal pattern for all macroionic distances, even in the case of d = 4.1 where the clouds almost touch each other. In other words, the counterion distribution in each cloud is approximately non-polarized, or namely, isotropic, while little deviation can be observed at θ = 0 and θ = π. Furthermore, the radial profile Pr of the counterion distribution probability is shown in Fig. 6. Again, the profile shows little difference between d = 4.1 and d = 20, which suggests that it should serve as a good approximation to use the same profile (case d = 20) for all distances, as the building block of our partition function.Hence the mean-field total energy of the two-macroion system can be expressed as follows:
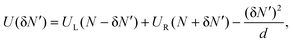 | (12) |
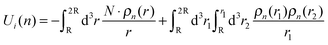 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(r) = 1, and assume that P(r) stays unchanged over all n, such that 4πr2ρn(r) = n·P(r). Therefore, eqn (13) becomes
P(r) = 1, and assume that P(r) stays unchanged over all n, such that 4πr2ρn(r) = n·P(r). Therefore, eqn (13) becomes| Ui(n) = −Nna1 + n2a2, | (14) |
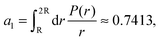 | (15) |
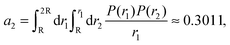 | (16) |
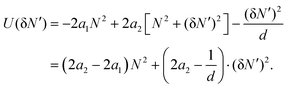 | (17) |
With the counterion number fluctuation δN considered, the canonical partition function of our system can now be written as
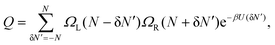 | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωi(n) is the ideal-gas entropy for the ith cell (i = L or R). With the help from eqn (17), and approximations used in eqn (9) and (10), we obtain
Ωi(n) is the ideal-gas entropy for the ith cell (i = L or R). With the help from eqn (17), and approximations used in eqn (9) and (10), we obtain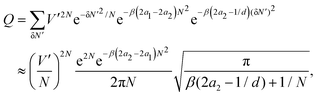 | (19) |
| δN = [2β(2a2 − 1/d) + 2/N]−1/2. | (20) |
This result is compared with the direct simulation result in Fig. 4. Our BW scheme, with the input from simulation data, does reproduce the quantity δN faithfully, as the largest deviation from simulation result is less than 0.7%.
We now turn to the thermodynamic quantities that follow our partition function. The Helmholtz free energy is
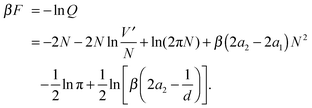 | (21) |
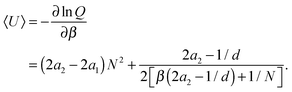 | (22) |
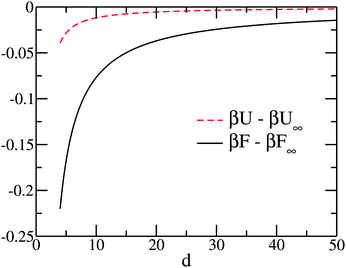 | ||
| Fig. 7 Free energy and electrostatic energy for the case N = 1000 and t = 100. The numerical values are derived via our BW theory in Section 5 (straight line: βF − βF∞; dashed line: βU − βU∞). | ||
Note that while we use a simple ideal-gas approximation for the number of configurations Ωi(n) in eqn (18), we adopt a better approximation for the factorials, which in return gives the δN′ dependence in the entropic factor. This dependence is crucial, and leads to the non-extensiveness in the high-temperature (ideal-gas) limit, as depicted in Section 2. On the other hand, one can follow a refined expression of Ωi(n), such as Ωi(n) = exp Si(n),34 where
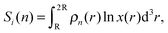 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ωi(n) becomes extensive instead and does not play a role in the summation of eqn (18).
Ωi(n) becomes extensive instead and does not play a role in the summation of eqn (18).
6 Conclusion
In this work we point out the existence of the non-extensive entropy upon joining together identical particles over two compartments. This non-extensive entropy, which can be understood easily via particle number fluctuations over the compartments, can provide extra physical insight for the theoretical treatment of macroionic systems. With extra consideration of electrostatic interactions, we look into this non-extensive entropy by monitoring the counterion number fluctuation in our computer simulations following a macroionic cell-model description, and find a long-range decay of the fluctuation over tens of the cell size.We then adopt the counterion distribution features extracted from our simulation result, into our BW partition function approach, as our theory provides a simple extension of the original BW mean-field theory by considering the number fluctuations over the two counterion clouds. The free energy derived thereafter clearly shows the predominance of the non-extensive entropy over the energy in the non-overlapping regime of counterion clouds. Thus it is strongly suggested that within our cell-model framework, the entropic mechanism should be responsible for the like-charge attraction.
The use of a cell model greatly facilitates our discussion on counterion fluctuations, and allows the possibility for computer simulations of macroionic systems over large separation distances. However, we have to address that the model is less physical in the aspects that the cell boundary is set in an ad hoc manner, and the effects of sparsely distributed ions outside the cells are neglected. To clarify the impact of these aspects, further ingredients can be incorporated into our current model. For example, we would anticipate a more significant increase in counterion number fluctuation as macroions get close, if the cell shape is allowed to deform. This is because more configurations would pop up upon the relief from the charge-neutral constraint. Moreover, cell volume fluctuation, the exchange of counterions with the ambient environment, and the shielding of sparsely-distributed ions, are also relevant mechanisms that need to be carefully examined. These aspects will be considered in our future works.
Note that a similar entropic mechanism of like-charge attraction has been previously proposed for a polyelectrolyte system.36 In that algorithm, the attraction arises because the volume of counterion condensation increases at an intermediate range of polyionic separation distance, as in return the translational entropy of the condensed counterions increases. In contrast to their approach, we fix the residence volume of counterions instead, and study their number fluctuation over the two cells. Therefore these two entropic mechanisms actually serve as complements to each other. While the counterion entropy has long been regarded responsible for the effective repulsion between macroions, it is remarkable to learn that such entropy can give rise to like-charge attraction.
Acknowledgements
This work has been supported by the National Science Council of the Republic of China under Grant No. NSC-100-2112-M-008-005 and NSC-99-2112-M-003-012-MY2. CLL thanks for the support from NCTS under focus group Life and Complexity.References
- G. M. Kepler and S. Fraden, Phys. Rev. Lett., 1994, 73, 356 CrossRef CAS.
- M. D. Carbajal-Tinoco, F. Castro-Roman and J. L. Arauz-Lara, Phys. Rev. E, 1996, 53, 3745 CrossRef CAS.
- J. C. Crocker and D. G. Grier, Phys. Rev. Lett., 1996, 77, 1897 CrossRef CAS.
- A. E. Larsen and D. G. Grier, Nature, 1997, 385, 230 CrossRef CAS.
- Y. Han and D. G. Grier, Phys. Rev. Lett., 2003, 91, 038302 CrossRef.
- B. V. R. Tata, P. S. Mohanty and M. C. Valsakumar, Solid State Commun., 2008, 147, 360 CrossRef CAS PubMed.
- E. Nagornyak, H. Yoo and G. H. Pollack, Soft Matter, 2009, 5, 3850 RSC.
- K. S. Schmitz, M. Lu, N. Singh and D. Ramsay, Biopolymers, 1984, 23, 1637 CrossRef CAS.
- K. S. Schmitz, Macroions in Solution and Colloidal Suspension, VCH Publishers, New York, 1993 Search PubMed.
- I. Rouzina and V. A. Bloomfield, J. Phys. Chem., 1996, 100, 9977 CrossRef CAS.
- J. X. Tang and P. A. Janmey, J. Biol. Chem., 1996, 271, 8556 CrossRef CAS PubMed.
- G. Liu, Y. Cai and T. Liu, J. Am. Chem. Soc., 2004, 126, 16690 CrossRef CAS PubMed.
- I. Sogami and N. Ise, J. Chem. Phys., 1984, 81, 6320 CrossRef.
- N. Ise and I. S. Sogami, Structure Formation in Solution: Ionic Polymers and Colloidal Particles, Springer-Verlag, 2005 Search PubMed.
- N. Ise, Phys. Chem. Chem. Phys., 2010, 12, 10279 RSC.
- J. Th. G. Overbeek, J. Chem. Phys., 1987, 87, 4406 CrossRef CAS.
- P. González-Mozuelos and M. D. Carbajal-Tinoco, J. Chem. Phys., 1998, 109, 11074 CrossRef.
- M. D. Carbajal-Tinoco and P. González-Mozuelos, J. Chem. Phys., 2002, 117, 2344 CrossRef CAS.
- T. M. Squires and M. P. Brenner, Phys. Rev. Lett., 2000, 85, 4976 CrossRef CAS.
- Y. Levin, Physica A, 1999, 265, 432 CrossRef CAS.
- Y. Levin, Rep. Prog. Phys., 2002, 65, 1577 CrossRef CAS.
- D. G. Grier and Y. Han, J. Phys.: Condens. Matter, 2004, 16, S4145 CrossRef CAS.
- J. Baumgartl, J. Luis Arauz-Lara and C. Bechinger, Soft Matter, 2006, 2, 631 RSC.
- M. Polin, D. G. Grier and Y. Han, Phys. Rev. E, 2007, 76, 041406 CrossRef.
- A. Cuetos, J. A. Anta and A. M. Puertas, J. Chem. Phys., 2010, 133, 154906 CrossRef PubMed.
- B. Y. Ha and A. J. Liu, Phys. Rev. Lett., 1997, 79, 1289 CrossRef CAS.
- T. E. Angelini, H. Liang, W. Wriggers and G. C. L. Wong, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8634 CrossRef CAS PubMed.
- C.-L. Lee and S.-K. Ng, J. Chem. Phys., 2010, 133, 084504 CrossRef PubMed.
- J. Ruiz-Garcia and B. I. Ivlev, Mol. Phys., 1998, 95, 371 CrossRef CAS.
- W. Chen, et al. , Phys. Rev. Lett., 2005, 95, 218301 CrossRef.
- J. Israelachvili, Intermolecular and Surface Forces, Academic, London, 2nd edn 1992 Search PubMed.
- M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover, New York, 1965 Search PubMed.
- M. Deserno and C. Holm, in Electrostatic Effects in Soft Matter and Biophysics, ed. C. Holm, P. Kékicheff and R. Podgornik, Kluwer, Dordrecht, NATO Science Series II - Mathematics, Physics and Chemistry, vol. 46, 2001 Search PubMed.
- J. Th. G. Overbeek, Colloids Surf., 1990, 51, 61 CrossRef CAS.
- K. Huang, Statistical Mechanics, Wiley, 2nd edn, 1987 Search PubMed.
- J. Ray and G. S. Manning, Langmuir, 1994, 10, 2450 CrossRef CAS.
| This journal is © the Owner Societies 2014 |