Nuclear spin circular dichroism in fullerenes: a computational study

Abstract

In the recently proposed phenomenon, nuclear spin-induced circular dichroism (NSCD), collective magnetisation of nuclei induces circular dichroism in a light beam passing through a molecular sample. Here we present the first computational predictions of NSCD for fullerenes C₆₀ and C₇₀. We show that the NSCD signal is nucleus-specific, like in NMR spectroscopy. Thus, NSCD may provide a new and promising, high-resolution observable for experimental identification of chemical compounds.

---

Nuclear magneto-optic spectroscopy (NMOS) techniques couple optical measurements of birefringence and dichroism with the use of the magnetisation of atomic nuclei to cause these changes in the polarisation state of light. NMOS methods have been a subject of growing interest and rapid development, due to their potential to provide a nucleus-specific spectroscopic signal.¹

An experimentally successful example of NMOS is nuclear spin optical rotation (NSOR), in which controlled magnetisation of nuclear spins along the light beam induces optical rotation of linearly polarised light (LPL) passing through the sample.^1a,d,e,j,k In the pilot study of Savukov, Lee, and Romalis^1a the NSOR signal was observed for the first time in liquid Xe and water samples. This work inspired further experimental^1d,e,j,k and theoretical^1c,g,h,j studies. It was also shown theoretically that different nuclear sites within a single molecule should provide different NSOR signals in analogy to nuclear magnetic resonance (NMR).^1c,j,n,q

A promising, novel candidate for spectroscopic characterisation of molecules is the nuclear spin circular dichroism (NSCD) recently formulated and implemented by Vaara et al.^1q The principle of NSCD is illustrated in Fig. 1. In this technique, the magnetically polarised nuclei induce ellipticity in linearly polarised light passing through a molecular sample, in a manner similar to magnetic circular dichroism (MCD),² where the CD effect is induced by an external magnetic field oriented along the light path. In practice, the MCD spectrum is obtained by measuring the differential absorption of the left- and right-circularly polarised components of LPL.

Fig. 1 Schematic illustration of NSCD, where ellipticity (ellipse on the left) is induced in the linearly polarised light (arrow on the right) by collective magnetisation of atomic nuclei (represented by local magnetic fields on H atoms).

NSCD and MCD are “mathematically” similar in their 3rd-order response theory expressions, where the dynamic molecular polarizability is modified by a static magnetic interaction.^1q However, the two phenomena are physically different. In MCD, the static magnetic interaction is the global Zeeman interaction with the external magnetic field, whereas in NSCD the local hyperfine interaction is involved. This provides NSCD with the exciting possibility of gaining local, nucleus-specific information. The signal obtained in MCD originates from the entire molecule. On the other hand, due to the hyperfine interactions, NSCD has potential to offer distinction of chemical environments, with atom-site specific signals, similar to NMR but by using optical detection.

In the proposed^1q but not yet performed NSCD experiment, nuclei are first magnetised (e.g., by using NMR magnets and coils) and then the differential absorption of the light passing through the sample is measured. To obtain the chemical resolution by the NSCD technique, two principal means suggested for NMOS^1c can be used: (i) wavelength tuning to localised excitations and (ii) selective magnetisation using NMR techniques. It has been suggested that by tuning the laser wavelength in NSOR experiments to the specific resonances, the NSOR signal can be localised to the different chromophores in molecules.^1c,q Numerous approaches for inducing and controlling the magnetisation of nuclei are known in NMR spectroscopy and have already been discussed and successfully tested in NSOR experiments.^1a,d,e,j,k

While the construction of the first experimental NSCD apparatus is on its way, it is crucial to provide a basic understanding of the NSCD observable to guide the future experiments. Here we present the first computational investigation† of NSCD for fullerenes C₆₀ and C₇₀, to illustrate the potential of the method. The calculated ¹³C NSCD spectra are analysed and compared to the available MCD spectra, recorded and calculated previously.³

The predicted†¹³C NSCD spectrum for C₆₀ is compared to the MCD one^3a in Fig. 2. Since all carbons in C₆₀ are equivalent, the total ¹³C NSCD signal in Fig. 2 was obtained by multiplying the calculated signal of a single carbon nucleus by the factor of 60.

Fig. 2 The calculated NSCD (B3LYP/def2-SV+P)† and MCD (B3LYP/6-31G*)^3a signals for C₆₀. The excitation wavelengths and transition dipole strengths D (B3LYP/def2-SV+P)† are shown in the lower panel for clarity.

The signs and relative intensities of the ¹³C NSCD bands do not fully correlate with those of the related MCD bands; some of the features have the same sign for both NSCD and MCD (Fig. 2 near 210 and 245 nm), while some have opposite signs (Fig. 2 near 320 nm). The positive NSCD band near 250 nm shows a rather strong relative intensity as compared to MCD one. This leads to a different overall shape of the NSCD and MCD signals.

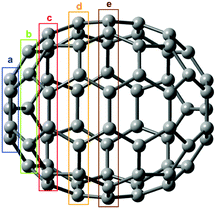
Let us now turn to C₇₀ fullerene with five distinct carbon atom types (Fig. 3). They have the following degeneracies: 10 × C_a, 10 × C_b, 20 × C_c, 20 × C_d, and 10 × C_e. This degeneracy is taken into account in Fig. 4 and 5, where the corresponding, calculated ¹³C NSCD intensities for single nuclei have been multiplied by the factors of 10, 10, 20, 20, and 10 for C_a–C_e, respectively.

Fig. 3 The five distinct symmetry-equivalent carbon types C_a–C_e in C₇₀.

Fig. 4 The calculated ¹³C NSCD (B3LYP/def2-SV+P, upper panel)† for the C_a–C_e nuclear sites and the MCD (B3LYP/6-31G*, middle panel)^3a in C₇₀. The total ¹³C NSCD signal (middle panel) is obtained as a sum of the signals for C_a–C_e. The excitation wavelengths and transition dipole strengths D (B3LYP/def2-SV+P)† are shown in the bottom panel. The spectral region 400–630 nm is shown.

Fig. 5 The calculated ¹³C NSCD (B3LYP/def2-SV+P, upper panel)† for the C_a–C_e nuclear sites and the MCD (B3LYP/6-31G*, middle panel)^3a in C₇₀. The total ¹³C NSCD signal (middle panel) is obtained as a sum of the signals for C_a–C_e. The excitation wavelengths and transition dipole strengths D (B3LYP/def2-SV+P)† are shown in the bottom panel. The spectral region 250–430 nm is shown.

The MCD signal for C₇₀ does not match the NSCD data in shape, neither for the individual C_a–C_e signals, nor for the total NSCD signal, Fig. 4 and 5. The individual C_a–C_e signals provide clearly distinct spectral patterns.

The intensity of the NSCD signals is rather different for the distinct carbon types at certain wavelengths, regardless of the degree of degeneracy. This is nicely seen in the NSCD signals for C_a and C_e in Fig. 4, both arising from 10-fold degenerate carbon types. Near 480 and 550 nm, C_e gives a rather weak signal as compared to C_a, while the opposite occurs near 270 nm. There, the signal corresponding to C_e is rather strong and C_a amounts only to about a third of it. More examples can be found in Fig. 5, e.g., near 270 and 370 nm.

Perhaps the most interesting observation in Fig. 4 and 5 is that the positions of the peaks and couplets on the wavelength axis are actually shifted off the corresponding resonances and this shift also depends on the carbon type, even when the corresponding ¹³C NSCD bands have the same sign and similar intensity. For example, in the region of 320–380 nm (Fig. 5) the negative couplet for C_c is found at a much higher wavelength than those for C_a and C_d. This is due to the different strengths of the NSCD signal at the three main resonances of 338, 340 and 376 nm (bottom panel of Fig. 5), which causes the different shapes and positions of these couplets. At some resonances that are hardly visible in the UV/vis spectra due to a small transition dipole strength, a large MCD signal may nevertheless emerge.³ This is also observed in NSCD, for example near 290 and 250 nm. This feature is also one of the reasons for the differential positions of the bands for the different carbon types. For example, the strong absorption calculated at 550 nm (exp. 544 nm)^3a is accompanied by a weak one near 518 nm, hardly visible in the experimental UV/vis spectra. Due to the linewidth and intensity effects, the maxima and minima for different carbon types are actually seen at different frequencies, compare, e.g., carbons C_a and C_d near 550 nm in Fig. 4.

The total ¹³C NSCD signal for C₇₀ shown in Fig. 4 and 5 is also rather different from the MCD signal and constitutes a candidate for the first possible experimental NSCD measurements, before the resolution of individual carbon signals is reached.

In summary, signals appropriate to the recently proposed nuclear spin-induced circular dichroism (NSCD) experiment were calculated for C₆₀ and C₇₀ fullerenes. We have shown that the NSCD signal is nucleus-specific, i.e., it may vary for distinct carbon sites. The signals from the distinct carbon atom types differ by their shape, band/couplet position on the wavelength axis, and intensity. Signals that are weak in absorption spectra can become visible in NSCD. The site-specificity suggests that NSCD spectroscopy may be amenable for experimental high-resolution identification of chemical compounds. In a recent study, closely related NSOR results were reported to provide nucleus-specific information on finite-size flakes of graphenic materials, including their defects (sp² islands in an sp³ environment and vice versa).^1r Similar applications can be foreseen for NSCD.

The project was supported by the Research Council of University of Oulu (MS and JV), the Czech Science Foundation (14-03564S, MS), the Czech Academy of Sciences (RVO-61388963, MS and PS), and the Academy of Finland (JV). The COST-CMTS Action CM1002 “Convergent Distributed Environment for Computational Spectroscopy (CODECS)” is acknowledged. Computational resources were provided by CSC-IT center for Science (Espoo, Finland) and the Finnish Grid Initiative as well as by CERIT Scientific Cloud, R&D Program, no. CZ.1.05/3.2.00/08.0144.

Notes and references

1. (a) I. M. Savukov, S. K. Lee and M. V. Romalis, Nature, 2006, 442, 1021–1024; (b) T.-t. Lu, M. He, D.-m. Chen, T.-j. He and F.-c. Liu, Chem. Phys. Lett., 2009, 479, 14–19; (c) S. Ikäläinen, M. V. Romalis, P. Lantto and J. Vaara, Phys. Rev. Lett., 2010, 105, 153001; (d) D. Pagliero, W. Dong, D. Sakellariou and C. A. Meriles, J. Chem. Phys., 2010, 133, 154505; (e) D. Pagliero and C. A. Meriles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19510–19515; (f) G.-h. Yao, M. He, D.-m. Chen, T.-j. He and F.-c. Liu, Chem. Phys., 2011, 387, 39–47; (g) T. S. Pennanen, S. Ikäläinen, P. Lantto and J. Vaara, J. Chem. Phys., 2012, 136, 184502; (h) S. Ikäläinen, P. Lantto and J. Vaara, J. Chem. Theory Comput., 2012, 8, 91–98; (i) G.-h. Yao, M. He, D.-m. Chen, T.-j. He and F.-c. Liu, ChemPhysChem, 2012, 13, 1325–1331; (j) J. Shi, S. Ikäläinen, J. Vaara and M. V. Romalis, J. Phys. Chem. Lett., 2013, 4, 437–441; (k) I. M. Savukov, H. Y. Chen, T. Karaulanov and C. Hilty, J. Magn. Reson., 2013, 232, 31–38; (l) L.-j. Fu, A. Rizzo and J. Vaara, J. Chem. Phys., 2013, 139, 181102; (m) L.-j. Fu and J. Vaara, J. Chem. Phys., 2013, 138, 204110; (n) F. Chen, G.-h. Yao, T.-j. He, D.-m. Chen and F.-c. Liu, Chem. Phys., 2014, 435, 57–61; (o) L.-j. Fu and J. Vaara, ChemPhysChem, 2014, 15, 2337–2350; (p) L.-j. Fu and J. Vaara, J. Chem. Phys., 2014, 140, 024103; (q) J. Vaara, A. Rizzo, J. Kauczor, P. Norman and S. Coriani, J. Chem. Phys., 2014, 140, 134103; (r) J. Vähäkangas, P. Lantto and J. Vaara, J. Phys. Chem. C, 2014, 118, 23996–24005.
2. R. W. Mason, A practical guide to magnetic circular dichroism spectroscopy, John Wiley & Sons, Inc., New Jersey, 2007.
3. (a) P. Štěpánek, M. Straka, V. Andrushchenko and P. Bouř, J. Chem. Phys., 2013, 138, 151103; (b) T. Fahleson, J. Kauczor, P. Norman and S. Coriani, Mol. Phys., 2013, 111, 1401–1404.
4. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
5. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
6. C. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829.
7. (a) K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani and P. Dahle, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284; (b) Dalton, a molecular electronic structure program, Release DALTON2014 (2014), see http://daltonprogram.org.
8. (a) J. Kauczor, P. Jørgensen and P. Norman, J. Chem. Theory Comput., 2011, 7, 1610–1630; (b) J. Kauczor and P. Norman, J. Chem. Theory Comput., 2014, 10, 2449–2455.
9. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785; (c) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
10. (a) J. Kaminský, M. Buděšínský, S. Taubert, P. Bouř and M. Straka, Phys. Chem. Chem. Phys., 2013, 15, 9223; (b) T. Kupka, M. Stachów, E. Chełmecka, K. Pasterny, M. Stobińska, L. Stobiński and J. Kaminský, J. Chem. Theory Comput., 2013, 9, 4275–4286.
11. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.

---

Footnote

† Methods. For a detailed account of the theoretical foundations and implementation of NSCD we refer to ref. 1q. Calculations on C₆₀ and C₇₀ fullerenes were carried out for molecules in their equilibrium ground-state geometries in vacuo, thus neglecting all vibronic and solvent effects. The structures were optimised using the Turbomole code, version 6.3.1., ref. 4, the BP86 density functional⁵ and the def-TZVP⁶ carbon basis set. NSCD calculations were done using the complex polarisation propagator (CPP) approach implemented^1q in the 2014 release version of the Dalton program package,⁷ which exploits the CPP response equation solver of ref. 8. The B3LYP density functional⁹ was employed in the calculations. The selection of B3LYP was strongly motivated by its good performance, using methodology similar to that of present work, for both the absorption and MCD spectra of C₆₀ and C₇₀, ref. 3a. B3LYP performed well also for the calculations of ¹³C NMR shielding in fullerenes.¹⁰ The basis set for NSCD calculations was constructed by augmenting the def2-SVP basis set¹¹ by an sp set of diffuse functions (α_s = 0.04363394 and α_p = 0.05089538). This combination gives a good balance of accuracy and computational cost, and is referred to as def2-SV+P. The empirical linewidth parameter required by the CPP approach was set to 1000 cm⁻¹ (0.00456 a.u.), following previous experience, e.g., ref. 1q and 3. The step between the consecutive frequencies was initially set equal to 0.0025 a.u. and then refined whenever needed.

---