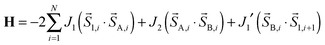Open Access Article
Open Access ArticleA single-chain magnet based on linear [MnIII2MnII] units†
Constantina
Papatriantafyllopoulou
a,
Sotiris
Zartilas
a,
Manolis J.
Manos‡
a,
Céline
Pichon
bc,
Rodolphe
Clérac
*bc and
Anastasios J.
Tasiopoulos
*a
aDepartment of Chemistry, University of Cyprus, 1678 Nicosia, Cyprus. E-mail: atasio@ucy.ac.cy; Fax: +357 22892801; Tel: +357 22892765
bCNRS, CRPP, UPR 8641, F-33600 Pessac, France. E-mail: clerac@crpp-bordeaux.cnrs.fr
cUniv. Bordeaux, CRPP, UPR 8641, F-33600 Pessac, France
First published on 30th September 2014
Abstract
The synthesis, structural characterization and magnetic properties of a 1D coordination polymer based on a linear mixed valent [MnIII2MnII] repeating unit are described. It displays single-chain magnet (SCM) behaviour with an energy barrier of ∼38 K and represents the first example of a mixed valent Mn–carboxylate SCM with a linear architecture.
Polynuclear Mn–carboxylate complexes and coordination polymers have attracted intense interest due to numerous reasons including their novel crystal structures and interesting magnetic properties.1 Such compounds often behave as single-molecule magnets (SMMs) or single-chain magnets (SCMs) displaying novel magnetic phenomena such as slow relaxation, large hysteresis and quantum tunneling of magnetisation (QTM).1–4 SMMs derive their properties from the combination of a large spin ground-state and Ising-type (easy-axis) magnetic anisotropy whereas SCMs possess strong intrachain exchange interactions without spin compensation between high spin anisotropic (Ising-type) units along the chain.1–3 Such magnetic species are remarkable results of the molecular approach to nanoscale magnetic materials and have been proposed as candidates for applications in high-density information storage, molecular spintronics and quantum computation.5
As a result, numerous Mn–carboxylate complexes and SMMs have been reported with a variety of topologies and nuclearities ranging from 2 to 84,1,6 but in contrast, only a small number of homospin manganese SCMs have been described.2 The largest category of Mn complexes in the field of molecular magnetism is possibly the trinuclear species since they often display ferromagnetic exchange interactions and SMM behaviour.1d,7 Such [Mn3] units have also been used as building blocks or modules for the construction of larger aggregates1d,8 and multidimensional coordination polymers, which display interesting magnetic properties.1d,9 Thus, several [Mn3] SMMs and a few [Mn3]∞ SCMs have been reported with the vast majority of these materials being based on oxido-centered triangular topology.1d,7–9
To the best of our knowledge, there are only four linear [Mn3] complexes that have been reported to exhibit SMM behaviour,10 whereas such moieties have never been observed to form SCM systems. In fact, SCMs consisting of linear polynuclear Mn–carboxylate repeating units are completely unknown. These simple 1D architectures built from linear modules are particularly interesting since they provide ideal model systems,2a,b which could become textbook examples for magnetochemists and physicists, allowing them to go further in the understanding of the SCM theory. Although SCMs with linear architectures are well known when rigid ligands that impose the geometry of the resultant compounds, such as cyanides,11 are employed, they are very rare in 3d metal carboxylate chemistry.12,13
We herein report the synthesis, crystal structure and magnetic properties of an 1D coordination polymer [Mn3(mpt)2(EtCO2)2(MeOH)2]∞ (1)∞ (H3mpt: 3-methylpentane-1,3,5-triol), based on a novel linear mixed valent trinuclear [MnIII2MnII] repeating unit. It displays SCM properties with a thermally activated relaxation time and an energy barrier of about 38 K. This compound represents not only the first example of a SCM based on a linear Mnx–carboxylate repeating unit but also the first mixed valent Mn–carboxylate SCM with a linear architecture.
The solvothermal reaction of Mn(O2CEt)2·2H2O and H3mpt in a ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
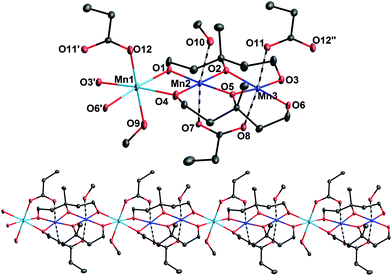
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio in MeOH at 100 °C for 24 h followed by slow cooling to room temperature gave brown rod-shaped crystals of (1)∞ in 35% yield; the dried solid was analysed satisfactorily as (1)∞§ (for synthetic details see the ESI†). The crystal structure§ of (1)∞ contains an 1D coordination polymer consisting of a linear trinuclear [Mn3(mpt)2(EtCO2)2(MeOH)2] (Fig. 1, top) repeating unit. Charge considerations, bond valence sum calculations14 and inspection of metric parameters indicate that the [Mn3] moiety is mixed-valent containing two MnIII (Mn2 and Mn3) and one MnII (Mn1) ions with the latter located in the one outer part of the linear [Mn3] unit.
2 molar ratio in MeOH at 100 °C for 24 h followed by slow cooling to room temperature gave brown rod-shaped crystals of (1)∞ in 35% yield; the dried solid was analysed satisfactorily as (1)∞§ (for synthetic details see the ESI†). The crystal structure§ of (1)∞ contains an 1D coordination polymer consisting of a linear trinuclear [Mn3(mpt)2(EtCO2)2(MeOH)2] (Fig. 1, top) repeating unit. Charge considerations, bond valence sum calculations14 and inspection of metric parameters indicate that the [Mn3] moiety is mixed-valent containing two MnIII (Mn2 and Mn3) and one MnII (Mn1) ions with the latter located in the one outer part of the linear [Mn3] unit.
The three Mn ions are held together by one EtCO2− group bridging in the usual syn, syn – η: η: μ fashion the two MnIII ions and two η2: η2: η2: μ4 mpt3− ligands. Two μ-OR arms of the latter together with an additional syn, syn – η: η: μ EtCO2− group link the neighbouring [Mn3] units resulting in the formation of the 1D coordination polymer of (1)∞ (Fig. 1, bottom). The MnIII–O–MnIII and Mn2III–O–Mn1II angles are ∼98.4(2)° and ∼100.5(2)°, respectively, whereas the Mn3III–O–Mn1II angle between the neighbouring units of (1)∞ is ∼97.1(2)°. The peripheral ligation is completed by two terminal methanol molecules connected to the central MnIII (Mn2) and MnII ions. The Mn ions are in very close proximity along the chain, with Mn⋯Mn separations of 3.120, 2.904 and 3.038 Å for Mn1⋯Mn2, Mn2⋯Mn3 and Mn3⋯Mn1, respectively. All Mn ions are six-coordinated adopting a distorted octahedral geometry with the two MnIII ions displaying the expected Jahn–Teller elongation axes (O7–Mn2–O10 and O8–Mn3–O11) which are nearly co-parallel (the angle between the JT axes is ∼7.6(1)°). These JT axes involve donor atoms either from methanol or propionate ligands, and thus all equatorial coordinating positions of the MnIII ions are occupied by the alkoxido O atoms of the two mpt3− ligands. It is also noticeable that the Mn ions within the chain are nearly co-linear with intrachain Mn–Mn–Mn angles being in the 170°–180° range. Examination of the crystal packing reveals that the chains run parallel to the a axis and there is no significant interchain hydrogen bonding interactions (Fig. S1, ESI†). Thus, the neighbouring chains are well separated, with the interchain Mn⋯Mn separations all being superior to 8.27 Å.
The 1D coordination polymer found in (1)∞ displays several attractive and unique structural features. In particular, (1)∞ is the first example of a coordination polymer, and a rare example of a metal complex in general, containing the H3mpt ligand in its neutral or anionic form.15 In addition, its structural architecture that can be described as a linear array of Mn2+ and Mn3+ ions tightly connected through both mono- and poly-atomic bridges (RO− and EtCO2− respectively), is unprecedented in Mn–carboxylate chemistry, although some chains consisting of mononuclear repeating units have been reported.12,16 Such compounds, especially those containing one or more trivalent Mn ions like (1)∞, are particularly attractive in the area of molecular magnetism since they could display SCM properties induced by the intrinsic magnetic anisotropy of their MnIII centers.
The magnetic properties of (1)∞ were investigated as a function of temperature (1.8–270 K) using dc magnetic fields up to 7 T. A plot of χT versus T for (1)∞, recorded at 1000 Oe, is shown in Fig. 2. The χT value steadily decreases from 7.9 cm3 mol−1 K at 270 K to 4.7 cm3 mol−1 K at 34 K and then rapidly increases to 6.8 cm3 mol−1 K at 4 K before it drops down to 5.5 cm3 mol−1 K at 1.85 K. The room temperature χT product is significantly smaller than the spin-only (g = 2) value of 10.375 cm3 mol−1 K expected for one MnII and two MnIII non-interacting centers. The overall profile of the χT versus T plot for (1)∞ reveals the existence of competing ferromagnetic and antiferromagnetic exchange interactions within the chain, the latter being responsible for the low χT product at 270 K. The χT value around 40 K suggests a virtual spin ground state (ST) of 5/2 for the [MnIII2MnII] repeating unit induced by significant antiferromagnetic interactions while the increase below 40 K reveals probably ferromagnetic interactions between these trinuclear magnetic moieties. The decrease of the χT value below 4 K is likely due to the existence of weak antiferromagnetic interchain interactions, magnetic anisotropy and Zeeman effects from the applied field.
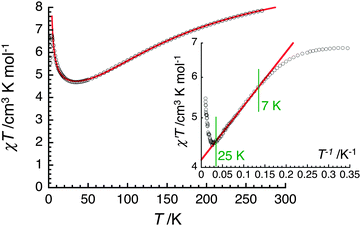 | ||
| Fig. 2 Temperature dependence of the χT product (χ is the magnetic susceptibility per mole of [Mn3] unit at 1000 Oe) between 1.8 and 270 K for a polycrystalline sample of (1)∞ (Fig. S2, ESI†). The solid red line is the best fit of the experimental data to the chain model (see text). Inset: the semi-logarithmic χ′T versus T−1 plot (χ′ being the in-phase ac susceptibility in zero dc field at 100 Hz and Hac = 3 Oe) with the best fit (red solid line) using the 1D Ising model between 7 and 25 K. | ||
In order to quantify the strength of the intrachain interactions in (1)∞, the magnetic susceptibility was modeled using the following classical spin chain Hamiltonian:
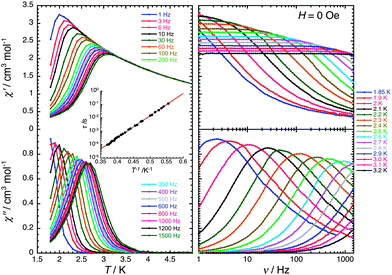
The τ versus 1/T data were fitted to the Arrhenius equation τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Δτ/kBT) (where Δτ is the energy barrier to reverse the magnetisation of a chain and τ0 is the intrinsic reversal time of the magnetically isolated spin unit of the chain in contact with the thermal bath) with Δτ/kB = 38 K and τ0 = 8.0 × 10−11 s, the latter value being in good agreement with those of reported SCMs.2,11,12 Considering that the correlation length, ξ, (∝χ′T) is saturating around 3 K (Fig. 2), the observed dynamics of magnetisation (below 3 K; Fig. 3) have been measured in the finite-size regime of SCM relaxation.2a,c Therefore the anisotropy barrier (ΔA) can be estimated at 35.5 K from Δξ and Δτ, as in this regime Δτ = Δξ + ΔA. This significant value of the magnetic anisotropy energy is in good agreement with the lack of saturation of magnetisation at fields up to 7 T (Fig. S3, ESI†).
exp(Δτ/kBT) (where Δτ is the energy barrier to reverse the magnetisation of a chain and τ0 is the intrinsic reversal time of the magnetically isolated spin unit of the chain in contact with the thermal bath) with Δτ/kB = 38 K and τ0 = 8.0 × 10−11 s, the latter value being in good agreement with those of reported SCMs.2,11,12 Considering that the correlation length, ξ, (∝χ′T) is saturating around 3 K (Fig. 2), the observed dynamics of magnetisation (below 3 K; Fig. 3) have been measured in the finite-size regime of SCM relaxation.2a,c Therefore the anisotropy barrier (ΔA) can be estimated at 35.5 K from Δξ and Δτ, as in this regime Δτ = Δξ + ΔA. This significant value of the magnetic anisotropy energy is in good agreement with the lack of saturation of magnetisation at fields up to 7 T (Fig. S3, ESI†).
In conclusion, the use of the triol H3mpt in Mn–carboxylate chemistry afforded a 1D coordination polymer, (1)∞, consisting of tightly connected [MnIII2MnII] linear repeating units. For only the second time in the family of Mn–carboxylate chains with a linear structural architecture and the first time for mixed valent ones, this system exhibits SCM properties with an appreciable relaxation energy barrier of 38 K. It should also be pointed out that the mpt3− ligand plays a crucial role not only in the formation but also in the appearance of SCM behaviour in (1)∞. In particular, its alkoxido bridging arms occupied all equatorial positions of the Mn ions directing the terminal solvent and carboxylate ligands to the axial ones thus contributing to the alignment of the local easy magnetic axes of the MnIII ions along the chain direction. Thus, this work reveals that H3mpt could be a valuable ligand for the isolation of novel carboxylate-based SCMs with simple spin and interaction topologies.
This work was supported by the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. PCIG09-GA-2011-293814, the Cyprus Research Promotion Foundation (PENEK–EVIΣX/0506/08), the University of Bordeaux, the ANR, the Région Aquitaine, and the CNRS.
Notes and references
- (a) R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011 RSC; (b) G. Aromi and E. K. Brechin, Struct. Bonding, 2006, 122, 1 CrossRef CAS; (c) A. J. Tasiopoulos and S. P. Perlepes, Dalton Trans., 2008, 5537 RSC; (d) R. Inglis, C. J. Milios, L. F. Jones, S. Piligkos and E. K. Brechin, Chem. Commun., 2012, 48, 181 RSC.
- (a) C. Coulon, H. Miyasaka and R. Clérac, Struct. Bonding, 2006, 122, 163 CrossRef CAS; (b) I.-R. Jeon and R. Clérac, Dalton Trans., 2012, 9569 RSC; (c) H. Miyasaka, M. Julve, M. Yamashita and R. Clérac, Inorg. Chem., 2009, 48, 3420 CrossRef CAS PubMed; (d) K. Bernot, J. Luzon, R. Sessoli, A. Vindigni, J. Thion, S. Richeter, D. Leclercq, J. Larionova and A. Van der Lee, J. Am. Chem. Soc., 2008, 130, 1619 CrossRef CAS PubMed; (e) T.-T. Wang, M. Ren, S.-S. Bao, B. Liu, L. Pi, Z.-S. Cai, Z.-H. Zheng, Z.-L. Xu and L.-M. Zheng, Inorg. Chem., 2014, 53, 3117 CrossRef CAS PubMed.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef CAS PubMed.
- (a) J. R. Friedman, M. P. Sarachik, J. Tejada and R. Ziolo, Phys. Rev. Lett., 1996, 76, 3830 CrossRef CAS; (b) L. Thomas, F. Lionti, R. Ballou, D. Gatteschi, R. Sessoli and B. Barbara, Nature, 1996, 383, 145 CrossRef CAS; (c) W. Wernsdorfer, R. Clérac, C. Coulon, L. Lecren and H. Miyasaka, Phys. Rev. Lett., 2005, 95, 237203 CrossRef CAS.
- (a) L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef CAS PubMed; (b) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS PubMed.
- (a) G. E. Kostakis, A. M. Ako and A. K. Powell, Chem. Soc. Rev., 2010, 39, 2238 RSC; (b) A. J. Tasiopoulos, A. Vinslava, W. Wernsdorfer, K. A. Abboud and G. Christou, Angew. Chem., Int. Ed., 2004, 43, 2117 CrossRef CAS PubMed.
- (a) T. C. Stamatatos, D. Foguet-Albiol, C. C. Stoumpos, C. P. Raptopoulou, A. Terzis, W. Wernsdorfer, S. P. Perlepes and G. Christou, J. Am. Chem. Soc., 2005, 127, 15380 CrossRef CAS PubMed; (b) T. C. Stamatatos, D. Foguet-Albiol, S.-C. Lee, C. C. Stoumpos, C. P. Raptopoulou, A. Terzis, W. Wernsdorfer, S. O. Hill, S. P. Perlepes and G. Christou, J. Am. Chem. Soc., 2007, 129, 9484 CrossRef CAS PubMed; (c) C.-I. Yang, W. Wernsdorfer, K.-H. Cheng, M. Nakano, G.-H. Lee and H.-L. Tsai, Inorg. Chem., 2008, 47, 10184 CrossRef CAS PubMed.
- (a) E. K. Brechin, Chem. Commun., 2005, 5141 RSC; (b) T. N. Nguyen, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2011, 133, 20688 CrossRef CAS PubMed; (c) B. Cordero, O. Roubeau, S. J. Teat and A. Escuer, Dalton Trans., 2011, 40, 7127 RSC; (d) A. M. Mowson, T. N. Nguyen, K. A. Abboud and G. Christou, Inorg. Chem., 2013, 52, 12320 CrossRef CAS PubMed.
- (a) Y.-L. Bai, J. Tao, W. Wernsdorfer, O. Sato, R.-B. Huang and L.-S. Zheng, J. Am. Chem. Soc., 2006, 128, 16428 CrossRef CAS PubMed; (b) C. M. Liu, D.-Q. Zhang and D.-B. Zhu, Inorg. Chem., 2009, 48, 4980 CrossRef CAS PubMed; (c) H.-B. Xu, B.-W. Wang, F. Pan, Z. Wang and S. Gao, Angew. Chem., Int. Ed., 2007, 46, 7388 CrossRef CAS PubMed.
- (a) A. Prescimone, J. Wolowska, G. Rajaraman, S. Parsons, W. Wernsdorfer, M. Murugesu, G. Christou, S. Piligkos, E. J. L. McInnes and E. K. Brechin, Dalton Trans., 2007, 5282 RSC; (b) P.-H. Lin, S. Gorelsky, D. Savard, T. J. Burchell, W. Wernsdorfer, R. Clérac and M. Murugesu, Dalton Trans., 2010, 39, 7650 RSC; (c) C.-L. Zhou, Z.-M. Wang, B.-W. Wang and S. Gao, Dalton Trans., 2012, 41, 13620 RSC; (d) F. Habib, G. Brunet, F. Loiseau, T. Pathmalingam, T. J. Burchell, A. M. Beauchemin, W. Wernsdorfer, R. Clérac and M. Murugesu, Inorg. Chem., 2013, 52, 1296 CrossRef CAS PubMed.
- (a) H. Miyasaka, T. Madanbashi, A. Saitoh, N. Motokawa, R. Ishikawa, M. Yamashita, S. Bahr, W. Wernsdorfer and R. Clérac, Chem. – Eur. J., 2012, 18, 3942 CrossRef CAS PubMed; (b) X. Feng, T. D. Harris and J. R. Long, Chem. Sci., 2011, 2, 1688 RSC; (c) T. D. Harris, M. V. Bennett, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2010, 132, 3980 CrossRef CAS PubMed.
- A. V. Prosvirin, H. Zhao and K. R. Dunbar, Inorg. Chim. Acta, 2012, 389, 118 CrossRef CAS PubMed.
- (a) X. N. Cheng, W. Xue, W.-X. Zhang and X.-M. Chen, Chem. Mater., 2008, 20, 5345 CrossRef CAS; (b) D.-R. Xiao, G.-J. Zhang, J.-L. Liu, L.-L. Fan, R. Yuan and M.-L. Tong, Dalton Trans., 2011, 40, 5680 RSC; (c) Y.-Z. Zheng, W. Xue, M. L. Tong, X.-M. Chen, F. Grandjean and J. J. Long, Inorg. Chem., 2008, 47, 4077 CrossRef CAS PubMed.
- (a) Bond Valence Sum calculations gave oxidation state values of 1.99 (MnII) and 3.00/3.01 (MnIII) for the Mn ions of (1)∞14b; (b) W. Liu and H.-H. Thorp, Inorg. Chem., 1993, 32, 4102 CrossRef CAS.
- (a) S. Nayak, M. Evangelisti, A. K. Powell and J. Reedijk, Chem. – Eur. J., 2010, 16, 12865 CrossRef CAS PubMed; (b) S. Zartilas, C. Papatriantafyllopoulou, T. C. Stamatatos, V. Nastopoulos, E. Cremades, E. Ruiz, G. Christou, C. Lampropoulos and A. J. Tasiopoulos, Inorg. Chem., 2013, 52, 12070 CrossRef CAS PubMed; (c) M. Charalambous, S. Z. Zartilas, E. E. Moushi, C. Papatriantafyllopoulou, M. J. Manos, T. C. Stamatatos, S. Mukherjee, V. Nastopoulos, G. Christou and A. J. Tasiopoulos, Chem. Commun., 2014, 50, 9090 RSC.
- (a) A. J. Tasiopoulos, N. C. Harden, K. A. Abboud and G. Christou, Polyhedron, 2003, 22, 133 CrossRef CAS; (b) D. J. Price, S. R. Batten, B. Moubaraki and K. S. Murray, Polyhedron, 2003, 22, 2161 CrossRef CAS; (c) A. J. Tasiopoulos, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2005, 44, 6324 CrossRef CAS PubMed.
- M. E. Fisher, Am. J. Phys., 1964, 32, 343 CrossRef.
- When J1 = J1′ is imposed in the fitting procedure, it is impossible to reproduce the experimental data in a satisfactory manner.
- (a) C. Palopoli, M. González-Sierra, G. Robles, F. Dahan, J.-P. Tuchagues and S. Signorella, J. Chem. Soc., Dalton Trans., 2002, 3813 RSC; (b) N. Berg, T. Rajeshkumar, S. M. Taylor, E. K. Brechin, G. Rajaraman and L. F. Jones, Chem. – Eur. J., 2012, 18, 5906 CrossRef CAS PubMed.
- (a) D. Mandal, P. B. Chatterjee, S. Bhattacharya, K.-Y. Choi, R. Clérac and M. Chaudhury, Inorg. Chem., 2009, 48, 1826 CrossRef CAS PubMed; (b) A. R. Schake, E. A. Schmitt, A. J. Conti, W. E. Streib, J. C. Huffman, D. N. Hendrickson and G. Christou, Inorg. Chem., 1991, 30, 3192 CrossRef CAS; (c) S. Gou, Q. Zeng, Z. Yu, M. Qian, J. Zhu, C. Duan and X. You, Inorg. Chim. Acta, 2000, 303, 175 CrossRef CAS.
- A general demonstration of the relationship between the correlation length and the zero-field magnetic susceptibility is reported by Fisher in ref. 17 (before applying to the classical Heisenberg model).
Footnotes |
| † Electronic supplementary information (ESI) available: Crystallographic data (CIF format) for (1)∞ and various structure and magnetism figures. CCDC 1015476. For the ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4cc05687f |
| ‡ Current address: Department of Chemistry, University of Ioannina, 45110, Ioannina, Greece. |
§ Vacuum-dried solid analysed (C and H) as (1)∞. Calcd (found): C, 37.69 (37.82) and H, 6.33 (6.01)%. Crystal data for (1)∞: C20H40Mn3O12, Mw = 637.34 g mol−1, triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 9.0326(8) Å, b = 9.208(2) Å, c = 17.277(2) Å, α = 102.92(2)°, β = 91.393(9)°, γ = 111.20(1)°, Z = 2, V = 1297.0(3) Å3, T = 100(2) K, ρcalcd = 1.632 g cm−3, 7567 reflections collected, 3361 reflections used, R1 [I > 2σ(I)] = 0.0476, wR2 = 0.1410. , a = 9.0326(8) Å, b = 9.208(2) Å, c = 17.277(2) Å, α = 102.92(2)°, β = 91.393(9)°, γ = 111.20(1)°, Z = 2, V = 1297.0(3) Å3, T = 100(2) K, ρcalcd = 1.632 g cm−3, 7567 reflections collected, 3361 reflections used, R1 [I > 2σ(I)] = 0.0476, wR2 = 0.1410. |
| This journal is © The Royal Society of Chemistry 2014 |