Correlating Fischer–Tropsch activity to Ru nanoparticle surface structure as probed by high-energy X-ray diffraction

Abstract

Synchrotron X-ray diffraction coupled to atomic pair distribution function analysis and Reverse Monte Carlo simulations is used to determine the atomic-scale structure of Ru nanoparticle catalysts for the Fischer–Tropsch reaction. The rate of CO hydrogenation strongly correlates with the abundance of surface atoms with coordination numbers of 10 and 11. DFT calculations confirm that CO dissociation proceeds with a low barrier on these Ru surface atom ensembles.

---

The concept of the active site in catalysis has been known for nearly a century by now,¹ yet identification of the locus of catalytic activity in many real-life catalysts remains elusive. Metal nanoparticles (NPs) are among the most important heterogeneous catalysts for such important industrial chemical reactions as ammonia synthesis, hydrogenation of unsaturated bonds and the Fischer–Tropsch (FT) reaction. Of considerable current interest is the dependence of catalytic rate on metal particle size. For instance, dissociation of diatomic molecules with π-bonds, e.g., NO, N₂ and CO, requires specific surface ensembles forming a step-edge.^2,3 Current knowledge of atomic ordering of catalytic surfaces is mostly based on model single crystal surfaces, for which particular sites can be straightforwardly identified and enumerated. The exact number of such sites on real NPs remains largely unknown. Advanced electron microscopy has been used to identify step-edge sites,^4,5 but such techniques have limited statistical accuracy, because two-dimensional representations of at best few NPs are used to draw conclusions on 3D atomic-scale structure of a large assembly of particles participating in the reaction. A more accurate approach involves a combination of characterization and modeling techniques.⁶ Typically, modeling using state-of-the-art density functional theory (DFT) based methods involves perfectly periodic nanocrystal-type structures. This is not necessarily the case with real NPs where the periodicity of the atomic ordering is essentially broken at their surface allowing for substantial atomic fluctuations. Local atomic disorder and non-uniformity in NPs a few nanometer in size have been proven by high-energy X-ray diffraction (XRD) coupled with atomic Pair Distribution Function (PDF) analysis.⁷

The Fischer–Tropsch reaction forms the basis of increasingly important industrial technology to convert synthesis gas (a mixture of CO and H₂) into clean and valuable transportation fuels. Step-edge sites are speculated to be the active sites for the FT reaction.⁸ DFT studies have shown that (H-assisted) CO dissociation, the essential reaction step to produce monomers for chain growth, occurs more easily on such steps than on other surfaces.⁹ Experimental evidence supporting this view is controversial. For Ru¹⁰ and Co,¹¹ the turnover frequency is independent of particle size and only decreases significantly for particles smaller than 7 to 10 nm. Various explanations for this dependence have been advocated including (i) strongly adsorbed species blocking active sites on small particles,^10b,11a (ii) slow H₂ dissociation on small particles limiting the rate of H-assisted CO dissociation¹² and (iii) absence of step-edge sites on small particles.⁸ Typically, FT synthesis is studied in gas- or slurry-phase reactors.¹³ Recently, aqueous-phase FT reactors have gained popularity in academic studies.^13d,14,15 Here, we present results from a study aimed at shedding light on the nature of active sites in the FT reaction by studying the change in the FT activity with the fraction of low-coordinated atoms in Ru particles smaller than 6 nm.

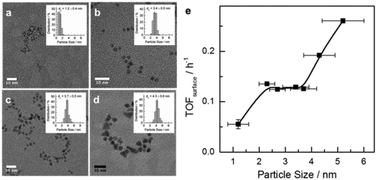
Colloidal Ru NPs between 1.2 to 5.2 nm were prepared by the polyol reduction method followed by reduction in H₂.^14b,15 FT reaction rates were determined at 150 °C. Together with the dispersion determined by TEM particle size analysis, surface-atom normalized turnover frequencies (TOF_surf defined in eqn (S2), ESI†) were computed (Fig. 1). TOF_surf increases with particle size from 1.2 to 5.2 nm with a plateau between 2.3 and 3.7 nm, this trend being consistent with available gas-phase FT data for Ru NPs.¹⁰ Such particle size dependence may be due to differences in the step-edge site density.^3,16 The usually argued maximum density of step-edge sites on 2 nm metal NPs^3,8,16 is based on highly idealized structures. Chorkendorff and co-workers have proposed that step-edge site density on Ru particles increases with size.¹⁷

Fig. 1 (left) TEM images of Ru NPs of increasing size (1.2, 3.4, 3.7 and 5.2 nm). (right) Surface-atom-normalized activity for aqueous phase FT reaction vs. Ru particle size. Aqueous-phase FT reaction was carried out at 150 °C and 30 bar syngas with H₂/CO = 2.

The alternative explanation that CO binds weaker to larger particles facilitating CO dissociation is not corroborated by IR data of adsorbed CO (Fig. S2, ESI†). Even though CO is adsorbed most strongly on the 1.2 nm NPs, the adsorption strength only varies slightly for NPs between 2.3 to 4.3 nm. The CO IR data further show that smaller particles carry more coordinatively unsaturated Ru atoms and the fraction of oxidized Ru is negligible (see the ESI†). This prompted us to investigate the atomic-scale structure of Ru NPs and look for a more adequate explanation for the particle size dependence in Fig. 1.

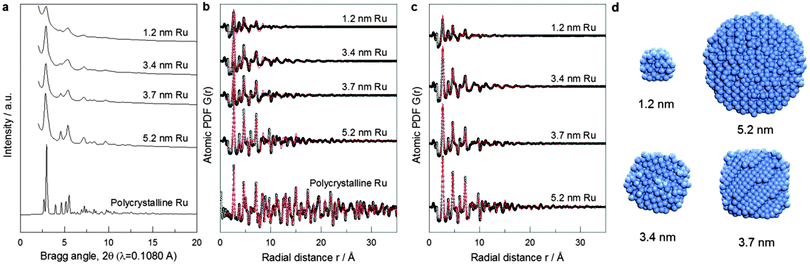
The XRD-PDF technique coupled to computer simulations has proven very well suited for characterizing the 3D structure of nanosized objects.⁷ XRD is a volume-sensitive technique. Atoms at the surface of particles smaller than 5 nm in size make up, however, about 20–80% of the total number of atoms, thus constituting a significant part of the NP volume. This renders XRD-PDF sensitive to both core and surface structure of small NPs. This information can be correlated to experimental catalytic activity data. Note XRD has a very good statistical accuracy since it samples a large number of NPs. Comparing NPs ensemble averaged XRD data to NPs ensemble averaged catalytic data puts structure–property correlations on the same footing. Fig. 2a shows the high-energy XRD patterns for Ru NPs of different sizes and also for a crystalline Ru standard. The XRD pattern of crystalline Ru shows well-defined Bragg peaks consistent with the hexagonal close packed (hcp)-type structure of bulk Ru. However, the XRD patterns for the Ru NPs are rather diffuse and cannot be analyzed in the traditional way. Therefore, we employed atomic PDF data analysis.⁷ Expectedly, the model reproduces the atomic PDF G(r) for polycrystalline Ru in very good detail as shown in Fig. 2b.¹⁸ This attests to the very good quality of the high-energy XRD data and the atomic PDFs derived from them. However, the model did not perform so well with the PDFs for Ru NPs with the performance increasingly worsening with diminishing NP size as indicated by the increasing values of the respective goodness-of-fit indicators shown in Fig. 2b. Visual inspection of experimental and hcp-model computed PDFs reveals that the worsening comes from a mismatch between both the position and intensity of PDF peaks (see Fig. S3a, ESI†). The low-r part of the experimental atomic PDF G(r) (Fig. S4, ESI†) shows that the first coordination distance, seen as a first peak in the atomic PDF data, is approximately 2.68 Å for all NP sizes. The same Ru bond distance has been obtained from EXAFS measurements at the Ru K edge (Table S2 and Fig. S3, ESI†). In addition, the experimental atomic PDFs show that with decreasing NP size the position of the second and third coordination spheres shift to higher r values (e.g., Fig. S5, ESI†), and the full width at half maximum (FWHM) of the first coordination sphere from crystalline Ru increases substantially when compared to that for polycrystalline Ru (Table S3, ESI†). The poor performance of the hcp-lattice constrained model with Ru NPs reflects the broken atomic ordering periodicity. The shift in the positions of the coordination spheres indicates local structural disorder, while the increase in FWHM points to increased degree of near-neighbor atomic fluctuations.^7c

Fig. 2 Synchrotron XRD for Ru particles. (a) XRD pattern. (b) Atomic PDFs: experimental data (symbols), hcp-lattice model fitting (red line). (c) RMC simulated model fitting (red lines). (d) Cross section of the atomic structure of Ru particles as generated from RMC simulations guided by XRD-PDF data.

To account for these observations we had to go beyond the limits of the perfectly periodic hcp lattice. For the purpose we employed reverse Monte Carlo (RMC) structure simulations.¹⁹ Details of the simulations are given in the ESI.† The simulations featured atomic configurations with the size and spherical shape of our Ru NPs. Representative atomic configurations for four differently sized Ru NP ensembles resulted from the RMC simulations are shown in Fig. 2d. The configurations reproduce the experimental PDFs much better than the hcp-lattice constrained model as evidenced by the respective goodness-of-fit indicators shown in Fig. 2b and c.

Visual inspection of the data in Fig. S4b (ESI†) illustrates the superiority of RMC constructed structure models in finer details. Analysis of these models reveals that 5.2 nm Ru particles exhibit overall hcp-type atomic ordering with some local surface structural disorder. On the other hand, only the cores of 3.4 and 3.7 nm Ru NPs exhibit hcp-type atomic ordering while atoms at their surface form structurally rather disordered shells. RMC simulations also reveal for the 1.2 nm Ru NP features a heavily disordered atomic configuration with little, if any, of the hcp-type structure features. Since the first minimum after the first coordination shell PDF peak is at about 3.4 Å (see Fig. S5, ESI†), first CNs in Ru NPs were determined by counting the number of metal atoms within a sphere with radius of 3.4 Å taking each metal atom from the respective RMC structure model as a center of such a sphere.

First CNs were then summarized in histograms showing the relative abundance of each CN found. So obtained distributions of first CNs in the Ru NPs studied here and that of first CNs in same size NPs with a perfectly periodic hcp-type structure are compared in Fig. S6 (ESI†). All atoms in bulk Ru with hcp-type structure have 12 first atomic neighbors. Due to finite size effects, atoms at the surface of Ru NPs have a first CN less than 12. Compared to the distribution of first CNs in hypothetical Ru NPs with a truncated but perfect hcp-type structure (grey bars in Fig. S6, ESI†), that of first CNs in the RMC constructed structure models (red bars in Fig. S6, ESI†) shows a much wider spread reflecting the substantial degree of atomic near-neighbor fluctuations, i.e., the presence of local structural disorder in the real NPs studied here. The fluctuations are particularly noticeable close to the NP's surface due to the greatest degrees of freedom surface atoms possess. The RMC models derived average first CN for Ru NPs are shown in Table S3 (ESI†). The average first CNs obtained by EXAFS experiments (Table S2, ESI†) are consistently lower than those obtained from the RMC models based on the experimental XRD/PDF data. This has most likely to do with the inefficiency of the EXAFS technique for materials with substantial local structural disorder. Note EXAFS fitting was done considering single scattering paths, i.e. not including partially overlapping metal–metal first coordination spheres that more often than not takes place in real NPs. An indication of the partial overlapping of the first and second coordination spheres in Ru NPs is the partial overlapping of the first and second peaks in experimental PDFs, clearly seen for 1.2 nm, 3.4 nm and 3.7 nm particles (Fig. 2c and Fig. S5, ESI†).

The evolution of the 3D atomic arrangement in Ru NPs, as revealed by inspecting the experimental PDF data alone (e.g., see Fig. S4, ESI†) and subsequent RMC simulations (e.g., see Fig. 3 and Fig. S6, ESI†), correlates well with the different activity regimes shown in Fig. 1. The correlation is as follows: (i) heavily disordered Ru NPs correspond to the regime with lowest activity below 2 nm, (ii) particles with a disordered shell and a hcp-type core, that is particles with size from 2.3 to 3.7 nm, fall in the regime with constant activity, and (iii) particles with little structural disorder and overall hcp-type atomic ordering correspond to the increase in activity. However, this correlation only provides a qualitative explanation of the catalytic activity data shown in Fig. 1. A quantitative explanation can be made by correlating the occurrence of particular CNs for atoms at the surface of Ru NPs, with the activity trend.

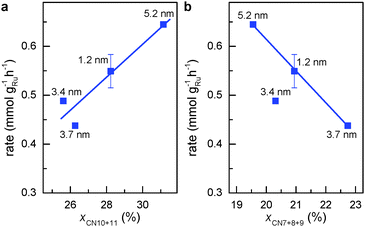Fig. 3 Activity for aqueous phase FT reaction vs. percentage of atomic sites coordinated with less than the ideal number of 12 atoms. (a) First CNs of 10 and 11. (b) First CNs of 7, 8 and 9.

Step-edge sites on the surface of Ru NPs can be identified by exploring the surface of the respective RMC models in detail (see Movies S1 to S4, ESI†). The sites involve Ru atoms that are at the bottom of the step-edges and so have a first CN of 10 or 11. Note that such coordination numbers are unique in a sense that they lie in between those of bulk (CN = 12) and those of atoms sitting on surfaces of Ru NPs (CN ≤ 9). The relative fraction of step-edge sites in the RMC structure models for Ru NPs was obtained very precisely by rigorous counting. Fig. 3a shows that the weight-based rate for aqueous-phase FT reaction increases linearly with the sum of fraction of surface atoms with first CNs of 10 and 11 (x_CN=10+11). This result demonstrates clearly that the FT activity closely relates to the presence of step-edge atomic sites. Correlating the activity to other first CNs did not yield similar relationships except for the sum of fractions of surface Ru atoms with first CN 7, 8 and 9 (x_CN=7+8+9). Unlike the trend observed for atoms with first CNs of 10 or 11, Fig. 3b shows that the FT rate is inversely proportional to the fraction of Ru atoms with first CN of 7, 8 or 9. This is to be expected since the FT reaction requires surface sites facilitating low barrier for CO dissociation.²⁰

Highlights of the different surface atomic configurations in Ru NPs are shown in Fig. S7 (ESI†). The highlights help recognize that surface atoms with first CN of 10 are indeed very much step-edge sites, while atoms with CN of 11 appear on more open than close-packed hcp-type surfaces. Other sites on more open surfaces may also be active for the FT reaction. For instance, previous DFT studies on Rh surfaces have shown that CO dissociates with lower activation energy on less-packed surfaces in comparison with close-packed surfaces. Yet this energy is only slightly higher with first CN of 10 or 11 than that on genuine step-edge sites.²¹ Hence, we hypothesize that both step-edge sites and open surface atomic sites with first CNs of 10 or 11 are active sites for the FT reaction. Fig. 4 shows that the TOF for aqueous phase FT normalized to x_CN=10+11 (TOF_CN=10+11, see eqn (S3), ESI† for definition) is independent of the Ru particle size. This implies that the chemical nature of the active sites for CO conversion remains unchanged for different particle sizes. Consequently, the change in FT activity with particle size in Fig. 1 is mainly due to the different concentration of sites with first CN of 10 or 11.

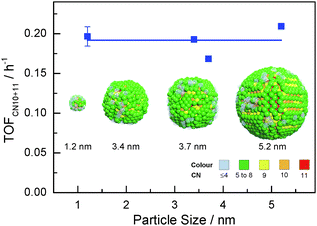Fig. 4 Ru particle size vs. activity of aqueous phase FT reaction normalized to the fraction of surface Ru atoms with CNs of 10 and 11 (colours represent different coordination numbers).

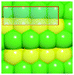
To verify that surface atomic configurations in close proximity to atoms with first CN of 10 or 11 can dissociate CO with low activation energy, DFT calculations were carried out focusing on few surface sites extracted from the RMC generated structure model (details given in the ESI†). Four potential sites were identified from the 5.2 nm Ru particle model (see Fig. S8, ESI†): (i) step sites involving surface atoms with CN of first 10 (B₅ sites), (ii) open surface sites involving surface atoms with first CN of 11 (so-called sawtooth sites), (iii) square planar sites with first CN = 8, and (iv) close-packed surfaces with first CN = 9. Calculations were performed by first extracting and freezing different parts of the RMC generated model for 5.2 nm particles that contained the four candidate sites. The geometries of these sites were then optimized before determining the barrier for CO dissociation.

Table 1 summarizes the calculated barriers for CO dissociation on these sites. The B₅ and sawtooth sites exhibit low barrier for CO dissociation of 49 and 135 kJ mol⁻¹, respectively. For the square planar and close-packed sites, the barriers for CO dissociation were found to be 174 and 232 kJ mol⁻¹, respectively. These values are to be compared to the values of 227 kJ mol⁻¹ for a closed-packed Ru(0001) surface and the 89, 65 and 47 kJ mol⁻¹ barrier for stepped Ru(1015),^9a Ru(112̄1)^9b and Ru(1010)²² surfaces, respectively. The DFT calculations thus indicated that CO dissociation is possible on B₅ and sawtooth sites, but not likely on square planar and sites on close-packed sites. The findings are consistent with trends for the FT reaction presented in Fig. 4, where the weight-based FT reaction rate is seen too increase with x_CN=10+11 and decreases with x_CN=7+8+9.

Table 1 Activation energy for CO dissociation on different sites identified on 5.2 nm Ru RMC model^a

B5^b	Sawtooth^b	Square planar^b	Close-packed^b
a DFT calculations performed by extracting parts of the RMC generated 5.2 nm Ru model (size roughly 1.5 nm, typically 150 atoms). b Colors represent coordination number: red (11), orange (10), yellow (9), green (5–8).
49 kJ mol^−1	135 kJ mol^−1	174 kJ mol^−1	232 kJ mol^−1

---

In summary, we demonstrated that high-energy XRD coupled with atomic PDF analysis and RMC simulations can be used to determine the core and surface atomic-scale structure of real NP catalysts smaller than 6 nm in very good detail. In particular, we show that step-edge and terrace sites on the surface of Ru NPs can not only be identified but also quantified. This study extends earlier XRD-PDF work on nanoparticle catalysts of the Chupas group.²³ Advantages of this approach are that particle-ensemble averaged structural and catalytic properties are compared without invoking the not quite realistic assumption of perfect crystalline-type NP structure and close-packed essentially flat NP surfaces. XRD-PDF measurements clearly show that unlike single crystal surfaces the surface of the real Ru particles can be corrugated and substantially disordered. A recent study of Ohyama et al. shows that Ru may be more susceptible to exposing such disordered surfaces than Pt.²⁴ The present study shows that the activity of the FT reaction scales linearly with the fraction of step-edge and open surface sites in Ru particles ranging in size from 1 to 6 nm. DFT calculations confirm that these sites catalyze low-barrier CO dissociation.

Notes and references

1. H. S. Taylor, Proc. R. Soc. London, Ser. A, 1925, 108, 105.
2. T. Zambelli, J. Wintterlin, J. Trost and G. Ertl, Science, 1996, 273, 1688.
3. K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Norskov, Science, 2005, 307, 555.
4. S. W. Lee, S. Chen, W. Sheng, N. Yabuuchi, Y.-T. Kim, T. Mitani, E. Vescovo and Y. Shao-Horn, J. Am. Chem. Soc., 2009, 131, 15669.
5. S. Van Aert, K. J. Batenburg, M. D. Rossell, R. Erni and G. Van Tendeloo, Nature, 2011, 470, 374.
6. A. M. Karim, V. Prasad, G. Mpourmpakis, W. W. Lonergan, A. I. Frenkel, J. G. Chen and D. G. Vlachos, J. Am. Chem. Soc., 2009, 131, 12230.
7. (a) V. Petkov, N. Bedford, M. R. Knecht, M. G. Weir, R. M. Crooks, W. Tang, G. Henkelman and A. Frenkel, J. Phys. Chem. C, 2008, 112, 8907; (b) N. Bedford, C. Dablemont, G. Viau, P. Chupas and V. Petkov, J. Phys. Chem. C, 2007, 111, 18214; (c) V. Petkov, Mater. Today, 2008, 11, 288.
8. R. A. van Santen, I. M. Ciobica, E. van Steen and M. M. Ghouri, Adv. Catal., 2011, 54, 127.
9. (a) I. M. Ciobica and R. A. van Santen, J. Phys. Chem. B, 2003, 107, 3808; (b) S. Shetty, A. P. J. Jansen and R. A. van Santen, J. Am. Chem. Soc., 2009, 131, 12874.
10. (a) J. Kang, S. Zhang, Q. Zhang and Y. Wang, Angew. Chem., Int. Ed., 2009, 48, 2565; (b) J. M. G. Carballo, et al. , J. Catal., 2011, 284, 102.
11. (a) G. L. Bezemer, et al. , J. Am. Chem. Soc., 2006, 128, 3956; (b) O. Borg, et al. , J. Catal., 2008, 259, 161.
12. A. Tuxen, et al. , J. Am. Chem. Soc., 2013, 135, 2273.
13. (a) Q. Zhang, J. Kang and Y. Wang, ChemCatChem, 2010, 2, 1030; (b) E. van Steen and M. Claeys, Chem. Eng. Technol., 2008, 31, 655; (c) H. M. Torres Galvis, et al. , Science, 2012, 335, 835; (d) H. Wang, et al. , J. Am. Chem. Soc., 2013, 135, 4149.
14. (a) C. X. Xiao, Z. P. Cai, T. Wang, Y. Kou and N. Yan, Angew. Chem., Int. Ed., 2008, 47, 746; (b) X. Y. Quek, Y. Guan, R. A. van Santen and E. J. M. Hensen, ChemCatChem, 2011, 3, 1735; (c) X. B. Fan, Z. Y. Tao, C. X. Xiao, F. Liu and Y. Kou, Green Chem., 2010, 12, 795.
15. X. Y. Quek, Y. Guan and E. J. M. Hensen, Catal. Today, 2012, 183, 72.
16. R. van Hardeveld and A. van Montfoort, Surf. Sci., 1966, 4, 396.
17. C. Strebel, S. Murphy, R. M. Nielsen, J. H. Nielsen and I. Chorkendorff, Phys. Chem. Chem. Phys., 2012, 14, 8005.
18. R. M. Nielsen, S. Murphy, C. Strebel, M. Johansson, I. Chorkendorff and J. H. Nielsen, J. Nanopart. Res., 2010, 12, 1249.
19. D. A. Keen and R. L. McGreevy, Nature, 1990, 344, 423.
20. A. J. Markvoort, R. A. van Santen, P. A. J. Hilbers and E. J. M. Hensen, Angew. Chem., Int. Ed., 2012, 51, 9015.
21. I. A. W. Filot, S. G. Shetty, E. J. M. Hensen and R. A. van Santen, J. Phys. Chem. C, 2011, 115, 14204.
22. S. Shetty and R. A. van Santen, Phys. Chem. Chem. Phys., 2010, 12, 6330.
23. S. Alayoglu, P. Zavalij, B. Eichhorn, Q. Wang, A. I. Frenkel and P. Chupas, ACS Nano, 2009, 3, 3127.
24. J. Ohyama, T. Sato, Y. Yamamoto, S. Arai and A. Satsuma, J. Am. Chem. Soc., 2013, 135, 8016.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods, computational details and supporting results. See DOI: 10.1039/c4cc01687d

---