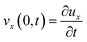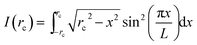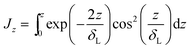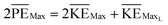Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Monitoring sessile droplet evaporation on a micromechanical device†
A.
Prasad
a,
A. T.-H.
Lin
b,
V. R.
Rao
c and
A. A.
Seshia
*a
aNanoscience Centre, Department of Engineering, University of Cambridge, 11 JJ Thomson Avenue, Cambridge, CB3 0FF, UK. E-mail: aas41@cam.ac.uk
bInstitute of Microelectronics, A*STAR, 11 Science Park Road, Singapore Science Park II, Singapore 117685
cCentre for Excellence in Nanoelectronics, Department of Electrical Engineering, IIT Bombay, Powai, Mumbai 400076, India
First published on 18th August 2014
Abstract
A bulk acoustic mode micro-electro-mechanical dual resonator platform is utilised to study the evaporation of sub-microliter water droplets from the surface of the resonator. An analytical formulation for the observed frequency shift and the measure dependence of resonant frequency on the modes of evaporation which is consistent with the optically derived data. The resonators access only a thin layer of the liquid through shear contact and, hence, the response is not affected by the bulk mass of the droplet to first order. A relationship between the droplet contact area and the elapsed time was established for the evaporation process and is used to derive a value of the diffusion coefficient of water in air that is found to be in reasonable agreement with literature values. This work introduces a new tool for the electro-mechanical monitoring of droplet evaporation with relevance to applications such as biosensing in liquid samples of sub-microliter volumes.
Introduction
Micro-Electro-Mechanical System (MEMS) technology enables batch fabrication of miniaturized mechanical devices that may be co-integrated with chip-scale electronics and microfluidic handling systems to realize miniaturized and portable platforms for bio-chemical sensing and environmental monitoring.1 Such platforms may utilize significantly smaller quantities of samples and reagents and potentially offer low cost routes towards volume manufacturing. Micro-/nano-mechanical sensors based on the modulation of mechanical properties on the interaction with the measurand have evoked much academic and translational interest in recent years.2 Particular implementations of such mechanical transducers are micro/nanomechanical resonators where the interaction between analyte/surrounding media and the resonator surface produces a shift in the resonant frequency response. These ‘dynamic’ mode sensors have shown an exquisite degree of sensitivity in vacuum enabling single molecule detection,3 zeptogram-scale mass sensing,4 and sub-attonewton force detection.5 However, when these sensors are operated in air and liquid environments, they suffer from degradation in performance due to high levels of fluidic damping. Viscous drag, squeeze film damping and acoustic radiation loss limit achievable resonator quality factors and, hence, the sensor resolution. Further, the presence of liquid can potentially interfere with the electrical transduction of the mechanical response. There has been much recent research in attempting to address the problems associated with operation in liquids and several innovative designs, for example embedding fluidic channels inside the resonator as in the case of suspended microchannel resonators,6–8 isolating the transduction element from the liquid as in the case of some piezoelectric devices,9 and electro-thermal actuation and piezoresistive sensing methods10 have been employed with promising results. However, these techniques require complex fabrication processes, and may be limited by transport issues in confined channel geometries and the lack of a precise chemical definition of the sensor surface.11An alternative approach to overcome the aforementioned issues has been previously reported by employing a dual-resonator platform (DRP).12 In this approach, two identical micromachined square plate resonators are coupled by a thin mechanical beam; one resonator is referred to as the transducer resonator (TR) and the other as the sensor resonator (SR). While the SR is interfaced with the liquid, the TR is electrically addressed to enable readout of the modulated frequency response. This scheme also allows relatively easy handling of liquid samples without significant constraints on electrical interfacing and device performance.
Apart from applications involving sensing of attached mass in air or vacuum environments (e.g. thin-film monitoring, particulate monitoring, etc.), the DRP can also be employed in situations where monitoring of physical processes in liquid media in contact with the SR is necessary. One such application is the monitoring of the evaporation of sessile droplets of liquids. Studies on the evaporation of droplets on flat surfaces have gathered tremendous interest over past decades with various studies being carried out to model the evaporation process.13–17 Evaporation of droplets is studied for understanding the general wetting behaviour of liquids,18 in the industrial context of spray cooling and inkjet printing,19–23 in the context of nanodispensing,24 in biology for mapping DNA on flat substrates,25 in microfluidics for optimizing device biochip designs,26 and dynamics of drying drops on nanostructured surfaces,27 and for understanding the various day-to-day phenomena involving the physical process of evaporation e.g. the coffee stain effect.28 These studies are also of relevance in a biochemical sensing context in fluid, where the very small volumes of fluid involved may evaporate rapidly from the sensor surface in a stop-flow mode.
The Quartz Crystal Microbalance (QCM) has been previously used to investigate sessile droplet evaporation.29,30 For instance, Joyce et al. used the QCM to monitor the extreme modes of droplet evaporation of a series of alcohols by modelling the evaporation process and its interaction with the radial sensitivity of the crystal. Previous work has also addressed M/NEMS based evaporation studies for investigating evaporation of microdroplets of diameters ranging from a few microns31 to tens of microns.32,33 These devices, based on the excitation of out-of-plane flexural resonances, are suitable for cases where droplet volumes are in the picoliter and femtoliter range. In contrast due to the in-plane nature of the excited mode shapes in the resonators used in our work, regardless of the bulk volume of the droplet, only a small thin layer of the droplet in shear contact with the resonator is effectively probed. Any changes in this thin layer (for e.g. due to changes in the contact area with the resonator and in some cases thickness of the layer itself) can be effectively sensed. Thus, these resonators find applications where modes of evaporation (associated with the shrinking droplet contact area) must be studied. The device platform reported in this paper can also be applied to study of the evaporation process of much larger droplet volumes (on the order of a few microliters or below), relevant to several practical applications outlined earlier, which are difficult to quantitatively analyze using existing optical techniques. Thus, the paper reports the use of the DRP to investigate evaporation of sessile droplets of DI water by direct electrical open-loop resonance frequency monitoring and the process of correlating the measured response due to the evaporating droplet with an analytical model of the physical process.
Theory
Liquid mass loading on the dual-resonator platform
The DRP consists of two identical thin silicon square plates, mechanically coupled by a thin coupling beam. The coupling beam is connected to the center points of the edges of the plate directly facing each other. The coupled system is driven in its coupled square-extensional (SE) modes and for analysis and experiments, the in-phase mode is monitored (Fig. 1).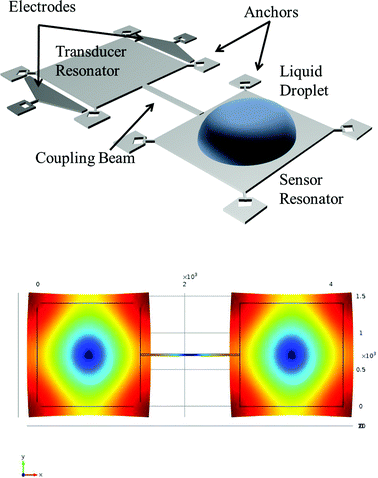 | ||
| Fig. 1 (Top) Schematic of the dual resonator platform with a liquid droplet spotted on the sensor resonator, and (bottom) COMSOL simulation of in-phase square-extensional (SE) mode. | ||
Using the Rayleigh–Ritz energy principle, the modal frequency ω of such a vibrating system can be approximately determined by equating the maximum potential energy (PEMax) to the maximum kinetic energy (KEMax) of the system. For a single square plate of side length L and thickness h, the SE mode shape can be approximated by the superposition of the following displacement functions:34
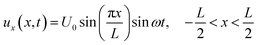 | (1a) |
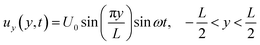 | (1b) |
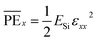 | (2) |
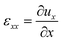 | (3) |
Hence, from eqn (2) and (3), we get:
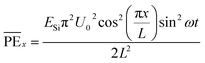 | (4) |
The strain energy stored in a differential element of volume dV(= dxdydz) at a distance x from the center is 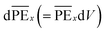 . Integrating for the whole plate, we get the component of stored strain energy in the vibrating plate which is then multiplied by a factor of 2 to get the time-dependent relationship of the stored PE for the DRP:
. Integrating for the whole plate, we get the component of stored strain energy in the vibrating plate which is then multiplied by a factor of 2 to get the time-dependent relationship of the stored PE for the DRP:
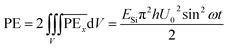 | (5) |
Hence,
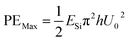 | (6) |
Similarly, to calculate the total kinetic energy of the vibrating square plate, we again consider the differential element of mass dm(= ρSidV) and proceed as follows:
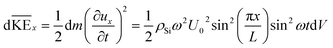 | (7a) |
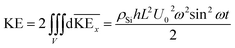 | (7b) |
Hence,
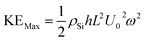 | (8) |
By equating the maximum values of PE and KE from eqn (6) and (8), we get
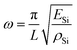 | (9a) |
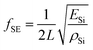 | (9b) |
In the case of a dual-resonator platform, the in-phase SE modal frequency can be approximated as ωDRP2 = 2PEMax/2KEMax or simply
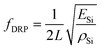 | (10) |
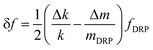 | (11) |
When a resonator surface comes in contact with a liquid deposit, an evanescent shear wave is formed at the liquid near the solid–liquid boundary. This shear wave dies off exponentially normal to the surface. Hence, to obtain the mass loading by the liquid and the resulting frequency shift, the modified PE and KE of the system must be re-calculated by applying Rayleigh's principle again as before. An effective thickness δL, also known as the penetration depth, of the liquid layer is defined35 as:
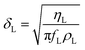 | (12) |
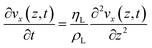 | (13) |
This is a one dimensional heat conduction equation whose solution is given by:
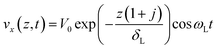 | (14a) |
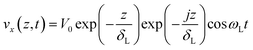 | (14b) |
At the point of contact (z = 0), assuming no-slip, the relative velocity between the liquid and the vibrating resonator surface should be zero. Hence, from eqn (1) and (14b) we get:
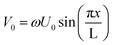 | (15) |
For a circular deposit of radius rc spotted at the center of one of the square plates of the DRP, the KE of a differential element within the liquid layer of thickness δL along the X-axis is given by:
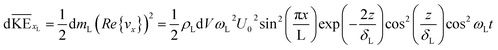 | (16) |
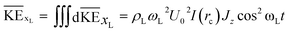 | (17) |
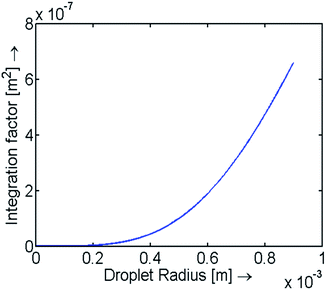
I(rc) is evaluated numerically and is plotted against droplet radii in Fig. 2. For droplets with a height much larger than δL, Jz = JδL. The maximum KE of the liquid deposit is
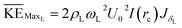 | (18) |
Hence, from eqn (6), (8) and (18), we have
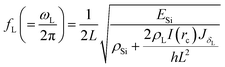 | (19) |
Therefore, for a measured “unloaded” frequency fU, the frequency shift due to liquid loading is approximately given by
| Δf = −S(rc, z)fU | (20) |
Modes of evaporation of the liquid droplet
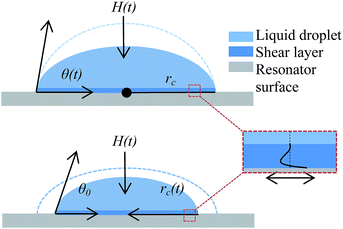
Evaporation of a liquid droplet is a diffusion driven process, where the concentration of the molecules (cs) reaches saturation just above the droplet surface while far away the concentration (c∞) depends on ambient conditions. This concentration gradient drives molecules away from the surface of the liquid droplet. The established evaporation rate is governed by Fick's law of diffusion where the diffusion flux ϕ is related to the concentration gradient and diffusion coefficient D by ϕ = −D∇c. Depending on the substrate surface and the liquid properties, there are two pure modes of evaporation for a slowly evaporating sessile droplet: pinned contact line mode and constant contact angle mode. The droplet can follow either of the two modes: a mixed mode in which both the modes occur in succession or a hybrid mode in which both occur at the same time. When the droplet contact line is fixed, the height and the contact angle of the droplet reduce with time whereas in the second constant contact angle mode, the contact area and height reduce with time while preserving the contact angle of the droplet. When the mixed mode of evaporation is observed, the droplet reaches a critical contact angle during the first mode, at which point, the second mode is triggered. For a sessile droplet of small volume, the shape at any instance can be approximated using a spherical cap geometry (bond number, Bo = ρLgrc2/γ ≅ 0.067, is less than 1 indicating the dominance of surface tension forces over gravitational). In our case, as indicated in the Experimental section later, it is observed that the contact line somewhat remains unchanged (pinned contact line mode) in the first phase of the experiment and then the evaporation seemingly transitions to a receding contact line mode for the remaining phase. As the initial height of the droplet is much larger than the penetration depth, we hypothesize the small corresponding change in the resonant frequency of the coupled system. Assuming that the second phase is the constant contact angle mode of evaporation, for a droplet of contact angle θ, spherical cap radius RS, and droplet volume Vc, following relationships can be established: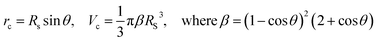 | (21) |
Now, the volume evolution of the drop is given by
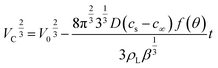 | (22) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/2
θ/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − cos
ln(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is a function of contact angle derived by Bourges-Monnier et al.36 to compensate for the horizontal contact surface. Simplifying the above equation in terms of the contact area Ac(= πrc2), we get
θ) is a function of contact angle derived by Bourges-Monnier et al.36 to compensate for the horizontal contact surface. Simplifying the above equation in terms of the contact area Ac(= πrc2), we get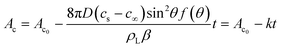 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf(θ)/ρLβ. Hence, the contact area is proportional to the evaporation and wetting parameters (diffusivity, temperature, humidity and contact angle). Unlike the first phase, where there is no change in the interfacial layer, the coupled system should “see” a change in mass with the shrinking droplet radius during this second phase of evaporation (Fig. 3).
θf(θ)/ρLβ. Hence, the contact area is proportional to the evaporation and wetting parameters (diffusivity, temperature, humidity and contact angle). Unlike the first phase, where there is no change in the interfacial layer, the coupled system should “see” a change in mass with the shrinking droplet radius during this second phase of evaporation (Fig. 3).
Experimental method
Device description
As explained earlier, the DRP consists of two identical micromachined square plate resonators that are coupled to a thin mechanical beam; one resonator is termed the transducer resonator (TR) and the other is termed the sensor resonator (SR). The device is fabricated by MEMSCAP Inc., USA using a standard silicon-on-insulator (SOIMUMPS) process. The resonators are suspended through T-shaped anchors at the corners while gold pads are patterned on the anchors and as well as on the electrodes for electrical interfacing. The geometrical parameters of the device are specified in Table 1. The device surface is not otherwise specifically treated and is used as it is received from the foundry.| Device design parameters | Values |
|---|---|
| Resonator edge length (L) | 1400 μm |
| Resonator thickness (h) | 25 μm |
| Coupling beam length | 1400 μm |
| Coupling beam width | 22 μm |
| SE in-phase resonance frequency (air, unloaded) | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142 142![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 Hz 969 Hz |
| Quality factor (air, unloaded) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
Actuation and sensing
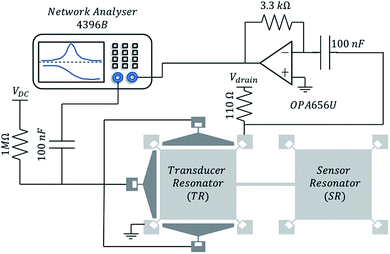
Coupled resonators are excited in their in-plane square extensional modes which inherently provide better quality factors compared to their out-of-plane flexural counterparts. The TR is electrically interfaced through the actuation electrodes, surrounding the resonator body, and the anchor pads. While the coupled device is capacitively excited, in an open loop, the motional current from the resonator body, through one of the anchor pads, is fed to the network analyzer (Agilent 4396B, RF Network Analyzer) following pre-amplification by a trans-impedance amplifier circuit (Fig. 4). The network analyzer is configured for obtaining S21 (electrical transmission) parameters of the device and is connected to a PC where the data are recorded for off-line analysis. As the signal is highly attenuated and damped, it is difficult to extract the resonance peak and other information from the output motional signal using conventional capacitive sensing techniques. Hence, to boost the signal, a piezoresistive sensing scheme is employed. When the resonators are excited in the square-extensional mode, anti-nodes result at the corners which are also the points of suspension of the resonator body. These suspension tethers connecting to the anchors are so designed so that the strain in these regions is maximized when the displacement of the square plate is maximized. By scaling the contribution of the piezoresistive signal from the T-shaped anchor relative to the resonator body, the piezoresistive response can be decoupled from the geometry of the resonator.Droplet dispensing and optical measurements
Distilled water droplets of volume 0.5–1 μL are dispensed on the SR by a micropipette. As the resonator surface area (1400 × 1400 μm2) and the droplet volumes are relatively large, the manual placement of the sessile drop on the resonator surface is relatively straightforward through this process may be automated for smaller dimensions and droplet volumes using microfluidics or robotic spotting techniques. A digital microscope (Keyence VHX-500F, Digital Microscope) is used to observe the evaporation of droplets from the top without interfering with the electronics setup. Images are taken periodically at an interval of 30 seconds and are later processed using ImageJ to obtain the radius of the droplet at various time intervals.Results and discussion
The DRP is first tested in air to obtain its unloaded frequency response. The resonance frequency fU and quality factor of the device are then extracted from the S21 (transmission) response in the unloaded state. The device is then extracted and spotted with a sessile droplet of DI water. Following this, the electrical transmission response and the optical images are recorded as a function of time as the droplet evaporates. The procedure is repeated several times to ascertain repeatability.Frequency response plots at various time instances for one of the evaporation experiments are shown in Fig. 5(a and b). As the motional current is swamped by the feedthrough current (parasitic and direct overlap capacitance), the original frequency and phase data are processed by subtracting the feedthrough component, obtained by supplying only the AC voltage to the device, from it. The corresponding feedthrough cancelled amplitude and phase frequency response curves are shown in Fig. 5(c and d).
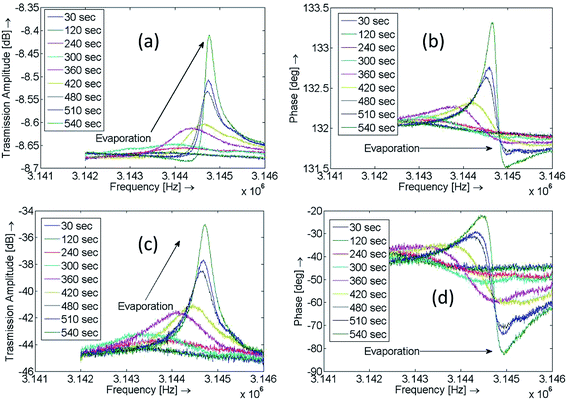 | ||
| Fig. 5 Transmission (S21) amplitude and phase plots at various time instances during evaporation of the droplet. (a and b) Raw data plots and (c and d) feedthrough cancelled data plots. | ||
Optical micrographs showing droplet evaporation from the DRP at different time instances is shown in Fig. 6. For the first 200 seconds (approximately), the size of the drop appears unchanged. Following this the drop rapidly starts to shrink and it eventually evaporates from the surface.
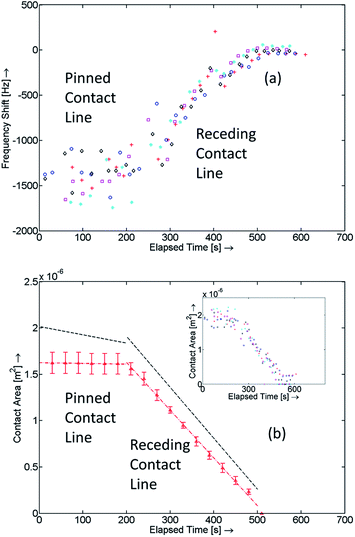
A scatter plot for the obtained frequency shifts, Δf, is plotted against time as shown in Fig. 7(a). The plot can be divided into three distinct zones, in the first zone, the resonant frequency is seen to fluctuate around a nominally value, in the second zone the frequency shift varies with time, and finally the frequency shift response flattens reaching a value close to zero indicating near-complete evaporation. The nature of frequency shifts throughout the experiments clearly indicates that the change in mass loading on the surface of the SR is different during different phases of the experiment. Further elaboration on this observation is discussed below when the optical images of droplet evaporation are compared with the observed frequency shifts. Anomalous frequency values and outliers were removed from these scatter plots.
The contact area is calculated using the optically measured droplet radii values (from ImageJ) and is plotted as a function of time as shown in Fig. 7(b) (inset). From the frequency shift data, using eqn (20), S(rc, z) and, hence, I(rc) is calculated. Values of the integration factor are then used to obtain the expected contact area (πrc2). Linear least-square fits for the optical and the modelled or frequency shift data for different regions are obtained. In both cases, the corner points are excluded from the fitting schemes (please refer to the ESI†). Sets of slopes for each individual experiment are extracted and average values designated k1,Opt, k2,Opt and k1,Mod, k2,Mod respectively are used for comparison. For the first phase k1,Mod = −8.942 × 10−10 compared to k1,Opt = −7.561 × 10−11 demonstrating a good match between the two techniques. The mode of evaporation during this stage can be said to be pinned contact line mode though contact line deformations can be seen occurring throughout this process. A reason for this could be because of slight non-uniformity of the surface energy distribution for the sensor as a result of contamination and exposure to air. Hence, as the height of the droplet reduces in the pinned contact line mode, the drop readjusts to maintain the smallest possible contact area. For the second stage, k2,Mod = −5.4983 × 10−9 compared to k2,Opt = −5.156 × 10−9 which is within 6.64% of the obtained value from optical observations of droplet evaporation. Under the given ambient conditions, T = 295.5 K and humidity = 31%, and the observed receding contact angle value of (48.85 ± 1.45)0 (please refer to the ESI†), we can estimate the value of the diffusion coefficient from the obtained slope k2,Mod. The experimentally obtained values for the diffusion coefficient of water are (2.8341 ± 0.105) × 10−5 [m2 s−1] compared to the reported value of 2.492 × 10−5 [m2 s−1] in the literature.37 While the match between the measured and theoretical values is relatively good (9–17% of the theoretical value), it should be emphasized here that the evaporation model itself is non-linear for smaller contact angles (please see the ESI†). Also, the diffusion constant is very responsive to local conditions and not one experiment is precisely equivalent to the other. However, it should be noted that by controlling the environmental conditions, the accuracy of the estimate could be further improved.
This analysis illustrates the usefulness of the technique in obtaining evaporation parameters. Alternatively, if the sample liquid is known (and, hence, its diffusion coefficient), one can easily find receding contact angle by analysing the slope obtained from the plot of the contact area against time. For example, in our case, if we assume the theoretical value of the diffusion coefficient of water vapour in air for the measurements, then the receding contact angle can be inferred to be approximately 44.17° compared to the observed value of 48.85°. This could be especially helpful in cases where sub-microliter/nanoliter droplet volumes need to be analysed where general imaging instruments and other techniques cannot be used. Also, as the surface properties of silicon can be readily modified, one possible application of the proposed device could be to study wetting properties of different liquids for different surfaces.
An interesting observation, revealed by comparing the time histories of the optical images and frequency response data, is that a change in the resonance frequency is observed even after the optical images appear to indicate that the droplet has completely evaporated. This can be attributed to the fact that since the thickness of the water layer seen by the sensor is only a few hundred nanometers, hence, a thin layer of water which is not captured by using the microscope is still present and contributes to the measured DRP frequency response until it evaporates completely. After evaporation of the droplet a visible residue is seen on the surface which contributes to “dry” mass loading.
Another observation from the data is that the expected contact area is always higher than what is measured optically. This implies that the coupled sensor is actually seeing more “mass” which could potentially be explained by the assumptions underlying the model described here. First, it is assumed that the liquid droplet is modelled by a symmetrically centred spherical cap geometry which, in reality, is not the case. The resulting difference in the spatial distribution of the droplet volume might result in a difference in the frequency shift observed experimentally. Also, the surface roughness could result in trapping of water molecules and, hence, higher mass loading. It has also been observed that inorganic residue can be deposited on the surface of the resonator resulting in additional mass loading due to miniscule amounts of contaminant residue.38 Also, fluctuations in temperature as the droplet evaporates have been neglected though such effects are expected to be small. A thorough analysis of such effects is left for future work.
The minimum optically observable radius of the droplet for the experiments where a change in frequency was recorded was around 250 μm. Below this radius, the droplet evaporated quickly thereby making it difficult to obtain a consistent value for the droplet radius. Assuming this to be the minimum contact radius that can be detected by the DRP, the corresponding mass and volume of the water in the shear layer is approximately 63 ng and 63 pL respectively and the total mass and volume of the droplet is approximately 20.4 μg and 20.4 nL respectively (please refer to the ESI†). In practice, the lowest detectable mass is related to the minimum detectable value of Δf as limited by the noise floor of the device and is smaller than the values reported above.12
One of the challenges associated with this technique is to control the positioning of the droplet on the resonator. Theoretically, if the droplet evaporates with the contact line pinned, the positioning of the droplet does not affect the response as the contact area, and hence, the mass sensed does not change throughout the evaporation process. In the case where the contact line recedes, if the recession is symmetric and the centre of the droplet remains fixed, then it is possible to account for the asymmetric positioning in the model if the initial position of the droplet is known (e.g. through a calibration process aided by surface structuring or a microfluidic interface to specify the initial position of the droplet) as the gradient of the frequency shift with respect to mass decrement is always positive. However, if the droplet moves over the surface of the resonator during evaporation or contracts asymmetrically during evaporation, then the interpretation of the response must account for this motion. In the current setup, these effects could be averaged out to a certain extent by using data across repeated experiments. Another drawback of this technique is the limited bandwidth of the open-loop frequency monitoring scheme. This can be addressed by embedding the DRP in the feedback loop of an electronic amplifier to construct an oscillator39 whose output tracks the resonance frequency enabling larger bandwidth applications. This approach would eliminate errors resulting from numerical extraction of parameters from the measured open-loop response. Finally, the device dimensions can be scaled to investigate evaporation of even smaller volumes of liquid and related physical processes, not accessible by standard optical techniques.
Conclusions
The dual-resonator platform, with its inherent advantages of relative ease of liquid handling without significant deterioration in response, offers a unique opportunity to investigate liquid-mediated surface processes as miniaturised microfabrication-compatible analogues of the QCM. The DRP is shown to be capable of detecting two modes of evaporation – viz. the pinned contact line mode and the receding contact line mode successfully and an analytical formulation of the frequency shift in the DRP is derived to understand the underlying correlation between the evaporating sessile droplet and the observed frequency shift. It was also shown that the device is very sensitive to small changes in the shape of the droplet as well as very small volumes of liquid. A good agreement was found between the experimentally derived value of diffusion coefficient of water derived from the measured data with literature values establishing the initial basis for this technique.Acknowledgements
Funding from the Royal Society and the Cambridge Trusts is acknowledged.Notes and references
- P. S. Waggoner and H. G. Craighead, Lab Chip, 2007, 7, 1238–1255 RSC
.
- J. L. Arlett, E. B. Myers and M. L. Roukes, Nat. Nanotechnol., 2011, 6, 203–215 CrossRef CAS PubMed
.
- A. K. Naik, M. S. Hanay, W. K. Hiebert, X. L. Feng and M. L. Roukes, Nat. Nanotechnol., 2009, 4, 445–450 CrossRef CAS PubMed
.
- Y. T. Yang, C. Callegari, X. L. Feng, K. L. Ekinci and M. L. Roukes, Nano Lett., 2006, 6, 583–586 CrossRef CAS PubMed
.
- H. J. Mamin and D. Rugar, Appl. Phys. Lett., 2001, 79, 3358–3360 CrossRef CAS PubMed
.
- T. P. Burg, M. Godin, S. M. Knudsen, W. Shen, G. Carlson, J. S. Foster, K. Babcock and S. R. Manalis, Nature, 2007, 446, 1066–1069 CrossRef CAS PubMed
.
- R. A. Barton, B. Ilic, S. S. Verbridge, B. R. Cipriany, J. M. Parpia and H. G. Craighead, Nano Lett., 2010, 10, 2058–2063 CrossRef CAS PubMed
.
- J. Lee, R. Chunara, W. Shen, K. Payer, K. Babcock, T. P. Burg and S. R. Manalis, Lab Chip, 2011, 11, 645–651 RSC
.
- H. Zhang, M. S. Marma, E. S. Kim, C. E. McKenna and M. E. Thompson, J. Micromech. Microeng., 2005, 15, 1911–1916 CrossRef
.
- J. H. Seo and O. Brand, J. Microelectromech. Syst., 2008, 17, 483–493 CrossRef CAS
.
- J. L. Arlett and M. L. Roukes, J. Appl. Phy., 2010, 108, 084701 CrossRef PubMed
.
- A. T. H. Lin, J. Yan and A. A. Seshia, J. Microelectromech. Syst., 2012, 21, 34–43 CrossRef CAS
.
- R. A. Meric and H. Y. Erbil, Langmuir, 1998, 14, 1915–1920 CrossRef CAS
.
- H. Y. Erbil, G. McHale and M. I. Newton, Langmuir, 2002, 18, 2636–2641 CrossRef CAS
.
- N. Shahidzadeh-Bonn, S. Rafai, A. Azouni and D. Bonn, J. Fluid Mech., 2006, 549, 307–313 CrossRef CAS
.
- N. Murisic and L. Kondic, J. Fluid Mech., 2011, 679, 219–246 CrossRef CAS
.
- L. Barash, T. Bigioni, V. Vinokur and L. Shchur, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 046301 CrossRef
.
- E. L. Talbot, A. Berson, P. S. Brown and C. D. Bain, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061604 CrossRef CAS
.
-
L. J. Turek, D. P. Rini, B. A. Saarloos and L. C. Chow, 2008 11th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, 2008, vol. 1–3, pp. 346–351 Search PubMed
.
- M. diMarzo and S. Tinker, Fire Saf. J., 1996, 27, 289–303 CrossRef CAS
.
- M. Sweetland and J. H. Lienhard, Int. J. Heat Mass Transfer, 2000, 43, 777–790 CrossRef
.
- J. Park and J. Moon, Langmuir, 2006, 22, 3506–3513 CrossRef CAS PubMed
.
- T. Lim, S. Han, J. Chung, J. T. Chung, S. Ko and C. P. Grigoropoulos, Int. J. Heat Mass Transfer, 2009, 52, 431–441 CrossRef CAS PubMed
.
- A. P. Fang, E. Dujardin and T. Ondarcuhu, Nano Lett., 2006, 6, 2368–2374 CrossRef CAS PubMed
.
- J. P. Jing, J. Reed, J. Huang, X. H. Hu, V. Clarke, J. Edington, D. Housman, T. S. Anantharaman, E. J. Huff, B. Mishra, B. Porter, A. Shenker, E. Wolfson, C. Hiort, R. Kantor, C. Aston and D. C. Schwartz, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 8046–8051 CrossRef CAS
.
- A. Ahmadi, M. D. Buat and M. Hoorfar, J. Micromech. Microeng., 2013, 23, 045001 CrossRef
.
- J. He, Q. Zhang, S. Gupta, T. Emrick, T. R. Russell and P. Thiyagarajan, Small, 2007, 3, 1214–1217 CrossRef CAS PubMed
.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS PubMed
.
- M. J. Joyce, P. Todaro, R. Penfold, S. N. Port, J. A. W. May, C. Barnes and A. J. Peyton, Langmuir, 2000, 16, 4024–4033 CrossRef CAS
.
- N. T. Pham, G. McHale, M. I. Newton, B. J. Carroll and S. M. Rowan, Langmuir, 2004, 20, 841–847 CrossRef CAS
.
- J. Arcamone, E. Dujardin, G. Rius, F. Perez-Murano and T. Ondarcuhu, J. Phys. Chem. B, 2007, 111, 13020–13027 CrossRef CAS PubMed
.
- C. Liu and E. Bonaccurso, Rev. Sci. Instrum., 2010, 81, 013702 CrossRef PubMed
.
- K. Park, N. Kim, D. T. Morisette, N. R. Aluru and R. Bashir, J. Microelectromech. Syst., 2012, 21, 702–711 CrossRef
.
- V. Kaajakari, T. Mattila, A. Qja, J. Kiihamaki and H. Seppa, IEEE Electron Device Lett., 2004, 25, 173–175 CrossRef CAS
.
- K. K. Kanazawa and J. G. Gordon, Anal. Chim. Acta, 1985, 175, 99–105 CrossRef CAS
.
- C. Bourges-Monnier and M. E. R. Shanahan, Langmuir, 1995, 11, 2820–2829 CrossRef CAS
.
-
R. E. Bolz and G. L. Tuve, Handbook of Tables for Applied Engineering Science, CRC Press, 2nd edn, 1976 Search PubMed
.
-
A. Prasad, A. Zielinsksi, M. Kalberer, R. L. Jones and A. A. Seshia, Proceedings of the 28th European Frequency and Time Forum (EFTF) conference, Neuchatel, Switzerland, June 23–26, 2014 Search PubMed
.
- J. E.-Y. Lee, B. Bahreyni, Y. Zhu and A. A. Seshia, IEEE Electron Device Lett., 2008, 29, 701–703 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4an01389a |
| This journal is © The Royal Society of Chemistry 2014 |