Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The application of non-linear curve fitting routines to the analysis of mid-infrared images obtained from single polymeric microparticles†
Hakan
Keles
a,
Andrew
Naylor
b,
Francis
Clegg
a and
Chris
Sammon
*a
aSheffield Hallam University, Materials and Engineering Research Institute, Sheffield, S1 1WB, UK. E-mail: C.Sammon@shu.ac.uk; Fax: +44 (0)114 225 3501; Tel: +44 (0)114 225 3069
bCritical Pharmaceuticals Limited, BioCity, Pennyfoot Street, Nottingham, NG1 1GF, UK
First published on 3rd March 2014
Abstract
For the first time, we report a series of time resolved images of a single PLGA microparticle undergoing hydrolysis at 70 °C that have been obtained using attenuated total reflectance-Fourier transform infrared spectroscopic (ATR-FTIR) imaging. A novel partially supervised non-linear curve fitting (NLCF) tool was developed to identify and fit peaks to the infrared spectrum obtained from each pixel within the 64 × 64 array. The output from the NLCF was evaluated by comparison with a traditional peak height (PH) data analysis approach and multivariate curve resolution alternating least squares (MCR-ALS) analysis for the same images, in order to understand the limitations and advantages of the NLCF methodology. The NLCF method was shown to facilitate consistent spatial resolution enhancement as defined using the step-edge approach on dry microparticle images when compared to images derived from both PH measurements and MCR-ALS. The NLCF method was shown to improve both the S/N and sharpness of images obtained during an evolving experiment, providing a better insight into the magnitude of hydration layers and particle dimension changes during hydrolysis. The NLCF approach facilitated the calculation of hydrolysis rate constants for both the glycolic (kG) and lactic (kL) acid segments of the PLGA copolymer. This represents a real advantage over MCR-ALS which could not distinguish between the two segments due to colinearity within the data. The NLCF approach made it possible to calculate the hydrolysis rate constants from a single pixel, unlike the peak height data analysis approach which suffered from poor S/N at each pixel. These findings show the potential value of applying NLCF to the study of real-time chemical processes at the micron scale, assisting in the understanding of the mechanisms of chemical processes that occur within microparticles and enhancing the value of the mid-IR ATR analysis.
Introduction
Multivariate analysis of hyperspectral imaging data is a rapidly developing research field and has received considerable attention over the last decade.1 Hyperspectral images that provide spatial and spectral information at the same time in an array of pixels and an individual pixel, respectively, can be obtained by a number of techniques including, X-ray tomography,2 X-ray fluorescence,3 Raman microscopy,4 and near infrared (NIR) imaging.5Over the last two decades Fourier transform infrared (FTIR) spectroscopic imaging has become routine, facilitating chemical characterization of multicomponent systems under both static and kinetic conditions.6,7 Currently more than 80% of all pharmaceutical formulations are delivered in a powder format8 and attenuated total reflectance (ATR) mode has proved advantageous, particularly for pharmaceutically relevant systems, because the sample can be in any phase, form or shape therefore no sample preparation is necessary.9 Micro-ATR-FTIR imaging with a germanium objective provides a higher spatial resolution compared to transmission and transflection due to the effective magnification imparted by the high refractive index of the ATR crystal material. Conveniently, ATR-FTIR imaging in macro mode, i.e. without the use of a microscope, provides a temperature controlled environment for studying dynamic systems with a larger field of view.10 In the macro ATR mode, kinetic processes can be probed with IR light such that each of the 2D array of pixels of the focal plane array detector acts as an individual detector, allowing the collection of thousands of IR spectra simultaneously. Consequently, a stack of 2D images at a range of IR wavelengths can be collected within a few minutes, proving good temporal resolution for relatively slow processes.11
The use of ATR sampling in infrared spectroscopy is based upon the fact that, although total internal reflection occurs at the sample–crystal interface, radiation does in fact penetrate a short distance into the sample, this is known as the evanescent field. The distance that the evanescent field can travel within a sample in direct contact with the ATR crystal is defined as the depth of penetration (dp). Harrick and duPre12 defined dp as the value at which the initial electric field strength (Eo) decays to a value of Eo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp−1 and can be given as;
exp−1 and can be given as;
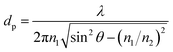 | (1) |
FTIR images, consisting of spectral and spatial information, must be analysed in detail to convert the data into chemically and physically significant information.6 Several methods for spectral and spatiotemporal data modelling can be used independently or in combination, however, the choice of analysis approach(es) for a series of hyperspectral image sets is determined by the nature and quality of the spectra and the information that needs to be extracted.15
The main challenge in hyperspectral image analysis on time-resolved multicomponent data sets is the extraction of the important information from the large volume of data generated including overlapping spectral features and noise. For time resolved experiments that continue for longer than a few hours unavoidable contributions from variations of atmospheric water vapour during the experiment has a huge effect particularly when the spectral region of interest is between 1500–1700 cm−1. This creates complications in the image analysis because the true peak centre, required for peak height measurements, may vary between pixels due to the superimposition of the rotational fine structure of atmospheric water onto the sample spectrum. Algorithms for subtracting atmospheric water vapour superimposed on the sample spectrum using a known water vapour spectrum can be employed for bulk ATR measurements collected using a single pixel detector. However, this does not always eliminate the problem in hyperspectral imaging, because of spectral variations between pixels emerging from the inherent low signal to noise ratio (S/R) compared to single point IR measurements. Applying a derivative is a common approach which eliminates baseline effects in univariate analysis but the water vapour bands are magnified by derivatives to such a degree that spectral information from the sample may be difficult to observe. Therefore spectra need to be deconvoluted by using soft or hard multivariate methods so that bands from the sample can be elucidated from the interfering water vapour signal. The most commonly applied multivariate tools to extract information from hyperspectral images include principal components analysis (PCA) and multivariate curve resolution (MCR) and comparisons between their application have been discussed elsewhere.1,16,17
The aim of this paper is to evaluate the advantages and limitations of univariate, hard and soft multivariate approaches for the analysis of ATR-FTIR images, collected during a dynamic process in real time. We also investigate the suitability of each of these analysis approaches for extracting quantitative information regarding the changes in the hydration and chemistry of a single poly(lactic-co-glycolic) acid (PLGA) microparticle and calculate the reaction rate during hydrolytic degradation.
Experimental
Materials
PLGA RG752H (75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 lactide
25 lactide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycolide, I.V. 0.16–0.24, Bohringer-Ingleheim) pharmaceutical grade CO2 (BOC Special Gasses) were used as received. Water used in the experiments was purified with the ELGA Purelab option-R water distillation apparatus (Up to 15 MΩ cm, Type II water) and degassed using a Fisherbrand FB11004 ultrasonic bath at ambient temperature and 100% ultrasound power for 15 minutes.
glycolide, I.V. 0.16–0.24, Bohringer-Ingleheim) pharmaceutical grade CO2 (BOC Special Gasses) were used as received. Water used in the experiments was purified with the ELGA Purelab option-R water distillation apparatus (Up to 15 MΩ cm, Type II water) and degassed using a Fisherbrand FB11004 ultrasonic bath at ambient temperature and 100% ultrasound power for 15 minutes.
CriticalMix™ process
PLGA is a random copolymer of poly(glycolic acid) (PGA), poly(lactic acid) (PLA), and is a U.S. Food and Drug Administration (FDA) approved, biodegradable18,19 synthetic polyester that is physically strong and highly processable.20 PLGA has suitable properties for biomedical applications as a scaffold21 and sustained release systems22 and has been comprehensively studied as carrier matrix for macromolecules such as proteins and peptides which are considered promising for the treatment of a range of conditions such as cancer, human growth deficiency, and multiple sclerosis.23 The manufacturing process used to produce the microparticles used in this study was a simple, one-step process which has been used recently to encapsulate protein based drugs with 100% encapsulation efficiency.22,24 When PLGA is exposed to scCO2 in a pressure vessel, the polymer is liquefied. If the liquid is depressurised through a nozzle, whereby the CO2 returns to a gaseous state, the polymer solidifies resulting in the production of microparticles. Careful control of the nozzle dimensions and depressurisation rate determines the particle size. Batches used in this study were prepared by adding 2.1 g of pre-weighed polymer, to the Particles from Gas Saturated Solutions (PGSS) apparatus. The apparatus was sealed, pressurised with CO2 to 700 psi (48 bar) and heated to 40 °C. Once at temperature, the pressure was increased to 2030 psi (140 bar). The liquefied polymer was then stirred at 150 rpm for 1 hour, after which time stirring was stopped and the mixture was depressurised through a nozzle generating microparticles. These were collected in a cyclone and recovered as a free flowing white powder.Real time ATR-FTIR imaging of reactions
Infrared images were collected using an Agilent 680-IR FT-IR spectrometer coupled with a liquid nitrogen cooled mercury cadmium telluride focal plane array detector MCT-FPA (64 × 64 pixels), capable of simultaneously collecting 4096 spectra from an image area of 640 μm × 640 μm using the Golden Gate™ Imaging Single Reflection ATR Accessory (Specac Ltd). This accessory has a diamond internal reflection element with corrective optics that adjusts the plane of best focus to sit on the crystal surface, eliminating any distortion, so that a symmetrical point spread function can be assumed. The angle of incidence of the infrared beam was 45° and the numerical aperture (NA) of the system was 0.32. Images were recorded in rapid scan mode and typical collection times were ∼5 minutes. The detector was mounted on a Large Sample (LS) external sample compartment and the infrared beam from the spectrometer was projected directly on to the FPA after passing through the ATR sampling accessory. The physical size of each FPA pixel is 40 μm × 40 μm and with 4× magnification, each pixel represents a 10 μm × 10 μm square in the image.To set up the hydrolysis experiment, a single PLGA microparticle was placed in direct contact with the ATR crystal using a 40× microscope standing on top of the ATR accessory and sufficient pressure was applied using the sapphire anvil to ensure good contact between the particle and the crystal resulting in some deformation of the spherical particle. The images collected were not circular, most likely showing some evidence of anamorphism despite the use of corrective optics and this issue when using such collection optics has been observed previously by Everall et al.25 and Chan et al.26 Once a satisfactory ‘dry’ image was collected water was introduced into the chamber in such a way that access to the particle was limited to the sides only as depicted in Fig. 1. Images were collected using the Agilent Technologies' ResolutionsPro FTIR Spectroscopy software version 5.2.0(CD846) at pre-determined time intervals and the collection parameters used were 128 co-added scans at a 4 cm−1 spectral resolution, in the mid-infrared (MIR) range (3800 to 950 cm−1). The raw processed images were obtained by ratioing against a background of the blank ATR crystal comprising of 256 co-added scans.
Data pre-processing
Raw processed image files were cropped between 1820 and 1000 cm−1 which provided a number of characteristic bands associated with PLGA and also included the water δ(OH) peak ∼1635 cm−1. In order to remove systematic discrepancies such as variations in detector sensitivity or sample thickness, raw images were vector normalised to minimise absorbance variance. Vector normalisation works such that each spectrum is divided to the vector length which is square root of the sum of all absorbance values squared. Instrumental factors such as fluctuations caused by the changes in the IR source intensity or temperature or detector sensitivity and optical artefacts caused by mismatch of the refractive index of species being imaged are known to cause a slope in the baseline in FTIR spectroscopy. In order to eliminate this slope, a second derivative can be applied, however caution is advised if there are very weak infrared bands of interest as a second derivative will magnify the noise and some low intensity peaks may be lost in the noise. However a first order baseline correction between the two end points of the previously cropped spectral range was found useful for elimination of the baseline drift when collecting an image. The full data pre-processing procedure is described in the ESI section including Fig. S1.†The MCR-ALS algorithm used in this paper32 has been developed for two-way data, therefore to use this approach, the 3D hyperspectral data cube must be unfolded into a two-dimensional matrix and refolded after analysis as shown in Fig. 2.
 | ||
| Fig. 2 Unfolding and re-folding spectroscopic imaging data to generate factor distribution images using MCR-ALS. | ||
FTIR images have a bilinear structure and it is assumed that some form of a Beer–Lambert relationship exists between spectral intensity and concentration.33 Therefore a bilinear model representing a spectroscopic image can be given as,
| Duxv = AuxzBzxv | (2) |
| A = (XBT)(BBT)−1 | (3) |
| B = (ATA)−1(ATD) | (4) |
To generate optimal matrices of A and B, one first needs to estimate their initial values. In this paper, a non-linear iterative partial least squares (NIPALS) decomposition method has been applied, the merits of which when compared to using random numbers, eigenvalue decomposition, or dissimilarity criterion is discussed in detail elsewhere.33 This is followed by the selection of the optimal number of factors to calculate and is achieved by considering the appropriateness of the initial estimate of the number of components. The final step, factor rotation, is a refining process where alternating least squares (ALS) is used to determine the optimal loadings and abstract factors matrices such that once recombined they most closely resemble the hyperspectral data matrix.
Although ALS is the most common method to decompose eqn (2) iteratively, a modified alternating least squares method (MALS) proposed by Wang et al.,34 which has been shown to overcome unstable convergence properties giving a non-optimum least squares solution, has been used for decomposition for all the MCR images generated here. The MCR-ALSv1.6 software was run from its graphical user interface (GUI) that allowed the user to input the number of factors (or components) to be estimated, number of iterations (used 500), and an ALS non negativity constraint (in this instance we used MALS-2D). The rationale for the use of 2 factors is justified based on the fact that the image quality (S/N, resolution) is better when using 2 factors than when using 3 or 4 factors and the same as using 5 factors, see ESI, Fig. S2.† And it is important to note that MCR results might be improved by using different strategies that were not covered in this paper and/or more soft constraints or hard constraints.35,36 For example, when the data were cropped down to the 1820–1500 cm−1 region which includes the PLGA carbonyl (∼1745 cm−1) and water δOH (∼1635 cm−1) MCR results were improved and although LA and GA peaks were not deconvoluted using MCR even when used cropped data between 1500 and 1300 cm−1, they were deconvoluted when 2 other PLGA compositions (PLGA100/0 and PLGA50/50) were included in the data set.
Another interesting, but rather lengthy, strategy that could have been considered was removing the solvent IR background contributions as developed and demonstrated by Kuligowski et al.37 in liquid chromatography infrared detection. They have estimated the solvent background successfully and by two different methods; principal component analysis and simple-to-use interactive self-modeling analysis (SIMPLISMA) and after subtracting the estimated background contributions from their data sets, MCR-ALS provided improved S/N ratios and resolved overlapping chromatographic peaks. As the shape of the δ(OH) band has been shown to change from pixel to pixel in FTIR imaging data, we considered that using the simple subtraction of a pure water spectrum at each pixel would introduce spurious peaks due to imperfect subtraction and hinder the MCR analysis. Therefore, for the purposes of this study and to keep the MCR analysis as a soft modelling approach, we decided to use no prior information of the pure components and utilise the whole fingerprint region of the IR spectra (1820–1000 cm−1) for the MCR analysis. We have not applied hard constraints such as pure spectra and/or different compositions of pure PLGA spectra as initial estimates of the MCR factors in the image set. Each of these would have been valid approaches but were beyond the scope of this work.
In order to use curve-fitting procedures, analytical functions must be used which describe the lineshapes of the peaks. Typical lineshapes encountered in spectroscopic studies are the Gaussian
| I(k) = I(k0)exp[−2.773(k − k0)/Δ2] | (5) |
| I(k) = I(k0)/[1 + (2(k − k0)/Δ)2] | (6) |
| I(k) = I(k0)[1 + P2]−M | (7) |
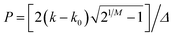 and M is known as the Pearson parameter. Eqn (7) reduces to the Lorentzian function when M = 1, approaches the Gaussian function when M becomes large and can approximate to the Voigt function for intermediate M.38 Modifying eqn (7) with an exponential term provides the required asymmetry and for M < 1 the distribution has very broad wings. The Pearson IV function is given in terms of this by
and M is known as the Pearson parameter. Eqn (7) reduces to the Lorentzian function when M = 1, approaches the Gaussian function when M becomes large and can approximate to the Voigt function for intermediate M.38 Modifying eqn (7) with an exponential term provides the required asymmetry and for M < 1 the distribution has very broad wings. The Pearson IV function is given in terms of this byI(k) = I(k0)[1 + P2]−M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−ν exp[−ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan−1 tan−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P] P] | (8) |
The exponential term has been shown to affect peak shapes when M is close to 1 (i.e. Lorentzian) more than it does for those where M is close to 10 (i.e. Gaussian).38
A routine in MATLAB Version 7.10 (R2010a), was developed to create fits for the each pixel within an IR imaging data set consisting of 4096 spectra individually. Peaks were detected using the algorithm described elsewhere41 and height and width of the peaks in the raw spectra at detected positions were used as initial guesses for the iterative loop. Application of non-linear curve-fitting to large two-dimensional experimental infrared spectroscopic arrays39 and a combination of non-linear curve-fitting and self-modelling curve resolution (SMCR)42 have been demonstrated. Software packages such as PyMCA, which is a non-linear least-squares fitting application have previously been developed for X-ray imaging data.43 However to the best of our knowledge, we are demonstrating a peak detecting non-linear optimisation algorithm applied to temporal ATR-FTIR imaging data for the first time.
The method by which we have approached this fitting procedure is described in detail in the ESI† and examples of the output from of the peak detection algorithm are given in Fig. S3.† To summarise our approach:
1. We select 18 spectra from the image based on their position; 6 from the water rich regions, 6 from the PLGA rich regions and 6 from the interface.
2. We iteratively and in a user supervised manner, adjust a peak detection threshold, such that all peaks in all 18 spectra are automatically detected by the peak detection algorithm. We fix the peak detection sensitivity parameter ‘Delta’.
3. Using the fixed peak detection parameter we apply the peak detection algorithm to all 4096 spectra in an unsupervised manner.
4. We then fit peaks of all 4096 spectra based on the number of detected peaks and their positions using a gradient search algorithm which finds the best fit for the measured data optimising the variables; peak height, peak width, peak centre, Pearson parameter and asymmetry parameter for each peak.
5. We then use the intensity of the peak ∼1635 cm−1 (selected in a supervised manner) to determine the distribution of water in the system and the sum of the intensity of all the peaks except the peak ∼1635 cm−1 to determine the distribution of PLGA.
6. The intensity of the peaks ∼1456 and ∼1424 cm−1, were used to calculate k values for lactic acid and glycolic acid units respectively.
Results and discussion
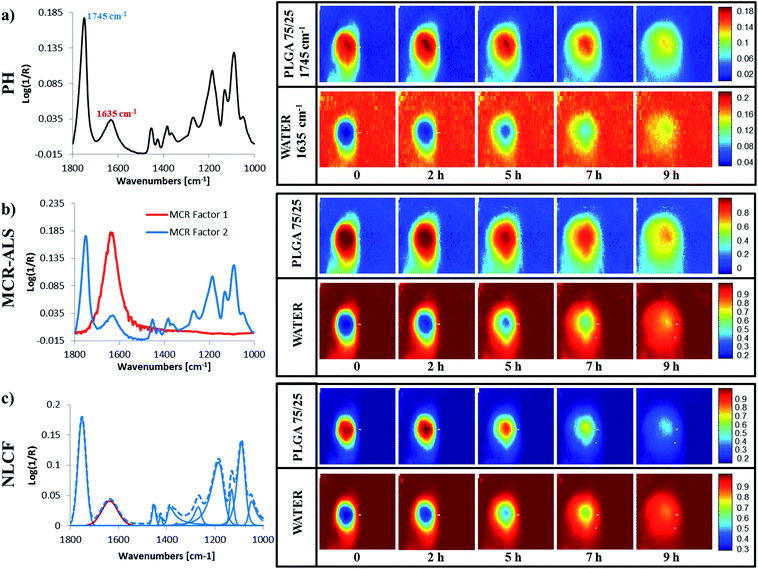
Fig. 3 shows the result of processing the same infrared image of a single PLGA microparticle in four different ways; using the peak height of a single peak in this case the ester carbonyl at ∼1745 cm−1 (Fig. 3(a)), plotting the distribution of a factor identified as deriving from PLGA in MCR-ALS (Fig. 3(b)), by plotting the sum of 10 peaks fitted between 1800 and 1000 cm−1 which does not include the peak ∼1635 cm−1 assigned to the water bending mode resulting from a NLCF procedure (Fig. 3(c)) and by plotting the sum of 10 peaks fitted between 1800 and 1000 cm−1 which does not include the peak ∼1635 cm−1 resulting from a peak fitting procedure using solely Gaussian lineshapes procedure (Fig. 3(d)). Images were generated from measurements conducted on an as received PLGA microparticle and on the same PLGA microparticle, immediately after water had been brought into contact with it. | ||
| Fig. 3 Data used to measure spatial resolution using the “step-edge” method for the dry PLGA particle (1st column of images and labelled ‘DRY’) and the same PLGA microparticle immediately after surrounding it with water as shown in Fig. 1 (2nd column of images and labelled ‘WET’) for images processed using peak height (a) PH, (b) MCR-ALS, (c) NLCF and (d) Gaussian. The raw data along the grey arrow in each image is shown in Fig. S3.† | ||
Spatial resolution comparison
The spatial resolution of a microscope is theoretically determined by the diffraction of radiation i.e. the Rayleigh criterion, which is defined in eqn (9) as | (9) |
A study on the effect of sample geometry on spatial resolution of the same ATR-FTIR imaging system used in this study has been conducted by Everall et al.25 for convex solid objects. They determined that this imaging system with a calculated NA of ∼2 was underestimating the size of 20–140 μm objects and approximating solid spheres, of varying dimensions, to be the same size (∼30 to 35 μm). The authors postulated that this was due to the shallow evanescent wave penetration (eqn (1)) and blurring caused by the finite spatial resolution. Our experiment however is different when compared to such a case, as the sample is a rather soft solid which, with a gentle anvil pressure, provides a flat central area that is quite large (∼100 μm) and the convex shape only occurs at the edges. As the main purpose of this paper is not to estimate the real size of the microparticle, but to compare the output of univariate, hard and soft multivariate tools, we are more interested in seeing how the different data analysis approaches impact upon measured spatial resolution and the sharpness of the interfaces. The measured spatial resolution for each of the data analysis methods is summarised in Table 1 and the spectra along the grey arrow on all spectra are shown in Fig. S4.†
| Method | Peak height | MCR-ALS | NLCF | Gaussian peak fitting |
|---|---|---|---|---|
| Dry | 70.2 ± 15.8 | 60.6 ± 0.4 | 42.7 ± 1.5 | 55.8 ± 4.1 |
| In water | 52.4 ± 4.7 | 48.8 ± 4.1 | 48.6 ± 4 | 49.2 ± 4.9 |
Table 1 shows that the NLCF approach improves the measured spatial resolution of a mid-IR image when there is a large discrepancy between the refractive index in adjoining pixels, i.e. an air/polymer interface. Lasch and Naumann have shown the application of Fourier self-deconvolution to IR microspectroscopy images has led to an improvement in the spatial resolution by improving the spectral resolution at each pixel.45 The NLCF approach we have used here, is also acting in a spectral resolution enhancement manner and the ability, when used in a supervised manner, to discriminate between species in adjoining pixels more readily than the peak height, MCR-ALS and Gaussian peak fitting approaches that limits the blurring effects at interfaces.
The comparison between the images generated using NLCF and the images generated using traditional Gaussian fitting is an interesting one. The results are showing that NLCF facilitated an improvement in spatial resolution compared to a Gaussian fit. This is likely to be mainly due to the optimisation algorithm (trust region) falling into local minima as a result of a lack of change between consecutive iterations due to the limited number of parameters in the Gaussian fitting protocol not allowing an improvement in fit, due to variations in the symmetry of bands between pixels. In order to make the algorithm robust for not only this but different data sets and as we know that IR bands are asymmetric, we chose to use the Pearson IV function despite the delay in computation time. The merits of using this function compared to Gaussian and or Lorentzian functions is also discussed in the text and in ref. 38 and 39.
When the refractive index change at an interface is small, such as when a PLGA microparticle is surrounded by water, the blurring of the interface is reduced and the spatial resolution determined by this step-edge approach is comparable between the each of the analysis approaches. It should be noted that for a sharp interface, such as the USAF (1951 1X 38257) target sample described in ref. 44, we have calculated the spatial resolution of the system to be ∼18 μm using the step edge method.
Image comparison
As indicated previously FTIR imaging is a powerful tool that facilitates the collection of spatially resolved chemically relevant data from samples in real time. By conducting such measurements in situ, we can minimise the perturbations to the system and follow chemical changes from the same region of the same sample. One of the challenges presented is the efficient analysis of the huge data matrices that are generated during such experiments (4096 spectra at each time point). To explore the relative merits of a number of different analysis approaches (univariate peak height image plotting, soft and hard multivariate modelling), we have taken single PLGA75/25 microparticle and followed its interaction with water as a function of time at 70 °C. The experiment is setup in such a way that the interaction between the particle and water will only occur at the interfaces that we are monitoring.Fig. 4(a) shows five false colour images obtained using the univariate peak height method and a spectrum taken from close to the ‘dry’ polymer/hydrated polymer interface in the t = 0 image. From this spectrum we are able to see both of the bands used to determine the polymer distribution (the ester carbonyl at ∼1745 cm−1) and the water distribution (the OH bending mode ∼1635 cm−1). The two images at the extreme left show the distribution of polymer (top) and water (bottom), within the ATR field of view, immediately after the experiment was started. Even at this short time (data collection was ∼5 minutes) there is evidence of an interface layer of hydrated PLGA around the particle, with an apparent concentration gradient from the particle centre outwards towards the aqueous media. As the contact time with water increases, a number of phenomena occur. Firstly the microparticle (defined by the red zone) initially appears to increase in size (2 h), which is indicative of swelling and the hydrated PLGA layer (yellow) becomes thicker. Images collected at times exceeding 2 hours show the particle decreasing in size and the boundaries of the particle becoming less well defined. The complementary images pertaining to water concentration show an inverse relationship, as one would expect in a binary system. The changes to the interface layer as a function of time will be discussed later. It is clear however, that the overlap between the bands used to determine the distribution of the two components in this system must influence the sharpness of this image and increase the magnitude of the measured interface.
Fig. 4(b) shows the equivalent false colour infrared images for the same data described in Fig. 4(a), this time, obtained using a MCR-ALS approach and 2 factors. The spectral features shown to the left hand side of this figure are the ‘pure component spectra’ for PLGA and water generated using this soft modelling method and are often referred to as factors. This data is in general agreement with the findings from the peak height measurement approach shown in Fig. 4(a). Closer inspection indicates that the interfaces in this set of images are blurred as were those observed in the univariate data set (Fig. 4(a)) and less sharp than those obtained using the hard modelling approach (Fig. 4(c)). But this data set does exhibit improved S/N compared to the univariate data (Fig. 4(a)). The blurring of the interfaces is the result of the ‘pure component spectrum’ representing PLGA still displaying a feature at ∼1635 cm−1 associated with water and due to the fact that the MCR factor for PLGA has fixed peak centres and band widths meaning they approximate rather than exactly replicate the spectrum at each pixel. The improvement in the S/N is the result of the elimination of water vapour in the pure spectral factors combined with the fact that the signal comes from many more spectral data points compared to the peak height data.
Fig. 4(c) shows 5 false colour images equivalent to those described in Fig. 4(a) and (b). However, this time they were obtained using the nonlinear curve-fitting approach and are the result of the summation of the peaks, generated during the fitting process, that have been assigned to PLGA (upper row) and water (lower row). The data to the left of these images shows the 11 component peaks used to fit the spectrum, from the same pixel used to obtain the peak height and MCR-ALS data within the PLGA/water interface. The dotted line denotes the synthetic spectrum generated from the combination of the fitted peaks, which matches the real spectrum at that pixel. The upper set of images shows the distribution of PLGA determined using all of the fitted peaks except the peak with a maximum at 1635 cm−1 which is used to obtain the distribution of the water within the ATR field of view. These images are, in general, in agreement with the data shown in Fig. 4(a) in that they indicate the formation of a hydrated region around a dry PLGA particle that increases in thickness over the first 2 hours and that this occurs concurrently with particle swelling. Closer inspection and comparison with the data in Fig. 4(b) indicates that the interfaces and boundaries in this set of images are much sharper and the data exhibits less noise, i.e. there is less variation in colour intensity between equivalent pixels. This (apparent) improvement in resolution and S/N in each image is achieved by the elimination of contributions from overlapping features at each pixel such as other chemical species, instrument noise and atmospheric water vapour. Another contributing factor to the broadening of the interfaces in the MCR-ALS images when compared with those generated using NLCF, is the fact that the NLCF peak centres are optimised for each peak within each pixel, whereas the MCR-ALS images used a fixed factor, with fixed peak centres and band widths. It is likely that during ALS optimisation, then a linear combination of the water and PLGA factors may give a better mathematical fit in some of the interface pixels resulting in a less well defined image, whereas the NLCF approach is better able to discriminate between water and PLGA. This does come at a considerable time and convenience penalty. The images shown in Fig. 4(a) can be obtained in seconds, whilst the data shown in Fig. 4(c) takes approximately 5 hours to generate using a PC with an Intel® Core™ i7-2620M CPU @ 2.7 GHz and 8 GB of RAM. In many applications this approach may not be feasible due to a number of considerations such as time, CPU availability and, more importantly, spectral data which is too challenging to fit due to a lack of knowledge of the species within that system Fortunately, the authors have amassed an understanding of the components within this system, i.e. water and PLGA thus generating confidence in the peak assignments. The MCR-ALS approach facilitates the collection of false colour images in a few minutes and thus offers an attractive/acceptable compromise between the slow but accurate hard modelling methodology and the rapid univariate approaches.
Interface analysis
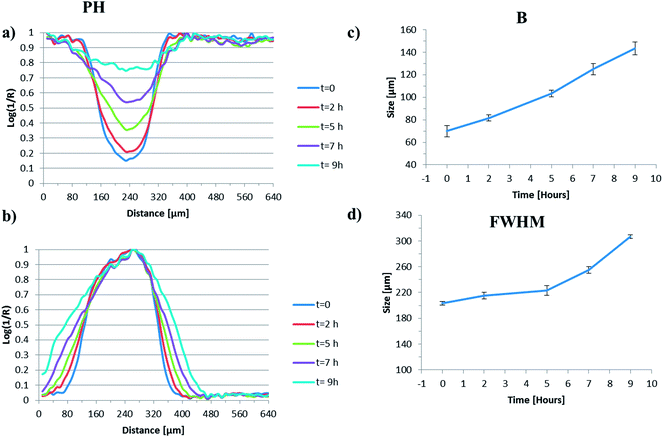
The generation of false colour images, from the mid-infrared imaging dataset highlighted here, facilitates the rapid assimilation of trends in physical processes such as particle swelling, particle shrinkage, hydration layer formation etc. but cannot readily be used to obtain quantitative information about such processes. This can be problematic when a particle is not uniform in shape and often the dimensions are estimated by assuming a particular geometry (circle, square etc.) that may not be appropriate. To compare the quality of the output generated using the NLCF approach with standard image generation strategies (peak heights and MCR-ALS) we have compared the findings along the centre line across the particle as a function of time. To facilitate comparison between the data analysis types we have defined two parameters; the full width at half maximum height of the normalised particle profile (A) and the dimensions of the right hand side interface (B). Their derivation is shown in the ESI, Fig. S5.†Fig. 5(a) and (b) show quantitative data extracted from across the centre line of the generated images shown in Fig. 4(a). Fig. 5(a) shows the evolution of the intensity of the water peak at each pixel across the image as a function of time and Fig. 5(b) shows the associated normalised plot of the full width at half height of the parameter ‘A’ for the images generated using peak heights.
From Fig. 5(a) it is possible to observe that the overall water concentration across the particle increases as a function of time as one might reasonably expect; rising from an intensity ∼15% of its maximum value at the local minimum at t = 0 h to a value of ∼75% of its maximum value at the local minimum at t = 9 h. The profile at t = 0, which is ∼5 minutes after the particle has been subjected to water, indicates that the initial ingress of water into the particle is rapid, most likely due to the porous nature of the scCO2 processed starting material. The shape of the profile initially appears to be fairly uniform and becomes less so as time progresses which may reflect the irregular shape of the particles. It is likely that initial compression onto the ATR crystal may make the analysed surface uniform (the ATR experiment collects data from the first 2–10 μm in direct contact with the crystal) but as the particle hydrates, swells and hydrolyses, the signal obtained via the ATR crystal will depend on the volume of the particle directly above the evanescent field and how it swells and or moves, potentially resulting in a loss of uniformity.
Fig. 5(b) shows the complementary data to that in Fig. 5(a) relating to the intensity of the polymer particle extracted from across the centre line of the peak height generated images. As the particle swells, the concentration of polymer measured within any given pixel will decrease and the concentration of water within that same pixel will increase. Therefore the intensity of the polymer peak (which should be the inverse of the water peak in this binary system) would provide an indication of the degree of swelling in the z-direction. Instead, we are using the change in width of the normalised intensity of the peak height of polymer peak, as a function of time, to provide an indication of the degree of swelling in the y-direction. We have chosen to normalise this data as it facilitates the observation of the change in full width at half height maximum (FWHHM) better than the equivalent data with the non-normalised y values, which decrease over time. For the peak height derived images we clearly see the width of this peak increasing as a function of time and this is plotted in Fig. 5(c).
When water is introduced into our system, there exist domains where we only measure water, others where polymer is the dominant signal and others where we observe a clear mixture of water and polymer; a hydrated zone. Determining the exact point where each domain ends and another domain begins is somewhat arbitrary, but some form of definition is necessary if we are to quantitatively compare data extracted from images generated using different approaches. As described above we have defined a hydrated zone ‘B’ where both the water intensity and the polymer band intensity are below a certain threshold (10% of the maximum value). Fig. 5(d) shows the plot of the B zone for the peak height derived images as a function of time. The size of this zone increases quite dramatically over the course of this experiment, with dimensions around 70 μm at t = 0 and expanding to 140 μm at t = 9 h. This increase in thickness of the outer hydration layer is an interesting finding and in broad agreement with confocal fluorescence images generated by Bajwa et al.46 of hydrating HPMC tablets. In the HPMC system an outer hydration layer of ∼100 μm increasing to 200 μm was measured over the course of a ‘wetting’ experiment. Clearly the timescales are different between the two systems due to the inherently different hydrophilicities, but nonetheless this adds credence to the nature of our measurements and our definition of B.
Fig. 6(a)–(d) show data comparable to that presented in Fig. 5, this time derived from the MCR-ALS generated images shown in Fig. 4(b). Fig. 6(a) and (b) show the evolution of the water intensity and the normalised plot of the polymer factor intensity respectively. The shape and the intensities of the profiles in these figures are similar to those derived from the peak height measurements, but there was less noise in the MCR derived data (most evident in Fig. 6(a)), particularly at longer time points, where the band intensities of the polymer peaks are quite low. This improvement of S/N occurs because the peak height data is derived from a single point and the MCR-ALS data is derived from a large number of data points. There is perhaps some evidence of the polymer band intensity profile being less sharp at longer time points and at its maximum, which could be related to the contribution of water within the extracted pure factor associated with the polymer (MCR factor 2; Fig. 4(b)) and will also be a function of the fixed lineshape of factor with its associated peak maxima and minima which will not be able to exactly match the spectrum at each pixel.
Both the B values (Fig. 6(c)) and the full width at half maximum height values (Fig. 6(d)) as a function of time are very similar to those shown in Fig. 5(c) and (d). This indicates that there is perhaps no significant improvement in the quality of output obtained for this system when performing an MCR-ALS analysis on the data when compared to the more rapid peak height approach. Of course the MCR-ALS method can be used without any prior knowledge of the system; therefore there is no need to identify a peak specific to each component within it, which could be advantageous in some instances.
Fig. 7(a)–(d) show data comparable to that shown in Fig. 5 and 6, this time derived from the NLCF generated images (Fig. 4(c)). Fig. 7(a) shows the intensity of the curve fitted water band as a function of time. Both the intensities and width of these profiles are somewhat different to those observed in those derived from the peak height (Fig. 5(a)) and MCR-ALS (Fig. 6(a)). Firstly the intensities are generally higher than those observed for the data derived using the other two approaches, this is more pronounced at short times, with the values at t = 0 being approximately 30% of their final intensity (cf. 15% for both peak heights and MCR-ALS). Some explanation is found in the consideration of the factors/bands used to generate the initial images from which these line profiles were generated. In the case of the peak height data, it is clear that the vector normalisation and baseline correction has enhanced S/N of the images (compare Fig. 4(a) with the data in ESI, Fig. S6†), but it is entirely feasible that this will exert some influence on the intensity values generated for each spectrum within a given pixel.
In the case of the MCR-ALS the extracted pure factor for the polymer contains a contribution from water (Fig. 4(b)) and therefore when the scores at each pixel for the pure water factor are calculated then they will be underestimated. As the NLCF approach is able to generate both a pure water signal and a pure polymer signal free from interference, we anticipate that the intensities presented in these profiles will be more likely to match the true concentration profile.
Fig. 7(b) is also somewhat different to the analogous peak height and MCR-ALS data; in that it is narrower and different in shape. Once more it is the convolution of the water and polymer bands in both the peak height and MCR-ALS spectra that contributes to the broadening of this profile, relative to the NLCF data.
Fig. 7(c) shows the increase in the B zone dimension as a function of time. The values plotted here are lower than those obtained via both the peak height and MCR-ALS approaches and the error determined at each time point is somewhat lower than the corresponding values for the other two methods. This is a clear indication of the ability of the NLCF procedures to eliminate noise from the processed images. Fig. 7(d) shows the FWHM of the normalised polymer band profile generated from the NLCF images (Fig. 4(c)) and this also shows a reduction in width in comparison with the analogous data generated using the other two methods. The reduction in size of the B zone and the FWHM in comparison with the data generated using peak heights and MCR-ALS is a reflection of the ability of the NLCF method to discriminate between the water and polymer contributions at each pixel, reducing the blurring effect of convoluted spectra.
Degradation rate calculation
Coupling the chemical selectivity of infrared spectroscopy with the regional selectivity of an FPA detector facilitates remarkable insight into a wide range of processes. PLGA microparticles can be used as sustained delivery vehicles, where the rate of hydrolysis will control the release rate. Parameters that govern the hydrolytic degradation of PLGA include molecular weight, structure and morphology and PLGA degradation dynamics. FTIR spectroscopy has routinely been used to follow hydrolysis kinetics, but we believe this is the first time that measurements have been undertaken on single microparticles in this manner. Two infrared bands have been observed at ∼1452 cm−1 and ∼1424 cm−1 that correspond to the antisymmetric bending of CH3 from the lactic acid units and the symmetric bending of CH2 from the glycolic acid units of the PLGA polymer. The relative intensities of these two bands can be used to estimate the relative quantity of glycolic and lactic acid units present in the polymer and has been used to determine the rate of hydrolysis of the two co-polymer segments within the same experiment. Work by Vey et al.47 has shown that the lactic acid units hydrolyse ∼1.3 times slower than the glycolic acid units. Unlike large-sized (a few mm) PLA/GA polymer devices, microspheres less than 300 μm in diameter have been shown to undergo homogeneous degradation with the rate of degradation of the core being equivalent to that at the surface.48,49 Therefore rate constants from different regions within a microparticle would be expected to give the same calculated rate.Fig. 8 shows typical single pixel spectra (Fig. 8(a)), spectra resulting from the binning of 5 × 5 pixels (Fig. 8(b)), the resultant peak fits from a single pixel (Fig. 8(c)) and the result of peak fits from the binning of 5 × 5 pixels (Fig. 8(d)) which have been used to calculate the rate constants, shown in ESI, Fig. S6.† It should be noted that due to a deviation from a linear relationship between the ln(intensity) versus time plot, no k values for the MCR data could be determined.
To compare the relative merit of each of the data analysis approaches used in this study, we have calculated the hydrolysis rates for both the glycolic and lactic blocks independently within the same experiment. MCR-ALS was unable to provide pure component spectra for both the lactic and glycolic segments of PLGA, probably due to the nature of the iterative extraction process. MCR-ALS relies on variance within spectral data sets to extract pure component factors and as the ratio between the glycolic and lactic units during hydrolysis is constant throughout the experiment (i.e. the data is co-linear) the algorithm does not detect any variance. Consequently a single ‘PLGA’ pure component is generated.
Hydrolysis rate constants for the lactic units (kL) and the glycolic units (kG) were calculated using both the peak height data and the NLCF data from the logarithmic plot of peak intensity versus degradation time (see ESI data S7†) using the band ∼1452 cm−1 for the lactic units and that at ∼1424 cm−1 for the glycolic units, using the spectra shown in Fig. 8. First order kinetics as defined in eqn (10) and (11) were assumed;
| ln(I) = −kLt + n | (10) |
| ln(I) = −kGt + n | (11) |
Rate constants were calculated by selecting the spectrum (or extracted factor) at 3 random pixels within each image. For comparison, the same positions were used for each of the peak height, MCR-ALS and NLCF image analysis approaches and the mean of the three values are shown in Table 2.
| Method | 5 × 5 pixels | Single pixel | ||
|---|---|---|---|---|
| k L | k G | k L | k G | |
| Peak height | 1.13 ± 0.2 | 1.41 ± 0.35 | 0.9 ± 0.53 | 1.53 ± 0.98 |
| NLCF | 1.47 ± 0.1 | 2.06 ± 0.13 | 1.29 ± 0.21 | 1.67 ± 0.34 |
Rate constants were also determined by binning the spectra/factor score from 3 areas of 5 × 5 pixels from random regions within each image. Once more the same regions were used for each of the peak height, MCR-ALS and NLCF image analysis approaches and the calculated rate data (where possible) are shown in Table 2 and are the result of the mean of three values.
Tracy et al.48 studied the degradation of poly(lactide-co-glycolide) microspheres in vivo and in vitro and determined degradation rate constants by measuring the polymer molecular weight as a function of time by gel-permeation chromatography. They found that the in vivo degradation rate was higher than in vitro degradation one. Their calculations of in vivo rate constant by GPC analysis for ester capped and uncapped (–COOH) PLGA50:50 microspheres were 0.033 ± 0.006 per day and 0.13 ± 0.05 respectively. Considering that the PLGA microparticle studied here was scCO2 processed therefore very porous, and a calibration (i.e. %GA or %LA versus IR absorbance) was not considered as in ref. 47, due to having one polymer composition, the k values calculated are in reasonable agreement with each other and with the values determined by Tracy et al.48 and, as one might anticipate, the error obtained when calculating rate constants by binning a number of spectra is somewhat lower than that obtained from a single pixel. The errors are larger for the peak height derived calculations than those from the NLCF measurements. It is also clear that the ratio of the rate constants calculated for the lactic and glycolic groups is also comparable with that determined by Vey et al.;47 we have determined the ratio of rate constants to be 1.2 (peak height binned pixels), 1.7 (peak height single pixels), 1.4 (NLCF binned pixels) and 1.3 (NLCF single pixels). Interestingly the error determined for the k calculations for the MCR-ALS processed images seemed to be independent of the number of pixels used to determine them. It is unclear if this finding is real or an anomaly of the pixels chosen to make the measurements.
Conclusions
A new algorithm for nonlinear curve fitting (NLCF) has been developed and applied to the analysis of mid-IR images of a single PLGA microparticle undergoing hydrolysis at 70 °C for the first time. The supervised NLCF approach has been shown to have several advantages over traditional peak height measurements and a commonly applied multivariate tool; MCR-ALS. Firstly the application of NLCF routines to such data has been shown to enhance the spatial resolution within a sample with (a) overlapping spectral signals and (b) containing interfaces with large discrepancies in the refractive index (i.e. air/polymer). Secondly it has been shown to improve S/N and sharpen features such as interfaces in processed images, due to its ability to discriminate between different species in a mixture, this is particularly pronounced when one compares this approach to standard peak height measurements. Thirdly as the approach does not appear to be greatly influenced by colinearity, unlike MCR-ALS, supervised NLCF can be used to extract chemical information from species changing at the same ratio during a kinetic process such as hydrolysis. Finally the high S/N at each pixel readily facilitates the calculation of rate constants from a single pixel with a low error when compared to traditional peak height approaches. All these advantages come at a significant time penalty; the NLCF algorithm described takes ∼5 hours to extract information from a single mid-IR image containing 4096 spectra, this compares to ∼2 seconds for peak height analysis and ∼1 minute for MCR-ALS on the same image using the same PC.With the help of fast developing computing hardware power, the supervised NLCF method developed here will be a useful IR imaging analysis tool providing high resolution images and quantitative analysis for many more cases particularly where hard modelling is the only option such as deconvoluting protein spectra when searching for changes in secondary structure.
Acknowledgements
The authors would like to thank the Engineering and Physical Sciences Research Council (EPSRC) grant number EP/I501665/1 for supporting this work.References
- J. M. Amigo, Anal. Bioanal. Chem., 2010, 398, 93–109 CrossRef CAS PubMed.
- S. Huotari, T. Pylkkanen, R. Verbeni, G. Monaco and K. Hamalainen, Nat. Mater., 2011, 10, 489–493 CrossRef CAS PubMed.
- G. Sciutto, P. Oliveri, S. Prati, M. Quaranta, S. Bersani and R. Mazzeo, Anal. Chim. Acta, 2012, 752, 30–38 CrossRef CAS PubMed.
- D. Zhang, P. Wang, M. N. Slipchenko, D. Ben-Amotz, A. M. Weiner and J. Cheng, Anal. Chem., 2013, 85, 98–106 CrossRef CAS PubMed.
- P. J. Williams, P. Geladi, T. J. Britz and M. Manley, Anal. Bioanal. Chem., 2012, 404, 1759–1769 CrossRef CAS PubMed.
- R. Bhargava, Appl. Spectrosc., 2012, 66, 1091–1120 CrossRef CAS PubMed.
- P. R. Griffiths and J. A. de Haseth, Fourier Transform Infrared Spectrometry, John Wiley & Sons Inc., Hoboken, New Jersey, 2nd edn, 2007 Search PubMed.
- P. Bassett, Drug Delivery Systems: Trends, Technologies and Market Opportunities, Drug & Market Development, Southborough, MA, USA, 2nd edn, 1999 Search PubMed.
- S. G. Kazarian and K. L. A. Chan, Biochim. Biophys. Acta, 2006, 1758, 858–867 CrossRef CAS PubMed.
- S. G. Kazarian and K. L. A. Chan, Appl. Spectrosc., 2010, 64, 135–152 CrossRef.
- S. G. Kazarian and K. L. A. Chan, Analyst, 2013, 138, 1940–1951 RSC.
- N. J. Harrick and F. K. duPre, Appl. Opt., 1966, 5, 1739 CrossRef CAS PubMed.
- F. M. Mirabella, J. Polym. Sci., Part B: Polym. Phys., 1983, 21, 2403 CrossRef CAS.
- G. Thomson and G. Poulter, US Pat., US20060261274 A1, 2006.
- A. A. Gowena, F. Marinib, C. Esquerrea, C. O'Donnella, G. Downey and A. c. J. Burger, Anal. Chim. Acta, 2011, 705, 272–282 CrossRef PubMed.
- B. Vajna, G. Patyi, Z. Nagy, A. Bodis, A. Farkas and G. Marosi, J. Raman Spectrosc., 2011, 42, 1977–1986 CrossRef CAS.
- M. Franssona, J. Johanssona, A. Sparéna and O. Svenssona, J. Chemom., 2010, 24, 674–680 CrossRef.
- U. Edlund and A. Albertsson, Adv. Polym. Sci., 2002, 157, 67–112 CrossRef CAS.
- D. Lemoine, D. C. Francois, F. Kedzierewicz, V. Preat, M. Hoffman and P. Maincent, Biomaterials, 1996, 17, 2191–2197 CrossRef CAS PubMed.
- C. Wischke and S. P. Schwendeman, Int. J. Pharm., 2008, 364, 298–327 CrossRef CAS PubMed.
- F. Danhier, E. Ansorena, J. M. Silva, R. Coco, A. Le Breton and V. Préat, J. Controlled Release, 2012, 161, 505–522 CrossRef CAS PubMed.
- F. Jordan, A. Naylor, C. A. Kelly, S. M. Howdle, A. Lewis and L. Illum, J. Controlled Release, 2010, 141, 153–160 CrossRef CAS PubMed.
- R. A. Jain, Biomaterials, 2000, 21, 2475–2490 CrossRef CAS PubMed.
- M. J. Whitaker, J. Ho, O. R. Davies, G. Serhatkulu, S. Stolnik-Trenkic, S. M. Howdle and K. M. Skakesheff, J. Controlled Release, 2005, 101, 85–92 CrossRef CAS PubMed.
- N. J. Everall, I. M. Priestnall, F. Clarke, L. Jayes, G. Poulter, D. Coombs and M. W. George, Appl. Spectrosc., 2009, 63, 313–320 CrossRef CAS PubMed.
- K. L. A. Chan and S. G. Kazarian, Appl. Spectrosc., 2003, 57, 381–389 CrossRef CAS PubMed.
- B. O. Budevska, S. T. Sum and T. J. Jones, Appl. Spectrosc., 2003, 57, 124–131 CrossRef CAS PubMed.
- T. M. Hancewicz and J. H. Wang, Chemom. Intell. Lab. Syst., 2005, 77, 18–31 CrossRef CAS.
- J. M. Prats-Montalbán, A. de Juan and A. Ferrer, Chemom. Intell. Lab. Syst., 2011, 107, 1–23 CrossRef.
- M. De Luca, S. Mas, G. Ioele, F. Oliverio, G. Ragno and R. Tauler, Int. J. Pharm., 2010, 386, 99–107 CrossRef CAS PubMed.
- A. de Juan and R. Tauler, Crit. Rev. Anal. Chem., 2006, 36, 163–176 CrossRef CAS.
- J. J. Andrew and T. M. Hancewicz, Appl. Spectrosc., 1998, 52, 797–807 CrossRef CAS.
- W. H. Lawton and E. A. Sylvestri, Technometrics, 1971, 13, 617–633 CrossRef.
- J. H. Wang, P. K. Hopke, T. M. Hancewicz and S. L. Zhang, Anal. Chim. Acta, 2003, 476, 93–109 CrossRef CAS.
- S. Piquerasa, L. Duponchel, R. Tauler and A. de Juan, Anal. Chim. Acta, 2011, 705, 182–192 CrossRef PubMed.
- S. Piqueras, J. Burger, R. Tauler and A. de Juan, Chemom. Intell. Lab. Syst., 2012, 117, 169–182 CrossRef CAS.
- J. Kuligowski, G. Quintas, R. Tauler, B. Lendl and M. de la Guardia, Anal. Chem., 2011, 83, 4855–4862 CrossRef CAS PubMed.
- A. G. Michette and S. J. Pfauntsch, J. Phys. D: Appl. Phys., 2000, 33, 1186–1190 CrossRef CAS.
- L. Chen and M. Garland, Appl. Spectrosc., 2003, 57, 323–330 CrossRef CAS PubMed.
- R. Bhargava, S. Q. Wang and J. L. Koenig, Appl. Spectrosc., 1998, 52, 323–328 CrossRef CAS.
- H. Eskandari, S. E. Salcudean and R. Rohling, IEEE Trans. on Ultrasonics, Ferroelectrics, and Frequency Control, 2007, 54, 1118–1130 CrossRef PubMed.
- W. Xu, K. Chen, D. Liang and W. Chew, Anal. Biochem., 2009, 387, 42–53 CrossRef CAS PubMed.
- V. A. Solé, E. Papillon, M. Cotte, P. H. Walter and J. Susini, Spectrochim. Acta, Part B, 2007, 62, 63–68 CrossRef.
- M. Offroy, Y. Roggo, P. Milanfar and L. Duponchel, Anal. Chim. Acta, 2010, 674, 220–226 CrossRef CAS PubMed.
- P. Lasch and D. Naumann, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 814–829 CrossRef CAS PubMed.
- G. S. Bajwa, K. Hoebler, C. Sammon, P. Timmins and C. D. Melia, J. Pharm. Sci., 2006, 95, 2145–2157 CrossRef CAS PubMed.
- E. Vey, C. Rodger, J. Booth, M. Claybourn, A. F. Miller and A. Saiani, Polym. Degrad. Stab., 2011, 96, 1882–1889 CrossRef CAS.
- M. A. Tracy, K. L. Ward, L. Firouzabadian, Y. Wang, N. Dong, R. Qian and Y. Zhang, Biomaterials, 1999, 20, 1057–1062 CrossRef CAS PubMed.
- G. Spenlehauer, M. Vert and J. P. Benoit, Biomaterials, 1989, 10, 557–563 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3an01879b |
| This journal is © The Royal Society of Chemistry 2014 |