SEDFIT–MSTAR: molecular weight and molecular weight distribution analysis of polymers by sedimentation equilibrium in the ultracentrifuge
Peter
Schuck
*a,
Richard B.
Gillis
b,
Tabot M. D.
Besong
b,
Fahad
Almutairi
b,
Gary G.
Adams
b,
Arthur J.
Rowe
b and
Stephen E.
Harding
*b
aNational Institute of Biomedical Imaging and Bioengineering, National Institutes of Health, Bldg. 13, Rm 3N17, 13 South Drive, Bethesda, MD 20892-5766, USA. E-mail: schuckp@mail.nih.gov
bNational Centre for Macromolecular Hydrodynamics, University of Nottingham, School of Biosciences, College Road, Sutton Bonington, LE12 5RD, UK. E-mail: steve.harding@nottingham.ac.uk
First published on 5th November 2013
Abstract
Sedimentation equilibrium (analytical ultracentrifugation) is one of the most inherently suitable methods for the determination of average molecular weights and molecular weight distributions of polymers, because of its absolute basis (no conformation assumptions) and inherent fractionation ability (without the need for columns or membranes and associated assumptions over inertness). With modern instrumentation it is also possible to run up to 21 samples simultaneously in a single run. Its application has been severely hampered because of difficulties in terms of baseline determination (incorporating estimation of the concentration at the air/solution meniscus) and complexity of the analysis procedures. We describe a new method for baseline determination based on a smart-smoothing principle and built into the highly popular platform SEDFIT for the analysis of the sedimentation behavior of natural and synthetic polymer materials. The SEDFIT–MSTAR procedure – which takes only a few minutes to perform – is tested with four synthetic data sets (including a significantly non-ideal system), a naturally occurring protein (human IgG1) and two naturally occurring carbohydrate polymers (pullulan and λ-carrageenan) in terms of (i) weight average molecular weight for the whole distribution of species in the sample (ii) the variation in “point” average molecular weight with local concentration in the ultracentrifuge cell and (iii) molecular weight distribution.
Introduction
The molecular weight (Da) or equivalently the ‘molar mass’ (g mol−1) is one of the most important parameters defining a polymer, although it is not trivial to measure, particularly for polydisperse systems. Sedimentation equilibrium (SE) in the analytical ultracentrifuge is a well established method for obtaining the molecular weights of polymers.1,2 It has an absolute basis (not requiring calibration standards or markers, or assumptions over conformation) and has an inherent fractionation ability, without the need for columns or membranes and associated assumptions over inertness. It is also not hampered by contamination through large supramolecular particles. With the use of multi-hole rotors and multi-channel cells, it is now possible to run up to 21 samples simultaneously in a single run. One drawback which has held back its wide application is that the procedures for data capture and analysis previously available have not made the method the easiest to apply.2 For studies on proteins and other molecules with well-defined molecular weights the last two decades has seen the development of powerful software procedures for the analysis of optical records from sedimentation equilibrium, taking advantage of on-line scanning of UV/visible optical records (absorption/fluorescence) or the on-line capture using a charge-coupled device (CCD) camera of the higher precision data yielded in the form of fringe displacements by the Rayleigh interferometric system. A characteristic feature of the analysis of protein interactions by SE is the direct fit of the measured signal profiles with a few discrete terms of Boltzmann exponentials, each corresponding to a different species of free protein or protein complex, and often linked in their amplitude by mass action law for reversibly interacting system. As recently reviewed,3 advanced strategies for SE analysis, such as implemented in the multi-method analysis platform SEDPHAT,4 include the global fitting of many SE signal profiles acquired at different loading concentrations, different rotor speeds, and different data acquisition with models that create constraints through implicit mass conservation and different interaction models, yielding binding affinities and stoichiometries.5The analysis of polymers with a quasi-continuous distribution of molecular weight – or suspensions of mixtures with a diverse distribution of molecular weight – poses different problems. In contrast to the quasi-discrete problem of protein interactions, where often the buoyant molar mass values and therefore the exponents of the Boltzmann terms for each species are known a priori, here the buoyant molecular weights are unknown and their averages and their entire distribution is estimated from the evaluation of the exponential SE profiles. This problem is further exacerbated by the steep rising of concentration profiles near the cell base, and the shadow of the cell base that leaves a fraction of material undetected and to be extrapolated. Conventional methods of estimating average molecular weights from extrapolation of Rayleigh fringe concentrations or UV/visible absorbancies to the base of the ultracentrifuge cell6 can lead to serious error particularly if the position of the bottom of the cell is poorly defined. A different approach was therefore introduced7 involving an operational point average molecular weight known as the M* function: this approach offered a significant advantage over conventional methods which involved concentration extrapolation to the cell base, since the M* function is a less sensitive function of radial position, permitting a more accurate evaluation of the (apparent) weight average molecular weight Mw,app for the macromolecular components in the solution. This procedure was initially built into a Wang Desktop calculator, extended into a mainframe FORTRAN algorithm8 and then into a QUICKBASIC version for PC.9 Besides providing a method of obtaining Mw,app the MSTAR programs also provided estimates of the local or point weight average molecular weights Mw,app(r) as a function of radial position (r) in the ultracentrifuge cell.8,9 The “app” signifies that the values obtained are apparent values, which will, at real solute concentration, be affected by thermodynamic non-ideality. Conventionally an “ideal” value is obtained by extrapolation of either Mw,app or Mw,app(r) to zero concentration, although at sufficiently low concentrations Mw,app ∼ Mw and Mw,app(r) ∼ Mw(r).
A limitation to the accuracy with which Mw (and Mw(r)) could be evaluated was the procedure employed to estimate the meniscus concentration, a long-standing problem with the analysis by fringe optics of sedimentation equilibrium data (see, e.g., ref. 6). Although for absorption optics this involved an extrapolation and an evaluation of the baseline or background absorbance of non-sedimenting species – and does not create too much difficulty, for Rayleigh interference – where the optical records are of the solute concentration relative to a reference position, conventionally taken as the air/solution meniscus10 – this involved either a rather complex mathematical manipulation of the data followed by an ill-conditioned extrapolation of two functions, based on a method of Teller et al.11 – the so-called intercept over slope method7 or a separate experiment involving synthetic boundary cells.12 We now present a completely new version of the program which (i) interfaces into the widely used SEDFIT platform for sedimentation analysis of macromolecules (ii) provides a much more rigorous method of obtaining the baseline and meniscus concentration for the Rayleigh interference optical system and (iii) provides an estimate for the distribution of molecular weight. We now describe the relevant theory behind the M* function, followed by a description of the algorithm, correcting for non-ideality where appropriate and then examples are given based on simulated data (single, two solute, data error and a significantly non-ideal system), a monodisperse protein preparation (human IgG1) a fractionated “standard” polysaccharide (pullulan P400) and an unfractionated polysaccharide (λ-carrageenan).
Theory
Average molecular weights and M*
Sedimentation equilibrium for a monodisperse ensemble of thermodynamically ideal macromolecules is characterized by the Boltzmann distribution, leading to a recorded signal | (1) |
k = (1 − ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ρ)ω2/2RT ρ)ω2/2RT | (2) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is the partial-specific volume, ρ the solvent density,13ω the rotor angular velocity, R the gas constant, and T the absolute temperature.1 The subscript ‘1’ in eqn (1) indicates that this relationship is for a single species.
is the partial-specific volume, ρ the solvent density,13ω the rotor angular velocity, R the gas constant, and T the absolute temperature.1 The subscript ‘1’ in eqn (1) indicates that this relationship is for a single species.
For an unknown sample, informed by eqn (1) one may examine a plot of ln(c) vs. r2 for an apparent weight average molecular weight
 | (3) |
Addressing this problem, an operational point average molecular weight was defined as7
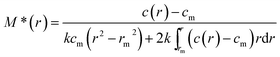 | (4) |
| M*(r = rb) = Mw,app | (5) |
First, conventional modes of analysis will require the evaluation of the baseline offset: in the ln(c) vs. r2 approach s0 needs to be explicitly known, whereas in the M* approach the macromolecular concentration at the meniscus cm needs to be distinguished from the total signal at the meniscus that will generally be superimposed by the offset s0, or cm = [s(rm) − s0](εd)−1. This problem can be posed differently for absorbance or interference optical systems:8 the absorbance system may allow for an experimental estimate of s0 to be determined, for example, from the signal close to the meniscus after a final overspeeding phase that leads to meniscus depletion conditions, or from scans performed at a wavelength where solute absorption is absent or minimal. Thus corrected, in absorbance the offset s0 is usually small. By contrast, the interference optical system fundamentally only allows us to measure fringe increments across the solution column, without an absolute reference.
Second, due to the derivative in eqn (3), when applied to noisy data it requires the data to be pre-smoothed to allow the determination of the numerical concentration derivative. This can be achieved, for example, with a ‘sliding strip’ procedure8,9 in the previous software MSTAR with a user-defined width, or with Chebyschev polynomial in the original MSTAR FORTRAN program,8 or now with the Savitzky–Golay smoothing and differentiation method14 in SEDFIT–MSTAR. By contrast, M* has the virtue of not requiring differentiation. In the calculation of M*, distortion of the signal and noise amplification can occur close to the meniscus, but the fraction in eqn (4) becomes increasingly more stable at higher radii with the growing integral in the denominator.
Finally, it is necessary for the application of M* to extrapolate the signal to the meniscus rm and, for the cell (i.e. whole distribution) average molecular weight, to extrapolate M* to the bottom of the solution column, rb. In MSTAR the extrapolation of signal to the meniscus is implemented as a linear or polynomial extrapolation,14 and similarly is available as an option in SEDFIT–MSTAR for both estimates of c(r = rm) and M*(r = rb).
The molecular weight distribution c(M)
In parallel, a method has been developed for the explicit determination of the entire molecular weight distribution, not restricted to its averages.5,15,16 It is based on the idea of direct modeling by least squares the experimental concentration distributions: | (6) |
One key difficulty in this approach is the ill-conditioned nature of this Fredholm integral equation, for which it can be shown that many different distributions c′(M) will invariably exist that fit the data indistinguishably well.11–14 However, in a Bayesian approach it is straightforward to determine from all distributions that fit the data with statistically indistinguishable quality the simplest distribution, for example, the smoothest distribution with Tikhonov regularization, or the distribution with highest information entropy with the maximum entropy regularization.15–19 This approach is available in the software SEDFIT and SEDPHAT.
A second difficulty is related to the fundamental problem that higher molecular weight species may sediment predominantly between the highest radius rup that can be optically accessed and the bottom of the solution column. This problem results in the c(M) method in undetermined distributions beyond an upper limit of molecular weight, Mup. It has been shown that this problem can be addressed by the global least squares modeling
 | (7) |
With regard to the computational implementation, SEDFIT–MSTAR solves eqn (6) and (7) as a linear least squares problem, which arises after discretization of the distribution c(M) into typically 50–100 molecular weight grid points, and from which all unknowns can be determined simultaneously in an algebraic operation employing normal equations.22 It should be noted that this includes the simultaneous optimization of both the exponential amplitudes and all baseline terms. This deviates fundamentally from the traditional sequential approach where first baselines are fixed, to be followed by the analysis of the SE gradient. The c(M) distribution at a reference radius r0 is normalized to units of (uniform) loading signal c0(M)dM that correspond to the estimated contributions to the SE profile, through analytical integration of eqn (1) for sector-shaped solution columns. Typically the analysis takes the order of 1 s with current personal computers.
Unfortunately, the solution of eqn (7) strictly as a linear least squares problem prohibits the additional consideration of radial-dependent baseline offsets s(r) (‘TI noise’) from multi-speed global SE analysis. Such radial-dependent baseline offsets are commonly determined as a byproduct of direct boundary modeling of families of concentration profiles in sedimentation velocity.23 While they can never be independently determined from a single concentration profile in SE, their consideration in the analysis of SE at multiple rotor speeds is complicated by the translation Δx of the radial-dependent features due to differential rotor stretching (which creates the non-linear constraint s(r + Δx,1) = s(r + Δx,2) etc.). Baseline profiles s(r) including rotor stretching can however be routinely evaluated in the global SE analysis of interacting systems.5,24 This is due to the description of the macromolecular concentration profiles governed by non-linear concentration parameters, which allows modified algebraic methods for the similar but translated baseline profile s(r + Δx).5 Along the same path, a potential future extension of SEDFIT–MSTAR may allow the consideration of radial-dependent baselines through treatment of the distribution as a family of non-linear parameters, although likely incurring significantly higher computational time.
On the other hand, dependent on the range of rotor speeds covered, and other experimental details such as the elasticity of the window cushion material25 the details of the radial-dependent noise may not necessarily remain identical after changing rotor speeds.5 In any event, for interference optical data acquisition the experimental determination and minimization of radial dependent baseline features, for example, through pre-aging of cell assemblies and recording of water blanks will be the method of choice. These considerations and the magnitude of the residual baseline uncertainty will also pose a limit on the useful concentration range for different types of studies in sedimentation equilibrium.
The removal of TI noise can also be effected experimentally, for interference data, by taking a series of scans immediately at the start of the run, averaging same, and subtracting this averaged set of radial values from the final (usually averaged) data set at equilibrium.26 This routine has been followed for all the experimental data reported here.
An executable form of the SEDFIT–MSTAR program can be obtained from the authors on request, or can be downloaded from https://sedfitsedphat.nibib.nih.gov/software/default.aspx or from https://www.nottingham.ac.uk/ncmh/unit/method.html#Software. A brief tutorial with screenshots and further information on its practical application can be obtained from http://www.analyticalultracentrifugation.com and via the SEDFIT-L forum (https://list.nih.gov/cgi-bin/wa.exe?SUBED1=SEDFIT-L%26A=1).
Relationship between c(M) and M* – exponential smoothing
Even though the motivation and computational approach of M* is very different from c(M) – the former being a data transformation to derive cell average molecular weights, and the latter attempting a low-resolution explicit representation of the molecular weight distribution in a direct least-squares fit – there is a high degree of synergy from the combined application of both.First, from the vantage point of M* the c(M) method can be regarded as a highly sophisticated method to smooth and extrapolate the data, and to estimate the baseline signals. To this end, we have implemented in SEDFIT–MSTAR the direct fit of the data with eqn (6) or (7). Even disregarding the specific form of c(M), with regard to the extrapolation of the signal to the meniscus for ca, the exponential superposition represents a special case of polynomial extrapolation (with infinite number of polynomials) that takes advantage of our specific knowledge of the expected functional form of the concentration distribution. As opposed to the polynomial extrapolation based on a trusted region close to the meniscus or cell base, here we use as the basis for extrapolation the entire solution column. Therefore, c(M) is an excellent method for determining baseline offsets, precisely because it takes advantage of data from the entire solution column and provides a best-fit baseline estimate on a least-squares basis.
Second, in addition to extracting these quantities from the c(M) fit, one can apply the M* transformation eqn (4) to the c(M) fit of the data, i.e. to the integral  with a result denoted in the following as M*c(M). These transformations of the c(M) fit to the raw data are shown as red lines in Panels (b) and (c) in Fig. 1–3 and 5–7. This not only honors the information on s0 and cm, but also produces a model for M*(r) across the entire solution column. Specifically, by design, this M*c(M) distribution will provide a natural extrapolation of M* to the bottom of the solution column. This extrapolation improves on the standard polynomial fit by taking into account the information from the entire solution column.
with a result denoted in the following as M*c(M). These transformations of the c(M) fit to the raw data are shown as red lines in Panels (b) and (c) in Fig. 1–3 and 5–7. This not only honors the information on s0 and cm, but also produces a model for M*(r) across the entire solution column. Specifically, by design, this M*c(M) distribution will provide a natural extrapolation of M* to the bottom of the solution column. This extrapolation improves on the standard polynomial fit by taking into account the information from the entire solution column.
Third, when the best-fit model of c(M) is transformed in the ln(c) vs. r2 plot, it provides a smooth fit of the noisy raw ln(c) vs. r2, data from which point averages as a function of signal Mw,app(c), or radius, Mw,app(r) can be easily determined across the entire solution column, provided the c(M) model yields an adequate fit of the data in the raw data space. Even though a fit of a transform will usually distort the statistics of the data errors, because the c(M) fit takes place in the original data space, it will have more appropriate weights than a fit and differentiation in the ln(c) domain.
In the implementation of SEDFIT–MSTAR, it is possible to switch from the M* representation of the data to the c(M) representation showing the raw sedimentation profiles, inspect the quality of fit of c(M) to the raw data and the residuals, and also to study the low-resolution molecular weight distribution c(M) directly. For example, multi-modal distributions may be resolved from suitable data. This can provide more insight in the molecular weight distribution, but in conjunction with information from M* gains robustness. For example, the M* perspective does not depend on regularization, and it may be advantageous when empirically applied to data with thermodynamic non-ideality.
When applied to the analysis of multiple sedimentation equilibrium data sets from the same sample acquired at multiple rotor speeds, the combination of M* with c(M) can be particularly powerful, especially if mass conservation and ideal sedimentation can be assumed. In this case, the global c(M) fit can serve to provide a single consistent interpretation of multiple individual M* transforms, which otherwise may be difficult to mutually reconcile and potentially result in different extrapolations and cell-average molecular weight estimates. An illustration of this with a pauci-disperse protein system has been given in Fig. 2 of ref. 5, where a multi-modal distribution was obtained from the global multi-speed analysis, but not in any of the single speed analyses. For the global analysis the question arises whether the baseline can be assumed to be rotor-speed independent or not. In SEDFIT–MSTAR, the data analysis can be carried out with both assumptions and the chi-squares of the c(M) fit can be compared. If a significant improvement in the quality of fit is achieved with rotor-speed dependent offsets s0,x (eqn (7), ‘RI noise’ option on) as compared to a fit with a single constant offset s0 (‘RI noise’ option off), then the analysis with individual offsets is justified. For interference optical data, the baseline cannot be expected to remain the same, as noted above.
In the implementation of this combined approach in SEDFIT–MSTAR, it is possible to either accept the results from the c(M) fit in the M* transformation, or override specific aspects, for example, to accommodate known baselines or meniscus concentrations. As outlined above, when globally analyzing data from multiple rotor speeds, the user can define whether they have a common baseline offset, or potentially different offsets at the different rotor speeds.
Hinge point-method for evaluation of Mw,app
SEDFIT–MSTAR also evaluates the apparent point weight average molecular weight Mw,app(r) as a function of radial position r using Savitzky–Golay smoothing and differentiation applied to eqn (3) as noted above. It also allows for the evaluation of the same parameter avoiding transformation of the data with the logarithm:6| Mw,app(r) = {1/k}{1/(r(s(r) − s0))}{d(s(r) − s0)/dr} | (8) |
Either eqn (3) or (8) can be used to define the molecular weight at the “hinge point” in the radial distribution – this is the radial position at which the local concentration (s(r) − s0) is equal to the initial cell loading concentration (in signal units). Hence Mw,app(r) at the hinge point will equal the weight average molecular mass of the whole distribution. Using for example eqn (8):
| Mw,app = {1/k}{1/(rhinge(s(rhinge) − s0))}{(d(s(r) − s0)/dr)hinge} | (9) |
SEDFIT–MSTAR provides the facility for obtaining the hinge point by evaluating the initial loading concentration from the conservation of mass equation:
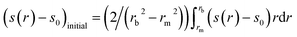 | (10) |
For non-sector-shaped channels (as found in the commonly used multi-channel centerpieces (3 pairs of channels)) the evaluation of the loading concentration presents difficulties for which there is no solution extant. However, by superimposition of early and late scans an empirical estimate of this parameter can be made, enabling the application of the ‘hinge point method’ described above.
Thermodynamic non-ideality
Thermodynamic non-ideality derives from macromolecular co-exclusion phenomena and, if the macromolecule is a polyelectrolyte, there will also be a contribution from any unsuppressed macro-ion charges, so all estimates for Mw and Mw(r) {and also the distribution c(M) vs. M, and Mz values} are apparent values (Mw,app, Mw,app(r), Mz,app(r) etc.). The charge contribution can be suppressed by working in a solvent of sufficient ionic strength (see, for example, ref. 27). Although for proteins at loading concentrations ∼1 mg ml−1 or less the effects of non-ideality are usually very small, for some polymers – particularly those with a high affinity for the solvent (such as polysaccharides in aqueous solvent), even at the lowest concentrations that can be used in a sedimentation equilibrium experiment (for polymers realistically ∼0.2–0.3 mg ml−1 with the longest cell path-length (20 mm) that can currently be employed), these effects can still be significant. Table 2 of ref. 28 for example gives a comparison of how Mw,app underestimate the true values for a series of polysaccharides at a loading concentration of 0.2 mg ml−1. If working at these low loading concentrations the approximations Mw ∼ Mw,app or Mz ∼ Mz,app are not valid, the conventional way of dealing with this situation is to perform a series of measurements at different loading concentration and extrapolate back to zero concentration where these effects tend to vanish. The form of the extrapolation can be linear or non-linear. For obtaining Mw,app using procedures that do not involve an integration, such as eqn (8), there is a simple relation relating Mw,app and Mw at dilution solution:| Mw,app = Mw{1/(1 + 2BMwc)} | (11) |
| Mw,app = Mw − 2BcMw2(1 + λ2Mz2/12) +… | (12) |
So although Mw,app from eqn (4) can generally be obtained to a higher precision than from the point average Mw,app evaluated from eqn (9) at the hinge point – and without assumptions over conservation of mass – the non-ideality effect will be greater. SEDFIT–MSTAR therefore includes both methods of Mw,app evaluation.
Application to simulated and real data
To illustrate the operation of SEDFIT–MSTAR we consider seven diverse examples, the first four of them based on simulated data (single solute, a mixture of two components, a mixture of two components with data error and a dataset with significant non-ideality). Simulated data was generated and where indicated normal random error added using custom-written plug-ins within the general software and graphical package pro Fit™ (Quantum Soft, Uitekon am See, Switzerland). Our routine level of normal random error is ±0.005 fringe (see, for example, ref. 26). In practice ‘real’ data sets will not, unlike simulated data sets, start from perfectly defined positions for the solution meniscus and the cell base: we therefore also consider the effects of systematic errors in these on the molecular weight evaluation. We also consider a significantly non-ideal system, with and without local random error of ±0.005 fringe. For our practical examples we consider the characterization of a monodisperse protein preparation (immunoglobulin IgG1) and two polysaccharides (a fractionated but still polydisperse preparation of pullulan and an unfractionated preparation of λ-carrageenan) are given.Simulation 1: single solute (no error)
As a point of reference and test for the correctness of the computations we first simulated noise-free data for a single solute. This is based on a Rinde32 type of simulation for a macromolecule of reduced molecular weight σ = kM = 2.000 (with k defined as in eqn (2)). For a solution density of 1.000 g ml−1, partial specific volume of 0.600 ml g−1, rotor speed of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and temperature of 293.15 K this corresponds to a molecular weight of 38
000 rpm and temperature of 293.15 K this corresponds to a molecular weight of 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 Da.
450 Da.
The radial position of the meniscus is at 6.90 cm and the base is at 7.15 cm. The true concentration at the meniscus in Rayleigh fringe units, cm (traditionally known as the “Ja value” – see ref. 6) is 0.108. The output consists of the signal plot a plot of log concentration versus radial displacement squared (r2) with fit (Fig. 1a), the M* versus r plot (with fit and extrapolation to r = rb) (Fig. 1b) a plot of the local or point weight average molecular weight Mw,app(r) vs. radial position r, or equivalently a plot of Mw,app(r) vs. concentration c(r) (Fig. 1c). Values of Ja = 0.108 and Mw,app = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 Da (from M*(cell base) = Mw,app and from the hinge point method) are correctly returned. The point average molecular weight plot (Mw,app(c) versus the corresponding local concentration in the ultracentrifuge cell, c or c(r)) reproduces this value also, and shows perfect monodispersity. Fig. 1d shows the estimated molecular weight distribution, again consistent with a monodisperse preparation of M = 38
450 Da (from M*(cell base) = Mw,app and from the hinge point method) are correctly returned. The point average molecular weight plot (Mw,app(c) versus the corresponding local concentration in the ultracentrifuge cell, c or c(r)) reproduces this value also, and shows perfect monodispersity. Fig. 1d shows the estimated molecular weight distribution, again consistent with a monodisperse preparation of M = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 Da.
450 Da.
Simulation 2: mixture of two solutes (no error)
The second simulation illustrates the effect of polydispersity, for clarity conducted in the absence of noise. Again based on Rinde, comprising an equal amount (by weight) of monomer, σ1 = 1.333 (M1 = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 Da) and dimer, σ2 = 2.667 (M2 = 51
630 Da) and dimer, σ2 = 2.667 (M2 = 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 Da). Solvent and sedimentation parameters are as in the first simulation, but with a radial position of the meniscus at 6.90 cm and the cell base at 7.10 cm. The true Ja value = 0.639. Fig. 2a shows the log concentration versus r2 plot, with the best-fit straight line (red) deviating from the data, as expected, due to the polydispersity. This is reflected also in the gradient of M* versus r (Fig. 2b), and the M*c(M) distribution (red line in Fig. 2b) that is based on the best-fit least-squares fit of the raw simulated c(r) data with the c(M) model eqn (5). As can be discerned from Fig. 2b, the same M*c(M) distribution allows the extrapolation to the cell base at r = rb. Fig. 2c shows the Mw,app(c) vs. concentration plot together with the c(M)-based best-fit (red line). From the SEDFIT–MSTAR analysis of the raw data, values of Ja = 0.65 and Mw,app = 38
260 Da). Solvent and sedimentation parameters are as in the first simulation, but with a radial position of the meniscus at 6.90 cm and the cell base at 7.10 cm. The true Ja value = 0.639. Fig. 2a shows the log concentration versus r2 plot, with the best-fit straight line (red) deviating from the data, as expected, due to the polydispersity. This is reflected also in the gradient of M* versus r (Fig. 2b), and the M*c(M) distribution (red line in Fig. 2b) that is based on the best-fit least-squares fit of the raw simulated c(r) data with the c(M) model eqn (5). As can be discerned from Fig. 2b, the same M*c(M) distribution allows the extrapolation to the cell base at r = rb. Fig. 2c shows the Mw,app(c) vs. concentration plot together with the c(M)-based best-fit (red line). From the SEDFIT–MSTAR analysis of the raw data, values of Ja = 0.65 and Mw,app = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 are returned, again in excellent (Ja) and exact (Mw) agreement with the true values. The hinge method also yields the same value for Mw, and finally the c(M) vs. M plot (Fig. 2d) also successfully resolves the two components, returning accurately the molecular weights (25
450 are returned, again in excellent (Ja) and exact (Mw) agreement with the true values. The hinge method also yields the same value for Mw, and finally the c(M) vs. M plot (Fig. 2d) also successfully resolves the two components, returning accurately the molecular weights (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 Da and 51
630 Da and 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 Da) and their relative proportions.
260 Da) and their relative proportions.
 | ||
Fig. 2 As Fig. 1 but for a simulated ‘perfect data’ 2-solute system, with 50% by weight of a monomer (M1 = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 Da) and 50% by weight of a dimer (M2 = 51 630 Da) and 50% by weight of a dimer (M2 = 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 Da). True Mw,app = Mw = 38 260 Da). True Mw,app = Mw = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 Da. Retrieved Mw,app (from extrapolation of M* to the cell base, and from the hinge point) = 38 450 Da. Retrieved Mw,app (from extrapolation of M* to the cell base, and from the hinge point) = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da. Fitted lines are as defined in the legend of Fig. 1. 500 Da. Fitted lines are as defined in the legend of Fig. 1. | ||
Simulation 3: mixture of two solutes with ±0.005 fringe random error
Next, we studied the effect of random error in the raw data on the different aspects of the analysis. Simulation parameters were identical to simulation 2, and corresponding results are shown in Fig. 3a–d. As may be discerned from Fig. 3c, the Savitzky–Golay filter sufficiently suppressed the random noise in the derivative of Mw,app. As expected M* is sensitive to the noise mainly close to the meniscus position, with increasing precision towards the base of the cell due to the accumulative effect of the integral in eqn (3). The biggest impact of the noise in the data is on the c(M) distribution: while it still serves as an excellent fit to both the M* and Mw,app values, the information on the true distribution degrades and the Tikhonov regularization returns a single broad distribution as the simplest distribution consistent with the noisy simulated c(r) data. This is by design, and required to avoid over-intepretation of the data, but, as illustrated here, leads to distributions that do not necessarily reflect the details of the true distribution. Nevertheless, the values of Ja = 0.65, and Mw,app = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 are returned, again in excellent agreement with the true values. An identical value for Mw,app is also returned from the hinge point method.
500 are returned, again in excellent agreement with the true values. An identical value for Mw,app is also returned from the hinge point method.
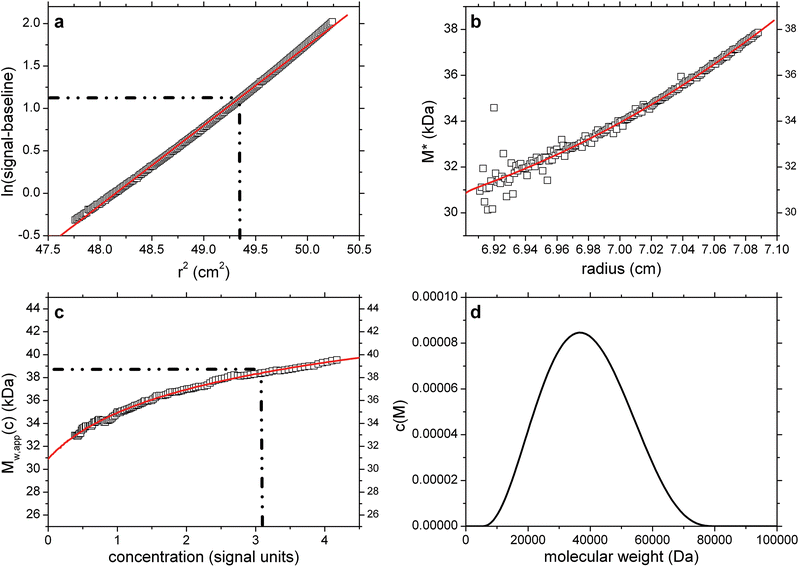 | ||
Fig. 3 As Fig. 2 but for concentration (Rayleigh fringe displacement) data with ±0.005 fringe random error with simulated random error. True Mw,app = Mw = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 Da. Retrieved Mw,app (from extrapolation of M* to the cell base, and from the hinge point) = 38 450 Da. Retrieved Mw,app (from extrapolation of M* to the cell base, and from the hinge point) = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da. Fitted lines are as defined in the legend of Fig. 1. 500 Da. Fitted lines are as defined in the legend of Fig. 1. | ||
We also explored a ‘worst case’ scenario, in which the meniscus position is in error by ±0.007 cm and the cell base position by ±0.005 cm: this returns Ja = 0.65 and Mw = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 Da an error of less than 1% from the true value.
700 Da an error of less than 1% from the true value.
Simulation 4: a significantly non-ideal system (with and without random error)
For our final simulation we look at a single solute system which shows significant non-ideality at a level comparable to that found in such a system where the molecular species under study for example is highly extended. The simulation is for a single solute, σ1 = 3 (M1 = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, rotor speed = 24
000 Da, rotor speed = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 rpm), Ja = 0.1276: baseline offset = 0, with 2BMwc = 0.144. This non-ideality is higher than that for most polysaccharides in dilute solution and greater than that for a bronchial mucin glycoprotein28 (Mw = 6 × 106 Da at c = 0.2 mg ml−1). It is equivalent to the non-ideality of a typical globular protein (ovalbumin, M = 44
721 rpm), Ja = 0.1276: baseline offset = 0, with 2BMwc = 0.144. This non-ideality is higher than that for most polysaccharides in dilute solution and greater than that for a bronchial mucin glycoprotein28 (Mw = 6 × 106 Da at c = 0.2 mg ml−1). It is equivalent to the non-ideality of a typical globular protein (ovalbumin, M = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da) at a high concentration (∼20 mg ml−1). The position of the meniscus is at 6.90 cm and the cell base is at 7.10 cm.
000 Da) at a high concentration (∼20 mg ml−1). The position of the meniscus is at 6.90 cm and the cell base is at 7.10 cm.
Fig. 4a shows the log concentration versus r2 plot, with the best-fit straight line (red) deviating from the data, as expected, due to the non-ideality. This is reflected also in the strong downward gradient of M* versus r (Fig. 4b), and also of the point average plot (Fig. 4c).
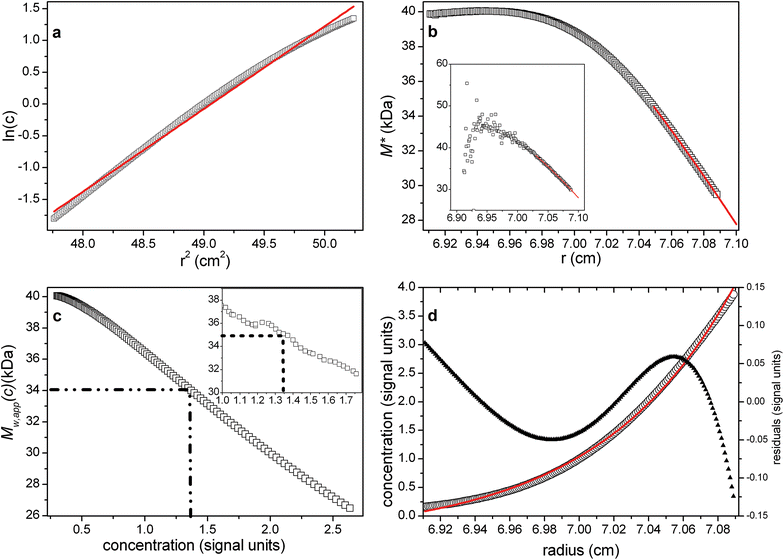 | ||
Fig. 4 As Fig. 1 but for a single solute system with significant non-ideality (2BMc = 0.144) σ = 3, rotor speed = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 rpm, True Mw = 40 721 rpm, True Mw = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. Expected Mw,app = 34 000 Da. Expected Mw,app = 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 Da (based on eqn (11)). From (b), a lower value is obtained ∼28 950 Da (based on eqn (11)). From (b), a lower value is obtained ∼28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, consistent with eqn (12). From (c) and the hinge point however (indicated by the dotted lines), the estimate for Mw,app ∼ 34 000 Da, consistent with eqn (12). From (c) and the hinge point however (indicated by the dotted lines), the estimate for Mw,app ∼ 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, close to the expected value. Fitted lines are (a) a linear regression, visually highlighting the characteristic negative curvature of non-ideal data in this transformation; (b) the polynomial extrapolation of M*. Inset (b and c) corresponding plots for random data with ±0.005 fringe error, yielding values for Mw,app ∼ 35 000 Da, close to the expected value. Fitted lines are (a) a linear regression, visually highlighting the characteristic negative curvature of non-ideal data in this transformation; (b) the polynomial extrapolation of M*. Inset (b and c) corresponding plots for random data with ±0.005 fringe error, yielding values for Mw,app ∼ 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da (hinge method) and ∼29 000 Da (hinge method) and ∼29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da (M* extrapolation). Note the failure of the smart-smooth procedure to obtain a c(M) plot due to the failure of obtaining an adequate fit of the raw c(r) data (d). For systems of low polydispersity this should be used as a diagnostic of the presence of significant non-ideality. 000 Da (M* extrapolation). Note the failure of the smart-smooth procedure to obtain a c(M) plot due to the failure of obtaining an adequate fit of the raw c(r) data (d). For systems of low polydispersity this should be used as a diagnostic of the presence of significant non-ideality. | ||
Note the failure of the smart-smooth procedure to obtain a satisfactory fit of c(M) to the raw data (Fig. 4d). This can be used as a diagnostic of the presence of significant non-ideality whose effects are unopposed by the presence of polydispersity (which causes upward curvature in a positive exponential way). When this is observed the radial region for the c(M) based baseline analysis should be restricted to a narrow data range close to the meniscus (maximal range that still leads to an adequate fit) to solely predict the baseline (Fig. 4d).
With this baseline, M* can be calculated, and traditional polynomial extrapolation to the cell base can be used to obtain Mw,app (red line in Fig. 4b). The hinge point estimation also successfully reveals Mw,app as before (Fig. 4c). The expected Mw,app = 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 Da (based on eqn (11)). From Fig. 4b, a lower value is obtained ∼(28
950 Da (based on eqn (11)). From Fig. 4b, a lower value is obtained ∼(28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 500) Da, consistent with eqn (12). From Fig. 4c and the hinge point however, the estimate for Mw,app ∼ (34
000 ± 500) Da, consistent with eqn (12). From Fig. 4c and the hinge point however, the estimate for Mw,app ∼ (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 500) Da, close to the expected value. For the same simulation with random error of ±0.005 fringe, similar values are returned for Mw,app of (29
000 ± 500) Da, close to the expected value. For the same simulation with random error of ±0.005 fringe, similar values are returned for Mw,app of (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000) Da from the M* extrapolation method and (35
000 ± 2000) Da from the M* extrapolation method and (35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 3000) Da from the hinge point method respectively (see insets to Fig. 4b and c).
000 ± 3000) Da from the hinge point method respectively (see insets to Fig. 4b and c).
Application to IgG1
A preparation of the chimeric human/murine IgG known as “Cetuximab” or “Erbitux”33 was studied (a gift of Professor R. Jefferis, University of Birmingham). Its amino-acid sequence molecular weight is 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782 Da. This antibody possesses two N-linked glycosylation sites and with covalently attached carbohydrate its total monomer molecular weight is ∼150
782 Da. This antibody possesses two N-linked glycosylation sites and with covalently attached carbohydrate its total monomer molecular weight is ∼150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. The preparation we studied had been shown to be monomeric by sedimentation velocity in the analytical ultracentrifuge. For the sedimentation equilibrium experiment using Rayleigh interference optics, the solvent was 0.1 M phosphate buffered saline at pH 7.0, which had a density of 1.00452 g ml−1 and a partial specific volume of 0.731 ml g−1 was employed. The rotor speed was 13
000 Da. The preparation we studied had been shown to be monomeric by sedimentation velocity in the analytical ultracentrifuge. For the sedimentation equilibrium experiment using Rayleigh interference optics, the solvent was 0.1 M phosphate buffered saline at pH 7.0, which had a density of 1.00452 g ml−1 and a partial specific volume of 0.731 ml g−1 was employed. The rotor speed was 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and controlled to a temperature of 20 °C. The sample had been dialysed against the solvent for 6 h and sample (at a loading concentration of 1.0 mg ml−1) and dialysate respectively were placed in the sample and reference sectors of the inner pair of channels in a multi-channel cell with sapphire windows. SEDFIT–MSTAR yields the results shown in Fig. 5. Fig. 5a shows a ∼linear plot of the log concentration versus r2, consistent with a monodisperse species. The M* plot shown in Fig. 5b yields a value for the apparent weight average molecular weight Mw,app of (148
000 rpm and controlled to a temperature of 20 °C. The sample had been dialysed against the solvent for 6 h and sample (at a loading concentration of 1.0 mg ml−1) and dialysate respectively were placed in the sample and reference sectors of the inner pair of channels in a multi-channel cell with sapphire windows. SEDFIT–MSTAR yields the results shown in Fig. 5. Fig. 5a shows a ∼linear plot of the log concentration versus r2, consistent with a monodisperse species. The M* plot shown in Fig. 5b yields a value for the apparent weight average molecular weight Mw,app of (148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000) Da. Fig. 5c shows the corresponding Mw,app(c) versus c(r) plot, with an estimate for the hinge point Mw,app of ∼147
000 ± 2000) Da. Fig. 5c shows the corresponding Mw,app(c) versus c(r) plot, with an estimate for the hinge point Mw,app of ∼147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da at a radial position 6.06 cm. As is typical for experimental data with more correlated noise and other unavoidable low-level imperfections, smoothing of these data prior to differentiation results in stronger non-random features in the Mw,app(c) data especially at lower radial positions and smaller concentration values.
500 Da at a radial position 6.06 cm. As is typical for experimental data with more correlated noise and other unavoidable low-level imperfections, smoothing of these data prior to differentiation results in stronger non-random features in the Mw,app(c) data especially at lower radial positions and smaller concentration values.
 | ||
Fig. 5 As Fig. 1 but for the analysis of a monodisperse preparation of human/murine IgG1 known as “Erbitux” at a loading concentration = 1 mg ml−1. True Mw ∼ 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. Retrieved Mw (from extrapolation of M* to the cell base) = (148 000 Da. Retrieved Mw (from extrapolation of M* to the cell base) = (148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000) Da, from c(M), Mw,app ∼ 148 000 ± 2000) Da, from c(M), Mw,app ∼ 148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da and from the hinge point ∼ 148 000 Da and from the hinge point ∼ 148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. Fitted lines are as defined in the legend to Fig. 1. 000 Da. Fitted lines are as defined in the legend to Fig. 1. | ||
Even though the resolution of c(M) (Fig. 5d) is not very high, it displays a single peak at Mw,app ∼ 148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da and is consistent with a single species. Notably, the c(M) method when considered as ‘exponential smoothing’ provides a single consistent ‘best-fit’ interpretation of both M*(r) and Mw,app(c) (red lines in Fig. 5b and c). All Mw,app values returned are slightly below the “ideal” value of ∼150
000 Da and is consistent with a single species. Notably, the c(M) method when considered as ‘exponential smoothing’ provides a single consistent ‘best-fit’ interpretation of both M*(r) and Mw,app(c) (red lines in Fig. 5b and c). All Mw,app values returned are slightly below the “ideal” value of ∼150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, the slight difference due to some thermodynamic non-ideality at c = 1.0 mg ml−1. The slight positive slope in the Mw,app(c) versus concentration plot is suggestive of a weak self-association (although our variously computed values for the whole distribution Mw,app do not directly reflect this fact), and this is currently the subject of further study.
000 Da, the slight difference due to some thermodynamic non-ideality at c = 1.0 mg ml−1. The slight positive slope in the Mw,app(c) versus concentration plot is suggestive of a weak self-association (although our variously computed values for the whole distribution Mw,app do not directly reflect this fact), and this is currently the subject of further study.
Application to pullulan P400
Pullulan P400 is one of a set of narrowly fractionated polysaccharide standards first prepared and characterized (using sedimentation equilibrium) by Kawahara & coworkers34 and then commercially produced as calibration standards for the size exclusion chromatography of polysaccharides. Pullulan P400 is listed as having a weight average molecular weight Mw ∼ 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da and we analysed a commercial sample from Polymer Laboratories (sample batch number 20907-2) dialysed against phosphate–chloride buffer (pH = 6.8, I = 0.1 M) and loaded into a 12 mm path length cell at a concentration of 2 mg ml−1, with dialysate in the reference sector. The sample was run at a rotor speed of 5000 rpm, temperature of 20.0 °C and equilibrium solute distributions recorded using Rayleigh interference optics. A value for the partial specific volume = 0.602 ml g−1 (ref. 34) was used in the analysis. Fig. 6a–d shows the results. The value obtained for P400 from the M* extrapolation of Mw,app of (400
000 Da and we analysed a commercial sample from Polymer Laboratories (sample batch number 20907-2) dialysed against phosphate–chloride buffer (pH = 6.8, I = 0.1 M) and loaded into a 12 mm path length cell at a concentration of 2 mg ml−1, with dialysate in the reference sector. The sample was run at a rotor speed of 5000 rpm, temperature of 20.0 °C and equilibrium solute distributions recorded using Rayleigh interference optics. A value for the partial specific volume = 0.602 ml g−1 (ref. 34) was used in the analysis. Fig. 6a–d shows the results. The value obtained for P400 from the M* extrapolation of Mw,app of (400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 5000) Da is in agreement with the commercially stated “standard” value and the findings of Kawahara et al.34 The hinge point method also gives a value close to this (395
000 ± 5000) Da is in agreement with the commercially stated “standard” value and the findings of Kawahara et al.34 The hinge point method also gives a value close to this (395![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 10
000 ± 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) Da.
000) Da.
 | ||
Fig. 6 As Fig. 1 but for the analysis of pullulan P400 at a loading concentration of 2 mg ml−1. True Mw ∼ 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. Retrieved Mw,app (from extrapolation of M* to the cell base – (b)) = 400 000 Da. Retrieved Mw,app (from extrapolation of M* to the cell base – (b)) = 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. (d) shows the presence of a trailing edge of a component of molecular weight < 20 000 Da. (d) shows the presence of a trailing edge of a component of molecular weight < 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, a presence comparable to that found from a corresponding experiment using sedimentation velocity analysis ((d) insert). The weighted average of the main + minor components ∼400 000 Da, a presence comparable to that found from a corresponding experiment using sedimentation velocity analysis ((d) insert). The weighted average of the main + minor components ∼400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. Fitted lines are as defined in the legend to Fig. 1. 000 Da. Fitted lines are as defined in the legend to Fig. 1. | ||
Interestingly, the c(M) vs. M plot reveals two peaks. One (main peak) with an estimated weight average molecular weight of ∼450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da and another, partially resolved peak appearing at low molecular weight (<20
000 Da and another, partially resolved peak appearing at low molecular weight (<20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da) (Fig. 6d). When c(M) is integrated across the entire distribution, a weight-average Mw of ∼400
000 Da) (Fig. 6d). When c(M) is integrated across the entire distribution, a weight-average Mw of ∼400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da is obtained in exact agreement with the extrapolated M* value, as is the M*c(M) distribution shown as a red line in Fig. 6b. Furthermore the bimodal nature of c(M) corresponds well to the profile from sedimentation velocity via application of least squares g*(s) procedure of SEDFIT35 (Fig. 6d – inset). Using the extended Fujita approach36 for conversion of the sedimentation coefficient distribution to a molecular weight distribution (assuming a conformation for the polymers – in this case a random coil), the main peak from the SV data is estimated to have an overall weight average molecular weight consistent with the value derived from c(M). Thus whilst information as concerns the presence of a lower weight component is yielded from the c(M) vs. M plot, the estimates of the mass and proportion of the individual ‘peaks’ displayed is approximate only.
000 Da is obtained in exact agreement with the extrapolated M* value, as is the M*c(M) distribution shown as a red line in Fig. 6b. Furthermore the bimodal nature of c(M) corresponds well to the profile from sedimentation velocity via application of least squares g*(s) procedure of SEDFIT35 (Fig. 6d – inset). Using the extended Fujita approach36 for conversion of the sedimentation coefficient distribution to a molecular weight distribution (assuming a conformation for the polymers – in this case a random coil), the main peak from the SV data is estimated to have an overall weight average molecular weight consistent with the value derived from c(M). Thus whilst information as concerns the presence of a lower weight component is yielded from the c(M) vs. M plot, the estimates of the mass and proportion of the individual ‘peaks’ displayed is approximate only.
Application to λ-carrageenan
For our final example we have chosen an unfractionated polysaccharide, λ-carrageenan (a gift from Dr T. Foster, University of Nottingham, School of Biosciences). This was dissolved in deionised distilled water (with the assistance of heating in a microwave for 30 seconds) and then dialysed for ∼24 hours against phosphate–chloride buffer (pH = 6.8, I = 0.1 M) and loaded into a 12 mm path length cell at a concentration of 0.3 mg ml−1, with dialysate in the reference sector. The sample was run at a rotor speed of 4000 rpm, temperature of 20.0 °C and equilibrium solute distributions recorded using Rayleigh interference optics. A value for the partial specific volume = 0.53 ml g−1 was used in the analysis. Fig. 7a–d show the results, yielding a value for Mw,app of (310![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 10
000 ± 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) Da which after allowance for non-ideality is in excellent agreement with the value obtained using SEC-MALS.37 The hinge point method gives a value in even better agreement (320
000) Da which after allowance for non-ideality is in excellent agreement with the value obtained using SEC-MALS.37 The hinge point method gives a value in even better agreement (320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 20
000 ± 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) Da, the extra noise/imprecision a consequence of working at very low loading concentration (0.3 mg ml−1).
000) Da, the extra noise/imprecision a consequence of working at very low loading concentration (0.3 mg ml−1).
 | ||
Fig. 7 As Fig. 1 but for the analysis of λ-carrageenan at a loading concentration of 0.3 mg ml−1. Mw,app (from extrapolation of M* to the cell base) = 310![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da. Fitted lines are as defined in the legend to Fig. 1. 000 Da. Fitted lines are as defined in the legend to Fig. 1. | ||
Discussion and perspectives
In the present work, we have developed an efficient and reliable approach for the sedimentation equilibrium analysis of virtually all polymer systems across a wide range of molecular weights – monodisperse, polydisperse and realistically non-ideal, and a high degree of confidence can be placed on the whole distribution weight average molecular weights computed. Our approach integrates the previously separate approaches of derivative-based and integral-based data transforms, which require various smoothing and/or extrapolation produces to determine distribution averages, with direct distribution fitting approaches which is a model-based least-squares fit of the data but is usually ill-conditioned. We found the combination provides a single consistent interpretation that offers information in parallel on different levels of detail. Running of the algorithm takes only a few minutes, in contrast to the time required previously to analyse sedimentation equilibrium data for polymers, and obviating the difficult and inconvenient procedures for obtaining adequate baselines encountered in earlier studies.2,12 A new method (MultiSig) for obtaining accurate values for the baseline offset (E) in fringe optics via multi-exponential fitting has recently been published.26 MultiSig returns the mean of 20 estimates using a Monte-Carlo type approach. Our currently described procedure we have found to return a precision very similar indeed to the individual estimates yielded by MultiSig. Thus a high degree of confidence can now be placed upon the whole-cell weight-averaged molecular weight (Mw) values computed. There are some important perspectives deriving from this work:(1) Solvent density. The assumption is made that this is constant throughout the solution column. In the case of the inclusion of dense solutes like caesium salts a short column is advised (and measurements made at least two rotor speeds to check for possible effects), otherwise the redistribution will need to be taken into account (the extreme case being isopycnic density gradient equilibrium where a density gradient is deliberately set up – see e.g., ref. 6 and 28).
(2) The non-ideality simulation we quoted was for a strongly non-ideal single solute system: the virtue of having two methods for extracting Mw,app – one, more precise but more affected by non-ideality, the other (hinge-point) less precise but less affected by non-ideality. When non-ideality is suspected an extrapolation to c = 0 is required to obtain Mw: this extrapolation is facilitated by the use of multi-channel cells. In the case of single solute, an extrapolation of the point average Mw,app(r)'s is possible – as shown in Fig. 4c: a good practical example is turnip yellow mosaic virus.38 For polydisperse systems such a procedure can lead to an underestimate of Mw because of redistribution of the molecular species of different molecular weight in the solution – unless ultra-short columns are used (see ref. 39). Although polydisperse non-ideal systems are almost impossible to simulate because of the complex non-linear way the separate virial coefficients Bk (and products BkMk) for each affect the fundamental equations of sedimentation equilibrium,40 it actually helps linearise the extrapolation to c = 0 to give Mw, since the effects of polydispersity (upward curvature in the concentration versus radial displacement plots) counteracts either partially or in some cases known as “pseudo-ideal” almost completely the effects of non-ideality (downward curvature). A good example of this behavior is for λ-carrageenan (Fig. 7). Although for proteins at loading concentrations ∼1 mg ml−1 or less the effects of non-ideality are usually very small (the example of non-ideality given in Fig. 4 is equivalent to a globular protein like ovalbumin at a concentration of ∼20 mg ml−1, which is 150× the minimum concentration needed for a sedimentation equilibrium experiment), for some polymers – particularly those with a high affinity for the solvent (such as polysaccharides in aqueous solvent), even at the lowest concentrations that can be used in a sedimentation equilibrium experiment (for polymers realistically ∼0.2–0.3 mg ml−1 with a long path-length (20 mm) cell), these effects can still be significant, and this is the case for λ-carrageenan (Fig. 7a–d) – the quasi-linear plot of ln(signal) versus r2 and the near flat plot of Mw,app(r) vs. c(r) is symptomatic of pseudo-non-ideality where the effects of polydispersity (causing upward curvature in both plots) are counteracted by the downward curvature caused by non-ideality. In such cases a conventional extrapolation of Mw,app (or 1/Mw,app) versus c to c = 0 is necessary. Non-ideality will also be apparent from the residuals of the best-fit c(M) model to the raw data, with the raw data showing less curvature than the best-fit model.
(3) With broad molecular weight distributions there is still the risk that a proportion of the higher molecular weight material is lost from optical registration at the cell base. If such a problem is suspected then experiments performed at least two different equilibrium speeds should be used and compared. SEDFIT–MSTAR allows the comparison of profiles at different speeds. This comparison can either be conducted in sequential analyses, or a single self-consistent interpretation can be achieved in a global analysis of data at multiple rotor speeds. The success of a global analysis will depend on the localisation of the base of the solution column, which can be treated as an adjustable fitting parameter within reasonable limits. If the self-consistent multi-speed extension of SEDFIT–MSTAR is successful, as can be assessed by the root-mean-square deviations of the global versus the individual single fits, c(M) with higher resolution can potentially achieved. This approach was demonstrated previously for discrete, ideal protein mixtures in ref. 5, and we will further explore this strategy in the context of M* analysis of polymers in future work.
(4) The procedure for taking an average of the final scans and subtracting an average of the initial scans, should be followed, and Ang & Rowe26 for example provide a useful protocol for doing this.
(5) In recently published work41 a complementary approach to sedimentation equilibrium analysis of polydisperse systems has been presented, with a focus on point average molecular weights at specific radial positions. The ‘MultiSig’ algorithm – based on a multi-exponential approach – (a) yields profiles of (reduced flotational) molecular weights (i.e. σ values) and returns all three of the principal averages (number-, weight- and z) to a good precision (b) yields profiles of c(σ) vs. s – i.e. c(M) vs. M if all components have a common partial specific volume – profiles which are shown by simulations using realistic error levels and by experiment to reflect the presence of multiple components or of continuous distributions. MultiSig does at the moment give a somewhat ‘coarse-grained’ (i.e. limited data pair sets) output over a modest range in σ, and is slow to run (∼30 minutes for optimal resolution), but these limitations can readily be overcome by the use of greater computational power.
These two approaches (MultiSig and SEDFIT–MSTAR) are thus seen to be complementary: the latter being a specialised technique for characterising whole cell Mw values; the former for defining distributions and interactions, in a range of mono-, oligo- and polydisperse systems. We are currently exploring the possibility of providing an easy interface between SEDFIT–MSTAR and MultiSig.
(6) Combination with sedimentation velocity data. Sedimentation velocity in the analytical ultracentrifuge – performed in the same instrumentation as sedimentation equilibrium – has a greater resolving power of components, although yields primarily sedimentation coefficient and sedimentation coefficient distributions and to obtain molecular weight distributions of polydisperse systems requires assumptions/knowledge of conformation or calibration using another technique. In an earlier paper30 we described a procedure for obtaining the distribution of molecular weight for a polymer based on extension of an earlier method by Fujita for transforming a sedimentation coefficient distribution from sedimentation velocity into a molecular weight distribution. The original Fujita method30 had been based on the assumption that the polymers adopted a random coil conformation. The Extended Fujita method36 covers molecular weight distributions of polymers for any conformation type including spheres and rods and conformations between the extremes of spheres, rods and coils. For its application, knowledge of the weight average sedimentation coefficient s20,w for at least one value of the weight average molecular weight Mw is required for calibration. Obtaining the weight average s20,w – and the distribution thereof – has been routine for over a decade now through regular application of SEDFIT to sedimentation velocity data.16 It is now fair to say that estimation of Mw is also routine using the application of SEDFIT–MSTAR to sedimentation equilibrium data for polymer solutions of wide ranging polydispersities and non-idealities.
Acknowledgements
This work was supported by the Intramural Research Programs of the National Institute of Biomedical Imaging and Bioengineering, National Institutes of Health (PS), the Royal Society (SEH) and the Biotechnology and Biological Sciences Research Council (SEH, GGA and RG)Notes and references
- T. Svedberg and K. O. Pedersen, The Ultracentrifuge, Oxford University Press, London, 1940 Search PubMed.
- S. E. Harding, A. J. Rowe and J. C. Horton, Analytical Ultracentrifugation in Biochemistry and Polymer Science, Royal Society of Chemistry, Cambridge, UK, 1992 Search PubMed.
- http://www.ncbi.nlm.nih.gov/pubmed/23377850 .
- https://sedfitsedphat.nibib.nih.gov/software/default.aspx .
- J. Vistica, J. Dam, A. Balbo, E. Yikilmaz, R. A. Mariuzza, T. A. Rouault and P. Schuck, Anal. Biochem., 2004, 326, 234–256 CrossRef CAS PubMed.
- J. M. Creeth and R. H. Pain, Prog. Biophys. Mol. Biol., 1967, 17, 219–287 CrossRef.
- J. M. Creeth and S. E. Harding, J. Biochem. Biophys. Methods, 1982, 7, 25–34 CrossRef CAS.
- S. E. Harding, J. C. Horton, and P. J. Morgan, in Analytical Ultracentrifugation in Biochemistry and Polymer Science, ed. S. E. Harding, A. J. Rowe and J. C. Horton, Royal Society of Chemistry, Cambridge, UK, 1992, pp. 275–294 Search PubMed.
- H. Cölfen and S. E. Harding, Eur. Biophys. J., 1997, 25, 333–346 CrossRef.
- D. C. Teller, Methods Enzymol., 1973, 27, 346–441 CrossRef CAS.
- D. C. Teller, J. A. Horbett, E. G. Richards and H. K. Schachman, Ann. N. Y. Acad. Sci., 1969, 164, 66–101 CrossRef CAS.
- D. R. Hall, S. E. Harding and D. J. Winzor, Prog. Colloid Polym. Sci., 1999, 113, 62–68 CrossRef CAS.
- E. Spruijt and P. M. Biesheuvel, J. Phys.: Condens. Matter, 2013 Search PubMed , http://iopscience.iop.org/0953-8984/page/Forthcoming%20articles.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C, Cambridge University Press, Cambridge, UK, 2nd edn, 1992 Search PubMed.
- S. W. Provencher, J. Chem. Phys., 1967, 46, 3229–3236 CrossRef CAS.
- D. R. Wiff and M. T. Gehatia, Biophys. Chem., 1976, 5, 199–206 CrossRef CAS.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 229–242 CrossRef.
- S. W. Provencher, in Light Scattering in Biochemistry, ed. S. E. Harding, D. B. Sattelle and V. A. Bloomfield, Royal Society of Chemistry, Cambridge, UK, 1992, pp. 92–111 Search PubMed.
- H. Zhao, C. A. Brautigam, R. Ghirlando and P. Schuck, Curr. Protoc. Protein Sci., 2013, 7, 20.12.1 Search PubMed.
- R. Ghirlando, Methods, 2011, 54, 145–156 CrossRef CAS PubMed.
- C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Prentice Hall, Englewood Cliffs, New Jersey USA, 1974 Search PubMed.
- P. Schuck and B. Demeler, Biophys. J., 1999, 76, 2288–2296 CrossRef CAS.
- http://www.ncbi.nlm.nih.gov/pubmed/?term=21167941 .
- A. T. Ansevin, D. E. Roark and D. A. Yphantis, Anal. Biochem., 1970, 34, 237–261 CrossRef CAS.
- S. Ang and A. J. Rowe, Macromol. Biosci., 2010, 10, 798–807 CrossRef CAS PubMed.
- S. E. Harding, J. C. Horton, S. Jones, J. M. Thornton and D. J. Winzor, Biophys. J., 1999, 76, 2432–2438 CrossRef CAS.
- S. E. Harding, in Analytical Ultracentrifugation in Biochemistry and Polymer Science, ed. S. E. Harding, A. J. Rowe and J. C. Horton, Royal Society of Chemistry, Cambridge, UK, 1992, pp. 495–516 Search PubMed.
- H. Fujita, J. Phys. Chem., 1959, 63, 1092–1095 CrossRef CAS.
- H. Fujita, Mathematical Theory of Sedimentation Analysis, Academic Press, New York, 1962 Search PubMed.
- H. Suzuki, in Analytical Ultracentrifugation in Biochemistry and Polymer Science, ed. S. E. Harding, A. J. Rowe and J. C. Horton, Royal Society of Chemistry, Cambridge, UK, 1992, pp. 568–592 Search PubMed.
- H. Rinde, The Distribution of the Sizes of Particles in Gold Sols Prepared According to the Nuclear Method, PhD Dissertation, University of Uppsala, Sweden, 1928 Search PubMed.
- Y. Qian, L. A. Diaz, J. Ye and S. H. Clarke, J. Immunol., 2007, 178, 5982–5990 CAS.
- K. Kawahara, K. Ohta, H. Miyamoto and S. Nakamura, Carbohydr. Polym., 1984, 4, 335–356 CrossRef CAS.
- P. Schuck, Biophys. J., 2000, 78, 1606–1619 CrossRef CAS.
- S. E. Harding, P. Schuck, A. S. Abdelhameed, G. Adams, M. S. Kökand and G. A. Morris, Methods, 2011, 54, 136–144 CrossRef CAS PubMed.
- F. M. Almutairi, G. G. Adams, M. S. Kök, C. J. Lawson, R. Gahler, S. Wood, T. J. A. J. Rowe and S. E. Harding, Carbohydr. Polym., 2013, 97, 203–209 CrossRef CAS PubMed.
- S. E. Harding and P. Johnson, Biochem. J., 1985, 231, 549–555 CAS.
- S. E. Harding, A. J. Rowe and J. M. Creeth, Biochem. J., 1983, 209, 893–896 CAS.
- S. E. Harding, Biophys. J., 1985, 47, 247–250 CrossRef CAS.
- R. Gillis, G. G. Adams, T. Heinze, M. Nikolajski, S. E. Harding and A. J. Rowe, Eur. Biophys. J., 2013, 42, 777–786 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |

