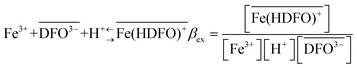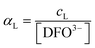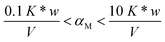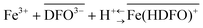Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Novel DFO-functionalized mesoporous silica for iron sensing. Part 2. Experimental detection of free iron concentration (pFe) in urine samples†
Giancarla
Alberti
*a,
Giovanni
Emma
a,
Roberta
Colleoni
a,
Maria
Pesavento
a,
Valeria Marina
Nurchi
b and
Raffaela
Biesuz
a
aDipartimento di Chimica, University of Pavia, via Taramelli 12, 27100 Pavia, Italy. E-mail: galberti@unipv.it; Fax: +39 0382 528544; Tel: +39 0382 987347
bDipartimento di Scienze Chimiche e Geologiche, University of Cagliari, Cittadella Universitaria, 09042 Monserrato-Cagliari, Italy. E-mail: nurchi@unica.it; Fax: +39 070 675 4478; Tel: +39 070 6754476
First published on 13th March 2014
Abstract
Successful in vivo chelation treatment of iron(III) overload pathologies requires that a significant fraction of the administered drug actually chelates the toxic metal. Increased mobilization of the iron(III) in experiments on animals or humans, most often evaluated from urinary output, is usually used as an assessment tool for chelation therapy. Alternatively, the efficiency of a drug is estimated by calculating the complexing ability of a chelating agent towards Fe(III). The latter is calculated by the pFe value, defined as the negative logarithm of the concentration of the free metal ion in a solution containing 10 μM total ligand and 1 μM total metal at a physiological pH of 7.4. In theory, pFe has to be calculated taking into account all the complexation equilibria involving the metal and the possible ligands. Nevertheless, complexation reactions in complex systems such as serum and urine may hardly be accurately modelled by computer software. The experimental determination of the bioavailable fraction of iron(III) in biological fluids would therefore be of the utmost relevance in the clinical practice. The efficiency of the therapy could be more easily estimated as well as the course of overload pathologies. In this context, the aim of the present work was the development of a sensor to assess the free iron directly in biological fluids (urine) of patients under treatment with chelating agents. In the proposed device (DFO-MS), the strong iron chelator deferoxamine (DFO) is immobilized on the MCM-41 mesoporous silica. The characterization of the iron(III) sorption on DFO-MS was undertaken, firstly in 0.1 M KNO3, then directly in urine samples, in order to identify the sorption mechanism. The stoichiometry of the reaction in the solid phase was found to be: 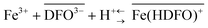 with an exchange constant (average value) of log
with an exchange constant (average value) of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex = 40(1). The application of DFO-MS to assess pFe in SPU (Simulating Pathology Urine) samples was also considered. The results obtained were very promising for a future validation and subsequent application of the sensor in samples of patients undergoing chelation therapy.
βex = 40(1). The application of DFO-MS to assess pFe in SPU (Simulating Pathology Urine) samples was also considered. The results obtained were very promising for a future validation and subsequent application of the sensor in samples of patients undergoing chelation therapy.
Introduction
The speciation of an element, either essential or toxic, is relevant, because the chemical form in which an element enters the body mostly determines its absorption and transport properties, and hence its biological and physiological activities.1Biological fluids are generally heterogeneous media that contain suspended or fragmented cells, proteins, or even crystalline particles. Many trace metal ions are present mostly bound to macromolecules (as proteins, but also nucleic acids, sugars, etc.) in biofluids. In addition to this quite strong and inert fraction, metal ions are also bound to the low molecular mass components of biofluids, such as amino acids, peptides, biophosphates, hydroxycarboxylic acids, inorganic anions, which are much more mobile.1
The determination of the concentration of each chemical form of the metal is clearly not feasible, due to the very complicated speciation. Fractionation is practically the most general procedure to assess at least classes of species in biological samples. However, it is difficult to apply any of the classical structure elucidation techniques, because of the small quantities, usually microgram, of the analyte.2–4 Identification is possible only for stable species and when standards are available for comparison.
If it is so complicated to evaluate the metal speciation in healthy individuals, more and more difficult will be the determination in the cases of overloaded metal-induced pathologies and human metal intoxications.
Iron is an important biological metal ion that plays an essential role in many metabolic pathways, such as the uptake and transport of oxygen to tissues, in the electron transport chain (respiration) and for reduction of carbon dioxide (photosynthesis).5
Under physiological conditions, the level of iron in the organism is controlled by homeostatic regulation that is mostly due to intestinal absorption or erythropoiesis in the bone marrow.6,7
It is well recognized that various human iron intoxications and overloaded metal-induced pathologies have been treated efficiently by administration of a chelating agent. However, complexation reactions in the human body are influenced by a multitude of factors, including competing metals and ligands, route of administration, dynamics of circulation, compartmentalization, bioavailability and metabolism of the chelating agent.8 Accordingly, in vivo chelation reactions may differ extensively from what would be expected from our chemical knowledge about metal/ligand protonation and complexation equilibria; anyway rigorous and specific simulation programs are not exhaustive to accurately describe a very complicated real system like the living organism. Chelating agents can affect metal toxicity by mobilizing the toxic metal into (mainly) urine or through the intestine. However, a number of variables and problems have to be considered in the choice of the opportune chelating therapy. In chronic metal-induced disease, where life-long chelation becomes fundamental, toxicity or side effects of the administered chelator must be taken into account. The metal selectivity of chelators is important because of the risk of depletion of the patient's stores of essential metals.8
The semi-empirical quantity widely used to quantify the complexing ability of a chelating agent towards a metal (M) ion is the pM value. It is defined as the negative logarithm of the concentration of the free metal ion in solution, as calculated for the 10 μM total ligand concentration and 1 μM total metal concentration, at pH 7.4.9
However, the mere knowledge of the calculated pM value is unable to describe the speciation of the metal/ligand system and to suggest the biologically active species at physiological pH; it does not contain any information on the donor-atom set and on the complex structure in solution; it is useless to predict the competition effects by other ligands or metal ions also present in the system.
Because of the complexity of biological systems, effects of antidotal chelators are often better described quantitatively from results of animal experiments or clinical treatments than by theoretical calculations. In part of the literature describing effects of chelators on acute metal toxicity, metal excretion or organ distribution was not quantified; accordingly, it is unclear to what extend increased excretion and decreased toxicity contributed to the observed alleviating effect of chelation treatment.10
Another relevant aspect concerns the speciation of the target metals. When trace elements are used as diagnostic tools during disease and/or to evaluate the efficiency of a therapy, it is important to know whether the metal is free or bound.4
The use of software enabling the calculation of multiple chemical equilibria was initially put forward as a powerful tool for tackling these issues. Soon after the first computer programs were developed, they were in fact actively applied by coordination chemists, not only for calculations on laboratory solutions but also for simulating naturally occurring mixtures of metal ions and ligands. The most complete database available, e.g., for blood plasma, includes a set of about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 complexes of ca. 10 essential and toxic metal ions, over 1000 ligands, and results for plasma conditions. Nevertheless, such an approach suffers from the lack of the necessary data to derive a reliable model.1 Thus in silico studies (performed on computer or via computer simulation) can only be complementary to the empirical approach (“in vitro” and “in vivo”), but they cannot be considered as a substitute to experimental measurements.
000 complexes of ca. 10 essential and toxic metal ions, over 1000 ligands, and results for plasma conditions. Nevertheless, such an approach suffers from the lack of the necessary data to derive a reliable model.1 Thus in silico studies (performed on computer or via computer simulation) can only be complementary to the empirical approach (“in vitro” and “in vivo”), but they cannot be considered as a substitute to experimental measurements.
In this regard, it is important to highlight the importance of the development of easy, fast and handily methods to directly assess the free metal, when it is possible, or at least the bioavailable fraction. Such experimental evaluations could also be employed to verify computer modeling of chemical speciation.
Through SPE techniques, it has been demonstrated that not only the pre-concentration and separation of a target analyte is possible, but also to have information about speciation of several metal ions. The solid materials were chelating resins and the application of that model permitted to evaluate total and free metal concentrations in samples at extremely low metal levels such as, the natural sample of pristine water like Antarctic seawater.11–13
Using a particular ratio quantity of the resin/volume of the sample solution, the information about metal species distribution in the original sample can be achieved from the competition between the ligand naturally present in the real sample and the resin. The sorbed metal fraction decreases, increasing the strength of the natural ligand and reducing the amount of the resin. When the capability of the resin to bind to the metal ion is known (the strength of the resin is quantified by the partition coefficient K*), it was demonstrated that it is possible to determine the collateral reaction coefficient,14αM = cM/[M]. From this parameter and knowing the total metal content (ctot), the free metal concentration [M] can be obtained. Using this method, the iminodiacetic resin (Chelex 100) was applied as a sensor to determine the free metal.11,15
According to this strategy, by using a selective metal sorbent, it is possible to assess the free iron(III) concentration in very complex matrixes, such as the blood plasma or urine. This information could be paramount to establish the efficiency of a chelator, and to estimate the Non-Transferrin-Bound Iron (NTBI) if the sensor is used directly to test biological fluids of iron overload patients.
Following this novel idea, deferoxamine (DFO), a strong selective iron(III) chelator, also used in chelation therapy, is immobilized on the MCM-41 mesoporous silica (DFO-MS)16 to develop a device capable of detecting iron(III), and evaluating its free concentration.
Urine was selected as the testing matrix, indeed the urine samples of iron overload patients have a high concentration of iron(III), complexed with the ligand employed in the chelation therapy. The amount of free iron in such samples is an indication about the effectiveness of the drug, depending on the nature of the ligand and on the integrity of the expelled ligand; so the possibility to assess the free iron is of overwhelming importance, either to establish to the NTBI, or to give information about drug half life.
For these reasons, we decided to demonstrate the feasibility of total and free iron determination directly in that biological medium, so we defined the Fe(III) sorption mechanism on DFO-MS in 0.1 M KNO3 and also in urine.
Materials and methods
Chemicals and apparatus
Mesoporous silica MCM-41 type (Sigma-Aldrich), (3-glycidyloxypropyl)trimethoxysilane (GPTMS, ≥98% Sigma-Aldrich), dimethyl sulfoxide (DMSO, anhydrous ≥99.9%, Sigma-Aldrich), deferoxamine mesylate salt (DFO, Novartis), acetonitrile (≥99.5% Carlo Erba), KNO3 (≥99.0%, Sigma-Aldrich), HNO3 for trace analysis (≥69.0%, Fluka) and NaOH (Carlo Erba) were used as received. Iron standard solution for ICP of 1000 mg L−1 (Fluka) was used to obtain the proper Fe(III) concentration in the solution phase. Solutions were prepared with ultrapure water (Milli-Q).The characterization of the solid material was obtained as previously described16 and most of characterization data were provided as ESI.†
An Orion420 pH-meter, with a combined glass electrode, was used to determine the pH of all the solutions. The metal determinations were performed by ICP-OES Perkin-Elmer Optima 3300 DV. The calibration curve was obtained according to the constructor indications. The LOD (3× standard deviation of the blank) and LOQ (10× standard deviation of the blank) are respectively 0.15 μM and 0.50 μM for Fe at 238.204 nm.
Synthesis
The DFO-mesoporous silica (MS) MCM-41 type self assembled monolayer (DFO-MS) was prepared according to the previously described and optimized pathways,16 as the scheme of Fig. 1, and here summarized.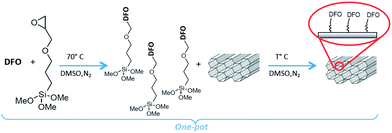 | ||
| Fig. 1 Synthesis of DFO-MS following the novel one pot scheme.16 | ||
About 0.32 g of DFO (mesylate salt or free ligand) were dissolved in 20 mL of DMSO with 0.1 mL of GPTMS and stirred overnight at 70 °C under nitrogen. 0.4 g of MS (MCM-41 or MSU-H type), previously dried at 130 °C were added to the mixture reaction, left stirring overnight under nitrogen, at thermostatted temperature. The DFO-MS was finally filtered off, washed several times with acetonitrile and dried under vacuum (see scheme in Fig. 1).
The DFO was used in the one pot reaction under two forms: mesylate salt, as received or free amine. In this second case, the mesylate salt was dissolved in methanol and an equivalent amount of NaOH was added to the solution; after 20 minutes, the solvent was removed and the residue was washed three times with acetonitrile and dried before use.
Procedure for sorption profiles (equilibrium studies)
The experimental sorption profiles represent the ratio of sorbed to total metal ion f reported vs. pH under the given conditions. The method, described in several of our papers (see for example ref. 15, 17 and 18) referred to chelating resins as the solid phase, enables us to establish the value of the partition coefficient K* of the metal ion between the solution and the solid phase.The same procedure was here applied to study the sorption of Fe(III) on DFO-MS. In particular, two different competition experiments were performed, following the idea that the equilibria of interest are those established at pH around neutrality.
The first method is as follows.
A constant amount of DFO-MS (50 mg) was immersed in a 0.1 M KNO3 solution with a fixed Fe(III) concentration (10–5 M) in the presence of EDTA. The first value of pH was fixed at around 2. After equilibration a small amount of solution was collected in a new disposable testing tube. Then small portions of NaOH were added and, after each addition, the pH at equilibrium was registered. The temperature was controlled at 25.0(5) °C. The pH range of investigation was between 2 and 9. All the collected samples were analyzed by ICP-OES for iron content. The sorbed iron(III), c, was determined as difference from the total. The sorption profiles were obtained by plotting the sorbed fraction, f, vs. pH.
In the second procedure, a desorption experiment was carried out. A known amount of Fe(III) (the mmol of Fe(III) were always in defect with respect to the active sites of the materials) was sorbed at pH around 3 on DFO-MS (about 30 mg) in 0.1 M KNO3 media. The solution was removed and the solid phase was washed several times with Milli-Q water. The Fe(III)-DFO-MS obtained was put to equilibrate in a 0.1 M KNO3 solution with PIPES buffer (10–2 M) at pH about 7. The solution was checked for the iron content and the concentration was always not significantly different from blank values. Then a competitive ligand (EDTA or other) was added. After each addition the system was left to equilibrate; then a small amount of solution was collected in a new disposable testing tube, and analyzed by ICP-OES for iron content. The desorption profiles were obtained by plotting f vs. ligand concentration.
Procedure for sorption studies on real samples
Urine samples of individuals, with no discernible pathology, were selected as test solutions. The fresh urine sample was filtered to eliminate all the solid material and methanol was added, in order to prevent bacteria growing. In all the original samples the concentration of Fe(III) was always below the LOD; consequently standard solution of Fe(III) was always added to the samples.A series of experiments was dedicated to assess the K* values in urine media. For this purpose, different subsamples of a unique urine previously enriched with iron(III) were left to equilibrate with DFO-MS. Then different competitive ligands were added to each subsample and the relative desorption curves were obtained. To be sure to obtain a reliable partition coefficient K*, not dependent on the media and on the variability of different samples, other experiments were performed considering iron(III) enriched urine of other individuals.
After determining K* in urine media, specific experiments were dedicated to asses the total and the free Fe(III) according to a strategy, previously successfully employed in a large variety of natural samples and beverages with commercial resins.11,13,15 To this purpose Fe(III) and a strong iron chelator (deferiprone) were added to urine samples to simulate a condition of an iron overload patient under chelation therapy. These samples were called SPU (Simulating Pathology Urine); the concentrations of the two added analytes were cFe = 1.4 × 10−5 M and cdeferiprone = 6 × 10−3 M. Four tubes with the same volume (V) of SPU samples were put in contact with different amounts of DFO-MS (w) and left to equilibrate overnight. The pH was measured, small amounts of solution were collected in new disposable testing tubes and analyzed for the iron content by ICP-OES. The total iron was checked directly in solution before equilibration with the sorbent, since the concentration was largely higher than the LOQ of the ICP-OES. The amount of sorbed iron, c, was determined in each tube as a difference from the total. From non-linear regression of c versus the V/w ratio, the free Fe(III) can be calculated as it will be explained below.
Results and discussion
Sorption profile for equilibrium studies
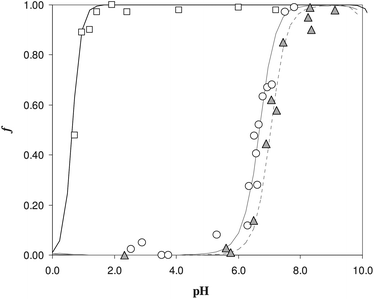
The complexing properties of the functionalized MS (DFO-MS) toward Fe(III) have to be verified. It is fundamental to accurately define the value of the partition coefficient K* to assess the free metal concentration. Instead of determining an operational value of K*, valid only in that strictly particular set of experimental conditions, we followed the strategy already reported for chelating resins.11,15,17 Once defined the sorption reactions and the exchange constants, it is possible to calculate the value of K* under any condition.In the case of the DFO-MS, it was assumed, in a rough estimate, that the protonation constants of the DFO, covalently bound on the MS, were the same of the ligand in solution. Of course, this is not proved, but it can be used in a first approximation, and if the exchange constants of Fe(III) on the solid phase, not significantly differ from those in solution, the approximation can be accepted. The DFO-MS, as already demonstrated,16 is able to sorb Fe(III) at very acidic pH (≤3). Because our purpose is to apply the material as a sensor in biological fluids, the characterization should also be extended at neutral pH; so the study of the sorption profile in the presence of a competitive ligand is indispensable to avoid the Fe(III) hydrolysis and to move the sorption profile curve towards basic values. In this way, the exchange properties are determined at a pH closer to that expected for the real samples.13
The sorption profiles of Fe(III), in the presence of EDTA as a competitive ligand, were reported in Fig. 2, at two different EDTA concentrations. It is clear the effect of competition, since the sorption profiles with EDTA (see triangles and empty circles) were moved to the neutral pH values with respect to the profile in the absence of ligand, reported with the empty squares.
The curves reported in Fig. 2 were calculated with a best fit of equation reported below (eqn (1)), according to the following sorption reaction (the overbar represents species in the solid phase):
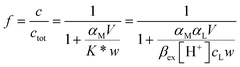 | (1) |
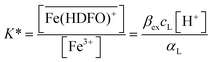 | (2) |
αM is the collateral reaction coefficient:
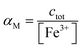 .
.
To compute the αM values, the hydrolysis constants of Fe(III) and complexation constants of Fe-EDTA have to be used; the thermodynamic data for Fe-EDTA were selected with IUPAC Database (SC-Database, http://www.acadsoft.co.uk) and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β are summarized in Table 1.
β are summarized in Table 1.
| Species | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β |
|---|---|
| a Amphoteric hydroxide. b Crystalline oxide. | |
| Fe(OH)2+ | −5.67 |
| Fe(OH)3 | −12.56 |
| Fe(OH)4− | −21.6 |
| Fe(OH)2+ | −2.19 |
| Fe(OH)3(am)a | −4.891 |
| Fe2O3(cr)b | −0.408 |
| HEDTA3− | 10.948 |
| H2EDTA2− | 17.221 |
| H3EDTA− | 20.359 |
| H4EDTA | 22.583 |
| H5EDTA+ | 24.083 |
| H6EDTA2+ | 23.859 |
| H4EDTA(s) | 26.1 |
| Fe(EDTA)− | 27.8 |
| Fe(EDTA)(OH)24− | 19.97 |
| Fe(HEDTA) | 29.3 |
| Fe2(EDTA)2(OH)24− | 41.8 |
| OH− | −14 |
MEDUSA program19 is applied to calculate αM at the ionic strength of interest and in function of the pH.
Considering the experiment reported in Fig. 2 with the white circles (experiment with lower EDTA concentration), the value of the exchange constant obtained was log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex = 40(1). The value is quite imprecise, but it is in pretty good agreement with the literature data for the Fe(III)/DFO complex in solution (log
βex = 40(1). The value is quite imprecise, but it is in pretty good agreement with the literature data for the Fe(III)/DFO complex in solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 41.01).20 For the gray triangles (experiment with higher EDTA concentration), it was impossible to evaluate a log
β = 41.01).20 For the gray triangles (experiment with higher EDTA concentration), it was impossible to evaluate a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex by the non-linear fitting, because of the few experimental points, but using the value of βex previously determined with low EDTA concentration, the calculated dotted curve describes the experimental points quite well.
βex by the non-linear fitting, because of the few experimental points, but using the value of βex previously determined with low EDTA concentration, the calculated dotted curve describes the experimental points quite well.
A first important conclusion is that, in the pH range of interest, i.e. working under physiological conditions, the behaviour of the DFO fixed on the silica seems to be the same of DFO in solution.
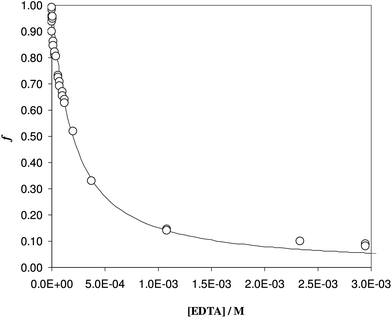
To be sure of our data, another experiment was carried out. The solid phase was left to equilibrate with Fe(III) at acidic pH, like for the isotherm studies; then the solution was removed and the Fe(III)-DFO-MS (after a cycle of washing with Milli-Q water) was immersed in a solution at pH 7.0 using PIPES as buffer. Then iron(III) was desorbed, step by step, increasing the concentration of EDTA from 0 to a quantity sufficient to permit the complete desorption of Fe(III). The plot obtained is presented in Fig. 3. The experimental data were fitted with eqn (1): in this case the variable K* was the unknown parameter. In the hypothesis that only the complex 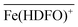 was formed, from K* it was possible to calculate the βex by the eqn (2). The value of log
was formed, from K* it was possible to calculate the βex by the eqn (2). The value of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex = 40.1(2) was found, in very pretty good agreement with the results obtained by the previous sorption profiles.
βex = 40.1(2) was found, in very pretty good agreement with the results obtained by the previous sorption profiles.
In this chapter eqn (1) is used to characterize the sorption reaction of iron(III) on DFO-SAMMS, as explained above, being βex the unknown parameter. We call this strategy, to apply eqn (1), “MODE 1”.
Sorption studies on real samples
As previously discussed, urine is an interesting matrix for the analysis of the free iron because the urine of iron overload patients usually exhibits a high concentration of iron(III), complexed with the ligand employed in the chelation therapy.Information about the speciation of iron at this stage is important for many reasons and, generally speaking, the possibility to assess the free iron in such media is of overwhelming importance, as already pointed out.
For the reasons, it was decided to investigate the Fe(III) sorption on the functionalized silica directly on this media.
The urine average composition, under normal conditions, is reported in Table 2.
| Urine composition (under normal conditions) | |
|---|---|
| H2O | 95% |
| Urea | 2% |
| Creatine | 0.1% |
| Uric acid | 0.03% |
| NH3 | 0.05% |
| pH | 5–7 |
| Ionic strength | 0.33–0.56 M |
| Na+ | 0.6% |
| Ca2+ | 0.015% |
| Mg2+ | 0.01% |
| Cl− | 0.6% |
| PO42− | 0.12% |
| SO42− | 0.18% |
| Others (ions, enzymes, hormones, carbohydrates, etc.) | 1.15% |
As it can be seen, the iron concentration in urine is not reported, because it is usually too low to be detected.
Our urine samples were collected from individuals, with no discernible pathology, with iron concentration below the LOD of the ICP-OES; for this reason, we have spiked the real samples with iron(III) to simulate the condition of an iron overload patient. In addition, to avoid the formation of microorganism, methanol was added in order to reach a 10% concentration in volume.
To evaluate the partition coefficient K* between Fe(III) and DFO-MS, in the range of pH and ionic strength of urine media, competitive ligands are needed. In Fig. 4, the sorption of iron(III) at pH 7 on DFO-MS in the presence of increasing amount of three different ligands (DFO, deferiprone, and oxalate) in solution is shown.
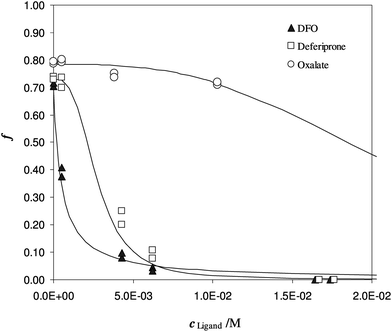 | ||
| Fig. 4 Competition of different ligands on Fe(III) enriched DFO-MS, in solution at pH 7. Different subsamples of V = 20 mL, I = 0.3 M, cFe(M) = 1.47 × 10−5, w = 35 mg. | ||
Another experiment was performed at pH 5.5, with DFO as the competitive ligand (Fig. 5). It is evident that, as the strength and the concentration of the added ligand increase, the metal exhibits higher difficulty to enter the solid phase. The values of αL and αM are known and depend on the ligand involved and on its concentration. They were calculated for the average ionic strength of urine, I = 0.3 M, by MEDUSA19 considering the contribution of iron(III) hydrolysis to αM and using the protonation and complexation constants selected for each ligand from the IUPAC Database (SC-Database, http://www.acadsoft.co.uk). From the fitting of the experimental data by eqn (1), the value of K* can be determined (note that we are using eqn (1) still in MODE 1). If a sorption model is supposed, and consequently a sorption reaction with precise stoichiometry, it is possible to obtain the exchange constant (βex) using eqn (2). The results of the fitting of the experimental points are shown in Table 3. The calculated sorption curve, reported in Fig. 4 and 5 as the continuous line, was obtained from eqn (1) with the values of Table 3.
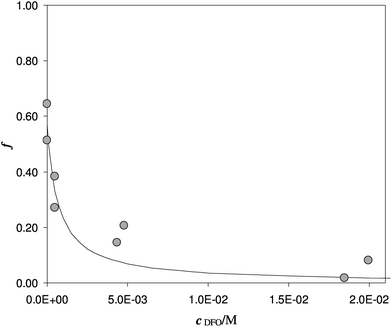 | ||
| Fig. 5 Competition of DFO on Fe(III) enriched DFO-MS in solution at pH 5.5. V = 20 mL, I = 0.3 M, cFe(M) = 1.7 × 10−5, w = 35 mg. | ||
A brief explanation of the parameter indicated as αfirst point in Table 3 is important. If the iron is free in solution, without any other iron chelator, a quantitative sorption of the metal into the solid phase is expected. Instead of that, as first point of the experiments, a sorption of around 70% was always registered. This value is justified by the presence of other ligands in urine, like proteins or inorganic anions (such as phosphate ion), responsible for iron(III) complexation and able to compete with the DFO anchored to the silica. It was also experimentally verified that the methanol added as the stabiliser in the urine media, did not interfere with Fe3+ binding since the same sorbed fraction was obtained both in the absence and presence of methanol (Fe(III) sorption 75% without methanol and 72% with methanol).
To understand the effect of diverse urine, samples obtained from different volunteers, spiked with the same Fe(III) concentration and equal additions of the deferiprone, were employed.
In Fig. 6 the sorbed ion is reported, for each urine sample, with symbols and the fitting with lines. In Table 4, the punctual values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex obtained from eqn (1) (MODE 1).
βex obtained from eqn (1) (MODE 1).
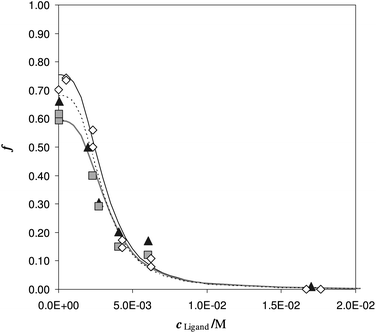 | ||
| Fig. 6 Competition of deferiprone on DFO-MS in different iron enriched urine samples, (reported with different symbols) at pH 7. V = 20 mL, cFe(M) = 1.47 × 10−5, w = 35 mg. | ||
| pH | I (M) | K* | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex βex |
|---|---|---|---|
| 5.94 | 0.14 | 3.5 × 1019 | 40.3 |
| 6.10 | 0.24 | 1.0 × 1020 | 40.3 |
| 7.19 | 0.08 | 5.0 × 1022 | 39.7 |
| 7.13 | 0.18 | 1.1 × 1023 | 40.3 |
The desorption profiles are described by the formation of the only single 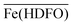 complex in the solid phase and the values of the log
complex in the solid phase and the values of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex, previously obtained in synthetic solutions and under different conditions are here confirmed in a real and complexed media, as human urine. Moreover the log
βex, previously obtained in synthetic solutions and under different conditions are here confirmed in a real and complexed media, as human urine. Moreover the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex is in reasonable agreement with the Fe(III)/DFO complexation constant in solution. It is important to highlight that the log
βex is in reasonable agreement with the Fe(III)/DFO complexation constant in solution. It is important to highlight that the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex was not affected by the changing of the ligand employed for competition, by the pH and the origin of the urine samples. Consequently the log
βex was not affected by the changing of the ligand employed for competition, by the pH and the origin of the urine samples. Consequently the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex value could be considered “universal” for urine samples, so we can calculate K* at any pH of any urine samples.
βex value could be considered “universal” for urine samples, so we can calculate K* at any pH of any urine samples.
The original tool to perform the free metal evaluation was now ready for use; the next item was a simulation of the in-field test. For this purpose we determined c at different V/w ratios, employing always eqn (1), but now the unknown parameters are ctot and αM. We call this strategy, to use eqn (1), “MODE 2”. This procedure is a sort of Fe(III) titration where the titrant is the DFO-MS.
The “free metal sensor” was tested on four SPU samples (A, B, C and D), treated as reported in the Experimental section.
To have an estimate of the ionic strength, the main ions were detected, and the pH was measured. The ionic composition of the samples is reported in Table 5.
| Sample | Na (M) | K (M) | Mg (M) | Ca (M) | I (M) |
|---|---|---|---|---|---|
| A | 0.09 | 4.65 × 10−2 | 7.1 × 10−4 | 8.3 × 10−4 | 0.14 |
| B | 0.16 | 8.49 × 10−2 | 1.6 × 10−3 | 1.5 × 10−3 | 0.25 |
| C | 0.05 | 2.86 × 10−2 | 5.5 × 10−4 | 7.7 × 10−4 | 0.08 |
| D | 0.07 | 1.55 × 10−2 | 5.7 × 10−4 | 4.8 × 10−4 | 0.09 |
As reported in the Experimental section, each sample was divided into different subsamples and put to equilibrate with different amounts of DFO-MS. After equilibration the solution was tested for iron content.
In Table 6 for each sample, the pH, the nominal deferiprone concentration (cL) and the amount of metal experimentally determined by direct quantification (ctot,dir) are reported (second, third and fourth columns). With these data, it is possible to calculate the theoretical values of αMt, reported in the fifth column.
| Samples | pH | c L (mM) | c tot,dir (μM) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αMt αMt |
c tot (μM) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αM αM |
pFe |
|---|---|---|---|---|---|---|---|
| A | 5.94 | 6.05 | 12.7 | 17.84 | 11.1(2) | 17.70(1) | 22.65(1) |
| B | 7.19 | 6.05 | 12.8 | 21.59 | 12(3) | 21.3(1) | 26.2(2) |
| C | 7.14 | 6.20 | 12.9 | 21.59 | 9.9(5) | 20.59(4) | 25.59(6) |
| D | 7.14 | 6.20 | 13.0 | 21.32 | 15(2) | 21.32(8) | 26.1(1) |
The experimental profiles of c as a function of different V/w ratios are shown in Fig. 7.
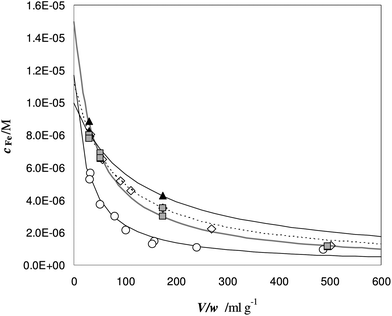 | ||
Fig. 7 Titration of Fe(III) in urine samples with DFO-MS. V = 18 mL, cL and ctot values are reported in Table 6. Samples: ◇ = A; ○ = B; ▲ = C;  = D. = D. | ||
At a low V/w ratio, almost the entire amount of iron(III) enters the solid phase. The DFO-MS competes with deferiprone in solution, but the strength of competition decreases for larger V/w values; indeed only a small fraction of iron(III) is still sorbed for V/w higher than 100 mL g−1.
It is important to highlight that the solid phase is able to compete with a ligand in solution for metal complexation only in case the collateral reaction coefficient is in between two limiting values. The “detection window” of the specific titration (obtained by eqn (1)) is:11
If the reaction coefficient αM is lower than 0.1 K* w/V, the metal ion is quantitatively sorbed by the solid phase (because M was either free or in complexes with very weak ligands). If αM is higher than 10 K* w/V, the metal ion is so strongly bound to the complexes in solution that it is not sorbed on the solid. The presence of such strongly complexing species cannot be excluded in real samples and, for their determination, one must select another solid material with active sites sufficiently strong.
From the non-linear regression of the eqn (1) MODE 2, it is possible to determine the value of ctot and αM for each sample.17 The results are reported in Table 6, sixth and seventh columns.
The values of ctot (obtained by the non-linear regression) could be considered in acceptable agreement with the “true” values i.e. the total concentration, directly measured on the initial spiked urine samples (ctot,dir). It is evident that, due to the iron concentration level of these samples, it is more convenient to assess the total content directly on the original samples. The case could be completely different when the concentration of metal is too low to be directly determined. In this case, thanks to the titration here proposed, ctot can be obtained from eqn (1) MODE 2, by extrapolation. This procedure has already been adopted in metal speciation studies on pristine seawater samples using a chelating resin as the sorbent.11
Nevertheless, the gold point of this procedure is the possibility to determine the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αM. First of all the accordance between the calculated values (log
αM. First of all the accordance between the calculated values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αMt) reported in the fifth column and those computed with the procedure (seventh column) of Table 6 is extremely important. These last values are found independently, since we only use for the calculation the log
αMt) reported in the fifth column and those computed with the procedure (seventh column) of Table 6 is extremely important. These last values are found independently, since we only use for the calculation the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex and the total iron concentration.
βex and the total iron concentration.
The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αM became much more informative, if we use it to obtain the pFe (−log[Fe]), from the simple relationship [Fe3+] = ctot/αM. The punctual values of pFe are reported for the four urine samples in Table 6, last column. They correspond to extremely low concentration, but of the same magnitude order to the values that are expected to be found in biological fluids of patients under chelation therapy.
αM became much more informative, if we use it to obtain the pFe (−log[Fe]), from the simple relationship [Fe3+] = ctot/αM. The punctual values of pFe are reported for the four urine samples in Table 6, last column. They correspond to extremely low concentration, but of the same magnitude order to the values that are expected to be found in biological fluids of patients under chelation therapy.
Here, as far as the authors know, a first attempt to measure the actual pFe is presented; the pFe values are found from the competition exerted by the designed solid phase: the DFO-MS.
Conclusions
The characterization of the iron(III) sorption on deferoxamine (DFO) immobilized on MCM-41 mesoporous silica (DFO-MS) in both synthetic solutions and real biological samples (urine) were presented. The exchange reaction of iron(III) on the active site of the new DFO-MS is:with an exchange constant (average value) log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βex = 40(1) in both media, in good agreement with the complexation reaction of Fe(III) with DFO in solution.
βex = 40(1) in both media, in good agreement with the complexation reaction of Fe(III) with DFO in solution.
Since a sufficient variety of samples was investigated, it was also confirmed that the monoprotonated species is the only complex formed in a large pH interval. This aspect is fundamental to calculate the partition coefficient between the solid phase and the solution, K*, indeed its determination is the key step to apply the solid material as a sensor for the free iron(III).
The assessment of the method was performed in SPU (Simulating Pathology Urine) samples. Portions of the same volume of the urine sample, enriched with deferiprone (one of the drugs currently employed in overloading therapy) and iron(III), were bought into contact with different amounts of DFO-MS to perform a titration of Fe(III) in the sample. As this experiment was a simulation, with both concentrations of deferiprone and total content of iron(III) known, it was possible to calculate a priori the pFe; this quantity was then compared with that obtained by the titration: a satisfactory agreement was obtained. This form of validation is the first step for developing a sensor for pFe. Of course, a lot of work has to be done and a much larger variety of samples, i.e. real urine samples of patients under therapy and other biological media, have to be tested.
We remind that in chelating therapy studies, the pFe is always simply computed from in silico studies. Here, we have experimentally determined the pFe in the solution of interest and it represents the actual pFe. In previous studies only the, “expected value”, i.e. the data only calculated by computer modeling of chemical speciation, is usually reported; so the possibility to verify these theoretical pFe values is a figure of merit of the proposed sensor. In any way, we also want to emphasize that actually the control of the trueness and the precision of speciation results are already difficult and are complicated even more by the fact that the certified samples are not available.
We are also quite sure that experimental methods devoted to determine, not the total iron content, but the free iron(III) concentration, at the moment, are not reported in the literature, consequently in our opinion this is the real novelty of our work. It is true that, at the present, we have analyzed only SPU samples, but in these examples we demonstrated that the free iron(III) obtained by the described experimental procedure was in pretty good agreement with the calculated value. This is not marginal, and we do believe that sensors of this kind can be employed in clinical analysis to validate the computer speciation simulation.
Another relevant aspect, not secondary to obtain a complete picture of benefits and limitations of the DFO-MS sensor, is the characteristics of the silica used here as the support for DFO. In this study we decided to apply a commercial mesoporous silica MCM-41 thanks to its high surface area and the relatively easy functionalization. We are aware that different promising materials could be used as the support for DFO aiming to obtain more stable and recyclable sensors. The reasons for the choice of mesoporous silica have been shelved in this first work, giving here more emphasis to the application of the DFO-MS as the sensor for the free iron(III).
Taking account of the satisfactory results we obtained, from the analytical point of view, we are confident to have room to develop DFO sensors based on different supports and with high sorption capacity for iron(III) (as, for example non-porous silica, and cellulose based materials).
Acknowledgements
We would like to thank NOVARTIS for DFO supply and FAR (Fondi Ateneo per la Ricerca) of the University of Pavia for funds.Notes and references
- T. Kiss and A. Odani, Bull. Chem. Soc. Jpn., 2007, 80, 1691 CrossRef CAS.
- J. A. Caruso, R. G. Wuilloud, J. C. Altamirano and W. R. Harris, J. Toxicol. Environ. Health, Part B, 2005, 9, 41 Search PubMed.
- R. A. Yokel, S. M. Lasley and D. C. Dorman, J. Toxicol. Environ. Health, Part B, 2006, 9, 63 CAS.
- P. Frisk, P. Ola Darnerud, G. Friman, J. Blomberg and N.-G. Ilbäck, J. Trace Elem. Med. Biol., 2007, 21, 29 CAS.
- G. Crisponi and M. Remelli, Coord. Chem. Rev., 2008, 252, 1225 CrossRef CAS PubMed.
- G. Faa and G. Crisponi, Coord. Chem. Rev., 1999, 184, 291 CrossRef CAS.
- International Commission on Radiological Protection, Report of the Task Group on Reference, Task Group on Reference Man, Oxford: Pergamon Press, New York, 1975 Search PubMed.
- O. Andersen and J. Aaseth, Environ. Health Perspect., 2002, 110, 887 CrossRef CAS.
- R. Abergel and K. Raymond, JBIC, J. Biol. Inorg. Chem., 2008, 13, 229 CrossRef CAS PubMed.
- O. Andersen, Chem. Rev., 1999, 99, 2683 CrossRef CAS PubMed.
- R. Biesuz, G. Alberti, G. D'Agostino, E. Magi and M. Pesavento, Mar. Chem., 2006, 101, 180 CrossRef CAS PubMed.
- M. Pesavento, R. Biesuz, M. Gallorini and A. Profumo, Anal. Chem., 1993, 65, 2522 CrossRef CAS.
- M. Pesavento, R. Biesuz, G. Alberti and M. Sturini, Anal. Bioanal. Chem., 2003, 376, 1023 CrossRef CAS PubMed.
- A. Ringbom and E. Still, Anal. Chim. Acta, 1972, 59, 143 CrossRef CAS.
- G. Alberti, R. Biesuz, A. Profumo and M. Pesavento, J. Inorg. Biochem., 2003, 97, 79 CrossRef CAS.
- R. Biesuz, G. Emma, C. Milanese, G. Dacarro, A. Taglietti, V. Nurchi and G. Alberti, Analyst, 2014 10.1039/C4AN00179F.
- G. Alberti, M. Pesavento and R. Biesuz, React. Funct. Polym., 2007, 67, 1083 CrossRef CAS PubMed.
- R. Biesuz, G. Alberti and M. Pesavento, J. Solution Chem., 2008, 37, 527 CrossRef CAS.
- I. Puigdomenech, MEDUSA - Chemical Equilibrium Diagrams program 32 bit vers, 16 Dec. 2010 Search PubMed.
- E. Farkas, E. A. Enyedy and H. Csoka, Polyhedron, 1999, 18, 2391 CrossRef CAS.
- M. Ronteltap, M. Maurer and W. Gujer, Water Res., 2007, 41, 977 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3an01488f |
| This journal is © The Royal Society of Chemistry 2014 |