Theory and simulation studies of effective interactions, phase behavior and morphology in polymer nanocomposites
Venkat
Ganesan
*a and
Arthi
Jayaraman
*b
aDepartment of Chemical Engineering, University of Texas, Austin, USA. E-mail: venkat@che.utexas.edu
bDepartment of Chemical and Biological Engineering, University of Colorado, Boulder, USA. E-mail: arthi.jayaraman@colorado.edu
First published on 23rd October 2013
Abstract
Polymer nanocomposites are a class of materials that consist of a polymer matrix filled with inorganic/organic nanoscale additives that enhance the inherent macroscopic (mechanical, optical and electronic) properties of the polymer matrix. Over the past few decades such materials have received tremendous attention from experimentalists, theoreticians, and computational scientists. These studies have revealed that the macroscopic properties of polymer nanocomposites depend strongly on the (microscopic) morphology of the constituent nanoscale additives in the polymer matrix. As a consequence, intense research efforts have been directed to understand the relationships between interactions, morphology, and the phase behavior of polymer nanocomposites. Theory and simulations have proven to be useful tools in this regard due to their ability to link molecular level features of the polymer and nanoparticle additives to the resulting morphology within the composite. In this article we review recent theory and simulation studies, presenting briefly the methodological developments underlying PRISM theories, density functional theory, self-consistent field theory approaches, and atomistic and coarse-grained molecular simulations. We first discuss the studies on polymer nanocomposites with bare or un-functionalized nanoparticles as additives, followed by a review of recent work on composites containing polymer grafted or functionalized nanoparticles as additives. We conclude each section with a brief outlook on some potential future directions.
I. Introduction
Materials that consist of mixtures of polymers and organic/inorganic particles, ranging from nanometers to microns, are used in a wide variety of applications.1 The role of the polymer in these mixtures has traditionally been as a colloidal stabilizer or rheological modifier, and characterized by the feature that the polymer size (i.e. the length scale controlling polymer physics, denoted generically as Rg) is much smaller than the size of the particle, R.2–5 This “colloid” limit constitutes the conventional regime for which many theoretical models and simulation approaches have been developed. At an equilibrium level, much information can be gleaned about this limit by studying the interactions between flat surfaces in polymeric media.6–9 At a dynamical level, much progress can be made by modeling the polymeric matrix as a continuum non-Newtonian fluid.10 More recent developments in nano- and biotechnology applications have however moved the polymer–particle mixtures from the “colloid limit” to the “nanoparticle limit” where Rg > R. For instance, in systems termed as polymer nanocomposites (PNCs), nanoparticles of sizes 5–50 nm (comparable to Rg) are routinely dispersed in polymeric matrices to enhance their properties.11–15 Examples of such materials include mixtures of a variety of homopolymers and multicomponent polymers blended with fillers such as clays, nanotubes, fullerenes, nanoscopic silica particles, etc.16–22 Initial interest in such materials arose from the significant property enhancements reported for the original polymer matrix even at extremely low loadings of the nanoparticles.23–25 These reports fueled intense research into the mechanical, electrical, barrier and fire retardancy properties of PNCs, leading to commercialization of technologies utilizing PNCs.26–28 More recent efforts have expanded the above class of studies and materials by examining the properties of nanocomposites involving polymer blends and block copolymers, where the potential to create multifunctional materials possessing novel electrical, magnetic and optical properties has been reported.29–32The above-discussed transition to the nanoparticle limit has also identified a number of new physical phenomena which have challenged the fundamental understanding of the properties of polymer–particle composites. For instance, at the equilibrium level, the curvature of the particle has been shown to play an important role in determining the interactions within the composite and the resulting phase behavior of the system.33–41 At a dynamical level, a number of observations have been reported where “continuum” theories seem to breakdown, leading to surprising and counter-intuitive phenomena.42–49 Not surprisingly, such observations have also spurred a number of theoretical and computational efforts aimed at elucidating the structure and properties of polymer nanocomposites. Recent review articles on this topic have described many of these theoretical and computational efforts alongside experimental work.50–53 In this article, we briefly review the results of some recent theoretical and computational efforts which have undertaken the task of modeling the structure and properties of polymer–nanoparticle mixtures. We primarily focus on theoretical and computational work in the context of mixtures of synthetic polymers and inorganic nanoparticles, and eschew discussion of systems of biological interest. For the same reason, our review mainly concerns charge neutral polymer–nanoparticle systems where the physics associated with electrostatic interactions is not the main concern. Finally, except for a few isolated instances, we do not discuss the vast literature accompanying the context of dynamical phenomena and rheological properties of polymer–nanoparticle mixtures. The latter topics are of extreme importance to a number of applications, but their thorough discussion would render this review too voluminous.
We divide the following review into two broad sections which focus on: (i) polymer–nanoparticle mixtures in which the particles are non-functionalized (termed as “bare particles” in our review); (ii) polymer–nanoparticle mixtures in which the nanoparticles are functionalized by polymer grafts. Within each section, we divide the discussion into the subcategories of theory and simulations. Within the context of the former, we primarily review the developments in the context of PRISM theories, density functional and self-consistent field theory approaches. Within the context of the latter, we discuss the recent developments in the context of both atomistic and coarse-grained simulations of the structure of polymer–nanoparticle composites. To maintain brevity, we do not discuss quantum mechanical simulation approaches and force field development efforts which play an important role underlying atomistic simulations. Within each section we also offer a brief perspective on some possible future directions within such a topic.
II. Bare particles
A. Theory
In this section, we review the theoretical efforts, emphasizing integral equation theories (specifically Polymer Reference Interaction Site Model, PRISM), density functional theory (DFT), self-consistent field theory (SCFT) and field theoretic approaches, to understand structure and phase behavior in polymer nanocomposites consisting of polymer matrices and bare particles (i.e. particles with no functionalization).| H(q) = Ω(q)C(q)[Ω(q) + H(q)] | (1a) |
| Hij(q) = ρiρjĥij(q) | (1b) |
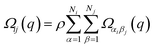 | (1c) |
| gij(r) = 0, r < σij | (2a) |
Outside the hard core, the PY approximation describes the direct correlation function between all pairs of sites (except particle–particle):
| cij(r) = (1 − eβUij(r))gij(r), r > σij | (2b) |
cCC(r) = hCC(r) − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gCC(r) − βUCC(r), r > D gCC(r) − βUCC(r), r > D | (2c) |
To efficiently solve this system of coupled nonlinear integral equations one can employ the KINSOL algorithm with the line search optimization strategy which minimizes the objective function along an optimum descent direction.64 KINSOL has significantly improved the convergence for these complex nonlinear integral equations as compared to the Picard iteration method that was used in many of the early PRISM studies. Once the solver converges to a solution, the inter-molecular pair correlation functions, gij(r), and the partial collective structure factors, Sij(q) for all identities of i and j sites in the system, are obtained.
In many early PRISM theory studies of polymer nanocomposites, with either bare particles or polymer grafted particles in a homopolymer matrix (focus of the next section in this review), the intra-molecular pair correlation, Ωij (an input to eqn (1)), was calculated by assuming ideal conformations of the grafted and/or matrix chains.54–63 Assuming ideal conformations for the matrix polymers is correct when studying an athermal polymer melt, where, according to the Flory theorem, the excluded volume interactions can be assumed to be screened.65 However, for systems where non-idealities in chain conformations (in grafted chains and/or matrix chains) arise, one needs to solve for a more accurate Ωij. One means to achieve such a task is to implement a self-consistent PRISM–MC approach. In essence, Monte Carlo (MC) simulations of the chain conformations in the presence of an external medium-induced potential obtained from PRISM theory are used to obtain the intra-molecular pair correlation functions Ωij. The latter are then input to the PRISM theory to provide an improved estimate of the external medium-induced potential. By repeating the preceding steps in an iterative manner a self-consistent convergence of PRISM theory and Ωij can be achieved. In implementing such a self-consistent PRISM–MC approach for homopolymer melts,66–71 and bare particles in a homopolymer melt,72,73 the self-consistent loop involves MC simulations of only one matrix polymer chain. In contrast, self-consistent PRISM–MC studies of polymer grafted nanoparticles in a polymer matrix require self-consistent loops for both the grafted and the matrix chains to account for the non-idealities both in the grafted and matrix chain conformations.74–78
The steps involved in the above-discussed self-consistent approach are as follows. First, the pair-wise decomposed medium-induced solvation potential, Δψij(r), is obtained from the PRISM equations and describes the interaction between any two sites i and j as mediated by all the remaining sites in the system, i.e., the matrix, grafts (if present) and particles themselves. The form of the medium-induced solvation potential depends on the approximation used in its derivation (see eqn (3a) and (b)).66–68,79–81
ΔψPYij(r) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[1 + cik(r)*skk′′(r)*ck′j(r)] ln[1 + cik(r)*skk′′(r)*ck′j(r)] | (3a) |
ΔψHNCij(r) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cik(r)*skk′′(r)*ck′j(r) cik(r)*skk′′(r)*ck′j(r) | (3b) |
| S(q) = Ω(q) + H(q) | (3c) |
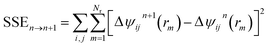 | (4a) |
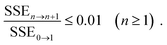 | (4b) |
Using PRISM theory without a self-consistent Monte Carlo loop, Hooper and Schweizer have conducted extensive studies of polymer nanocomposites to predict the structure, effective forces, and thermodynamics in polymer nanocomposites with hard spherical fillers and homopolymers, at an athermal limit (absence of attractive interactions) as well as in the presence of polymer–particle attraction, for single and two particle limits, and at increasing (finite) filler fractions.54–56 In the athermal limit they observed a transition from “monotonic decaying, attractive depletion interactions” between the particles, to a much stronger “repulsive–attractive oscillatory depletion” at approximately the semidilute–concentrated solution boundary.56 Under melt conditions, they found that the depletion force is extremely large and attractive at contact, but is followed by a high repulsive barrier. They found that PRISM calculations based on HNC closure for particle–particle direct correlations and PY closure for other pairs of direct correlations captured many of the rich features found in the simulations.56 With increasing nanoparticle volume fraction, the inter-filler packing changed from a bridged or sterically stabilized particle organization in the infinite dilution limit to more diffuse liquid-like packing with clustering of particles. Additionally, the presence of particle–polymer attraction led to a significant bound polymer layer on the particles marked by a microphase-separation-like scattering peak at a length scale that is indicative of distinct bound polymer layers.
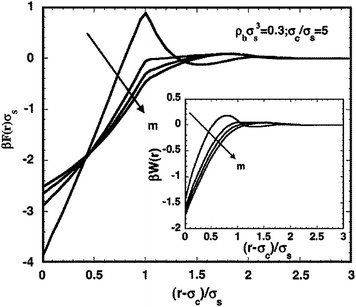
The results from PRISM theory have shown agreement with small angle neutron scattering studies on polystyrene loaded with spherical silica nanoparticles under contrast-matched conditions.41 Hall and Schweizer extended the above PRISM theory based calculations to cover the entire compositional range from the polymer melt (0% filler loading) to the hard sphere fluid (100% filler loading), with attractive interactions between polymers and nanoparticles for several interaction strengths and nanoparticle sizes.58 By focusing on high filler volume fractions they were able to fully account for many-body correlation effects in the determination of the spinodal phase separation instabilities. They observed entropic depletion-like lower critical temperature at low filler volume fraction (<10%) and a bridging-induced upper critical temperature at high (95%) filler volume fraction. Hall et al. have also presented PRISM theory studies in conjunction with experiments for a system of silica nanoparticles in miscible poly(ethylene oxide) (PEO) and polytetrahydrofuran (PTHF) nanocomposites.57 Structural characterization from PRISM calculations has been compared directly with results from small-angle X-ray scattering experiments to show that the PRISM approach shows qualitative and quantitative agreement with experimental structures for a range of filler loading and interfacial cohesion between the polymer and particle. Using potential of mean force (PMF) calculations Hall et al. presented a criterion for the onset of depletion or bridging-induced kinetic gelation; their criterion is consistent with the experimental observation of complete miscibility for the PEO nanocomposite, and a non-equilibrium behavior in the PTHF nanocomposite.
Additional comparisons of PRISM theory and experimental results from small angle neutron scattering (SANS) have been presented by Kim et al. that show the ability of PRISM theory to reproduce the adsorbed polymer layer on the additives expected in experiments and qualitative failure of random phase approximation (RPA).82 Kim et al. have gone beyond binary mixtures of fillers and polymers, and also used ultrasmall-angle X-ray scattering to probe the local and long wavelength structure of ternary mixtures of silica nanoparticles suspended in concentrated solutions of polyethyleneglycol (PEG) in the good solvent ethanol to study how the fillers organize at varying polymer concentrations.83 While at the dilute polymer limit, the silica fillers are dispersed via electrostatic repulsions, at intermediate polymer concentrations they observed filler aggregation. As expected at the polymer melt limit they observed a homogeneous phase due to the formation of adsorbed polymer layers on the nanoparticles. These SAXS measurements were quantitatively compared with predictions of the two-site PRISM theory, where the solvent is modeled implicitly through an effective contact strength of attraction between the polymer and filler. They found good agreement between theory and experiment with the assumption that the contact strength of attraction between the polymer and filler linearly decreases with solvent volume fraction.
So far, all of the studies we have discussed were focused on bare spherical particles in a matrix of linear polymers. Going beyond linear polymer architectures in the matrix, Zhao et al. employed PRISM theory to study nanocomposites, where the matrix polymers are star polymers and the fillers are spherical particles, in the presence of particle–polymer attraction.84,85 The star architecture was found to promote contact aggregation of particles at weak nanoparticle–monomer attraction, suppress polymer bridging between particles at moderate nanoparticle–monomer attraction, and promote the particle–polymer aggregation through polymer bridging at large nanoparticle–monomer attraction. They systematically studied effects of varying arm length and number of arms, and found that in the case of short arm lengths, the network phase (formed by polymer bridging) boundary shifts towards reduced miscibility with increasing number of arms. In the case of long arm lengths, the network phase boundaries show opposite trends compared to short arm lengths.
Going beyond spherical fillers, Hall and Schweizer have studied the equilibrium properties of nanocomposites with linear polymers and fillers with rod-like, disk-like, and cubic shapes.59 They found that the depletion attractions, stabilization of the fillers via polymer adsorption, or bridging of the fillers by polymer chains are all shape-dependent. Additionally, they found that often, but not always, the trends are monotonic with increasing filler dimensionality. Chakrabarti et al. used a small scale Monte Carlo method plus PRISM theory to study two models of fractal-like aggregates relevant to non-compact carbon black or silica aggregates in polymer nanocomposites and suspensions.86 They found that the effective potential between the centers of mass of the fractal aggregates has a distinctive soft repulsion form that depends on whether geometric disorder at the single aggregate level is included. The aggregate fluids show a considerable amount of interpenetration and complex non-hard-sphere packing features in their pair correlation functions. Calculations of the collective static structure factor and compressibility (or inverse bulk modulus) were in qualitative agreement with scattering experiments on suspensions of fumed silica hard fractals.
In summary, PRISM theory has been used extensively to elucidate effective interactions and equilibrium structure in bare particle–polymer nanocomposites for varying particle shapes, polymer architecture and intermolecular interactions. Moreover, as discussed above, results from PRISM theory show excellent agreement (qualitative and some quantitative) with experiments and simulation results. While most of these PRISM approaches have studied the phase behavior in the bulk, there is a need for understanding spatial organization of the components of the composites near surfaces to capture the effect of substrates in thin film systems. There has not been much development in PRISM approaches to address this aspect, and could be a direction for future development.
| βF[ρpα(r), ρcγ(r)] = βFpol[ρpα(r)] + βFpar[ρcγ(r)] + βFintpol,par[ρpα(r), ρcγ(r)] | (5) |
In the above, ρpα(r) and ρcγ(r) denote, respectively, the (inhomogeneous) polymer and particle density fields (the indices α and γ denote, respectively, the different polymer and particle species, if any). The terms Fpol[ρpα(r)] and Fpar[ρcγ(r)] denote the free energies of a system containing only the polymer and particle components, and the term Fintpol,par[ρpα(r), ρcγ(r)] embodies the effects of the polymer–particle interactions. The equilibrium density profiles ρpα(r), ρcγ(r) are then obtained as the fields which minimize the corresponding grand free energy.92
A standard approach of both DFT and SCFT is to identify the free energies Fpol[ρpα(r)] and Fpar[ρcγ(r)] above as a combination of an ideal term, Fid, corresponding to a system of noninteracting molecules, and an “excess” term, Fex, which accounts for the interactions between the molecules.92,93 While both DFT and SCFT approaches share such a feature, they however differ in the functional forms adopted for Fid and Fex. In the context of simple fluids and particulate phases, it is common to associate Fid with the ideal gas free energy of a non-interacting system of particles as
Fid[ρ(r)] = ∫drρ(r)[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ(r) − 1] ρ(r) − 1] | (6) |
Some DFT approaches for polymeric materials have also adopted the above approach of modeling the ideal gas term as that corresponding to a fluid of unconnected monomers.94 In contrast, in SCFT and in some versions of DFTs, the polymer connectivity is explicitly accounted for within the ideal gas term.95 In such situations, Fid[ρ(r)] represents the free energy of an inhomogeneous polymeric system (with density ρ(r)) in which all the bonded interactions are assumed to be present, but the nonbonded interactions are ignored. Unfortunately, for such situations, an explicit expression for Fid[ρ(r)] cannot be obtained, and hence one uses either Monte Carlo simulations87 or a mapping of the partition function to a random walk problem followed by the solution of a diffusion equation to obtain Fid[ρ(r)].91,93
A number of different models have been proposed for Fex[ρ(r)] to capture the interaction effects within particle and polymer systems. For simple fluids and the particle phases, excluded volume interactions play an important role in determining the structural characteristics. As a consequence, models used in such contexts are designed to account for the structural correlations arising from harsh repulsive interactions.92 The early versions of such theories used a weighted measure of the inhomogeneous densities within free energy models for homogeneous systems to determine the excess free energies.96–98 In contrast, more recent models use sophisticated approaches, in particular, the fundamental measure theories to account for the interaction features arising from excluded volume interactions.99,100 In the context of polymeric systems, different approaches are used within the SCFT and DFT frameworks for representing Fex[ρ(r)]. DFT frameworks are typically employed when a proper accounting of the correlations resulting from monomer level excluded volume interactions is desired (such as for characterizing the short range features of polymer density profiles near surfaces). In such cases, the weighted density functional and/or fundamental measure theory approaches, originally proposed for simple fluid systems, have been generalized to characterize the interactions between polymer segments.87,90,95,101 Moreover, if the ideal gas free energy, Fid, ignored connectivity, then Fex[ρ(r)] is also augmented through an “association” like term to account for the connectivity of the monomers.102,103 In contrast to the DFT frameworks, SCFT approaches typically do not strive for an accurate representation of monomer level correlations. In such methodologies, simple “local” density functional forms (such as a virial expansion) are often adopted to characterize Fex[ρ(r)].91,93,104
In a manner similar to the excess free energy contributions for the polymer and particle phases, a number of models have been proposed for Fintpol,par[ρpα(r), ρcγ(r)] depending on whether explicit treatment of excluded volume interactions between particles and polymers is desired. In cases where the short range correlations arising from the hard core repulsions between the polymer monomers and the particles are important or desired to be incorporated, DFT approaches such as fundamental measure theories have been adapted to account for the different sizes of polymer monomers and the particles to model Fintpol,par[ρpα(r), ρcγ(r)].105–109 Attractions and long range van der Waals interactions between the polymer and particles, if any, are often incorporated through a mean-field formalism which ignores the correlations between the polymer monomers and the particles.108 In SCFT approaches, the interactions between the polymer and particles are again modeled through simple local density functionals which ignore the monomer level structural characteristics of the polymer.110,111
The above ingredients have been used in different combinations to study the equilibrium characteristics of polymer–bare particle mixtures. Below we classify them broadly into two categories, and discuss some of the studies pertaining to the case of polymers mixed with bare (ungrafted) nanoparticles:
(i) Insertion free energies and interparticle interactions in polymer solutions and melts: a number of studies have examined the insertion free energies and interparticle interactions in polymer melts and solutions using DFT and SCFT approaches. In such contexts, it is common to fix the particle(s) and model it as an external excluded volume interaction potential to deduce the effect on the polymer structure and its free energies. By calculating the free energy changes resulting from the insertion of one and two particles, the infinite dilution limit of the insertion free energies and the polymer-mediated interparticle interactions are deduced.
Calculations in the above spirit have had a long history, beginning with the characterization of polymer-mediated interparticle interactions between large colloidal particles by Asakura and Oosawa.112,113 Subsequently, a number of studies extended such a treatment to account for effects such as interpolymer interactions and solvent quality. However, it was only recently that such approaches were extended to study the interactions between nanoparticles (i.e. particles whose sizes are comparable or even smaller than the polymer) in polymer solutions and melts. For instance, Surve and coworkers used a SCFT implementation for a polymer solution in an implicit solvent representation to study the effects of curvature, polymer–particle interactions and particle shape upon the interactions between nanoparticles.36,37,114 Their studies presented explicit results for the influence of curvature upon the effective interactions between nanoparticles and also deduced the resulting phase diagrams by using such interactions within a virial expansion approach. Yang and coworkers used a SCFT approach to study the conformational characteristics of polymers adsorbed on spherical particles, and quantified the loop and tail distributions as a function of particle size115 (see also ref. 114). Such studies demonstrated the increased preference of the polymers to form tails and bridges during adsorption on nanoparticles. Such conformational features were also shown to lead to an enhanced propensity to form polymer bridged gels in nanoparticle systems.37 Lekkerkerker, Tunier and coworkers used the adsorption method in conjunction with other approximations to account for the particle curvature and calculated the depletion interactions between particles in polymer solution.116,117 From the interaction potential between two spheres they deduced the osmotic second virial coefficient, B2, for various polymer–colloid size ratios.4 They found that when the polymers become smaller than the spheres, B2 remained positive in the dilute regime, and thereby demonstrated that the depletion interaction is ineffective in causing phase separation of relatively small spheres. Most of the preceding studies used a mean-field approximation to solve the equilibrium characteristics of the polymer matrix. In contrast, Eisenreigler and coworkers used more sophisticated field theoretic techniques (which went beyond the mean-field limit) to study polymer depletion effects near mesoscopic particles of different shapes and demonstrated the importance of accounting for interpolymer interactions.118–120 In the context of polymer melts, Vaia and Gianellis used a SCFT approach to study the free energy of polymer–organo-clay mixtures as a function of clay platelet separation.121 Using such a methodology, they delineated the parameters controlling the states of dispersion, intercalation and aggregation of the clay platelets in the polymer matrix. Their results suggested that strong polymer–particle attractions are a requisite for efficient dispersion of nanoparticles.
A number of studies have also used a DFT framework for the polymer to study the energetics of one and two particle systems in polymer solutions and melts. For instance, Freasier and Woodward used an integral equation based DFT for the polymer solution to calculate the structure of the polymers around spherical particles.122 Patel and Egorov used DFT (with the bonded interactions included in Fid) to study the interactions between nanoparticles in polymer solutions, and clarified the roles of attractive interactions between the polymer and the particles and the solvent quality in influencing such interactions.123,124 The microstructure and depletion forces in polymer–colloid mixtures were studied using the DFT model of interfacial statistical associating fluid theory by Chapman and coworkers (see Fig. 1).125 Using such a framework, they characterized the role of polymer concentration, particle/polymer-segment size ratio, and polymer chain length on the structure, polymer induced depletion forces, and the colloid–colloid osmotic second virial coefficients. Recently, Frischknecht and Yethiraj studied the multibody effects between nanoparticles in a polymer and demonstrated that three body interactions could become significant, and that the pair-wise interactions deduced at infinite dilutions may provide only a partial description of the physics at finite particle concentrations.126
Variants of the SCFT approaches have also been used to study the insertion free energies and interparticle interactions arising in the structured polymeric media such as polymer brushes and block copolymer morphologies. For instance, Reister and Fredrickson used the SCFT approach to examine the potential of the mean force between particles embedded in the lamellar phase of block copolymers.127 The physics of nanoparticles in polymer brushes has also been addressed within the SCFT framework by Kim and O’Shaughnessy,128 Kim and Matsen,129 Chen and Ma,130 Egorov131 and more recently by Halperin, Kroger and Zhulina.132 These studies have clarified the influence of particle sizes, solvent quality and brush grafting densities upon the insertion free energies and interactions between nanoparticles.
(ii) Phase behavior and structure of polymer–nanoparticle mixtures: a number of studies have examined the phase behavior and structural characteristics in mixtures of polymer–nanoparticle mixtures at finite concentrations of particles using SCFT and DFT approaches. The different studies in this regard themselves fall into three broad categories:
The first class of studies has used an SCFT framework for polymers coupled to an explicit representation and simulation of the particles. This framework represents an extension of the one and two particle studies discussed in category (i) above, in which the particles are modeled as an interaction potential which excludes the polymers from its interior (attractive interactions are modeled in a mean-field manner). However, in contrast to studies in (i), the particle degrees of freedom are not fixed, and instead a simultaneous equilibration of both the particle and polymer degrees of freedom is affected. Typically, this entails in each step the solution of the equilibrium characteristics of the polymers for a specified configuration of the particles, followed by particle moves based on the forces experienced by the particles (Brownian dynamics) or the energy of the system (Monte Carlo). Such hybrid methods were pioneered for polymer–particle systems by Fredrickson and coworkers,111 and have been primarily used to address the structural features of particle assemblies within self-assembled block copolymer matrices.133,134 In its first application, Fredrickson and coworkers used such an approach to study the segregation of nanoparticles within lamellar block copolymer phases.111 Subsequent applications have studied the influence of nanoparticles on order–disorder transitions,30 the combined self-assembly of block copolymers and anisotropic fillers,135 the influence of confinement on such nanoparticle assemblies,136 and the influence of external magnetic fields on the assembly of such nanoparticles.134 Ginzburg, Balazs and coworkers have pursued similar approaches wherein a mesoscopic time-dependent Landau–Ginzburg formalism is combined with a Brownian dynamics framework for the particles.137,138 Unlike the hybrid methodologies discussed in the context of block copolymers, the latter does not enforce particle–polymer exclusion in a rigorous manner, and has primarily been used to study the dynamics and the influence of shear upon the phase separation processes of particles mixed with binary polymeric mixtures.
A second class of approaches uses a hybrid DFT–SCFT framework for polymer–particle systems. Such approaches combine the SCFT framework describing the polymer degrees of freedom (DOF) along with a DFT framework for the particle DOF. The interactions between the polymer and particles are expressed at a mean-field level as a free energy functional of the density of the polymers and particles, and as a consequence, such approaches do not enforce explicit exclusion of polymers from the particle interiors. Such approaches were pioneered by Balazs, Ginzburg and coworkers who used such models to study the phase behavior of nanoparticles of different shapes mixed with homopolymers and diblock copolymers. In their initial studies they combined an Onsager-type DFT for hard, anisotropic particles, with mean-field free energy functionals for the polymer and studied liquid crystalline phase transitions.137,139 The resulting phase diagrams were shown to be strongly dependent on the anisotropy of the particles, the polymer chain length and polymer–particle interactions. In subsequent studies, they extended such a framework to study the combined self-assembly of multicomponent polymers and particles.110,140,141 Using such approaches, they delineated the influence of particle sizes, concentrations110,140,141 and confinement142 upon the self-assembly of block copolymer matrices and the arrangement of particles in such morphologies. A number of subsequent studies have extended such a framework to study similar issues in the context of other classes of multicomponent polymer systems.143,144
In the third category of studies, a DFT framework is employed for both the particles and polymers to study issues related to the phase behavior of such mixtures. Wu and coworkers used such an approach to study the dispersion of nanoparticles in block copolymer phases, while quantifying the effects of particle sizes, concentrations and surface energies.106,107 More recently, Feng and Chapman extended the interfacial statistical associating fluid theory to study the order–disorder transitions and concentration profiles in block copolymer–nanoparticle mixtures.109 Frischknecht, Mackay and coworkers have used such approaches in a series of articles to study the phase behavior of polymer–nanoparticle mixtures near substrates. They modeled both the nanoparticles and the polymer segments as hard spheres, and used a density functional that is based on the fundamental measure theory of hard sphere liquids while enforcing the bonding constraints. Using such a framework they predicted (in agreement with experiments) the presence of a first order transition in which the particles segregate to the surface by expelling the polymers.105,108,145
In sum, it is evident from the above discussion that the combination of DFT and SCFT approaches has led to significant advances in the understanding of the interaction and phase behavioral characteristics of polymer–nanoparticle mixtures. Such theories have been extended to multicomponent polymeric systems and the structural outcomes have been used in property prediction tools to characterize the influence of morphologies on the optical and mechanical properties.146,147 Possible next steps in this context should address similar issues in the context of anisotropic particles and/or multicomponent polymers possessing more complicated conformational characteristics.135 While pioneering early work of Balazs and coworkers did consider the phase behavior of anisotropic particles mixed with polymers, their model was based on the combined SCFT + DFT approach.148,149 Extensions of the more rigorous hybrid modeling and/or DFT approaches have not been accomplished. In such systems interplay of liquid crystalline ordering and block copolymer phase behavior is expected to lead to rich morphological characteristics. In a similar light, consideration of the phase behavior of nanoparticles mixed with polymeric systems such as rod–coil copolymers, graft copolymers etc. is also expected to suggest new directions for manipulation of nanoparticle assemblies.
B. Simulations
With regard to the structure of a polymer matrix in the vicinity of a single filler, Rissanou and Harmandaris have used atomistic simulations to characterize the interface in graphene–poly(methyl-methacrylate) (PMMA) nanocomposites.152 Upon comparing the density, structure and dynamics of the polymer chains in the bulk and at varying distances from the graphene layer, they found a strong effect of graphene layers on the polymer properties. For example, they found that the density of PMMA polymer chains close to graphene layers up to distances of about 1.0–1.5 nm is larger than that of the bulk PMMA chains. Additionally, the chain conformations were perturbed for distances up to about 2–3 radii of gyration from graphene, with the segmental dynamics of PMMA chains being much slower when the chains were within 2–3 nm of the graphene surface. Pandey and Doxastakis have applied preferential sampling techniques and connectivity-altering Monte Carlo algorithms along with detailed atomistic models of polyethylene and realistic structures for silica surfaces and fullerene particles to understand the conformations of the chains in a polyethylene melt near a surface and a highly curved nanoparticle.153 They found that when particles have sizes comparable to the Kuhn length of the polymer, formation of long trains is disfavored and it competes with the enthalpic interactions gained by forming polymer layers around the particles. They also state that a more accurate description of polymer rigidity at these small lengths is necessary to capture these competitions correctly. Kuppa et al. have used atomistic simulations to investigate the structure and morphology of poly(ethylene oxide) (PEO) chains confined in 1 nm slit pores defined by montmorillonite silicate layers.154 They found that the PEO chains are more disordered within these montmorillonite silicate layers than they are in the bulk, in agreement with experimental observations. A similar study by Lay et al. used atomistic simulations to study polymer aqueous solution (one poly-vinyl alcohol, PVA, chain in water) between two SiO2 surfaces.155 They found that the mobility of the system components decreased with increasing drying, i.e. increasing polymer to water ratio, due to the increased portion of the hydrogen bonded water molecules.
Going beyond the single/dilute filler limit, Lin and Khare have presented an efficient method involving simulated annealing and mimicking polymerization to create atomistically detailed model structures of cross-linked polymer nanocomposites, specifically cross-linked epoxy–POSS (i.e., polyhedral oligomeric silsesquioxane) nanocomposite.156 Using these atomistic models they found that incorporation of POSS fillers (at 5 wt%) in the cross-linked epoxy matrix leads to a weak lowering of the coefficient of volume thermal expansion without any significant change to the glass transition temperature. Yani and Lamm have also used atomistic molecular dynamics to study POSS molecules blended with a polyimide (PI) polymer chain, in particular two types of POSS molecules, (i) POSS with hydrogen functional groups (OHS) and (ii) POSS with aminophenyl functional groups (OAPS), to understand how the morphology within the composite varies with increasing POSS loading and POSS functionalization.157 They found that adding OAPS into the PI matrix showed an increase in the glass transition temperatures, while adding OHS into the PI matrix showed a decrease in the glass transition temperature. Also, they found that OHS molecules displayed a higher order compared to the OAPS molecules in the nanocomposite, and the PI chains packed more efficiently around OHS than around OAPS.
Using atomistic simulations, Scocchi et al. have estimated the interaction parameters for a coarse-grained nylon-6–clay composite system for use in dissipative particle dynamics (DPD) simulations (discussed in more detail in the next section).158 They mapped the corresponding coarse-grained simulation's energy values to those from atomistic molecular dynamics simulations. Using these atomistically based interaction parameters, the structural information of nylon-6–MMT composite obtained from the mesoscale DPD simulations showed excellent agreement with experimental observations. Other coarse-grained approaches are discussed in detail in the next section.
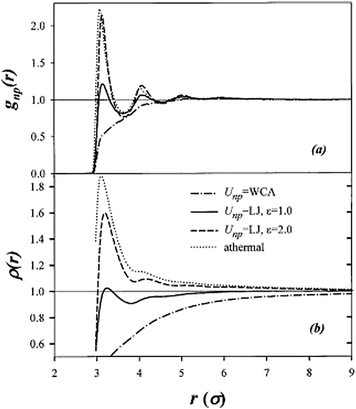
Molecular dynamics simulations have been extensively used in studying the equilibrium (and more often, the dynamical) characteristics of polymer–nanoparticle mixtures. Starr, Schroder and Glotzer performed one of the first such studies in which they used a bead–spring model of the polymer containing an icosahedral shaped particle to examine the polymer structuring and its influence on the dynamics of polymer segments near nanoparticle surfaces.159,160 They found a gradual change of the polymer dynamics in the vicinity of the nanoparticle surface, with the magnitude of change being correlated with the strength of interaction between the nanoparticle and polymer monomers. In a later study, they extended the model to study the structure of the nanoparticles in quiescent and steady shear conditions.161 They observed particle aggregation driven by the influence of polymer–particle interactions, and quantified the clustering characteristics and the influence of such aggregates upon the macroscopic rheology. A similar model, albeit involving spherical nanoparticles, was used by Smith and coworkers to study the matrix-induced effective interactions between the nanoparticles.162 They observed that when the polymer–nanoparticle interactions were relatively weak (see Fig. 2), the polymer matrix promoted nanoparticle aggregation (akin to the depletion effects discussed earlier), whereas, attractive nanoparticle–polymer interactions led to strong adsorption of the polymer chains on the surface of the nanoparticles and promoted dispersion of the nanoparticles. A number of studies that followed have used variants of such models to study the dispersion characteristics of polymer–nanoparticle mixtures, the interfacial characteristics of polymer layers around the particles and the specific influence of polymer–particle interaction energies.163–165 In other contexts, the model of spherical nanoparticles in a bead–spring polymer melt has also been used to study the polymer chain diffusion processes in polymer nanocomposites,166,167 the origins underlying the mechanical properties of polymer nanocomposites,168–173 and the influence of multibody effective interactions upon the structure of polymer–nanoparticle mixtures.174
Alternative approaches using dissipative particle dynamics methodology have also proven popular for studying the morphology and properties of polymer–nanoparticle mixtures.175,176 Such methodologies typically use a softer interaction potential (relative to Lennard-Jones potentials) between the polymer monomers, and hence have been able to study longer time scale processes.177,178 Moreover, by appropriate choice of dissipative forces, such methodologies can also be adapted to conserve momentum and study hydrodynamical phenomena. For instance, Pryamitsyn and Ganesan used such simulations to study the dynamical properties of polymer–nanoparticle mixtures and demonstrated that the polymer–particle interactions play an important role in modulating the polymer dynamics and as a consequence the macroscopic rheology of the mixture.175,176 In a follow-up study, they used such a methodology to identify the breakdown of continuum theories for diffusivity and viscosity of suspensions.179
Both MD and DPD simulation approaches have also proven especially popular for studying the self-assembly and organization of nanoparticles in multicomponent systems such as block copolymers and polymer blends. MD simulations of Schultz, Genzer and Hall presented results for the organization of nanoparticles in lamellar phases of block copolymers.180 They presented phase diagrams for composites containing nanoparticles of various sizes and interactions. They also identified the concentration profiles perpendicular to the lamellar interface, and in this manner identified the critical role played by the size of the nanoparticles relative to the block copolymer. Skenpnek et al. used MD to study the phase diagram of block copolymer–nanoparticle systems wherein the end group of the block copolymers was functionalized to have an affinity to the nanoparticles.181 Using MD simulations they identified a range of self-assembled morphological phases. Pryamitsyn and Ganesan used the DPD simulation approach and supporting scaling arguments to rationalize the organization of nanoparticles within the lamellar phases of the block copolymer as a function of the block copolymer–nanoparticle interactions and the size of the nanoparticle. Their work also identified the possibility of formation of bicontinuous phases in such systems which was verified in later experimental studies.182 A number of studies which have followed later have used the DPD simulation approach to study the influence of shear,183–185 finite concentration of particles,186 asymmetry and anisotropy of the nanoparticles in their organization within block copolymers.187–189
In comparison to MD (and DPD) simulations, Monte Carlo simulation approaches have found much less use to study the properties of mixtures of nanoparticles with homopolymer and diblock copolymer systems. Mainly, the difficulties inherent in attempting moves involving nanoparticles (due to the exclusion of polymer segments) have rendered MC simulations to be applied primarily to problems in which the nanoparticles can be envisioned to be stationary.190 Vacatello performed one of the first such simulations examining the structure of polymer chains in a system containing nanoparticle fillers. His simulations indicated that the polymer units were arranged in densely packed and ordered shells analogous to those found near planar solid surfaces.191–194 In a later work, he examined the influence of nanoparticles on chain dimensions to demonstrate that addition of nanoparticles can cause modest swelling of the polymer chains.195 A similarly motivated study was also conducted by Kumar and coworkers to identify the statistics of polymer conformations in nanoparticle systems and concluded that nanoparticles do not affect the equilibrium melt chain conformations.196
Seeking to quantify the interaction characteristics of nanoparticles in polymer systems, Marla and Meredith used an expanded ensemble MC simulation approach to study the colloid chemical potentials and polymer adsorption on nanocolloids dispersed in a freely adsorbing polymer solution.197,198 An important outcome of their work was the demonstration that the polymer adsorption behavior dominated the polymer chain length dependence of the chemical potential of the colloids, which suggested a mechanism to explain the stability of nanoparticles in adsorbing polymer solutions. Zhang and Archer used off-lattice MC simulations to study the interactions between long polymer chains and strongly adsorbing colloidal particles of comparable size to the polymer coils.199 They calculated the polymer–particle interactions and identified contributions arising from chain density fluctuations and polymer confinement. They predicted that at thermodynamic equilibrium, particle aggregation and polymer–particle network are formed around a volume fraction of 10%. More recently, Binder and coworkers developed a methodology to study the insertion free energy of nanoparticles in polymer brushes.200 Using such an approach they demonstrated that the forces exerted on the particle by the brush depend on the proximity of the particle to the grafted substrate.
De Pablo and coworkers have developed a number of MC techniques to study the structure and properties of polymer–nanoparticle mixtures.201,202 In an early work, they incorporated nanoparticles in polymer melts and studied the dependence of the mechanical properties as a function of the polymer–nanoparticle interactions.169 More recently, they have proposed an approach similar to particle-to-mesh schemes, in which the particles were explicitly present in the simulations but represented through density fields on grid points.203,204 Polymer beads were also represented in a density field representation for the characterization of their interactions. Using such an approach they demonstrated that MC simulations could be executed in which both the particles and polymers can be equilibrated simultaneously. They applied such a methodology to study the equilibrium characteristics of homopolymers and block copolymers mixed with nanoparticles.
Finally, we note that Bolhuis, Louis, Hansen and coworkers have developed a “soft-particle” approach to polymer–nanoparticle mixtures which enables one to study the structure and phase behavior of such systems.205–207 In such a framework, the polymers are coarse-grained to a soft particle which possesses a single degree of freedom. By developing effective interaction potentials between such soft polymer units, and between the polymer unit and the particle, they have studied the dependence of the resulting phase behavior on the nanoparticle sizes, polymer excluded volume interactions, etc. While such an approach has proven to be extremely useful, nevertheless, such a framework is limited to lower ranges of polymer concentrations for which the polymer can be envisioned as non-overlapping individual units.
In summary, coarse-grained simulation tools have played an important role in advancing our understanding of the characteristics of polymer–nanoparticle mixtures. Such tools, especially MD approaches, have served to fill an important void in the context of the earlier discussed approaches, viz., the treatment of nonequilibrium phenomena. Not surprisingly, there is presently intense effort in developing methodologies which can link the parameters underlying such approaches to more fine scale, atomistic and united atom descriptions of the system.208 Successful development of such approaches will lead to truly multiscale simulations of equilibrium and non-equilibrium properties of polymer–nanoparticle mixtures.
III. Grafted particles
Modification of the surface of nanoparticle fillers by functionalization with polymers or organic ligands has emerged as a popular strategy for controlling the inter-particle interactions and dispersion in polymeric solutions and melts. In this section, we review the many recent theory and simulation efforts that have focused on understanding the effect of the grafted polymer chemistry, molecular weight, grafting density, matrix polymer chemistry and molecular weights on the effective interactions between the polymer grafted particles in the polymer matrix, and the resulting morphology of composites with polymer grafted nanoparticle fillers.A. Theory (SCFT, DFT and PRISM approaches)
A number of early studies in the context of grafted particles considered the structure and interactions between polymer grafted flat surfaces dispersed in polymer melts and solutions. The first studies in this regard were pioneered by deGennes and Alexander in which they used scaling arguments to identify the density profile of the graft chain monomers, the effective interactions between the surfaces as a function of the grafting density, solvent quality etc.8,209 Subsequently, strong stretching theory based calculations of Semenov,210 Milner–Witten–Cates,211 Borisov and coworkers212 helped formalize the scaling theory ideas and also identified quantitatively accurate expressions for the effective interactions between surfaces, the influence of molecular weight polydispersity etc. More recently, researchers have used polymer self-consistent theory213–215 and density functional theory216,217 to address quantitative aspects of grafted polymer layers including regimes which are beyond the range of applicability of strong stretching theories. A number of excellent reviews have presented a comprehensive summary of these early studies.218–220When the grafted surfaces are present in a polymer melt medium, the simplest model system which has attracted the most attention from both an experimental and theoretical perspective is one where the grafted polymer is chemically identical to the matrix polymer (termed the “autophobic” case), and as a consequence, there are no enthalpic interactions. In such cases, the polymer-mediated interactions arise primarily from the entropic effects pertaining to the grafted polymer and the matrix chains. Much of the theoretical developments in this area have grown out of the descriptions of the wetting and dewetting of polymer melts on polymer brushes advanced by Leibler and coworkers.221,222 Explicitly, using scaling ideas and strong segregation theory calculations they delineated the parameters for which the matrix chains completely penetrate the brush, termed as the “wetting” case, and the regimes for which matrix chains are either expelled or penetrate only a finite zone into the grafting layer, termed as the “dewetting” and “partial wetting” cases, respectively.222 Situations corresponding to the wetting regime constitute a favorable interaction between the polymer melt and the grafted surface, and hence promote dispersion of the grafted surfaces. In contrast, the dewetting regime is likened to a situation of unfavorable interactions between the matrix and the surface, and thereby promotes aggregation of the surfaces. The occurrence of wetting and dewetting regimes themselves was predicted to depend on the degree of polymerization of the grafted chains (Ngraft), the chain grafting density (σ, expressed as the number of grafted chains per unit area) and the degree of polymerization (Nmatrix) of the free host chains. For the situation of flat surfaces, when 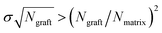 dewetting of the matrix chains was predicted. In other words, situations involving short matrix polymers and/or sparsely grafted polymer ligands are expected to be more conducive to wetting. Subsequent studies by Matsen and others have used SCFT to quantify the polymer brush structure, interfacial energies and the effective interactions between grafted surfaces immersed in polymer melts.223,224 Such studies confirmed the validity of the qualitative features of the ideas advanced by Leibler and coworkers, but have also identified quantitatively important corrections not captured by scaling theories. Similar results were also predicted by Chapman, and by Wu and coworkers by the use of DFT approaches.225–227
dewetting of the matrix chains was predicted. In other words, situations involving short matrix polymers and/or sparsely grafted polymer ligands are expected to be more conducive to wetting. Subsequent studies by Matsen and others have used SCFT to quantify the polymer brush structure, interfacial energies and the effective interactions between grafted surfaces immersed in polymer melts.223,224 Such studies confirmed the validity of the qualitative features of the ideas advanced by Leibler and coworkers, but have also identified quantitatively important corrections not captured by scaling theories. Similar results were also predicted by Chapman, and by Wu and coworkers by the use of DFT approaches.225–227
In contrast to the extensive number of articles which have reported studies of the case wherein the chemical identities of the polymer melt and the grafts are the same, far fewer studies exist for the situation in which the polymer melt and grafts are of differing chemical identities. In a seminal article, Leibler and Borukhov used scaling theories to examine the case in which there are favorable interactions between the grafted polymer and the polymer matrix.228,229 They demonstrated that such situations lead to a considerable expansion of the parameter space promoting dispersion of the surfaces. Another scaling based study of Ryu, Ganesan and coworkers considered the case in which the matrix polymers exhibit unfavorable interactions with the grafts.230 Their results indicated a dominance of the entropic effects and that the behavior predicted for autophobic regimes persists even up to very large molecular weights of the brush polymer. In a more recent study, Ganesan and coworkers studied the interfacial properties of random copolymer brushes in a matrix of homopolymers.231 In such a context, they demonstrated that the brush may rearrange its segments so as to promote favorable interactions with the matrix and thereby achieve much lower interfacial energies than may be anticipated based on the composition of the polymer brush.
Most of the above-discussed studies were based on results obtained by considering the behavior of flat grafted surfaces. Early studies used the Derjaguin approximation to extrapolate such findings to curved surfaces and derived results pertinent to large, colloidal scale particles.6 However, such approximations are limited in the range of curvatures over which they can be applied, and fail to account for the structural effects which manifest in highly curved systems such as nanoparticles, nanorods, etc. To address such a limitation, a number of recent studies have used density functional theories, SCFT approaches and PRISM theories to tackle the particle curvature effects in a much more direct manner. Below, we briefly review some of these studies which are specific to the context of spherical nanoparticles.
When polymers are grafted on a curved surface at a high grafting density, the curved surface provides more volume for the grafted monomers than flat surfaces and alleviates the crowding and packing frustration in a densely grafted polymer brush. As a consequence, the interactions between particles are in general expected to become weakened with an increase in the curvature of the grafting surface. In separate studies, Matsen and Kim, and Roan accurately accounted for the effects of curvature within self-consistent field theories to study the interaction between two brush coated spheres in a good solvent.232,233 Their studies confirmed the purely repulsive nature of such interactions and also suggested that the intensity of such interactions becomes weaker with increasing particle curvature.232,234 A follow-up study by Trombly and Ganesan studied the interactions between a grafted nanoparticle and a bare particle (of differing sizes), and quantified the resulting interaction energies as a function of the radii of the grafted and bare particles.235 They also found a universal scaling law for the interaction potential which exhibited a power-law dependence on both particle sizes, a linear dependence on grafting density, and a logarithmic dependence on interparticle distance with an interaction range that scaled with the brush height. More recently, Egorov and coworkers used both SCFT and DFT approaches to study the influence of solvent quality effects on the interactions between grafted particles in solvents.234,236–238 Their results suggested that richer interparticle interaction characteristics which include both attractions and repulsions can manifest depending on the solvent quality.
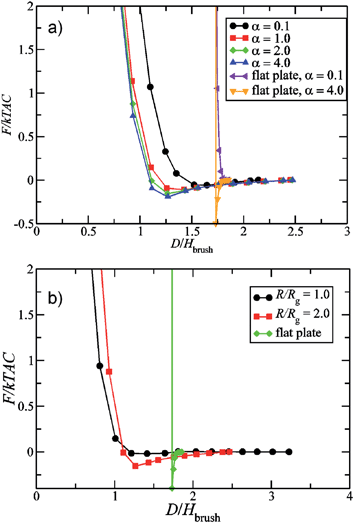
When the brush coated nanoparticles are placed in a melt of free homopolymer chains, the chemistry of the free and grafted polymers and ratio of the molecular weights of the free and grafted polymer govern the effective interparticle interactions. Recent SCFT studies for grafted nanoparticles in polymer melts of the same chemical identity have examined in more detail the effects of particle size and grafting density upon the interparticle interactions.239,240 The results of such studies suggest that the considerations deduced from the results for polymers grafted on flat plates are still qualitatively applicable. Overall, such studies have confirmed that the interactions between grafted nanoparticles are purely repulsive in a polymer melt of sufficiently low molecular weight (relative to the graft MW). In contrast, for the case when the polymer melt MW is sufficiently large, the potential of mean force between two grafted particles is repulsive at short separations and weakly attractive at intermediate separations. This weak mid-range attraction is due to a depletion-like effect where the free homopolymers in the solution are excluded from interacting polymer brushes on the particles. There is a depletion of free homopolymer chains in between two grafted particles due to the associated conformational entropy losses of the free chains and the stretching energy entailed by the brush chains in the penetration by the matrix chains. Interestingly, the MW ratios which characterize the boundary between the purely repulsive case and the repulsive–attractive cases are dependent on the size of the nanoparticle in addition to the grafting densities. For smaller particles the effective particle interaction is always repulsive. Increasing the particle size at a fixed grafting density has an effect which is similar to that of increasing the grafting density itself and leads to an attractive interaction for some ranges of matrix MW and grafting densities (see Fig. 3).
A number of recent studies have examined the implications of the above results for the dispersion and stability of polymer–nanoparticle mixtures. In one of the early mean field theory studies, Harton and Kumar used simple mean-field considerations to suggest that dispersion is achieved when the molecular weight of the matrix polymer < κ times the grafted polymer molecular weight, where the factor κ scales with the particle radius R as κ ∼ R−0.35 for brushes on small spherical particles.241 Subsequent experimental studies and supporting theoretical calculations suggested a much richer morphological behavior in which the polymer grafted particles aggregated into a variety of cluster morphologies as a function of the ratio of grafted polymer molecular weight to matrix polymer molecular weight (Ngraft/Nmatrix) and grafting densities (σ).242,243 These cluster morphologies were argued to result as a consequence of the competition between the brush entropic effects arising from the aggregation of many particles on the one hand and the direct van der Waals interactions on the other hand. Spherical aggregates were observed at low values of Ngraft/Nmatrix and σ, connected sheets and string shaped aggregates at intermediate values of Ngraft/Nmatrix and σ, and a dispersed morphology results at large σ.
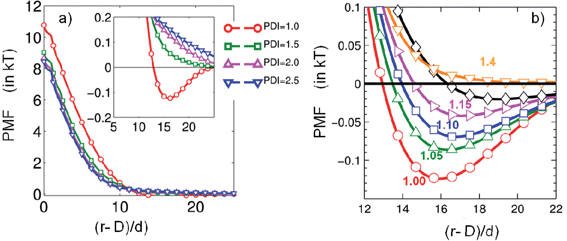
While the studies discussed so far were at the monodisperse molecular weight (graft and matrix) limit, Jayaraman and coworkers have used self-consistent PRISM–MC approaches to elucidate the effect of bidisperse and polydisperse distribution of graft molecular weights on the effective interactions of polymer grafted particles in a chemically identical polymer matrix.75,77,78 For the bidisperse graft lengths, the potential of mean force (PMF) between two grafted particles in a polymer matrix suggested two regimes: the shorter grafts dictate the value of the PMF at contact and at small inter-particle distances, while longer grafts dictate the long-range characteristics of the PMF. This is expected since earlier work on monodisperse grafted particles has shown that the length of the repulsive tail in the PMF is dependent on the graft length.63 However, more interestingly, at intermediate inter-particle distances the presence of bidispersity in grafts, i.e. short and long chains, eliminates the mild-attractive well seen for monodisperse short chains. Similarly, they also found that a polydisperse MW distribution of grafted polymer also weakened the attractive well at intermediate inter-particle distances, completely eliminating the attractive well at intermediate inter-particle distances at some critical polydispersity index (PDI)77,78 (see Fig. 4). The elimination of the mid-range attractive well is due to (a) the longer grafts in the polydisperse graft length distribution that introduce longer range steric repulsion, and (b) reduced monomer crowding in the grafted layer brought about by the polydisperse graft lengths that improves the wetting of the grafted layer by matrix chains. These recent theoretical predictions suggest that polydispersity in graft length can be used to stabilize dispersions of grafted nanoparticles in a polymer matrix at conditions where monodisperse grafts would cause aggregation. In agreement with these predictions, recent experiments by Rungta et al. with a polystyrene matrix and silica particles with a bidisperse polystyrene grafts (synthesized using step-by-step RAFT polymerization) found better dispersion as compared to silica particles with monodisperse polymer grafts of comparable length.244
Most of the above-discussed studies pertain to the situation in which the polymers are grafted on particles at moderate to high grafting densities corresponding to the brush regime. The other limit, corresponding to the case of low grafting densities, has been studied extensively by Jayaraman and Schweizer through PRISM theories.60,61 Such studies have predicted strong concentration fluctuations indicative of aggregate formation and/or a tendency for microphase separation as the nanoparticle attraction strength increases at 100% filler fraction. Melts and dense solutions of ∼2 to 5 nm spherical nanoparticles with one, two and four polymer grafts (no matrix) are expected to display a system-specific power law dependence of the microphase spinodal temperature on packing fraction. Jayaraman and Schweizer observed good agreement between the microphase spinodal curve for particles with one polymer graft with the order–disorder transition curve seen in large scale simulations by Glotzer and coworkers.60,61,245,246 When mixed with a melt or a dense solution of polymers, these lightly grafted particles exhibit behavior distinctly different from the densely grafted particles. The matrix molecular weight has a minimal effect on the potential of mean force (PMF) between the grafted particles, and instead the PMF is more sensitive to the amount of particle surface that remains exposed or unshielded by the grafted polymers.
Moving beyond homopolymer grafts, Nair and Jayaraman used the self-consistent PRISM–MC approach to study AB copolymer-grafted spherical nanoparticles at low grafting density (with the copolymer chains grafted on the particle through A monomer) placed in the A or B homopolymer matrix.74 They calculated the potential of mean force (PMF) between copolymer-grafted nanoparticles in a homopolymer matrix, at low grafting density, as a function of monomer sequence (alternating versus diblock) in the grafted chain, molecular weight of the grafted and matrix chains, particle size, matrix packing fraction (dense polymer solutions to melts) and monomer attractions. They found that the PMF between two alternating AB copolymer grafted particles in a homopolymer matrix was insensitive to the chemistry of the homopolymer matrix (A- or B-homopolymer) in the case of a weak A–B χ parameter, and behaved similar to homopolymer grafted particles in a chemically similar homopolymer matrix. In contrast, the shape of the PMF of two AB diblock copolymer grafted particles in a homopolymer matrix changed with matrix chemistry; the different shapes of the PMF suggest that AB diblock copolymer grafted particles would display different morphologies in A and B homopolymer matrices.
In summary, the above discussion highlights the extensive theoretical developments that have accompanied the understanding of interactions between polymer grafted spherical nanoparticles in polymer solutions and melts. In contrast however, far fewer theoretical studies exist regarding the phase behavior of such systems (except for some isolated examples) and/or the organization of grafted nanoparticles in multicomponent polymer matrices.127 We note that the latter topic has emerged as an important consideration for applications aiming to template the self-assembly of block copolymers by using grafted nanoparticles and/or for directing the assembly of block copolymers by the addition of suitably functionalized nanoparticles. The overall self-assembly in such systems is expected to depend on an intricate interplay of brush conformations and enthalpic effects within self-assembled phases. The only work we are aware of in this context is that of Matsen and Kim in which they studied the organization of nanoparticles grafted with a mixture of A and B chains dispersed in the lamellar phase of block copolymers.247 By numerically solving the SCFT equations using a multi-coordinate system algorithm they identified the parameters controlling the segregation of the nanoparticles into the different regions of the lamellar phase. Further developments along these lines can be expected to emerge as an important direction of future research.
In the context of non-spherical particles, much of the work has focused on the situation of grafted rod-like nanoparticles. Frischknecht used density functional theory to model the interactions between end adsorbed polymer coated nanorods in a polymer melt of identical chemistry.248 End adsorbed polymers (polymers with sticky ends adsorbing on the nanorod surface) differ from permanently grafted polymers because the end adsorbed polymers are in equilibrium with the polymers in the bulk. The PMF between end adsorbed nanorods was found to be purely repulsive when the matrix polymer length is equal to the end adsorbed polymer length. For longer matrix polymers, nanorods were found to exhibit strong repulsion at short interparticle separations, and a weak attraction at intermediate separations due to the entropically caused dewetting of the polymer brush by the matrix polymer. The depth of the attractive well increased with surface coverage and matrix polymer length.
In a more recent study, Frischknecht and coworkers used DFT and SCFT to study the interactions between polymer grafted nanorods (NR) in a polymer melt as a function of molecular weights of the polymer and graft.249 Both theories predicted a gradual transition from a “wet” to a “dry” brush as the grafting density, the nanorod radius, and/or the ratio of matrix to brush chain lengths are increased. DFT calculations of the interaction free energy between two NRs found an attractive well at intermediate NR separations, with a repulsive barrier at closer separations. The strength of the attraction was found to increase as the brushes became more dewetted. By including the van der Waals attractions between the NRs they predicted at which values of the system parameters the NRs are dispersed or aggregated, and demonstrated good agreement with experimental observations of dispersed and aggregated nanorods. Another study by Hore and Composto considered the density profiles of a miscible polymer blend in contact with a nanorod.250 They demonstrated that a partitioning of the matrix chains occurs within the brush, which modulates the interactions of the grafted particle with the polymer matrix.
Only few studies have considered the interaction between other models of anisotropically shaped objects and the influence of polymer grafts. For instance, Yang and co-workers used a 2D version of SCFT to study the interactions between two polymer grafted nanosheets immersed in a polymer melt.251 Their results point to the length of the clay sheet being an important parameter for controlling inter-particle interactions. At constant grafting density, when the length of the clay sheet is much greater than the radius of gyration of grafted length the effective interaction was found to be repulsive at small inter-sheet separations and attractive at intermediate separations. When the length of the clay sheet was much smaller than the radius of gyration of grafted length the effective interaction was found to be repulsive at all distances.
B. Simulations
Smith et al. have conducted atomistic MD simulations of poly(dimethylsiloxane) (PDMS) melts with bare silica and hydroxyl and trimethylsiloxy groups modified silica surfaces using a quantum chemistry-based force field.256 In addition to matching some of the structures obtained by neutron scattering experiments, they found the density of PDMS near the bare silica surface to be much greater, and the dynamics of interfacial PDMS much slower than that observed for unperturbed PDMS melts. They attributed such results to the strong van der Waals dispersion forces between PDMS and the silica surface. The presence of hydroxyl and trimethylsiloxy groups on the silica surface resulted in a decrease in the density of interfacial PDMS and a speedup in polymer dynamics relative to those observed for PDMS near the bare silica surface due to increased separation between PDMS and the silica surface and a corresponding decrease in the strength of the dispersion attraction between the polymer and the surface.
In summary, these atomistic simulations have provided detailed structural information and to some extent dynamical insight into polymer nanocomposites with polymer grafted particles. However, the computational intensity of these atomistically detailed simulations has limited the system sizes that have been investigated. With the speedups that are possible now with graphical processing units (GPUs) and molecular dynamics packages being developed for GPUs we anticipate that atomistically detailed studies will move to larger system sizes. This GPU based computing is discussed in more detail in the Future outlook section of this review.
Shen et al. also used coarse-grained simulations of multiple polymer grafted particles in an explicit matrix to show that in addition to the expectation that particles will aggregate when the matrix length is much greater than the graft length at high grafting density, there exists an optimum grafting density, σc, for observing dispersion of the grafted nanoparticles in the polymer matrix and that optimal grafting density scales with NmatrixK/NgraftL where K, L > 0, and Nmatrix and Ngraft are the length of the matrix and grafted chains respectively.261 Lin et al. have used DPD simulations to investigate the self-assembly of polymer grafted nanoparticles to study the effect of varying nanoparticle shape, from hexagonal nanoplatelets to nanorods.262 The assembly of these polymer grafted particles was studied in a small molecule and oligomeric, good and theta solvent. They found that in general the solvophilicity of the grafted particle increased with increasing number of polymer grafts and length of grafted polymers. They calculated the morphology of the assembled particles (e.g. strings, ribbons, fillets, or dispersed phase) as a function of the shape of the particle (or aspect ratio) and the solvophilicity of the grafted particles. They found that the matrix length, which ranged from 1 coarse-grained bead to 4 coarse-grained beads, did not affect the morphology of the assembled structure; however the sizes of aggregates were smaller with larger matrix lengths.
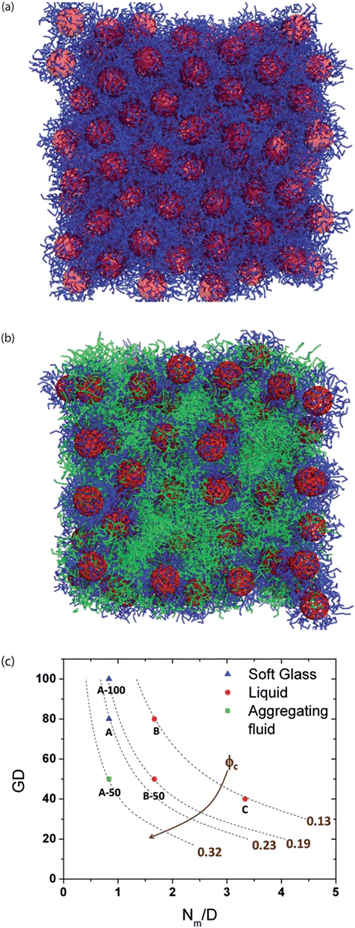
Chremos and Panagiotopolous have used coarse-grained MD simulations to study structural transitions within a system of polymer grafted nanoparticles in the absence of a matrix polymer or a solvent (melt-like conditions), at varying grafting density and varying particle size.263 At high grafting density, even with a sufficiently large core, they found that the behavior of polymer grafted particles was similar to star polymers, “where the thermal expansion of the corona traps the nanoparticles and a glassy behavior is observed.” In contrast, at low enough grafting density, the corona cannot prevent neighboring nanoparticles from aggregating, in agreement with prior theoretical studies. Goyal and Escobedo performed coarse-grained molecular dynamics simulations of polymer grafted nanoparticles in the absence and presence of a matrix consisting of a polymer melt to investigate how particle core concentration, polymer grafting density, and polymer length affected the particle mobility and viscous response.264 They carried out constant strain-rate simulations to calculate viscosities and constant-stress simulations to calculate yield stresses. They found that in the systems of polymer grafted nanoparticles the structural order and viscosity decrease and diffusivity increases with increasing length of the grafted chains for a given core concentration or grafting density. Depending on the combination of the grafting density and graft length employed, pure polymer grafted nanoparticles exhibited distinctive fluid behavior, as shown in Fig. 5.
In summary, it is clear from the above discussion that both atomistic and coarse-grained simulations have made considerable advances in studying the interactions and the structural details in the context of grafted nanoparticles in polymer melts. However, as a natural consequence of the computational effort required, most of these studies have been mostly restricted to the context of single and two particle systems. Future advances in this regard are likely to occur in the direction of the development of methodologies which can extend the computational frameworks to study the phase behavior and structural characteristics at a finite concentration of nanoparticles. Another potential direction is the use of computer simulation to study the interactions and phase behavior between anisotropically shaped objects in a polymer matrix.
IV. Future outlook
In the previous sections we reviewed some of the salient theoretical and simulation studies which have addressed the interactions and structure in polymer–nanoparticle mixtures. In some instances, these theory and simulation studies have served to elucidate the physical phenomena underlying the experimental observations, and in other instances, the theoretical predictions have led to new experimental efforts. In the conclusion of each sub-section, we also presented some perspective on potential future directions with the theme of the section. In this final section, we conclude by discussing few general aspects which are likely to witness increased activity in the near future.A. Effect of substrates
Most of the studies discussed in the previous sections related to the behavior of polymer–nanoparticle (grafted and ungrafted) mixtures in the limit of “bulk” systems, i.e. far from the influence of substrates and/or confinement. However, many of the recent technological developments in the context of polymer–nanoparticle mixtures involve systems which are either confined in nanoscale channels or near the substrate.51,142,145,265–268 In such contexts, the interactions between the nanoparticles and their structure are expected to be influenced by the presence of the substrate(s) in addition to the factors discussed earlier in the review. Despite the growing importance there has been only very limited work in addressing directly the role of surfaces and confinement in the interactions and phase behavior of polymer–nanoparticle mixtures.142,145 We anticipate that in the near future there is likely to be increased activity in developing methodologies and predictions pertinent to such situations.B. Capturing processing effects in simulations
With the exception of isolated instances, this review primarily dealt with the studies and developments related to the equilibrium aspects of polymer–nanoparticle mixtures. However, nonequilibrium effects resulting from filler aggregation and/or external fields (flow, electric fields) are important for many applications of PNCs, especially for situations involving anisotropic fillers. The time and length scales which can be probed through present-day computer simulations do not necessarily overlap with experimental regimes. Moreover, issues unique to PNCs, such as the anisotropy of the fillers, potentially long-ranged interparticle interactions (mediated by the polymers), and the dynamical and rheological response of the polymer matrix, do not have direct counterparts in the composites literature pertinent to micron sized and larger particles. Hence, there is a need for the development of appropriate theoretical models and computational frameworks which can enable the study of nonequilibrium issues as well as the influence of external fields on the structure and dispersion of nanoparticles in polymer matrices.C. Use of graphical processing units (GPUs) based molecular simulations
Most of the atomistic simulations and coarse-grained simulations presented in this review were conducted on high performance parallel central processing unit (CPU) machines, where the simulation length and time scale were limited by the computational intensity of the simulations on CPUs. The recent progress in graphics processing units (GPUs) and simultaneous development of molecular simulation algorithms designed for or adapted to run optimally on GPUs should allow molecular modelers to dream of “larger” and “longer” simulations of polymer nanocomposites than has been done so far.269 The release of both CUDA, a GPU programming toolkit that enables parallel execution of functions called ‘kernel’ on NVIDIA GPUs, and OpenCL, a multi-platform data-parallel programming interface for computing on GPUs, has enabled many molecular dynamics (MD) packages to incorporate GPU acceleration. MD simulations of polymers and polymer nanocomposites are perfect for implementation on GPUs due to their computational complexity and parallelism. While packages that were originally designed for studying macromolecular systems in parallel CPU implementation, like GROMACs150 and LAMMPs151 have now incorporated GPU compatibility, there are other new packages like HOOMD-blue270 that have been designed purely for GPU execution. With these developments, one is able to achieve significant speedup compared to the same simulations on CPUs in a variety of coarse-grained particle simulations that would have been impractical without access to enormous computational resources, as shown in a recent study.271 In addition to obtaining MD trajectories, data analysis of trajectories involving histograms can also be performed well on GPUs due to their inherent parallelism. For example, a recent paper shows how radial distribution function histogramming can be implemented on multiple NVIDIA GPUs allowing intensive data analysis on large trajectories to be conducted in seconds–few minutes.272 These new advances in GPU based packages are going to make studying polymer nanocomposites with atomistic or more detailed coarse-grained models, at experimentally relevant length scales and time scales, and at higher filler fractions tractable in the near future.Acknowledgements
The authors thank Dr Amalie Frischknecht for useful comments on a preprint. The authors are grateful to M. Ashtiani and T. B. Martin for their help with references and C. Estridge for help with TOC graphic. VG acknowledges financial support from Robert A. Welch Foundation (Grant F1599), National Science Foundation (DMR 1005739 and 1306844) and the US Army Research Office under grant W911NF-07-1-0268. AJ acknowledges financial support from Department of Energy (Grant DE-SC0003912).References
- A. Kelly, Composites in Context, Compos. Sci. Technol., 1985, 23, 171–199 CrossRef
.
- C. Cabane, K. Wong and R. Duplessix, Macromolecules for Control of Distances in Colloidal Dispersions, ACS Symp. Ser., 1989, 384, 312–327 CrossRef CAS
.
- E. Dickinson, Colloid science of mixed ingredients, Soft Matter, 2006, 2, 642–652 RSC
.
- E. Dickinson, Milk protein interfacial layers and the relationship to emulsion stability and rheology, Colloids Surf., B, 2001, 20, 197–210 CrossRef CAS PubMed
.
- J. M. Brader, Nonlinear rheology of colloidal dispersions, J. Phys.: Condens. Matter, 2010, 22, 363101 CrossRef CAS PubMed
.
- J. F. Joanny, L. Leibler and P. G. DeGennes, Effects of Polymer-Solutions on Colloid Stability, J. Polym. Sci., Part B: Polym. Phys., 1979, 17, 1073–1084 CrossRef CAS
.
- P. G. DeGennes, Polymer-Solutions Near an Interface .1. Adsorption and Depletion Layers, Macromolecules, 1981, 14, 1637–1644 CrossRef CAS
.
- P. G. Degennes, Conformations of polymers attached to an interface, Macromolecules, 1980, 13, 1069–1075 CrossRef CAS
.
- P. A. Pincus, C. J. Sandroff and T. A. Witten, Polymer Adsorption on Colloidal Particles, J. Phys., 1984, 45, 725–729 CAS
.
-
R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, New York, 1999 Search PubMed
.
- A. C. Balazs, T. Emrick and T. P. Russell, Nanoparticle–polymer composites: Where two small worlds meet, Science, 2006, 314, 1107–1110 CrossRef CAS PubMed
.
- R. Krishnamoorti and R. A. Vaia, Polymer nanocomposites, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 3252–3256 CrossRef CAS
.
- V. Ganesan, C. J. Ellison and V. Pryamitsyn, Mean-field models of structure and dispersion of polymer–nanoparticle mixtures, Soft Matter, 2010, 6, 4010–4025 RSC
.
- K. I. Winey and R. A. Vaia, Polymer nanocomposites, MRS Bull., 2007, 32, 314–319 CrossRef CAS
.
- A. J. Crosby and J. Y. Lee, Polymer nanocomposites: The “nano” effect on mechanical properties, Polym. Rev., 2007, 47, 217–229 CrossRef CAS
.
- R. Andrews and M. C. Weisenberger, Carbon nanotube polymer composites, Curr. Opin. Solid State Mater. Sci., 2004, 8, 31–37 CrossRef CAS
.
- P. J. Yoon, T. D. Fornes and D. R. Paul, Thermal expansion behavior of nylon 6 nanocomposites, Polymer, 2002, 43, 6727–6741 CrossRef CAS
.
- F. M. Du, J. E. Fischer and K. I. Winey, Effect of nanotube alignment on percolation conductivity in carbon nanotube/polymer composites, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 121404 CrossRef
.
- T. Erb, U. Zhokhavets, G. Gobsch, S. Raleva, B. Stuhn, P. Schilinsky, C. Waldauf and C. J. Brabec, Correlation between structural and optical properties of composite polymer/fullerene films for organic solar cells, Adv. Funct. Mater., 2005, 15, 1193–1196 CrossRef CAS
.
- M. Moniruzzaman and K. I. Winey, Polymer nanocomposites containing carbon nanotubes, Macromolecules, 2006, 39, 5194–5205 CrossRef CAS
.
- L. J. A. Koster, S. E. Shaheen and J. C. Hummelen, Pathways to a New Efficiency Regime for Organic Solar Cells, Adv. Energy Mater., 2012, 1246–1253 CrossRef CAS
.
- J. M. Kropka, K. W. Putz, V. Pryamitsyn, V. Ganesan and P. F. Green, Origin of dynamical properties in PMMA-C-60 nanocomposites, Macromolecules, 2007, 40, 5424–5432 CrossRef CAS
.
-
E. P. Giannelis, R. Krishnamoorti and E. Manias, Polymer–silicate nanocomposites: Model systems for confined polymers and polymer brushes, Polymers In Confined Environments, 1999, vol. 138, pp. 107–147 Search PubMed
.
- T. D. Fornes, P. J. Yoon, H. Keskkula and D. R. Paul, Nylon 6 nanocomposites: the effect of matrix molecular weight, Polymer, 2001, 42, 9929–9940 CrossRef CAS
.
- R. Krishnamoorti and K. Yurekli, Rheology of polymer layered silicate nanocomposites, Curr. Opin. Solid State Mater. Sci., 2001, 6, 464–470 CAS
.
- S. Takahashi, H. A. Goldberg, C. A. Feeney, D. P. Karim, M. Farrell, K. O'Leary and D. R. Paul, Gas barrier properties of butyl rubber/vermiculite nanocomposite coatings, Polymer, 2006, 47, 3083–3093 CrossRef CAS
.
- T. C. Merkel, B. D. Freeman, R. J. Spontak, Z. He, I. Pinnau, P. Meakin and A. J. Hill, Ultrapermeable, reverse-selective nanocomposite membranes, Science, 2002, 296, 519–522 CrossRef CAS PubMed
.
- N. Grossiord, J. Loos, O. Regev and C. E. Koning, Toolbox for dispersing carbon nanotubes into polymers to get conductive nanocomposites, Chem. Mater., 2006, 18, 1089–1099 CrossRef CAS
.
- M. R. Bockstaller, Y. Lapetnikov, S. Margel and E. L. Thomas, Size-selective organization of enthalpic compatibilized nanocrystals in ternary block copolymer/particle mixtures, J. Am. Chem. Soc., 2003, 125, 5276–5277 CrossRef CAS PubMed
.
- M. K. Gaines, S. D. Smith, J. Samseth, M. R. Bockstaller, R. B. Thompson, K. O. Rasmussen and R. J. Spontak, Nanoparticle-regulated phase behavior of ordered block copolymers, Soft Matter, 2008, 4, 1609–1612 RSC
.
- B. J. Kim, J. Bang, C. J. Hawker, J. J. Chiu, D. J. Pine, S. G. Jang, S. M. Yang and E. J. Kramer, Creating surfactant nanoparticles for block copolymer composites through surface chemistry, Langmuir, 2007, 23, 12693–12703 CrossRef CAS PubMed
.
- B. J. Kim, G. H. Fredrickson, C. J. Hawker and E. J. Kramer, Nanoparticle surfactants as a route to bicontinuous block copolymer morphologies, Langmuir, 2007, 23, 7804–7809 CrossRef CAS PubMed
.
- I. Lynch, S. Cornen and L. Piculell, Investigation of the segregative phase separation induced by addition of polystyrene to AOT oil-continuous microemulsions, J. Phys. Chem. B, 2004, 108, 5443–5452 CrossRef CAS
.
- M. E. Mackay, A. Tuteja, P. M. Duxbury, C. J. Hawker, B. Van Horn, Z. B. Guan, G. H. Chen and R. S. Krishnan, General strategies for nanoparticle dispersion, Science, 2006, 311, 1740–1743 CrossRef CAS PubMed
.
- Q. Zhang and L. A. Archer, Poly(ethylene oxide)/silica nanocomposites: Structure and rheology, Langmuir, 2002, 18, 10435–10442 CrossRef CAS
.
- M. Surve, V. Pryamitsyn and V. Ganesan, Polymer-bridged gels of nanoparticles in solutions of adsorbing polymers, J. Chem. Phys., 2006, 125, 064903 CrossRef PubMed
.
- M. Surve, V. Pryamitsyn and V. Ganesan, Depletion and pair interactions of proteins in polymer solutions, J. Chem. Phys., 2005, 122, 154901 CrossRef PubMed
.
- G. F. Schneider and G. Decher, From “Nano-bags” to “Micro-pouches”. Understanding and Tweaking Flocculation-based Processes for the Preparation of New Nanoparticle-Composites, Nano Lett., 2008, 8, 3598–3604 CrossRef CAS PubMed
.
- M. Kamibayashi, H. Ogura and Y. Otsubo, Shear-thickening flow of nanoparticle suspensions flocculated by polymer bridging, J. Colloid Interface Sci., 2008, 321, 294–301 CrossRef CAS PubMed
.
- S. Srivastava, P. Agarwal and L. A. Archer, Tethered Nanoparticle–Polymer Composites: Phase Stability and Curvature, Langmuir, 2012, 28, 6276–6281 CrossRef CAS PubMed
.
- S. Sen, Y. Xie, S. K. Kumar, H. Yang, A. Bansal, D. L. Ho, L. Hall, J. B. Hooper and K. S. Schweizer, Chain conformations and bound-layer correlations in polymer nanocomposites, Phys. Rev. Lett., 2007, 98, 128302 CrossRef PubMed
.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho, B. Van Horn, H. C. Kim and C. J. Hawker, Nanoscale effects leading to non-Einstein-like decrease in viscosity, Nat. Mater., 2003, 2, 762–766 CrossRef CAS PubMed
.
- K. Nusser, G. J. Schneider, W. Pyckhout-Hintzen and D. Richter, Viscosity Decrease and Reinforcement in Polymer–Silsesquioxane Composites, Macromolecules, 2011, 44, 7820–7830 CrossRef CAS
.
- U. Yamamoto and K. S. Schweizer, Theory of nanoparticle diffusion in unentangled and entangled polymer melts, J. Chem. Phys., 2011, 135, 224902 CrossRef PubMed
.
- A. Tuteja, M. E. Mackay, S. Narayanan, S. Asokan and M. S. Wong, Breakdown of the continuum Stokes–Einstein relation for nanoparticle diffusion, Nano Lett., 2007, 7, 1276–1281 CrossRef CAS PubMed
.
- A. Tuteja, P. M. Duxbury and M. E. Mackay, Polymer chain swelling induced by dispersed nanoparticles, Phys. Rev. Lett., 2008, 100, 077801 CrossRef PubMed
.
- S. Y. Kim and C. F. Zukoski, Super- and sub-Einstein intrinsic viscosities of spherical nanoparticles in concentrated low molecular weight polymer solutions, Soft Matter, 2012, 8, 1801–1810 RSC
.
- I. Kohli and A. Mukhopadhyay, Diffusion of Nanoparticles in Semidilute Polymer Solutions: Effect of Different Length Scales, Macromolecules, 2012, 45, 6143–6149 CrossRef CAS
.
- J. T. Kalathi, G. S. Grest and S. K. Kumar, Universal Viscosity Behavior of Polymer Nanocomposites, Phys. Rev. Lett., 2012, 109, 198301 CrossRef PubMed
.
- S. K. Kumar and R. Krishnamoorthi, Nanocomposites: Structure, Phase Behavior, and Properties, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 37–58 CrossRef CAS PubMed
.
- S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Nanocomposites with Polymer Grafted Nanoparticles, Macromolecules, 2013, 46, 3199–3214 CrossRef CAS
.
- P. F. Green, The structure of chain end-grafted nanoparticle/homopolymer nanocomposites, Soft Matter, 2011, 7, 7914–7926 RSC
.
- L. M. Hall, A. Jayaraman and K. S. Schweizer, Molecular theories of polymer nanocomposites, Curr. Opin. Solid State Mater. Sci., 2010, 14, 38–48 CrossRef CAS
.
- J. B. Hooper and K. S. Schweizer, Contact aggregation, bridging, and steric stabilization in dense polymer–particle mixtures, Macromolecules, 2005, 38, 8858–8869 CrossRef CAS
.
- J. B. Hooper and K. S. Schweizer, Theory of phase separation in polymer nanocomposites, Macromolecules, 2006, 39, 5133–5142 CrossRef CAS
.
- J. B. Hooper, K. S. Schweizer, T. G. Desai, R. Koshy and P. Keblinski, Structure, surface excess and effective interactions in polymer nanocomposite melts and concentrated solutions, J. Chem. Phys., 2004, 121, 6986–6997 CrossRef CAS PubMed
.
- L. M. Hall, B. J. Anderson, C. F. Zukoski and K. S. Shweizer, Concentration Fluctuations, Local Order, and the Collective Structure of Polymer Nanocomposites, Macromolecules, 2009, 42, 8435–8442 CrossRef CAS
.
- L. M. Hall and K. S. Schweizer, Many body effects on the phase separation and structure of dense polymer–particle melts, J. Chem. Phys., 2008, 128, 234901 CrossRef PubMed
.
- L. M. Hall and K. S. Schweizer, Structure, scattering patterns and phase behavior of polymer nanocomposites with nonspherical fillers, Soft Matter, 2010, 6, 1015–1025 RSC
.
- A. Jayaraman and K. S. Schweizer, Structure and Assembly of Dense Solutions and Melts of Single Tethered Nanoparticles, J. Chem. Phys., 2008, 128, 164904 CrossRef PubMed
.
- A. Jayaraman and K. S. Schweizer, Effect of the number and placement of polymer tethers on the structure of dense solutions of hybrid nanoparticles, Langmuir, 2008, 24, 11119–11130 CrossRef CAS PubMed
.
- A. Jayaraman and K. S. Schweizer, Effective Interactions, Structure, and Phase Behavior of Lightly Tethered Nanoparticles in Polymer Melts, Macromolecules, 2008, 41, 9430–9438 CrossRef CAS
.
- A. Jayaraman and K. S. Schweizer, Effective Interactions and Self-Assembly of Hybrid Polymer Grafted Nanoparticles in a Homopolymer Matrix, Macromolecules, 2009, 42, 8423–8434 CrossRef CAS
.
- A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker and C. S. Woodward, SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers, ACM Transactions on Mathematical Software, 2005, 31, 363–396 CrossRef
.
- K. S. Schweizer and J. G. Curro, Integral equation theories of the structure, thermodynamics, and phase transitions of polymer fluids, Adv. Chem. Phys., 1997, 98, 1–142 CrossRef CAS
.
- C. J. Grayce, A. Yethiraj and K. S. Schweizer, Liquid state theory of the density dependent conformation of nonpolar linear polymers, J. Chem. Phys., 1994, 100, 6857–6872 CrossRef CAS
.
- J. Melenkevitz, K. S. Schweizer and J. G. Curro, Self consistent integral eqn theory for the eqbm properties of polymer solns, Macromolecules, 1993, 26, 6190–6196 CrossRef CAS
.
- P. G. Khalatur and A. R. Khokhlov, Hybrid MC/RISM technique for simulation of polymer solutions: MC+RISM integral eqns, Mol. Phys., 1998, 93, 555–572 CAS
.
- S. Mendez, J. G. Curro, M. Putz, D. Bedrov and G. D. Smith, An integral equation theory for polymer solutions: explicit inclusion of the solvent molecules, J. Chem. Phys., 2001, 115, 5669–5678 CrossRef CAS
.
- M. Putz, J. G. Curro and G. S. Grest, Self-consistent integral equation theory for polyolefins: comparison to molecular dynamics simulations and X-ray scattering, J. Chem. Phys., 2001, 114, 2847–2860 CrossRef CAS
.
- A. Yethiraj and C. K. Hall, Monte Carlo simulations and integral equation theory for microscopic correlations in polymeric fluids, J. Chem. Phys., 1991, 96, 797–807 CrossRef
.
- A. L. Frischknecht, E. S. McGarrity and M. E. Mackay, Expanded chain dimensions in polymer melts with nanoparticle fillers, J. Chem. Phys., 2010, 132, 204901 CrossRef PubMed
.
- P. G. Khalatur, L. V. Zherenkova and A. R. Khokhlov, Entropy-driven polymer collapse: Application of the hybrid MC/RISM method to the study of conformational transitions in macromolecules interacting with hard colloidal particles, Eur. Phys. J. B, 1998, 5, 881–897 CrossRef CAS
.
- N. Nair and A. Jayaraman, Self-Consistent PRISM Theory-Monte Carlo Simulation Studies of Copolymer Grafted Nanoparticles in a Homopolymer Matrix, Macromolecules, 2010, 43, 8251–8263 CrossRef CAS
.
- N. Nair, N. Wentzel and A. Jayaraman, Effect of bidispersity in grafted chain length on grafted chain conformations and potential of mean force between polymer grafted nanoparticles in a homopolymer matrix, J. Chem. Phys., 2011, 134, 194906 CrossRef PubMed
.
- A. Jayaraman and N. Nair, Integrating PRISM theory and Monte Carlo simulation to study polymer-functionalised particles and polymer nanocomposites, Mol. Simul., 2012, 38, 751–761 CrossRef CAS
.
- T. B. Martin, P. M. Dodd and A. Jayaraman, Polydispersity for tuning potential of mean force between polymer grafted nanoparticles in a polymer matrix, Phys. Rev. Lett., 2013, 110, 018301 CrossRef PubMed
.
- T. B. Martin and A. Jayaraman, Polydisperse homopolymer grafted spherical nanoparticle in a chemically identical homopolymer matrix, Soft Matter, 2013, 9, 6876–6889 RSC
.
- K. S. Schweizer and J. G. Curro, Integral equation theory of polymer melts: intramolecular structure local order, and the correlation hole, Macromolecules, 1988, 21, 3070–3081 CrossRef CAS
.
- C. J. Grayce and K. S. Schweizer, Solvn potentials for macromolecules, J. Chem. Phys., 1994, 100, 6846–6856 CrossRef CAS
.
- K. S. Schweizer and J. G. Curro, PRISM Theory of the Structure, Thermodynamics, and Phase-Transitions of Polymer Liquids and Alloys, Adv. Polym. Sci., 1994, 116, 319–377 CrossRef CAS
.
- S. Y. Kim, K. S. Schweizer and C. F. Zukoski, Multiscale Structure, Interfacial Cohesion, Adsorbed Layers, and Thermodynamics in Dense Polymer–Nanoparticle Mixtures, Phys. Rev. Lett., 2011, 107, 225504 CrossRef PubMed
.
- S. Y. Kim, L. M. Hall, K. S. Schweizer and C. F. Zukoski, Long Wavelength Concentration Fluctuations and Cage Scale Ordering of Nanoparticles in Concentrated Polymer Solutions, Macromolecules, 2010, 43, 10123–10131 CrossRef CAS
.
- L. Zhao, Y.-G. Li and C. Zhong, Integral equation theory study on the structure and effective interactions
in star polymer nanocomposite melts, J. Chem. Phys., 2007, 126, 014906 CrossRef PubMed
.
- L. Zhao, Y.-G. Li and C. Zhong, Integral equation theory study on the phase separation in star polymer nanocomposite melts, J. Chem. Phys., 2007, 127, 154909 CrossRef PubMed
.
- R. Chakrabarti, J. Y. Delannoy, M. Couty and K. S. Schweizer, Packing correlations, collective scattering and compressibility of fractal-like aggregates in polymer nanocomposites and suspensions, Soft Matter, 2011, 7, 5397–5407 RSC
.
- C. E. Woodward and A. A. Yethiraj, Density-functional theory for inhomogeneous polymer-solutions, J. Chem. Phys., 1994, 100, 3181–3186 CrossRef CAS
.
- A. Yethiraj, Polymer melts at solid surfaces, Adv. Chem. Phys., 2002, 121, 89–139 CrossRef CAS
.
- A. Yethiraj, Molecular modeling of polymers at surfaces, Chem. Eng. J., 1999, 74, 109–115 CrossRef CAS
.
- J. B. Hooper, J. D. McCoy and J. G. Curro, Density functional theory of simple polymers in a slit pore. I. Theory and efficient algorithm, J. Chem. Phys., 2000, 112, 3090–3093 CrossRef CAS
.
-
G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, 2006 Search PubMed
.
-
J. P. Hansen and I. R. McDonald, Theory of simple liquids, Elsevier Academic Press, 2006 Search PubMed
.
- K. F. Freed, Interrelation between density functional and self-consistent-field formulations for inhomogeneous polymer systems, J. Chem. Phys., 1995, 103, 3230 CrossRef CAS
.
- C. P. Emborsky, Z. Feng, K. R. Cox and W. G. Chapman, Recent advances in classical density functional theory for associating and polyatomic molecules, Fluid Phase Equilib., 2011, 306, 15–30 CrossRef CAS
.
- A. Yethiraj and C. E. Woodward, Monte-Carlo Density-Functional Theory of Nonuniform Polymer Melts, J. Chem. Phys., 1995, 102, 5499–5505 CrossRef CAS
.
- P. Tarazona and R. Evans, A Simple Density Functional Theory for Inhomogeneous Liquids – Wetting by Gas at a Solid–Liquid Interface, Mol. Phys., 1984, 52, 847–857 CrossRef CAS
.
- W. A. Curtin and N. W. Ashcroft, Weighted-density-functional theory of inhomogeneous liquids and the freezing transition, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 2909–2919 CrossRef CAS
.
- R. Evans, Nature of the liquid–vapor interface and other topics in the statistical-mechanics of nonuniform, classical fluids, Adv. Phys., 1979, 28, 143–200 CrossRef CAS
.
- Y. Rosenfeld, M. Schmidt, H. Lowen and P. Tarazona, Dimensional crossover and the freezing transition in density functional theory, J. Phys.: Condens. Matter, 1996, 8, L577–L581 CrossRef CAS
.
- Y. Rosenfeld, M. Schmidt, H. Lowen and P. Tarazona, Fundamental-measure free-energy density functional for hard spheres: Dimensional crossover and freezing, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4245–4263 CrossRef CAS
.
- Y.-X. Yu and J. Wu, Density functional theory for inhomogeneous mixtures of polymeric fluids, J. Chem. Phys., 2002, 117, 2368–2376 CrossRef CAS
.
- S. Tripathi and W. G. Chapman, Microstructure and Thermodynamics of Inhomogeneous Polymer Blends and Solutions, Phys. Rev. Lett., 2005, 94, 087801 CrossRef PubMed
.
- Y. X. Yu and J. Z. Wu, A fundamental-measure theory for inhomogeneous associating fluids, J. Chem. Phys., 2002, 116, 7094–7103 CrossRef CAS
.
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1986 Search PubMed
.
- E. S. McGarrity, A. L. Frischknecht, L. J. D. Frink and M. E. Mackay, Surface-induced first-order transition in athermal polymer–nanoparticle blends, Phys. Rev. Lett., 2007, 99, 238302 CrossRef CAS PubMed
.
- D. P. Cao and J. Z. Wu, Density functional theory for a primitive model of nanoparticle-block copolymer mixtures, J. Chem. Phys., 2007, 126, 144912 CrossRef PubMed
.
- J. H. Jin and J. Z. Wu, A theoretical study for nanoparticle partitioning in the lamellae of diblock copolymers, J. Chem. Phys., 2008, 128, 074901 CrossRef PubMed
.
- A. L. Frischknecht, V. Padmanabhan and M. E. Mackay, Surface-induced
phase behavior of polymer/nanoparticle blends with attractions, J. Chem. Phys., 2012, 136, 164904 CrossRef PubMed
.
- Z. Z. Feng and W. G. Chapman, Revisited Block Copolymer/Nanoparticle Composites: Extension of Interfacial Statistical Associating Fluid Theory, Macromolecules, 2012, 45, 6658–6668 CrossRef CAS
.
- R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Predicting the mesophases of copolymer–nanoparticle composites, Science, 2001, 292, 2469–2472 CrossRef CAS PubMed
.
- S. W. Sides, B. J. Kim, E. J. Kramer and G. H. Fredrickson, Hybrid particle-field simulations of polymer nanocomposites, Phys. Rev. Lett., 2006, 96, 250601 CrossRef PubMed
.
- S. Asakura and F. Oosawa, On Interaction Between 2 Bodies Immersed in a Solution of Macromolecules, J. Chem. Phys., 1954, 22, 1255–1256 CAS
.
- S. Asakura and F. Oosawa, Interaction between particles suspended in solutions of macromolecules, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS
.
- M. Surve, V. Pryamitsyn and V. Ganesan, Nanoparticles in solutions of adsorbing polymers: Pair interactions, percolation, and phase behavior, Langmuir, 2006, 22, 969–981 CrossRef CAS PubMed
.
- S. Yang, D. D. Yan and A. C. Shi, Structure of adsorbed polymers on a colloid particle, Macromolecules, 2006, 39, 4168–4174 CrossRef CAS
.
- R. Tuinier, D. G. A. L. Aarts, H. H. Wensink and H. N. W. Lekkerkerker, Pair interaction and phase separation in mixtures of colloids and excluded volume polymers, Phys. Chem. Chem. Phys., 2003, 5, 3707–3715 RSC
.
- R. Tuinier, J. Rieger and C. G. de Kruif, Depletion-induced phase separation in colloid–polymer mixtures, Adv. Colloid Interface Sci., 2003, 103, 1–31 CrossRef CAS PubMed
.
- A. Bringer, E. Eisenriegler, F. Schlesener and A. Hanke, Polymer depletion interaction between a particle and a wall, Eur. Phys. J. B, 1999, 11, 101–119 CrossRef CAS
.
- E. Eisenriegler, Small mesoscopic particles in dilute and semidilute solutions of nonadsorbing polymers, J. Chem. Phys., 2000, 113, 5091–5097 CrossRef CAS
.
- A. Hanke, E. Eisenriegler and S. Dietrich, Polymer depletion effects near mesoscopic particles, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 6853–6878 CrossRef CAS
.
- R. A. Vaia and E. P. Giannelis, Polymer melt intercalation in organically-modified layered silicates: Model predictions and experiment, Macromolecules, 1997, 30, 8000–8009 CrossRef CAS
.
- B. C. Freasier and C. E. Woodward, Structure of polymer fluids in colloidal dispersions, Comput. Theor. Polym. Sci., 1999, 9, 141–152 CrossRef CAS
.
- N. Patel and S. A. Egorov, Interactions between colloidal particles in polymer solutions: A density functional theory study, J. Chem. Phys., 2004, 121, 4987–4997 CrossRef CAS PubMed
.
- N. Patel and S. A. Egorov, Interactions between nanocolloidal particles in polymer solutions: Effect of attractive interactions, J. Chem. Phys., 2005, 123, 144916 CrossRef CAS PubMed
.
- A. Bymaster, S. Jain and W. G. Chapman, Microstructure and depletion forces in polymer–colloid mixtures from an interfacial statistical associating fluid theory, J. Chem. Phys., 2008, 128, 164910 CrossRef PubMed
.
- A. L. Frischknecht and A. Yethiraj, Two- and three-body interactions among nanoparticles in a polymer melt, J. Chem. Phys., 2011, 134, 174901 CrossRef PubMed
.
- E. Reister and G. H. Fredrickson, Phase behavior of a blend of polymer-tethered nanoparticles with diblock copolymers, J. Chem. Phys., 2005, 123, 214903 CrossRef PubMed
.
- J. U. Kim and B. O'Shaughnessy, Nanoinclusions in dry polymer brushes, Macromolecules, 2006, 39, 413–425 CrossRef CAS
.
- J. U. Kim and M. W. Matsen, Repulsion exerted on a spherical particle by a polymer brush, Macromolecules, 2008, 41, 246–252 CrossRef CAS
.
- K. Chen and Y. Q. Ma, Interactions between colloidal particles induced by polymer brushes grafted onto the substrate, J. Phys. Chem. B, 2005, 109, 17617–17622 CrossRef CAS PubMed
.
- S. A. Egorov, Insertion
of nanoparticles into polymer brush under variable solvent conditions, J. Chem. Phys., 2012, 137, 134905 CrossRef CAS PubMed
.
- A. Halperin, M. Kroger and E. B. Zhulina, Colloid–Brush Interactions: The Effect of Solvent Quality, Macromolecules, 2011, 44, 3622–3638 CrossRef CAS
.
- S. H. Kim and E. W. Cochran, Localization of spherical nanoparticles within lamellar AB diblock copolymer melts through self-consistent field theory, Polymer, 2011, 52, 2328–2339 CrossRef CAS
.
- V. Raman, A. Bose, B. D. Olsen and T. A. Hatton, Long-Range Ordering of Symmetric Block Copolymer Domains by Chaining of Superparamagnetic Nanoparticles in External Magnetic Fields, Macromolecules, 2012, 45, 9373–9382 CrossRef CAS
.
- Q. Y. Tang and Y. Q. Ma, Self-Assembly of Rod-Shaped Particles in Diblock-Copolymer Templates, J. Phys. Chem. B, 2009, 113, 10117–10120 CrossRef CAS PubMed
.
- Q. Y. Pan, C. H. Tong and Y. J. Zhu, Self-Consistent-Field and Hybrid Particle-Field Theory Simulation of Confined Copolymer and Nanoparticle Mixtures, ACS Nano, 2011, 5, 123–128 CrossRef CAS PubMed
.
- V. V. Ginzburg, G. Peng, F. Qiu, D. Jasnow and A. C. Balazs, Kinetic model of phase separation in binary mixtures with hard mobile impurities, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4352–4359 CrossRef CAS
.
- G. W. Peng, F. Qiu, V. V. Ginzburg, D. Jasnow and A. C. Balazs, Forming supramolecular networks from nanoscale rods in binary, phase-separating mixtures, Science, 2000, 288, 1802–1804 CrossRef CAS PubMed
.
- V. V. Ginzburg, C. Gibbons, F. Qiu, G. W. Peng and A. C. Balazs, Modeling the dynamic behavior of diblock copolymer/particle composites, Macromolecules, 2000, 33, 6140–6147 CrossRef CAS
.
- J. Huh, V. V. Ginzburg and A. C. Balazs, Thermodynamic behavior of particle/diblock copolymer mixtures: Simulation and theory, Macromolecules, 2000, 33, 8085–8096 CrossRef CAS
.
- R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Block copolymer-directed assembly of nanoparticles: Forming mesoscopically ordered hybrid materials, Macromolecules, 2002, 35, 1060–1071 CrossRef CAS
.
- J. Y. Lee, Z. Shou and A. C. Balazs, Modeling the self-assembly of copolymer–nanoparticle mixtures confined between solid surfaces, Phys. Rev. Lett., 2003, 91, 136103 CrossRef PubMed
.
- Q. Y. Pan, C. H. Tong, Y. J. Zhu and Q. H. Yang, Phase behaviors of bidisperse nanoparticle/block copolymer mixtures in dilute solutions, Polymer, 2010, 51, 4571–4579 CrossRef CAS
.
- L. S. Zhang and J. P. Lin, Hierarchically Ordered Nanocomposites Self-Assembled from Linear-Alternating Block Copolymer/Nanoparticle Mixture, Macromolecules, 2009, 42, 1410–1414 CrossRef CAS
.
- E. S. McGarrity, A. L. Frischknecht and M. E. Mackay, Phase behavior of polymer/nanoparticle blends near a substrate, J. Chem. Phys., 2008, 128, 154904 CrossRef CAS PubMed
.
- G. A. Buxton and A. C. Balazs, Simulating the morphology and mechanical properties of filled diblock copolymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031802 CrossRef
.
- G. A. Buxton, J. Y. Lee and A. C. Balazs, Computer simulation of morphologies and optical properties of filled diblock copolymers, Macromolecules, 2003, 36, 9631–9637 CrossRef CAS
.
- V. V. Ginzburg and A. C. Balazs, Calculating phase diagrams of polymer–platelet mixtures using density functional theory: Implications for polymer/clay composites, Macromolecules, 1999, 32, 5681–5688 CrossRef CAS
.
- V. V. Ginzburg, C. Singh and A. C. Balazs, Theoretical phase diagrams of polymer/clay composites: The role of grafted organic modifiers, Macromolecules, 2000, 33, 1089–1099 CrossRef CAS
.
- H. J. C. Berendsen, D. Vanderspoel and R. Vandrunen, GROMACS – A Message-Passing Parallel Molecular-Dynamics Implementation, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS
.
- S. Plimpton, Fast Parallel Algorithms For Short-Range Molecular-Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- A. N. Rissanou and V. Harmandaris, Structure and dynamics of poly(methylmethacrylate)/graphene systems through atomistic molecular dynamics simulations, J. Nanopart. Res., 2013, 15, 1589 CrossRef
.
- Y. N. Pandey and M. Doxastakis, Detailed atomistic Monte Carlo simulations of a polymer melt on a solid surface and around a nanoparticle, J. Chem. Phys., 2012, 136, 094901 CrossRef PubMed
.
- V. Kuppa and E. Manias, Dynamics of poly(ethylene oxide) in nanoscale confinements: A computer simulations perspective, J. Chem. Phys., 2003, 118, 3421–3429 CrossRef CAS
.
- H. C. Lay, M. J. S. Spencer, E. J. Evans and I. Yarovsky, Molecular simulation study of polymer interactions with silica particles in aqueous solution, J. Phys. Chem. B, 2003, 107, 9681–9691 CrossRef CAS
.
- P.-H. Lin and R. Khare, Molecular Simulation of Cross-Linked Epoxy and Epoxy–POSS Nanocomposite, Macromolecules, 2009, 42, 4319–4327 CrossRef CAS
.
- Y. Yani and M. H. Lamm, Molecular dynamics simulation of mixed matrix nanocomposites containing polyimide and polyhedral oligomeric silsesquioxane (POSS), Polymer, 2009, 50, 1324–1332 CrossRef CAS
.
- G. Scocchi, P. Posocco, M. Fermeglia and S. Pricl, Polymer–clay nanocomposites: A multiscale molecular modeling approach, J. Phys. Chem. B, 2007, 111, 2143–2151 CrossRef CAS PubMed
.
- F. W. Starr, T. B. Schroder and S. C. Glotzer, Effects of a nanoscopic filler on the structure and dynamics of a simulated polymer melt and the relationship to ultrathin films, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021802 CrossRef CAS
.
- F. W. Starr, T. B. Schroder and S. C. Glotzer, Molecular dynamics simulation of a polymer melt with a nanoscopic particle, Macromolecules, 2002, 35, 4481–4492 CrossRef CAS
.
- F. W. Starr, J. F. Douglas and S. C. Glotzer, Origin of particle clustering in a simulated polymer nanocomposite and its impact on rheology, J. Chem. Phys., 2003, 119, 1777–1788 CrossRef CAS
.
- J. S. Smith, D. Bedrov and G. D. Smith, A molecular dynamics simulation study of nanoparticle interactions in a model polymer–nanoparticle composite, Compos. Sci. Technol., 2003, 63, 1599–1605 CrossRef CAS
.
- D. Brown, P. Mele, S. Marceau and N. D. Alberola, A molecular dynamics study of a model nanoparticle embedded in a polymer matrix, Macromolecules, 2003, 36, 1395–1406 CrossRef CAS
.
- M. Goswami and B. G. Sumpter, Effect of polymer–filler interaction strengths on the thermodynamic and dynamic properties of polymer nanocomposites, J. Chem. Phys., 2009, 130, 134910 CrossRef PubMed
.
- J. Liu, Y. Wu, J. X. Shen, Y. Y. Gao, L. Q. Zhang and D. P. Cao, Polymer–nanoparticle interfacial behavior revisited: A molecular dynamics study, Phys. Chem. Chem. Phys., 2011, 13, 13058–13069 RSC
.
- M. Goswami and B. G. Sumpter, Anomalous chain diffusion in polymer nanocomposites for varying polymer–filler interaction strengths, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041801 CrossRef
.
- T. Desai, P. Keblinski and S. K. Kumar, Molecular dynamics simulations of polymer transport in nanocomposites, J. Chem. Phys., 2005, 122, 134910 CrossRef PubMed
.
- J. Liu, S. Z. Wu, L. Q. Zhang, W. C. Wang and D. P. Cao, Molecular dynamics simulation for insight into microscopic mechanism of polymer reinforcement, Phys. Chem. Chem. Phys., 2011, 13, 518–529 RSC
.
- G. J. Papakonstantopoulos, M. Doxastakis, P. F. Nealey, J. L. Barrat and J. J. de Pablo, Calculation of local mechanical properties of filled polymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 031803 CrossRef
.
- S. T. Knauert, J. F. Douglas and F. W. Starr, The effect of nanoparticle shape on polymer-nanocomposite rheology and tensile strength, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1882–1897 CrossRef CAS
.
- A. Adnan, C. T. Sun and H. Mahfuz, A molecular dynamics simulation study to investigate the effect of filler size on elastic properties of polymer nanocomposites, Compos. Sci. Technol., 2007, 67, 348–356 CrossRef CAS
.
- J. Cho, M. S. Joshi and C. T. Sun, Effect of inclusion size on mechanical properties of polymeric composites with micro and nano particles, Compos. Sci. Technol., 2006, 66, 1941–1952 CrossRef CAS
.
- J. Cho and C. T. Sun, A molecular dynamics simulation study of inclusion size effect on polymeric nanocomposites, Comput. Mater. Sci., 2007, 41, 54–62 CrossRef
.
- L. Khounlavong, V. Pryamitsyn and V. Ganesan, Many-body interactions and coarse-grained simulations of structure of nanoparticle–polymer melt mixtures, J. Chem. Phys., 2010, 133, 144904 CrossRef PubMed
.
- V. Pryamitsyn and V. Ganesan, Mechanisms of steady-shear rheology in polymer–nanoparticle composites, J. Rheol., 2006, 50, 655–683 CrossRef CAS
.
- V. Pryamitsyn and V. Ganesan, Origins of linear viscoelastic behavior of polymer–nanoparticle composites, Macromolecules, 2006, 39, 844–856 CrossRef CAS
.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating Microscopic Hydrodynamic Phenomena With Dissipative Particle Dynamics, Europhys. Lett., 1992, 19, 155–160 CrossRef
.
- R. D. Groot and P. B. Warren, Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation RID D-1682-2009, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS
.
- V. Ganesan, V. Pryamitsyn, M. Surve and B. Narayanan, Noncontinuum effects in nanoparticle dynamics in polymers, J. Chem. Phys., 2006, 124, 221102 CrossRef PubMed
.
- A. J. Schultz, C. K. Hall and J. Genzer, Computer simulation of block copolymer/nanoparticle composites, Macromolecules, 2005, 38, 3007–3016 CrossRef CAS
.
- R. Sknepnek, J. A. Anderson, M. H. Lamm, J. Schmalian and A. Travesset, Nanoparticle ordering via functionalized block copolymers in solution, ACS Nano, 2008, 2, 1259–1265 CrossRef CAS PubMed
.
- V. Pryamitsyn and V. Ganesan, Strong segregation theory of block copolymer–nanoparticle composites, Macromolecules, 2006, 39, 8499–8510 CrossRef CAS
.
- V. Kalra and Y. L. Joo, Coarse-grained molecular dynamics study of block copolymer/nanoparticle composites under elongational flow, J. Chem. Phys., 2009, 131, 214904 CrossRef PubMed
.
- V. Kalra, S. Mendez, F. Escobedo and Y. L. Joo, Coarse-grained molecular dynamics simulation on the placement of nanoparticles within symmetric diblock copolymers under shear flow, J. Chem. Phys., 2008, 128, 164909 CrossRef PubMed
.
- L. L. He, Z. Q. Pan, L. X. Zhang and H. J. Liang, Microphase transitions of block copolymer/nanorod composites under shear flow, Soft Matter, 2011, 7, 1147–1160 RSC
.
- L. L. He, L. X. Zhang and H. J. Liang, The effects of nanoparticles on the lamellar phase separation of diblock copolymers, J. Phys. Chem. B, 2008, 112, 4194–4203 CrossRef CAS PubMed
.
- L. L. He, L. X. Zhang, A. Xia and H. J. Liang, Effect of nanorods on the mesophase structure of diblock copolymers, J. Chem. Phys., 2009, 130, 144907 CrossRef PubMed
.
- L. L. He, L. X. Zhang and H. J. Liang, Mono- or bidisperse nanorods mixtures in diblock copolymers, Polymer, 2010, 51, 3303–3314 CrossRef CAS
.
- L. L. He, L. X. Zhang, H. P. Chen and H. J. Liang, The phase behaviors of cylindrical diblock copolymers and rigid nanorods' mixtures, Polymer, 2009, 50, 3403–3410 CrossRef CAS
.
- G. G. Vogiatzis, E. Voyiatzis and D. N. Theodorou, Monte Carlo simulations of a coarse grained model for an athermal all-polystyrene nanocomposite system, Eur. Polym. J., 2011, 47, 699–712 CrossRef CAS
.
- M. Vacatello, Phantom chain simulations of realistically sized polymer-based nanocomposites, Macromol. Theory Simul., 2006, 15, 303–310 CrossRef CAS
.
- M. Vacatello, Phantom chain simulations of polymer–nanofiller systems, Macromolecules, 2003, 36, 3411–3416 CrossRef
.
- M. Vacatello, Molecular arrangements in polymer-based nanocomposites, Macromol. Theory Simul., 2002, 11, 757–765 CrossRef CAS
.
- M. Vacatello, Monte Carlo simulations of polymer melts filled
with solid nanoparticles, Macromolecules, 2001, 34, 1946–1952 CrossRef CAS
.
- M. Vacatello, Chain dimensions in filled polymers: An intriguing problem, Macromolecules, 2002, 35, 8191–8193 CrossRef CAS
.
- M. S. Ozmusul, C. R. Picu, S. S. Sternstein and S. K. Kumar, Lattice Monte Carlo simulations of chain conformations in polymer nanocomposites, Macromolecules, 2005, 38, 4495–4500 CrossRef CAS
.
- K. T. Marla and J. C. Meredith, Simulation of interaction forces between nanoparticles: End-grafted polymer modifiers, J. Chem. Theory Comput., 2006, 2, 1624–1631 CrossRef CAS
.
- K. T. Marla and J. C. Meredith, Simulation of interaction forces between nanoparticles in the presence of Lennard-Jones polymers: Freely adsorbing homopolymer modifiers, Langmuir, 2005, 21, 487–497 CrossRef CAS PubMed
.
- Q. Zhang and L. A. Archer, Monte Carlo simulation of structure and nanoscale interactions in polymer nanocomposites, J. Chem. Phys., 2004, 121, 10814–10824 CrossRef CAS PubMed
.
- A. Milchev, D. I. Dirnitrova and K. Binder, Excess free energy of nanoparticles in a polymer brush, Polymer, 2008, 49, 3611–3618 CrossRef CAS
.
- M. Doxastakis, Y. L. Chen, O. Guzman and J. J. de Pablo, Polymer–particle mixtures: Depletion and packing effects, J. Chem. Phys., 2004, 120, 9335–9342 CrossRef CAS PubMed
.
- M. Doxastakis, Y. L. Chen and J. J. de Pablo, Potential of mean force between two nanometer-scale particles in a polymer solution, J. Chem. Phys., 2005, 123, 034901 CrossRef CAS PubMed
.
- D. Q. Pike, F. A. Detcheverry, M. Muller and J. J. de Pablo, Theoretically informed coarse grain simulations of polymeric systems, J. Chem. Phys., 2009, 131, 084903 CrossRef PubMed
.
- F. A. Detcheverry, H. M. Kang, K. C. Daoulas, M. Muller, P. F. Nealey and J. J. de Pablo, Monte Carlo simulations of a coarse grain model for block copolymers and nanocomposites, Macromolecules, 2008, 41, 4989–5001 CrossRef CAS
.
- A. A. Louis, P. G. Bolhuis, E. J. Meijer and J. P. Hansen, Polymer induced depletion potentials in polymer–colloid mixtures, J. Chem. Phys., 2002, 117, 1893–1907 CrossRef CAS
.
- P. G. Bolhuis, E. J. Meijer and A. A. Louis, Colloid–polymer mixtures in the protein limit, Phys. Rev. Lett., 2003, 90, 068304 CrossRef PubMed
.
- P. G. Bolhuis, A. A. Louis and J. P. Hansen, Influence of polymer-excluded volume on the phase-behavior of colloid–polymer mixtures, Phys. Rev. Lett., 2002, 89, 128302 CrossRef CAS PubMed
.
- C. Peter and K. Kremer, Multiscale simulation of soft matter systems – from the atomistic to the coarse-grained level and back, Soft Matter, 2009, 5, 4357–4366 RSC
.
- S. Alexander, Adsorption of chain molecules with a polar head a-scaling description, J. Phys., 1977, 38, 983–987 CAS
.
- A. N. Semenov, Contribution to the theory of microphase layering in block-copolymer melts, Zhurnal Eksperimentalnoi I Teoreticheskoi Fiziki, 1985, 88, 1242–1256 CAS
.
- S. T. Milner, T. A. Witten and M. E. Cates, Theory of the Grafted Polymer Brush, Macromolecules, 1988, 21, 2610–2619 CrossRef CAS
.
- Y. B. Zhulina, V. A. Pryamitsyn and O. V. Borisov, Structure and Conformational Transitions in Grafted Polymer-Chains Layers – New Theory, Vysokomolekulyarnye Soedineniya Seriya A, 1989, 31, 185–194 Search PubMed
.
- M. W. Matsen and J. M. Gardiner, Corrections to the strong-stretching theory of polymer brushes due to the proximal layer, J. Chem. Phys., 2003, 118, 3775–3781 CrossRef CAS
.
- H. Tang and I. Szleifer, Phase-behavior of Grafted Polymers in Poor Solvents, Europhys. Lett., 1994, 28, 19–24 CrossRef CAS
.
- M. A. Carignano and I. Szleifer, Statistical Thermodynamic Theory of Grafted Polymeric Layers, J. Chem. Phys., 1993, 98, 5006–5018 CrossRef CAS
.
- Y. Ye, J. D. McCoy and J. G. Curro, Application of density functional theory to tethered polymer chains: Effect of intermolecular attractions, J. Chem. Phys., 2003, 119, 555–564 CrossRef CAS
.
- J. D. McCoy, Y. Ye and J. G. Curro, Application of density functional theory to tethered polymer chains: Athermal systems, J. Chem. Phys., 2002, 117, 2975–2986 CrossRef CAS
.
- S. T. Milner, Polymer Brushes, Science, 1991, 251, 905–914 CrossRef CAS PubMed
.
- I. Szleifer and M. A. Carignano, Tethered polymer layers, Adv. Chem. Phys., 1996, 94, 165–260 CrossRef CAS
.
- A. Halperin, M. Tirrell and T. P. Lodge, Tethered Chains In Polymer Microstructures, Adv. Polym. Sci., 1992, 100, 31–71 CrossRef CAS
.
- L. Leibler and A. Mourran, Wetting on grafted polymer films, MRS Bull., 1997, 22, 33–37 CAS
.
-
L. Leibler, A. Ajdari, A. Mourran, G. Coulon and D. Chatenay, Wetting of Grafted Polymer Surfaces by Compatible Chains, in Ordering in Macromolecular Systems 1994, ed. A. Teramoto, M. Kobayashi and T. Norisuye, Springer-Verlag, Berlin, 1994, pp. 301–311 Search PubMed
.
- P. G. Ferreira, A. Ajdari and L. Leibler, Scaling law for entropic effects at interfaces between grafted layers and polymer melts, Macromolecules, 1998, 31, 3994–4003 CrossRef CAS
.
- M. W. Matsen and J. M. Gardiner, Autophobic dewetting of homopolymer on a brush and entropic attraction between opposing brushes in a homopolymer matrix, J. Chem. Phys., 2001, 115, 2794–2804 CrossRef CAS
.
- S. Jain, V. V. Ginzburg, P. Jog, J. Weinhold, R. Srivastava and W. G. Chapman, Modeling polymer-induced interactions between two grafted surfaces: Comparison between interfacial statistical associating fluid theory and self-consistent field theory, J. Chem. Phys., 2009, 131, 044908 CrossRef PubMed
.
- K. Gong and W. G. Chapman, Solvent response of mixed polymer brushes, J. Chem. Phys., 2011, 135, 214901 CrossRef PubMed
.
- X. F. Xu, D. P. Cao and J. Z. Wu, Density functional theory for predicting polymeric forces against surface fouling, Soft Matter, 2010, 6, 4631–4646 RSC
.
- I. Borukhov and L. Leibler, Enthalpic stabilization of brush-coated particles in a polymer melt, Macromolecules, 2002, 35, 5171–5182 CrossRef CAS
.
- I. Borukhov and L. Leibler, Stabilizing grafted colloids in a polymer melt: Favorable enthalpic interactions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, R41–R44 CrossRef CAS
.
- B. Kim, D. Y. Ryu, V. Pryamitsyn and V. Ganesan, Dewetting of PMMA on PS-Brush Substrates, Macromolecules, 2009, 42, 7919–7923 CrossRef CAS
.
- D. M. Trombly, V. Pryamitsyn and V. Ganesan, Interfacial properties of statistical copolymer brushes in contact with homopolymer melts, J. Chem. Phys., 2011, 134, 154903 CrossRef PubMed
.
- J. U. Kim and M. W. Matsen, Interaction between polymer-grafted particles, Macromolecules, 2008, 41, 4435–4443 CrossRef CAS
.
- J. R. Roan and T. Kawakatsu, Self-consistent-field theory for interacting polymeric assemblies. I. Formulation, implementation, and benchmark tests, J. Chem. Phys., 2002, 116, 7283–7294 CrossRef CAS
.
- A. Striolo and S. A. Egorov, Steric stabilization of spherical colloidal particles: Implicit and explicit solvent, J. Chem. Phys., 2007, 126, 014902 CrossRef PubMed
.
- D. Trombly and V. Ganesan, Interactions between Polymer-Grafted Particles and Bare Particles for Biocompatibility Applications, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 2566–2577 CrossRef CAS
.
- F. LoVerso, S. A. Egorov and K. Binder, Interaction Between Polymer Brush-Coated Spherical Nanoparticles: Effect of Solvent Quality, Macromolecules, 2012, 45, 8892–8902 CrossRef CAS
.
- S. A. Egorov and K. Binder, Effect of solvent quality on the dispersibility of polymer-grafted spherical nanoparticles in polymer solutions, J. Chem. Phys., 2012, 137, 094901 CrossRef CAS PubMed
.
- S. A. Egorov, Interactions between polymer brushes in solvents of variable quality: A density functional theory study, J. Chem. Phys., 2008, 129, 064901 CrossRef CAS PubMed
.
- J. J. Xu, F. Qiu, H. D. Zhang and Y. L. Yang, Morphology and interactions of polymer brush-coated spheres in a polymer matrix, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2811–2820 CrossRef CAS
.
- D. M. Trombly and V. Ganesan, Curvature effects upon interactions of polymer-grafted nanoparticles in chemically identical polymer matrices, J. Chem. Phys., 2010, 133, 154904 CrossRef PubMed
.
- S. E. Harton and S. K. Kumar, Mean-field theoretical analysis of brush-coated nanoparticle dispersion in polymer matrices, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 351–358 CrossRef CAS
.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos and V. Pryamitsyn,
et al., Anisotropic self-assembly of polymer-decorated spherical nanoparticles, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed
.
- V. Pryamitsyn, V. Ganesan, A. Z. Panagiotopoulos, H. Liu and S. K. Kumar, Modeling the anisotropic self-assembly of spherical polymer-grafted nanoparticles, J. Chem. Phys., 2009, 131, 221102 CrossRef PubMed
.
- A. Rungta, B. Natarajan, T. Neely, D. Dukes, L. S. Schadler and B. C. Benicewicz, Grafting Bimodal Polymer Brushes on Nanoparticles Using Controlled Radical Polymerization, Macromolecules, 2012, 45, 9303–9311 CrossRef CAS
.
- C. R. Iacovella, A. S. Keys, M. A. Horsch and S. C. Glotzer, Icosahedral packing of polymer-tethered nanospheres and stabilization of the gyroid phase, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 040801 CrossRef
.
- C. R. Iacovella, M. A. Horsch, Z. Zhang and S. C. Glotzer, Phase diagrams of self-assembled mono-tethered nanospheres from molecular simulation and comparison to surfactants, Langmuir, 2005, 21, 9488–9494 CrossRef CAS PubMed
.
- J. U. Kim and M. W. Matsen, Positioning Janus Nanoparticles in Block Copolymer Scaffolds, Phys. Rev. Lett., 2009, 102, 078303 CrossRef PubMed
.
- A. L. Frischknecht, Forces between nanorods with end-adsorbed chains in a homopolymer melt, J. Chem. Phys., 2008, 128, 224902 CrossRef PubMed
.
- A. L. Frischknecht, M. J. A. Hore, J. Ford and R. J. Composto, Dispersion of Polymer-Grafted Nanorods in Homopolymer Films: Theory and Experiment, Macromolecules, 2013, 46, 2856–2869 CrossRef CAS
.
- M. J. A. Hore and R. J. Composto, Using Miscible Polymer Blends To Control Depletion–Attraction Forces between Au Nanorods in Nanocomposite Films, Macromolecules, 2012, 45, 6078–6086 CrossRef CAS
.
- R. Wang, F. Qiu, H. D. Zhang and Y. L. Yang, Interactions between brush-coated clay sheets in a polymer matrix, J. Chem. Phys., 2003, 118, 9447–9456 CrossRef CAS
.
- T. V. M. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Bohm and F. Muller-Plathe, Interface of Grafted and Ungrafted Silica Nanoparticles with a Polystyrene Matrix: Atomistic Molecular Dynamics Simulations, Macromolecules, 2011, 44, 2316–2327 CrossRef CAS
.
- P. V. Komarov, I. V. Mikhailov, Y. T. Chiu, S. M. Chen and P. G. Khalatur, Molecular Dynamics Study of Interface Structure in Composites Comprising Surface-Modified SiO2 Nanoparticles and a Polyimide Matrix, Macromol. Theory Simul., 2013, 22, 187–197 CrossRef CAS
.
- B. L. Peters, J. M. D. Lane, A. E. Ismail and G. S. Grest, Fully Atomistic Simulations of the Response of Silica Nanoparticle Coatings to Alkane Solvents, Langmuir, 2012, 28, 17443–17449 CrossRef CAS PubMed
.
- J. M. D. Lane, A. E. Ismail, M. Chandross, C. D. Lorenz and G. S. Grest, Forces between functionalized silica nanoparticles in solution, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 050501 CrossRef
.
- J. S. Smith, O. Borodin, G. D. Smith and E. M. Kober, A molecular dynamics simulation and quantum chemistry study of poly(dimethylsiloxane)–silica nanoparticle interactions, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1599–1615 CrossRef CAS
.
- D. Meng, S. K. Kumar, J. M. D. Lane and G. S. Grest, Effective interactions between grafted nanoparticles in a polymer matrix, Soft Matter, 2012, 8, 5002–5010 RSC
.
- J. Kalb, D. Dukes, S. K. Kumar, R. S. Hoy and G. S. Grest, End grafted polymer–nanoparticles in a polymeric matrix: Effect of coverage and curvature, Soft Matter, 2010, 7, 1418–1425 RSC
.
- J. Klos and T. Pakula, Computer simulations of chains end-grafted onto a spherical surface. Effect of matrix polymer, Macromolecules, 2004, 37, 8145–8151 CrossRef CAS
.
- G. D. Smith and D. Bedrov, Dispersing Nanoparticles in a Polymer Matrix: Are Long, Dense Polymer Tethers Really Necessary?, Langmuir, 2009, 25, 11239–11243 CrossRef CAS PubMed
.
- J. X. Shen, J. Liu, Y. Y. Gao, D. P. Cao and L. Q. Zhang, Revisiting the Dispersion Mechanism of Grafted Nanoparticles in Polymer Matrix: A Detailed Molecular Dynamics Simulation, Langmuir, 2011, 27, 15213–15222 CrossRef CAS PubMed
.
- Y. L. Lin, C. S. Chiou, S. K. Kumar, J. J. Lin, Y. J. Sheng and H. K. Tsao, Self-Assembled Superstructures of Polymer-Grafted Nanoparticles: Effects of Particle Shape and Matrix Polymer, J. Phys. Chem. C, 2011, 115, 5566–5577 CAS
.
- A. Chremos and A. Z. Panagiotopoulos, Structural Transitions of Solvent-Free Oligomer-Grafted Nanoparticles, Phys. Rev. Lett., 2011, 107, 105503 CrossRef PubMed
.
- S. Goyal and F. A. Escobedo, Structure and transport properties of polymer grafted nanoparticles, J. Chem. Phys., 2011, 135, 184902 CrossRef PubMed
.
- V. Pryamitsyn and V. Ganesan, Effect of confinement on polymer-induced depletion interactions between nanoparticles, J. Chem. Phys., 2013, 138, 234905 CrossRef PubMed
.
- L. Meli, A. Arceo and P. F. Green, Control of the entropic interactions and phase behavior of athermal nanoparticle/homopolymer thin film mixtures, Soft Matter, 2009, 5, 533–537 RSC
.
- D. Maillard, S. K. Kumar, B. Fragneaud, J. W. Kysar, A. Rungta, B. C. Benicewicz, H. Deng, L. C. Brinson and J. F. Douglas, Mechanical Properties of Thin Glassy Polymer Films Filled with Spherical Polymer-Grafted Nanoparticles, Nano Lett., 2012, 12, 3909–3914 CrossRef CAS PubMed
.
- X. C. Chen and P. F. Green, Control of Morphology and Its Effects on the Optical Properties of Polymer Nanocomposites, Langmuir, 2010, 26, 3659–3665 CrossRef CAS PubMed
.
- J. E. Stone, D. J. Hardy, I. S. Ufimtsev and K. Schulten, GPU-accelerated molecular modeling coming of age, J. Mol. Graphics Modell., 2010, 29, 116–125 CrossRef CAS PubMed
.
- J. A. Anderson and A. Travesset, Molecular dynamics on graphic processing units: HOOMD to the rescue, Comput. Sci. Eng., 2008, 10, 5342–5359 CrossRef
.
- E. Jankowski, H. S. Marsh and A. Jayaraman, Computationally Linking Molecular Features of Conjugated Polymers and Fullerene Derivatives to Bulk Heterojunction Morphology, Macromolecules, 2013, 46, 5775–5785 CrossRef CAS
.
- B. G. Levine, J. E. Stone and A. Kohlmeyer, Fast analysis of molecular dynamics trajectories with graphics processing units-Radial distribution function histogramming, J. Comput. Phys., 2011, 230, 3556–3569 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2014 |