DOI:
10.1039/C3SM51680F
(Paper)
Soft Matter, 2013,
9, 9907-9917
Mechanical properties and microdomain separation of fluid membranes with anchored polymers
Received 18th June 2013, Accepted 22nd August 2013
First published on 23rd August 2013
Abstract
The entropic effects of anchored polymers on biomembranes are studied using simulations of a meshless membrane model combined with anchored linear polymer chains. The bending rigidity and spontaneous curvature are investigated for anchored ideal and excluded-volume polymer chains. Our results are in good agreement with the previous theoretical predictions. It is found that the polymer reduces the line tension of membrane edges, as well as the interfacial line tension between membrane domains, leading to microdomain formation. Instead of the mixing of two phases as observed in typical binary fluids, densely anchored polymers stabilize small domains. A mean field theory is proposed for the edge line tension reduced by anchored ideal chains, which reproduces our simulation results well.
1 Introduction
Our knowledge of the heterogeneous structure of biomembranes has advanced from the primitive fluid mosaic model1 to the modern raft model2,3 over the past decades. According to this modern model, membrane proteins are not randomly distributed in lipid membranes but concentrated in local microdomains, called lipid rafts, with a diameter of 10–100 nm.4–6 The raft contains high concentrations of glycosphingolipids and cholesterol, and plays important roles in many intra- and intercellular processes including signal transduction and membrane protein trafficking.In the last decade, phase separation in multi-component lipid membranes has been intensively investigated in three-component systems of saturated and unsaturated phospholipids and cholesterol.7–15 Lipid domains exhibit various interesting patterns on the micrometer scale, which can be reproduced by theoretical calculations and simulations. Various shapes of lipid domains can be also formed at the air–water interface.16–18 However, the formation mechanism of microdomains on the 10–100 nm scale has not been understood so far. In lipid rafts, glycolipids contain glycan chains. Recently, network-shaped domains and small scattered domains have been observed in lipid membranes with PEG-conjugated cholesterol.19 The effects of anchored polymers have been well investigated in the case of uniform anchoring on membranes, but the effects on the lipid domains and line tension have not been well investigated. In this paper, we focus on the effects of anchored polymers on the properties of biomembranes, in particular, on lipid domains.
It is well known that anchored polymers modify membrane properties. The polymer anchoring induces a positive spontaneous curvature C0 of the membranes and increases the bending rigidity κ. These relationships are analytically derived using the Green's function method for the mushroom region20,21 and confirmed by Monte Carlo simulations.22–25 The membrane properties in the brush region are analyzed by a scaling method.20,21,26 Experimentally, the κ increase is measured by micropipette aspiration of liposomes.27 Polymer decoration can enhance the stability of lipid membranes. PEG-conjugated lipids can reduce protein adsorption and adhesion on cellular surfaces, whereby PEG-coated liposomes can be used as drug carriers in drug-delivery systems.28,29
When vesicles are formed from the self-assembly of surfactant molecules via micelle growth, the vesicle size is determined kinetically by the competition between the bending energy and the line tension energy of the membrane edge.30–38 Recently, Bressel et al. reported that the addition of an amphiphilic copolymer induces the formation of larger vesicles.39 A polymer-anchoring-induced liposome-to-micelle transition is also observed.26,40,41 The line tension of the membrane edge is considered to be reduced by polymer anchoring, but it has not been systematically investigated so far. In this study, we simulate the edge line tension for anchored ideal and excluded-volume chains and analytically investigate the polymer effects on the edge tension for ideal chains.
In order to simulate the polymer-anchoring effects on biomembranes, we employ one of the solvent-free meshless membrane models.42,43 Since we focus on the entropic effects of polymer chains, the detailed structures of the bilayer can be neglected, and thus the membranes can be treated as curved surfaces. In the meshless model, a membrane particle represents a patch of bilayer membrane and membrane properties can be easily controlled.
In sec. II, the membrane model and simulation method are described. In sec. III, the bending rigidity and spontaneous curvature are estimated from the axial force measurement of cylindrical membranes and are also compared with the previous theoretical predictions. The reduction in the edge tension is discussed for both ideal chains and excluded-volume chains in sec IV. In sec V, we present our investigation on how polymer anchoring modifies membrane phase separation. Finally, a summary and discussion are provided in sec VI.
2 Model and method
In this study, we employ a coarse-grained meshless membrane model43 with anchored linear polymer chains. One membrane particle possesses only translational degrees of freedom. The membrane particles form a quasi-two-dimensional (2D) membrane according to a curvature potential based on the moving least-squares (MLS) method.43 Polymer particles are linked by a harmonic potential, and freely move as a self-avoiding chain with a soft-core repulsion. One end of each polymer chain is anchored on a single membrane particle with a harmonic potential and a soft-core repulsion.44 First, we simulate a single-phase membrane, where all membrane particles including polymer-anchored particles are the same type (A) of membrane particles. Then, we investigate membrane phase separation, where a membrane consists of two types (A and B) of membrane particles. The polymers are anchored to the type A particles.We consider a single- or multi-component membrane composed of Nmb membrane particles. Among them, Nchain membrane particles are anchored by polymer chains. Each polymer chain consists of Np polymer beads with an anchored membrane particle. The membrane and polymer particles interact with each other via a potential
| | | Utot = Urep + Umb + Up + UAB, | (1) |
where
Urep is an excluded-volume potential,
Umb is a membrane potential,
Up is a polymer potential, and
UAB is a repulsive potential between different species of membrane particles.
All particles have a soft-core excluded-volume potential with a diameter of σ.
| |  | (2) |
in which
kBT is the thermal energy and
rij is the distance between membrane (or polymer) particles
i and
j. The diameter
σ is used as the length unit,
B = 0.126, and
fcut (
s) is a
C∞ cutoff function
| |  | (3) |
with
n = 12,
A = 1 and
scut = 1.2.
For excluded-volume polymer chains, all pairs of particles including pairs of polymer beads have the repulsive interaction given in eqn (2). In contrast, for ideal polymer chains, polymer beads have the excluded-volume interactions only with membrane particles to prevent polymer beads from passing through the membrane.
2.1 Meshless membrane model
The membrane potential Umb consists of attractive and curvature potentials,| |  | (4) |
where the summation is taken only over the membrane particles. The attractive multibody potential is employed to mimic the “hydrophobic” interaction.| | Uatt(ρi) = 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln{1 + exp[−4(ρi − ρ*)]}−C, ln{1 + exp[−4(ρi − ρ*)]}−C, | (5) |
which is a function of the local density of membrane particles  , with shalf = 1.8 and scut = shalf + 0.3, where fcut(shalf) = 0.5, which implies A = ln(2){(scut/shalf)12 − 1}. The constant C is set for Uatt(0) = 0. Here we use ρ* = 6 in order to simulate a 2D fluid membrane. For ρi ≲ ρ*, Uatt acts as a pairwise potential with
, with shalf = 1.8 and scut = shalf + 0.3, where fcut(shalf) = 0.5, which implies A = ln(2){(scut/shalf)12 − 1}. The constant C is set for Uatt(0) = 0. Here we use ρ* = 6 in order to simulate a 2D fluid membrane. For ρi ≲ ρ*, Uatt acts as a pairwise potential with  , and for ρi ≳ ρ*, this potential saturates to the constant −C.
, and for ρi ≳ ρ*, this potential saturates to the constant −C.The curvature potential is expressed by the shape parameter called “aplanarity”, which is defined by
| | 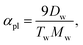 | (6) |
with the determinant
Dw =
λ1λ2λ3, the trace
Tw =
λ1 +
λ2 +
λ3, and the sum of the principal minors
Mw =
λ1λ2 +
λ2λ3 +
λ3λ1. The aplanarity
αpl scales the degree of deviation from the planar shape, and
λ1,
λ2, and
λ3 are three eigenvalues of the weighted gyration tensor
| |  | (7) |
where
α,
β, ∈{
x,
y,
z}, and the mass center of a local region of the membrane

. A truncated Gaussian function is employed to calculate the weight of the gyration tensor
| |  | (8) |
which is smoothly cut off at
rij =
rcc. Here we use the parameters
rga = 0.5
rcc and
rcc = 3
σ. The bending rigidity and the edge tension are linearly dependent on
kα and
ε, respectively, for
kα ≳ 10, so that they can be independently varied by changing
kα and
ε, respectively.
2.2 Anchored polymer chain
We consider flexible linear polymer chains anchored on the membrane. Polymer particles are connected by a harmonic spring potential,| |  | (9) |
where kbond is the spring constant for the harmonic potential and b = 1.2σ is the Kuhn length of the polymer chain. The summation is taken only between neighboring particles along polymer chains and between the end polymer particles and the anchored membrane particles (a total of Np springs in each chain).2.3 Phase separation in membranes
Two types of membrane particles, A and B, are considered in sec. 5. Numbers of these particles are NA and NB, respectively. To investigate phase separation, we apply a repulsive term UAB in eqn (1) to reduce the chemical affinity between different types of membrane particles.45 The potential UAB is a monotonic decreasing function:  with n = 1, A = 1, rcut = 2.1σ, and A1 = exp[σ/(rcut − σ)] to set UAB(σ) = 1.
with n = 1, A = 1, rcut = 2.1σ, and A1 = exp[σ/(rcut − σ)] to set UAB(σ) = 1.2.4 Simulation method
The NVT ensemble (constant number of particles N, volume V, and temperature T) is used with periodic boundary conditions in a simulation box of dimensions Lx × Ly × Lz. For planar membranes, the projected area Lx × Ly is set for the tensionless state. The dynamics of both the membrane and anchored flexible polymers are calculated by using underdamped Langevin dynamics. The motions of membrane and polymer particles are governed by| |  | (10) |
where m is the mass of a particle (membrane or polymer particle) and ζ is the friction constant. gi(t) is a Gaussian white noise, which obeys the fluctuation-dissipation theorem. We employ the time unit τ = ζσ2/kBT with m = ζτ. The Langevin equations are integrated by the leapfrog algorithm46 with a time step of Δt = 0.005τ.We use Np = 10, ε = 4, kα = 10, and kbond = 10 throughout this study. In the absence of anchored polymer chains, the tensionless membranes have a bending rigidity κ/kBT = 21 ± 0.5, the edge tension Γedσ/kBT = 4.5 and the area a0 = 1.44σ2 per membrane particle.47 For the single-phase membranes, the number of membrane particles is fixed as Nmb = 1200 and the number fraction ϕ = Nchain/Nmb of polymer-anchored membrane particles is varied. To investigate phase separation, the number of the type A membrane particles is fixed as NA = 400, and the number of the type B particles is chosen as NB = 400 and 2100 for a striped domain and a circular domain, respectively. The polymer chains are anchored to the type A particles and the polymer fraction ϕ = Nchain/NA is varied. To confirm that the membranes are in thermal equilibrium, we compare the results between two initial states, stretching or shrinking, and check that no hysteresis has occurred. We slowly stretch and shrink cylindrical or striped membranes in the axial direction with a speed less than dLz/dt = 10−6σ/τ and then equilibrate them for t/τ = 6 × 104 before the measurements. For the simulations of circular domains, the membranes were equilibrated for a duration of 6 × 104τ after step-wise changes of εAB. The error bars are calculated from six independent runs.
3 Bending rigidity and spontaneous curvature of membranes
A cylindrical membrane with polymer chains anchored outside the membrane is used to estimate the polymer-induced spontaneous curvature and bending rigidity (see Fig. 1). For a cylindrical membrane with radius R and length Lz, the Helfrich curvature elastic free energy is given by| |  | (11) |
where C1 and C2 are the principal curvatures at each position on the membrane surface, and the membrane area A = 2πRLz. The coefficients κ and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) are the bending rigidity and the saddle-splay modulus, respectively, and C0 is the spontaneous curvature. In the absence of the anchored polymers (we call it a pure membrane hereinafter), the membrane has zero spontaneous curvature, C0 = 0.
are the bending rigidity and the saddle-splay modulus, respectively, and C0 is the spontaneous curvature. In the absence of the anchored polymers (we call it a pure membrane hereinafter), the membrane has zero spontaneous curvature, C0 = 0. |
| | Fig. 1 Front and side views of a snapshot of a cylindrical membrane with anchored excluded-volume polymer chains at a polymer density ϕ = 0.167 and cylinder axial length Lz = 45.3σ. The red and green particles represent membrane and polymer particles, respectively. | |
The membrane also has an area compression energy Far(A): Far(A) = KA(A − A0)2/2A0 for A − A0 ≪ A0, where A0 is the area of the tensionless membrane. The radius R is determined by free-energy minimization ∂F/∂R|Lz = 0 for F = Fcv + Far(A). Since the curvature energy increases with increasing Lz, a contractile force,
| | 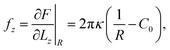 | (12) |
is generated along the cylindrical axis.
Fig. 2 shows the axial force fz calculated from the pressure tensors,
| |  | (13) |
for
α ∈ {
x,
y,
z}, where the summation is taken over all membrane and polymer particles. When the potential interaction crosses the periodic boundary, the periodic image
αi +
nLα is employed for
Pαα calculation. The force
fz increases linearly with 1/
R.
44 Thus,
C0 and
κ of the anchored membranes can be estimated from a linear fitting method to
eqn (12). For both anchored ideal chains and excluded-volume chains, the obtained values of
C0 and
κ are shown in
Fig. 3. For the pure membranes, the value of
κ is in very good agreement with those estimated from the height fluctuations of planar membranes
47 and membrane buckling.
48 The estimated value of
C0 for the pure membrane deviates slightly from the exact value, zero. This small deviation would be caused by a higher-order term of the curvature energy
49 or finite size effects as discussed in
ref. 47.
 |
| | Fig. 2 Force fz dependence on the radius R of the cylindrical membranes with anchored excluded-volume chains at ϕ = 0.083, 0.125, 0.167, and 0.250. The solid lines are obtained by linear least-squares fits. | |
 |
| | Fig. 3 Polymer density ϕ dependence of (a) the spontaneous curvature C0 and (b) bending rigidity κ of the membranes with anchored ideal chains and excluded-volume chains. The dashed lines in (a) and (b) represent the prediction of the linear theory (eqn (14) and (15)) for the ideal chains. The solid lines in (a) and (b) represent the prediction of the scaling theory (eqn (16) and (17)) in the brush region. | |
The anchored polymer generates a positive spontaneous curvature, and enhances the bending rigidity κ. Both quantities increase with increasing polymer chain density, and for the excluded-volume chains, these increases are enhanced by the repulsive interactions between the neighboring chains.
In the mushroom region, the spontaneous curvature and bending rigidity are linearly dependent on the polymer density ϕ. Analytically, the relationships20,21
| | | κΔC0 = 2aspkBTRendϕ/a0, | (14) |
are predicted, where Δ
C0 and Δ
κ are the differences of the spontaneous curvatures and bending rigidities between the polymer-decorated membrane and the pure membrane, respectively, and
Rend is the mean end-to-end distance of the polymer chain. The factor 2 in
eqn (14) appears because in our definition the spontaneous curvature is twice as large as that in the previous studies.
20–23 The coefficients are derived analytically using the Green's function
20,21 and also estimated by Monte Carlo simulations of single anchored polymer chains:
23aκ = 0.21 and 0.2 and
asp = 0.18 and 0.17 for ideal and excluded-volume chains, respectively. Our results for the ideal chains are in very good agreement with these previous predictions (compare the dashed lines and symbols in
Fig. 3). To draw the dashed line in
Fig. 3(a), the end-to-end distance is estimated from the simulation;
Rend = 4.16
σ, which is slightly larger than a free polymer chain

. Note that anchored ideal polymer chains are in the mushroom region for any density
ϕ, since the polymer chains do not directly interact with each other.
For excluded-volume chains, our results deviate from the theoretical predictions (eqn (14)) for the mushroom region at ϕ ≳ 0.1. Thus, in the high density of anchored polymer chains, the interactions between polymer chains are not negligible. We compare our results with a scaling theory based on a blob picture for the brush region in ref. 21. For a cylindrical membrane, the spontaneous curvature is derived from the free-energy minimization with respect to the radius of the cylinder,21
| |  | (16) |
where
fc(
x) = [{1 + (1 +
ν)
x/
ν}
ν/(1+ν) − 1]/
x − 1,
κ0 is the bending rigidity of the pure membrane, and the reduced spontaneous curvature
x =
h0C0/2 for the height of a brush on a flat surface
h0 =
Np![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) (1−ν)/2νb
(1−ν)/2νb. The polymer coverage on the membrane is normalized by the maximum coverage as
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif)
=
Γ/
Γmax =
b2ϕ/
a0, and the exponent
ν = 0.6 is used for excluded-volume chains. The bending rigidity is given by
| |  | (17) |
in the small curvature limit.
21 Our results are qualitatively in agreement with these predictions from the scaling theory (see
Fig. 3). The deviation is likely due to the polymer length (
Np = 10) in the simulation, which is too short to apply the blob picture in the scaling theory.
4 Edge line tension
4.1 Simulation results
Next, we investigate the edge line tension with various anchored polymer densities for both ideal chains and excluded-volume chains. A strip of single-phase membrane with anchored polymers is used to estimate the edge tension Γed (see Fig. 4). The edge tension Γed can be calculated by using47,50,51| |  | (18) |
since the total edge length is 2Ly. The pressure Pxx = Pzz ≈ 0 for solvent-free simulation with a negligibly low critical micelle concentration. We checked that the edge tension is independent of the edge length for pure membranes as well as for polymer-decorated membranes (see Fig. 5). |
| | Fig. 4 Top and side views of a snapshot of a membrane strip with anchored excluded-volume chains at ϕ = 0.15 and the length Ly = 57.6σ of each membrane edge. | |
 |
| | Fig. 5 Edge line tension Γed of a membrane strip with anchored excluded-volume chains estimated for different edge lengths Ly at ϕ = 0, 0.1, 0.15, 0.2, and 0.25. | |
Fig. 6 shows that the edge tension Γed decreases with increasing polymer density ϕ. The reduction for excluded-volume chains is much larger than that for ideal chains, similar to polymer effects on the bending rigidity. The polymer chains prefer staying on the edge, since there is more space to move so that they can gain entropy. Fig. 7(a) shows that the polymer density distribution ρchain is nonuniform at the distance dw from the strip's central axis. High peaks of ρchain are found close to the edges for both ideal chains and excluded-volume chains, while the density ρmb of all membrane particles has only very small peak. The relative polymer density ρchain/ρmb more rapidly increases at the edges for larger mean density ϕ [see Fig. 7(b)]. The mean polymer density ϕ1 at the edges is calculated as an average  for the right region of the peak (dmaxw) of ρmb in Fig. 7(a). The density difference from the mean value Δϕ = ϕ1 − ϕ increases with increasing ϕ as shown in Fig. 8. The excluded volume chains induce higher polymer concentration at the edges than the ideal chains.
for the right region of the peak (dmaxw) of ρmb in Fig. 7(a). The density difference from the mean value Δϕ = ϕ1 − ϕ increases with increasing ϕ as shown in Fig. 8. The excluded volume chains induce higher polymer concentration at the edges than the ideal chains.
 |
| | Fig. 6 Polymer density dependence ϕ of the edge line tension for ideal and excluded-volume chains. The dashed line represents our theoretical prediction by eqn (23). | |
 |
| | Fig. 7 Density distribution in the membrane strip. (a) Density of polymer-anchored membrane particles ρchain, and the total density ρmb at ϕ = 0.25. The solid lines with symbols and dashed lines represent the data for the excluded-volume chains and ideal chains, respectively. (b) Density ratio ρchain/ρmb for the excluded-volume chains. The distance dw from the center of the strip is taken in the direction perpendicular to the edge. The membrane lengths are Lst = 60σ perpendicular to the edge and Ly = 28.8σ along the edge. | |
 |
| | Fig. 8 Excess polymer density Δϕ ≡ ϕ1 − ϕ at the membrane edge as a function of the mean polymer density ϕ. The solid lines with circles and squares represent our simulation results for the ideal chains and excluded volume chains, respectively. The dashed line represents our theoretical prediction for the ideal chains by eqn (21). | |
4.2 Theoretical analysis
Here we propose a mean field theory for the edge line tension induced by the anchored polymers in the mushroom region. According to the nonuniform polymer distribution on the membrane strip, we divide the membrane into two regions, an edge (region 1) and middle region (region 2). The polymer density is assumed to be uniform in each region. The area fractions of the two regions are n1 and n2 with n1 + n2 = 1, and the polymer densities are ϕ1 and ϕ2 with ϕ = n1ϕ1 + n2ϕ2. The width of region 1 is considered as the radius of gyration of polymer Rg, so that the area fraction is given by| |  | (19) |
The free energy of the membrane strip is written as
| |  | (20) |
where
f0 is the free energy contribution of the membrane without polymer anchoring. The first four terms are the mixing entropy for regions 1 and 2. When a polymer chain moves from the middle region to the open edges, it gains the conformational entropy Δ
S.
The partition function of a single anchored polymer chain is expressed as Zp = qNpW, where q is the number of the nearest neighbors in the lattice model (q = 6 in a cubic lattice). The restricted weight of a polymer anchored on the flat membrane is  , where erf(x) is the error function and lan is the anchor length.20,21 On the other hand, the free end of a polymer anchored on the edge can also move in the other half space, and has a larger value of weight Wed. We numerically counted the weights Wed and Whs in a cubic lattice. The ratio Wed/Whs increases with increasing Np, and Wed/Whs ≃ 2 for Np = 10. Thus, the excess entropy is estimated as ΔS = ln(Wed/Whs) ≃ ln
, where erf(x) is the error function and lan is the anchor length.20,21 On the other hand, the free end of a polymer anchored on the edge can also move in the other half space, and has a larger value of weight Wed. We numerically counted the weights Wed and Whs in a cubic lattice. The ratio Wed/Whs increases with increasing Np, and Wed/Whs ≃ 2 for Np = 10. Thus, the excess entropy is estimated as ΔS = ln(Wed/Whs) ≃ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 under our simulation condition.
2 under our simulation condition.
Using minimization of Fed, the polymer density ϕ1 in the edge region is analytically derived as
| |  | (21) |
where
Q = exp(Δ
S) and
s = 1 + (
Q − 1) (
ϕ +
n1). At
Q = 2 and
n1 ≪ 1, the density difference is simply Δ
ϕ ≡
ϕ1 −
ϕ =
ϕ (1 −
ϕ)/(1 +
ϕ), which is in good agreement with the simulation results (see
Fig. 8).
The edge tension is derived as Γed = ∂Fed/∂Led, where Led is the total edge length Led = 2Ly. Thus, the polymer-induced edge tension ΔΓed is given by
| |  | (22) |
At Q = 2, the Taylor expansion gives
| |  | (23) |
Thus, the edge tension Γed decreases with increasing ϕ and is independent of the edge length Ly for n1 ≪ 1. Fig. 6 shows the comparison of edge tensions between our simulation and the theoretical results for ideal chains; the agreement is excellent. As the membrane strip becomes narrower (n1 increases), the polymer effect on the edge tension Γed is reduced by the loss of mixing entropy in region 2, and Γed increases with increasing edge length Ly.
For the excluded-volume polymer chains, the membrane cannot be simply divided into two regions because of the repulsive interaction between polymer chains. The effects of the membrane edges may be considered as an increase in the average volume for each chain. For a flat membrane without edges, the volume per chain is given by Vpf = 2RendLxLy/Nchain. The membrane strip has an additional space πRend2Ly around the edges so that the polymer volume becomes Vpe = Vpf + πRend2Ly/Nchain. Thus, the polymer chains gain additional conformational entropy not only at the edges but in the middle of the strip.
5 Membrane domains with anchored polymers
In this section, we focus on the effects of anchored polymers on membrane phase separation. First, in sec. 5.1 we estimate the line tension of polymer-anchored membrane domains, and then in sec. 5.2 we investigate the polymer effects on domain separation and domain shape transformation. Here, we investigate only the membranes with excluded-volume chains, since the effects of the ideal chains are considered to be very small. As described in sec. 3, polymers can induce an effective spontaneous curvature in the membrane. In order to diminish the influence of the induced spontaneous curvature, we symmetrically anchor polymer chains on both sides of the membrane as shown in Fig. 9. Half of the chains (Nchain/2) are anchored on the upper (lower) side of the membrane, and each chain is anchored on one membrane particle. Then, the net curvature effects induced on both sides of the membrane cancel each other out. |
| | Fig. 9 Snapshots of (a) striped and (b) circular domains with anchored excluded-volume chains in planar membranes at NA = 400 and ϕ = 0.3. Type A and B membrane particles are displayed in red and blue, respectively. | |
5.1 Interfacial line tension between two membrane domains
The line tension ΓAB between the type A and B domains is estimated by two methods using a striped domain and a circular domain. For the striped domain shown in Fig. 9(a), the line tension is calculated by using| | | ΓAB = 〈Pxx − Pyy〉LxLz/2. | (24) |
The obtained line tension for tensionless membranes is shown by solid lines in Fig. 10. We ensured that ΓAB is independent of the boundary length Ly for 24 < Ly/σ < 48 (data not shown). The line tension ΓAB decreases with increasing ϕ, while ΓAB increases with increasing εAB. Thus, the same value of ΓAB can be obtained for different polymer densities ϕ by adjusting εAB.
 |
| | Fig. 10 Interfacial line tension ΓAB between membrane domains as a function of (a) ϕ and (b) εAB. The solid and dashed lines represent ΓAB estimated from the striped domain and the circular domain, respectively. | |
Before investigating polymer effects on the domain shape in the next subsection, we also estimate ΓAB from the circular domain shown in Fig. 9(b). The line tension ΓAB is calculated from the 2D Laplace pressure,45,50
| | ΓAB = ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) Δγ, Δγ, | (25) |
where
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif)
is the average radius of the domain, and Δ
γ is the difference of surface tension between the type A and B domains: Δ
γ =
γin −
γout, where
γin is the surface tension of the inner (type A) domain and
γout is that of the outer (type B) domain. Both of them can be estimated from the pressure tensors of the local regions
| | | γα = 〈Pαzz − (Pαxx + Pαyy)/2〉Lz, | (26) |
where
α represents “in” or “out”;
Pαxx,
Pαyy, and
Pαzz are the diagonal components of the pressure tensors calculated in the local membrane regions. The outer surface tension
γout can also be calculated from the pressure tensors for the whole area.
To estimate γin and γout, we extract the inner and outer regions as follows. First, domains of type A particles are calculated. The particles are considered to belong to the same cluster (domain) when their distance is less than rcut = 2.1σ. Then the radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) of the largest domain is calculated. Type A particles contacting type B particles (closer than rcut) are considered domain boundary particles. The number of boundary particles is Nbd. In the largest domain, the distance of the domain particles from the center rG of the domain is averaged by RA = (1/Nbd)Σ|r − rG|. For the mean radius of the domain boundary, the half boundary width
of the largest domain is calculated. Type A particles contacting type B particles (closer than rcut) are considered domain boundary particles. The number of boundary particles is Nbd. In the largest domain, the distance of the domain particles from the center rG of the domain is averaged by RA = (1/Nbd)Σ|r − rG|. For the mean radius of the domain boundary, the half boundary width  is added so that
is added so that ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) = RA + 0.6σ. Then, the maximum fluctuation amplitude ΔR around
= RA + 0.6σ. Then, the maximum fluctuation amplitude ΔR around ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is calculated. The surface tension γin is estimated within the area inside the circular region with radius
is calculated. The surface tension γin is estimated within the area inside the circular region with radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) − ΔR − 0.5σ, while γout is estimated within the area outside the circular region with radius
− ΔR − 0.5σ, while γout is estimated within the area outside the circular region with radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) + ΔR + 0.5σ. Note that a few type B particles can enter the type A domain at small ΓABσ/kBT ∼ 1 so the type A particles neighboring these isolated particles are not taken into account for estimation of
+ ΔR + 0.5σ. Note that a few type B particles can enter the type A domain at small ΓABσ/kBT ∼ 1 so the type A particles neighboring these isolated particles are not taken into account for estimation of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and ΔR.
and ΔR.
The line tension estimated from the 2D Laplace pressure is shown by dashed lines in Fig. 10. For the pure membrane, the obtained values are in very good agreement with those from the membrane strip. However, they are slightly larger for the polymer-anchored membranes. This deviation is likely caused by the relative larger boundary region of the circular domain than the striped domain. It is a similar dependence obtained for the membrane edges (see eqn (23)).
The phase behavior of the pure membranes (εAB = 0) belongs to the universality class of the 2D Ising model.52 For the polymer-anchored membranes, however, the line tension dependence of the boundary curvature is not explained by the universality class. Thus, the polymer effects cannot be treated as an effective potential between neighboring membrane particles.
5.2 Domain separation and microdomain formation
To clarify the anchored polymer effects, we compare the shape changes of the type A membrane domains with increasing ϕ and with decreasing εAB. In both cases, the interfacial line tension ΓAB decreases and the low line tension leads to the breakup of domains. However, the resultant states are quite different as shown in Fig. 11. As the repulsive interaction between the type A and B particles is reduced with decreasing εAB, the obtained phase behavior is similar to that of typical binary fluids. At ΓABσ ≃ kBT (εAB = 2), the domain boundary undergoes large fluctuation and a few (type A or B) particles leave their domain to dissolve in the other domain. As εAB decreases further, the domain breaks up into small domains, and finally the two types of particles are completely mixed. |
| | Fig. 11 Sequential snapshots of domain separations as (left from (a) to (d)) εAB decreases at ϕ = 0 or (right from (a) to (g)) as the polymer density ϕ increases at εAB = 4. Red and blue particles represent the A and B type membrane particles, respectively. To show microdomain separation and shape transformation clearly, polymer particles are not displayed. | |
On the other hand, the anchored polymers induce formation of small stable domains (called microdomains) instead of a mixing state, although it can reduce the line tension to ΓABσ ≲ kBT (see Fig. 11(g)). At ϕ ≤ 0.45, the type A domain remains as one domain but exhibits an elongated shape at ϕ = 0.45. At ϕ ≥ 0.5, it starts separating into microdomains. Note that the membrane is considered in a mixed state even at ϕ = 0.45, if ΓAB for the straight boundary is extrapolated (see Fig. 10). In contrast to the reduction in εAB, the boundary of the elongated domain is rather smooth (compare snapshots in Fig. 11(c) and (f)). We confirmed that these small domains are also formed from random distribution of initial states. Thus, it is a thermodynamically stable state.
Let us discuss the effects of the polymer anchoring on the domain formation. First, we remind that the polymer beads have only repulsive interactions with the other beads and membrane particles except for the membrane-anchored head particles. The polymer effects seem suppressed for shorter lengths than the polymer size ∼Rend = 4σ. A smaller boundary undulation than the polymer size does not yield additional space for the polymer brush. A similar suppression in the short length scale was reported on the bending rigidity induced by the polymer anchoring.24 When the domain size is comparable to the polymer length, most of the particles already stay at the domain boundary, so that an additional increase in the boundary length likely yields much less gain in the average volume per polymer and the polymer conformational entropy. As explained in sec. 5.1, the line tension of the circular domain is larger than the straight boundary. For the smaller domains, this difference would be enhanced, although the domains are too small for direct estimation of ΓAB by Laplace's law.
To investigate the changes of domains in greater detail, we calculate the mean cluster size ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm and a reduced excess domain length ΔLbd. The cluster size
dm and a reduced excess domain length ΔLbd. The cluster size ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm is defined as
dm is defined as
| |  | (27) |
where
ni is the number of clusters with size
ic. The reduced excess domain length for the mother (largest) domains Δ
Lbd is defined as
| |  | (28) |
where
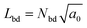
is the boundary length of the mother domains and
Adm =
NAa0 is the domain area. The length
Lbd is normalized by the length of a circular domain

so that Δ
Lbd = 0 for the circular domain.
Fig. 12 shows the development of ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm and ΔLbd. In the εAB reduction, the transition to the mixing state occurs sharply between εAB = 1.5 and 1. However, for polymer anchoring, a gradual decrease in
dm and ΔLbd. In the εAB reduction, the transition to the mixing state occurs sharply between εAB = 1.5 and 1. However, for polymer anchoring, a gradual decrease in ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm represents the formation of microdomains (see Fig. 12(c)). Around the transition points, ΔLbd is increased less by polymer anchoring than by lowering εAB, while both domains are similarly elongated (see Fig. 11). This difference is caused by the weaker undulation of polymer-decorated domain boundaries.
dm represents the formation of microdomains (see Fig. 12(c)). Around the transition points, ΔLbd is increased less by polymer anchoring than by lowering εAB, while both domains are similarly elongated (see Fig. 11). This difference is caused by the weaker undulation of polymer-decorated domain boundaries.
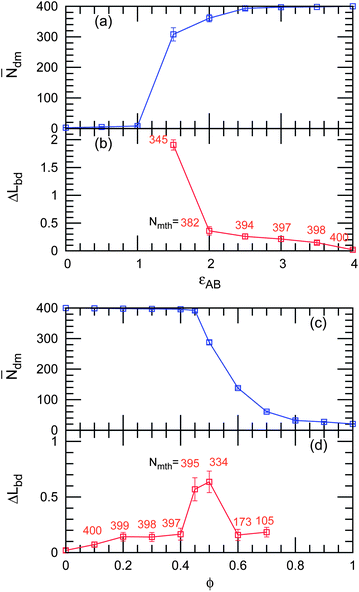 |
| | Fig. 12 Domain shape changes and domain separation as (a,b) εAB decreases at ϕ = 0 and (c and d) ϕ increases at εAB = 4. (a and c) The average cluster size ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm of the mother (largest) domains and (b and d) the reduced excess domain length ΔLbd of the mother domains. The mean number Nmth of the membrane particles in the mother domains at each stage is shown in light red color. dm of the mother (largest) domains and (b and d) the reduced excess domain length ΔLbd of the mother domains. The mean number Nmth of the membrane particles in the mother domains at each stage is shown in light red color. | |
We calculated the fraction of polymer chain anchors on the mother domain ϕmth after the microdomain separation (see Fig. 13). Interestingly, it is lower than the initial density ϕ. Thus, detached small domains have higher polymer densities than their mother domain. This is caused thermodynamically by the entropy gain of polymers anchored on small domains and also kinetically by a higher density at the domain boundary.
 |
| | Fig. 13 Mean polymer density ϕ dependence of the number fraction ϕmth of polymer chain anchors on the mother (largest) domain. | |
6 Summary and discussion
We have systematically studied the entropic effects of anchored polymers on various types of mechanical and interfacial properties of biomembranes using particle-based membrane simulations. First, we reconfirm the previous theoretical predictions for the spontaneous curvature and bending rigidity by simulating cylindrical membranes. They increase with the anchored polymer density ϕ linearly in the mushroom region, but they sharply increase in the brush region.Second, we investigated the polymer anchoring effects on the edge line tension for ideal and excluded-volume chains. It is revealed that polymer anchoring significantly reduces the edge tension. For ideal polymer chains, it is also investigated by a mean field theory. It is clarified that the entropy gain of polymer conformation at the membrane edge reduces the edge tension. Experimentally, it is known that polymer anchoring induces the formation of large vesicles39 and spherical or discoidal micelles.41 Since the ratio between the edge tension and the bending rigidity determines the vesicle radius Rves formed by the membrane disks as Rves ∼ (2κ + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) )/Γed, the reduction in the edge tension increases the vesicle radius. Our results are consistent with these experimental observations.
)/Γed, the reduction in the edge tension increases the vesicle radius. Our results are consistent with these experimental observations.
Finally, we investigated the polymer anchoring effects on phase separation in membranes for excluded-volume chains. The line tension of the domain boundary is reduced by anchoring polymers. It is found that densely anchored polymers can stabilize microdomains, whereas large domains are unstable. Although we did not investigate polymer length dependence here, it is expected that the domain size can be controlled by the polymer length. In living cells, lipid rafts contain a large amount of glycosphingolipids.4–6 Our simulation results suggest that the entropic effects of glycosphingolipids may play a significant role in stabilizing microdomains ≲100 nm. At a moderate polymer density, elongated shapes of membrane domains are obtained. In lipid membranes with PEG-conjugated cholesterol, the domain shapes depend on the anchored polymer density ϕPEG; at a high ϕPEG, small domains are scattered, while at a slightly lower ϕPEG, small elongated domains are connected with each other to form a network.19 The elongated domains in our simulations may form a network, if much larger domains are simulated. A further study is needed to clarify the polymer-anchoring effects on large-scale domain patterns.
Our present study highlights entropic effects of anchored polymers on the microdomain formation via the reduction in domain boundary tension on quasi-2D biomembranes. It is well known that high line tension can induce budding of membranes.8,9,52 Nonzero spontaneous curvature induced by proteins and anchored polymers can lead to various liposome shapes, such as tube formation and pearling.53–58 Shape transformation of vesicles induced by polymer-decorated domains is an interesting topic for further studies.
Acknowledgements
We would like to thank G. Gompper, P. A. Pincus, T. Auth, T. Taniguchi, V. N. Manoharan, and S. Komura for informative discussions. This study is partially supported by KAKENHI (25400425) from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan. HW is supported by a MEXT scholarship.References
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CAS.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569–572 CrossRef CAS PubMed.
- E. Ikonen, Curr. Opin. Cell Biol., 2001, 13, 470–477 CrossRef CAS PubMed.
- G. Vereb, J. Szöllősi, J. Matko, P. Nagy, T. Farkas, L. Vigh, L. Matyus, T. A. Waldmann and S. Damjanovich, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8053–8058 CrossRef CAS PubMed.
- Z. Korade and A. K. Kenworthy, Neuropharmacology, 2008, 55, 1265–1273 CrossRef CAS PubMed.
- L. J. Pike, J. Lipid Res., 2009, 50, S323–S328 CrossRef PubMed.
- A. R. Honerkamp-Smith, S. L. Veatch and S. L. Keller, Biochim. Biophys. Acta, 2009, 1788, 53–63 CrossRef CAS PubMed.
- R. Lipowsky and R. Dimova, J. Phys.: Condens. Matter, 2003, 15, S31–S45 CrossRef CAS.
- L. Bagatolli and P. B. S. Kumar, Soft Matter, 2009, 5, 3234–3248 RSC.
- S. L. Veatch and S. L. Keller, Phys. Rev. Lett., 2002, 89, 268101 CrossRef PubMed.
- T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821–824 CrossRef CAS PubMed.
- A. T. Hammond, F. A. Heberle, T. Baumgart, D. Holowka, B. Baird and G. W. Feigenson, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6320–6325 CrossRef CAS PubMed.
- P. I. Kuzmin, S. A. Akimov, Y. A. Chizmadzhev, J. Zimmerberg and F. S. Cohen, Biophys. J., 2005, 88, 1120–1133 CrossRef CAS PubMed.
- M. Yanagisawa, M. Imai and T. Taniguchi, Phys. Rev. Lett., 2008, 100, 148102 CrossRef PubMed.
- G. G. Putzel and M. Schick, Biophys. J., 2009, 96, 4935–4940 CrossRef CAS PubMed.
- H. M. McConnell and V. T. Moy, J. Phys. Chem., 1988, 92, 4520–4525 CrossRef CAS.
- H. Wu and Z. C. Tu, J. Chem. Phys., 2009, 130, 045103 CrossRef PubMed.
- M. Iwamoto, F. Liu and Z.-c. Ou-Yang, EPL, 2010, 91, 16004 CrossRef.
- M. Yanagisawa, N. Shimokawa, M. Ichikawa and K. Yoshikawa, Soft Matter, 2012, 8, 488–495 RSC.
- R. Lipowsky, Europhys. Lett., 1995, 30, 197–202 CrossRef CAS.
- C. Hiergeist and R. Lipowsky, J. Phys. II, 1996, 6, 1465–1481 CrossRef CAS.
- M. Breidenich, P. R. Netz and R. Lipowsky, Europhys. Lett., 2000, 49, 431–437 CrossRef CAS.
- T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051801 CrossRef PubMed.
- T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031904 CrossRef PubMed.
- M. Werner and J.-U. Sommer, Eur. Phys. J. E, 2010, 31, 383–392 CrossRef CAS.
- D. Marsh, R. Bartucci and L. Sportelli, Biochim. Biophys. Acta, 2003, 1615, 33–59 CrossRef CAS.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1997, 79, 2379–2382 CrossRef CAS.
- D. D. Lasic, Angew. Chem., Int. Ed. Engl., 1994, 33, 1685–1698 CrossRef.
- A. S. Hoffman, J. Controlled Release, 2008, 132, 153–163 CrossRef CAS PubMed.
- W. Helfrich, Phys. Lett. A, 1974, 50, 115–116 CrossRef.
- P. Fromherz, Chem. Phys. Lett., 1983, 94, 259–266 CrossRef CAS.
- E. W. Kaler, A. K. Murthy, B. E. Rodriguez and J. A. N. Zasadzinski, Science, 1989, 245, 1371–1374 CAS.
- T. M. Weiss, T. Narayanan, C. Wolf, M. Gradzielski, P. Panine, S. Finet and W. I. Helsby, Phys. Rev. Lett., 2005, 94, 038303 CrossRef CAS PubMed.
- J. Leng, S. U. Egelhaaf and M. E. Cates, Europhys. Lett., 2002, 59, 311–317 CrossRef CAS.
- D. Madenci, A. Salonen, P. Schurtenberger, J. S. Pedersen and S. U. Egelhaaf, Phys. Chem. Chem. Phys., 2011, 13, 3171–3178 RSC.
- K. Bryskhe, S. Bulut and U. Olsson, J. Phys. Chem. B, 2005, 109, 9265–9274 CrossRef CAS PubMed.
- H. Noguchi and G. Gompper, J. Chem. Phys., 2006, 125, 164908 CrossRef PubMed.
- H. Noguchi, J. Chem. Phys., 2013, 138, 024907 CrossRef PubMed.
- K. Bressel, M. Muthig, S. Prevost, J. Gummel, T. Narayanan and M. Gradzielski, ACS Nano, 2012, 6, 5858–5865 CrossRef CAS PubMed.
- A. Schalchli-Plaszczynski and L. Auvray, Eur. Phys. J. E, 2002, 7, 339–344 CAS.
- M. Johnsson and K. Edwards, Biophys. J., 2003, 85, 3839–3847 CrossRef CAS PubMed.
- H. Noguchi, J. Phys. Soc. Jpn., 2009, 78, 041007 CrossRef.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021903 CrossRef PubMed.
- H. Wu and H. Noguchi, AIP Conf. Proc., 2013, 1518, 649–653 CrossRef CAS.
- H. Noguchi, Soft Matter, 2012, 8, 8926–8935 RSC.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987 Search PubMed.
- H. Shiba and H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031926 CrossRef PubMed.
- H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061919 CrossRef PubMed.
- V. A. Harmandaris and M. Deserno, J. Chem. Phys., 2006, 125, 204905 CrossRef PubMed.
- T. V. Tolpekina, W. K. den Otter and W. J. Briels, J. Chem. Phys., 2004, 121, 8014 CrossRef CAS PubMed.
- B. J. Reynwar and M. Deserno, Biointerphases, 2008, 3, FA117–FA124 CrossRef PubMed.
- R. Lipowsky, J. Phys. II, 1992, 2, 1825–1840 CrossRef CAS.
- R. Phillips, T. Ursell, P. Wiggins and P. Sens, Nature, 2009, 459, 379–385 CrossRef CAS PubMed.
- A. V. Shnyrova, V. A. Frolov and J. Zimmerberg, Curr. Biol., 2009, 19, R772–R780 CrossRef CAS PubMed.
- I. Tsafrir, D. Sagi, T. Arzi, M.-A. Guedeau-Boudeville, V. Frette, D. Kandel and J. Stavans, Phys. Rev. Lett., 2001, 86, 1138–1141 CrossRef CAS PubMed.
- K. Akiyoshi, A. Itaya, S. M. Nomura, N. Ono and K. Yoshikawa, FEBS Lett., 2003, 534, 33–38 CrossRef CAS PubMed.
- K. Guo, J. Wang, F. Qiu, H. Zhang and Y. Yang, Soft Matter, 2009, 5, 1646–1655 RSC.
- T. Baumgart, B. R. Capraro, C. Zhu and S. L. Das, Annu. Rev. Phys. Chem., 2011, 62, 483–507 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln{1 + exp[−4(ρi − ρ*)]}−C,
ln{1 + exp[−4(ρi − ρ*)]}−C, , with shalf = 1.8 and scut = shalf + 0.3, where fcut(shalf) = 0.5, which implies A = ln(2){(scut/shalf)12 − 1}. The constant C is set for Uatt(0) = 0. Here we use ρ* = 6 in order to simulate a 2D fluid membrane. For ρi ≲ ρ*, Uatt acts as a pairwise potential with
, with shalf = 1.8 and scut = shalf + 0.3, where fcut(shalf) = 0.5, which implies A = ln(2){(scut/shalf)12 − 1}. The constant C is set for Uatt(0) = 0. Here we use ρ* = 6 in order to simulate a 2D fluid membrane. For ρi ≲ ρ*, Uatt acts as a pairwise potential with  , and for ρi ≳ ρ*, this potential saturates to the constant −C.
, and for ρi ≳ ρ*, this potential saturates to the constant −C.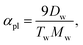

 . A truncated Gaussian function is employed to calculate the weight of the gyration tensor
. A truncated Gaussian function is employed to calculate the weight of the gyration tensor

 with n = 1, A = 1, rcut = 2.1σ, and A1 = exp[σ/(rcut − σ)] to set UAB(σ) = 1.
with n = 1, A = 1, rcut = 2.1σ, and A1 = exp[σ/(rcut − σ)] to set UAB(σ) = 1.

![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) are the bending rigidity and the saddle-splay modulus, respectively, and C0 is the spontaneous curvature. In the absence of the anchored polymers (we call it a pure membrane hereinafter), the membrane has zero spontaneous curvature, C0 = 0.
are the bending rigidity and the saddle-splay modulus, respectively, and C0 is the spontaneous curvature. In the absence of the anchored polymers (we call it a pure membrane hereinafter), the membrane has zero spontaneous curvature, C0 = 0.
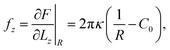



 . Note that anchored ideal polymer chains are in the mushroom region for any density ϕ, since the polymer chains do not directly interact with each other.
. Note that anchored ideal polymer chains are in the mushroom region for any density ϕ, since the polymer chains do not directly interact with each other.
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) (1−ν)/2νb. The polymer coverage on the membrane is normalized by the maximum coverage as
(1−ν)/2νb. The polymer coverage on the membrane is normalized by the maximum coverage as ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) = Γ/Γmax = b2ϕ/a0, and the exponent ν = 0.6 is used for excluded-volume chains. The bending rigidity is given by
= Γ/Γmax = b2ϕ/a0, and the exponent ν = 0.6 is used for excluded-volume chains. The bending rigidity is given by



 for the right region of the peak (dmaxw) of ρmb in Fig. 7(a). The density difference from the mean value Δϕ = ϕ1 − ϕ increases with increasing ϕ as shown in Fig. 8. The excluded volume chains induce higher polymer concentration at the edges than the ideal chains.
for the right region of the peak (dmaxw) of ρmb in Fig. 7(a). The density difference from the mean value Δϕ = ϕ1 − ϕ increases with increasing ϕ as shown in Fig. 8. The excluded volume chains induce higher polymer concentration at the edges than the ideal chains.




 , where erf(x) is the error function and lan is the anchor length.20,21 On the other hand, the free end of a polymer anchored on the edge can also move in the other half space, and has a larger value of weight Wed. We numerically counted the weights Wed and Whs in a cubic lattice. The ratio Wed/Whs increases with increasing Np, and Wed/Whs ≃ 2 for Np = 10. Thus, the excess entropy is estimated as ΔS = ln(Wed/Whs) ≃ ln
, where erf(x) is the error function and lan is the anchor length.20,21 On the other hand, the free end of a polymer anchored on the edge can also move in the other half space, and has a larger value of weight Wed. We numerically counted the weights Wed and Whs in a cubic lattice. The ratio Wed/Whs increases with increasing Np, and Wed/Whs ≃ 2 for Np = 10. Thus, the excess entropy is estimated as ΔS = ln(Wed/Whs) ≃ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 under our simulation condition.
2 under our simulation condition.




![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) Δγ,
Δγ,![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is the average radius of the domain, and Δγ is the difference of surface tension between the type A and B domains: Δγ = γin − γout, where γin is the surface tension of the inner (type A) domain and γout is that of the outer (type B) domain. Both of them can be estimated from the pressure tensors of the local regions
is the average radius of the domain, and Δγ is the difference of surface tension between the type A and B domains: Δγ = γin − γout, where γin is the surface tension of the inner (type A) domain and γout is that of the outer (type B) domain. Both of them can be estimated from the pressure tensors of the local regions![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) of the largest domain is calculated. Type A particles contacting type B particles (closer than rcut) are considered domain boundary particles. The number of boundary particles is Nbd. In the largest domain, the distance of the domain particles from the center rG of the domain is averaged by RA = (1/Nbd)Σ|r − rG|. For the mean radius of the domain boundary, the half boundary width
of the largest domain is calculated. Type A particles contacting type B particles (closer than rcut) are considered domain boundary particles. The number of boundary particles is Nbd. In the largest domain, the distance of the domain particles from the center rG of the domain is averaged by RA = (1/Nbd)Σ|r − rG|. For the mean radius of the domain boundary, the half boundary width  is added so that
is added so that ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) = RA + 0.6σ. Then, the maximum fluctuation amplitude ΔR around
= RA + 0.6σ. Then, the maximum fluctuation amplitude ΔR around ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is calculated. The surface tension γin is estimated within the area inside the circular region with radius
is calculated. The surface tension γin is estimated within the area inside the circular region with radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) − ΔR − 0.5σ, while γout is estimated within the area outside the circular region with radius
− ΔR − 0.5σ, while γout is estimated within the area outside the circular region with radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) + ΔR + 0.5σ. Note that a few type B particles can enter the type A domain at small ΓABσ/kBT ∼ 1 so the type A particles neighboring these isolated particles are not taken into account for estimation of
+ ΔR + 0.5σ. Note that a few type B particles can enter the type A domain at small ΓABσ/kBT ∼ 1 so the type A particles neighboring these isolated particles are not taken into account for estimation of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) and ΔR.
and ΔR.
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm and a reduced excess domain length ΔLbd. The cluster size
dm and a reduced excess domain length ΔLbd. The cluster size ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm is defined as
dm is defined as

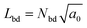 is the boundary length of the mother domains and Adm = NAa0 is the domain area. The length Lbd is normalized by the length of a circular domain
is the boundary length of the mother domains and Adm = NAa0 is the domain area. The length Lbd is normalized by the length of a circular domain  so that ΔLbd = 0 for the circular domain.
so that ΔLbd = 0 for the circular domain.![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm and ΔLbd. In the εAB reduction, the transition to the mixing state occurs sharply between εAB = 1.5 and 1. However, for polymer anchoring, a gradual decrease in
dm and ΔLbd. In the εAB reduction, the transition to the mixing state occurs sharply between εAB = 1.5 and 1. However, for polymer anchoring, a gradual decrease in ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm represents the formation of microdomains (see Fig. 12(c)). Around the transition points, ΔLbd is increased less by polymer anchoring than by lowering εAB, while both domains are similarly elongated (see Fig. 11). This difference is caused by the weaker undulation of polymer-decorated domain boundaries.
dm represents the formation of microdomains (see Fig. 12(c)). Around the transition points, ΔLbd is increased less by polymer anchoring than by lowering εAB, while both domains are similarly elongated (see Fig. 11). This difference is caused by the weaker undulation of polymer-decorated domain boundaries.
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) dm of the mother (largest) domains and (b and d) the reduced excess domain length ΔLbd of the mother domains. The mean number Nmth of the membrane particles in the mother domains at each stage is shown in light red color.
dm of the mother (largest) domains and (b and d) the reduced excess domain length ΔLbd of the mother domains. The mean number Nmth of the membrane particles in the mother domains at each stage is shown in light red color.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) )/Γed, the reduction in the edge tension increases the vesicle radius. Our results are consistent with these experimental observations.
)/Γed, the reduction in the edge tension increases the vesicle radius. Our results are consistent with these experimental observations.